Behavioral Relevance of the Dynamics of the Functional Brain Connectome

Abstract

While many previous studies assumed the functional connectivity (FC) between brain regions to be stationary, recent studies have demonstrated that FC dynamically varies across time. However, two challenges have limited the interpretability of dynamic FC information. First, a principled framework for selecting the temporal extent of the window used to examine the dynamics is lacking and this has resulted in ad-hoc selections of window lengths and subsequent divergent results. Second, it is unclear whether there is any behavioral relevance to the dynamics of the functional connectome in addition to that obtained from conventional static FC (SFC). In this work, we address these challenges by first proposing a principled framework for selecting the extent of the temporal windows in a dynamic and data-driven fashion based on statistical tests of the stationarity of time series. Further, we propose a method involving three levels of clustering—across space, time, and subjects—which allow for group-level inferences of the dynamics. Next, using a large resting-state functional magnetic resonance imaging and behavioral dataset from the Human Connectome Project, we demonstrate that metrics derived from dynamic FC can explain more than twice the variance in 75 behaviors across different domains (alertness, cognition, emotion, and personality traits) as compared with SFC in healthy individuals. Further, we found that individuals with brain networks exhibiting greater dynamics performed more favorably in behavioral tasks. This indicates that the ease with which brain regions engage or disengage may provide potential biomarkers for disorders involving altered neural circuitry.

Introduction

With the advent of functional magnetic resonance imaging (fMRI), different methods for characterizing brain connectivity and functional integration have received a lot of attention (Friston, 1994). Functional connectivity (FC) measures the instantaneous (zero-lag) temporal correlation of mainly resting-state fMRI signals obtained from different brain regions. One of the imports of investigating brain connectivity lies in its diagnostic implications as well as its link to human behavior. Previous works have shown that FCs between brain regions are more informative in predicting behavior than activity of functional regions in isolation (Cole et al., 2012). Further, aberrant behaviors in subjects with mental disorders have been linked to alterations in FC of specific brain networks (Filippi et al., 2012). Notably, recent works have linked both inter-individual and intra-individual variability in FC to corresponding variability in behavior (Thompson et al., 2013). However, previous studies mainly investigated FC by obtaining one connectivity value for the entire duration of the experiment based on the assumption that connectivity did not change significantly over time (Greicius et al., 2007; van de Ven et al., 2004). Given that the brain is a dynamic and adaptive system whose state is likely to change over time, the stationarity assumption has been relaxed by some recent works that explored the dynamics of FC in time and frequency domains (Britz et al., 2010; Chang and Glover, 2010; Chang et al., 2011, 2013; Chapuis et al., 2013; Deshpande et al., 2006; Handwerker et al., 2012; Hutchison et al., 2013; Keilholz et al., 2013; Leonardi et al., 2013; Majeed et al., 2011; Sakoğlu et al., 2010; Sato et al., 2006; Tagliazucchi et al., 2012). But unlike static FC (SFC), the behavioral relevance of the dynamic variations in FC is yet to be established, although preliminary reports support this notion (Madhyastha et al., 2014). Here we surmise that greater temporal variability of FC increases the adaptability and efficiency of brain networks, leading to better behavioral performance. Accordingly, we hypothesize that dynamics of the whole-brain resting-state functional connectome will predict human behavior in various domains, such as alertness, cognition, emotion, and personality traits, better than conventional SFC measures. To test this hypothesis, we correlated dynamic and static FC-based metrics with behavioral data.

In this article, we address the following outstanding issues related to evaluation of dynamic FC in order to test the aforementioned hypothesis: (1) the choice of the length of the sliding window within which connectivity is evaluated, (2) characterization of dynamic changes in both nodal and connectivity configurations using first-level adaptive clustering, (3) definition of metrics that capture the dynamics described previously, (4) investigation of dynamic connectivity patterns that are consistent across time and across subjects using second and third levels of clustering, respectively, and (5) strategies for performing the aforementioned analyses at a whole-brain level. In the later paragraphs, we briefly elaborate on the just-mentioned themes.

To capture dynamics of FC, previous studies used sliding windows of fixed length (Handwerker et al., 2012; Leonardi et al., 2013). However, it cannot be assumed that nonstationary dynamics imply fixed stationary windows. Cribben et al. (2012) employed dynamic connectivity regression to detect temporal change points in FC, which essentially allows window lengths to vary with time. However, their method makes a restrictive assumption that, within each partition/window, the connectivity configuration is the same across subjects. Though such an assumption may be valid for task-based studies where all subjects are forced to perform a given task in the window under consideration, it is not applicable in resting state wherein different subjects may be engaged in different mental processes within a given window. To address this issue, we propose an approach capable of capturing FC temporal variations by employing dynamic windows of changing length such that time series across the entire brain are statistically guaranteed to be stationary within a given window. The feasibility of this approach is demonstrated using simulations followed by application to human resting-state fMRI data from the Human Connectome Project (HCP) (Q3 release, 40 subjects; http://humanconnectome.org).

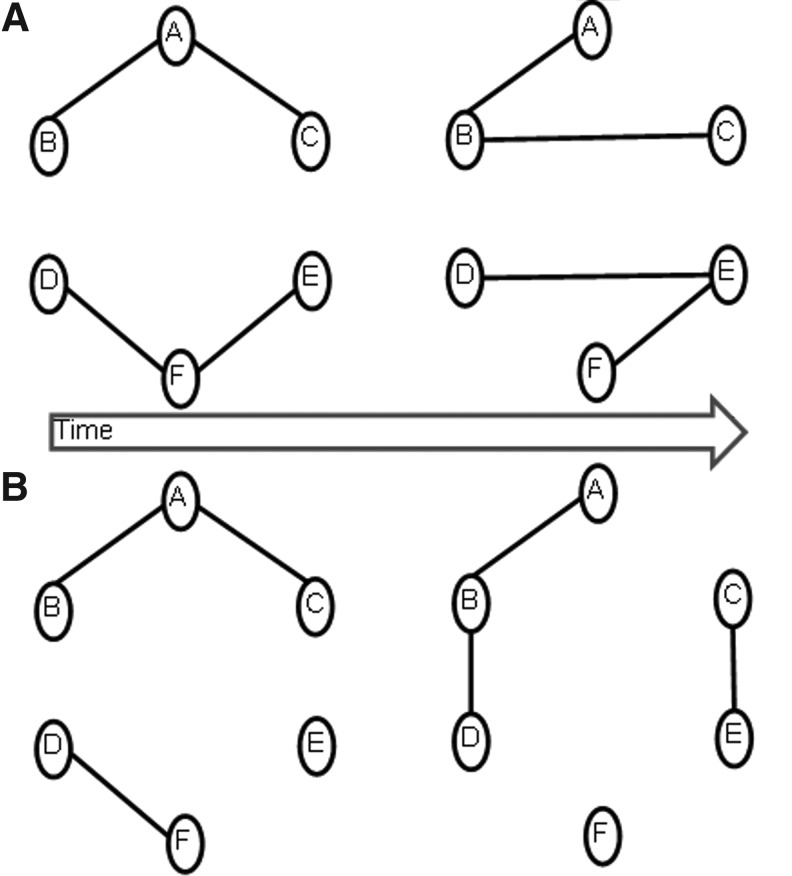
Once dynamics of FC have been obtained between multiple brain regions, ad-hoc approaches have been used to characterize and represent the information obtained. Since the amount of information obtained from the assessment of dynamic FC can be quite large, it has been often difficult to interpret the underlying neuroscientific meaning (Chang and Glover, 2010). Some previous studies showed snapshots of FC at various points during the experiment by using different window lengths (Handwerker et al., 2012; Lee et al., 2013) or template pattern matching (Majeed et al., 2011). Even though such approaches are good exploratory techniques, the results and interpretation from them can become subjective, depending on the window length and frames chosen. One principled approach adopted by some recent reports is to find connectivity configurations that are quasi-stable for a certain period of time (Li et al., 2014). This follows from similar quasi-stable scalp voltage configurations, called microstates, obtained from agglomerative clustering of electroencephalographic (EEG) data (Britz et al., 2010; Musso et al., 2010). Such approaches assume that a single functional configuration exists across the whole brain at any given time instant. Additionally, they also assume that the dynamics of connectivity are essentially due to the brain changing from one across-the-brain connectivity configuration to another. These assumptions to some extent lose generality. For example, the nodal configuration of each of the two networks shown in Figure 1A does not change over time (having the same nodes), but the connections between network nodes change with time. Though previous studies have attempted to capture this type of dynamics, the example showed in Figure 1B, wherein both connections between nodes and the nodal configuration of the networks themselves change with time (having different nodes at different time instants), represents a more general scenario of FC dynamic changes. To capture the latter type of dynamics, we propose an approach based on adaptive evolutionary clustering (AEC) (Xu et al., 2014) for finding brain network FC configurations at each time instant. Based on this first-level clustering, metrics were defined for objectively characterizing the dynamic changes in FC configurations. Using a regression model, we investigated whether those metrics capturing FC dynamics can predict behavior better than conventional SFC. Further, first-level dynamic connectivity patterns that occurred consistently across time and subjects were identified using second- and third-level clustering, respectively.

FIG. 1.

Schematic of two types of temporally dynamic network configurations. (A) The first type illustrating a dynamic network configuration wherein all nodes are part of the same network, only the connections between them change with time. (B) The second type illustrating a dynamic network configuration wherein both connections between nodes and the networks themselves are changing with time.

Materials and Methods

Data acquisition and preprocessing

The resting-state fMRI (rfMRI) session1 minimally preprocessed data from HCP were used in this work. This dataset included 40 unrelated subjects (age range=22–35 years, 21 women), each having two runs. During the scan, subjects were instructed to lie at rest with eyes open and fixated on bright cross-hair on a dark background. For each subject, oblique axial acquisitions alternated between phase encoding in a right-to-left direction in one run and phase encoding in a left-to-right direction in the other run. rfMRI raw images were collected with a multiplexed gradient echo planar imaging sequence and the following parameters: 1200 volumes, field of view (FOV)=208×180 mm²; flip angle (FA)=52°; TR (repetition time)/TE (echo time)=720 msec/33.1 msec, in-plane matrix: 104×90; 72 slices per volume with slice thickness=2 mm; multiband factor=8; and echo spacing=0.58 msec. The acquired data were minimally preprocessed involving removal of spatial distortions, motion correction, normalization to Montreal Neurological Institute (MNI) space, reduction of bias field, and masking out of regions outside the brain. For more details about data acquisition and “minimal” preprocessing of the data, please see HCP Q3 release reference manual (http://humanconnectome.org/documentation/Q3/Q3_Release_Reference_Manual.pdf).

We performed additional preprocessing using Data Processing Assistant for Resting-State fMRI software (DPARSF) (Chao-Gan and Yu-Feng, 2010), including mean and linear trend removal for each voxel time series, temporal filtering with passing band: 0.01–0.1 Hz, and regressing out the white matter and cerebrospinal fluid (CSF) signals. Subsequently, the 190-region version of the CC200 brain atlas (Craddock et al., 2012), which contains a parcellation of all gray matter voxels in the brain to 190 homogeneous functional regions based on spectral clustering, was employed for Region of Interest (ROI) definition (for anatomical labels corresponding to the 190 regions, please see Supplementary Table S1; Supplementary Data are available online at www.liebertpub.com/brain). We extracted the mean time series from all 190 regions for subsequent use.

Behavioral and individual difference measures

Apart from rfMRI data, we also used HCP's behavioral data from the same subjects to investigate the relevance of the dynamics of FC to human behavior as compared with conventional SFC. The HCP collected behavioral measures developed for the NIH Toolbox Assessment of Neurological and Behavioral function (www.nihtoolbox.org) and several additional measures to assess domains not covered by the NIH Toolbox. The behavioral measures were categorized into several domains and the domains that were employed in this work were alertness, cognition, personality, and emotion. We did not incorporate categories of motor and sensory functions into our analysis since they were relatively less relevant to resting-state data. Supplementary Table S2 gives full details of individual behavioral measures.

Dynamic FC model

Pearson's correlation calculated over entire time series reflects the average or static FC (SFC) over the entire length of the experiment. For capturing the dynamic variations in FC, we used sliding-windowed Pearson's correlation along the time axis. Previous reports have used fixed window length with rectangular (Leonardi et al., 2013) or Hamming windows (Handwerker et al., 2012). But there was no evidence supporting the superiority of any given window shape over others. Therefore, we employed a rectangular window shape for simplicity. However, for fixed window length, the length adopted mattered very much and different lengths produced different smoothing effects (Chang and Glover, 2010). This is because previous studies made arbitrary choices for the length of the fixed window. On the contrary, we employed an approach wherein the stationarity of the time series under consideration dictated the length of the window. To guarantee that the time series within the length of the window were locally stationary, we employed the Dickey-Fuller test (DF test) (Said and Dickey, 1984) to determine the window length. The DF test is a hypothesis test for the existence of unit root in a given time series with zero mean. A given time series y(t) can be modeled as follows:

Where t is the time index, α is a coefficient, and ɛ(t) is the error term. A unit root is present when α=1, in which case, the mean and variance of y(t) are a function of time t, implying that y(t) is nonstationary. The DF test has a null hypothesis that a unit root exists and the time series are nonstationary. The test procedure in our work was as follows. At a given time point t₁, we chose the initial window length to be m₋ (m₋=14 TRs in this work. The deduction of this initial window length is described in the “Selection of the Range of Sliding Window Length” section in Supplementary Data), and did the DF test on time series within [t₁-m₋+1, t₁] from all 190 regions. If no unit root existed for all 190 time series, then we assumed that they were consistently stationary and used these windowed time series to calculate Pearson's correlation for time point t₁. Otherwise, the window length was increased by one time point (or one TR) such that the windowed time series started from t₁-m₋ to t₁, and then we redid the DF test. We iterated this procedure until consistent stationarity was achieved or the maximum window length was reached. The maximum window length m₊ was chosen as 140 TRs (see “Selection of the Range of Sliding Window Length” section in Supplementary Data for mathematical deduction). The sliding window was moved forward one TR each time, that is, from t₁ to t₁+1, and we repeated the just-mentioned procedure to calculate the window length. The first 140 data points of the time series were utilized for the DF test of the first sliding window. Thus, t₁ was started from the 141st time point and dynamic FC had a length of 1060 time points (1200 is the total number of time points).

It is noteworthy that using the aforementioned procedure, the entire length of the time series was partitioned into variable length segments wherein all 190 regions covering the entire brain had stationary temporal activity. Statistically, this does not guarantee that the covariance between these regions will also be stationary within the given segment. However, it is physiologically unlikely that when the activity in the entire brain exhibits stationarity, interactions between them will be nonstationary. Future studies must design experiments to test the validity of this assumption.

Clustering

First-level clustering

The input to the first-level clustering algorithm was a distance matrix constructed from the dynamic FC matrix. We assumed that higher the absolute value of FC, the closer the two regions are in feature space. Note that we did not differentiate between “correlated” and “anticorrelated” interregional relationships in this work. It is noteworthy that lack of positive zero-lag correlation between regions does not imply that they are disconnected as they may have other types of associations (Deshpande et al., 2011). Therefore, it is reasonable to assume that the absolute value of the correlation coefficient is a measure of association between ROI time series. We do plan to add an additional layer of complexity in future work by distinguishing “correlated” and “anticorrelated” interregional relationships.

We cannot directly use interregional FC as the “distance measure” for the following reasons. First, the closer the two regions in feature space, the smaller their distance should be, but their connectivity's absolute value should be bigger. This implies that a monotonically decreasing transformation is required to convert FC to a distance measure. Second, distances should be nonnegative, with the value being zero if and only if the distance is between one region and to itself. But the FCs have negative values and the FC from one region to itself is one. To meet these requirements, we used a distance measure D, defined by D=1 − |P|, where Pearson's correlation P ranges between −1 and 1. This transform is monotonically decreasing, the result is nonnegative, and the distance from one region to itself is zero. Other requirements of distance measures, including reciprocity (the distance from one region to another should be same as the other way around) and triangular inequality, are also met by D.

After the distance matrix D was obtained for each time instant, it was fed to the AEC algorithm (Xu et al., 2014). This algorithm was used for determining the regions that cluster together, based on the distances between them obtained from Pearson's correlation at each time point, such that the smoothness of the transition of the whole-brain clustering of FC patterns from one time point to the next is controlled by a forgetting factor. The weighting of previous clustering configurations on the current time instant was calculated through a forgetting factor determined by Bayesian information criterion (Roebroeck et al., 2005). The hierarchical model (Joe and Ward, 1963) was chosen as the clustering method.

The choice of the number of clusters in any clustering algorithm can be based on mathematical criteria, such as the silhouette index (Rousseeuw, 1987), or based on heuristics and prior information regarding the underlying variables. Heuristics and prior information can guide us for selecting the range of the number of clusters within which the silhouette index is calculated. Specifically with respect to the number of FC networks in the brain, many previous works used methods, such as fuzzy clustering (Lee et al., 2012); independent component analysis (ICA)–based methods, especially probabilistic ICA (PICA) (De Luca et al., 2006) and tensor PICA (Damoiseaux et al., 2006); graph-theory-based network analysis (Moussa et al., 2012); and fully exploratory network ICA (FENICA) (Kalcher et al., 2012; Schöpf et al., 2010; Wang et al., 2012), to find the number of consistent resting-state networks (RSNs). The current understanding of human RSNs comprises a set of 10 confirmed networks that are specialized in functionality: visual network, working memory network, executive network, dorsal attention network (DAN), ventral attention network, auditory network, sensorimotor network, basal ganglia network, language network, as well as the well-known default mode network (DMN). Further, the RSNs are hierarchically organized (Kalcher et al., 2012; Lee et al., 2012). This implies that when the number of networks or clusters increases, some networks will split into subnetworks, usually into left and right lateral parts or peripheral and foveal parts, rather than reshape into a new network that seemingly has no relation with the previous ones. Previous studies have demonstrated that if the number of networks is two, then the brain can be functionally divided into task-positive and task-negative networks (Lee et al., 2012). However, if the number of clusters/networks increases to a number between 5 and 10, then aforementioned 10 networks emerge gradually one by one (Damoiseaux et al., 2006; Lee et al., 2012). Specifically, Damoiseaux et al. (2006) used tensor PICA in which a three-dimensional tensor represented spatial, temporal, and subject-specific loadings to find group representatives of these 10 networks. Further, Kalcher et al. (2012) investigated the effect of the length of the time series (or scan time) on the number of networks based on which 10 seems to be appropriate choice for the scan times used in this work. Given these factors, we specified 2 to 20 as the search range for number of clusters during first-level clustering so that the number of clusters (for each time point) returned by the silhouette index is physiologically meaningful.

Second-level clustering

We investigated which of the first-level clustering (spatial) configurations consistently occurred over time using second-level clustering. Thus, second-level clustering was a clustering of the first-level results over time. Unlike first-level clustering that was dynamic in nature (i.e., clustering configurations at each time instant impacted those at later time instants), second-level clustering was static in nature. Hierarchical approach to clustering was employed and the number of clusters was determined by silhouette index (with a search range between 2 and 20). The search range was determined according to the current understanding of the number of quasi-stable FC configurations that recur over time during the course of an experiment. The number of temporal FC patterns found by previous works is normally <20. For example, Li et al. (2014) found 16 reproducible temporal FC patterns across healthy people via effective dictionary learning and sparse coding algorithms. Zhang et al. (2014) found 12 representative functional states using a dynamic Bayesian variable partition model. Besides, the number of temporally quasi-stable patterns of EEG topography, called microstates, found by previous studies is also generally <20. Britz et al. (2010) found the optimal number to be 4; Musso et al. (2010) found 10 recurrent microstates. Thus, we used the search range to be 2–20 to accommodate all possibilities.

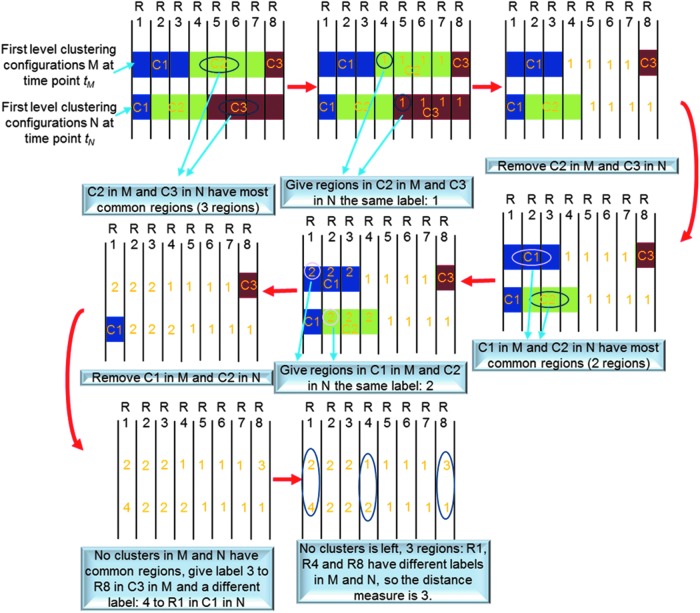
The distance measure between two first-level clustering configurations was calculated using a procedure illustrated in Figure 2. Suppose at time point t_m, the first-level clustering result was called M and, at a different time point t_n, the first-level clustering result was called N. M has 10 clusters represented by m_i, where 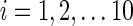, and N has 10 clusters represented by n_j, where 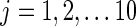. First, we compared the number of common regions (common members) between each possible pair m_i, n_j, and then among them we selected the pair m_i*, n_j* that had the maximal number of common regions, and we assigned the same label to all regions in m_i* and all regions in n_j*. Then, we removed this pair and found the next pair that had the maximal number of common regions in remaining possible pairs, and assigned regions belonging to this pair the same label (this label was different from previous labels.). Then, we removed this pair and this procedure continued. If the maximal number of common regions became zero for remaining possible pairs, then we assigned all regions in all remaining clusters in M a label different from all previous labels, and all regions in all remaining clusters in N a different label (also different from all previous labels). Consequently, no pairs were left in M and N and all regions were labeled in both M and N. Finally, the distance measure was devised to be the number of regions having different labels in M and N. It is evident that this distance measure meets requirements of reciprocity, nonnegativeness, triangular inequality, and self-distance being zero.

FIG. 2.

A schematic illustrating the calculation of distance measure in second-level clustering. The schematic starts with any two first-level clustering configurations at different time points as shown on the upper left corner. Red arrows indicate the direction of the procedure (R1,…, R8 denote region #1 to region #8, and C1, C2, and C3 denote cluster #1, cluster #2, and cluster #3).

Each second-level cluster had a number of clusters with first-level configurations as its members. For each second-level cluster, we calculated the mean matrix from first-level distance matrices D_i of all its members, wherein i indexes all members in the given second-level cluster. The member whose distance matrix was closest to 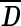in the Euclidean sense was chosen to represent the centroid of the second-level cluster. The Euclidean distance E between 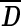and D_i was calculated using Equation 2.

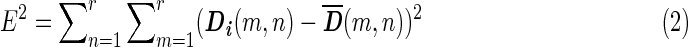Where r represents the number of columns (or rows), which is equal to the number of regions, in the corresponding matrix.

Third-level clustering

Second-level brain network patterns that occurred consistently across runs/subjects were identified using a third-level clustering across all runs/subjects. Dominating second-level centroids were predicated based on the histogram of second-level clusters' occurrence times obtained from all runs/subjects (Supplementary Fig. S1). It is evident that the majority of second-level clusters had occurrence times <100 TRs. Therefore, second-level clusters with occurrence times >100 TRs were considered to be dominating, which were then input to third-level clustering. Transient second-level patterns with occurrence times <100 TRs were inconsistent and hence were not input to third-level clustering since the objective of performing third-level clustering was to find dominant and consistent second-level patterns across subjects/runs.

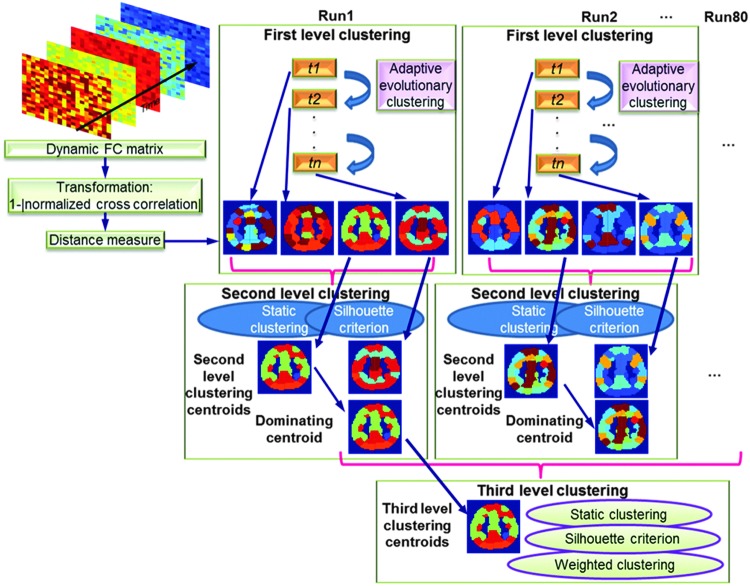
To calculate the distance measure between dominating second-level centroids, the strategy adopted in second-level clustering is not feasible since each centroid had a weight, that is, the occurrence times of the second-level cluster it represented. Therefore, we performed weighted clustering. For any dominating second-level centroid i, we had its FC distance matrix D_i. We picked out all the lower (or upper) triangular elements of D_i and vectorized them to represent their corresponding points in feature space. The diagonal elements were not considered. Then, weighted K-means algorithm was employed to cluster these points in feature space. The number of clusters was determined by silhouette criterion and each cluster's centroid was calculated by weighted mean. Similar to the second-level clustering, the member whose distance matrix was nearest to the theoretical centroid was selected as the third-level centroid. The procedure for all three levels of clustering is schematically illustrated in Figure 3.

FIG. 3.

Schematic of the procedure for all three levels of clustering. The top left part illustrates the transformation of dynamic FC to a distance measure; top right part is the first-level clustering. Second- and third-level clustering is illustrated below that. Since each of the 40 subjects had 2 runs, we had a total of 80 runs. FC, functional connectivity.

Simulations

To validate our proposed method for dynamic FC calculation and clustering, simulations were performed on artificial data. We simulated time series from 12 regions, each with 1000 time points, using a multivariate vector autoregressive model (MVAR) given as follows:

Where V(t) denotes the matrix of signals from 12 regions, A_i is the regression coefficient matrix, and ɛ represents noise vector with covariance matrix C, which has autocorrelation coefficients normalized to 1. To test time-varying FC, three scenarios were used.

• (i) A_is were all zero matrices (thus, time-lagged connectivity was excluded, and there was no need to specify p), C was constant over time, and time series of 12 regions were divided into four clusters, each having three members connected to each other (regions 1, 2, and 3 were in one cluster; regions 4, 5, and 6 were in one cluster;…; regions 10, 11, and 12 were in one cluster). In this case, C was a blocked symmetric positive definite matrix with 3×3 blocks on the diagonal.

• (ii) Same as first scenario except that every nonzero element in C was slowly varying over time in a sinusoidal manner with period equal to 200π and randomized phases. The belongingness of each region was not changed compared with scenario (i).

• (iii) Same as first scenario except after every 200 time points, C was circularly shifted by one column and one row such that the membership of each time series changed with respect to its cluster.

Note that the lower and upper limits of sliding window length for DF test were set to 10 and 100 time points as derived in the “Selection of the Range of Sliding Window Length” section in Supplementary Data. Moreover, the windowed Pearson's correlation calculated was the “valid” section of it, that is, only those parts that were calculated without the zero-padded edges. The sliding window moved forward one time point each time, and the [1, 100] section of simulated time series was preserved for DF test of the first sliding window. Thus, the resultant time series of dynamic FC had 900 time points, corresponding to [100, 1000] section of simulated MVAR time series. Aforementioned rule was applied to HCP fMRI data analysis also. It is noteworthy that the objective of our simulation was to demonstrate the ability of the proposed method for tracking connectivity dynamics and hence we generated synthetic data using a simple MVAR model. While many previous studies have used more realistic generative dynamic causal modeling-based synthetic fMRI data (Friston et al., 2003), the physiological basis of time-varying FC is yet unclear (Keilholz, 2014). When more clarity is available on this aspect, more realistic simulations may be performed in future studies.

Characterization of dynamic and static FCs and their behavioral relevance from experimental data

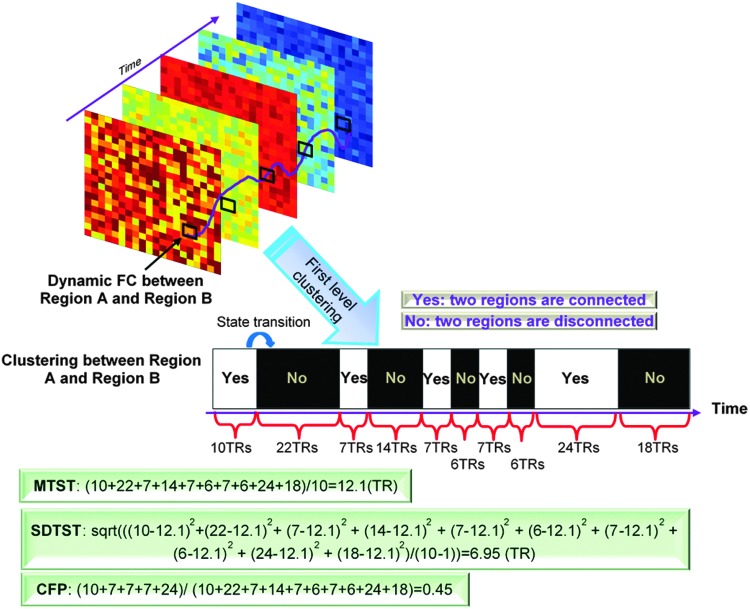
We defined three metrics to characterize dynamic FC based on the first-level clustering result. The first is the mean time that two regions are in connected (or disconnected) state before transitioning into a disconnected (or connected) state, called mean time before state transition (MTST). The second is standard deviation of the time before state transition (SDTST). The third is called clustering frequency percentage (CFP), which measures the percentage of total time that two regions are clustered relative to total scanning time. In addition, the conventional SFC was adopted as the fourth metric.

We used these metrics to find their relevance to behavior measures. An illustrative example demonstrating state transitions and the procedure to calculate these metrics are shown in Figure 4. The behavioral scores from a variety of behavioral tests were input into a general linear model (GLM) as the dependent variables with dynamic and static FC metrics as explanatory variables as given below:

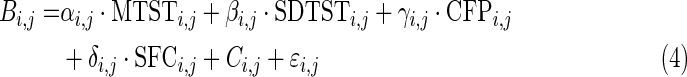FIG. 4.

An illustrative example of the calculation of three metrics: MTST, SDTST, and CFP. The first-level clustering result leads to a series of state transitions for every pair of regions between clustered and unclustered states. Specifically, two regions either belong to the same cluster (connected, clustered state) or different clusters (disconnected, unclustered state), and switch between these two states, as reflected in the black-and-white bar with “Yes” and “No” indicating whether they are clustered or not. Then, the three metrics MTST, SDTST, and CFP are calculated as in corresponding boxes. Note the fourth metric SFC that is widely known and thus not illustrated here. CFP, clustering frequency percentage; MTST, mean time before state transition; SDTST, standard deviation of the time before state transition; SFC, static FC; TR, repetition time.

Where i indexes different behavioral tests, j indexes the FCs between different pairs of regions, B_i,j is a vector of behavioral scores for all subjects, and MTST_i,j, SDTST_i,j, CFP_i,j, and SFC_i,j are vectors of corresponding metrics for all subjects. α_i,j, β_i,j, γ_i,j, and δ_i,j are their coefficients, respectively; C_i,j is a constant term; and ɛ_i,j is a residual. It should be noted that we had the four metrics from 80 runs (2 runs for each of the 40 subjects), but behavioral scores only from 40 subjects. So each subject's behavioral score was used twice in the GLM corresponding to its two runs. The coefficients from this GLM were estimated using a standard least squares procedure and were tested for statistical significance using a z-test. A Bonferroni corrected p-value threshold of p=0.05/(75×N), where 75 is the number of behaviors and N is the number of paired connections, was used in this test. Then, the variance explained in this GLM by each metric was calculated. For example, 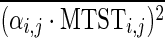is the variance explained by MTST. The overline denotes mean operation over all is and js. And 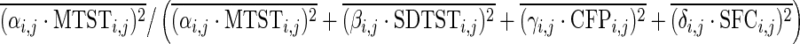represents the relative percentage of variance explained by MTST.

Results

Simulation results

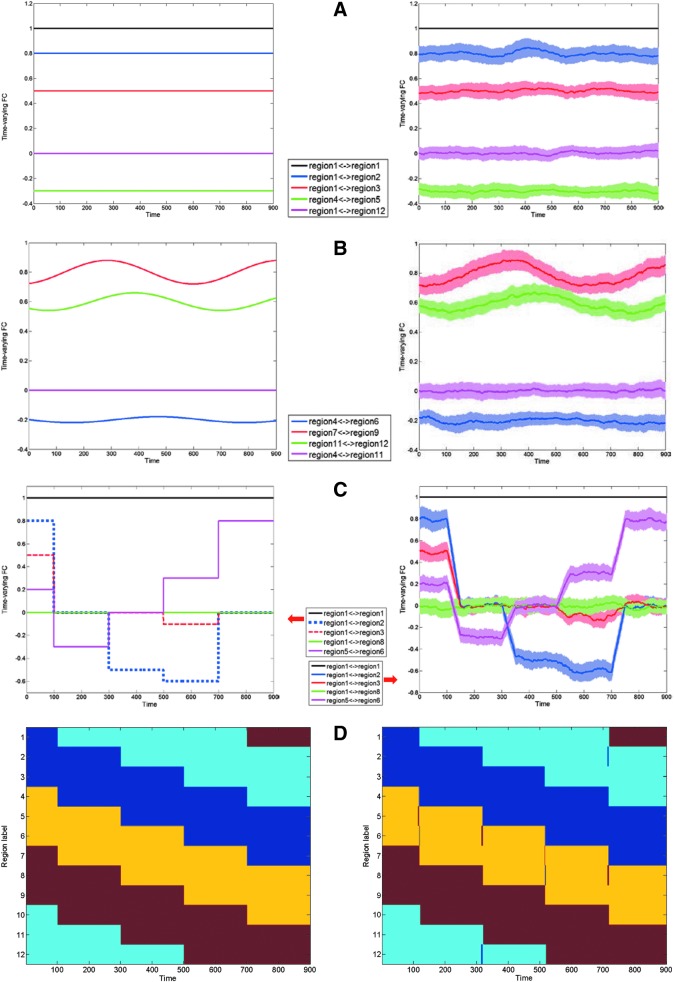
Simulations described before were conducted 100 times for each scenario and the corresponding results are shown in Figure 5. The mean and standard deviation (over all 100 iterations) of the resulting time-varying FC time series from several representative regions are illustrated. Figure 5A corresponds to scenario (i) specifically showing the connections from region 1. The estimated time-varying FCs approach the ground truth very well and the autocorrelation is constantly one. Figure 5B and C shows the results corresponding to scenarios (ii) and (iii) wherein the estimated time-varying FCs track the ground truth sufficiently well, and the regions belonging to different clusters (regions 4 and 11 in Fig. 5B and regions 1 and 8 in Fig. 5C) have nearly zero correlation, indicating no false positives. In particular, when the simulated cluster belongingness changes in Figure 5C, the estimated time-varying FCs respond to it swiftly and converge quickly. Figure 5D demonstrates one representative realization of AEC algorithm over time (first-level clustering) for simulated time-varying FCs of scenario (iii). After every 200 time points, the cluster belongingness (and hence the nodal configuration for the networks) was circularly shifted once. For example, from time points 1 to 200, regions 1, 2, and 3 were clustered together; region 4, 5, and 6 were clustered together; and so on. Then from time points 201 to 400, regions 2, 3, and 4 belonged to the same network; regions 5, 6, and 7 belonged to the same network;…; regions 11, 12, and 1 belonged to the same network. This switching pattern is tracked correctly, with only short transitional time. Note that since the time-varying FC time series correspond to [100, 1000] section of MVAR time series, the cluster belongingness switches occur at time points 100, 300, 500, and 700.

FIG. 5.

Simulation results for time-varying FC and first-level clustering. The simulated MVAR processes consisted of 12 regional time series, each with 1000 time points. (A) Left: example showing simulated ground truth for time-varying FCs of scenario (i); right: estimated mean and standard deviation (std) of simulated time-varying FCs. Color bands span [mean − std, mean+std] with mean in the middle. (B) Left: example showing simulated ground truth for time-varying FCs of scenario (ii); right: estimated mean and standard deviation of simulated time-varying FCs. (C) Left: example showing simulated ground truth for time-varying FCs of scenario (iii); right: estimated mean and standard deviation of simulated time-varying FCs. (D) Left: ground truth clustering pattern for one representative example of simulated time-varying FCs corresponding to scenario (iii); right: corresponding estimated clustering pattern using AEC algorithm. Regions rendered with the same color are connected to each other and hence belong to the same cluster. AEC, adaptive evolutionary clustering; MVAR, multivariate vector autoregressive model.

Characterization and quantification of dynamic and static FCs using HCP data

First-level clustering

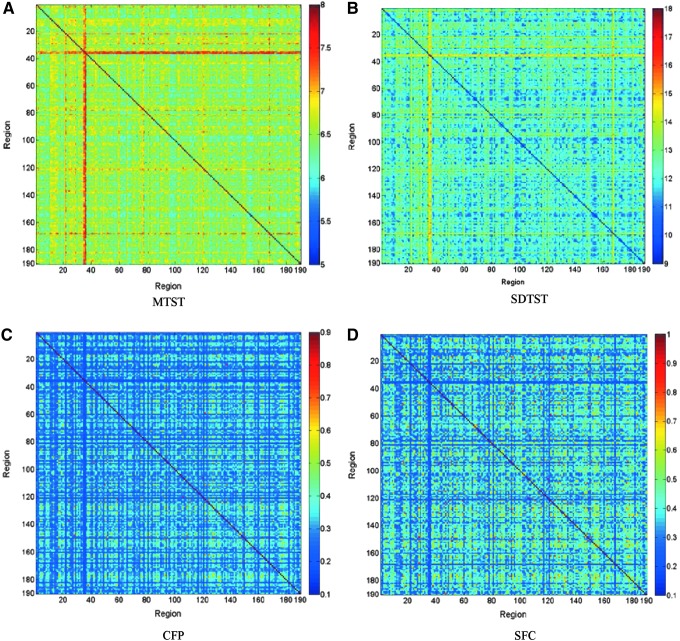
Figure 6 shows interregional MTST, SDTST, CFP, and SFC matrices averaged over all runs and subjects. Generally, a higher value of MTST indicates lesser dynamic variations of FC between regions. We can observe that several regions have much less dynamics of FC in relation to other regions, such as regions 35 and 36 and region 168, corresponding to brainstem and right rectus gyrus (for corresponding AAL anatomical area of each region, please see Supplementary Table S1). In theory, a high value of MTST could be obtained regardless of whether a pair of regions spend most of their time with strong correlation or weak correlation. However, from Figure 6, we can observe that connections having higher MTSTs generally have lower CFPs and SFCs. This negative correlation between MTST and CFP/SFC indicates that, in the context of the human brain, higher MTST implies that the corresponding regions spend most of their time having weak correlation. Accordingly, regions, such as brainstem and rectal gyrus, with high MTSTs are connected with other regions for a very short period of time.

FIG. 6.

Interregional MTST, SDTST, CFP, and SFC matrices averaged over all runs. Numbers along horizontal and vertical axes are region labels. For the automatic anatomical labeling (AAL) nomenclature corresponding to these numeric labels, please see Supplementary Table S1. (A) MTST, (B) SDTST, (C) CFP, and (D) SFC (Note: for each matrix, diagonal elements represent the dynamic or static FC metric between a given region and itself. Therefore, the colors of diagonal elements have no meaning and not comparable to off-diagonal elements).

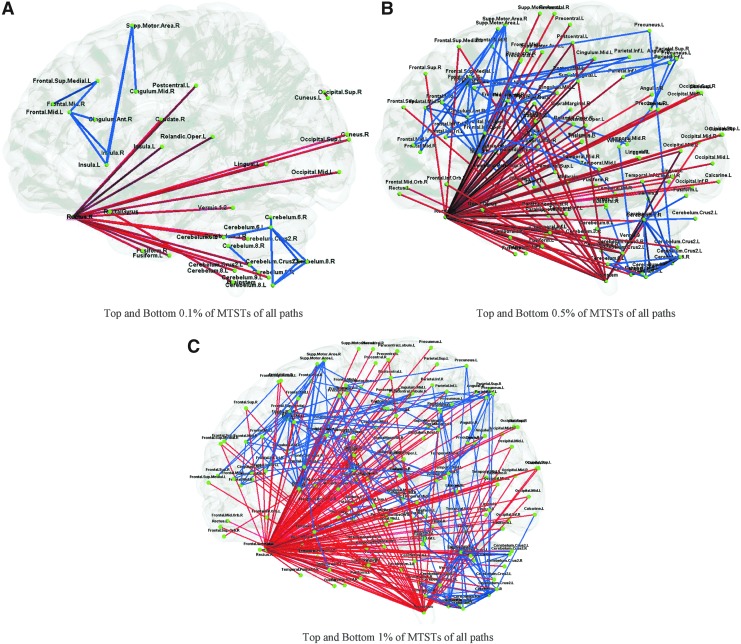
Figure 7 shows the paths (connections between regions) with MTSTs within the top and bottom 0.1%, 0.5%, and 1% of MTSTs of all paths. The MTSTs here are averaged over all runs and subjects. Figure 7A is intended to improve visualization such that paths with most significance could be emphasized. These results reinforce the point we made about large MTSTs for the rectal gyrus and brainstem that they were seldom clustered (at the first level) with other regions for most of the time, implying that they had very weak dynamic FCs with other regions. The blue paths with low MTSTs represent connections with highly dynamic FC. One network involving the mid-frontal cortex, anterior and mid cingulate, insula, and supplemental motor area as well as another intra-cerebellar network stand out in Figure 7A. These two networks were connected to each other by multiple intermediary nodes in the temporal and parietal cortices at a lower threshold (Fig. 7C).

FIG. 7.

Paths with top and bottom 0.1% MTSTs in (A), top and bottom 0.5% MTSTs in (B), and top and bottom 1% MTSTs in (C). The red paths represent interregional MTSTs whose values are among the top 0.1% of all MTSTs in (A), top 0.5% of all MTSTs in (B), and top 1% of all MTSTs in (C), and blue paths represent interregional MTSTs whose values are among the bottom 0.1% of all MTSTs in (A), bottom 0.5% of all MTSTs in (B), and bottom 1% of all MTSTs in (C). The MTSTs mentioned here have been averaged over all runs and subjects. If the threshold is set beyond 1%, the number of paths is too big such that it prevents any meaningful visualization.

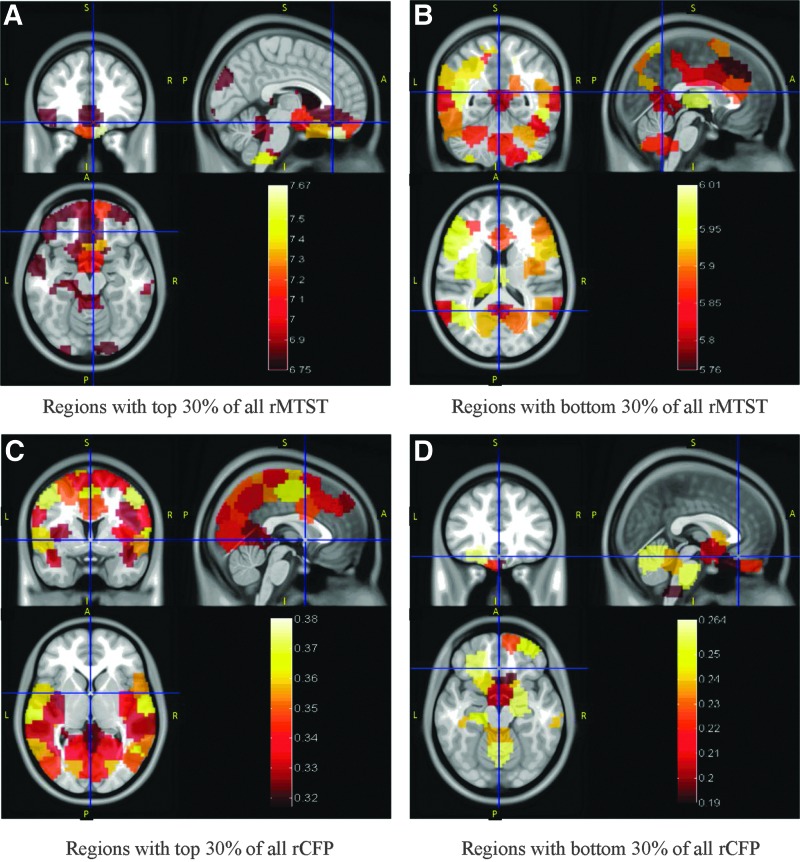
We defined a metric, regional MTST (rMTST), by finding the mean MTST of all paths associated with a given region. Brain regions with rMTST in the top 30% and bottom 30% are shown in Figure 8A and B, respectively. Similarly, regional CFP (rCFP) was defined as the mean CFP of all paths associated with a given region and regions with rCFP in the top 30% and bottom 30% are shown in Figure 8C and D, respectively. At this proportion of 30%, known RSNs are revealed. For comparison, Supplementary Figure S2 shows regions with top and bottom 20% rMTST and rCFP. Compared with Figure 8, there are fewer regions highlighted and some important RSNs are even missing in Supplementary Figure S2, such as the visual network in Figure 8A, and so are some important regions, such as posterior cingulate cortex (PCC), in Figure 8C. This implies that Supplementary Figure S2 is not as informative as Figure 8. Therefore, we only elaborate on Figure 8 here. It can be seen from Figure 8 that the brainstem and rectus have highest rMTST and lowest rCFP, which is in agreement with the results presented earlier, that is, low dynamics and unconnected to other regions for a major portion of the experiment. Also, DMN, DAN, and fronto-parietal control network (FPCN) (Vincent et al., 2008) have low rMTST, indicating high dynamics of FC. Especially DMN has the lowest rMTST, that is, highest dynamics of FC. Most occipital, temporal, superior frontal, and parietal areas have high CFP, indicating that they generally have strong FC to other regions for most of the time.

FIG. 8.

Regions with top and bottom 30% rMTST and rCFP. Regions with top 30% of all rMTST are shown in (A) and with bottom 30% of all rMTST are shown in (B). Corresponding maps for top and bottom 30% rCFP are shown in (C) and (D), respectively. Hot colormap is used to represent the numeric value of corresponding metric for each region shown (A, anterior; P, posterior; S, superior; I, inferior; L, left; R, right). rCFP, regional CFP; rMTST, regional MTST.

Third-level clustering

Supplementary Figure S3 shows the eight centroids obtained from third-level clustering, which represent whole-brain FC patterns appearing consistently across space, time, and subjects. In this figure, brain regions with the same color are functionally connected to each other. A statistical summary of third-level clusters is listed in Table 1, including number of members (dominating second-level centroids), and the sum of occurrence times of members in TRs. Together, these two metrics determine the relative dominance of each third-level cluster. We obtained 8 third-level clusters according to the silhouette criterion (Boyett-Anderson et al., 2003). It is clear that clusters #1, #2, #6, and #7 are more dominant than others, and cluster #8 is the least dominant. Note that the numbers assigned to clusters are incidental and carry no particular meaning. Also, the cluster centroids in Figure S3 are in the same order as in Table 1. The DMN can be observed in the centroids of clusters #3, #4, #6, and #8. These four clusters accounted for ∼32% of the total occurrence times of dominating second-level clusters (OTDSLCs). Also, the regions of the DMN were connected to regions outside the DMN in addition to being connected to each other in clusters #2, #5, and #7. Taken together, this implies that the regions of the DMN were connected to each other and appeared as part of the same cluster for ∼78% of OTDSLCs. The visual network, comprising of primary and secondary visual cortices, appeared in centroids #1, #3, #4, #5, and #6, with #6 having only occipital area, #3 having occipital-parietal-frontal interaction (merged with DAN), and others having frontal-occipital interaction. They accounted for 57% of OTDSLCs. The language network appeared in centroid #6 and clustered with cerebellar regions. This network accounted for 15% of OTDSLCs. The sensorimotor network appeared in centroid #1 and splits into bilateral parts in centroid #4, accounting for 33% of OTDSLCs. The DAN merged with the visual network in centroid #3 and appeared as an individual network in centroid #6. So, in total it accounted for 19% of OTDSLCs. The executive network can be seen only in centroid #4, which accounted for 11% of OTDSLCs. The ventral attention network appears as a clear network (dark red) only in centroid #8, which accounted for 11% of OTDSLCs. The limbic network can be seen in its entirety in centroid #1, which accounted for 22% of OTDSLCs, and split into several parts (thalamus, caudate, basal ganglia, etc.) with each part having connections with cortical regions in centroids #3, #5, and #7. Brainstem appears as an individual cluster in centroid #2. Also in centroid #2 we can observe that the ventral frontal areas shaped into individual clusters, such as rectus, indicating that they have weak FC with other areas. It should be noted that since many networks co-occur in certain centroids, percentages of the total OTDSLCs for all RSNs do not sum to 100%.

Table 1.

Statistical Summary of Third-Level Clustering

Third-level cluster	Cluster #1	Cluster #2	Cluster #3	Cluster #4	Cluster #5	Cluster #6	Cluster #7	Cluster #8	Sum
No. of cluster members	33	19	7	19	4	15	15	1	113
Sum of all members' occurrence times (TR)	13,776	14,702	2787	6838	2744	9140	11,209	813	62,009

TR, repetition time.

Behavioral relevance of dynamic and static FCs

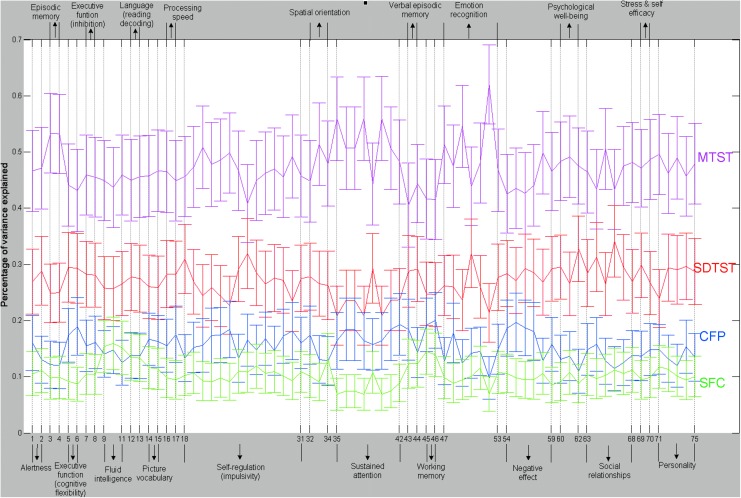
Figure 9, which presents the relative percentage of variance explained by MTST, SDTST, CFP, and SFC for 75 behavioral scores pertaining to alertness, cognition, emotion, and personality (please see Supplementary Table S2 for details of individual behavioral measures), is the most important contribution of this article. It is remarkable that the variances explained by dynamic FC metrics MTST and SDTST are clearly higher than those by CFP and SFC for every behavioral measure. MTST in particular, has much more power in explaining behavioral variability than the other three. This is significant because it implies that the dynamics of FC can be a better predictor of human behavior than conventional SFC. Visual inspection of scatter plots of behavioral data against each of the four metrics revealed that the correlations were not driven by outliers.

FIG. 9.

Percentage of variances in behavioral measures explained by dynamic and static FC metrics. Percentage of variances is shown as error bars with mean and standard deviation derived across all paths between the 190 regions. Along the horizontal axis are labels for 75 behavioral tests (please refer to Supplementary Table S2 for behavioral test details). The broad behavioral domains of groups of behavioral tests are indicated above and below the figure. Note that a value of 0.6 on the y-axis indicates that 60% of the variance in behavior is explained by the corresponding connectivity metric.

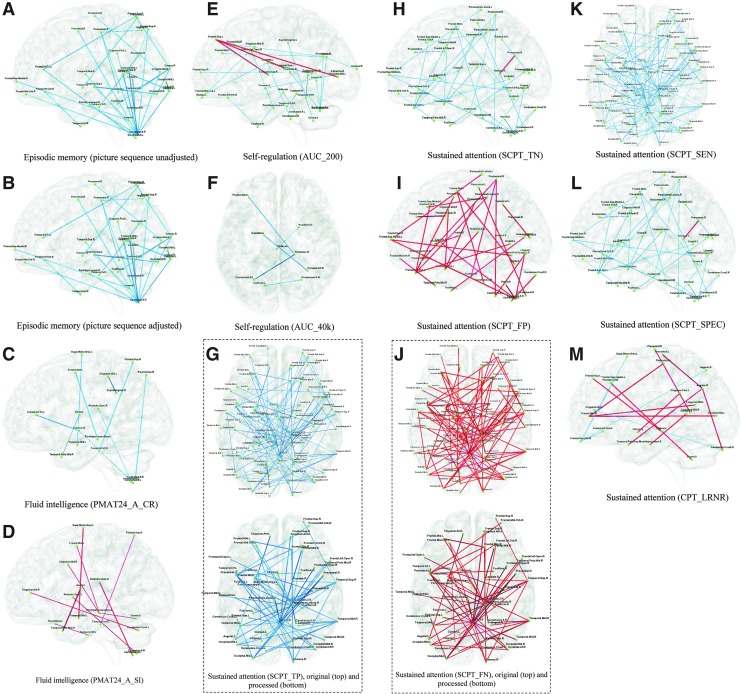
Figure 10 shows the paths whose MTSTs significantly predicted several selected behavioral measures. Note that Figure panels 10G and J both have two subfigures, one being original and the other having been further processed. Since there were a lot of paths whose MTSTs significantly correlated with true positives and false negatives of SCPT task, we obtained a distribution of the number of paths emanating from each region and found that only 10% of regions had more than four paths emanating from them. Based on this, we retained only those paths that connected at least one of the regions with a nodal degree of 5 or more to obtain the processed subfigures. In this way, we were able to identify only the prominent hubs for proper visualization. However, all of our conclusions would still be valid with the original subfigures. In Figure 10A and B, all paths are cobalt blue, implying that higher the episodic memory score, lower the MTST and greater the dynamics of FC. Many of these paths involve the cerebellum, which makes sense given previous reports of its role in episodic memory retrieval (Andreasen et al., 1999; Wiggs et al., 1999). Other important areas include frontal cortex, occipital cortex, temporal cortex, parahippocampal, precentral, and parietal areas. Previous works have shown that these areas are activated in an episodic-memory-retrieval task (Tsukiura et al., 2002; Wiggs et al., 1999). Figure 10C shows paths significantly predicting correct responses for the fluid intelligence behavioral test and Figure 10D shows paths significantly predicting skipped items (a measure of error rate) in the same test. They show that individuals with more correct responses had lower MTST and greater dynamic FC while increased error rate was predicted by lower dynamics of FC. Areas associated with this pattern include inferior and medial frontal cortices as well as the parietal cortex, which have been previously implicated in fluid intelligence (Geake and Hansen, 2005; Gray et al., 2003). Also, fluid intelligence is mediated by a composite of working memory systems and many regions involved in fluid intelligence are associated with working memory, including regions in the temporal lobe, hippocampus, and cerebellum (Prabhakaran et al., 1997), as in Figure 10C and D. Besides, pallidum in the basal ganglia has also been shown to be involved in fluid intelligence (Rhein et al., 2014). In Figure 10E and F, MTSTs of most paths are significantly negatively correlated with self-regulation. Many regions seen in these two figures, that is, prefrontal cortex, especially its ventral area (Jimura et al., 2013); lateral intraparietal cortex (Louie and Glimcher, 2010); thalamus; and caudate (Kinnison et al., 2012; Komura et al., 2001), have been previously implicated in self-regulation. Figure 10G–M belongs to the behavior test of the same category: sustained attention, also termed vigilance. It is conspicuous that Figure 10G and J is exactly the same except for the polarity (cobalt blue and red), and so is Figure 10H and I. Also, Figure 10K is the same as Figure 10G, and Figure 10L is the same as Figure 10H, except for polarity. Taken together, these imply that lower MTST and hence greater dynamics of FC are associated with better performance on SCPT. The specific paths whose MTSTs predict behavioral variability involved brain regions, such as frontal cortex, precentral cortex, insula, occipital cortex, temporal cortex, inferior parietal cortex, and cingulate gyrus, which have been previously implicated in sustained attention and vigilance (Breckel et al., 2013; Olbrich et al., 2009; Seidman et al., 1998).

FIG. 10.

Paths whose MTSTs significantly predicted variability in selected behavioral measures. The predictive ability is quantified by the regression coefficient α for each MTST in the GLM shown in Equation 4 in the main text. The coefficient α is passed through a z-test and Bonferroni corrected for multiple comparisons (corrected p<0.05). In each subfigure, cobalt blue paths have negative α values, and red paths have positive α values. The behavior tests for subfigures are as follows: (A) Episodic memory (picture sequence test, unadjusted). (B) Episodic memory (picture sequence test, adjusted). (C) Fluid intelligence (PMAT24_A_CR). (D) Fluid intelligence (PMAT24_A_SI). (E) Self-regulation (AUC_200). (F) Self-regulation (AUC_40k). (G) Sustained attention (SCPT_TP). The top one is the original figure. Since it has too many paths that hamper visualization, we show the processed figure as the bottom one with only paths that connect to nodes with five or more paths. (H) Sustained attention (SCPT_TN). (I) Sustained attention (SCPT_FP). (J) Sustained attention (SCPT_FN). The top one is the original figure. Since it has too many paths that hamper visualization, we show the processed figure as the bottom one with only paths that connect to nodes with five or more paths. (K) Sustained attention (SCPT_SEN). (L) Sustained attention (SCPT_SPEC). (M) Sustained attention (CPT_LRNR). Please refer to Supplementary Table S2 for details about specific metrics referred to for each behavior. GLM, general linear model.

It is noteworthy that even though MTST explained a higher percentage variance in behavior compared with other metrics across the whole range of tasks, different paths/networks were involved in explaining each behavior. This indicates that our findings are unlikely to be driven by correlation between behaviors themselves.

Discussion

In this work, we have proposed a framework for estimating dynamic FC between functionally homogeneous regions across the entire brain using adaptive windowing based on time series stationarity. The multidimensional FCs obtained from each subject were subjected to three levels of clustering across space, time, and subjects in order to derive metrics for capturing connectivity dynamics as well as to find brain FC network patterns that are dynamic in time, yet consistent across subjects. Both dynamic and static FC metrics were correlated with behavioral variables to find their ability to predict human behaviors.

This section is organized as follows. We first discuss the third-level clustering results that show the most consistent whole-brain connectivity patterns across time and subjects. Second, we discuss the implications of paths as well as regions that exhibit highest and lowest dynamics. Third, we discuss the behavioral relevance of the dynamics of FC and support for our central hypothesis that temporal variations in connectivity are a better predictor of human behavior than static connectivity. Fourth, we discuss methodological issues surrounding group comparisons using different window lengths and the effect of parcellation schemes on the results. Finally, we list certain limitations of the current study and future directions that may be worth pursuing.

First, among the RSNs revealed by third-level clustering results shown in Supplementary Figure S3, DMN and visual network occupy more than 50% of the total OTDSLCs, apparently higher than other RSNs. This is expected since the DMN (Greicius et al., 2003) and visual networks (Patriat et al., 2013) have been shown to be predominant and highly reproducible networks in the resting human brain by many previous reports.

Second, results shown in Figures 6–8 consistently indicate that rectal gyrus has very weak SFC and low dynamics of FC with other regions reflected as high MTST, low CFP, and low SFC. This indicates that it seldom clusters with other regions; that is, it appears as an individual cluster. The function of rectal gyrus is currently yet unclear, but anterior parts of the orbito-frontal cortex in general have been implicated in the processing of motivational information (Kringelbach and Rolls, 2004). Given that there is little motivational information to process during a resting state scan with eyes open and fixed on a target, it is understandable that there is very little static connectivity as well as its dynamics associated with this region. This region is generally known to possess susceptibility-based distortion. However, the HCP preprocessing pipeline contains many steps for removing this artifact based on field maps (Glasser et al., 2013). Therefore further studies that employ more appropriate acquisition strategies (as opposed to postprocessing employed here for artifact removal) are required to confirm the functional significance of low FC and high MTST in the rectal gyrus. The brainstem also had low FC and high MTST with other regions. The brainstem plays an important role in regulating cardiac and respiratory functions, maintaining consciousness and regulating sleep. However, resting-state FC between the brainstem and the neocortex is tightly coupled with corresponding variations in physiological fluctuations (Chang et al., 2013). Therefore, further research is required to assess the impact of the presence (and removal) of the dynamics of physiological fluctuations on corresponding dynamics of resting-state FC between the brainstem and the neocortex.

On the other hand, a network consisting of the mid-frontal cortex, anterior and mid cingulate, insula, and supplemental motor area as well as an intra-cerebellum network stand out as having highly dynamic FC (Fig. 7A). Results with a more liberal threshold of 0.5% indicate that these two networks are connected by paths converging to the parietal cortex (Fig. 7B). In other words, the fontal-parietal-cerebellar circuit displays high FC dynamics. When the threshold is further relaxed to 1% (Fig. 7C), direct fronto-cerebellar paths emerge. These regions are involved in a range of functions that are too exhaustive to be listed here. Briefly, the mid-frontal cortex is implicated in planning complicated cognitive processes (Ridderinkhof et al., 2004), while the anterior cingulate plays a role in many cognitive functions, such as initiation, motivation, and goal-directed behaviors (Devinsky et al., 1995). Insula plays a role in various functions, including perception, motor control, self-awareness, cognitive functioning, and interpersonal experience (Karnath et al., 2005). High FC dynamics associated with the insula may be supported by the virtue of the fact that it was identified as one of the hubs in the “rich-club” organization of the brain's structural connectome (van den Heuvel and Sporns, 2011). Further, the role of the insula in functional integration (Kurth et al., 2010) and dynamic switching as part of the “Salience” network (Menon and Uddin, 2010), along with the anterior cingulate cortex, may be supported by high FC dynamics of both the insula and anterior cingulate observed in this study. Stoodley and Schmahmann (2010) suggest that different regions of the cerebellum containing sensorimotor, cognitive, and limbic representations interact with the parietal cortex. Taken together, fronto-parietal, intra-cerebellar, and cortico-cerebellar networks that support a large range of brain functions appear to display highest dynamics of FC.

A closer look at regions having high dynamics of FC to all other brain regions in Figure 8B reveals that nodes of common RSNs, such as DMN, DAN, and FPCN, have similar level of dynamics. As pointed out by Vincent et al. (Vincent et al., 2008), DAN and DMN are two opposing brain networks that are implicated in attention to the external world versus internally directed mentation, respectively, and the FPCN (which includes regions implicated in cognitive control and is structurally located in between DMN and DAN regions) controls the switching between DAN and DMN. This controlling mechanism and the competing roles of DAN and DMN may underlie its high dynamics of FC. The PCC and precuneus have high dynamic FC and high CFP, probably as a result of strong FC paths with high dynamics linking it to frontal and cerebellar regions as discussed previously.

The regions of the DMN were connected to each other for a large portion of the total time as well as exhibited high connectivity dynamics with other brain regions. This finding needs to be understood in the context of resting state being defined as “Random Episodic Silent Thinking” (Andreasen et al., 1995). We believe that it is the “randomness” of resting state that is being supported by frequent state changes accompanying high connectivity dynamics. Since this state dominates during a resting-state scan, DMN regions not only display high dynamics, but are also connected to each other for a large portion of the experiment. DMN's purported role in social cognition, autobiographical memory, and mind wandering (Buckner et al., 2008) supports the aforementioned notion. For example, mind wandering, autobiographical/episodic memory, and internal mentation require processing different contexts of past, present, or future. In addition, social cognition is also characterized by “largely unconstrained decision making, including reliance on potentially multiple instances of recursive thinking” (Mars et al., 2012). Supporting the mental processes described previously requires flexible engagement and disengagement with multiple brain regions, which fits the pattern of high dynamics and occurrence of the DMN during rest.

Third, emerging evidence suggests that important individual differences can be associated with patterns of resting-state brain connectivity, and the variability of SFC patterns across individuals can be reflected in corresponding variability of important cognitive and behavioral variables (Cole et al., 2012; Filippi et al., 2012; He et al., 2012). Recent reports indicate that dynamic FC is also predictive of behavioral performance in healthy individuals (Kelly et al., 2008; Madhyastha et al., 2014; Thompson et al., 2013). However, it is yet unclear whether dynamic FC can provide additional predictive value over that provided by SFC. To answer this question, we obtained the predictive power of both dynamic and static FCs on behavioral performance using a single GLM. Our results clearly demonstrate that dynamic FC metrics, especially MTST, have much more power in explaining variance in behavioral performance tasks than SFC metric for all of the 75 behavioral tests considered, covering domains of alertness, cognition, emotion, and personality. Further, results from Figures 9 and 10 demonstrate that higher dynamics of FC are predictive of superior/favorable behavioral performance. For example, higher episodic memory score, better sustained attention, higher self-regulation, and lower impulsivity are predicted by lower MTST and hence greater dynamics of FC. This supports our hypothesis that information derived from dynamic variations in FC better predicts behavior as compared with conventional static measures and that greater dynamic variability supports superior behavioral performance in healthy individuals.

The results presented here have profound implications for our understanding of what constitutes a healthy and desirable brain. Conventional wisdom dictates that deviations of SFC from what one would typically observe in a matched control population represent altered neural circuitry underlying various disorders. For example, hyperconnectivity has been observed in psychiatric disorders, such as psychosis (Wotruba et al., 2014), schizophrenia (Shinn et al., 2013), and post-traumatic stress disorder (Qin et al., 2012; Yin et al., 2011), and hypoconnectivity has been observed in disorders, such as autism (von dem Hagen et al., 2013). In addition to the SFC value, the amount of variability of FC values over time may provide additional dimensions on which brain alterations may be assessed. For example, the inability to disengage from a state of altered connectivity may explain why one observes altered static connectivity in the first place. The fact that higher dynamics predicted better behavioral performance in healthy individuals indicates that the ease with which brain regions engage or disengage may be potential biomarkers for disorders involving altered neural circuitry. Specific examples of the application of this hypothesis to patient populations have begun to emerge. For example, a recent study showed that the inability of brain connections to dynamically adapt may be linked to behavioral inflexibility in autism (Uddin et al., 2014). Therefore, further exploration of this hypothesis in patient populations will likely emerge as a promising area of research.

Fourth, we discuss certain methodological issues arising from our study. Since the windows are allowed to be of varying lengths in our method, time-varying correlations cannot be directly compared across different populations. Rather, metrics, such as MTST, that capture state transitions due to time-varying connectivity dynamics are indeed comparable. Shorter windows due to inherent nonstationarity in the time series are likely to result in more state transitions at shorter intervals resulting in smaller MTST. This indicates greater dynamics, which could potentially be significantly different in a patient population as compared with controls. In addition, simpler metrics, such as variance of time-varying connectivity calculated over time, can also be compared across groups.

Another methodological issue concerns the choice of the parcellation scheme we have used to reduce the dimensionality of the dataset. There is an abundance of resting-state connectivity studies that have examined specific networks, usually involving <10 anatomically identified regions, rather than the entire brain. These studies are motivated by specific hypotheses regarding the functionality of specific networks. The methods used for this purpose include seed-based correlation (Greicius et al., 2003), as well as principle component analysis and ICA-based analysis (Radua et al., 2010; Soldati et al., 2013). Even though convenient for testing targeted hypotheses, the effect of other regions in the brain cannot be ignored and it is difficult to obtain the complete picture when investigating brain networks of a few regions in isolation. Accordingly, many studies explored whole-brain SFC (Shirer et al., 2012) and even whole-brain dynamic FC patterns (Allen et al., 2014; Leonardi et al., 2013). However, they suffered from the following limitations: (i) some works (Leonardi et al., 2013) employed a partitioning of the whole brain according to AAL atlas whose segmentation is solely based on anatomy, thus making the ROIs (regions of interest) functionally heterogeneous, and (ii) ICA-based functional definition (Allen et al., 2014) of ROIs combined distant regions into a single ROI, which is really not an appropriate parcellation scheme. We recognize that dimensionality reduction is essential given that dynamic evaluation of connectivity from all voxels in the brain can be computationally expensive. Therefore, unlike previous studies, we adopted a dimensionality reduction strategy that parcellated voxel time series into 190 functionally homogeneous gray matter regions using spectral clustering (Craddock et al., 2012). This 190-region atlas was derived using a large resting-state dataset (Craddock et al., 2012) (for corresponding AAL anatomical areas of the 190 regions, please see Supplementary Table S1). We extracted mean time series from each of the 190 regions and fed them into dynamic FC model. Here, we would like to note the differences between the parcellation schemes that we have adopted and other schemes in the literature. One set of methods rely on FC itself to generate parcellation of brain regions (Wig et al., 2014; Yeo et al., 2011). Although useful for exploring underlying neurophysiology, using such methods to generate ROIs in our context amounts to double dipping since we are interested in investigating connectivity dynamics between regions. However, another set of methods relies on the homogeneity of fMRI time series in spatially contiguous regions and such methods are more suited as a method for ROI definition for subsequent connectivity analysis. Spectral clustering, the one we have used (Craddock et al., 2012), is one such method. However, certain recent advancements, such as the one by Ryali et al. (2013), provide more robust performance. Future studies may investigate the performance of our proposed model on ROIs generated by such superior parcellation schemes.

Finally, we note a few limitations of this study and suggest that future work should be oriented in these directions. First, for dynamic FC calculation, we did not differentiate between “correlated” and “anticorrelated” interregional relationships in this work, and we plan to add this additional layer of complexity in a future study. This is important because in addition to characterizing functional associations between regions, the nature of such associations can be characterized by including the sign. Second, fluctuations of brain states represented by RSNs measured by fMRI should coordinate with EEG microstates (Van de Ville et al., 2010). Thus, it is necessary to conduct a similar analysis using simultaneously acquired EEG data. Third, some form of cross-validation would also be helpful in determining stable ranges for the major free parameters used in the proposed method, which would be important if this method is to be successfully extended to other datasets. Fourth, the sensitivity of the proposed method to an improper choice of the search range for the number of clusters needs to be investigated. Fifth, it is yet unclear whether metrics of dynamic FC obtained from simpler approaches, such as fixed window sliding correlation, are also capable of explaining as much variance in behavior as the proposed adaptive windowing method. If so, it may reduce computational complexity and future studies must investigate this aspect. Sixth, since our focus was to investigate the behavioral relevance of dynamic FC metrics, we used them in a regression model to predict behavior and did not perform tests to determine the statistical significance of metrics such as MTST. Future studies can develop nonparametric permutation tests in order to address this issue. Finally, FC does not provide information on the directionality (or causality) of connections. Previous reports have shown that causal relationships provide a complimentary mode of communication between brain regions in resting state and that regions that seem to be dissociated at zero-lag might as well have time-lagged relationships (Deshpande et al., 2011). Therefore, a similar analysis must be carried out using causal effective connectivity (EC). Further, the predictive ability of dynamic EC on human behavior must be deduced and compared with that of dynamic FC and static EC.

Acknowledgments

Data were provided by the HCP, WU-Minn Consortium (principal investigators: David Van Essen and Kamil Ugurbil; grant No. 1U54MH091657) funded by the 16 NIH institutes and centers that support the NIH Blueprint for Neuroscience Research, and by the McDonnell Center for Systems Neuroscience at Washington University.

Author Disclosure Statement

No competing financial interests exist.