Assessing Effects of Cholera Vaccination in the Presence of Interference

Summary

Interference occurs when the treatment of one person affects the outcome of another. For example, in infectious diseases, whether one individual is vaccinated may affect whether another individual becomes infected or develops disease. Quantifying such indirect (or spillover) effects of vaccination could have important public health or policy implications. In this paper we use recently developed inverse-probability weighted (IPW) estimators of treatment effects in the presence of interference to analyze an individually-randomized, placebo-controlled trial of cholera vaccination that targeted 121,982 individuals in Matlab, Bangladesh. Because these IPW estimators have not been employed previously, a simulation study was also conducted to assess the empirical behavior of the estimators in settings similar to the cholera vaccine trial. Simulation study results demonstrate the IPW estimators can yield unbiased estimates of the direct, indirect, total and overall effects of vaccination when there is interference provided the untestable no unmeasured confounders assumption holds and the group-level propensity score model is correctly specified. Application of the IPW estimators to the cholera vaccine trial indicates the presence of interference. For example, the IPW estimates suggest on average 5.29 fewer cases of cholera per 1000 person-years (95% confidence interval 2.61, 7.96) will occur among unvaccinated individuals within neighborhoods with 60% vaccine coverage compared to neighborhoods with 32% coverage. Our analysis also demonstrates how not accounting for interference can render misleading conclusions about the public health utility of vaccination.

1. Introduction

1.1 Background and Motivating Example

When assessing the effect of a treatment or exposure, often it is assumed the outcomes of one individual are not affected by the treatment received by other individuals, i.e., there is no interference between individuals. However, in many contexts, the no interference assumption is likely violated. For example, in the context of infectious diseases, whether one individual is vaccinated may affect whether another individual becomes infected or develops disease (Halloran and Struchiner 1995). Consider the following motivating example.

An individually-randomized placebo-controlled trial was conducted in Matlab, Bangladesh between 1985–88 to assess the efficacy of two oral cholera vaccines (Clemens et al. 1988). All children (2–15 yrs old) and women (>15 yrs old) were randomly assigned with equal probability to one of three treatment assignments: (1) B subunit-killed whole-cell oral cholera vaccine, (2) killed whole-cell-only cholera vaccine, or (3) E. coli K12 placebo. Although all women and children were randomized, only a subset participated in the trial. Of the total eligible sample population (N = 121,982), 49,300 women and children received two or more doses of vaccine. Surveillance of the Matlab population for diarrhea was conducted at three diarrheal treatment centers, and data for all eligible individuals were obtained from the International Centre for Diarrhoeal Disease Research, Bangladesh. Cholera cases were defined according to the following criteria: Vibrio cholerae 01 isolation from fecal samples, presentation of non-bloody diarrhea, and registration at a treatment center upon presentation of symptoms. Risk of cholera among the total eligible study population was 4.52 cases per 1000 people in the first year of follow-up. In the original vaccine trial, efficacy (defined as percent reduction in cholera incidence in vaccinated individuals compared to placebo recipients) was estimated to be 62% for the vaccine with B subunit and 53% for the vaccine without B subunit at one year of follow-up (Clemens et al. 1988).

Previous analyses of the cholera vaccine trial suggest that vaccination of individuals may have affected the outcomes of other individuals. For example, Ali et al. (2005) found spatial variation in vaccine efficacy was associated with spatial heterogeneity in vaccine coverage (i.e., the proportion of vaccinated individuals), whereby the estimated efficacy was lower in areas of higher vaccine coverage. They also found that risk of disease among placebo recipients was inversely associated with the level of vaccine coverage in their respective neighborhoods. These results suggest possible interference between individuals in spatial proximity to one another. Similarly, Root et al. (2011) found that incidence of cholera among placebo recipients declined with increasing vaccine coverage within an individual’s kinship network.

The analysis of the Matlab cholera vaccine trial presented in this paper goes beyond the association-type analyses described above. Instead, inference is drawn about different effects of vaccination by utilizing recently developed methods for causal inference in the presence of interference. The results have straight-forward interpretations in terms of the expected number of cases of cholera averted due to vaccination, allowing investigators and public health officials who determine vaccine policy to better understand the direct and indirect effects of cholera vaccination.

1.2 Methods for Interference

Recently increasing attention has been placed on developing methods for assessing treatment effects in the presence of interference (see Tchetgen Tchetgen and VanderWeele (2012) and references therein). Inference in this setting is particularly interesting, yet challenging, because a treatment may have different types of effects in the presence of interference. One approach has been to assume individuals can be partitioned into groups such that interference is possible within groups but not across groups (i.e., there is no interference between individuals in different groups). This assumption is sometimes called ‘partial interference’ (Sobel 2006) and should approximately hold if individuals can be clustered in space, time, or some other fashion.

Drawing inference about treatment effects generally requires knowledge or modeling of the mechanism by which individuals select or are assigned treatment. Under the partial interference assumption, one possible assignment mechanism is a sequential two stage randomization design, where in stage one groups are randomized to different treatment allocation strategies and in stage two individuals are randomized to treatment or control conditional on the strategy assigned to their group in the first stage (Hudgens and Halloran 2008). For example, schools might be randomized to low or high vaccine coverage, and then students in the schools randomized to control or vaccine with vaccination probability dependent on whether their school was assigned to low or high coverage (Longini et al. 2002).

In many settings, however, randomization may only occur at the group level, at the individual level, or neither. Tchetgen Tchetgen and VanderWeele (2012; henceforth TV) proposed estimators for treatment effects in the presence of interference which do not require randomization of individuals or groups. The estimators proposed by TV entail estimating mean potential outcomes by taking weighted averages of the observed responses where the weights include the inverse of group-level propensity scores (Rosenbaum and Rubin 1983). TV proved that when the group-level propensity scores are known, these inverse-probability weighted (IPW) estimators are unbiased. However, to date the finite sample properties of their proposed IPW estimators have not been evaluated when the group-level propensity score is unknown and therefore must be estimated, nor have these estimators been employed in an application.

1.3 Outline

The remainder of this paper is organized as follows. In Section 2 we introduce notation and provide general definitions of estimands and estimators to be used in subsequent sections. In Section 3 finite sample properties of the IPW estimators are assessed in a simulation study. In Section 4 we use these methods to analyze the cholera vaccine trial data described in Section 1.1. Finally, in Section 5 we discuss our findings and highlight potential future methods for addressing interference.

2. Methods

2.1 Notation and Estimands

Consider a finite population of N individuals. Suppose the individuals can be partitioned into m groups (e.g., neighborhoods) with n_i individuals in group i for i = 1, …, m, such that ${\sum }_{i=1}^m{n}_i=N$. Suppose individuals are either vaccinated (a = 1) or not vaccinated (a = 0). Let A_ij = 1 if individual j in group i is vaccinated, and 0 otherwise. Let A_i = (A_i1, …, A_ini) denote the vector of vaccination indicators of all individuals in group i. Let A_i,−j = (A_i1, …, A_ij−1, A_ij+1, …, A_ini) denote the vector of vaccination indicators for all individuals in group i except individual j. Let a_i and a_i,−j denote realizations of A_i and A_i,−j. Let 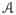(n) be the set of 2ⁿ possible vaccination vectors for a group of size n, such that a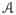_i ∈ (n_i).

Assume there is partial interference, i.e., there is no interference between individuals in different groups. Let y_ij(a_i) denote the potential disease outcome (1 if disease or infection, 0 otherwise) for individual j in group i if A_i = a_i, such that each individual in group i has 2^n_i potential outcomes. Sometimes it is helpful to express the potential outcome for individual j as a function of his/her vaccination status a_ij and the vaccination status of other individuals in his/her group a_i,−j, in which case we write y_ij(a_ij; a_i,−j). Let Y_ij = y_ij(A_i) denote the observed infection outcome for individual j in group i, and let Y_i = (Y_i1, …, Y_ini) denote the vector of observed outcomes for all individuals in group i.

For the cholera vaccine study motivating example, individuals may have chosen to participate or not in the trial. The potential outcomes defined above can be defined more generally as a function of vaccination status and participation status. In particular, let B_ij = 1 if individual j in group i chose to participate in the trial, let B_ij = 0 otherwise, and define B_i = (B_i1, …, B_ini). Let y_ij(a_i, b_i) denote the potential disease outcome for individual j in group i if A_i = a_i and B_i = b_i. We assume that participation has no effect on an individual’s outcome for fixed vaccination status of their group, i.e., $y_{ij}({\mathbf{a}}_i,{\mathbf{b}}_i)=y_{ij}({\mathbf{a}}_i,{\mathbf{b}}_i^{\prime })$ for all b_i, ${\mathbf{b}}_i^{\prime }$. Under this assumption the simpler notation y_ij(a_i) in the preceding paragraph is sufficient to describe all potential outcomes for individual j in the presence of partial interference.

Various vaccine effects can be defined according to differences in average potential outcomes associated with a particular group allocation strategy and individual treatment assignment. Here we consider allocation strategies, denoted by α or α′, corresponding to different levels of vaccine coverage. Define the individual average potential outcome for individual vaccine assignment a and group-level vaccination coverage α by ȳ_ij(a; α) = y_ij(a; a_i,−j)π(a_i,−j; α), where π(a_i,−j; α) denotes the conditional probability Pr(A_i,−j = a_i,−j|A_ij = a) under vaccine coverage α. Assume under allocation strategy α individuals receive vaccine independently from each other with probability α such that $\pi ({\mathbf{a}}_{i,-j};\alpha )={\prod }_{k=1,k\ne j}^{n_i}{\alpha }^{a_{ik}}{(1-\alpha )}^{1-a_{ik}}$. The marginal individual average potential outcome can be defined similarly as ȳ_ij(α) = 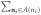y_ij(a_i)π(a_i; α), with $\pi ({\mathbf{a}}_i;\alpha )={\prod }_{j=1}^{n_i}{\alpha }^{a_{ij}}{(1-\alpha )}^{1-a_{ij}}$. Define the group average potential outcomes as ${\overline{y}}_i(a;\alpha )={\sum }_{j=1}^{n_i}{\overline{y}}_{ij}(a;\alpha )/n_i$. Population average potential outcomes are defined as $\overline{y}(a;\alpha )={\sum }_{i=1}^m{\overline{y}}_i(a;\alpha )/m$, and marginal group and population average potential outcomes are defined as ${\overline{y}}_i(\alpha )={\sum }_{j=1}^{n_i}{\overline{y}}_{ij}(\alpha )/n_i$ and $\overline{y}(\alpha )={\sum }_{i=1}^m{\overline{y}}_i(\alpha )/m$, respectively.

Following Halloran and Struchiner (1995) and Hudgens and Halloran (2008), the direct effect of vaccination corresponds to the difference in the risk of infection when an individual is vaccinated compared to when an individual is not vaccinated, all other things being equal. Formally, define the population average direct effect when vaccine coverage is α as $\overline{DE}(\alpha )=\overline{y}(0;\alpha )-\overline{y}(1;\alpha )$. Indirect effects of vaccination correspond to the difference in infection risk of an unvaccinated individual under two different levels of vaccine coverage. The population average indirect effect is formally defined as $\overline{IE}(\alpha ,{\alpha }^{\prime })=\overline{y}(0;\alpha )-\overline{y}(0;{\alpha }^{\prime })$. Indirect effects can be defined analogously for vaccinated individuals (a = 1), but for simplicity only indirect effects in unvaccinated individuals are considered in the sequel. The total effects of vaccination combine both direct and indirect effects, and correspond to the difference between the risk of infection for unvaccinated individuals under one vaccine coverage level compared to the risk of infection for vaccinated individuals under another vaccine coverage level. Specifically, the population average total effect is defined by $\overline{TE}(\alpha ,{\alpha }^{\prime })=\overline{y}(0;\alpha )-\overline{y}(1;{\alpha }^{\prime })$. The overall effect of vaccination corresponds to the difference in the risk of infection under one group allocation strategy relative to another strategy, i.e., $\overline{OE}(\alpha ,{\alpha }^{\prime })=\overline{y}(\alpha )-\overline{y}({\alpha }^{\prime })$. If there is no interference between individuals, then the direct, indirect, and total effects do not differ across allocation strategies α and α′, the indirect effects equal zero, and the total effects equal the direct effects (Hudgens and Halloran 2008). In the next section we consider estimators that, under certain assumptions, can be used to draw inference from observational data about average potential outcomes under different allocation strategies α and α′ and, in turn, the four effects defined above.

2.2 Estimators

In the absence of randomization at the group and/or individual level, TV proposed IPW estimators of the direct, indirect, total, and overall effects. The IPW estimators are constructed by weighting the observed individual responses Y_ij by the inverse of the group-level propensity score, i.e., the probability a group of individuals receives a particular vaccination vector (defined below). When this group-level propensity score is known, TV proved the IPW estimators are unbiased under two assumptions: conditional independence and positivity. Under the conditional independence assumption

$$Pr({\mathbf{A}}_i={\mathbf{a}}_i\mid {\mathbf{X}}_i,{\mathbf{y}}_i)=Pr({\mathbf{A}}_i={\mathbf{a}}_i\mid {\mathbf{X}}_i),$$ (1)

where y_i denotes the potential outcomes for all individuals in group i, and X_i = (X_i1, …, X_ini) is an n_i × p matrix with X_ij a 1 × p vector of covariates for individual j in group i. The right side of (1) is the group-level propensity score used in constructing the IPW estimators. Under the positivity assumption

$$Pr({\mathbf{A}}_i={\mathbf{a}}_i\mid {\mathbf{X}}_i)>0,\forall {\mathbf{a}}_i\in \mathcal{A}(n_i).$$ (2)

Assumptions (1) and (2) are group-level generalizations of the usual no unmeasured confounders and positivity assumptions made at the individual level in the analysis of observational studies when interference is not present.

In general in observational studies the true propensity score will not be known. In this particular setting TV proposed fitting mixed effects models to estimate the propensity scores. For the cholera vaccine trial, individuals were randomized to vaccine or not, such that whether or not an individual was vaccinated was determined by his/her choice to participate in the trial as well as his/her randomization assignment. Therefore, to estimate the group-level propensity scores, the individual probability of trial participation will be estimated using a mixed effects logit model, and this will be combined with the known probability of vaccine assignment (2/3) conditional on participation in the trial. We assume that the decision of an individual to participate in the trial was independent of their vaccine assignment, which is plausible because by design individuals had no way of knowing their randomization assignment prior to deciding whether or not to participate in the trial. Recall B_ij is an indicator of participation for individual j in group i. The joint probability of vaccination for a group is modeled as

$$Pr({\mathbf{A}}_i\mid {\mathbf{X}}_i;\mathit{\varphi })=\int \prod _{j=1}^{n_i}{\{(2/3)h_{ij}(b_i)\}}^{A_{ij}}{\{1-(2/3)h_{ij}(b_i)\}}^{(1-A_{ij})}{f}_b(b_i;{\varphi }_b){db}_i$$ (3)

where h_ij(b_i) = Pr (B_ij = 1|X_ij, b_i) = logit⁻¹ (X_ijϕ_a + b_i) is the probability of participation in the trial conditional on covariates X_ij for individual j and random effect b_i for group i, f_b(·; ϕ_b) denotes the density function of b_i which is assumed b_i ~ N(0, ϕ_b), and ϕ = (ϕ_a, ϕ_b) denotes the vector of model parameters.

When the group-level propensity scores (3) are unknown and must be estimated, the IPW estimators of the group-level average potential outcomes are:

$${\widehat{Y}}_i^{\mathit{ipw}}(a;\alpha )=\frac{{\sum }_{j=1}^{n_i}\pi ({\mathbf{A}}_{i,-j};\alpha )I(A_{ij}=a)Y_{ij}}{Pr({\mathbf{A}}_i\mid {\mathbf{X}}_i;\widehat{\mathit{\varphi }})n_i}$$ (4)

$${\widehat{Y}}_i^{\mathit{ipw}}(\alpha )=\frac{{\sum }_{j=1}^{n_i}\pi ({\mathbf{A}}_i;\alpha )Y_{ij}}{Pr({\mathbf{A}}_i\mid {\mathbf{X}}_i;\widehat{\mathit{\varphi }})n_i}$$ (5)

where ϕ̂ is an estimator of ϕ (discussed further below). The estimators for population average potential outcomes and marginal population average potential outcomes are ${\widehat{Y}}^{\mathit{ipw}}(a;\alpha )={\sum }_{i=1}^m{\widehat{Y}}_i^{\mathit{ipw}}(a;\alpha )/m$ and ${\widehat{Y}}^{\mathit{ipw}}(\alpha )={\sum }_{i=1}^m{Y}_i^{\mathit{ipw}}(\alpha )/m$. Estimators for direct, indirect, total, and overall effects are given by:

$$\begin{array}{l}\widehat{DE}(\alpha )={\widehat{Y}}^{\mathit{ipw}}(0;\alpha )-{\widehat{Y}}^{\mathit{ipw}}(1;\alpha )\\ \widehat{IE}(\alpha ,{\alpha }^{\prime })={\widehat{Y}}^{\mathit{ipw}}(0;\alpha )-{\widehat{Y}}^{\mathit{ipw}}(0;{\alpha }^{\prime })\\ \widehat{TE}(\alpha ,{\alpha }^{\prime })={\widehat{Y}}^{\mathit{ipw}}(0;\alpha )-{\widehat{Y}}^{\mathit{ipw}}(1;{\alpha }^{\prime })\\ \widehat{OE}(\alpha ,{\alpha }^{\prime })={\widehat{Y}}^{\mathit{ipw}}(\alpha )-{\widehat{Y}}^{\mathit{ipw}}({\alpha }^{\prime })\end{array}$$ (6)

In the results below these estimators were computed with ϕ̂ estimated by fitting a mixed effects logit model of the probabilty of participation using maximum likelihood. Mixed effects models were fit using the glmer function in the lme4 package (Bates, Maechler and Bolker 2011), and the denominators of (4) and (5) were evaluated numerically using the integrate function in R (R Core Team 2013).

TV did not provide variance estimators of the estimators given in (6), although they did suggest that large sample variance estimators should be straightforward to obtain under standard regularity conditions. In Web Appendix A the large sample distributions of the estimators in (6) are derived using M-estimation theory (Stefanski and Boos 2002). The estimators are shown to be consistent and asymptotically normal, and sandwich-type variance estimators are derived. In the sequel, the variance estimator given in equation (5) of Web Appendix A is used to compute Wald type confidence intervals (CIs) for the different effects.

3. Simulation Study

A simulation study was implemented to assess the accuracy of the IPW estimators (6) in scenarios similar to the cholera vaccine trial. The steps taken in the simulation study are listed below.

• (0)
  The simulated population, which was held fixed across simulation runs, consisted of 10,000 individuals who were randomly allocated to one of 500 neighborhoods (median: 20 people per neighborhood, IQR: 17 – 23). Let y_ij(a, k) represent the cholera status of individual j given individual j receives treatment a and k individuals in neighborhood i excluding individual j are vaccinated. For each individual, y_ij(a, k) was generated by randomly sampling from a Bernoulli distribution with expectation logit⁻¹(0.500−0.788a−2.953α_i−0.098X_ij1−0.145X_ij2+0.351aα_i) where α_i = (a+k)/n_i, X_ij1 represented an individual’s age (in decades), and X_ij2 represented an individual’s distance to the nearest river (in km). Individual ages were randomly generated using an exponential distribution with mean 20; ages above 100 were set to 100 and then ages were divided by 10 (making the units decades). Neighborhood distances to river were randomly generated using a log-normal distribution such that the log distance mean and standard deviation were 0 and 0.75, respectively. Individual-level distances were then generated by adding random variation to neighborhood-level distances in the form of normal random deviates with mean 0 and standard deviation of 0.05; individual-level distances below 0 were set to 0. The parameter values for the above outcome model were chosen based on logistic regression modeling of the cholera vaccine trial data. Under this parameterization if no individuals were vaccinated in a neighborhood, the risk of infection for individuals age 20 (X_ij1 = 2) living one km to the nearest river (X_ij2 = 1) was approximately 0.54. The average potential outcomes for individual j in neighborhood i were then calculated as

  $${\overline{y}}_{ij}(a;\alpha )=\sum _{k=0}^{n_i-1}{y}_{ij}(a,k)\left(\begin{array}{c}{n}_i-1\\ k\end{array}\right){\alpha }^k{(1-\alpha )}^{n_i-k-1}$$

  and ȳ_ij(α) = αȳ_ij(1; α) + (1 − α)ȳ_ij(0; α). Finally the causal estimands of interest as defined in Section 2.1 were computed.

• (1)For each individual the indicator of participation in the trial B_ij was randomly generated from a Bernoulli distribution with mean logit⁻¹ (0.2727 − 0.0387X_ij1 + 0.2179X_ij2 + b_i), where X_ij1 and X_ij2 were from step 0, and b_i was a neighborhood-level random effect generated from a Normal distribution with mean 0 and variance ϕ_b = 1.0859. As in step 0, the choice of parameter values was based on fitting a logistic mixed effects model to the cholera vaccine trial data. For individuals with B_ij = 1, treatment assignment A_ij was generated from a Bernoulli distribution with mean 2/3. Otherwise, if B_ij = 0, then A_ij = 0.
• (2)Based on the potential outcomes generated in step 0 and the treatment assignment from step 1, the observed outcomes were set to $Y_{ij}=y_{ij}(a=A_{ij},k={\sum }_{j^{\prime }=1,j^{\prime }\ne j}^{n_i}{\mathbf{A}}_{{ij}^{\prime }})$, and the estimates ${\widehat{Y}}_i^{\mathit{ipw}}(a;\alpha )$ and ${\widehat{Y}}_i^{\mathit{ipw}}(\alpha )$ were calculated for a ∈ {0, 1} and α ∈ [0.2, 0.8] using the IPW estimators (4)–(5). Then, the direct, indirect, total, and overall effect estimates (6) were calculated, along with the corresponding sandwich-type variance estimates given in Web Appendix A and Wald CIs.
• (3)Steps 1–2 were repeated 1000 times.

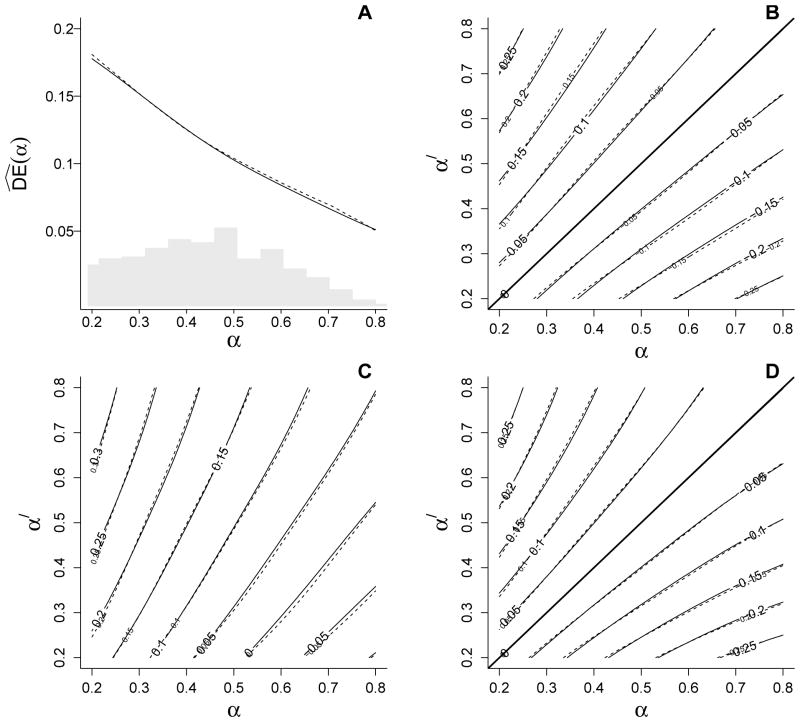
The plots in Figure 1 display the average of the 1000 IPW estimates of the direct, indirect, total, and overall effects, as well as the corresponding true effects (calculated based on the population generated in step 0 above). Figure 1A shows the direct effects as a function of group-level allocation strategies, i.e., α. Figures 1B–1D depict the indirect, total, and overall effects of vaccination across all combinations of α and α′. The true direct effects decline with increasing vaccine coverage α, while indirect, total, and overall effects increase with α′ across all values of α. Note that plots for $\widehat{IE}(\alpha ,{\alpha }^{\prime })$ and $\widehat{OE}(\alpha ,{\alpha }^{\prime })$ are symmetric in absolute value because Ŷ^ipw(0; α) − Ŷ^ipw(0; α′) = −{Ŷ^ipw(0; α′) − Ŷ^ipw(0; α)} and Ŷ^ipw(α) − Ŷ^ipw(α′) = −{Ŷ^ipw(α′) − Ŷ^ipw(α)}. In general, the empirical bias of the IPW estimators was negligible. Similarly, the average sandwich-type variance estimates approximately equaled the empirical variance, and the empirical coverage of the Wald 95% CIs was close to the nominal coverage probability (see Web Table 1).

Figure 1.

IPW estimates of (A) direct $\overline{DE}(\alpha )$, (B) indirect $\overline{IE}(\alpha ,{\alpha }^{\prime })$, (C) total $\overline{TE}(\alpha ,{\alpha }^{\prime })$, and (D) overall $\overline{OE}(\alpha ,{\alpha }^{\prime })$ effects from the simulation study. Solid lines represent the true effects, and dashed lines represent average effect estimates obtained using the IPW estimators. The histogram in (A) represents the distribution of vaccine coverage observed from the simulated data. Note that plots for $\widehat{IE}(\alpha ,{\alpha }^{\prime })$ and $\widehat{OE}(\alpha ,{\alpha }^{\prime })$ are symmetric in absolute value because Ŷ(0; α) − Ŷ(0; α′) = −{Ŷ(0; α′) − Ŷ(0; α)} and Ŷ(α) − Ŷ(α′) = −{Ŷ(α′) − Ŷ(α)}.

For each simulation we also computed naive estimators based on simple averages of observed outcomes for comparison with the IPW estimators. For each group we computed the average observed outcomes ${\stackrel{\sim }{Y}}_i(a)={\sum }_{j=1}^{n_i}{Y}_{ij}I(A_{ij}=a)/{\sum }_{j=1}^{n_i}I(A_{ij}=a)$ for each level of treatment a = 0, 1, where I(·) is the usual indicator function. The average overall outcome ${\stackrel{\sim }{Y}}_i={\sum }_{j=1}^{n_i}{Y}_{ij}/n_i$ was also computed, and these group level averages were then averaged across groups having vaccine coverage approximately equal to α. Specifically, we let $\stackrel{\sim }{Y}(a;\alpha )={\sum }_{i=1}^m{\stackrel{\sim }{Y}}_i(a)I({\alpha }_i\in [\alpha -h/2,\alpha +h/2))/{\sum }_{i=1}^{m}I({\alpha }_i\in [\alpha -h/2,\alpha +h/2))$ and $\stackrel{\sim }{Y}(\alpha )={\sum }_{i=1}^m{\stackrel{\sim }{Y}}_{i}I({\alpha }_i\in [\alpha -h/2,\alpha +h/2))/{\sum }_{i=1}^{m}I({\alpha }_i\in [\alpha -h/2,\alpha +h/2))$, where ${\alpha }_i={\sum }_{j=1}^{n_i}{A}_{ij}/n_i$ denotes the observed vaccine coverage in neighborhood i and h = (0.8 − 0.2)/50 = 0.012. The estimators Ỹ(a; α) and Ỹ(α) were evaluated at the same values of a and α as the IPW estimators. Naive estimates for the direct, indirect, total, and overall effects were then computed by substituting Ỹ(a; α) for Ŷ^ipw(a; α) and Ỹ(α) for Ŷ^ipw(α) in (6). The empirical bias of the naive estimators (Web Figure 1) was substantially larger than the bias of the IPW estimators (Figure 1). These results are not surprising given that, unlike the IPW estimators, the naive estimators make no attempt to adjust for possible confounding (in this case by age X_ij1 and distance to a river X_ij2).

As an alternative to the IPW estimators that does attempt to adjust for confounding, outcome model-based estimators of the different vaccine effects were also computed for each simulated data set. In particular, as in Ali et al. (2005) the following population average logistic regression model logit(Pr[Y_ij = 1]) = β₀ + β₁A_ij + β₂α_i + β₃A_ijα_i + β₄X_ij1 + β₅X_ij2 was fit using generalized estimating equations assuming an independence working correlation structure between individuals within the same neighborhoods (groups). The coefficients from the logistic regression model could not directly be interpreted in terms of the estimands of interest because the vaccine effects given in Section 2.1 are defined as counterfactual risk differences. Therefore, following Austin (2010), the predicted risk of Y_ij = 1 was computed for each individual for a = 0, 1 and α ∈ [0.2, 0.8] based on the fitted model. These individual predicted risks were averaged across individuals within groups, and then the group averages were averaged across groups to obtain estimates of Ȳ(a; α) and Ȳ(α), which were then substituted for Ŷ^ipw(a; α) and Ŷ^ipw(α) in (6). Like the naive estimators, the outcome model-based estimators were substantially more biased than the IPW estimators (Web Figure 2).

Finally, to examine sensitivity of the IPW estimators to misspecification of the propensity score model, for each simulation the IPW estimators were also computed based on an incorrectly specified propensity score model wherein the river distance covariate (X_ij2) was erroneously omitted. Results in Web Figure 3 show that negligible bias was introduced when the propensity score model was incorrect, demonstrating the IPW estimators may in some circumstance be fairly robust to such model misspecification. However, it is difficult to draw general conclusions from a single simulation study, and one might expect the bias of the IPW estimator to be dependent on the strength of association of the omitted covariate(s) with participation and risk of cholera infection.

4. Analysis of the cholera vaccine trial

4.1 Data

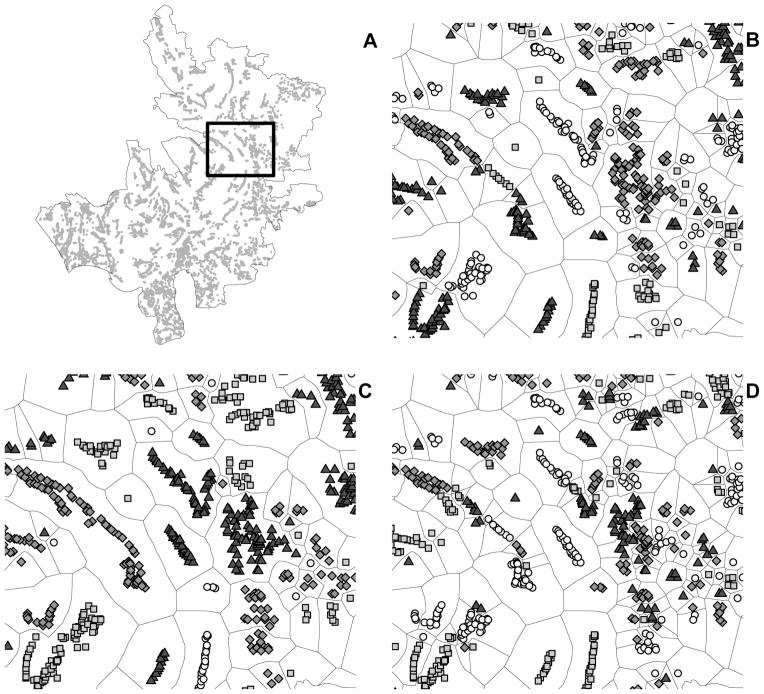
As in Ali et al. (2005), individuals were considered to be trial participants if they received two or more doses of either vaccine or placebo. Unvaccinated individuals included eligible non-participants and placebo recipients. Vaccinated individuals included recipients of B subunit-killed whole-cell oral cholera vaccine and killed whole-cell-only vaccine, with no distinction made in the analysis between the two types of vaccine (N = 49,300). A total of 121,982 eligible individuals from 6,415 baris, i.e., clustered patrilineal households were included in the analysis (Figure 2A).

Figure 2.

Definition of neighborhoods from geo-referenced data. Household clusters, i.e., baris, which are represented as gray dots in (A), were partitioned into distinct neighborhoods, i.e., groups, according to a single-linkage agglomerative clustering procedure. The rectangle in (A) is magnified in (B), (C), and (D). The total number of groups was set to (B) 700 neighborhoods for the main analysis, and (C) 400 and (D) 1100 neighborhoods for the sensitivity analysis.

4.2 Neighborhood Definition

Because group membership was not predefined in this individually randomized trial, groups (neighborhoods) were defined according to the spatial clustering of baris. Discrete neighborhoods were determined according to a single linkage agglomerative clustering method (Everitt et al. 2011). Each individual therefore belonged to a neighborhood defined by the spatial distribution of baris. We assumed no interference between individuals in different neighborhoods. The total number of neighborhoods was pre-specified to equal 700, which resulted in a median of 64 (IQR: 21 – 191) eligible individuals per neighborhood (Figure 2B). A sensitivity analysis was conducted to address how neighborhood scale, i.e., group definition, could influence results. Specifically, the analysis was repeated using cluster definitions in which the pre-determined total number of groups equaled 400 and 1100 (Figure 2C–D).

4.3 Analysis

Because individuals who did not participate in the trial are included in this analysis, methods suitable for an observational study design, such as IPW type approaches, are necessary to draw valid inference about the effects of vaccination. To implement the IPW estimators from Section 2.2 using the cholera vaccine trial data, a logistic mixed effects model of the probability of participating in the trial was fit to estimate the group-level propensity scores (3). Following VanderWeele and Shpitser (2011), we considered for inclusion in the propensity score model measured baseline covariates that were believed to possibly cause participation, cholera infection, or both. Based on this criterion and analyses examining associations of covariates with participation or cholera infection, the untestable no unmeasured confounders assumption (1) was assumed to hold conditional on age and distance to the nearest river. Analyses suggested that the associations between the log odds of participation and the covariates age and river were non-linear; therefore quadratic age and river terms were also included in the propensity score model. The fitted propensity score model indicated that the odds of trial participation was significantly associated with age (for age in decades centered at 28 years, ϕ̂_a,age = −0.060, estimated standard error $\widehat{\text{se}}=0.004$ and ϕ̂_a,age² = 0.032, $\widehat{\text{se}}=0.002$) and distance to the nearest river (ϕ̂_a,river = 0.147, $\widehat{\text{se}}=0.048$ and ϕ̂_a,river² = 0.020, $\widehat{\text{se}}=0.012$), and that there was significant correlation between individuals in the same neighborhood (ϕ̂_b = 1.20, $\widehat{\text{se}}=0.08$). The Tchetgen Tchetgen-Coull (2006) diagnostic test suggested the normal random effects model provided adequate fit (p = 0.13). Estimators (4) and (5) can be viewed as weighted averages of individual observed responses with weights w_ij = π(A_i,−j; α)/Pr(A_i|X_i; ϕ̂) and w_i = π(A_i; α)/Pr(A_i|X_i; ϕ̂). For the primary results presented below, w_ij ranged from 1.08 to 3.74 and w_i ranged from 0.92 to 1.16 for the values of α considered. Sensitivity analyses were conducted by considering group-level propensity score models including other covariates in addition to age and distance to the nearest river. Group level propensity score estimates were used to compute the IPW estimates (6) of the direct, indirect, total and overall effects for vaccine coverage values α and α′ between 0.30 and 0.60. The ranges of α and α′ were chosen because 75% of individuals were members of neighborhoods with vaccine coverage between 30% and 60%.

4.4 Results

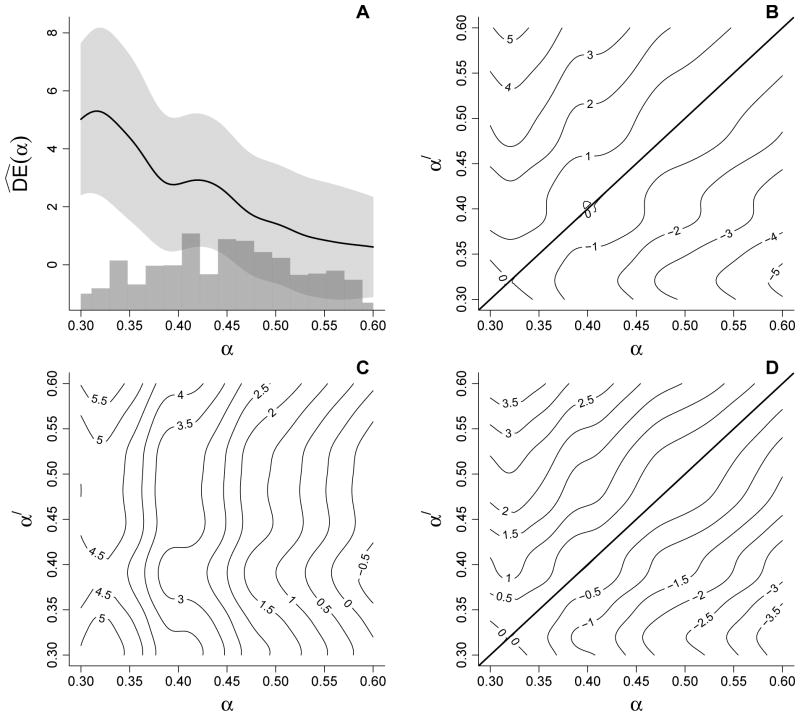
IPW estimates of the direct, indirect, total, and overall effects based on 700 neighborhoods are shown in Figure 3. The estimates are given in units of cases of cholera per 1000 individuals per year. The direct effect estimates (Figure 3A) generally decrease with increasing α. The largest estimate of the direct effect occurs at 32% vaccine coverage level: $\widehat{DE}(0.32)=5.30$, 95% CI 2.48, 8.12. In other words, in neighborhoods with 32% vaccine coverage we would expect 5.30 fewer cases of cholera per 1000 person-years among vaccinated individuals compared to unvaccinated individuals. In contrast, the smallest direct effect estimate occurs at 60% coverage: $\widehat{DE}(0.60)=0.61$, 95% CI −1.11, 2.33. These two inferences about the direct effect come to very different conclusions about the vaccine, in terms of both the magnitude and significance of its effect, illustrating the limitations of analyses that only consider direct effects when interference may be present. Moreover, were only $\widehat{DE}(0.60)$ and the corresponding CI considered, the vaccine would be dismissed as having no utility. Analyses based on $\widehat{DE}(0.32)$ and the other effect estimates below indicate this conclusion would be incorrect.

Figure 3.

IPW estimates of (A) direct $\overline{DE}(\alpha )$, (B) indirect $\overline{IE}(\alpha ,{\alpha }^{\prime })$, (C) total $\overline{TE}(\alpha ,{\alpha }^{\prime })$, and (D) overall $\overline{OE}(\alpha ,{\alpha }^{\prime })$ effects based on the cholera vaccine trial data. In (A) the light gray region represents approximate pointwise 95% confidence intervals and the histogram below depicts the distribution of observed neighborhood vaccine coverage.

The indirect effect estimates are displayed in the contour plot in Figure 3B. Not surprisingly the estimates tend to increase with α′ − α. The largest estimate of the indirect effect occurs between 60% and 32% coverage levels: $\widehat{IE}(0.32,0.60)=5.29$, 95% CI 2.61, 7.96. That is, we would expect 5.29 fewer cases of cholera per 1000 person-years in unvaccinated individuals within neighborhoods with 60% coverage compared to within neighborhoods with 32% coverage.

The total effect estimates in Figure 3C exhibit quite a different pattern from the indirect effect estimates, reflecting the direct effect of the vaccine. Whereas the indirect effect estimates along the line α = α′ in Figure 3B necessarily equal zero, the total effect estimates along the line α = α′ in Figure 3C necessarily equal the direct effect estimates in Figure 3A. In general, the contours in Figure 3C have a roughly vertical orientation, indicating that the estimated risk of cholera when vaccinated tends to be the same regardless of coverage, i.e., Ŷ(1; α′) is relatively constant as a function of α′. The hyperplane below the line α = α′ in Figure 3C includes the contour where the total effect estimate equals zero, corresponding to situations where being vaccinated in a low coverage neighborhood affords the same estimated risk of cholera as being unvaccinated in a high coverage neighborhood. On the other hand, the largest total effect estimate $\widehat{TE}(0.32,0.60)=5.90$ (95% CI: 2.98, 8.82) corresponds, as one might expect, to being vaccinated in a high coverage (60%) neighborhood relative to being unvaccinated in a low coverage (32%) neighborhood. In contrast to inference about $\overline{DE}(0.60)$, the total effect estimate $\widehat{TE}(0.32,0.60)$ is an order of magnitude greater and the corresponding 95% CI easily excludes the null value of zero, suggesting a significant total vaccine effect.

Estimates of the overall effects (Figure 3D) exhibit a similar pattern to the indirect effect estimates. The largest overall effect estimate $\widehat{OE}(0.32,0.60)=3.96$ (95% CI: 2.06, 5.86) provides a single summary measure of the neighborhood-level effect of vaccination. In words, 3.96 fewer cases of cholera per 1000 individuals per year are expected if 60% of individuals are vaccinated compared to if only 32% are vaccinated.

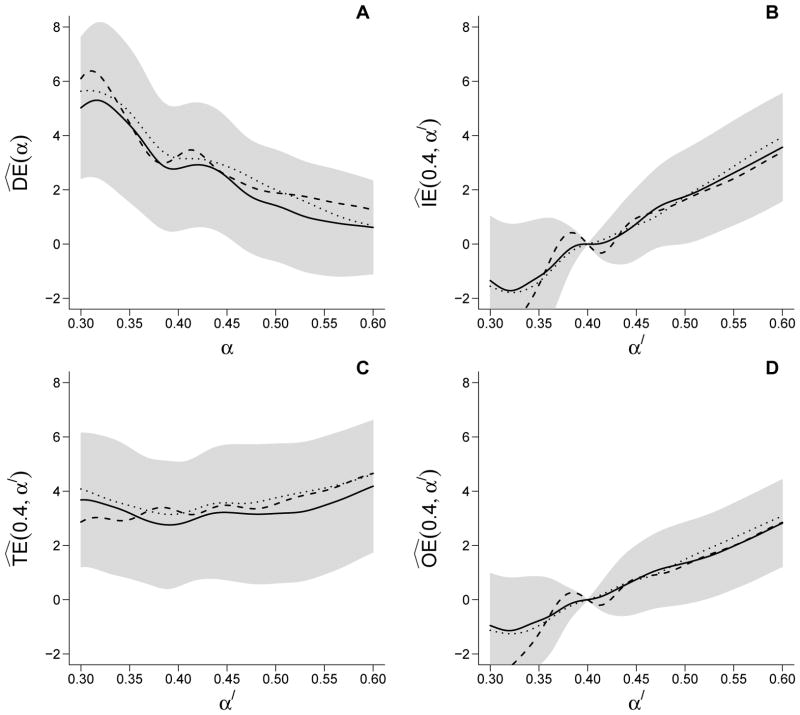
Effect estimates obtained using alternative group definitions (i.e., 400 and 1100 total neighborhoods) were similar and within the 95% CIs from the 700 neighborhoods analysis (Figure 4). Estimates were also similar when using an alternative propensity score model that conditioned on age (linear and quadratic), distance to the nearest river (linear and quadratic), distance to the nearest treatment center (linear), and religion (Hindu versus non-Hindu); see Web Figure 4.

Figure 4.

IPW estimates of (A) direct $\overline{DE}(\alpha )$, (B) indirect $\overline{IE}(0.40,{\alpha }^{\prime })$, (C) total $\overline{TE}(0.40,{\alpha }^{\prime })$, and (D) overall $\overline{OE}(0.40,{\alpha }^{\prime })$ effects based on the cholera vaccine trial data. The solid line gives the estimates using the 700 neighborhood partition. The dashed and dotted lines correspond to estimates using the 400 and 1100 neighborhood partitions. The gray regions around the effect estimates represent approximate pointwise 95% confidence intervals using the 700 group partition.

5. Discussion

The Matlab cholera vaccine trial analysis presented in this paper extends previous association-type analyses of population-level vaccine efficacy (Ali et al. 2005, 2009; Root et al. 2011) to inference about the different causal effects of the vaccine(s). Such inference quantifies the expected number of cholera cases prevented for different levels of vaccine coverage in both vaccinated and unvaccinated individuals, providing clearer interpretation of and additional insight into the population-level impact of vaccination for investigators and policy makers. The analysis in this paper also demonstrates the importance of considering both individual and group-level vaccine effects when interference may be present. Otherwise, an analysis that focuses only on the individual (i.e., direct) effect may fail to recognize a vaccine with potential public health benefit.

A two-stage randomized trial as described in Section 1.2 would be an ideal study design for drawing inference about different vaccine effects in the presence of interference. However, in many settings two-stage randomization may not be feasible, in which case alternative analytical strategies that adjust for the lack of randomization at one or both stages are needed to estimate the effects of vaccination. In contrast to two-stage randomized trials, in individually randomized vaccine trials the group-level vaccine coverage will depend on the proportion of individuals within groups that elect to participate in the trial (assuming the vaccine is not available otherwise), which may vary between groups. For instance, Ali et al. (2009) found significant heterogeneity in the spatial distribution of vaccine coverage across villages in the cholera vaccine trial area. Such heterogeneity may be associated with the infection risk of individuals within the groups, and thus comparisons between groups with different vaccine coverage levels may be susceptible to confounding. The methods employed in our analysis use inverse probability weighting to control for such confounding. In particular, we found that age and distance to the nearest river were associated with trial participation and cholera infection, and thus assumed the no unmeasured confounders assumption (1) held conditional on these covariates. Sensitivity analysis to this assumption suggested the results were fairly robust to the choice of confounders included in the propensity score model.

Nonetheless, it is always possible in observational studies that unmeasured confounding exists. Predicting the impact of such confounding on the IPW estimates of the cholera vaccine’s effects is challenging. At the individual level, if in the absence of vaccination trial participants would have been at lower risk for developing cholera than non-participants (conditional on measured covariates), then we might predict the direct effect estimates to be positively biased. This might have occurred if individuals who participated in the trial tended to also take additional precautionary measures to lower their risk of acquiring cholera relative to non-participants. On the other hand, if in the absence of vaccination trial participants would have been at greater risk for developing cholera than non-participants, then we might predict the direct effect estimates to be negatively biased. This might have occurred if trial participants correctly self-identified themselves as being at high risk of acquiring cholera relative to non-participants. Similarly, at the group level, if in the absence of vaccination those neighborhoods with high trial participation rates would have had lower (higher) cholera incidence on average, then we might expect estimates of the indirect effect IE(α, α′) to be positively (negatively) biased for α ≤ α′.

There are several avenues of possible future research related to drawing inference about treatment effects in the presence of interference. We demonstrated that IPW estimators proposed by Tchetgen Tchetgen and VanderWeele (2012) performed well in simulations. However, it is well known that IPW estimators having a Horvitz-Thompson-type form can be highly variable. Future research could explore the utility of stabilized IPW estimators having a Hajek-estimator-type form in this setting. Additionally, the IPW estimators employed in this study require the unverifiable assumption of no unmeasured confounders; further research could develop formal methods for assessing the sensitivity of these estimators to unmeasured confounders. Following Ali et al. (2005), in the cholera vaccine trial analysis presented in Section 4 no distinction was made between the two types of vaccines. An analysis that distinguishes between the different vaccines and the placebo would require extending the methods employed in this paper to allow for more than two levels of A_ij.

Partial interference, i.e., no interference between individuals in different groups, is another key assumption of the IPW estimators. We examined the impact of the partial interference assumption in the cholera vaccine trial through a sensitivity analysis and found that results obtained using different neighborhood scales were similar. Although we defined neighborhoods using a single-linkage agglomerative clustering method, other clustering techniques (e.g., complete linkage agglomerative clustering, arithmetic average clustering, centroid clustering, non-hierarchical k-means clustering) could have also been employed to differentiate between spatial neighborhoods (Everitt et al. 2011). Future research could entail relaxing the partial interference assumption. For instance, following Ali et al. (2005), one approach might entail allowing each individual to have their own possibly unique set of individuals with whom they interfere; e.g., the potential outcomes of individual j might be allowed to depend only on the treatment received by individuals within a 500 m circular area of the residence of individual j. Hierarchical models of interference might also be considered that posit different levels of interference, e.g., between individuals within the same household and also between individuals within the same neighborhood but different households. The extent to which the observable data can be used to identify the form of interference or test assumptions about the assumed interference structure is an open question.

An additional extension of the work presented here might include incorporating a monotone treatment response assumption. In certain settings it may be plausible to assume that the vaccine does no harm, either directly or indirectly. For example, a no direct harm assumption might suppose ȳ(0; α) ≥ ȳ(1; α), i.e., the risk of infection when an individual is not vaccinated is at least as great as when vaccinated, conditional on a group allocation strategy. A no indirect harm assumption might suppose for a = 0, 1 that ȳ(a; α) ≥ ȳ(a; α′) for any two strategies α, α′ such that α < α′, i.e, the risk of infection is a monotonically decreasing function of coverage conditional on the individual vaccination status. IPW estimators could then be constructed which satisfy constraints imposed by the monotone treatment response assumptions. For example, assuming no indirect harm, the estimator of the indirect effect $\overline{IE}(0.40,{\alpha }^{\prime })$ would be guaranteed to be non-negative for all α < α′. These and other similar assumptions might be considered in the future development and application of IPW estimators for assessing treatment effects in the presence of interference.