Costs and benefits of group living with disease: a case study of pneumonia in bighorn lambs (Ovis canadensis)

Abstract

Group living facilitates pathogen transmission among social hosts, yet temporally stable host social organizations can actually limit transmission of some pathogens. When there are few between-subpopulation contacts for the duration of a disease event, transmission becomes localized to subpopulations. The number of per capita infectious contacts approaches the subpopulation size as pathogen infectiousness increases. Here, we illustrate that this is the case during epidemics of highly infectious pneumonia in bighorn lambs (Ovis canadensis). We classified individually marked bighorn ewes into disjoint seasonal subpopulations, and decomposed the variance in lamb survival to weaning into components associated with individual ewes, subpopulations, populations and years. During epidemics, lamb survival varied substantially more between ewe-subpopulations than across populations or years, suggesting localized pathogen transmission. This pattern of lamb survival was not observed during years when disease was absent. Additionally, group sizes in ewe-subpopulations were independent of population size, but the number of ewe-subpopulations increased with population size. Consequently, although one might reasonably assume that force of infection for this highly communicable disease scales with population size, in fact, host social behaviour modulates transmission such that disease is frequency-dependent within populations, and some groups remain protected during epidemic events.

1. Introduction

Host aggregation can facilitate pathogen transmission, and this is thought to be a major cost of group living [1,2]. The extent to which host social dynamics shape transmission depends on both the ease with which the pathogen is transmitted from host to host, and host group stability during epidemics. For easily transmitted pathogens, such as those with aerosolized transmission routes, transmission is often modelled as density-dependent: the rate at which susceptible hosts become infected is thought to increase with increasing population size, with the consequence that pathogen persistence and epidemic size are both directly related to population size [3]. By contrast, pathogens that require more intense contact for transmission, such as those relying on sexual transmission routes, have forces of infection independent of population size [3]. This is because the number of disease-transmitting contacts is expected to be similar, regardless of population size—a transmission function often referred to as ‘frequency-dependent’.

For hosts living in highly compartmentalized societies with consistent group sizes and rare between-group interactions, however, stable social bonds can modulate transmission. Although transmission may be higher in larger groups (density-dependent within groups), the per capita infection rate cannot exceed group size, making transmission appear frequency-dependent when viewed from the population level. This occurs when infectious agents are isolated to specific host groups [4], as was shown for bovine tuberculosis transmission among badgers in the UK [5], and for the single-host enzootic phase of Yersinia pestis outbreaks among prairie dogs [6]. Pathogen sequestration to particular social groups is predicted even for highly infectious agents that might otherwise be assumed to have density-dependent transmission. In these settings, predictions from mean-field models that describe disease at the population scale are incorrect, because the population does not accurately represent the pool of susceptible hosts [3,7–9].

Contact estimates based on population-wide mixing may be biased high during periods of group stability, with important ramifications for intervention during disease epidemics in human, domestic and free-living animal populations. First, because individual contacts are biased high, transmission and disease-induced mortality rates estimated at the population level will be biased low [10]. Second, choices about management actions such as culling, antibiotic treatment or vaccine application which aim at altering the number of susceptible hosts may be misguided, because these decisions rely on theoretical threshold values which make assumptions about the relevant number of susceptible hosts [7]. Third, theory suggests that if transmission scales with population size (i.e. transmission is density-dependent), then pathogens cannot invade and persist in host populations below a threshold population size [8,11]. Thresholds, however, do not exist if disease-transmitting contact rates and population size are decoupled owing to host contact structure (i.e. transmission is frequency-dependent) [12]. As a consequence, while pathogens subjected to density-dependent transmission are generally predicted to fade out prior to driving their hosts extinct, frequency-dependent transmission is both theoretically [13,14] and empirically [15] linked to host population collapse.

Alternatively, group stability may sometimes benefit social hosts during infectious disease events. While extensive empirical work explores the role of well-connected ‘super-spreader’ individuals in increasing epidemic size [16], relatively few studies investigate the inverse effect, e.g. whether temporally stable host aggregations inhibit pathogen transmission. This is true despite the fact that many animal species live in genetically well-mixed populations which consistently break into discrete subpopulations for portions of the year. For example, the social dynamics of harem breeding species such as zebras [17] and horses [18], or species such as mouflon [19] and saiga antelope [20] which rear their offspring in stable nursery groups, may serve to buffer those populations against pathogen transmission during periods of increased susceptibility simply by eliminating social bridges along which pathogens could move. For these species, group stability may temporarily limit pathogen transmission by acting as a form of organizational social immunity [21].

Here, we address the question: how does spatio-temporal stability in social connections affect disease-induced mortality patterns in a social host? We then explore how the relationship between social patterns and observed mortality events relates to the choice of pathogen transmission function, and consider the implications of that choice on management of wildlife species which experience high levels of disease-induced mortality. We treat these questions in the context of a detailed study of an infectious pneumonia which regularly produces epidemics in populations of bighorn sheep. Existing work on this system focuses on preventing and managing all-age mortality associated with pathogen spillover from domestic sheep and goats [22–24]. Here, we focus instead on the enzootic phase of disease characterized by recurrent annual pneumonia outbreaks among bighorn lambs [25,26]. By analysing lamb mortalities as they relate to ewe social connections, we find that disease impacts some portions of bighorn populations much more intensely than others, and explain why disease events in chronically infected populations may be unlikely to respond to population-level management strategies.

2. Material and methods

(a). Study system

Epidemics of contagious pneumonia challenge bighorn sheep restoration throughout the western United States [23,24]. Pneumonia epidemics in bighorn sheep are attributed to spillover of directly transmitted bacteria from domestic sheep [27,28]. Following pathogen introduction, initial disease events affect all age classes with ewe mortality rates ranging from 30% to 60% [25]. Subsequently, some populations continue to experience periodic outbreaks of pneumonia in lambs prior to weaning for a decade or more [25].

Bighorn sheep live in sexually segregated societies for much of the year [29]. During summer, ewes rear their lambs in nursery groups. Pneumonia outbreaks probably start with transmission from one or more chronically infected ewes to their lambs [22,25,30], with gregarious juvenile behaviour providing a plausible mechanism for subsequent lamb-to-lamb transmission. This study focused on animals living in the Hells Canyon area of Idaho, Washington and Oregon (figure 1a). The preponderance of diagnosed lamb mortality in Hells Canyon during the study period was attributable to infectious pneumonia (true for 92 of 104 necropsied lambs for whom a cause of death could be confirmed) [25]. In the light of this observation, we assumed that lamb mortality was a reasonable proxy for lamb infection throughout this analysis. Lamb mortality rates varied dramatically from year to year, regardless of whether disease was present (figure 1b).

Figure 1.

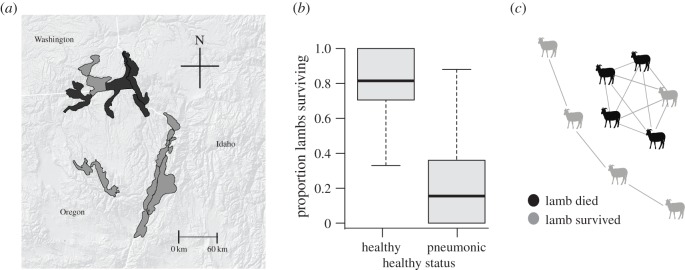
(a) Map of Hells Canyon region, with the five study populations shaded in dark grey, and all other populations show in light grey. (b) Summer lamb survival in years classified as healthy for lambs, or pneumonia present in lambs. (c) Example summer ewe social contact network. Grey nodes represent ewes whose lambs survived through 1 October; black nodes represent ewes whose lambs died.

We investigated the capacity of four factors to account for variability in lamb mortality: population, year, ewe-subpopulation and individual ewe. We used these factors to specify a hierarchy of four possible transmission scales during enzootic lamb pneumonia events. Follow-up analyses examined the relationship between ewe-subpopulation size and population size. If most lamb mortalities result from direct ewe-to-lamb transmission, then we would expect that some (presumably chronically infected) ewes would consistently lose their lambs while others would consistently rear theirs successfully, producing heterogeneity and high variation in individual ewe outcomes. If disease is localized within ewe-subpopulations, then we would expect some subpopulations to experience very poor lamb survival, whereas other subpopulations in that same year might have high lamb survival. This would produce heterogeneity and high variation at the subpopulation level. If transmission is localized to populations, we would expect some populations to consistently have high summer lamb survival, whereas other populations would consistently perform poorly, producing high variation at the population level. Follow-up analyses examined the relationship between ewe-subpopulation size and population size.

(b). Data collection and preparation

We followed lambs born to marked ewes from 1997 through to 2010 in four intensively monitored bighorn sheep populations in Hells Canyon (figure 1a). Location data from 162 radio-collared ewes over a combined 664 ewe-summers in the Asotin, WA; Black Butte, WA; Imnaha, OR; Redbird, ID; and Wenaha, OR and WA populations were used to build summer contact networks for 66 lamb cohorts born in the years following an all-age pneumonia outbreak in 1995–1996 [25,31]. We defined populations as geographically distinct groups, with no exchange of females and low levels of mixing by males. A lamb cohort was defined as a year-class of lambs within a population. As in previous analyses [25,26], each lamb cohort was considered an independent observation from its population, because there are no clear trends in disease severity or population trajectories once pathogens were present in the study populations (electronic supplementary material, figure S1). The resulting dataset includes between 10 and 13 cohorts from five populations (electronic supplementary material, table S1). The median proportion of ewes radio-collared per population was 0.25 (electronic supplementary material, table S1). Ewes almost always gave birth to a single lamb in May (85%) and weaned the lamb at approximately four months of age [32]. We excluded seven cohorts where the median interval between successive locations of a given ewe was greater than 10 days. Lambs were dependent on, and tightly paired with, their dams throughout the summer (1 May–30 September). A detailed description of summer ewe social network construction, including details on the data used in construction, is included in the electronic supplementary material. We used ewe social networks as a basis for identifying temporally stable ewe-subpopulations, which we defined as clusters of marked ewes observed associating directly or indirectly (i.e. were not observed directly associating, but were both observed associating with a third marked individual at different points in time; figure 1c) over the course of the summer. All ewe-subpopulations were entirely nested within populations in this study.

Daily group size and composition were recorded at each observation; in this analysis, we use ‘group size’ to refer to the number of sheep seen together in these ‘daily groups’. Ewes were classified as having a lamb when they were observed nursing, bedded with or in body contact with a lamb. The survival of lambs born to marked ewes was calculated through to 30 September (age approx. 18–20 weeks). Diseased and healthy cohorts were classified on the basis of the presence or absence of recorded or suspected lamb pneumonia [25,31], and were analysed separately. Electronic supplementary material, table S1 contains information on each cohort, including the number of ewes and lambs followed, population health status, number of relocation events, and number and size of all ewe-subpopulations.

(c). Analysis

Bootstrap-based methods were used to check for relationships between number of detected ewe-subpopulations and number of radiocollars, and for differences in numbers of groups between diseased and healthy years (see the electronic supplementary material, figure S3). Network-based autocorrelation approaches [33] were used to evaluate the stability of ewe-subpopulation membership from year to year, and are included in the electronic supplementary material.

To determine the spatial and temporal scales of pneumonia transmission, we decomposed variance in summer lamb survival using a hierarchical logistic regression model. We estimated variance attributable to: populations, years within populations (‘years’), ewe-subpopulations and ewes. Because daily group membership was not stable over the timescale of epidemic events, we omitted daily groups from the variance decomposition in favour of the coarser, but more realistic ewe-subpopulation membership. We took years to be nested in populations, because disease severity was not temporally synchronized across all Hells Canyon populations (electronic supplementary material, figure S1). The nested structure allowed each population to experience a unique disease status in the same year. Ewe effects were estimated across all years during which a ewe reproduced, regardless of that year's disease status. Because ewe effects are estimated across all years that she was observed with a lamb, they are partially crossed with all other terms in the model. Comparisons were based on a variance decomposition performed using a hierarchical logistic regression model with random effects for ewes, ewe-subpopulations, years and populations. Let p_i be the binary outcome of summer lamb survival (0 = died; 1 = survived) for the ith lamb. For the ith lamb born to the jth ewe in the kth ewe-subpopulation during the lth year in the mth population, this corresponded to the following hierarchical linear model:

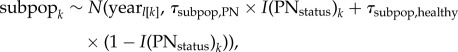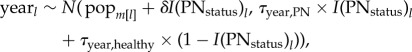and

we use the subscript notation z_q[r] to denote which of the q levels of factor z was experienced by individual r. For example ewe_j[i] indicates which of the j ewes produced lamb i. I(PN_status) are indicator terms that take on the value 0 for years classified as healthy, and 1 otherwise. These terms control the variance estimate to which each observation contributes. Indicator terms were generated separately for each level of the model, but always retained the same meaning: any ewe-subpopulation present in a year classified as having pneumonia is assigned an I(PN_status) term of 1, as is any year classified as having pneumonia. A schematic of model hierarchy is shown in figure 2a.

Figure 2.

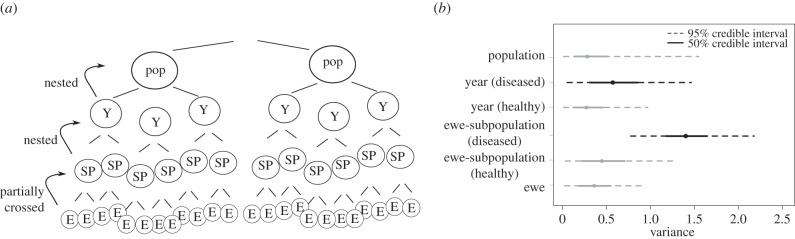
(a) Schematic of hierarchical structure of variance decomposition. Y, ‘year’, SP, ‘subpopulation’, E, ‘ewe’. (b) Variance attributed to each random effect (ewe-subpopulations, years, specific ewes). Grey lines indicate 95% posterior credible intervals associated with each variance component. Black is used for variance decomposition when disease is present; grey is used in years when no disease was detected. Variance decompositions are based only on years with multiple components. Ewe and population effects were estimated across all years (healthy and diseased), and are thus shown as a single distribution applied across all disease classes. Variance in the hierarchical (ewe, subpopulation, year, population) logistic regression model in diseased cohorts was estimated to be 1.41 at the subpopulation level (95% credible interval from 0.77 to 2.21), and 0.58 at the year level (95% credible interval from 0.03 to 1.45). In healthy years, variance based on 167 lambs was estimated as 0.43 at the subpopulation level (95% credible interval from 0.02 to 1.32), and 0.279 (95% credible interval from 0.01 to 0.96) at the year level. Variance attributable to ewe effects across all years was estimated at 0.406 (95% credible interval from 0.02 to 0.95); variance attributable to population was estimated at 0.280 (95% credible interval from 0.01 to 1.46).

For our purposes, the critical attributes of this model were the precision parameters, τ_subpop,PN, τ_{subpop,healthy}, τ_year,PN, τ_year,healthy, τ_pop and τ_ewe, which we inverted to variances following model fitting. We were particularly interested in the relative size of each variance component. High variance at a particular level indicated that lamb survival differed between units at this level, whereas low variance meant that lamb survival did not differ. Because we were specifically interested in whether models that incorporated ewe-subpopulations outperformed mean-field models which treated all ewes in a population as well-mixed, we used the deviance information criterion (DIC) to compare models with and without a ewe-subpopulation level in their hierarchical structures.

We then tested whether the number of ewe-subpopulations during the lth study year in the mth population (λ_l) depended on population size. Population size was estimated from the total number of ewes counted in annual aerial surveys. We used a hierarchical Poisson model containing a fixed effect for total ewes counted (‘TotEwes’), a random intercept for each population (‘pop’), and an overdispersion term, φ [34], to evaluate this relationship. Formally, this model was

and

In this model, our inferential focus was on the posterior density associated with the β₁ parameter, which links the observed number of ewe-subpopulations to the total number of ewes in the population. We used a similar structure to model median daily group size as a function of total number of ewes, however, in that case, we used an identity link function, and treated the residuals as normally distributed. See the electronic supplementary material for detailed descriptions of statistical methods and model fits.

We fitted a piecewise linear regression model [35] to describe how the number of ewe-subpopulations related to median daily group size. Piecewise regression allows a process to abruptly change forms at some (model-estimated) point along a covariate axis. Median daily group sizes were modelled as a function of the number of ewe-subpopulations present in each population, in a framework that allowed for a possible change in the relationship between daily group size and number of subpopulations. In this model, λ_k represents the median daily group size observed for members of the kth subpopulation in the jth year. Let β₁ be the linear relationship between number of subpopulations (‘NumSubpops’) and median daily group size prior to the changepoint; let U be the changepoint, and let γ be the adjustment to the relationship between number of subpopulations and daily group size for numbers of subpopulations exceeding the changepoint. Then, the changepoint model is

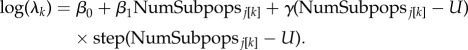Our inferential focus was on whether the relationship between daily group size and number of subpopulations was constant over the range of number of subpopulations observed. We were also interested in the specific shape of that relationship. Thus, inference was based on estimates of β₁, γ and U.

The hierarchical linear models were fitted using the lmer package [36], and the piecewise regression model was fitted using the SiZer package [37] in R [38]. The variance decomposition was fitted using Markov chain Monte Carlo (MCMC) samplers implemented in JAGS [39] and accessed through R. Five chains of length 100 000 were run for each model, with the first 50 000 steps omitted for burn-in. Gelman–Rubin statistics [40] was used to evaluate chain mixing and model convergence. Credible intervals were extracted from the joint posterior distributions produced by the MCMC algorithm following convergence. We used non-informative priors wherever possible. Specific parametrizations, convergence diagnostics and posterior estimates for all emergent quantities are included in the electronic supplementary material.

3. Results

The number of ewe-subpopulations that contributed to a lamb cohort ranged from one to nine, with a median of 3 (electronic supplementary material, figure S2). Twenty-eight of the 53 cohorts with multiple ewe-subpopulations were classified as healthy, and 25 as diseased. To test for ewe-subpopulation-specific effects on lamb survival in diseased years, we analysed survival of the 274 lambs born in cohorts with more than one ewe-subpopulation present. In years with lamb disease events, 50.8% of the observed variation in lamb mortalities was attributed to ewe-subpopulations (95% posterior credible interval: 28.6%, 77.0%), whereas in healthy years, subpopulations accounted for only 28.9% of observed variation (95% posterior credible interval from 2.2% to 64.6%). The subpopulation a lamb was reared in explained more variation than year or ewe during years when disease was detected, whereas in healthy years, group explained no more variation than individual or year (figure 2b). Furthermore, a model that did not incorporate ewe-subpopulation was a significantly poorer fit than a model that included ewe-subpopulations (DIC for the full model = 580.5; DIC for the reduced model = 600.8). The variance in lamb survival among subpopulation was significantly higher in years with disease. Lambs in a subpopulation with survival 1 s.d. below average have greater than three times the odds of mortality in an average subpopulation [exp(sqrt(1.46)) = 3.35] when epidemics were detected. By contrast, in healthy years, the odds of mortality for lambs born in a subpopulation with survival 1 s.d. below average was less than twice [exp(sqrt(0.42)) = 1.91] those of lambs born in an average subpopulation. In an analysis that excluded ewe-subpopulation, ewe-subpopulation-level effects in diseased years were reattributed to years, whereas healthy year effects remained relatively unchanged (electronic supplementary material, figure S4).

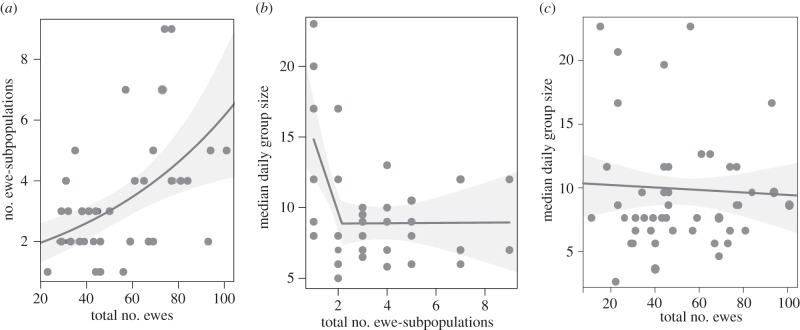
Ewe-subpopulations were defined such they that were never observed to mix with one another over the course of the summer. While some unobserved mixing between subpopulations almost certainly occurred, our sampling intensity limits the likelihood that strong connections between marked animals (e.g. ‘bridge vertices’) escaped detection in this dataset. However, subpopulations did undergo internal fission–fusion dynamics, with some subpopulation members forming ephemeral groups that lasted one or several days before splitting. Median total daily group size was 9 (approx. six ewes with a mixture of three juveniles and (usually young) rams). The number of ewe-subpopulations did not differ between healthy and diseased years (p = 0.289 on 10 000 bootstrapped replicates; electronic supplementary material). The number of ewe-subpopulations increased when the population size increased (β_TotEwes = 0.013; 95% confidence interval (CI) = (0.0024, 0.0245); figure 3a). The relationship between number of ewe-subpopulations and ewe-subpopulation size was characterized by an abrupt change once multiple ewe-subpopulations were present. Median daily group size declined dramatically when the number of ewe-subpopulations increased from one to two, but remained relatively constant for two or more subpopulations (95% CI for slope with less than three groups = (−14.176, −0.228); 95% CI for slope with two or more ewe-subpopulations = (−0.725, 3.215); figure 3b). The number of ewe-subpopulations did not differ by health classification (healthy and diseased; p = 0.289 on 10 000 bootstrapped replicates). We found no compelling evidence of a relationship between total number of ewes observed and daily group size (95% CI for β_TotEwes = (−0.064, 0.042); figure 3c); daily group size remained relatively constant across a range of observed population sizes. We observed similar patterns, regardless of whether we used total daily group size or number of ewes in a group in these models.

Figure 3.

(a) Number of ewe-subpopulations by estimated number of ewes in the population. Grey shading indicates the 95% confidence regions associated with the fit from a Poisson mixed effects model describing number of components as a function of total number of ewes with random slopes and intercepts for each population. (b) Median observed group size by number of ewe-subpopulations. Grey shading indicates 95% confidence regions for the structure of the piecewise linear relationship. (c) Median daily observed group size by estimated number of ewes in the population for all population-years included in this study. Grey shading indicates 95% confidence regions estimated from a Poisson mixed effects model relating total number of ewes in a given population-year to daily observed ewe group sizes.

4. Discussion

We found that lamb mortalities were affected by female social connections during years when disease was present, but not in the absence of disease. Ewe-subpopulations accounted for most of the variation in lamb mortality, while individual ewe, year and population-level variation were relatively unimportant. Mortalities were structured at the subpopulation scale and therefore the assumption that all ewes in a population mix homogeneously during lamb disease epidemics is not supported.

For the five months following parturition, ewe group sizes were independent of population size (figure 3b,c). Group size during lamb-rearing may represent an ecologically optimal aggregation for foraging efficiency or protection from predators [41], but the size and stability of these aggregations also have consequences for disease transmission and management. Specifically, our data suggest that lamb mortality, and by proxy pathogen transmission, is largely localized within ewe-subpopulations. These results have several important ramifications. First, disease-induced mortality rates calculated at the population level probably underestimate true impacts on exposed lambs. Rather than successfully controlling their own infections, surviving lambs may simply be protected by social barriers that reduce or eliminate their risk of exposure. In this situation, ewe social connections provide a form of organizational social immunity [21] in which some individuals remain protected simply because existing contact processes do not provide a direct chain of transmission linking them to infected individuals. In this way, stable female-offspring groups may provide population-level resilience in the face of infectious disease despite high juvenile susceptibility. This resilience comes at a cost, however: because ewes in this system appear to consistently form groups of similar sizes, regardless of population size, disease die-offs are likely to precipitate social reorganization patterns that may foster continued pathogen transmission even as populations decrease in size. In short, the advantage of a critical population size below which pathogens fade out may be lost.

Choice of transmission function often shifts from density-dependent to frequency-dependent when systems are viewed from increasingly coarse scales. While phocine distemper in harbour seals generally follows density-dependent transmission processes within cohorts, between-cohorts transmission is frequency-dependent [42]. The relative role of different transmission modes shifts dramatically between spillover (between-species) and enzootic (within-species) persistence in prairie dog populations infected with Y. pestis [6,43]. Seasonally variable host aggregation and disease incidence patterns are consistent with a shift between frequency- and density-dependent transmission of chronic wasting disease incidence in white tailed deer [44]. However, despite the growing empirical support for scale-dependent approaches to transmission function, transmission in a system is still usually assumed to follow the same process: it is either frequency- or density-dependent, regardless of the scale of observation (but see [45]). This assumption may hinder model development and disease management, especially for systems transitioning from spillover to endemic, or with long-lived infectious stages [46].

Research on the relationship between group stability and disease often focuses on systems in which transmission is enhanced during periods of increased group mixing or group size. This is the case, for example, in measles among school children [47], and brucellosis in elk [48]. In this study, we explore the other end of that spectrum. Disease events in our system occur when populations are compartmentalized into subpopulations, and we argue that this compartmentalization constrains epidemic size. This finding has important implications about the evolutionary pressures that pathogens place on host societies.

As is inevitable with analysis of field data, ours has a number of assumptions and limitations. First, because not all ewes were marked, we were unable to build saturated contact networks for each cohort. This may have resulted in an underestimate of the amount of mixing among subpopulations and introduced some upward bias on the number of subpopulations detected. The relationship between number of collared ewes and ewe-subpopulations was not significant after accounting for population size, however (electronic supplementary material). Frequent relocations and the general fidelity of collared ewes to their resident groups (electronic supplementary material, figure S5) suggest that this weakness does not jeopardize our overall findings. Second, we could not directly measure ewe-subpopulation size. Although subpopulations were defined based on associations of marked individuals, they also consisted of an unknown number of unmarked sheep that were not individually identifiable. Because the number of subpopulations increased with population size but daily group size did not (figure 3), we assumed that the number, but not the sizes of both subpopulations and groups were linked with population size. Third, this analysis focuses entirely on enzootic disease events in ewes and lambs; the potential roles of adult rams and domestic sheep during lamb pneumonia events are not considered here. Disease in lambs is unlikely to come from rams because, consistent with previous work [29], we rarely observed adult rams with ewes and lambs during summer. Apparent population closure paired with high ewe survival during lamb epidemics is consistent with the hypothesis that infection in lambs is not due to spillover, but owing to chronically infected ewes.

Finally, we attribute the observed variation in lamb mortality between subpopulations to disease transmission, but subpopulations may be subjected to varying risk from other sources, particularly genetic susceptibility and habitat. We feel confident attributing risk to contact as opposed to genetic factors, because ewes are not completely nested in subpopulations. Instead, some reshuffling in subpopulation membership occurs between years (electronic supplementary material, figure S5). If genetics drive susceptibility in this system, then a strong ewe effect should have emerged in the variance decomposition, but no such effect was observed. From a habitat perspective, while there could be some microsite differences between populations, all populations studied here are at low density, and are unlikely to be nutritionally limited and forage quality and availability are unlikely to vary substantially between ewe-subpopulations.

Our results reflect a growing resource allocation dilemma for bighorn sheep management: research and management efforts have focused on all-age die-offs that occur after pneumonia is first introduced to a naive population; however, the long-term enzootic persistence of pneumonia may be the greater threat to species recovery. Management aimed at reducing disease transmission through limiting or reducing population size would probably result in fewer ewe-subpopulations of the same size and might have no effect on the probability of within-subpopulation disease transmission during lamb rearing. A reduction in population size without a corresponding change in ewe group size is unlikely to alter contact rates within ewe-subpopulations, which appear to be most critical for disease transmission to juveniles. An alternative strategy is to target removal efforts at animals that are likely to be chronically infected, a strategy we are currently exploring in the Hells Canyon system. Although disease transmission within subpopulations may proceed via density-dependent transmission, transmission is frequency-dependent when viewed from the population scale [9]. As a consequence, the critical community size required for pathogen persistence may be much lower than previously expected, and this will hamper efforts to manage enzootic disease by limiting population size.

Limited knowledge of the mechanisms underlying pathogen persistence inhibits our ability to make management decisions that facilitate population recovery after disease invasion. Reducing spillover risk is unquestionably critical for bighorn sheep restoration, but following spillover, risk mitigation is not necessarily sufficient to spur pathogen fade-out and population recovery. We showed that when groups are stable, social structure can be directly linked to mortality patterns, and that this relationship may be discernible from commonly available data such as the relocation dataset used here. Such a relationship can serve as a basis for drawing inference about the extent of disease transmission, with direct implications on disease management. Incorporating social networks into survival analyses is a powerful yet underused approach for investigating and managing disease in wildlife.

Ethics statement

Animals were handled by state wildlife agencies in accordance with approved protocols.

Funding statement

Data collection was supported by the wildlife agencies of Idaho, Washington and Oregon, with assistance from the US Forest Service, Bureau of Land Management, and support from the Wild Sheep Foundation national, chapters and affiliates, Shikar-Safari Club International and the Oregon Hunters Association. Funding was also provided by Federal Aid to Wildlife Restoration Project W-160-R administered through Idaho Department of Fish and Game. Analysis was supported through Morris Animal Foundation grant number (D13ZO-081), and by an academic computing fellowship from Pennsylvania State University for K.R.M. R.K.P. was supported by the Cedar Tree Foundation and P. Thye, P.J.H. was supported by the Research and Policy for Infectious Disease Dynamics (RAPIDD) programme of the Science and Technology Directorate, Department of Homeland Security and Fogarty International Center, National Institutes of Health.