Juxtacrine Signaling Is Inherently Noisy

Abstract

Juxtacrine signaling is an important class of signaling systems that plays a crucial role in various developmental processes ranging from coordination of differentiation between neighboring cells to guiding axon growth during neurogenesis. Such signaling systems rely on the interaction between receptors on one cell and trans-membrane ligands on the membrane of a neighboring cell. Like other signaling systems, the ability of signal-receiving cells to accurately determine the concentration of ligands, is affected by stochastic diffusion processes. However, it is not clear how restriction of ligand movement to the two-dimensional (2D) cell membrane in juxtacrine signaling affects the accuracy of ligand sensing. In this study, we use a statistical mechanics approach, to show that long integration times, from around one second to several hours, are required to reach high-sensing accuracy (better than 10%). Surprisingly, the accuracy of sensing cannot be significantly improved, neither by increasing the number of receptors above three to five receptors per contact area, nor by increasing the contact area between cells. We show that these results impose stringent constraints on the dynamics of processes relying on juxtacrine signaling systems, such as axon guidance mediated by Ephrins and developmental patterns mediated by the Notch pathway.

Introduction

Noise is a fundamental property of biological systems that affects biological functions ranging from transcriptional processes and chemotactic behavior at the single cell level to tissue development at the organismal level (1). Although many biological systems have to find ways to deal with noise to function reproducibly, other systems use noise for generating random processes or bet hedging strategies (2). One source of noise is the inherently stochastic behavior attributable to random diffusion of molecules in the environment. Such a diffusion driven noise, limits the accuracy at which the concentration of the ligand can be measured by cell surface receptors. This problem was first addressed by Berg and Purcell in 1977, who estimated the statistical fluctuations in ligand concentration and its effect on the accuracy of measurement by the cell (3). They showed that ligand diffusion introduces a counting error at the receptors, setting a noise floor for measuring ligand concentration. Based on the probability of a receptor to be occupied, they computed the fluctuation in receptor occupancy. Finally, relating the fluctuation in receptor occupancy with the uncertainty in ligand concentration at equilibrium, they obtained the relative uncertainty in the determination of the ligand concentration. This computation was also generalized for a system of many receptors.

A different approach using statistical mechanics and the fluctuation dissipation theorem was used to generalize the results of Berg and Purcell to a broader range of cases (4–6). This approach was based on using the fluctuations in receptor occupancy as a form of thermal noise, which allows using the fluctuation dissipation theorem rather than considering the microscopic details of the receptor-ligand interactions. They were able to separate noise coming from the binding/unbinding from the noise due to the ligand diffusion. The noise floor attributable to diffusion coincides with the results obtained by Berg and Purcell.

These methods provided an expression for the accuracy of the determination of ligand concentration, $\delta c/\overline{c}$, given an average ligand concentration, $\overline{c}$. For one receptor and for ligands diffusing in three dimensions (3D), the accuracy attributable to random diffusion of ligands is given by the following (3,4):

$$\frac{\delta c}{\overline{c}}\approx \frac{1}{\sqrt{\pi D_3\overline{c}\tau a}},$$ (1)

where D₃ is the ligand diffusion coefficient in 3D, $\tau$ is the measurement integration time, and a is the radius of the receptor.

It was also shown that increasing the number of receptors, m, which are used for sensing ligands, improves the accuracy. This improvement in accuracy is proportional to $1/\sqrt{m}$ at low m, but reaches saturation for high values of m. This saturation of the accuracy occurs because at some level no additional information is provided by adding more receptors, given a finite cell size (or finite size of receptor cluster).

Later works extended the analysis to include more detailed or cooperative ligand-receptor interactions (7–12), lateral diffusion of receptors on the membrane (5), endocytosis of bound receptor-ligand pairs (6), and combined 3D and one dimensional (1D) diffusion for the case of transcription factors binding to DNA (13). The analysis was applied to several biological sensing processes including bacterial chemotaxis, intracellular signaling in Escherichia coli (E. coli), regulation by transcription factors, dynamics of flagellar motors, and neurotransmission in neural synapses (4,5).

In this study, we consider the effect of noise in an important class of signaling systems, termed juxtacrine signaling systems, in which the receptors on the membrane of one cell interact with ligands diffusing along the membrane of a neighboring cell (Fig. 1). Examples for such systems include the Notch signaling pathway, ephrins, semaphorins, and T-cell receptor-antigen interactions (14–17). The main difference between these systems and the systems considered previously is that both receptors and ligands diffuse in two dimensions (2D).

Figure 1.

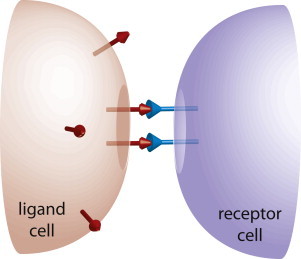
Schematic representation of a juxtacrine signaling system. We consider a geometry in which receptors on one cell (blue symbols in right cell) interact with ligands diffusing on the membrane of a neighboring cell (red symbols in the left cell). Ligands are assumed to diffuse freely on the membrane of the ligand cell and interact with receptors located at the contact area between the cells.

We show that the accuracy of sensing in 2D exhibits a very weak, logarithmic, dependence on the relevant length scales of the system. As a result of this weak dependence, the accuracy of ligand sensing is not significantly improved by having more than three to five receptors on the contact area between cells. Furthermore, increasing the contact area itself does not improve the accuracy either. We show that relatively long integration times, from around one second to several hours are required to reach accuracy of better than 10% (compared to milliseconds in typical 3D signaling systems). We discuss the implications of these results for biological processes relying on juxtacrine signaling systems, such as lateral inhibition and boundary formation mediated by the Notch signaling pathway and axon guidance mediated by cues from the ephrin signaling pathway.

Methods

Calculation of ligand concentration fluctuations in the 2D case

In our analysis, we consider one cell that expresses receptors (receptor cell) that comes in contact with a cell that expresses membrane-bound ligands (ligand cell, Fig. 1). We assume that the contact area is small compared with the total surface area of the cell membrane. We assume that the concentration of receptors is much smaller than that of the ligands, so that the receptors can be considered in terms of a discrete variable whereas the ligands are considered as continuous concentration. In the opposite case, where there are few ligands and many receptors, the ligands can be treated as a discrete variable and the receptors as a continuous concentration. The calculation of fluctuations in both cases is equivalent with the exception that the variables for receptors and ligands are exchanged. The special case where the concentrations of receptors and ligands are similar is not considered here.

We define the ligand concentration on the membrane of the ligand cell by c(x,t). We also assume that ligands are continuously recycled in and out of the membrane uniformly (e.g., through endocytosis and exocytosis (18,19)) with rates $k_{endo}$ and $k_{exo}$, respectively. The pursuing ligand dynamics is dictated by the following diffusion equation:

$$\frac{\partial c\left(\mathit{x},t\right)}{\partial t}+\nabla \cdot j=-k_{endo}c\left(\mathit{x},t\right)+k_{exo}{c}_{cyto},$$ (2)

where j is the ligands diffusion current on the cell membrane and to first order can be written as $j=-D_2\nabla c$, with D₂ being the 2D diffusion coefficient for the ligands on the cell membrane. $c_{cyto}$ is the concentration of a cytoplasmic pool of the ligands that is assumed to be constant in this study. Given our assumption that the cell area is much larger than the contact area, we impose boundary conditions such that the concentration far from the contact is equal to the average concentration, namely, $c\left(\infty ,t\right)=\overline{c}=k_{exo}{c}_{cyto}/k_{endo}$.

Following standard procedure in statistical mechanics (20), we add noise to the system by assuming a random perturbation in the chemical potential (see Supporting Material for detailed derivation). We allow a small perturbation, $\delta c^{\ast }\left(\mathit{x},t\right)$, around the mean ligand concentration, $\overline{c}$ such that $c=\overline{c}+\delta c^{\ast }$ and calculate the power spectrum of $\delta c^{\ast }$ defined by the following:

$$S\left(\omega ,\mathit{k}\right)\equiv \langle \delta c^{\ast }\left(\omega ,\mathit{k}\right)\delta c^{\ast }\left(-\omega ,-\mathit{k}\right)\rangle .$$ (3)

Here, 〈…〉 represents an ensemble average and $\delta c^{\ast }\left(\omega ,\mathit{k}\right)$ is a Fourier transform of $\delta c^{\ast }\left(\mathit{x},t\right)$ over all temporal and spatial frequencies ω and k:

$$\delta c^{\ast }\left(\omega ,\mathit{k}\right)=\int dt\int d^{2}x{e}^{i\left(-\mathit{k}\cdot \mathit{x}+\omega t\right)}\delta c^{\ast }\left(\mathit{x},t\right).$$ (4)

Performing the calculation for the 2D case, the expression for the power spectrum is given by the following:

$$S\left(\omega ,\mathit{k}\right)=\frac{2\overline{c}\left(D_2{k}^2+k_{endo}\right)}{{\omega }^2+{\left(D_2{k}^2+k_{endo}\right)}^2}.$$ (5)

Calculation of accuracy of measurement by a single receptor

Next, we consider a single receptor that can measure ligand concentration in a radius roughly equivalent to its size, a, over an integration time, $\tau$. We take the limit where the ligands that arrive at the receptors bind and are immediately released. This limit corresponds to the perfect monitoring disk approximation where the receptor simply counts the number of ligands diffusing through an area a (3,21). The effect of finite binding and unbinding has been previously taken into account (for the 3D case) and only reduces the accuracy of measurement (3,4). The average ligand concentration measured by a receptor will be given by the following:

$$\tilde{c}\left(t,\mathit{x}\right)=\int d^2{x}^{\text{′}}d{t}^{\text{′}}{w}_r\left(\mathit{x}-{\mathit{x}}^{\text{′}}\right)k_r\left(t-t^{\text{′}}\right)c\left(t^{\text{′}},{\mathit{x}}^{\text{′}}\right),$$ (6)

where the function $w_r\left(\mathit{x}-{\mathit{x}}^{\text{′}}\right)$ defines the receptor spatial distribution and $k_r\left(t-t^{\text{′}}\right)$ defines the receptor temporal response. We choose Gaussian distribution profiles for $w_r\left(\mathit{x}-{\mathit{x}}^{\text{′}}\right)$ and $k_r\left(t-t^{\text{′}}\right)$ with standard deviations of a and $\tau$, respectively. We then calculate the fluctuations measured by the receptor using (see Supporting Material) the following:

$$\langle \delta \tilde{c}\left(t,\mathit{x}\right)\delta \tilde{c}\left(t,\mathit{x}\right)\rangle =\int \frac{d\omega d^{2}k}{{\left(2\pi \right)}^3}S\left(\omega ,\mathit{k}\right)e^{-{\tau }^2{\omega }^2}{e}^{-a^2{k}^2}$$ (7)

The accuracy of measurement of ligand concentration by a single receptor can now be defined as $\delta c/\overline{c}\equiv \sqrt{\langle \delta {\tilde{c}}^2\rangle }/\overline{c}$.

Performing the integration in Eq. 7 we obtain an expression for the accuracy (see Supporting Material) that can be approximated by the following:

$$\frac{\delta c}{\overline{c}}\approx \frac{1}{\sqrt{\pi D_2\overline{c}\tau }}\sqrt{\ln \left(\frac{\lambda }{a}\right)},$$ (8)

where, $\lambda$, is the diffusion length scale of the ligand on the cell membrane. If the integration time is longer than the typical endocytosis time, namely when $\tau \gg k_{endo}^{-1}$, then the diffusion length scale is defined by $\lambda \equiv \sqrt{D_2/k_{endo}}$. In the opposite limit, if the integration time is shorter than the typical endocytosis time, namely when $\tau \ll k_{endo}^{-1}$, then the diffusion length scale is defined by ${\lambda }^{\ast }\equiv \sqrt{D_2\tau }$. Equation 8 is valid for $\lambda ,{\lambda }^{\ast }\gg a$, which is typically the case because both $\lambda \text{and}{\lambda }^{\ast }$ are expected to be of the order of few microns (based on typical diffusion constants, exchange rates, and integration times—see Table 1 (22–30)) and a is ∼ 1 to 10 nm for typical receptors.

Table 1.

Summary of typical biological parameters and estimated integration times to reach accuracy of 10% in measuring ligand concentration

Parameter	Value	Reference
D2	0.01 to 0.1 μm2/s	(22,23)
kendo	0.001 to 0.01 1/s	(24–27)
C	1 to 100 μm−2	(22,28–30)
S	0.1 to 5 μm	Small range corresponds to filopodia, large range corresponds to epithelial contacts.
${\tau }_{min}\left(toreach\frac{\delta c}{c}=0.1\right)$	0.91 s∗	Calculated based on Eq. 12
${\tau }_{max}\left(toreach\frac{\delta c}{c}=0.1\right)$	3.22 h∗∗	Calculated based on Eq. 13
${\tau }_{3D,typical}\left(toreach\frac{\delta c}{c}=0.1\right)$	0.03 s ∗∗∗	Calculated based on (4)

All quantities were calculated using the limit of large number of receptors.

^∗τ_min ∼ 0.91 s is calculated by numerically solving the equation, ${\left(\delta c/\overline{c}\right)}^2=1/\pi m{D}_2\tau \overline{c}\left[\ln \left({\lambda }^{\ast }/a\right)+{\sum }_{i=1}^{m-1}{K}_0\left(\left(2s/{\lambda }^{\ast }\right)\sin \left(\pi i/m\right)\right)\right]$, and assuming the following parameters: k_endo = 10⁻² 1/s, D₂=10⁻¹ μm ²/s, $\overline{c}$ = 100 1/μm ², $\delta c/\overline{c}=0.1$, s = 5 μm, and m = 20.

^∗∗${\text{τ}}_{\text{max}}$ ∼ 3.22 h is calculated by solving Eq. 13 with $\lambda =\sqrt{D_2/k_{endo}}$, and assuming the following parameters: k_endo = 10⁻³ 1/s, D₂ = 10⁻² μm ²/s, $\overline{c}$ = 1 1/μm ², $\delta c/\overline{c}=0.1$, s = 0.1 μm, and m = 20. We note that in this limit solving the exact formula (Eq. 12) gives the same result.

^∗∗∗${\text{τ}}_{3\text{D},\text{typical}}$ ∼ 0.03 s is calculated using ${\tau }_{3D}\approx 1/{2\pi D_3\overline{c}a\left(\delta c/\overline{c}\right)}^2$ (4) by assuming the following parameters: D₃ = 10 μm ²/s, $\overline{c}=100nM$, a = 1 μm.

Calculation of accuracy of measurement by multiple receptors

Now we consider m receptors located on the contact surface between the cells (Fig. 1). Ligands are assumed to diffuse freely in 2D and are measured by the receptors at the contact area. We neglect for simplicity receptor diffusion, the effect of receptor internalization upon ligand binding, and cooperative effects in receptor-ligand binding (5–7,9).

To take into account the presence of m multiple receptors with radius a, we assume similarly to the case of one receptor that

$$\delta \tilde{c}\left(t,\mathit{x}\right)={\sum }_{\mu =1}^m\int d^2{x}^{\text{′}}d{t}^{\text{′}}{w}_r\left({\mathit{x}}_{\mu }-{\mathit{x}}^{\text{′}}\right)k_r\left(t-t^{\text{′}}\right)\delta c^{\ast }\left(t^{\text{′}},{\mathit{x}}^{\text{′}}\right),$$ (9)

where ${\mathit{x}}_{\mu }$ is the position of the $\mu$-receptor. Eq. 7 then becomes the following:

$$\langle \delta \tilde{c}\left(t,\mathit{x}\right)\delta \tilde{c}\left(t,\mathit{x}\right)\rangle ={\sum }_{\mu ,\nu }\int d\omega \frac{d^{2}k}{{\left(2\pi \right)}^3}{e}^{-{\tau }^2{\omega }^2}{e}^{-a^2{k}^2}\left(\frac{1}{m}\right)e^{i\mathit{k}\cdot {\mathit{x}}_{\mu }}\left(\frac{1}{m}\right)e^{-i\mathit{k}\cdot x_{\nu }}\frac{2\overline{c}\left(D_2{k}^2+k_{endo}\right)}{{\omega }^2+{\left(D_2{k}^2+k_{endo}\right)}^2}.$$ (10)

Equation 10 can be estimated by taking the limit $\omega \approx 0$ (see Supporting Material):

$$\langle \delta \tilde{c}\left(t,\mathit{x}\right)\delta \tilde{c}\left(t,\mathit{x}\right)\rangle \approx {\sum }_{\mu \ne \nu }\left(\frac{1}{m^2}\right)\frac{\overline{c}}{\tau D_2\pi }{K}_0\left(\frac{\left|{\mathit{x}}_{\mu }-{\mathit{x}}_{\nu }\right|}{\lambda }\right)+\frac{\overline{c}}{\pi D_2\tau m}\ln \left(\frac{\lambda }{a}\right),$$ (11)

where $K_0$ is the modified Bessel function (31).

We now assume that the m receptors are distributed uniformly along the circumference of a contact area with radius s (Here, we take the same assumption as (4) regarding the geometry involved). This assumption allows us to simplify Eq. 11. In this case we obtain the following:

$${\left(\frac{\delta c}{\overline{c}}\right)}^2\approx \frac{1}{\pi D_2\overline{c}\tau m}\left[\ln \left(\frac{\lambda }{a}\right)+{\sum }_{i=1}^{m-1}{K}_0\left(\frac{2s}{\lambda }\sin \left(\frac{\pi i}{m}\right)\right)\right]$$ (12)

In the limiting case where $\lambda \gg s$ we can use the asymptotic expansion for the modified Bessel function K₀ (31) to obtain the accuracy of ligand measurement by multiple receptors:

$$\frac{\delta c}{\overline{c}}\approx \frac{1}{\sqrt{\pi D_2\overline{c}\tau }}\sqrt{\frac{\ln \left(\frac{\lambda }{ma}\right)}{m}+\left(\frac{m-1}{m}\right)\ln \left(1.1228\frac{\lambda }{s}\right)}.$$ (13)

Similar to the case of one receptor, $\lambda$ is replaced by ${\lambda }^{\ast }$ when $\tau \ll k_{endo}^{-1}$ (see Supporting Material).

In the Supporting Material we also provide the derivation of the results (Eqs. 8 and 13) using an alternative method based on the fluctuation dissipation theorem (4). As expected, the binding-unbinding kinetics introduce an additional term to the accuracy similar to the one described in the 3D case (4).

Calculation of accuracy in the limit of a perfect absorber

In the calculation above we have taken the assumption of a perfect monitoring disk where ligands are immediately released upon binding to the receptors. It is useful to consider the opposite limit of a perfect absorber where the ligands are immediately removed from the contact area, for example by cleavage and internalization of the receptor-ligand pair. We have calculated the accuracy of sensing for this case based on a simple argument initially discussed in (3). In this calculation we directly integrate Eq. 2 with an additional boundary condition $c\left(a,t>0\right)=0$, to obtain the total current impinging on a disk with radius a. Assuming a Poisson distribution, the accuracy of sensing would simply be proportional to $1/\sqrt{N}$, where N is the total number of ligands arriving at the receptor during the integration time. The accuracy obtained for this case is given by the following (see Supporting Material):

$$\frac{\delta c}{\overline{c}}\approx \frac{1}{\sqrt{2\pi D_2\overline{c}\tau }}\sqrt{\ln \left(\frac{\lambda }{a}\right)}$$ (14)

Hence, for the case of a perfect absorber, the accuracy improves by a factor of $\sqrt{2}$, compared with the case of a perfect monitoring disk (Eq. 8).

Results

Accuracy of ligand measurement for the one receptor case

Using statistical mechanics formalism, we have first calculated the measurement accuracy of the 2D ligand concentration by a single receptor on the membrane of the receptor cell (Fig. 1). We show in the methods that the expression we get for the accuracy of measurement in this case is given by the following:

$$\frac{\delta c}{\overline{c}}\approx \frac{1}{\sqrt{\pi D_2\overline{c}\tau }}\sqrt{\ln \left(\frac{\lambda }{a}\right)}$$ (15)

For short integration times $\left(\tau \ll k_{endo}^{-1}\right)$, the diffusion length scale in Eq. 15, $\lambda =\sqrt{D_2/k_{endo}}$ is replaced by ${\lambda }^{\ast }=\sqrt{D_2\tau }$. This result differs from the 3D accuracy (Eq. 1) in several important ways. First, the accuracy improves (i.e., $\delta c/\overline{c}$ decreases) in a logarithmic manner as the receptor radius grows. Such logarithmic dependence appears in other quantities related to diffusion in 2D (32). Furthermore, the accuracy now depends on the diffusion length scale in the system, $\lambda$ (or ${\lambda }^{\ast }$ ), which is the typical length scale from which ligands can diffuse into the contact area before they endocytose (or during the measurement integration time). This logarithmic dependence means that the accuracy now depends very weakly on the relevant length scales of the system (apart from the standard dependence on the length scale associated with the integration time $\sqrt{D_2\tau }$).

Accuracy improves very little with increasing number of receptors

One possible strategy to improve the accuracy is to add more receptors at the contact area between cells. The number of receptors that come in contact with the ligands in a neighboring cell depends on the concentration of receptors on the cell membrane and on the contact area between cells. We therefore calculated how the accuracy changes both with the total number of receptors, m, in the contact area and with the radius of the contact area, s.

The accuracy of ligand concentration measurement for the case of m receptors, located on the contact surface between the cells (Fig. 1) are given by Eq. 12 (exact solution valid for any $\lambda \gg a$ ) and Eq. 13 (approximated solution for $\lambda >s$ ). Fig. 2 A and B show the dependence of the accuracy, $\delta c/\overline{c}$, on the number of receptors, different contact diameters between cells, and different integration times. For relatively short integration time ( $\tau$ = 30 s, Fig. 2 A) we use Eq. 12 with ${\lambda }^{\ast }$ instead of $\lambda$, and for relatively long integration times ( $\tau$ = 600 s, Fig. 2 B) we use Eq. 13. For the case of one receptor (m = 1) we consistently recover the expression given by Eq. 15. As expected, increasing the number of receptors, m, improves the accuracy (see Fig. 2 A and B) but, surprisingly, this improvement saturates when the number of receptors is greater than three to five receptors. The accuracy at saturation is simply the accuracy one would get if the whole contact area was considered to be one large receptor. Namely, for large m, Eq. 13 takes a similar form to the one receptor result (Eq. 15) but with the receptor radius, a, replaced by the radius of the contact area, s. Simple analysis of Eq. 13 shows that the saturation value, $m_{sat}$, depends on the ratio between two logarithms, $m_{sat}\cong 1+\left(\ln \left(\lambda /a\right)/\ln \left(\lambda /s\right)\right)$, and hence depends very weakly on all the relevant length scales in Eq. 13 (i.e., diffusion length scale, size of the receptor, and size of the contact area). The effect of adding more receptors is therefore much weaker in this 2D geometry compared with the 3D geometry, where this saturation is reached when $m_{sat}\cong 2s/a$ that can range from several hundreds to several thousands receptors (4). Longer integration times naturally improve the accuracy, but the weak dependence on the number of receptors, remains (Fig. 2 B). Hence, unlike the 3D case, the accuracy cannot be significantly improved by adding more receptors.

Figure 2.

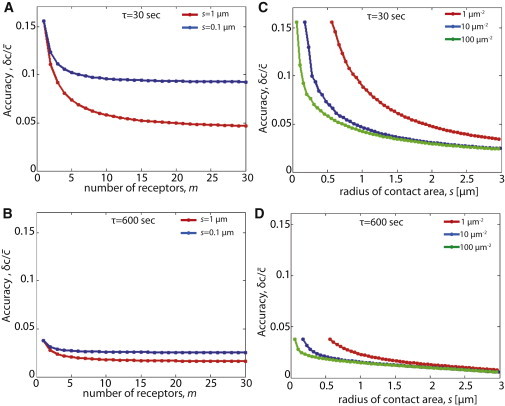
Dependence of measurement accuracy on number of receptors, contact area, and integration time. (A–B) Dependence of measurement accuracy of ligand concentration, $\delta c/\overline{c}$, on the number of receptors at the contact area, m, for relatively short integration time (A, $\tau$ = 30 s) and for relatively long integration time (B, $\tau$ = 600 s). The accuracy in all cases saturates at around three to five receptors. The accuracy is calculated using the exact solution, Eq. 12, for A, and the approximate solution, Eq. 13, for B (because the condition for approximation, $s<\lambda$, can only be applied in B). The following parameters are used: D₂ = 0.03 μm²/s, $\overline{c}$ = 100 molecules/μm², K_endo = 3^∗10⁻³ 1/s, a = 1 nm, and the radius of the contact area, s, as indicated in the figure legend. Because in A $\tau <k_{endo}$, we use ${\lambda }^{\ast }=\sqrt{D_2\tau }$ instead of $\lambda =\sqrt{D_2/k_{endo}}$ for this case. (C–D) Dependence of measurement accuracy of ligand concentration, $\delta c/\overline{c}$, on the radius of the contact area, s, for relatively short integration time (C, $\tau$ = 30 s) and for relatively long integration time (D, $\tau$ = 600 s). The plot shows that the accuracy does not significantly improve when s > 0.5 to 1.5 μm. As in A–B, the accuracy is calculated using the exact solution, Eq. 12, for A, and the approximate solution, Eq. 13, for B. The number of receptors for each value of s was calculated using $m=\pi s^2{\sigma }_R$, where ${\sigma }_R$ is the receptor density. In the exact calculation m was rounded to the nearest integer number. D₂ = 0.03 μm²/s, $\overline{c}$ = 100 molecules/μm², K_endo = 3^∗10⁻³ 1/s, a = 1 nm, ${\sigma }_R$ as indicated in the figure legend. Comparison of the exact and approximate solutions is provided in Fig. S1.

Accuracy improves very little with increasing contact area

It is interesting to ask whether the accuracy is affected by the contact area between cells. For a fixed concentration of receptors, increasing the contact area increases both m and s. Fig. 2 C and D show the dependence of the accuracy on contact radius for different receptor concentrations and different integration times. For typical values of ligand concentrations, the accuracy saturates when the contact radius is above a few microns, corresponding to the radius in which the number of receptors in the contact area reaches the saturation value, $m_{sat}$. Longer integration times (Fig. 2 D) improve the accuracy (compared with shorter integration time, Fig. 2 C) but show saturation at similar contact areas. As in the previous section, we use Eq. 12 with ${\lambda }^{\ast }$ instead of $\lambda$ for short integration times ( $\tau$ = 30 s, Fig. 2C), and Eq. 13 for relatively long integration times ( $\tau$ = 600 s, Fig. 2 B). We note that, the approximated solution in Eq. 13 works nicely for longer integration times but breaks down (as expected) in the limit of large contact radii and short integration time (Fig. S1). This result suggests that there is almost no advantage in terms of accuracy of measurement in having large contact area between cells.

Another way to understand this weak dependence of the accuracy on the number of receptors and the contact area is by realizing that diffusion in 2D is known to exhibit long-range density fluctuations (logarithmic dependence) (33). These long-range correlations limit the ability of the receptor cell to accurately determine the average ligand concentration even when the whole contact area can be treated as one effective receptor with large contact area.

Integration times of up to several hours are required to reach high accuracy

How long would it typically take for a receptor cell to accurately determine ligand concentration in a neighboring cell? Using Eqs. 12 and 13 (applied in different parameter regimes) we can estimate the typical time it would take to reach an accuracy of 10% $\left(\delta c/\overline{c}=0.1\right)$. For typical values of parameters, we find that cells may need to integrate between around 1 second to 3 hours (see Table 1). These are considerably longer times than the time it would take an eukaryotic cell to accurately measure the concentration of a ligand diffusing in 3D, which is typically in the millisecond range (see Table 1 and (5)). It is interesting to note, that developmental processes, in which juxtacrine signaling systems are being used, may occur over periods of time that are shorter than the typical integration times calculated above. It is therefore not clear how signaling can be accurately determined in these systems.

Averaging over several neighboring cells modestly improve accuracy

Cells in higher organisms typically come in contact with several neighboring cells, raising the question of how the accuracy of sensing changes when a receptor cell is in contact with multiple ligand cells. Assuming that the receptor cell integrates over the signal from all its neighbors and that fluctuations are uncorrelated between cells, it is easy to show that the accuracy improves modestly by a factor of $1/\sqrt{N}$, where N is the number of neighbors (see Supporting Material). For cells in an epithelial cell layer, which have six neighbors in average this would correspond to improving the accuracy by a factor of ∼ 2.5.

Processing of receptor-ligand pair improves accuracy by a factor of up to $\sqrt{2}$

Some juxtacrine signaling systems undergo processing upon receptor-ligand binding; for example, the Notch receptor is cleaved once bound to its ligand and its extracellular domain trans-endocytose into the ligand expressing cell (34). Such processing prevents the unbinding of the ligand and the possibility of measuring the same ligand more than once (6). In the limit of very fast processing, namely, that processing rate is much faster than the unbinding rate, one can consider the receptor as a perfect absorber that counts and removes all the ligands impinging on it (3,21) (we assume each processed receptor is immediately replaced by a new one). The accuracy of measurement by a perfect absorber in the 3D case was previously shown to be better than the accuracy of a perfect monitoring sphere by a numerical factor (21). We perform a similar calculation for the accuracy of a perfect absorber for the 2D case, taking into account endocytosis and exocytosis. We show that the accuracy improves by a factor of $\sqrt{2}$ compared with the result in Eq. 8 (see Methods and Supporting Material). Note that, receptor-ligand processing may also reduce the accuracy if it takes time for the processed receptor to be replaced by a new one.

Discussion

From the point of view of the receptor cell, there are two general strategies to improve accuracy of detection. One strategy is to integrate the signal over longer times. Although this strategy certainly improves accuracy it comes with a price: a longer integration time means a slower response time of the system. We show that for typical values of parameters, integration times ranging from around one second to 3 h are required to reach accuracy better than 10%. Many biological systems may be required to operate on faster time scales.

The second strategy is to improve detection by adding more receptors. This strategy seems to work well in 3D signaling systems, where the accuracy can be improved significantly by increasing the number of receptors. In this case, the improvement in accuracy reaches saturation when $m_{sat}\cong 2s/a$. For chemotactic receptors in E. coli, this threshold value may reach many hundreds of receptors (3,4). In contrast, the behavior of the accuracy in the 2D juxtacrine signaling system is dramatically different. Although adding additional receptors initially improves accuracy, it reaches saturation when $m_{sat}\cong 1+\left(\ln \left(\lambda /a\right)/\ln \left(\lambda /s\right)\right)\cong 3-5$, for typical values of parameters (Fig. 2 A and B). Similarly, increasing the contact area between cells (Fig. 2 C and D) or averaging over signal from multiple neighbors does not significantly improve the accuracy. This result has striking implications on the ability of cells to sense signaling from their neighbors in an accurate manner.

Reduced accuracy imposes a constraint on speed of axon growth

What are the implications of these results on specific biological processes that rely on juxtacrine signaling? One such process is axon guidance, in which neurons send out axons to their correct targets during neural development (35). This process is mediated by juxtacrine signaling systems such as the ephrin signaling pathway (but also other signaling systems may be involved). Ephrins from the target cells interact with Eph receptors on the growth cone of the axon. The axons in this process often respond to gradients of ephrins expressed in the target tissue and stop growing when they reach specific ligand concentration (36) (see Fig. 3 A). Our results suggest that there may be a constraint on the growth rate of the axons because the growing neurons may require long integration times to accurately determine the ephrin concentration in the target tissue. Assuming growing axons need to distinguish between ephrin concentrations that are ∼ 10% different (37), presented on cells 10 μm in diameter, we estimate that the maximal growth rate of the axons for typical parameters (assuming 1 min integration time) should not exceed 10 μm/min. Interestingly, some axons have been shown to reach growth rates as fast as 5 μm/min (38,39), suggesting that growth rate may indeed be limited by the ability to accurately measure ephrin concentration during axon guidance.

Figure 3.

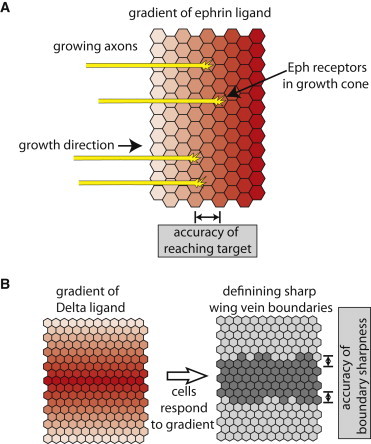
Implications of accuracy constraints on ephrin mediated axon guidance and Notch mediated patterning. (A) An illustration of axon guidance mediated by ephrin signaling. During axon development, axons (yellow) that express Eph receptors in their growth cones, grow into the target tissue that express a gradient of ephrin ligands (red). Eph signaling is used for the determination of target positions for the axons. The limit on accuracy of measurement in juxtacrine signaling imposes a constraint on the growth rate of axons. For example, assuming that 1 min integration time is required for reaching an accuracy enough to distinguish between ephrin concentration in neighboring cells (say 10% difference between cells that are 10 μm apart), imposes a limit on the growth rate of axons to 10 μm/min. (B) A simplified illustration of Notch mediated wing vein development in Drosophila. During wing vein formation, a gradient of Delta expression in the future vein region (red) is used for defining the boundary between vein (dark gray) and intervein (light gray) regions. Here, the limit on accuracy of measurement in juxtacrine signaling may impose a constraint on the developmental time required for achieving sharp boundaries (see text).

Implications of result to Notch mediated patterning

Another example for processes that may be affected by our results are Notch mediated patterning processes. The Notch signaling pathway is involved in different developmental processes in which neighboring cells adopt different fates. For example, during wing development in Drosophila melanogaster, the Notch pathway is used in defining sharp vein boundaries (40,41). In this system, a gradient of Delta expression is converted into a sharp Notch signaling response that translates to a sharp boundary defined by an almost perfect 1D line of cells (Fig. 3 B). It has been shown that such a mechanism may be very sensitive to noise in Notch signaling (42). Although this process certainly involves more complex regulatory processes, it is useful to ask, in the context of a simple Notch readout model, what would be the typical integration time required to achieve such accurate patterning. Given that the concentration of Delta may vary by an estimated 10% to 20% over one cell diameter (estimated from (40)), we can estimate that achieving such spatial accuracy would require up to 10 min. Although the process of wing vein formation takes several hours, it is not clear at what stage during wing development are cell fates determined. It has been shown that target genes downstream of Notch signaling may exhibit transient response lasting only a few minutes (43), which may suggest that this process may also be limited by the time it takes to accurately determine Delta concentration along the gradient.

Notch is also involved in patterning processes in which small initial differences between cells are amplified to generate alternating salt-and-pepper differentiation patterns in a process termed lateral inhibition (44,45). It is possible that our finding that such signaling systems are inherently noisy may be useful in this context. Such noise may help generate large initial differences between cells that can help generating patterned states more quickly (42).

The conclusions discussed above rely on several simplifying assumptions including assuming that the receptors do not diffuse, that the concentrations of receptors and ligands are unmatched, and that the biochemical details of the signaling pathway such as clustering of receptors are neglected. The contribution of some of these effects has been addressed elsewhere for the 3D case and is beyond the scope of this study (5–7,9). Given that the source of noise for juxtacrine signaling is the long-range density fluctuations in 2D diffusion, we expect that the exact details of the biochemistry would not dramatically improve the accuracy of sensing. Similarly, we do not expect that the accuracy would be significantly improved for the special case where receptor and ligand concentrations are similar. Nevertheless, it would be interesting to explore the effect of receptor-ligand binding-unbinding on the accuracy in juxtacrine signaling as has been done in 3D systems (7–12).

Regarding the role of receptor diffusion, one way to look at this problem is to say that receptor diffusion effectively increases the diameter of the area probed by the receptor (a in Eq. 15). Because this diameter goes into the logarithmic term, we do not expect receptor diffusion to affect the uncertainty much. Nevertheless, it would be interesting to explore these effects in detail in the future. Finally, it will be interesting to consider the implications of our results on other developmental processes such as planar cell polarity and the immune system relying on different signaling pathways than the ones discussed in this study.

Supporting Citations

References (46–54) appear in the Supporting Material.