Deactivation of a Negative Regulator: A Distinct Signal Transduction Mechanism, Pronounced in Akt Signaling

Abstract

Kinase cascades, in which enzymes are sequentially activated by phosphorylation, are quintessential signaling pathways. Signal transduction is not always achieved by direct activation, however. Often, kinases activate pathways by deactivation of a negative regulator; this indirect mechanism, pervasive in Akt signaling, has yet to be systematically explored. Here, we show that the indirect mechanism has properties that are distinct from direct activation. With comparable parameters, the indirect mechanism yields a broader range of sensitivity to the input, beyond saturation of regulator phosphorylation, and kinetics that become progressively slower, not faster, with increasing input strength. These properties can be integrated in network motifs to produce desired responses, as in the case of feedforward loops.

Phosphorylation of proteins and lipids, catalyzed by specific kinase enzymes, is ubiquitous in intracellular signal transduction. A classic example in eukaryotes is the canonical structure of the mitogen-activated protein kinase cascades, in which three kinases are sequentially activated by phosphorylation (1). Another example is the PI3K (phosphoinositide 3-kinase)/Akt pathway, which (like the mammalian mitogen-activated protein kinases) is prominently dysregulated in human cancers (2). Type-I PI3Ks phosphorylate a lipid substrate to produce the lipid second messenger, PIP₃, which recruits the protein kinase Akt and mediates its activation by phosphorylation (3,4). In no small part because of these important pathways, we typically think of phosphorylation as a direct means of activating molecular interactions and reactions in signal transduction. This is not the only way to increase the flux through a signaling pathway, however. Consider signaling downstream of Akt, which phosphorylates a host of protein substrates to affect diverse functions. A survey of the Akt signaling hub shows that many of these reactions result in a decrease, rather than an increase, in activity/function of the substrates (3). And, among those substrates, the four listed in Table 1 are considered negative, not positive, regulators of downstream signaling (see Fig. S1 in the Supporting Material). Whereas negative regulators are appreciated for their roles in feedback adaptation of signaling, the implications of deactivating a negative regulator as an indirect mechanism of pathway activation has yet to be explored.

Table 1.

Survey of Akt substrates and downstream signaling

Substrate (site)	Effect on substrate	Outcome
TSC2 (T1462)	GAP activity ↓	Rheb, mTOR ↑
PRAS40 (T246)	mTOR binding ↓	mTOR ↑
GSK3α/β (S21/S9)	kinase activity ↓	β-catenin ↑
BAD (S136)	Bcl-2/xL binding ↓	Bcl-2/xL ↑

Here, we use simple kinetic models to elucidate the basic properties of pathway activation by deactivation of a negative regulator (hereafter referred to as mechanism II), as compared with the standard activation of a positive regulator (mechanism I). The analysis is presented in the context of protein phosphorylation, but the conclusions may be generalized to other reversible modifications or to allosteric binding interactions. The common first step is phosphorylation of the regulatory molecule by the kinase. The activity of the upstream kinase such as Akt may be represented by a dimensionless, time (t)-dependent input signal function, s(t). We assume that the total amount of regulator is constant and define its phosphorylated fraction as ϕ(t). Neglecting concentration gradients and saturation of the upstream kinase and of the opposing (constitutively active) phosphatase(s), the conservation of phosphorylated regulator is expressed as follows (see Text S1 in the Supporting Material):

$$\frac{d\varphi }{dt}=k_p\left[s\left(1-\varphi \right)-\varphi \right];\varphi \left(0\right)=0.$$ (1)

The parameter k_p is the pseudo-first-order rate constant of protein dephosphorylation. In the case of s = constant (i.e., subject to a step change at t = 0), the properties of this simplified kinetic equation are well known (5) and may be summarized as follows. As the magnitude of the signal strength s increases, the steady-state value of ϕ, ϕ_ss, increases in a saturable fashion; when s >> 1, ϕ_ss approaches its maximum value of 1 and is insensitive to further increases in s. The kinetics of ϕ(t) approaching ϕ_ss become progressively faster as s increases, however.

Next, we model the influence of the regulator on a downstream response. Defining the fractional response as ρ and following analogous assumptions as above, we formulate equations for mechanisms I and II as follows:

$$\frac{d\rho }{dt}=\{\begin{array}{c}\left[k_{a,0}+\left(k_{a,\max }-k_{a,0}\right)\varphi \right]\left(1-\rho \right)-k_{d,0}\rho \left(\text{I}\right)\\ k_{a,0}\left(1-\rho \right)-\left[k_{d,0}-\left(k_{d,0}-k_{d,\min }\right)\varphi \right]\rho \left(\text{II}\right).\end{array}$$ (2)

In each equation, the first term on the right-hand side describes activation, and the second, deactivation. In mechanism I, the effective rate constant of activation increases linearly with ϕ, from a minimum value of k_a,0 when ϕ = 0 up to a maximum value of k_a,max when ϕ = 1; the deactivation rate constant is fixed at k_d,0. Conversely, in mechanism II, the effective rate constant of deactivation decreases linearly with ϕ, from a maximum value of k_d,0 when ϕ = 0 down to a minimum value of k_d,min when ϕ = 1; in this mechanism, the activation rate constant is fixed at k_a,0. The initial condition is assigned so that ρ is stationary when ϕ = 0. To further set the two mechanisms on a common basis, we define dimensionless parameters such that the maximum steady-state value of ρ (with ϕ_ss = 1) is the same for both mechanisms I and II,

$$g=k_{a,\max }/k_{a,0}=k_{d,0}/k_{d,\min };K=k_{a,0}/k_{d,0}.$$ (3)

With these definitions, each conservation equation is reduced to the following dimensionless form:

$$\frac{1}{k_{d,0}}\frac{d\rho }{dt}=\{\begin{array}{l}K\left[1+\left(g-1\right)\varphi \right]\left(1-\rho \right)-\rho \left(\text{I}\right)\hfill \\ K\left(1-\rho \right)-\left[1-\left(1-g^{-1}\right)\varphi \right]\rho \left(\text{II}\right).\hfill \end{array}$$ (4)

Mechanisms I and II (Fig. 1 a) are compared first at the level of their steady-state solutions, ρ_ss, for stationary s. Equation 1 yields the familiar hyperbolic dependence of ϕ_ss on s, and ρ_ss(s) has the same shape for both mechanisms. However, whereas ρ_ss of mechanism I shows saturation at a lower value of s than ϕ_ss, the opposite is true of mechanism II (Fig. 1 b). Thus, mechanism II retains sensitivity to the input even while phosphorylation of the upstream regulator shows saturation. This is perhaps more readily seen when ϕ_ss(s) is replaced with a sigmoidal Hill function (i.e., with s replaced by sⁿ in Eq. 1) (Fig. 1 c). The key parameter that affects the relative sensitivities of mechanisms I and II and the disparity between them is the gain constant, g (see Text S1 in the Supporting Material). As this parameter is increased, ρ_ss of mechanism I becomes increasingly saturable with respect to ϕ_ss (Fig. 1 d), whereas ρ_ss of mechanism II gains sensitivity as ϕ_ss approaches 1 (Fig. 1 e). As an illustrative example, consider that when ϕ_ss is increased from 0.90 to 0.95, or from 0.98 to 0.99, the amount of the negative regulator in the active state is reduced by a factor of 2 (see Fig. S2).

Figure 1.

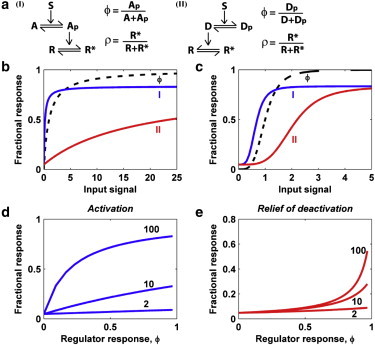
Steady-state properties of mechanisms I and II. (a) Schematics of direct (I) and indirect (II) activation. (b) Steady-state dose responses, ρ_ss(s), of mechanisms I and II along with phosphorylation of the upstream regulator, ϕ_ss(s) (Eq. 1 at steady state); K = 0.05, g = 100. (c) Same as panel b, except with a sigmoidal ϕ_ss(s) (Hill function with n = 4). (d) Steady-state output, ρ_ss, of mechanism I vs. ϕ_ss for K = 0.05 and indicated values of the gain constant, g. (e) Same as panel d, but for mechanism II. To see this figure in color, go online.

The two mechanisms also show distinct temporal responses. In the response of mechanism I to a step increase in s, ρ(t) approaches ρ_ss with a timescale that generally becomes faster as s increases. Unless the kinetics of ϕ(t) are rate-limiting, the timescale is ∼k_d,0^–1(1–ρ_ss) (Fig. 2 a; see also Text S1 and Fig. S3 in the Supporting Material). Conversely, the response of mechanism II generally becomes slower as s increases, inasmuch as the frequency of deactivation decreases whereas that of activation is constant, with a timescale of ∼k_a,0^–1ρ_ss (Fig. 2 b). To approximate a transient input, we model s(t) as a step increase followed by a decay. For mechanism I, the response ρ(t) is such that the variation in the time of the peak, as a function of the step size, is modest. The subsequent decay is prolonged when ϕ(t) hovers close to saturation (Fig. 2 c). Such kinetic schemes have been analyzed in some detail previously (6,7). In contrast, the response of mechanism II to the transient input is such that the system retains sensitivity and consistent decay kinetics beyond the saturation of ϕ(t). The distinctive feature is that ρ(t) peaks noticeably later in time as the magnitude of the peak increases (Fig. 2 d).

Figure 2.

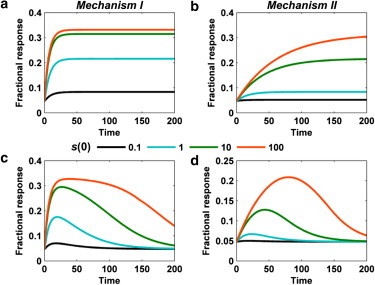
Kinetic properties of mechanisms I and II. (a) Response of mechanism I to a step change in s from zero to the indicated s(0). Time is given in units of k_pt; parameters are K = 0.05, g = 10, and k_d,0 = 0.1k_p. (b) Same as panel a, but for mechanism II. (c) Same as panel a, but for a transient input, s(t) = s(0)exp(–0.03k_pt). d) Same as panel c, but for mechanism II. To see this figure in color, go online.

Having established the basic steady state and kinetic properties of mechanism II as compared with the canonical mechanism I, we considered what outcomes could be achieved by linking these motifs in series or in parallel. Such schemes are identified in the Akt/mTOR signaling network, for example (see Fig. S4). In a standard kinase activation cascade, it is understood that the properties of saturation and sensitivity are compounded with each step of the cascade (8). Thus, two sequential steps of mechanism I yield progressive saturation of the steady-state output at lower s (Fig. 3 a), and the desaturating effect of mechanism II is likewise compounded (Fig. 3 b). By corollary it follows that a sequence of mechanisms I and II will show an intermediate dose response; that is, the mechanism II step offsets the saturation effect of mechanism I.

Figure 3.

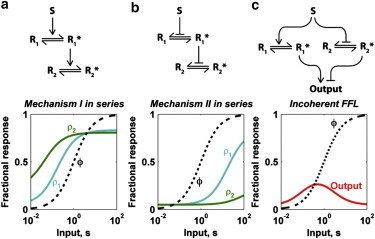
Serial and parallel schemes incorporating mechanism I or/and II. (a) Steady-state outputs of two response elements, ρ₁ and ρ₂, activated by mechanism I in series. At each level, K = 0.05, g = 100. (b) Same as panel a, but for mechanism II in series. (c) Incoherent feedforward loop (FFL) in which mechanisms I and II are activated in parallel to activate and inhibit, respectively, the terminal output. For both mechanisms I and II, K = 0.05, g = 100. The parameters for Eq. 5 are α = 2.5, β = 50. To see this figure in color, go online.

A more complex scheme is to combine the two mechanisms in parallel, as in an incoherent feedforward loop (FFL) connected to an “AND NOT” output as follows:

$$\text{Output}=\alpha {\rho }_I/\left(1+\alpha {\rho }_I+\beta {\rho }_{II}\right).$$ (5)

Given the differential saturation properties of mechanisms I and II, this scheme readily yields the expected biphasic dose response (9) without the need for disparate values of the parameters (Fig. 3 c). Regarding the kinetics, the analysis shown in Fig. 2 makes it clear that mechanism II naturally introduces time delays in cascades or network motifs. Thus, for the incoherent FFL at high, constant s, activation of inhibition by mechanism II would tend to yield a dynamic response marked by a peak followed by adaptation (see Fig. S5). Analogous calculations were carried out for a coherent FFL as well (see Fig. S6).

To summarize our conclusions and their implications for signaling downstream of Akt and other kinases, we have described a distinct, indirect signal transduction mechanism characterized by deactivation of a negative regulator. This motif shows steady-state sensitivity beyond saturation, and therefore the activity of the upstream kinase, such as Akt, can be relatively high. By comparison, the direct activation of signaling by phosphorylation requires that activity of the kinase be regulated, or specifically countered by high phosphatase activity, to maintain sensitivity and avoid saturation of the response. The mechanism described here also introduces relatively slow kinetics (for comparable parameter values). This property, together with its extended range of sensitivity, would allow the motif to be incorporated in signaling networks to yield desired steady and unsteady responses in a robust manner. Considering that key signaling processes mediated by Akt (notably activation of the mammalian target of rapamycin (mTOR) pathway) are achieved by deactivation of negative regulators, we assert that greater recognition of this mechanism and of its distinct properties is warranted.