Free-energy calculations for semi-flexible macromolecules: Applications to DNA knotting and looping

Abstract

We present a method to obtain numerically accurate values of configurational free energies of semiflexible macromolecular systems, based on the technique of thermodynamic integration combined with normal-mode analysis of a reference system subject to harmonic constraints. Compared with previous free-energy calculations that depend on a reference state, our approach introduces two innovations, namely, the use of internal coordinates to constrain the reference states and the ability to freely select these reference states. As a consequence, it is possible to explore systems that undergo substantially larger fluctuations than those considered in previous calculations, including semiflexible biopolymers having arbitrary ratios of contour length L to persistence length P. To validate the method, high accuracy is demonstrated for free energies of prime DNA knots with L/P = 20 and L/P = 40, corresponding to DNA lengths of 3000 and 6000 base pairs, respectively. We then apply the method to study the free-energy landscape for a model of a synaptic nucleoprotein complex containing a pair of looped domains, revealing a bifurcation in the location of optimal synapse (crossover) sites. This transition is relevant to target-site selection by DNA-binding proteins that occupy multiple DNA sites separated by large linear distances along the genome, a problem that arises naturally in gene regulation, DNA recombination, and the action of type-II topoisomerases.

I. INTRODUCTION

Free-energy changes govern the direction of all chemical and biophysical processes in biological systems. A quantitative treatment of free-energy landscapes is central to understanding protein and RNA folding,¹ motion and energy transduction in molecular machines,² macromolecule-ligand interactions,^3,4 genome organization,^5,6 and many other biological phenomena. For macromolecular systems, obtaining accurate estimates of the free energy is one of the most challenging problems in computational biology and chemistry.^7–9 Systems involving intermediate length scales such as semi-flexible DNA-protein structures are abundant in living cells; however, this class of problems has generally eluded standard computational free-energy methods because the inherent flexibility of molecules on these elevated length scales results in large conformational fluctuations in rugged potential energy landscapes.¹⁰

The free energy, F, of a system in the canonical ensemble, i.e., at constant number of particles N, volume V, and temperature T, is defined as

$$F=⟨U⟩-TS=-k_{B}T\ln \left(Q\right),$$ (1)

where ⟨U⟩ is the mean energy, S is the entropy, and Q is the canonical partition function of the system (k_B is Boltzmann's constant). For simplicity, we restrict ourselves to a classical system of N point particles with Cartesian position coordinates r_i, i = 1, …, N in a volume V. Assuming that the kinetic energy of the system is independent of the particle positions, Q reduces to the configuration integral

$$Q=\underset{V}{\int }\frac{d^3{r}_1}{a^3}...\underset{V}{\int }\frac{d^3{r}_N}{a^3}\exp \left[-\beta U\left(\stackrel{\rightharpoonup }{r}\right)\right],$$ (2)

where β = (k_BT)⁻¹ and $U\left(\stackrel{\rightharpoonup }{r}\right)$ is the total potential energy (also referred to as force field) for a full-system configuration $\stackrel{\rightharpoonup }{r}=\left({\mathbf{r}}_1,...,{\mathbf{r}}_N\right)$. The constant a in Eq. (2) is a microscopic length required to make Q dimensionless; e.g., for a system of point particles of mass m undergoing Newtonian dynamics, the length a corresponds to the thermal wavelength, Λ = h/(2πmk_BT)^1/2, where h is Planck's constant. Equilibrium ensembles of full-system configurations distributed according to the Boltzmann distribution $p\left(\stackrel{\rightharpoonup }{r}\right)\propto \exp \left[-\beta U\left(\stackrel{\rightharpoonup }{r}\right)\right]$ can be generated by using molecular dynamics, Markov-chain Monte Carlo, and Langevin dynamics simulations, for example. To enhance sampling, various schemes have been employed such as parallel tempering (replica-exchange sampling), multicanonical (flat histogram) sampling, and umbrella sampling.^11–15

A typical application of computational free-energy methods is to compute the difference in free energy between two macromolecular states A, B, i.e.,

$$\Delta F_{AB}=F_B-F_A=-k_{B}T\ln \left(\frac{Q_B}{Q_A}\right).$$ (3)

If the two states coexist in a simulation, ΔF_AB can be estimated directly by using a counting method, because the ratio of partition functions Q_B/Q_A in Eq. (3) is equal to the probability ratio P_B/P_A of observing states B and A, respectively. Thus, counting the respective numbers of times the system visited states A and B during the simulation, Ω_A, Ω_B, and using Q_B/Q_A = Ω_B/Ω_A in Eq. (3), yields ΔF_AB. In cases where the states A and B do not coexist, alternative sampling methods based on free energy perturbation can be used, such as thermodynamic integration (TI).^7–9 These approaches have been used to compute solvation free energies,^16,17 ligand-receptor binding affinities,^18–20 free energies of protein and RNA folding,^21–24 and in a number of other applications. Thermodynamic integration is used when the two states A, B are significantly different from one another, and amounts to sub-dividing (staging) the transformation from A to B into a path of intermediates along a suitable reaction coordinate. Since ΔF_AB is independent of the path between the terminal states A, B, the intermediates do not have to be physically realistic, which implies that computationally favorable paths may be chosen; however, in the rugged potential energy landscape $U\left(\stackrel{\rightharpoonup }{r}\right)$ typical of macromolecular systems the task of finding the most favorable paths is difficult in general.²⁵

Another class of methods estimates the absolute free energy of a macromolecular system for a given force field $U\left(\stackrel{\rightharpoonup }{r}\right)$. For small systems, limited to harmonic fluctuations about a mechanical-equilibrium ground state, the absolute free energy can be computed by treating fluctuations harmonically about an energy-minimized ground state (the harmonic approximation, or HA), normal mode analysis (NMA),^26–28 or use of the so-called quasi-harmonic approximation (QHA).^29,30 However, for larger systems with multiple occupied energy wells, QHA tends to significantly overestimate the configurational entropy.^30,31 To overcome this limitation, the method has been extended by applying QHA to each local minimum (basin) of the potential-energy landscape separately.^32,33 Since the number of basins to be considered increases exponentially with system size, such minima-mining approaches have been limited to protein subdomains and other small systems.¹⁰ Other methods for estimating absolute free energies of macromolecules are based on expressing the full-system probability distribution $p\left(\stackrel{\rightharpoonup }{r}\right)$ in terms of distributions of molecular fragments, by using an expansion of mutual information terms³⁴ and polymer growth models.^35–37 In the latter approach, new monomers are added one at a time to an ensemble of partially grown configurations while keeping track of appropriate statistical weights. These techniques have been applied to simple model proteins,³⁸ RNA secondary structures,³⁹ all-atom models of peptides and small protein subdomains,^9,40,41 and a number of other systems (see also Ref. 42). A general challenge for polymer growth methods, which becomes more severe for increasing system size, is that configurations important in the full system may have low statistical probability in early stages of growth, so that biasing toward structural information known for the full system is required.⁴³

A widely used strategy to estimate the absolute free energy of a given target system, effectively combining methods for relative and absolute free energies described above, employs a reference system, “ref,” for which the absolute free energy, F_ref, is available.^11,44–47 The free energy of the target system, A, is calculated as

$$F_A=F_{ref}+\Delta F_{ref\to A},$$ (4)

where ΔF_{ref → A} is the free-energy difference between the reference system and the target system, which can be estimated, e.g., by free-energy perturbation or thermodynamic integration. This strategy was introduced for a molecular system using a reference state constrained by external harmonic wells.⁴⁴ Using Eq. (4) for two arbitrary target states, A, B, yields a path-independent method to calculate the free-energy difference ΔF_AB = F_B − F_A in terms of a thermodynamic cycle, without the need of transforming one state to the other.⁴⁵ In Ref. 46, rather than using harmonic constraints, the reference state was constructed by generating histograms of the coordinates of the target system obtained in a finite-time simulation, and choosing an ensemble of reference configurations at random from the histograms. This approach was later generalized to larger molecules by using pre-calculated molecular fragments as reference states.⁴⁷

In the limit of long, flexible (synthetic) polymer chains powerful tools in statistical physics, such as scaling approaches and the renormalization group, have been widely used to study equilibrium properties of these systems.^48–53 Likewise, the free-energy change associated with spatially confining a long, semi-flexible polymer chain with contour length L and persistence length P, e.g., into a cylindrical tube or spherical cavity of diameter D, have been studied in the asymptotic limit L ≫ P, D by combining scaling approaches with Monte Carlo simulations.^54,55 These approaches thus complement methods applicable to the small systems described above. However, semi-flexible macromolecular systems involving intermediate length scales remain notoriously difficult to handle, because such systems are in general out of reach of methods developed for the limiting cases of small, stiff systems and large, flexible systems, respectively.

Critical aspects of DNA replication,⁵⁶ recombination,^57,58 repair,^59,60 and gene regulation^61–64 depend on interactions between DNA-bound protein molecules that are separated by large linear distances along the genome, entailing the formation of DNA or chromatin loops. For more than two decades, many details of these processes have been worked out from in vitro and in vivo model studies using plasmid DNAs. The use of circular DNA has been an especially powerful tool in elucidating the mechanisms of recombinases and topoisomerases through topological analysis of knotted and linked products that are trapped by loop formation.^65–68 Loop formation in circular DNA is distinct from that in linear molecules; even in the simplest case of a single pair of interacting sites on circular DNA, there is an excess entropy loss relative to that for forming a pair of independent loops.⁶⁹ Thus, the thermodynamics of loop formation within a circular domain has remained an unsolved problem for semi-flexible systems. Combined with recent computational and experimental results suggesting that DNA-loop-mediated processes are driven thermodynamically rather than kinetically,^70–72 there is strong motivation to develop new methods for more generally evaluating the free energies of looped, semiflexible DNA structures.

In this work, we present a method to obtain configurational free energies of semiflexible macromolecular systems by combining TI with NMA. Following the strategy in Eq. (4), an arbitrary molecular state A is gradually transformed into a harmonically constrained reference state A₀ and the associated change in free energy is computed by TI. The free energy of the reference state A₀ is then computed separately and accurately by means of NMA. Compared with previous free-energy calculations that depend on the use of a reference state,^{11,44–46,73} our method introduces two innovations, namely, the use of internal coordinates to harmonically constrain the reference states, and the ability to freely select the reference states. As a consequence, it is now possible to explore systems that undergo substantially larger fluctuations than those considered in previous calculations. In addition, using freely selectable reference states avoids problems associated with locating the actual minimum of a rugged potential-energy landscape.¹⁰ The general procedure is numerically accurate, free of uncontrolled approximations, and applies to models of any macromolecular system for which internal geometric constraints can be specified. In particular, our method is applicable to biopolymers having arbitrary ratios of contour length L to persistence length P. As a test of our method we show that free energies of prime DNA knots containing up to six crossings can be accurately computed for large, semiflexible DNAs 3000 and 6000 base pairs in size (Fig. 1).

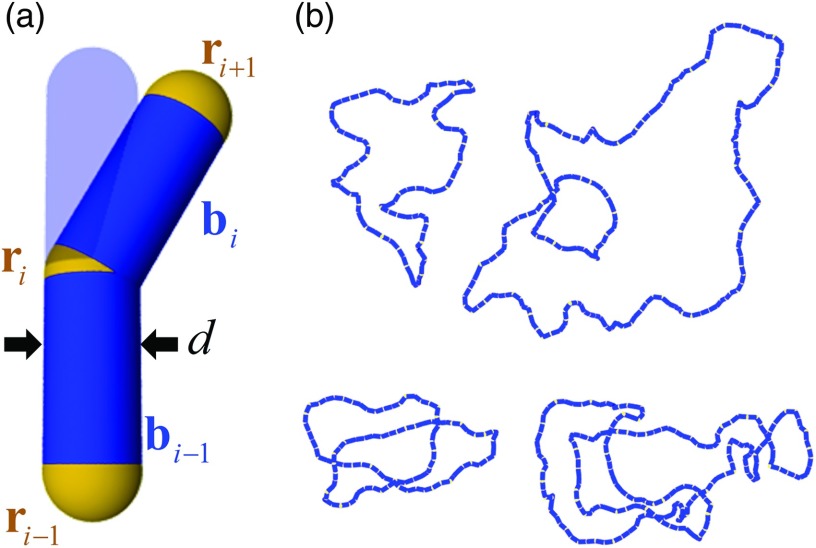
FIG. 1.

Coarse-grained DNA model. (a) Definition of chain segments b_i, vertices r_i, and segment diameter d. The equilibrium position of segment b_i is shown by the translucent surface. (b) Typical chain conformations generated by Monte Carlo simulation. Shown are chains with N = 100 segments (L = 20 P, 3000 base pairs) (left) and chains with N = 200 segments (L = 40 P, 6000 base pairs) (right). The top chains are unknotted and the bottom chains are knotted (4₁, figure-eight).

We then apply our method to an open problem, namely, investigating the free-energy landscape of circular DNA molecules partitioned into two looped domains by a nucleoprotein complex bound simultaneously to two DNA sites (Fig. 2). These structures are appropriate models for double-strand-passage intermediates in type-II topoisomerase reactions,⁷⁴ synaptic complexes (sc) in recombination reactions taking place on DNA circles,⁶⁸ and promoter selection in enhancer-multiple promoter interactions,^{61,62,75–77} among other systems. For a circle of total contour length L, synapsis between sites separated by a linear distance ℓ generates looped domains with lengths ℓ and L − ℓ, respectively. By evaluating the free-energy landscape F(ℓ, L; P) we find that the location of optimal synapse sites on a circular DNA molecule depends strongly on the ratio L/P; in particular, we find a bifurcation in the location of optimal synapse sites at a critical value L/P ≈ 10.7 (about 1600 base pairs for P = 50 nm).

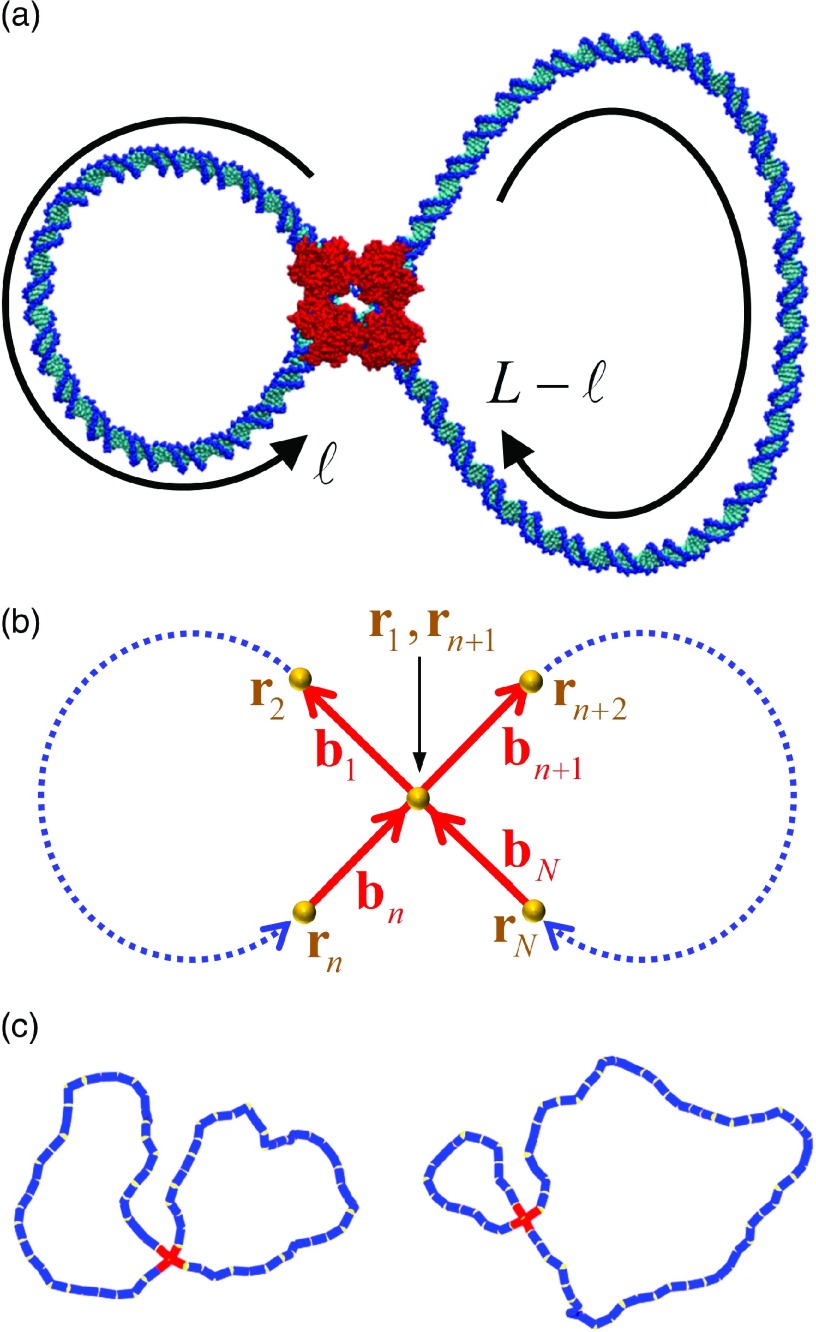
FIG. 2.

Dual-loop synaptic complex. (a) Atomistic model of a nucleoprotein synaptic complex (Cre-LoxP, adapted from PDB ID 3CRX) formed on a circular DNA substrate. Cre-protein atoms are shown in red. (b) Definition of segment vectors forming the synaptic junction (see text for details). (c) Typical chain conformations generated by Monte Carlo simulation. Both chains have the same total length L = 16 P (2400 base pairs), but different locations of the synapse (red chain segments). At left, the synapse is located at ℓ = L/2, forming two loops of equal length ℓ = 8P. At right, the synapse is located at ℓ = L/4, forming loops with lengths ℓ = 4 P and L − ℓ = 12 P, respectively.

II. METHODS

A. DNA model: Extensible harmonic chain

We consider a semi-flexible harmonic chain as a coarse-grained mesoscopic model for duplex DNA.^78,79 Chain elements are extensible, cylindrical segments with equilibrium length b₀ and fixed diameter d, connected end-to-end by semi-flexible joints located at vertices r_i, i = 1, …, N (Fig. 1(a)). Segments are described by displacement vectors b_i = r_{i + 1} − r_i with length b_i and unit-length direction vectors ${\widehat{\mathbf{b}}}_i={\mathbf{b}}_i/b_i$. The total potential energy for a given conformation $\stackrel{\rightharpoonup }{r}=\left({\mathbf{r}}_1,...,{\mathbf{r}}_N\right)$ is defined as

$$U\left(\stackrel{\rightharpoonup }{r}\right)=U_{el}+U_{ev}+U_K,$$ (5)

where U_el is the elastic energy of the chain (cf. Eq. (6) below) and U_ev, U_K describe infinite potential barriers associated with excluded volume (overlapping chain segments) and changes in knot type K, respectively (cf. supplementary material⁸⁰). These contributions are U_ev = 0 if none of the cylinders overlap and U_ev = ∞ otherwise. Similarly, U_K = 0 if the chain has knot type K and U_K = ∞ otherwise.

In this work, we consider two distinct topological models, namely, knotted, circular DNA and an unknotted, dual-loop synaptic nucleoprotein complex. Knotted, circular DNA with overall contour length L is modeled as a chain of N segments (Fig. 1). Such knotted chains are formed, e.g., through random closure of linear DNA or via strand passage mediated by topoisomerases or site-specific recombinases. The closure (boundary) condition for circular chains is enforced by the constraint r₁ ≡ r_{N + 1}. In this work, we consider the elastic energy due to bending and stretching of the chain only, as appropriate for nicked DNA. The elastic energy for a conformation $\stackrel{\rightharpoonup }{r}$ is defined as

$$U_{el}\left(\stackrel{\rightharpoonup }{r}\right)=U_{sc}+k_{B}T\sum _{i=1}^N\left[c_b\left(1-{\widehat{\mathbf{b}}}_i·{\widehat{\mathbf{b}}}_{i+1}\right)+\frac{c_s}{2}{\left(\frac{b_i}{b_0}-1\right)}^2\right],$$ (6)

where c_b, c_s are bending and stretching elastic constants, respectively. Elastic energy constants are set so that each segment represents approximately 30 base pairs of DNA (segment length b₀ = 0.2P) in 0.15 M NaCl (cf. supplementary material⁸⁰). The term U_sc in Eq. (6) represents the elastic energy associated with deformations of the sc (cf. Eq. (7) below) and does not contribute to the energy of unlooped circular chains.

Dual-loop synaptic complexes consist of a circular DNA molecule having two loci bound to a single protein complex (Fig. 2). The circular contour with length L is therefore partitioned into domains of length ℓ and L − ℓ, respectively, where ℓ is the contour length of one of the loops. The loops are modeled as chains having n and N − n segments, respectively, where N is the total number of chain segments and n is the number of segments in the loop of length ℓ. Both loops are connected at a common vertex r₁, which joins 4 segments (b₁, b_n, b_{n + 1}, b_N) at a four-way junction. The closure (boundary) condition at the junction is enforced by the constraint r₁ ≡ r_{n + 1} ≡ r_{N + 1}. The elastic energy of the sc is given by Fig. 2,

$$U_{sc}=k_{B}T\frac{c_b}{2}\left({\widehat{\mathbf{b}}}_1·{\widehat{\mathbf{b}}}_n+{\widehat{\mathbf{b}}}_1·{\widehat{\mathbf{b}}}_{n+1}+{\widehat{\mathbf{b}}}_n·{\widehat{\mathbf{b}}}_N+{\widehat{\mathbf{b}}}_{n+1}·{\widehat{\mathbf{b}}}_N\right).$$ (7)

Thus, the preferred geometry of the synapse in this model is that of a square-planar crossing, which has been proposed as a prototype Holliday-junction geometry in the phage-λ integrase superfamily of site-specific recombinases.^81–83

B. Free-energy calculations using TI-NMA

We used a Metropolis Monte Carlo procedure to generate equilibrium ensembles of chain conformations (cf. supplementary material⁸⁰). Free energies of knotted, circular chains and dual-loop synaptic complex models were obtained by combining TI with NMA, a scheme henceforth referred to as TI-NMA. NMA requires the system to obey harmonic fluctuations about a well-defined minimum-energy configuration. To this end, we use an auxiliary potential energy function, $U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)$, which exhibits a single, well-defined minimum at ${\stackrel{\rightharpoonup }{r}}_0$ such that $U_{ha}\left(\stackrel{\rightharpoonup }{r}={\stackrel{\rightharpoonup }{r}}_0\right)\equiv 0$. The ground-state conformation ${\stackrel{\rightharpoonup }{r}}_0$ may be selected arbitrarily (cf. Sec. II C. below). To calculate $U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)$, we associate basis vectors $\left\{{\widehat{\mathbf{x}}}_i,{\widehat{\mathbf{y}}}_i,{\widehat{\mathbf{b}}}_i\right\}$ with all segments b_i as follows. Position vectors r_i are given relative to the chain's center of mass, ${\mathbf{R}}_{cm}=N^{-1}{\sum }_i^N{\mathbf{r}}_i$, where each vertex of the chain at position r_i is taken to have unit mass. The z-axes of the frames are defined as the unit-length direction vectors ${\widehat{\mathbf{b}}}_i$, y-axes are defined as ${\widehat{\mathbf{y}}}_i={\mathbf{r}}_i\times {\widehat{\mathbf{b}}}_i/\left|{\mathbf{r}}_i\times {\widehat{\mathbf{b}}}_i\right|$, and x-axes are defined as ${\widehat{\mathbf{x}}}_i={\widehat{\mathbf{y}}}_i\times {\widehat{\mathbf{b}}}_i$ (Fig. 3). The potential U_ha is then defined as

$$\begin{array}{ccc}\hfill U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)& =& U_{sc}+k_{B}T\sum _{i=1}^N[\frac{c_b}{2}\left(2-{\widehat{\mathbf{b}}}_{i+1}·{\widehat{\mathbf{b}}}_{i+1}^p\right.\hfill \\ & & \left.-{\widehat{\mathbf{b}}}_{i-1}·{\widehat{\mathbf{b}}}_{i-1}^p\right)+\frac{c_s}{2}{\left(\frac{b_i}{b_0}-1\right)}^2],\hfill \end{array}$$ (8)

where ${\widehat{\mathbf{b}}}_{i+1}^p$, ${\widehat{\mathbf{b}}}_{i-1}^p$ are the preferred orientations of segment vectors adjacent to b_i in frame $\left\{{\widehat{\mathbf{x}}}_i,{\widehat{\mathbf{y}}}_i,{\widehat{\mathbf{b}}}_i\right\}$. The preferred segment directions are given by the orientations of segments ${\widehat{\mathbf{b}}}_{i+1}^0$, ${\widehat{\mathbf{b}}}_{i-1}^0$ within frames $\left\{{\widehat{\mathbf{x}}}_i^0,{\widehat{\mathbf{y}}}_i^0,{\widehat{\mathbf{z}}}_i^0\right\}$ of the reference configuration ${\stackrel{\rightharpoonup }{r}}_0$ (cf. Sec. II C. below).

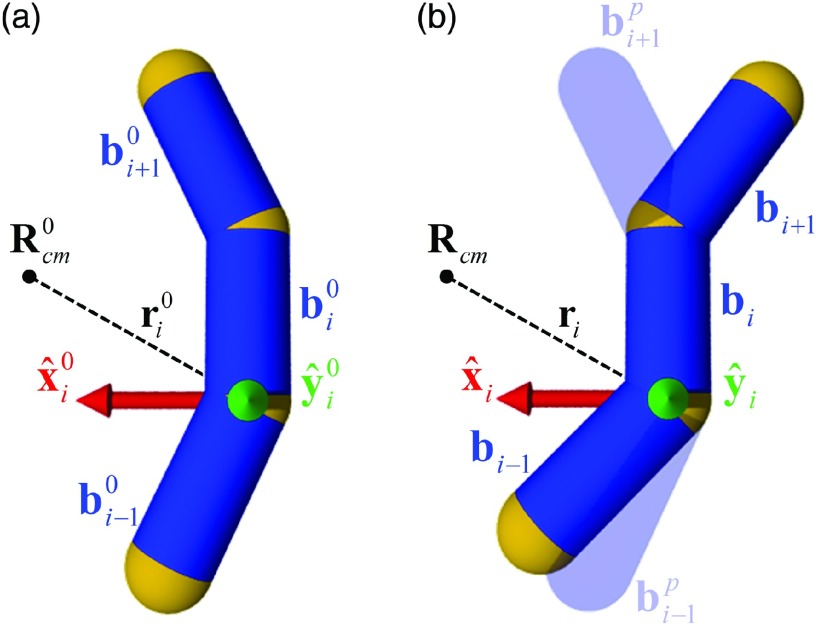
FIG. 3.

Internal-coordinate constraints. (a) For a given ground state conformation ${\stackrel{\rightharpoonup }{r}}_0$ with center of mass ${\mathbf{R}}_{cm}^0$, the basis frames $\left\{{\widehat{\mathbf{x}}}_i^0,{\widehat{\mathbf{y}}}_i^0,{\widehat{\mathbf{b}}}_i^0\right\}$ are obtained for each segment ${\mathbf{b}}_i^0$ such that axis ${\widehat{\mathbf{x}}}_i^0$ lies in the plane defined by the point ${\mathbf{R}}_{cm}^0$ and the vector ${\mathbf{b}}_i^0$, and points towards ${\mathbf{R}}_{cm}^0$. (b) For an arbitrary conformation $\stackrel{\rightharpoonup }{r}$, frames $\left\{{\widehat{\mathbf{x}}}_i,{\widehat{\mathbf{y}}}_i,{\widehat{\mathbf{b}}}_i\right\}$ are obtained in the same way as in (a). The equilibrium (preferred) orientations ${\mathbf{b}}_{i+1}^p$, ${\mathbf{b}}_{i-1}^p$ (shown as translucent surfaces) of segments b_{i + 1}, b_{i − 1} in the frame $\left\{{\widehat{\mathbf{x}}}_i,{\widehat{\mathbf{y}}}_i,{\widehat{\mathbf{b}}}_i\right\}$ correspond to the orientations ${\mathbf{b}}_{i+1}^0$, ${\mathbf{b}}_{i-1}^0$ in the frame $\left\{{\widehat{\mathbf{x}}}_i^0,{\widehat{\mathbf{y}}}_i^0,{\widehat{\mathbf{b}}}_i^0\right\}$.

The objective is to replace the energy function of the original, semi-flexible system described by Eq. (5) with a potential function suitable for NMA, and to calculate the associated change in free energy by TI (Fig. 4). To this end, we define

$$U\left(\lambda \right)=\left\{\begin{array}{cc}\lambda U_{ha}+\left(1-\lambda \right)U_{el}+U_{ev}+U_K,\hfill & 0\le \lambda \le 1\hfill \\ \lambda U_{ha}+U_{ev}+U_K,\hfill & 1\le \lambda \le {\lambda }_{max}\hfill \end{array}\right.,$$ (9)

where the parameter λ serves to switch between the limits U_el + U_ev + U_K at λ = 0 and λ_maxU_ha + U_ev + U_K at λ = λ_max. The first phase of TI, 0 ⩽ λ ⩽ 1, replaces the original elastic potential energy $U_{el}\left(\stackrel{\rightharpoonup }{r}\right)$ with the new potential $U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)$. The second phase of TI further increases λ to a value λ_max which is chosen large enough so that the system is fully constrained to harmonic fluctuations about the reference ground state ${\stackrel{\rightharpoonup }{r}}_0$. This process is shown for selected knotted and dual-loop sc models in supplementary material⁸⁰ (Movies 1(a)-1(j)). Finally, NMA is applied to the ground state configuration ${\stackrel{\rightharpoonup }{r}}_0$ and the total free energy F is obtained as

$$F=F_0-\Delta F_1-\Delta F_2.$$ (10)

ΔF₁ and ΔF₂ are the free-energy changes associated with the two phases of TI described above and F₀ is the free energy of the reference ground state ${\stackrel{\rightharpoonup }{r}}_0$ obtained by NMA. Selected normal modes for knotted and dual-loop sc models are shown in supplementary material⁸⁰ (Movies 2(a)-2(j)). Carrying out this procedure for two different semi-flexible systems A, B, e.g., two different DNA knots, yields the free-energy difference ΔF_AB = F_B − F_A in terms of the thermodynamic cycle shown in Fig. 4.

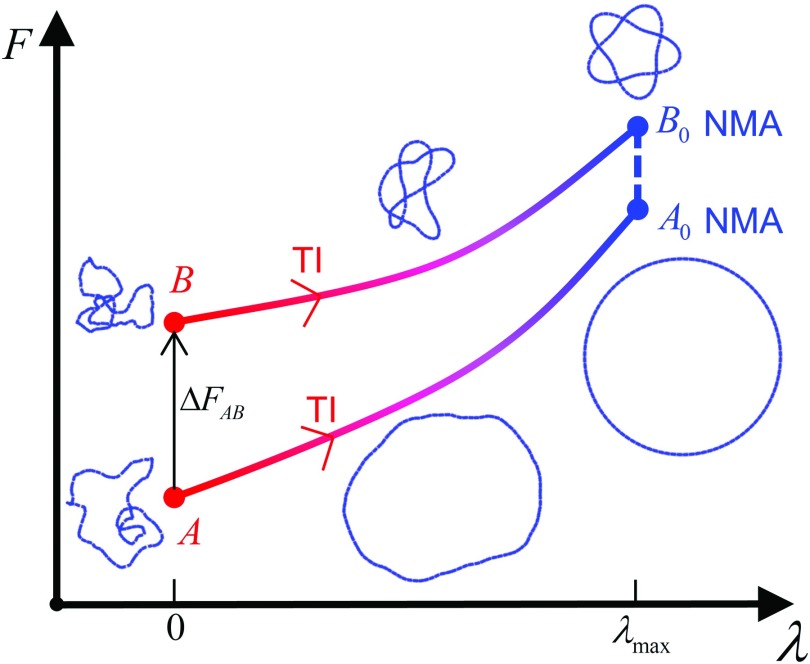
FIG. 4.

Thermodynamic cycle yielding the free-energy difference between states A and B (red section of the curves). Thermodynamic integration (TI) computes the change in free energy as each of the states A (unknotted), B (knotted, 5₁) is transformed into ground-state conformations A₀, B₀ (blue section of the curves). Normal mode analysis (NMA) gives the free energy of the ground-state conformations for the states A₀, B₀, completing the cycle (dashed blue line). Typical Monte Carlo conformations are shown for the TI portion of the cycle. Ground-state conformations of unknotted and knotted chains used for NMA are shown on the far right.

C. Reference systems

A major advantage of our method is the ability to freely select, in principle, any arbitrary full-system configuration as a possible reference state. These states can be chosen on the basis of computational convenience, the final computed difference in free energy being independent of the reference states. For the present calculations, reference conformations ${\stackrel{\rightharpoonup }{r}}_0$ for knotted chains were idealized knot conformations having unit-length segments, which were generated by the program KnotPlot.⁸⁴ Conformations ${\stackrel{\rightharpoonup }{r}}_0$ for the dual-loop synapse model were obtained by gradient-descent energy minimization of U_el in Eq. (6). The reference conformations used in our calculations are shown in supplementary material⁸⁰ (Fig. S2). In what follows, we assign preferred segment orientations ${\widehat{\mathbf{b}}}_{i+1}^p$, ${\widehat{\mathbf{b}}}_{i-1}^p$ for the segment vectors adjacent to b_i to be used in the auxiliary potential energy function $U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)$ in Eq. (8). At first, segment frames $\left\{{\widehat{\mathbf{x}}}_i^0,{\widehat{\mathbf{y}}}_i^0,{\widehat{\mathbf{b}}}_i^0\right\}$ are obtained for the chosen ground state configuration ${\stackrel{\rightharpoonup }{r}}_0$ (cf. Fig. 3(a)). Displacement vectors ${\widehat{\mathbf{b}}}_{i+1}^0$, ${\widehat{\mathbf{b}}}_{i-1}^0$ are expanded in the frame $\left\{{\widehat{\mathbf{x}}}_i^0,{\widehat{\mathbf{y}}}_i^0,{\widehat{\mathbf{b}}}_i^0\right\}$ with expansion coefficients

$$b_{i+1,x}^0={\widehat{\mathbf{b}}}_{i+1}^0·{\widehat{\mathbf{x}}}_i^0,b_{i+1,y}^0={\widehat{\mathbf{b}}}_{i+1}^0·{\widehat{\mathbf{y}}}_i^0,b_{i+1,z}^0={\widehat{\mathbf{b}}}_{i+1}^0·{\widehat{\mathbf{b}}}_i^0,$$ (11)

$$b_{i-1,x}^0={\widehat{\mathbf{b}}}_{i-1}^0·{\widehat{\mathbf{x}}}_i^0,b_{i-1,y}^0={\widehat{\mathbf{b}}}_{i-1}^0·{\widehat{\mathbf{y}}}_i^0,b_{i-1,z}^0={\widehat{\mathbf{b}}}_{i-1}^0·{\widehat{\mathbf{b}}}_i^0.$$ (12)

The above 6N parameters are then used to define preferred orientations ${\widehat{\mathbf{b}}}_{i+1}^p$, ${\widehat{\mathbf{b}}}_{i-1}^p$ for an arbitrary configuration $\stackrel{\rightharpoonup }{r}$, with segment frames $\left\{{\widehat{\mathbf{x}}}_i,{\widehat{\mathbf{y}}}_i,{\widehat{\mathbf{b}}}_i\right\}$ (cf. Fig. 3(b)), as

$${\widehat{\mathbf{b}}}_{i+1}^p=b_{i+1,x}^0{\widehat{\mathbf{x}}}_i+b_{i+1,y}^0{\widehat{\mathbf{y}}}_i+b_{i+1,z}^0{\widehat{\mathbf{b}}}_i,$$ (13)

$${\widehat{\mathbf{b}}}_{i-1}^p=b_{i-1,x}^0{\widehat{\mathbf{x}}}_i+b_{i-1,y}^0{\widehat{\mathbf{y}}}_i+b_{i-1,z}^0{\widehat{\mathbf{b}}}_i.$$ (14)

D. Thermodynamic integration

In the first phase of TI, for 0 ⩽ λ ⩽ 1, we replace the elastic potential energy U_el by the potential U_ha which constrains the chain to a reference ground state ${\stackrel{\rightharpoonup }{r}}_0$. The free-energy change associated with this process is given by

$$\Delta F_1=\underset{0}{\overset{1}{\int }}d\lambda {⟨\frac{dU}{d\lambda }⟩}_{\lambda }=\underset{0}{\overset{1}{\int }}d\lambda {⟨U_{ha}-U_{el}⟩}_{\lambda },$$ (15)

where the subscript indicates that evaluation takes place at a specific value of λ. Values of ⟨U_ha − U_el⟩_λ for 21 equally spaced values of λ = {0, 0.05, 0.1, …, 1} were obtained by Monte Carlo simulation and the results were interpolated and integrated according to Eq. (15) (cf. supplementary material⁸⁰). In the second phase of TI, for 1 ⩽ λ ⩽ λ_max, we further increased λ until the system was fully constrained to harmonic fluctuations about the reference ground state ${\stackrel{\rightharpoonup }{r}}_0$. We found that λ_max = 200 was sufficient to achieve high numerical accuracy in all calculations presented here; in particular, we verified that ⟨U(λ)⟩_λ, with U(λ) given in Eq. (9), converged to k_BT(3N − 6)/2 as expected for harmonic behavior according to the equipartition theorem.⁸⁵ The free-energy change associated with this process is given by

$$\Delta F_2=\underset{1}{\overset{{\lambda }_{max}}{\int }}d\lambda {⟨\frac{dU}{d\lambda }⟩}_{\lambda }=\underset{1}{\overset{{\lambda }_{max}}{\int }}d\lambda {⟨U_{ha}⟩}_{\lambda }.$$ (16)

Values of ⟨U_ha⟩_λ for 100 exponentially increasing values of λ from 1 to λ_max were obtained by Monte Carlo simulation and the results were interpolated and integrated according to Eq. (16) (cf. supplementary material⁸⁰).

E. Normal mode analysis

The Hessian matrix of mixed second derivatives, $H_{ij}=\beta b_0^2\frac{{\partial }^{2}U\left(\stackrel{\rightharpoonup }{r}\right)}{\partial r_i\partial r_j}$, i, j = 1, …, 3N, is calculated and diagonalized to obtain eigenvalues ν_m, m = 1, …, 3N, representing force constants for each normal mode m (cf. the supplementary material⁸⁰). When ordered smallest to largest, one finds ν_m = 0 for m = 1, …, 6 and ν_m > 0 for m = 7, …, 3N. The 6 zero eigenvalues m = 1, …, 6 are associated with rigid translations and rotations of the whole system and thus do not incur any energetic cost. The 3N − 6 nonzero eigenvalues m = 7, …, 3N are associated with internal vibrations of the chain about the minimum energy configuration ${\stackrel{\rightharpoonup }{r}}_0$. The free energy is obtained as

$$-\frac{F_0}{k_{B}T}=\rho +\ln \left(N^{3/2}\right)+\ln \left(8{\pi }^2\sqrt{I_x{I}_y{I}_z}\right)+\frac{1}{2}\sum _{m=7}^{3N}\ln \left(\frac{2\pi }{{\nu }_m}\right),$$ (17)

where I_x, I_y, I_z are the principal moments of inertia of the minimum energy configuration ${\stackrel{\rightharpoonup }{r}}_0$ in units of b₀ (cf. Eq. (8)). The quantity ρ depends on the discretization of the system, but is constant for molecules of the same size (number of segments) and thus does not appear in differences (cf. the supplementary material⁸⁰). Note that the potential energy of the minimum configuration ${\stackrel{\rightharpoonup }{r}}_0$ is zero according to the definition of $U_{ha}\left(\stackrel{\rightharpoonup }{r},{\stackrel{\rightharpoonup }{r}}_0\right)$ in Eq. (8) and is therefore absent in Eq. (17).

III. RESULTS

A. Equilibrium distributions of knotted, circular molecules

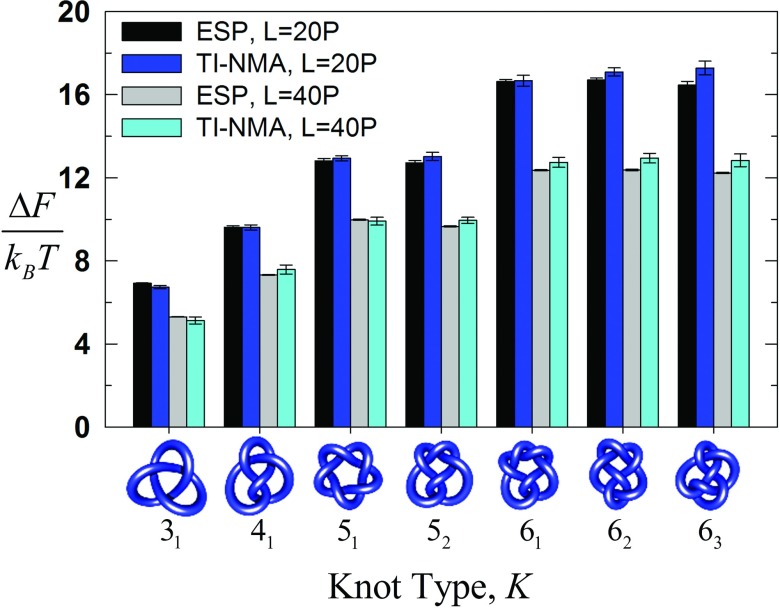
To verify the numerical accuracy of the TI-NMA method, we calculated free energies of DNA prime knots having up to 6 irreducible crossings. Computations were done for two different DNA lengths, namely, L/P = 20 (N = 100 segments) and L/P = 40 (N = 200 segments), corresponding to nicked-circular DNA molecules 3000 and 6000 base pairs in size (see supplementary material,⁸⁰ Table S1). Our results for the free energies of DNA knots obtained by TI-NMA are compared directly to the knots’ probabilities of occurrence in ensembles of chains generated by random segment passage during successive deformations of the chain (Equilibrium Segment Passage, ESP) (Fig. 5). Such ensembles sample equilibrium distributions of knot types.⁸⁶ Here we extend the ESP method to ensembles in which knots with the highest probability of occurrence were excluded during the simulation. Restricted ensembles produce more efficient sampling and thus higher numerical accuracy for knots with low probability, i.e., high free energy (cf. supplementary material⁸⁰ for details). Figure 5 shows that values of the free energy for DNAs up to 6000 base pairs (40 P) obtained by TI-NMA are numerically accurate to within fractions of k_BT.

FIG. 5.

Knotting free energies of DNA circles relative to an unknot of identical size calculated for different knot types using TI-NMA (blue, cyan bars) and ESP (black, gray bars). Black and blue bars show results for chains with length L = 20 P (N = 100, 3000 base pairs), whereas gray and cyan bars show results for chains with length L = 40 P (N = 200, 6000 base pairs).

1. Convergence of free-energy values for increasing ensemble size

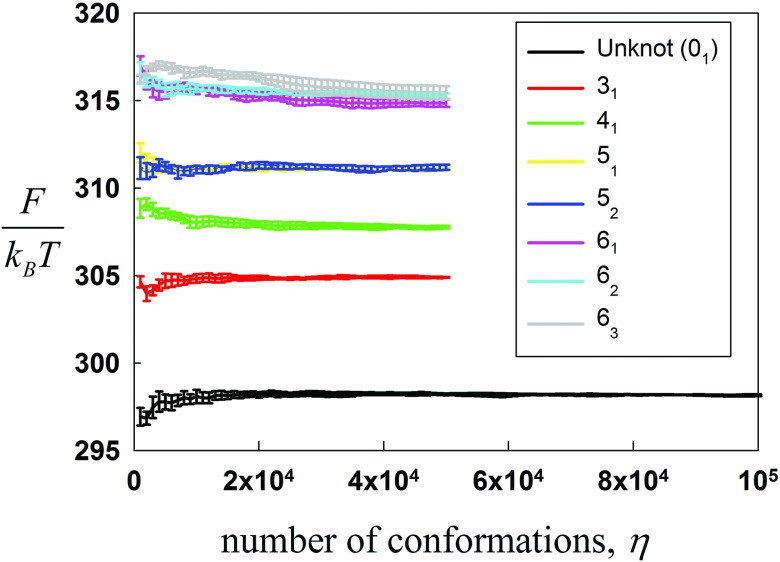
Absolute free energies of chains with the same overall length but with different knot types were calculated for increasing ensemble sizes (Fig. 6). Simulations were performed at 120 different values of λ, each producing an ensemble containing η independent conformations. The absolute free energy F = F₀ − ΔF_TI was then plotted for increasing η.

FIG. 6.

Free energies of chains with N = 100 segments (L/P = 20, 3000 base-pairs) are shown for each knot type and for increasing ensemble sizes.

2. Independence of the free energy on the reference system

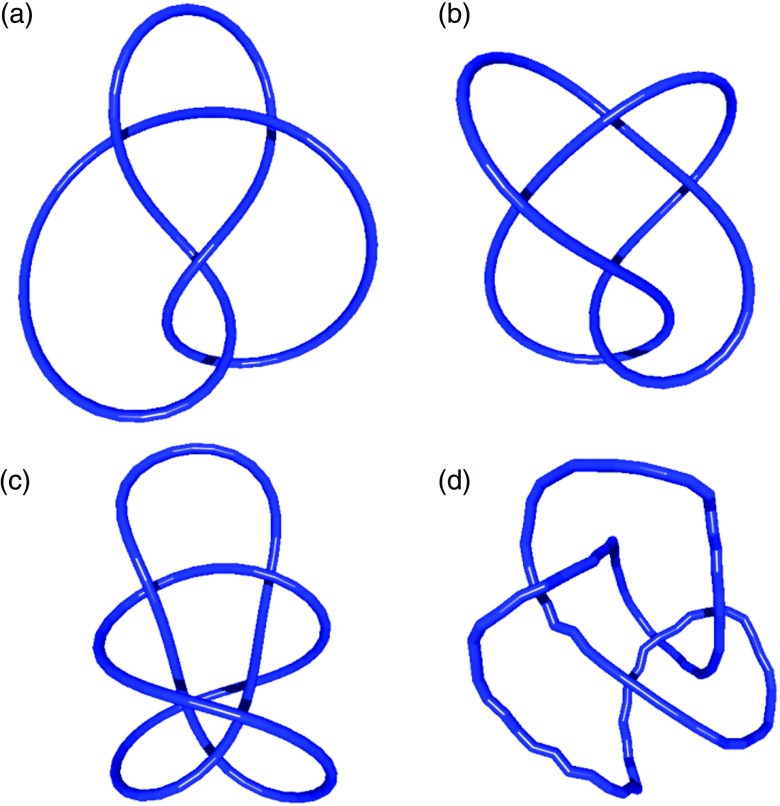
Final computed values for the difference in free energy between two states are independent of the chosen reference states (see Sec. II C). This is demonstrated here by calculating the free energy of a knotted DNA molecule for several arbitrary choices of the reference conformation (Fig. 7). The computed free-energy values are found to coincide within fractions of k_BT (Table I).

FIG. 7.

Reference conformations used to calculate the free energy of a figure-eight (4.1) DNA knot, demonstrating the independence of the computed free energy on chosen reference conformations. Each conformation (a)-(d) has overall length L = 20P (N = 100segments). Conformation (a) was used as the reference state for the 4.1 knot with L = 20P in Fig. 5. The final free-energy values obtained using these different reference conformations coincide within fractions of k_BT (cf. Table I).

Table I.

Comparison of free energies obtained for different reference conformations.

Conformationa	βF(λ = 0)b	βF0(λ = 200)	βΔFTI(λ = 0 → 200)
a	308.36(0.16)c	1077.85	769.49(0.16)
b	307.94(0.08)	1076.71	768.77(0.08)
c	308.54(0.07)	1076.45	767.91(0.07)
d	308.10(0.14)	1078.62	770.52(0.14)

^aCf. Fig. 7.

^bβ = (k_BT)⁻¹.

^cValues in parentheses represent error (SEM, 5 trials, η = 5 × 10⁵ in each trial).

B. Free-energy landscapes for dual-looped synapse models

We used our approach to compute the free energy landscape F(ℓ, L; P) of a synaptic DNA complex containing an internal synapse at two specified DNA segments. ΔF_TI = ΔF₁ + ΔF₂ and F₀ were individually fitted to continuous functions of loop length ℓ for specific ratios of L/P (cf. the supplementary material⁸⁰ for details). The free energy landscape F(ℓ, L; P) was obtained by interpolating these results for intermediate values L/P. Figure 8(a) shows ΔF = F(ℓ, L; P) − F(L/2, L; P) as a function of ℓ/L and L/P.

FIG. 8.

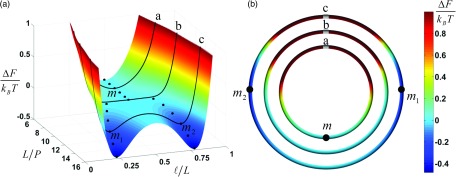
Free-energy landscape ΔF(ℓ, L; P) of a dual-loop DNA synaptic complex. (a) ΔF as a function of contour to persistence length ratio, L/P, and fractional contour length ℓ/L (cf. Fig. 2). At a critical value L/P ≈ 10.7, the minimum for ΔF (black dots) bifurcates from a single minimum at m = L/2 into two separate minima at m₁ < L/2 and m₂ = (L − m₁) > L/2, respectively. Black curves labeled a, b, c represent free energy profiles for fixed ratio L/P. (b) ΔF along a circular DNA molecule with fixed ratio L/P, corresponding to curves a, b, c in (a), as a function of the separation ℓ (to scale). One of the synapse sites is located at the top of each circle. Values of ΔF are represented by colors as shown. Chain a: L/P = 8 (about 1200 base pairs), with a single minimum m; chain b: critical value L/P ≈ 10.7 (about 1600 base pairs); chain c: L/P = 14 (about 2100 base pairs), with two separate minima m₁ and m₂.

The behavior of ΔF as a function of ℓ for fixed L/P depends strongly on the value of L/P. For small L/P, we find a single minimum for ΔF at m = L/2. At the critical value L/P ≈ 10.7, the single minimum at m = L/2 bifurcates into two separate minima at m₁ < L/2 and m₂ = (L − m₁) > L/2, respectively. The two minima tend to m₁/L → 0 and m₂/L → 1 as L/P is further increased. The onset of the bifurcation depends on the ratio L/P and may thus be controlled, for fixed length L, by varying the persistence length P of the DNA. Figure 8(b) shows ΔF along a circular DNA molecule with fixed length L as a function of the separation ℓ between synapse sites, where one synapse site is located at the top of each circle. Clearly, the locations of the minima in ΔF, corresponding to optimal locations of synapse sites, changes dramatically as the size of the molecule increases from 1200 to 2100 base pairs.

IV. DISCUSSION

We have developed a general approach for estimating the configurational free energy of semi-flexible macromolecules that combines TI with NMA of a harmonically constrained reference system. Our approach introduces two important innovations, namely, the use of internal coordinates to harmonically constrain reference states, along with the ability to freely select these reference states. As a result, it is now possible to study systems that undergo substantially larger fluctuations than those considered in previous calculations.

By using Eq. (10), the TI-NMA method yields the absolute free energy of a macromolecular system for given force field $U\left(\stackrel{\rightharpoonup }{r}\right)$. Applying Eq. (10) to two arbitrary configurations yields the free-energy difference by means of a thermodynamic cycle, without the need to transform one state into the other (cf. Fig. 4). The TI-NMA method can thereby compute free-energy differences for macromolecular states that are significantly different from one another. We consider one such case here, namely, circular DNA molecules of different knot types (cf. Fig. 5). Topological barriers render energy-perturbation methods (including TI) ineffective because there is no well-defined reaction coordinate that continuously connects different topological states. Similar difficulties arise in connection with problems involving phase transitions, such as unfolded and folded states of a protein separated by a first-order collapse transition.⁸⁷ Our method is thus applicable to a wide range of problems involving biomolecular organization, beyond free energies of DNA knotting and looping in circular DNA (cf. Figs. 5 and 8). The polymer-length scale we address corresponds to that of plasmid-sized DNA circles, a size regime that is highly challenging to other approaches.

In this work, the difference in free energy, ΔF, between reference and target states was computed directly by applying TI to results for ⟨U⟩_λ obtained by MC simulation (cf. Eqs. (15) and (16)). Figure 6 shows that convergence of the free energy can be achieved with ensembles as small as 20 000–40 000 chains; these ensembles are on the order of 100 times smaller than those required by other methods (data not shown). However, in more complex systems, accuracy in ΔF may require enhanced sampling techniques such as parallel tempering, multicanonical sampling, or umbrella sampling.^11–15

Applications of the TI-NMA method are particularly appropriate in cases where the topology and/or geometry of a semi-flexible polymer domain is fixed. Examples include topologically closed domains that may be simultaneously knotted and supercoiled. Previous studies assessing the effect of supercoiling on the free energy of knot formation were based on models similar to ours, but led to conflicting conclusions because of differences in imputed changes in DNA supercoiling.^86,88 Such ambiguities can be avoided in our methodology, which can rigorously and systematically address a broad range of problems involving the formation of topologically closed DNA domains.

Our results for the free-energy landscape F(ℓ, L; P) of a dual-looped synaptic DNA complex reveal a bifurcation in the optimal location of synapse sites, coinciding with the minima in the free-energy landscape F(ℓ, L; P), as the parameter L/P is changed (Fig. 8). The notion of bifurcations was originally introduced in the mathematical study of dynamical systems. In this context, a bifurcation corresponds to a qualitative change in the behavior of a dynamical system when a parameter changes, e.g., the appearance or disappearance of equilibrium points.⁸⁹ Similarly, the bifurcation in the location of optimal synapse sites in a synaptic DNA complex found here corresponds to a change in the shape of the free-energy landscape F(ℓ, L; P) as a function of ℓ/L when the parameter L/P is changed (for example, by changing P for fixed L). By identifying and characterizing the bifurcation we are able to address the problem of target-site selection by DNA-binding proteins and protein complexes that occupy multiple DNA sites separated by large linear distances. This problem arises naturally in gene-regulatory contexts that involve interactions between enhancer and multiple promoter sequences, in the action of type-II topoisomerases, and in other sequence-specific and non-specific protein-DNA interactions. We note that topological transitions in Gaussian chains (i.e., without bending energy) constrained by slip-links, which are driven purely by entropy upon changing the through-space distance between chain ends, have been known for some time.^90,91 In contrast, the bifurcation in the locations of optimal synapse sites found here results from competition between energetic and entropic contributions to the full free energy of a semi-flexible system.

We note that probing the complete free energy landscape F(ℓ, L; P) (Fig. 8) directly by simulating an equilibrium set of conformations of circular chains and counting the number of conformations which happen to have a crosslink at different positions along the chain during the simulation is computationally inefficient. This problem is particularly severe for combinations of parameters (ℓ, L; P) for which the free energy F(ℓ, L; P) is large (i.e., the probability of occurrence of these states is small). Moreover, the detailed geometric constraints imposed by the synaptic complex on the DNA loops cannot realistically be implemented in such a model. The TI-NMA method avoids this problem by computing the free energy of the whole protein-DNA synaptic complex for individual combinations of parameters (ℓ, L; P), taking into account realistic geometric parameters for the complex.

In the asymptotic limit of long, flexible chains, our results for F(ℓ, L; P) (Fig. 8) are consistent with the phenomenon of knot localization found previously, i.e., the statistically most-probable conformations minimizing F(ℓ, L; P) are those for which one of the loop sizes is much smaller than the other.^69,92–95 The TI-NMA method allows us to go beyond this result and to obtain realistic values for the free energy F(ℓ, L; P) of semi-flexible polymers with arbitrary ratios L/P. Our method can be readily extended to finding optimal synapse spacing as a function of the ionic environment, supercoiling, and locations of additional DNA-binding proteins.