A Model for an Early Stage of Tomato Fruit Development: Cell Multiplication and Cessation of the Cell Proliferative Activity

Abstract

Changes in cell number during the early period of tomato fruit development were analysed by means of a deterministic model of cell multiplication. The period commenced at the seed stage with one theoretical cell undergoing intensive cell division, and ended when the cell number became nearly constant. The model takes into consideration the proliferative activity of the fruit cell population which, a few days before flower anthesis, begins to decrease progressively after each mitotic cycle. Model parameters, namely the time at which proliferative activity diminishes, its rate of decrease and the length of the cell cycle, were estimated by fitting the model to observed cell population dynamics in tomato fruits growing in three different positions on the truss. It is hypothesized that the molecular mechanism responsible for the cessation of mitosis in growing fruits is associated with shortening of telomeric ends of nuclear DNA, as suggested previously for other growing cell populations.

INTRODUCTION

Cell multiplication is a recurrent process. Division of a cell creates two or several cells that resemble the mother cell and which, in turn, undergo division. A certain proportion of cells in a population is non‐dividing and, in many cases, the proportion of cells that divides in each successive cycle declines progressively, i.e. there is a decrease in cell proliferative activity. In culture, most normal cells, e.g. mammalian somatic cells, terminate their proliferation after a period of vigorous growth, and double only a limited number of times (Matsumura, 2000). There are also numerous examples of proliferative activity loss in growing plant tissues. In their study on sunflower, tobacco and pea leaves, Granier et al. (2000b) observed that cell number per leaf increased exponentially during early leaf development, but it became constant later. Analysis of cell number dynamics in leaves (Milthorpe and Newton, 1963; Dale, 1970, 1976) led to the conclusion that the proportion of proliferating cells declines with time.

Fruit growth starts after bloom, with intensive cell division, but the proliferative activity of the cells slows down as development proceeds, mitosis stops and the cell population enters a stage of cell enlargement. In apple fruit, evidence supports the view that after a few weeks of development fruit growth is a matter of cell enlargement (Bain and Robertson, 1951). In peach fruit, cell numbers in the mesocarp and endocarp appear to be fixed several weeks after full bloom, and subsequent growth of the fruit is exclusively supported by cell enlargement and formation of intercellular spaces (Masia et al., 1992; Zanchin et al., 1994; Ognjanov et al., 1995; Yamaguchi et al., 2002). Gillaspy et al. (1993) noted that in its early stages, tomato fruit growth is primarily the result of cell division, but cell division then ceases and fruit growth continues mostly by cell expansion.

The diminution of proliferative activity, especially in cultured populations under controlled conditions, signifies that the progeny do not return exactly to the state from which replication began. Certain transformations that are responsible for arresting proliferation must occur in the cells. Olovnikov and other authors (Olovnikov, 1973; Harley et al., 1990; Bodnar et al., 1998; Weinberg, 1998; see reviews by Matsumura, 2000, and Perrem and Reddel, 2000) have hypothesized that the cessation of cell proliferative activity is eventually caused by progressive shortening of telomeres during mitosis. Telomeres are specialized polynucleotide structures that are located at the ends of all linear eukaryotic chromosomes. Because of technical limitations, it is difficult to determine the extent to which telomeres shorten at each cell division; therefore quantitative information on these phenomena is restricted. It has been shown (Harley et al., 1990) that the length of telomeric DNA in human fibroblasts is inversely correlated with the number of population doublings. In plant tissues, the decrease in telomeric repeats at the chromosome ends of barley (Hordeum vulgare L.) embryos during in vivo ageing has been evaluated (Kilian et al., 1995), and the absolute value of the telomere decrease per population doubling was much greater than that estimated from mammalian DNA shortening.

Our previous model for fruit growth (Fishman and Génard, 1998) described a stage when cell division was arrested and the number of cells in the fruit became constant. The model was based on biophysical analysis of water and dry material transport contributing to cell enlargement. The aim of the present study was to analyse the early phase of fruit growth that started before anthesis and finished when cell multiplication was arrested. To describe this period, a model of cell multiplication is needed that takes into account a proliferative activity that diminishes progressively after each round of cell division. Models of cell division may be either mechanistic or phenomenological. Choice of the model depends on the experimental observations available for analysis. Molecular mechanisms controlling cell proliferation have been studied extensively over recent years. It has been shown that oscillations in the activity of cyclin‐dependent kinases promote the cell cycle (King et al., 1996). Novac and Tyson (1993) developed a comprehensive model of mitotic phase control in the Xenopus embryo. A similar system of differential equations was used in the mathematical model describing the molecular basis for mitotic control during early development of the sea urchin embryo (Ciliberto and Tyson, 2000). These models contain up to 30 parameters, and a quantitative investigation of underlying biochemical processes is needed for parameter estimation otherwise the models can be compared only qualitatively with observations. On the other hand, phenomenological models involve several parameters that may be estimated by curve fitting to the observed cell number dynamics. The parameters obtained in such models may be important characteristics of biological phenomena. For instance, Dale (1970) examined negative logistic and negative exponential functions of time to describe the cell number increase in developing leaves of Phaseolus vulgaris, concluding that the negative exponential model fitted observed data when the average division time is 12 h. Thornley (1981) also used the negative exponential function to describe the cessation of meristematic activity in a leaf.

The model analysed in the present study is comparable with the continuous phenomenological models of Dale (1970) and Thornley (1981), but it is a discrete one considering a succession of division steps. The rate of decrease of proliferating activity of fruit cells after a single division step is one of the model parameters that was estimated by applying the model to our observations of the cell population dynamics in tomato (Lycopersicon esculentum Mill.) fruits. Accepting the hypothesis that cessation of mitosis in the growing fruits is associated with nuclear DNA shortening, as was assumed for the cultured cell populations, the rate of decline of the proliferative activity, evaluated by means of the deterministic discrete model, was compared with rates of telomeric DNA shortening reported in the literature (Harley et al., 1990; Kilian et al., 1995).

MATERIALS AND METHODS

Plant material and cultural conditions

The experiment was carried out in an 8·75 m² (21 m³) climatic growth chamber under controlled environmental conditions. Tomato seeds (Lycopersicon esculentum Mill. ‘Raïssa’) were sown in sand, and 12 plants were pricked out at a developmental stage of about six visible leaves into 10 l pots filled with a balanced oxygenated nutrient solution, whose composition was checked every week and readjusted when necessary. Sowing took place in the climatic growth chamber. A day‐night air temperature of 25–20 °C was maintained continuously from sowing until the end of measurements. A photon flux of about 500 µmol m^–2 s^–1 PAR above the canopy was applied from 0800 to 2000 h. Air relative humidity was approx. 70 %, and the atmosphere was enriched to 600 µl CO₂ l^–1 after anthesis of the first truss. The first inflorescence (or truss) was pruned to six flowers when necessary, and the second inflorescence was pruned to two flowers. Plants were topped at a level of two leaves above the second truss. Flowers were pollinated as they opened using an ‘electrical bee’, and all side shoots were removed as they appeared.

Experimental design and developmental observations

To assess the dynamics of cell number during fruit development, many successive plantings were made under the conditions described above. At the first planting date, 12 plants were placed in the phytotron in two parallel lines of four plants, with one perpendicular line of four plants placed at the end of the two rows. At each sampling date, four successive plants were collected as fruits reached the developmental stage of interest, and were immediately replaced by young plants (six visible leaves) sown about 1 month previously under the same conditions. A total of 17 sowings was made to maintain a permanent pool of 12 plants in the phytotron. The age of each individual reproductive organ was assessed by noting the dates of full flower opening (anthesis). As fruits developed, the diameter of the six fruits on the first truss was measured once a week to monitor whether fruit growth was similar among plants.

Determination of fruit cell number

Numbers of pericarp cells were recorded in the first, third and fifth fruits of the first truss, using a method adapted from that of Bünger‐Kibler and Bangerth (1983). Fruits smaller than 2·5 cm in diameter were picked and fixed in a solution of ethanol, formaldehyde and acetic acid (90 : 5 : 5). After washing in water, the whole fruit pericarp was isolated under a binocular microscope and its volume was measured by water displacement. It was then put into a maceration solution of 3·5 % pectinase + 0·1 m EDTA + 0·4 m mannitol at pH 4 for 2–3 d at 32 °C. Similarly, pericarps of fruits >2·5 cm were isolated after picking, and their volume and fresh weight were measured. They were then macerated for at least 24 h at ambient temperature in a solution of 0·05 m EDTA + 0·4 m mannitol at pH 10·3. After maceration, samples were stirred for 15 min on a magnetic stirrer and diluted with an 87 % solution of glycerol. Cell number in an aliquot of the suspension was counted in counting chambers under a microscope (Fuchs‐Rosenthal chamber, 0·2 mm deep for large fruits; Bürker chamber, 0·1 mm deep for small fruits). A minimum of five samples per fruit were counted, and more in cases of high variability (coefficient of variation >10 %). The total number of cells in the whole fruit pericarp was calculated from volumes of the counting chamber, maceration solution and pericarp.

Computation methods

For numerical computations of the dynamics of the cell population predicted by the model, a computer program based on Splus language (Chambers and Hastie, 1992) was written. The parameters of the model were estimated using the Splus non‐linear procedure. The goodness‐of‐fit of the model was evaluated by the root mean squared error (e), a criterion commonly used to quantify the mean difference between simulation and measurement (Kobayashi and Us Salam, 2000), here defined as:

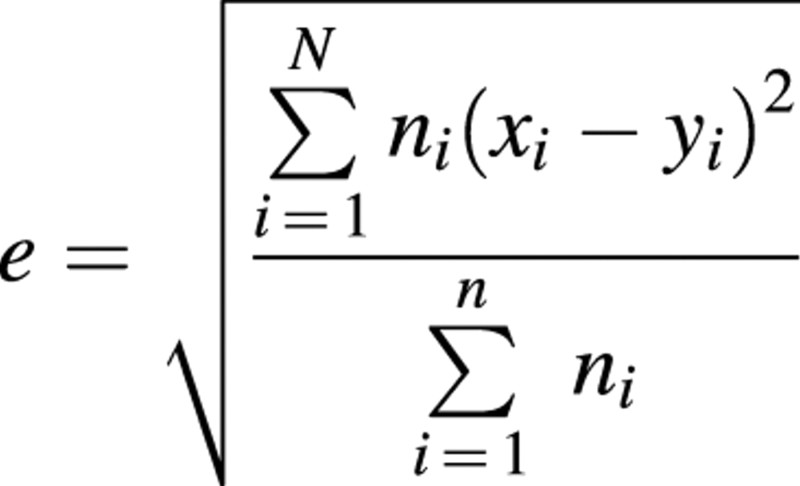
with x_i being the simulation result and y_i the mean of observed data at date t_i. N is the number of sampling dates and n_i is the sample size at date t_i. The smaller the e in comparison to measurements, the better the goodness‐of‐fit. This idea can be represented through relative e:

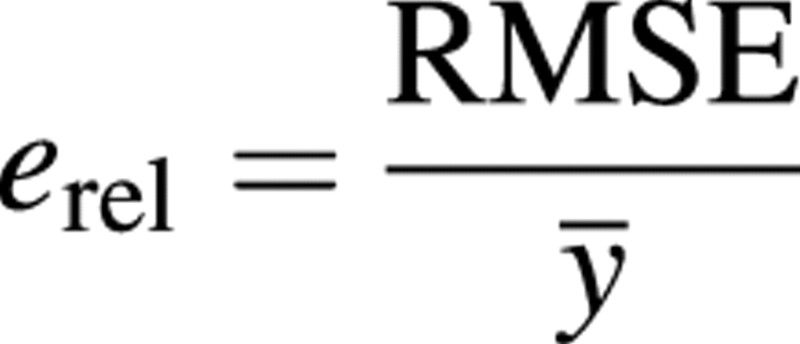
where ȳ is the mean of all observed values.

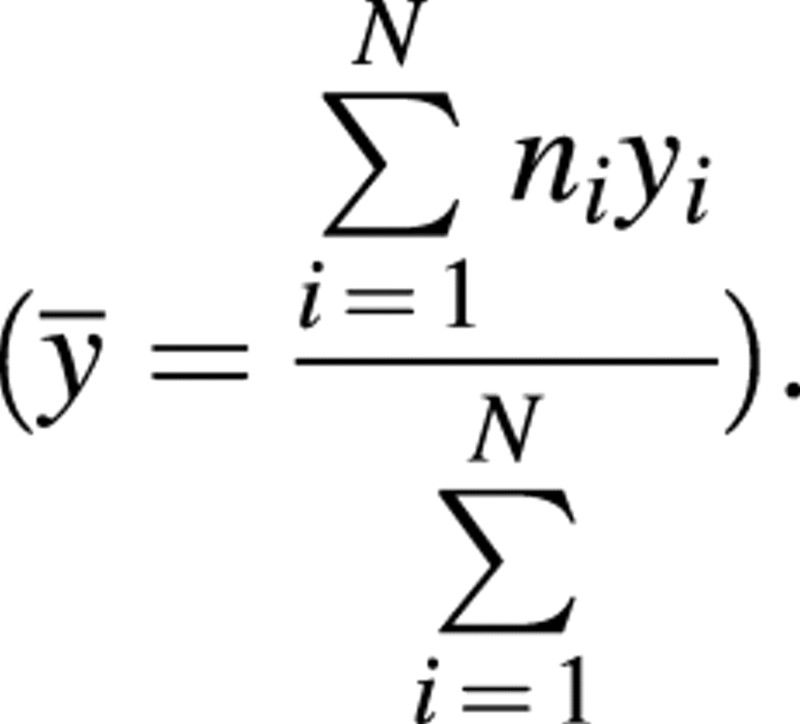
Each of the model parameters could be considered as constant or dependent on fruit position. To test for the ‘best’ model, several alternatives were tested by comparing nested models, as presented by Chambers and Hastie (1992). The statistic used to compare two nested models with p and q parameters, respectively (p > q), was:

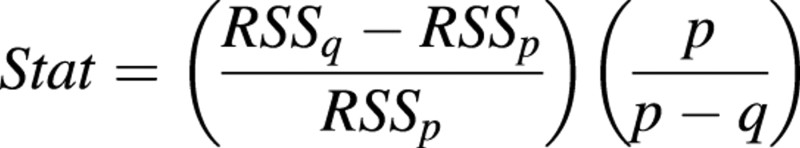
which follows an F‐distribution with degrees of freedom p – q and n – q, where n is the sample size and R_j is the residual sum of squares of the model with j parameters. Among two models showing no significant difference, the simpler was preferred.

MODEL DESCRIPTION

We considered a model in which the proliferating cells divide by binary fission. The average number of cells in the population at time t_i is denoted as N(t_i), where t_i is the running time after the ith division cycle. The total cell cycle duration, τ_i, is the sum of the interphase and mitosis phase lengths. The time after the ith division is given by:

where τ_c(E) symbolizes the dependence of the cth cell cycle on environmental and internal control factors, E, and the summation is performed over all cycles (1 ≤ c ≤ i). If the affecting factors are constant during the simulation time then t_i = iτ.

The model was assumed to start at time S from the first ‘mother’ cell, theoretically at the seed stage, with an exponential increase in cell number. At time B, considered to be the end of exponential division, the proportion of dividing cells begins to diminish after each division. At times S and B, numbers of cells are, respectively, N(S) = 1 and N(B) = 2(B – S)/τ.

From time B, the model assumes that a certain proportion, θ, of cells divides. This proportion is a measure of the proliferating activity. The proportion of non‐proliferating cells is 1 – θ. The proliferating activity is assumed to diminish after each division event, so that θ varies according to the rule: θ_i = θ_{i – 1}δ, where 0 ≤ θ_i ≤ 1 and 0 ≤ δ ≤ 1. Iteration according to this rule leads to:

θ_m = θ_{m– 1}δ = θ_{m– 2}δ² = ... = θ₁δ^{m– 1}(2)

where θ_B = θ₁ = 1, and m – 1 is the number of cell cycles performed after time B.

During the first cycle after time B, among the total number of cells n = N(B), δn cells divide, giving 2δn offspring, and (1 – δ)n cells are non‐proliferating. At any time after B, the number of cells entering the mth cycle is doubled after the end of the cycle, and a proportion θ_{m+ 1 =}δ^m of them continue to multiply. Cell population dynamics are represented by the scheme shown in Fig. 1. According to this scheme, the number of proliferating cells at time t_i, is equal to:

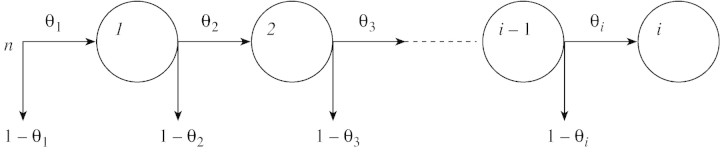
Fig. 1. Schematic representation of the algorithm of the model after time B when the proliferative activity decreases after each cell cycle. Circles symbolize the mitotic cycles. Arrows pointing downwards show the proportion of non‐proliferating cells that appears after each cycle. θ₁ = 1 and θ_i = θ₁δ^{i – 1} where i – 1 is the number of cell cycles performed after time B.

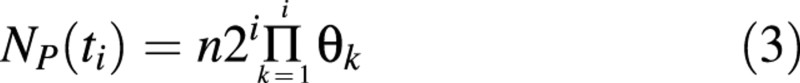
Taking into account eqn (2) and using series summation for an arithmetical progression, we obtained:

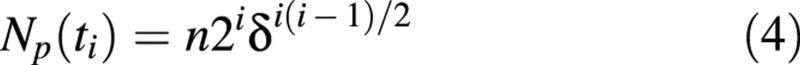
The number of non‐proliferating (growing, in the case of the cell population in developing fruit) cells which appeared before the mth division, at time t = t_{m – 1} (m ≥ 1), is denoted as N_G,m, and is given by:

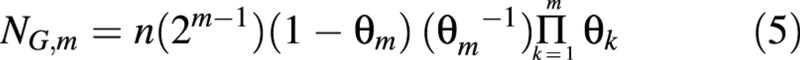
which, in combination with eqn (2), gives:

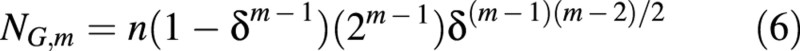
The total number of non‐proliferating cells accumulated before time t_i, N_G(t_i), is:

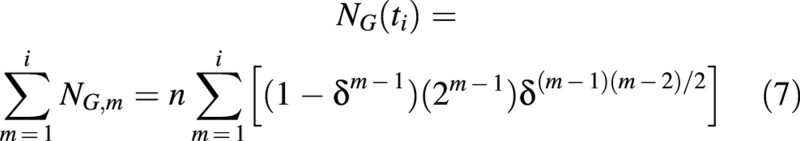
The total number of cells in the population may be calculated from eqns (4) and (7) as:

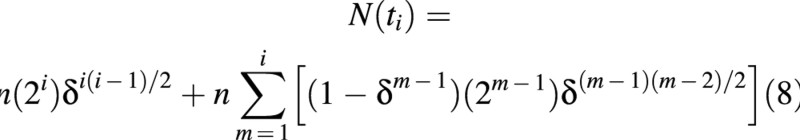
where t_iand _i are related by eqn (1).

EXPERIMENTAL RESULTS AND MODEL PARAMETERIZATION

To simulate the dynamic behaviour of the cell community, three parameters must be estimated: B, the time at which θ, the cell proliferative activity, starts to decrease; δ, the relative decrease in proliferative activity; and τ, the duration of one cell cycle. Three sets of experimental data obtained for fruits situated at positions 1, 3 and 5 were used to estimate these parameters. Since the number of pericarp cells varied with fruit position within the inflorescence, it was assumed that some of these parameters also varied with fruit position. To check which of the parameters was most appropriate to accommodate the effect of fruit position on cell number, sub‐models considering either one, two or three parameters depending on fruit position were compared (see computation method). Statistically, only one model was worse than all others, namely that in which all three parameters were constant, i.e. independent of fruit position. All other sub‐models with one, two or three changing parameters were not statistically different. It was therefore considered that the ‘best’ model should include only one parameter depending on fruit position, but statistically it was not possible to detect which of the three parameters best described differences among fruit positions because the residuals were similar. Figure 2 shows the experimental data set together with the simulation obtained by the model, considering one of the three parameters as dependent on fruit position. Results of the parameterization are given in Table 1. In any case, the model fitted the experimental data well and e_rel ranged between 14 and 16 %.

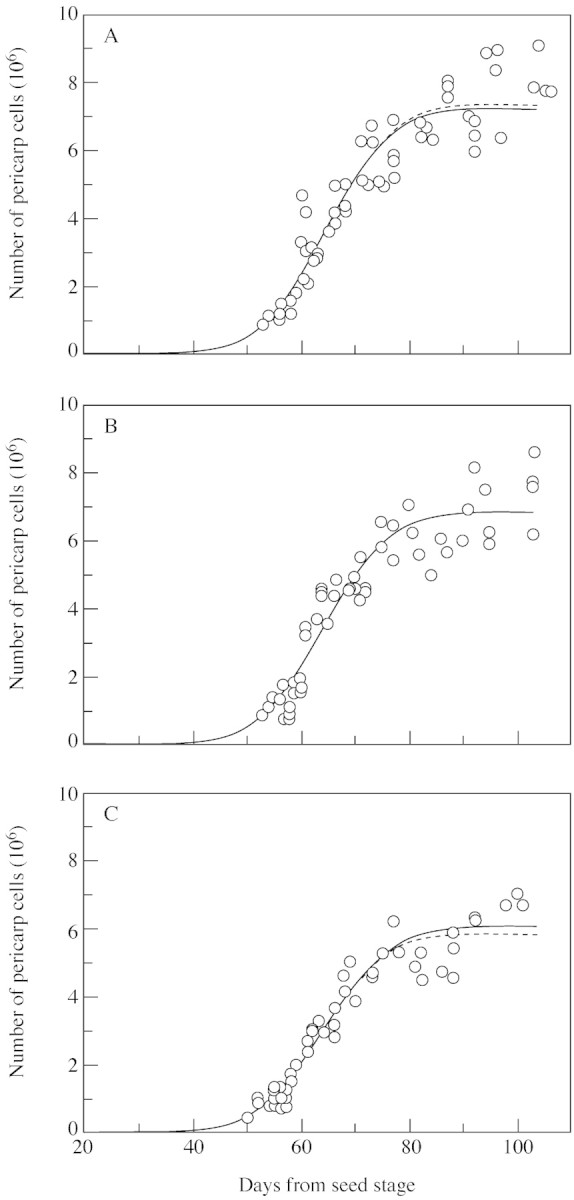
Fig. 2. Comparison between the observed dynamics of cell number in tomato fruits at positions 1 (A), 3 (B) and 5 (C) in the truss (symbols) and the curves calculated by the model, considering either τ (bold line), δ (thin line) or B (broken line) to be dependent on fruit position.

Table 1.

Values of estimated parameters of the cell division model for three fruit positions within the inflorescence

	Fruit 1	Fruit 3	Fruit 5
Sub‐model 1 B = ƒ(fruit)
B	44·84	44·57	44·08
τ	2·593	–	–
δ	0·915	–	–
erel	0·140	0·157	0·157
Sub‐model 2 τ = ƒ(fruit)
B	44·48	–	–
τ	2·577	2·591	2·614
δ	0·916	–	–
erel	0·141	0·158	0·161
Sub‐model 3 δ = ƒ(fruit)
B	44·49	–	–
τ	2·591	–	–
δ	0·918	0·916	0·911
erel	0·139	0·157	0·155

Each of the three sub‐models considers one of the parameters as being dependent on fruit position, the other two being constant. B (day) is the time at which θ, the cell proliferative activity, starts to decrease; δ is the relative decrease in proliferative activity; and τ (day) is the duration of one cell cycle .

Day 0 is considered as the seedling stage with one theoretical cell.

e_rel, relative root mean squared error.

SENSITIVITY ANALYSIS

The sensitivity analysis was performed on the model adjusted for fruit 1 considering that B was dependent on fruit position. To examine the sensitivity of the model to individual parameters, the computations of eqn (8) were compared after a ± 1 % variation of the parameter value. The later the decrease of the proliferative activity starts (increase of B), or the less one cell cycle lasts (decrease of τ), the higher the final number of cells (Fig. 3A and B). A 1 % increase in B or decrease in τ induces a 13 % increase in final cell number, while the opposite variation of B and τ induces an 11 % decrease in final cell number. The model was most sensitive to the relative decrease of proliferative activity after each cell cycle, δ, since a 1 % increase or decrease in δ induces, respectively, a 50 % increase or a 28 % decrease in final cell number.

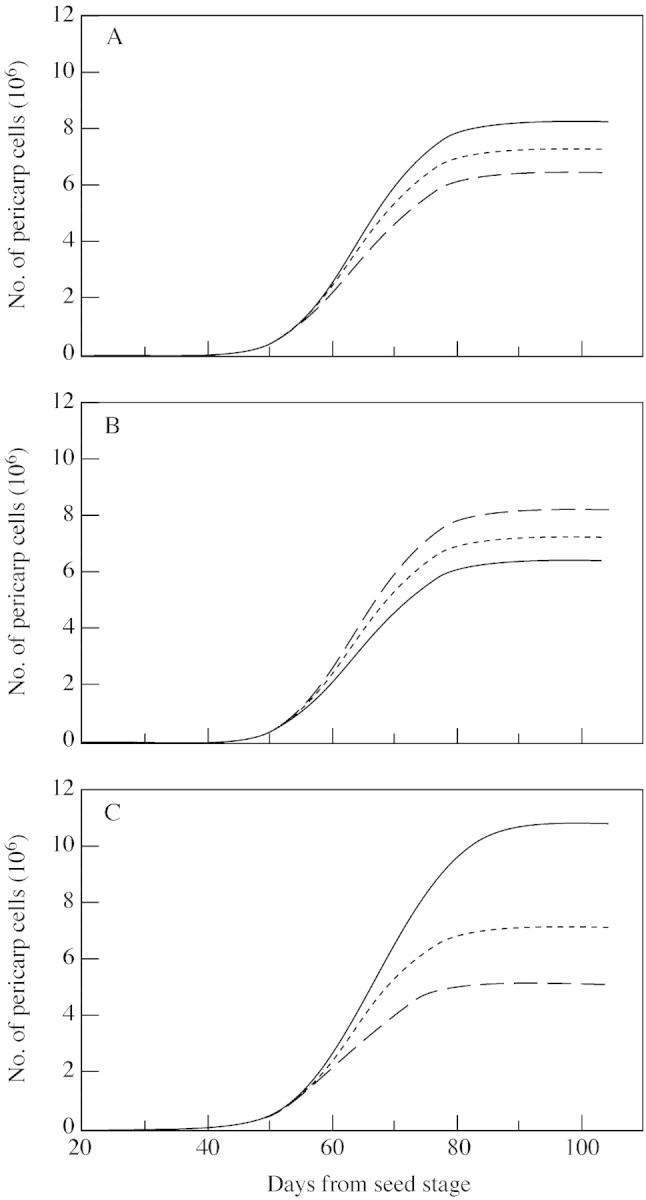
Fig. 3. Sensitivity analysis of the model to a ± 1 % variation of parameter B (A), τ (B) and δ (C). Broken lines represent the number of cells calculated by the model adjusted on experimental data obtained for fruit 1. Bold and thin lines are the number of cells calculated by the model after a respective 1 % increase or 1 % decrease of the parameter value.

To investigate the interaction between parameters, the sensitivity analysis was extended by increasing or decreasing simultaneously two of the three parameters. The parameters B and τ have opposite and additive effects since increasing or decreasing both of these parameters does not change the model output (Fig. 4A). The interaction between δ and B was more than additive when B was increased, and less than additive when B was decreased (Fig. 5B and C). For instance, a 1 % increase in both δ and B increased the final cell number by 69 %, which is more than the sum of the 50 and 13 % increases, respectively, obtained after the individual increase of δ and B. On the contrary, a 1 % decrease in both δ and B induces a 36 % decrease in final cell number, which is less than the sum of individual effects of δ and B (–28 % and –11 %, respectively). The interaction between δ and τ was similar to that between δ and B, taking into account that increasing τ or decreasing B amounts to the same thing, and vice versa.

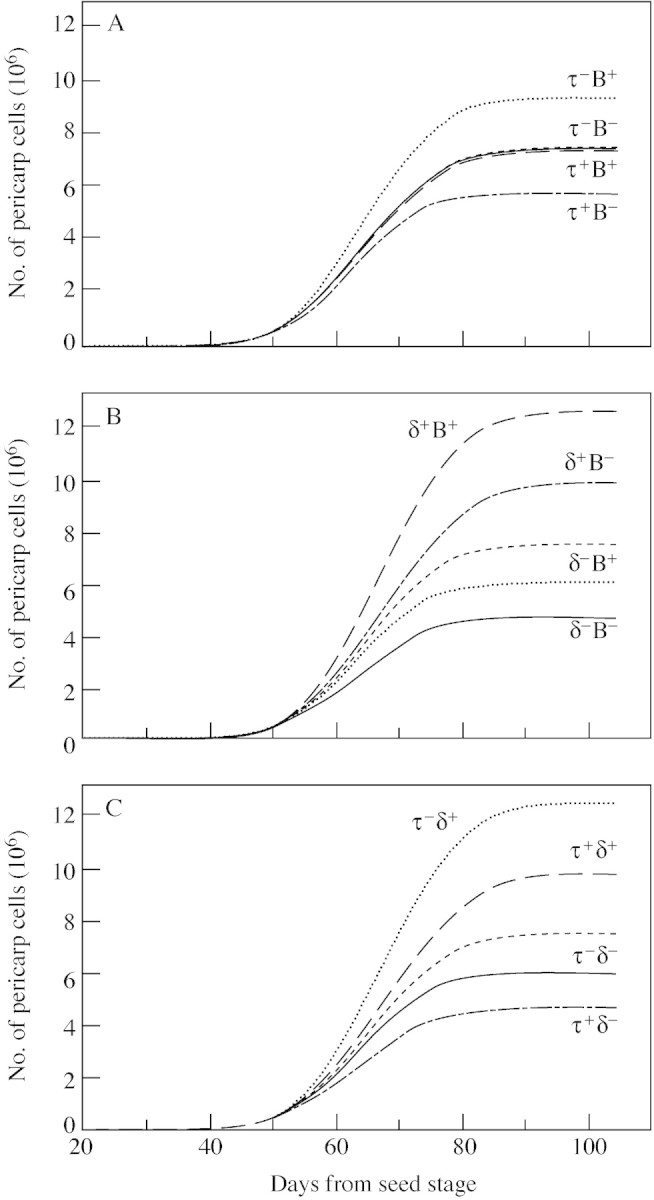
Fig. 4. Sensitivity analysis of the model to the simultaneous variation of two parameters by ± 1 %: B and τ (A); B and δ (B); and τ and δ (C). Broken lines represent the number of cells calculated by the model adjusted on experimental data obtained for fruit 1. + and – indicate, respectively, 1 % increase or 1 % decrease of the parameter value.

A 1 % variation in all three parameters (not shown) induces variations of final cell number ranging from –28 % (increasing τ and decreasing δ and B) to +91 % (decreasing τ and increasing δ and B).

DISCUSSION

The deterministic model suggested here for the analysis of cell multiplication in growing fruit involves an exponential proliferative activity of cells from sowing to time B, which corresponds to about 10 d before anthesis of the first truss under the conditions described in the Materials and Methods. After this period, proliferative activity diminishes progressively as cell division proceeds. The model is adequate to describe the sigmoid growth of the fruit cell populations observed in tomato. The discrete model analysed here is comparable with the equation presented by Thornley (1976, 1981) in a continuous and differential form, with the dependence of the multiplication activity (which is in parallel to θ) on the population age being given as an empirical negative‐exponential function.

The question remains as to which of the three parameters is most dependent on fruit position. The duration of the division cycle may be influenced by environmental factors, such as temperature (López‐Sáez et al., 1969; Brown, 1976; Granier et al., 2000a), light (Brown, 1976) and soil water content (Granier and Tardieu, 1999; Granier et al., 2000a). In the present experiment, the environmental conditions were constant, which is why we assumed that τ was independent of fruit position. Ho et al. (1982/1983) pointed out that in tomato fruits, final cell number may be determined by the cell division activity during the first 1–2 weeks after fertilization. Comparing two fruit positions in the truss, Bohner and Bangerth (1988) concluded that a smaller number of cells at flower anthesis was responsible for a smaller final number of cells in tip fruit. Our model is in agreement with these hypotheses since, at anthesis, the simulated number of cells decreased from fruit 1 to fruit 5. For instance, when B was considered to depend on fruit position, the numbers of cells calculated at anthesis were 1·46 × 10⁶, 1·39 × 10⁶ and 1·27 × 10⁶ for fruits 1, 3 and 5, respectively. In the model, the final cell number is indeed affected by the proliferation activity before anthesis, which depends both on the time B at which the proliferation activity, θ, starts to decrease, and on the relative decrease of the proliferative activity, δ. δ may be assumed to be an intrinsic characteristic of cell division, thus independent of fruit position under stable environmental conditions. Finally, B would be the most appropriate parameter to account for differences in final cell number among fruits within the inflorescence. Assuming that all fruits from one truss were initiated from a single meristematic cell, cells of tip fruits have a longer history and have undergone more divisions, which may explain why the proliferative activity starts decreasing earlier.

Cell cycle duration, τ, was estimated as 2·6 d. This figure can be compared with observations of the cycle duration in other species. Richard et al. (2001) observed a cell cycle duration in Arabidopsis thaliana cell suspension culture of around 2 d during the first 5 d after dilution. Cell cycle duration in sunflower leaves was 1·3–1·7 d during the period of exponential increase in cell number (Granier and Tardieu, 1998). López‐Sáez et al. (1966) measured cycle duration in root meristems of Allium cepa at various temperatures, and found that as the temperature rose from 5 to 35 °C, the duration of the cycle decreased from 5·4 to 0·45 d. The duration of the mitotic cycle for fruit cells, as estimated in the present study, was comparable with values reported by Richard et al. (2001) for Arabidopsis thaliana cells and by López‐Sáez et al. (1966) for cells in root meristems.

The parameter δ describes the proportion of cell proliferative capacity remaining after a replication cycle. From eqn (2), it is apparent that (θ_m – θ_{m + 1})/θ_m = 1 – δ is the relative rate of decrease in proliferative activity after one division cycle. From our estimations, this relative rate was about 0·08 for cells of tomato fruit. This result can now be examined from the point of view of the hypothesis that the progressive shortening of telomeric DNA which accompanies the cell divisions is eventually the cause of the decrease in proliferative activity. If there were a linear relation between the rate of decrease of proliferative activity and the rate of shortening of telomeric DNA, and if the linearity coefficients were dependent on species, age of the individual and, perhaps, on other factors, the relative rate of the decrease in proliferative activity would have to be compared with the relative rate of shortening of telomeric DNA. Kilian et al. (1995) estimated the diminution in the number of telomeric repeats as 1·43 kb per cell division in barley, and noted that this value was much higher (by about an order of magnitude) than the respective value reported for human telomeres (Harley et al., 1990). However, the total human telomere length is approx. ten times less than that of barley. Therefore, we suggested that the comparison should be between relative changes in the numbers of telomeric repeats. The relative rate of telomeric DNA decrease in barley was 0·02 per cell division, and relative rates in human fibroblast in vitro population doublings were estimated from the data presented by Harley et al. (1990), as 0·01 per cell division in the foetal and newborn cell strains, and as 0·021 and 0·023 per cell division in the old and young adult strains, respectively. Thus, rates of relative DNA shortening for barley and human cells are comparable, and the relative DNA shortening rates are also comparable with the relative rate of proliferative activity decrease estimated above as 0·08 for tomato fruit.

If telomere loss ‘is the intrinsic timing mechanism that controls the number of cell divisions’ (Bodnar et al., 1998), this ‘biological clock’ may control the length of the period of intensive cell replication in fruit. The genetic timer (if not ‘destroyed’ by application of specific enzymes or hormones, as reviewed by Perrem and Reddel, 2000) counts and restricts the number of mitotic cycles, whereas the duration of each cycle depends on external conditions, such as temperature, radiation, etc. Hence, variations in the external conditions may change the total duration of the cell replicative stage of fruit growth. By studying the dynamics of fruit cell number and estimating the important parameters in the cell division process, we have been able to connect the eventual genetic mechanism underlying the early period of fruit development with the ecological factors that control this stage of growth.

Received: 14 August 2002; Returned for revision: 20 January 2003; Accepted: 25 March 2003