New Automated Single-Cell Technique for Segmentation and Quantitation of Lipid Droplets

Abstract

Lipid droplets are the major organelle for intracellular storage of triglycerides and cholesterol esters. Various methods have been attempted for automated quantitation of fluorescently stained lipid droplets using either thresholding or watershed methods. We find that thresholding methods deal poorly with clusters of lipid droplets, whereas watershed methods require a smoothing step that must be optimized to remove image noise. We describe here a novel three-stage hybrid method for automated segmentation and quantitation of lipid droplets. In this method, objects are initially identified by thresholding. They are then tested for circularity to distinguish single lipid droplets from clusters. Clusters are subjected to a secondary watershed segmentation. We provide a characterization of this method in simulated images. Additionally, we apply this method to images of fixed cells containing stained lipid droplets and GFP-tagged proteins to provide a proof-of-principle that this method can be used for colocalization studies. The circularity measure can additionally prove useful for the identification of inappropriate segmentation in an automated way; for example, of non-cellular material. We will make the programs and source code available to the community under the Gnu Public License. We believe this technique will be of interest to cell biologists for light microscopic studies of lipid droplet biology.

Introduction

Lipid droplets (LDs) are the primary storage organelle for triglycerides and cholesterol esters in eukaryotic cells (reviewed in Fujimoto and Parton 2011; Thiam et al. 2013). LDs can be found in virtually all mammalian cell types but are more prominent in some specialized cells. LDs in adipocytes are the primary site of long-term fatty acid storage in mammals, whereas LDs in hepatocytes are the major site of storage of fat in the liver. Excessive fat storage in the liver is common in individuals who consume a Western diet and is associated with metabolic syndrome, hypertension, atherosclerosis and an increased risk of type 2 diabetes mellitus (Krahmer et al. 2013). Excessive cholesterol accumulation in LDs in macrophages results in their conversion to foam cells, which play an important role in initiating the formation of atherosclerotic lesions (Adams et al. 1971; Krahmer et al. 2013).

Whereas LDs were previously considered inert stores of lipids, it is now appreciated that they are highly dynamic organelles (Farese and Walther 2009). The formation and destruction of LDs, as well as the multiple processes by which triglycerides and cholesterol are transferred to and removed from LDs are now active subjects of research by many cell biologists. Quantitative methods are needed to answer certain questions, such as whether new lipid is stored preferentially into existing or de novo LDs; whether there are distinct populations of LDs, as suggested by several studies (Hsieh et al. 2012; Martin et al. 2005; Wilfling et al. 2013; Wolins et al. 2005); and whether LDs undergo maturation processes at different stages of their life history.

LDs can be visualized with a variety of bright, hydrophobic dyes, including Bodipy (Harris et al. 2013), 1,6-diphenylhexatriene (Ranall et al. 2011) and Nile Red (Greenspan et al. 1985), permitting observation by fluorescence microscopy. Most LDs range in size from several hundred nanometers to several microns. LDs in adipocytes can be much larger, filling much of the cell volume, whereas some LDs may be 0.4 µm or smaller in diameter.

Smaller LDs are visualized as circular spots by light microscopy, which correspond to the point-spread function of the microscope and the focal plane. The shape of larger LDs is also typically circular or nearly circular, whereas clusters tend to be more irregularly shaped. The presence of clusters of LDs complicates quantitative image analysis, as individual LDs cannot be easily separated by thresholding (see Fig. 1). Watershed methods, originally developed to separate whole cells labeled with volume or surface markers, have also been used to segment LDs within single cells (Wilfling et al. 2013). Whereas watershed methods are more robust to LD clustering, they are highly sensitive to image noise and generally require some smoothing, which leads to a loss of resolution in order to prevent severe over-segmentation.

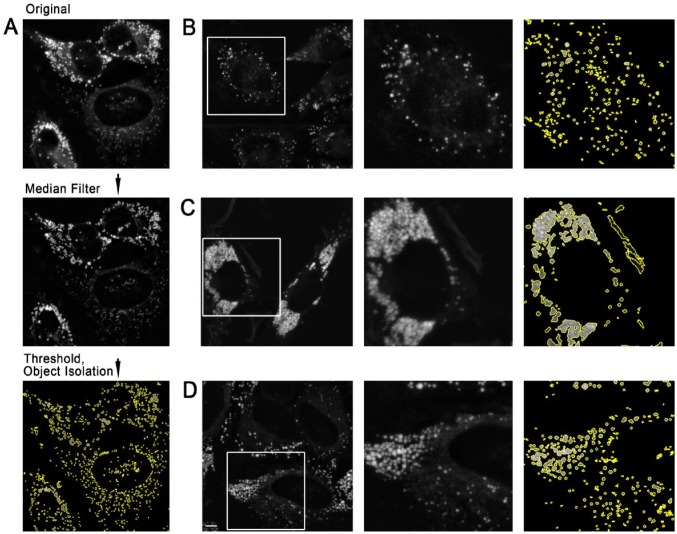
Figure 1.

Thresholding-based identification of lipid droplets (LDs) in HeLa cells with varying LD density. (A) Object identification strategy. A median-filtered background (neighborhood size, 128 pixels) was subtracted from the original image. The image was then thresholded, with pixels measuring <15% of the maximum pixel intensity set to zero. All contiguous sets of pixels were identified, and pixels in each cluster with a value less than 50% of the maximum pixel value for that cluster were set to zero. (B) HeLa cells incubated with 350 mM oleic acid for 24 hr and then stained with Nile Red. The field shown was selected to show an example with well-separated LDs. (C) HeLa cells incubated with 2 mM oleic acid for 24 hr and stained with Nile Red to generate large areas of near-confluent LDs. (D) HeLa cells incubated and stained as in (A), but field chosen to illustrate some degree of LD clustering under moderate labeling conditions. All source images (left; B, C, D) were prepared by projection and median filter background correction of z-stacks following the procedure detailed in the Materials & Methods. Scale, 5 µm.

In this study, we take advantage of the generally spherical nature of LDs to create a novel three-step hybrid method. In this method, an image containing candidate LDs and clusters is first segmented based on global and local thresholding, and each segmented object is then tested for circularity using a least-squares fit to a circular boundary. Objects established as nearly circular (within a threshold) are accepted as LDs. Remaining objects are accepted as clusters and are segmented using the standard Vincent and Solle watershed algorithm (Vincent and Soille 1991). An interesting feature of our method is that the circularity measure can also act as a quality control on the overall segmentation. We supply characterization and testing of the performance and limits of this method both on actual and simulated LD images, and additionally demonstrate the use of this methodology in the context of a proof-of-principle application. The current version is in the form of Unix command-line programs, which we have tested on Mac OSX but which should be portable to a variety of platforms. We have made this software available as open source under the Gnu Public License. Source code can be obtained from github.com/jfpresley2/lipid-droplet-segmentation.

Materials & Methods

Reagents

Defatted bovine serum albumin (defatted BSA), Nile Red, nocodazole, paraformaldehyde and oleic acid were obtained from Sigma-Aldrich (Oakville, ON, Canada). The Tip47-GFP expression vector was a kind gift of N. Wolins (St. Louis, MO). The GFP-Rab7 is previously described (Dejgaard et al. 2008). The GalTase-GFP (Cole et al. 1996b) is a kind gift of J. Lippincott-Schwartz (Bethesda, MD).

Cell Culture and Lipid Droplet Induction

HeLa cells obtained from the American Type Culture Collection (Manassas, VA) were grown as described (Dejgaard et al. 2008) in Dulbecco’s Modified Eagle’s Medium (DMEM) supplemented with 10% fetal calf serum, 2 mM glutamine, 150 mg/ml penicillin and 100 U/ml streptomycin (Invitrogen; Burlington, ON). Cells were grown in an incubator at 37C with 5% CO₂. HeLa cells were grown in MatTek dishes (MatTek, Inc.; Ashland, MD) for imaging. LD formation was induced by the addition of 50 µM, 350 µM, or 2 mM oleic acid conjugated to defatted BSA, as described in Martin and Parton (2008). Transfections were performed using Fugene HD Transfection Reagent (Roche Applied Science; Mannheim, Germany) according to manufacturer’s instructions. Cells were fixed 24–48 hr after oleic acid addition in 4% formaldehyde/PBS (pH 7.2) for 10 min. Cells were then washed with PBS, and stored at 4C immersed in PBS. Nile Red was prepared as a 1 mg/ml stock solution in DMSO. Prior to imaging, cells were stained with 30 ng/ml Nile Red in PBS (10 min, 37C) to visualize LDs, and taken immediately to the microscope stage.

Image Acquisition and Analysis

Image z-stacks were taken using a Zeiss LSM510 confocal microscope (Zeiss; Toronto, ON) using a numerical aperture (NA) 1.4, 63× plan-apochromat oil immersion, and a pixel size of 0.1 µm. Nile Red was visualized using the 543-nm line of a He-Ne laser, and a 560–615-nm band-pass filter. GFP was visualized using the 488-nm line of an Argon laser and a 505–530-nm BP emission filter. To increase the signal, the pinhole was set for a slice thickness of 2 µm, with an interval between slices of 1 µm. This resulted in an improved signal at the expenses of some out-of-focus fluorescence in the projected images. Line averaging of 4–8× was also used to minimize noise, which could interfere with the analysis. Images were exported as 12-bit TIFF files using the microscope software. For analysis, TIFF images were converted to PGM or PPM using the program “convert” in the open source ImageMagick package (http://www.imagemagick.org/). The other programs used were created for this project, and are described in the text. The included program “project” was used to perform a slice-by-slice background correction and additive projection. Briefly, a median-filtered background was calculated for each pixel utilizing a 128×128 background region centered on the pixel. The background was subtracted and negative pixels then zeroed. Images were projected by integer addition of the corresponding background-corrected pixels in each slice. The brightest pixel of the projected image was determined and the projected image was rescaled to a maximum value of 4095 prior to further analysis by a floating point division of each pixel by the maximum pixel value in the image followed by multiplication of the result by 4095.0 and rounding to the nearest integer value.

Creation of Simulated Images

Simulated images were created by first calculating LD diameters and locations in 2-D depending on the pattern desired, or at locations generated at random. Uniformly fluorescent spheres with the appropriate diameters were projected onto the selected locations on the 2-D grid, with the fluorescence intensity of each pixel representing the integrated projected fluorescence over that pixel. All simulated images were created to approximate the resolution expected on an image with 0.1-µm pixels taken with an objective with a numerical aperture of 1.4. This was done by subjecting the image to a Gaussian convolution with a standard deviation of 2.576 pixels. The image was then rescaled so that the brightest pixel had a value of 4095 followed by the addition of photon shot noise (always specified as the number of photons required to give a fluorescence value of 4095).

Photon shot noise is a major contributor to noise found in confocal images and arises from the fact that, in a single acquisition, the number of photons that contribute to an individual pixel while it is being recorded can be very small. Thus, the number of photons actually measured will be drawn from a Poisson distribution centered on the expected mean value. We modeled shot noise in the simulated images by assigning a fixed number of photons to the maximum pixel value (4095), which, in the simulation images, was generally also the brightest pixel in a simulated LD or cluster. A conversion factor (fluorescence per photon; FPP) could then be calculated; e.g., 400 photons/maximum pixel would indicate that the arrival of a single photon was equivalent to an FPP of 4095/400 or 10.2375 fluorescence units. A new pixel value was then calculated as follows, using the function gsl_ran_poisson() and the function gsl_ran_gaussian() from the open-source Gnu Scientific Library (Galassi et al. 2009). Calculations were done as follows, using double-precision floating point arithmetic, except for gsl_ran_poisson(), which returns integer values, with the final result rounded to an integer value and stored in a copy of the original image. First, the pixel value was converted to a mean photon count and this count was randomized as follows using gsl_rnd_poisson:

$$\text{mean photon count}=\text{pixel value}/\text{FPP}$$

$$\text{count}=gsl\_rnd\_poisson(meanphotoncount)$$

A new pixel value was generated by adding a Gaussian-distributed random number to count with a mean of 0 and a standard deviation of 1 (to ensure the final values are a continuous distribution). The result was then multiplied by the FPP to rescale it to the original range and the result converted to an integer by rounding.

$$\text{new value}=\text{FPP X}(\text{count}+gsl\_rnd\_gauss(1.0))$$

For mean photon counts of 10 or higher (i.e., well below threshold values set to zero), the distributions produced were close to a Gaussian with an SD of the square root of the count. Thus, for the purposes of this study, this model closely approximates other models of counting noise that use Gaussian distributions (e.g., in Constantino et al. 2005).

Software

Software was written in the D programming language (Alexandrescu 2010) as a series of programs designed to be run from a Unix command line. Programs were compiled using the freely available dmd compiler (Alexandrescu 2010) and run using the command-line interface under Mac OS10.6.8 (Snow Leopard). Source codes for the programs used for image analysis are hosted at github.com/jfpresley2/lipid-droplet-segmentation, along with a makefile and compilation instructions. These programs are designed to operate in a Unix or Unix-like environment and may be used or modified under the terms of the GNU General Public License version 2. Translation of the code to other C-family languages (e.g., C++, Java) should be straightforward.

Results

Background Correction and Thresholding Fail to Distinguish Correctly Segmented LDs from Clusters

We wished to test whether approaches previously developed to isolate and quantitate fluorescently labeled endosomes based on global and local thresholding would be sufficient to identify and quantitate LDs in fluorescence microscope images (Dunn et al. 1989). We therefore loaded HeLa cells with 50 µM–2 mM oleic acid for 24–48 hr, as described in the Materials & Methods, in order to obtain a range of LD densities for tests. As we found that LD density in HeLa cells was reduced at high confluence, we also varied the plating density. Low LD densities were defined as densities in which 75% or more of LDs were visibly separated from neighboring LDs. Under these low density conditions, objects isolated after thresholding were near-circular, consistent with LD morphology (Fig. 1A, 1B). In cells treated with 2 mM oleic acid, the highest concentration tested, the cytoplasm was full of LDs, which were adjacent (Fig. 1C). After thresholding and segmentation, more than 75% of fluorescence was found in large and irregular objects, which appeared to consist of multiple, circular structures that were touching, consistent with failure to segment large clusters of LDs (Fig. 1C). Some high-density LD clusters were also found localized to small regions of the cytoplasm (Fig. 1D) under lipid loading conditions (50–350 µM oleic acid), which have been frequently used in published experiments; thus, the problem cannot be easily bypassed simply by avoiding heavy loading conditions. We also found high-density LD clusters in HepG2, Chinese Hamster Ovary and COS7 cells upon moderate oleic acid loading (data not shown), suggesting that the tendency of LDs to cluster must be taken into account in any quantitation strategy.

Development of a Test to Distinguish Single LDs from Clusters

LDs are typically circular in fluorescence images, and are often nearly circular in electron microscopic images. We reasoned that clusters of LDs would be more irregularly shaped and that an automated test for circularity could validate correctly segmented LDs while flagging unsegmented clusters for special attention. To test for circularity, we modified our object isolation algorithm to extract the location of the boundary pixels of each spot. The array of pixel coordinates was then fitted to the equation of a circle using the Späth best-fit algorithm (Spath 1996). The standard deviation of the boundary pixels with respect to the circle was then computed and expressed in units of best-fit circle radius (Fig. 2A), giving a measure of quality-of-fit that can be compared between structures which may be of different sizes.

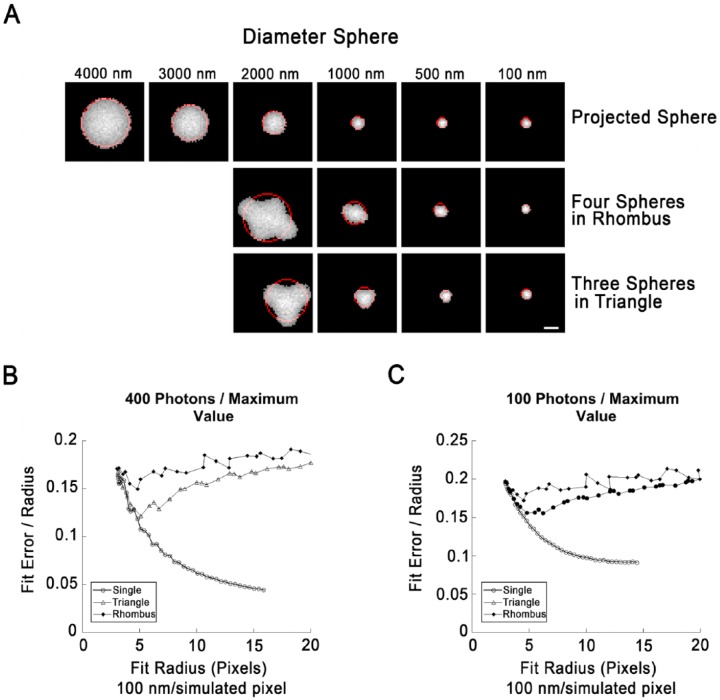
Figure 2.

Fits of circle to boundaries of single lipid droplets (LDs) or LD clusters in simulated images. (A) Illustration of simulated LDs arranged singly (top row) or as indicated. Simulated images were created by projection of a sphere onto a plane, preserving the integrated fluorescence intensity for each 2D pixel. The radius indicated at the top is the radius on the simulated image prior to processing (100 nm/pixel). The objects shown have been subjected to a Gaussian blur to simulate the effects of diffraction, followed by the application of simulated photon shot noise (400 photons/maximum pixel value), and clipping to their full width half maximum (FWHM). The boundary pixels were then extracted and the best-fit circle determined (red). (B) Fit error (SDBFC; standard-deviation best-fit-circle) as a function of fit circle radius for single LDs, clusters of three arranged in a triangle or clusters of four arranged in a rhombus created and processed exactly as described for (A). LDs in clusters were overlapped by 20% to prevent segmentation by the thresholding routine. Each point represents the mean value of 1000 simulations. Error bars are not shown since standard deviation of simulation runs was <0.1% for 100 nm LDs (the smallest size tested) for all three geometries. (C) Fit error as a function of circle radius exactly as in (B) except that shot noise was increased to 100 photons/maximum pixel value. Each point represents the mean of 1000 simulation runs. Standard deviation was <0.2% for 100 nm LDs for all three geometries. Scale, 10 simulated pixels (1.0 simulated µm).

To gain insight into whether this strategy could distinguish between single LDs and clusters, we created a simulation that projected spherical LD images onto a plane and added simulated photon shot noise to the image. Single or multiple LDs could be projected onto the same image. LD diameters (Fig. 2A) were assumed as 100 nm/simulated pixel. Projections were then subjected to a Gaussian blur (SD, 2.576 pixels) to approximate the effects of image blurring due to diffraction, assuming an NA 1.4-objective and 560-nm fluorescence imaging. Shot noise was then applied, with the brightest pixel of the LD corresponding to either 100 or 400 photons. These are realistic estimates because (1) Nile Red is brightly fluorescent and this facilitates the acquisition of low-noise images, and (2) confocal images are typically averages of several acquisitions.

Simulated images were created containing a single projected LD, three LDs arranged in an equilateral triangle with 20% overlap, or four LDs arranged in a rhombus with 20% overlap (Fig. 2A). Sizes of LDs were varied from 4 µm to 100 nm in 100 nm increments. Simulated objects were clipped to their full width half maximum (FWHM), as done for endosomal isolation, and a circle fit to the boundary pixels of the object using the Späth algorithm (Spath 1996). The standard deviation between the boundary pixels and the best-fit circle were calculated, and expressed in units of radius of the best-fit circle (standard-deviation best-fit-circle; SDBFC).

Under low-noise conditions (400 photons/max pixel), the spherical geometry could be easily distinguished from rhombi and triangles at large fit radii, with fit errors of 0.1 or less for the spheres, and ~0.13–15 for the other geometries. At fit radii of 5 pixels or less, the calculated fit error was similar under all conditions, suggesting, as expected, that this discriminator breaks down at small object sizes. Increased noise (100 photons/brightest pixel) gave similar results, but with increased fit error (<0.15 for sphere with radius ≥5 pixels). Clusters are likely to be more irregular than the test geometries (triangle and rhombus), which were intentionally chosen to approximate a circular object. This analysis suggests that an LD with a diameter >1 µm could be distinguished from a cluster in most cases utilizing SDBFC.

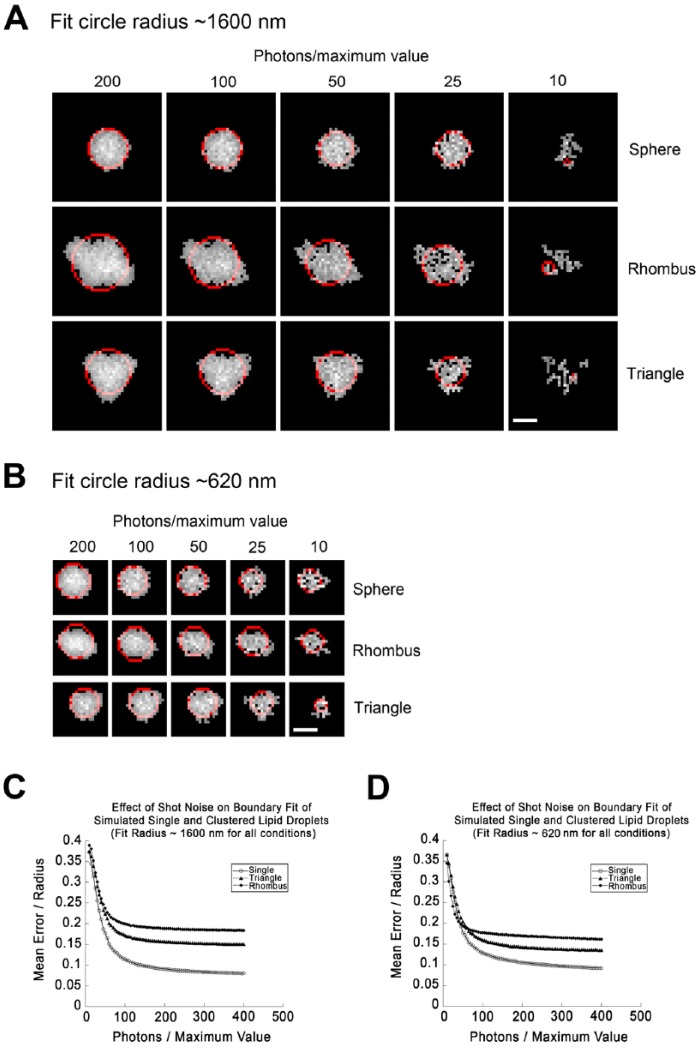
As SDBFC was noticeably affected by image noise (compare Fig. 2B and 2C), we conducted additional simulations in which we progressively increased image noise from 200 photons/maximum pixel to 10 photons/maximum pixel while holding the fit circle diameter at either of two values ~1600 nm (large) or ~620 nm (marginal). Image definition was markedly reduced by <50 photons/maximum pixel value (Fig. 3A, 3B), and extremely poor at 10 photons/maximum pixel value. Single LDs were well distinguished from clusters at 100 photons/maximum value, with discrimination dramatically reduced <80 photons/maximum value (Fig. 3C, 3D). This suggests that SDBFC can be used as a discriminator to distinguish LDs from clusters but that the image noise must be kept low by utilizing bright dyes to minimize detector gain and by image averaging or increasing integration times.

Figure 3.

Effects of increased noise on the ability to distinguish simulated spherical lipid droplets (LDs) from clusters. (A) LDs were simulated as described for Figure 2 to give a diameter for the fit circle of roughly 1600 nm. This corresponded to an initial simulated size of 2300 nm for a single LD, 1300 nm for each LD arranged in a triangle, and 1100 nm for each LD arranged in a rhombus. LDs were subjected to simulated photon shot noise with the brightest simulated pixel set to the indicated number of photons/pixel. Noised images were then thresholded to their full width half maximum (FWHM) and the boundary extracted and fit to a circle (red). Note that images degrade significantly as smaller numbers of simulated photons are sampled. (B) LDs simulated as in (A), but with sizes of LDs set to give a fit circle diameter near 620 nm for each geometry. This corresponds to an initial radius prior to processing of 400 nm for single LDs and 200 nm for each LD arranged in a rhombus or triangle. (C) Fit error (SDBFC; standard-deviation best-fit-circle) as a function of fit circle radius for single LDs, clusters of three arranged in a triangle, or clusters of four arranged in a rhombus with an overlap of 20% created and processed such that the fit circle diameter approximates 16 pixels (1600 nm) exactly as described for (A). Each point represents the mean value of 1000 simulations. Simulations were not included in the average if the structure was broken into more than one contiguous area. This was <5% of total simulations at 40 photons/maximum value for all geometries, but rejections for this reason rapidly increased at higher noise levels. (D) Effect of shot noise on fit error exactly as in (C) but with a fit circle diameter approximating 600 nm. Scale, 10 simulated pixels (1.0 simulated µm).

Assessing LD Segmentation Accuracy in Images of Cells

Overall, this analysis suggests that SDBFC can discriminate LDs from clusters in simulations, using plausible image acquisition conditions. To test whether SDBFC could discriminate LD clusters on real images of cells, we re-analyzed the same images shown in Figure 1, and additionally an image of cells stained for the Golgi protein GM130, which is not found on LDs, but instead on the Golgi apparatus, which consists of a ribbon of typically non-spherical stacks. Objects were considered circular if the fit circle was greater than 500 nm in radius (1 µm in diameter) and SDBFC was greater than 0.15. The SDBFC requirement was made less stringent for smaller objects (0.25 for radius 400–500 nm; 0.3 for radius 300–400 nm; 0.35 for radius <300 nm).

In an image with moderate LD clustering (Fig. 1D), spherical LDs were separated from non-spherical clusters consistent with expectations from visual inspection (Fig. 4, top row). Whereas a surprisingly large proportion of the fluorescent mass was in clusters, many clusters consisted of LDs connected by only a few pixels, suggesting that they could be resolved either with modification of the original segmentation algorithm or with a secondary segmentation step.

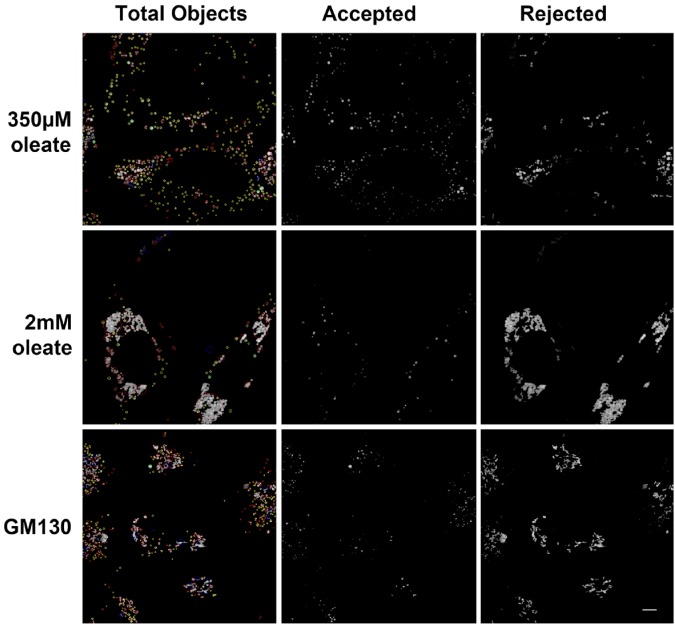
Figure 4.

Assessment of accuracy of lipid droplet (LD) segmentation by fitting a circle to boundary pixels. LDs in Nile Red stained HeLa cells from Figure 1 (top, middle) or the Golgi protein GM130 stained with a primary antibody against GM130 (Nakamura et al. 1995) and a Cy3-labeled secondary (bottom) were identified by background correction followed by local thresholding as described for Figure 1. The best-fit circle was determined for the boundary pixels of each object and goodness of fit calculated as SD of boundary pixels from the best-fit circle expressed in units of circle radius. Green and yellow circles indicate objects meeting the criteria for acceptance as LDs. In the left panel in each set of green circles indicates goodness of fit of 0.15 or less for objects with a radius of 5 pixels or larger. Yellow circles indicate goodness of fit of 0.35 or less for objects with a radius less than 5 pixels. Accepted objects are shown in the middle panels. Red and blue circles indicate objects rejected as not meeting the criteria for single LDs. Red circles indicate objects that did not meet these criteria, whereas blue circles indicate gross failures of fit. A blue circle indicates either that the area of the best-fit circle differs from the area of the object by >50%, or that the center of the circle is outside of the smallest bounding box encompassing all of the pixels of the objects. All rejected objects are shown in the right panels. Left panels were prepared by projection and median filter background correction of z-stacks following the procedure detailed in the Materials & Methods. Scale, 5 µm.

In an image of cells with severe LD clustering (Fig. 1C), the algorithm identified a small number of round structures, and correctly identified that most of the fluorescent mass was in clusters (Fig. 4, middle row). Whereas the clusters could be visually separated into LDs, it was not obvious if further automated processing was possible.

Overall, this analysis suggests that single LDs could be separated from clusters in real images, but also that LD clusters are a significant portion of the total LD mass even at moderate levels of oleic acid loading. Nevertheless, a strategy was suggested to target clusters for a secondary segmentation step.

Secondary Watershed Screening

Watershed algorithms are a family of algorithms that divide an image into regions surrounding local minima, expanding the minima until the regions meet, and creating boundaries at the meeting points (Roerdink and Meijster 2001). Watershed algorithms are frequently used to segment cells in high-throughput screening applications. We reasoned that inversion of pixel values in an image of fluorescent LDs (e.g., Fig. 1C) would result in local minima at the center of many LDs, and that application of a watershed algorithm to such an image could serve as an effective secondary segmentation step.

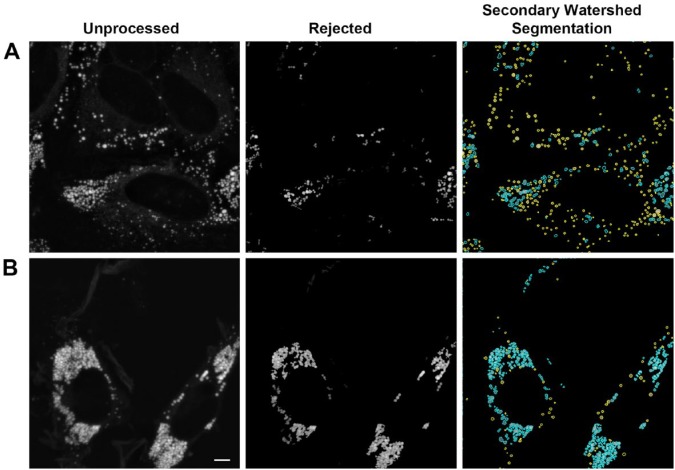
We implemented the Vincent and Soille watershed algorithm (Vincent and Soille 1991), and integrated it with our previous segmentation approach. In the hybrid approach, we first segmented the image as previously described, and then passed regions that did not pass the test for circularity onto the watershed algorithm. To reduce the effect of image noise on the algorithm prior to application of the watershed algorithm, we applied a Gaussian blur with a standard deviation of 2.5 pixels. After applying the watershed algorithm to the images, pixels at watershed boundaries were set to zero. This permitted the simple definitions of objects as contiguous areas of pixels as done previously for thresholding-defined objects. Objects with less than six pixels were deleted, both in the first and the second object isolation stage. Clusters were broken up into objects that appeared to correspond to individual LDs, both in images with moderate clustering (Fig. 5A; blue outlines in right panel) and those with severe clustering (Fig. 5B; blue outlines in right panel). The isolated structures often appeared less circular than LDs isolated by thresholding alone. This non-circularity was often visible in the original images, suggesting that LDs in clusters may sometimes have their shape distorted due to packing interactions. However, when the watershed algorithm was applied without a pre-smoothing step or was applied to invalid data in the form of a reflection image of the coverslip, dramatically non-circular shapes were obtained, suggesting that the same circularity measure used for the initial separation of LDs from clusters would be useful as an overall quality control measure.

Figure 5.

Processing of lipid droplet clusters with watershed segmentation. Images from the top two rows of Figure 4 are shown. Left panel shows the unprocessed image (previously prepared by projection and median filter background correction of z-stacks following the procedure detailed in the Methods & Materials). Middle panel shows structures that fail to meet the criteria for identification as LDs (identical to right panel, Figure 4). Right panel shows all LDs originally accepted (yellow boundaries), and the result of applying a watershed segmentation to the rejected structures (blue boundaries). Scale, 5 µm.

Effectiveness of Three-Stage Segmentation Compared to Thresholding on Simulated Images

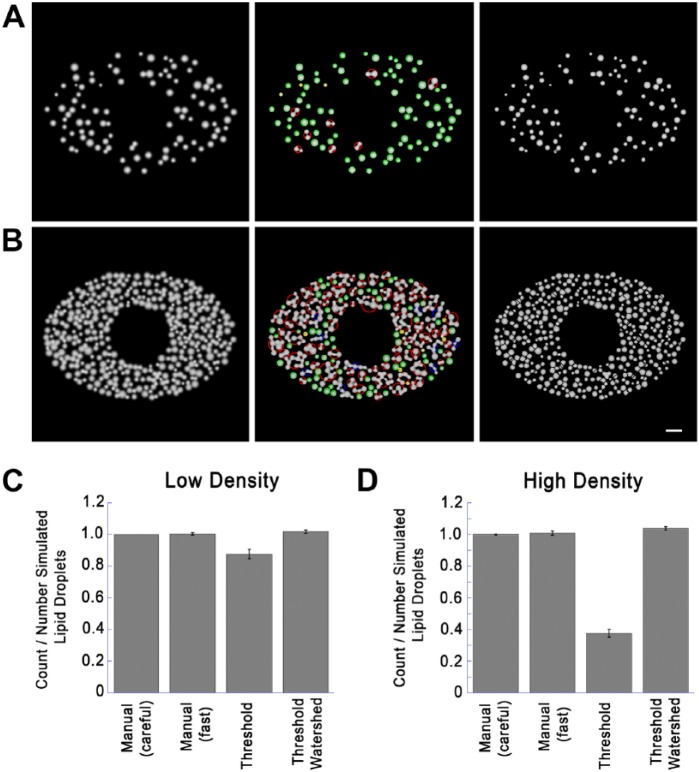
To assess the effectiveness of the three-stage segmentation technique described here compared to the most commonly used techniques, we generated images containing random patterns of LDs in simulated cells at preselected low or high densities. Simulated LDs were placed at random into an ellipse with a major axis of 300 pixels and a minor axis of 200 pixels with the exception of a 100 pixel exclusion zone to simulate the nucleus (Fig. 6A, 6B). LD diameter was taken from a Gaussian distribution (mean diameter 20 pixels or 2.0 simulated microns; standard deviation 4 pixels). Images were then blurred using a Gaussian convolution (SD, 2.576 pixels) to approximate the resolution of a NA 1.4 objective at a pixel size of 0.1 µM pixels and shot noise added as described in Methods (400 photons / maximum pixel). Droplets were added at random until >20% of the total usable area (the inside of the ellipse excluding the nucleus) was covered (low density) or >70% of the usable area was covered (high density). Droplets were allowed to overlap up to 20% of their diameters. To compare the effectiveness of three-stage segmentation to other techniques we generated ten low-density images (95 – 102 lipid droplets / image) and ten high-density images (378-403 lipid droplets / image). Representative images generated can be found in Figure 6a (low density) and 6b (high density). All images were quantitated using simple thresholding and object isolation, by careful or rapid manual counting, or with the same three-stage segmentation procedure used for the analysis described in Figure 5. Manual counting was done blindly without knowledge of the true number of lipid droplet in the simulated images. “Careful” manual counting was done with instructions to obtain as close as possible the true number even if additional time was required (up to 15 min. / images for the high density images). “Rapid” manual counting was done quickly on printouts of images, marking each droplet when counted. Simple thresholding and three-stage segmentation were done using the procedures in Figure 1 and Figure 5 respectively. Results were then divided by the true number of droplets, and results from the ten images averaged. Results are shown in Figure 6c (low density) and Figure 6d (high density).

Figure 6.

Comparison of Quantitation Techniques on Simulated Images. (A) Low density simulated cell images created with a low density of lipid droplets (LDs; 20% of cell area covered, as described in detail in the text. Left image shows the image before processing. Middle image is after thresholding and testing for circularity. Green and yellow circles indicate structures accepted as circular, exactly as in Figure 4. Red and blue circles indicate structures not accepted as circular, and passed to the watershed routine for further segmentation. Right image is a composite showing circular structures without further processing and non-circular structures segmented by setting watershed boundaries to zero. (B) Simulated image was created and processed identically as in the panels in (A) but with LDs added until 70% of the usable area was covered (high density). Left panel shows the original image. Middle image shows identification of circular and non-circular structures color-coded as in (A). Right image is a composite showing circular structures without further processing, and non-circular structures segmented by setting watershed boundaries to zero. (C) Ten low-density images were created exactly as described for the left panel in (A) with random LD patterns (20% of usable image area covered). The number of simulated LDs was recorded for each image, and LD number was then determined as indicated. Shown for each condition is the mean ± SD of counted/actual LDs. Details on each method used are described in the text. (D) Ten high-density images were created and processed exactly as described for the left panel in (B) (70% of simulated cytoplasm covered). LD count was then determined by the indicated techniques as described for (C) and divided by the number LDs rendered. Shown is the mean ± SD of counted/actual LDs. Micron bar 50 pixels (5 simulated µm).

We found that both rapid and careful manual counting gave accurate results on the test images (Fig. 6C, 6D); although, a time frame of 5–15 min was required per image to count the LDs on the high-density images. In contrast, simple thresholding and three-stage segmentation required less than 1 sec/image. Thresholding followed by object isolation was effective on the low-density images (Fig. 6C) but severely undercounted LDs on the high density images (Fig. 6D). Three-stage segmentation counted LDs almost as accurately as manual counting on both the low-density and high-density images, although there was some over-segmentation by the watershed routine leading to a count slightly higher than the true count (Fig. 6C, 6D). Thus, the three-stage segmentation routine was remarkably accurate, even for LDs at a high density, where simple thresholding was not effective.

Colocalization of LDs Identified by Three-Stage Segmentation with Fluorescently Tagged Organelle Markers

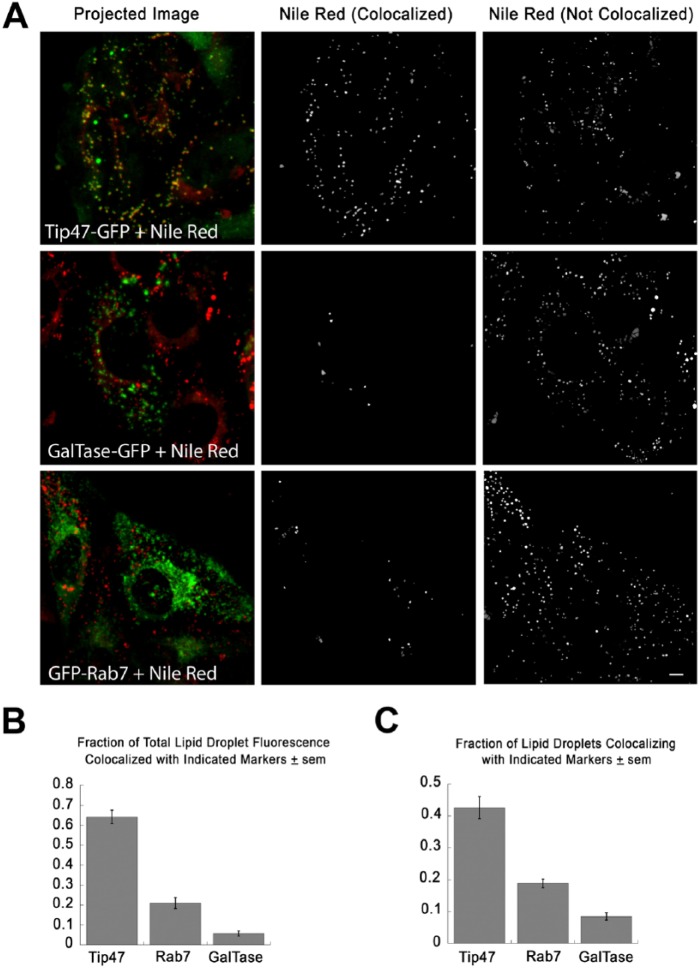
To test if the three-stage segmentation described could be applied to a realistic problem, we transfected HeLa cells with (1) PAT protein, Tip47-GFP, which is known to associate with LDs (Wolins et al. 2005); (2) GFP-Rab7, which associates with late endosomes/lysosomes (Jordens et al. 2001); or (3) GalTase-GFP (Cole et al. 1996b), which associates with the Golgi apparatus. Cells were then incubated with 350 µM oleic acid for 24 hr. For the last 6 hr, cells transfected with GalTase-GFP were additionally treated with 5 µg/ml nocodazole to break the Golgi into small mini-stacks localized randomly in the cytoplasm (Cole et al. 1996a), but not known to associate with LDs. Cells were then fixed, stained with Nile Red, and images (10 images per condition) acquired as described in the Materials & Methods. Confocal z-stacks were background-corrected and projected as described in the Materials & Methods. Red and green channels in each image were then processed separately using the two-step segmentation previously described. Objects in the Nile Red image were scored as colocalized if >30% of the pixels overlapped with objects in the green image. Remaining objects were scored as non-colocalized. All steps were incorporated into a procedure, which outputs the colocalized and non-colocalized objects into separate images (Fig. 7A; middle and right column, respectively) and also generated text output with statistics on each object (summarized in Fig. 7B and 7C). Cell areas were selected manually with an ImageJ (NIH, Bethesda, MD) macro, and output text filtered using a script written in the open-source Ruby language to compile object statistics for individual cells. A minimum of 12 cells were scored for each condition.

Figure 7.

Use of three-stage segmentation to assess colocalization of lipid droplets (LDs) with GFP-tagged proteins. (A) HeLa cells were transfected with the indicated proteins and incubated for 24 hr with 350 µM oleic acid, fixed and stained with Nile Red. GalTase-transfected cells were additionally treated with 5 µg/ml nocodazole for 6 hr to break the Golgi into large numbers of mini-stacks. The left panels show the merged images. Note that the LD protein Tip47-GFP (green) colocalizes well with LDs (red), whereas GalTase-GFP and GFP-Rab7 colocalize less well. Images were processed using the three-stage segmentation described in Figure 5. Nile Red-stained structures, in which 30% or more of total pixels overlap with objects in the similarly processed GFP image (colocalized), are shown in the middle panels, and all of the other Nile Red-stained structures (not colocalized) are shown in the right panels. (B) Sum of fluorescence of LDs colocalized with each of the protein markers tested and divided by total LD fluorescence in the same cell. Each bar shows the mean calculated from at least 12 cells ± SEM. All differences were significant using a student’s t-test (p<0.0001). The “Projected Images” (Left) were previously prepared by projection and median filter background correction of z-stacks, as detailed in the Materials & Methods. (C) Fraction of total isolated LDs colocalized with each of the protein markers tested. Each bar shows the mean of at least 12 cells ± SEM. All differences were significant as determined using a student’s t-test (p<0.0001). Scale, 5 µm.

The majority of Nile Red-stained fluorescence (>60% of fluorescence in colocalized structure) was found to colocalize with Tip47-GFP by this measure (Fig. 7A, 7B), whereas only a small proportion of Nile Red-stained fluorescence colocalized with GalTase-GFP. There was an intermediate level of colocalization (<20%) with Rab7-GFP. This could be random colocalization due to the very high density of Rab7-labeled punctae, or might represent autophagic delivery of LDs to lysosomes. Overall, the results were consistent with our expectations, and suggest that the procedures described here may be useful for quantifying colocalization of LDs with tagged markers.

The current study demonstrates one possible strategy for the quantitation of LDs in microscope images and, under our test conditions, the three-stage segmentation procedure provides good results in assessing colocalization of LDs with marker proteins. This suggests its use in a number of applications, including scoring the association of LDs with PAT proteins, Rab proteins, or proteins involved in lipolysis. The total image processing time, including all curve fits, and both the primary and secondary segmentation routines was typically ~3 sec for a 1000×1000 pixel image with several hundred objects in each channel. This is adequate for use in general cell biology applications, and could likely be sped-up considerably if needed for high-throughput routines, as a major portion of the total running time is spent in curve fits of circular boundaries using a reliable but fairly slow iterative algorithm (Spath 1996) run for a fixed (rather large) number of iterations.

Discussion

Colocalization of structures can be assayed by methods applied to pixels throughout the entire image (e.g., Pearson’s Correlation Coefficient) or by identifying objects and measuring overlap. The first approach requires no special pre-processing of the image but does not distinguish between object-localized fluorescence and non-object-localized fluorescence (for instance, the large, relatively uniform cytoplasmic pool of Rab7). If colocalization is assayed object-by-object using a measure of overlap (e.g., by individual LDs), accurate segmentation becomes important. Examining colocalization at the level of individual endosomes is important in defining and distinguishing sorting endosomes that contain transferrin and LDL from recycling and late endosomes, which contain only one of the two markers (Dunn and Maxfield 1992). Each of these approaches has strengths and weaknesses and may be applied in particular cases. One case where the analysis of colocalization at the level of individual LDs could be important would be following lipid tracers in pulse-chase experiments or following the fates of distinct lipid species, which may go, in some cases, to distinct populations of LDs (Hsieh et al. 2012). In this case, the approaches described here may prove useful. A further advantage of identifying LDs with circular boundaries is that, in cells stained with volume dyes (e.g., Nile Red), it may be possible to estimate the volume of a subset of spherical LDs of known diameter, and to use these as calibration standards to estimate the total volume of LDs on a per-cell basis. We are currently assessing the feasibility of this approach.