A Relationship between the Transient Structure in the Monomeric State and the Aggregation Propensities of α-Synuclein and β-Synuclein

Abstract

α-Synuclein is an intrinsically disordered protein whose aggregation is implicated in Parkinson’s disease. A second member of the synuclein family, β-synuclein, shares significant sequence similarity with α-synuclein but is much more resistant to aggregation. β-Synuclein is missing an 11-residue stretch in the central non-β-amyloid component region that forms the core of α-synuclein amyloid fibrils, yet insertion of these residues into β-synuclein to produce the βS_HC construct does not markedly increase the aggregation propensity. To investigate the structural basis of these different behaviors, quantitative nuclear magnetic resonance data, in the form of paramagnetic relaxation enhancement-derived interatomic distances, are combined with molecular dynamics simulations to generate ensembles of structures representative of the solution states of α-synuclein, β-synuclein, and βS_HC. Comparison of these ensembles reveals that the differing aggregation propensities of α-synuclein and β-synuclein are associated with differences in the degree of residual structure in the C-terminus coupled to the shorter separation between the N- and C-termini in β-synuclein and βS_HC, making protective intramolecular contacts more likely.

Intrinsically disordered proteins (IDPs) are involved in myriad biological processes, including cellular signaling, molecular recognition, and transcriptional regulation.¹⁻⁵ Additionally, members of this class of proteins have been implicated in a number of debilitating protein misfolding disorders.⁶ For instance, Aβ peptides and α-synuclein (αS) are the primary constituents of the amyloid deposits found in Alzheimer’s disease and Parkinson’s disease, respectively.⁷⁻⁹ A description of the native state ensembles of IDPs in terms of the constituent structures and their relative populations is vital to understanding both the function and the aggregation process of these proteins. The absence of persistent secondary and tertiary structure elements in IDPs does not preclude the presence of well-defined conformational preferences. Indeed, residual structure, often in the form of transient long-range contacts, has been detected in many IDPs,¹⁰⁻²² and some exhibit pockets of structure that have a propensity to bind small molecules.^23,24

The heterogeneity and broadness of the ensembles of structures characteristic of disordered states of proteins make the determination of the conformational properties of IDPs particularly challenging. For example, nuclear Overhauser effect (NOE)-based nuclear magnetic resonance (NMR) measurements are sensitive only up to separations of ∼0.5 nm, the result being that transient tertiary interactions in disordered states are unlikely to be detected using this approach. Despite this limitation, it has been possible to extract some structural information about disordered states from certain types of X-ray techniques and NMR spectroscopy measurements. For instance, small-angle X-ray scattering (SAXS)^25,26 and diffusion NMR spectroscopy²⁷ have been used to determine the molecular dimensions of IDPs. NMR observables such as residual dipolar couplings (RDCs) have proven to be a useful source of detailed structural information about disordered states,^{10,14,16,28−33} and methods are also emerging for utilizing chemical shifts.^{18−22,34−37}

Paramagnetic relaxation enhancement (PRE) experiments overcome the limitations of NOE measurements in probing the conformational properties of IDPs by utilizing the longer-range dipolar interactions between unpaired electrons in paramagnetic probes and atomic nuclei, which can be detected experimentally at distances up to ∼2.0 nm. The paramagnetic probe is often a free radical, typically a nitroxide spin-label covalently attached to a cysteine residue introduced into the protein of interest by site-specific mutagenesis. ¹H–¹⁵N HSQC spectra are then recorded with the spin-label in its paramagnetic (oxidized) and diamagnetic (reduced) states. The enhancement of the transverse relaxation of each proton due to the free electron of the oxidized spin-label can be quantified by comparing the intensities of each proton resonance measured for each spin-label state.³⁸ From the resultant intensity ratios (I_ox/I_red), the r^–6 average of the distance between the free electron and each proton (typically the backbone amide hydrogen) in the protein can be deduced.³⁸⁻⁴⁰ The fact that this distance is a time and ensemble average over the duration of the experiment and the ensemble of molecules present is an important consideration in the analysis of PRE data. When PRE–NMR experiments are conducted with the spin-label attached at a number of different positions in the protein, sufficient distances for characterizing key features of the conformational ensemble of the protein can be obtained.¹⁷

IDPs have also been characterized using molecular dynamics (MD) simulations,⁴¹⁻⁴⁶ although such techniques are hampered by the need to explore very large regions of conformational space. Because this is computationally expensive, implicit solvent models are often used.^17,47−53 Regardless of whether implicit or explicit solvent models are used, however, compact structures tend to be favored relative to more extended conformational states, most likely because most force fields have been parametrized to reproduce structural data for natively folded proteins. This is, however, an area of intense research in which rapid progress can be expected. Conducting the simulations at high temperatures allows more expanded structures to be sampled, but with the concomitant risk of compromising the physical relevance of the structures that are explored. Adding restraints derived from experimental data can, however, help to overcome this problem, while simultaneously biasing sampling toward relevant structures and restricting the conformational space that is explored, thereby reducing the simulation time and computational expense required for converged simulations.^17,54,55 Such restrained MD simulations can also be seen to aid the interpretation of experimental data in terms of structures and their populations, particularly for IDPs where the experimental data are in general averages over many disparate structures. Because of this factor, it is important to apply the restraints as averages, which can be achieved by averaging over time^56,57 or space,⁵⁸⁻⁶¹ i.e., over ensembles of structures. Care must be taken, however, to ensure that there are sufficient data to warrant the additional degrees of freedom that result from averaging over multiple replicas or time points. Additionally, nonlinearly averaged restraints can result in over- or underestimation of the population of structures with short distances.^62,63 In this context, it has been recently recognized that the use of replica averaging represents an implementation of the maximum entropy principle to incorporate the experimental information into the molecular dynamics simulations.⁶²⁻⁶⁵

In this work, we consider two related and similarly sized (127 and 140 residues) IDPs, α-synuclein (αS) and β-synuclein (βS).⁶⁶⁻⁶⁸ Despite their significant sequence similarity (Figure 1), these two proteins differ considerably in their behavior and medical significance. In particular, while αS aggregates to form the Lewy bodies characteristic of Parkinson’s disease, βS does not appear to aggregate in vivo and has even been shown to inhibit fibril formation by αS.^69,70 To explore the reasons for such differences between αS and βS, we introduced a construct of βS, βS_HC,⁷¹ which incorporates residues 71–82 of the non-β-amyloid component (NAC) region of αS (Figure 1) to determine whether this highly hydrophobic 11-residue region, which is absent in the sequence of βS, is sufficient to induce αS-like aggregation behavior in βS. Despite the fact that the NAC region is thought to be the primary determinant of αS aggregation⁷² and to be necessary for fibril formation, particularly residues 63–74,^73,74 the aggregation properties of βS_HC are closer to those of βS,⁷¹ which is much less aggregation prone than αS.

Figure 1.

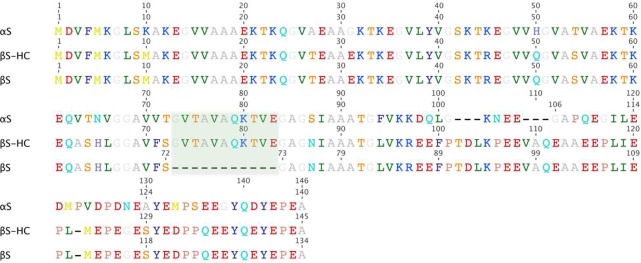
Alignment of the amino acid sequences of αS, βS, and βS_HC. Amino acids are colored according to the chemical nature of their side chains. The region shaded in Cambridge blue indicates the 11 residues from αS that were inserted into βS to form βS_HC.

To fully understand the reasons for these differing aggregation behaviors, it is necessary to characterize the ensemble of structures sampled by each protein under the same conditions under which aggregation occurs. αS in solution has been the subject of very many experimental,⁷⁵⁻⁸⁶ computational,^83,87 and hybrid^{10−12,17,19,20,88−92} investigations. While each study has highlighted different structural features, there is a general agreement that in solution, the C-terminal region of αS appears to provide some protection to the remainder of the protein, including the aggregation prone central NAC region. To date, the structural propensities of βS have been characterized only experimentally.^13,15,93 To build upon this, PRE–NMR experiments were conducted on βS and βS_HC, and distances derived from the experimental data were used as replica-averaged restraints in MD simulations to generate ensembles of structures representative of the native states of these proteins. Comparison of these ensembles and the ensemble of structures previously generated for αS reveals specific differences in the structural preferences of the three proteins and allows the effects of the hydrophobic core on the structural properties of these forms of synuclein, including their different aggregation propensities, to be examined at a molecular level.

Methods

Protein Preparation

¹⁵N-labeled βS and βS_HC were expressed and purified as described previously.⁷¹ A QuickChange (Stratagene) site-directed mutagenesis kit was used to engineer cysteine mutations at positions A30, S42, S64, F89, A102, S118, and A134 in βS and A30, S42, S64, A113, and A145 in βS_HC. Mutation sites were selected to minimize structural perturbations and to correspond as closely as possible to the αS mutation sites (Q24, S42, Q62, S87, N103, and N122). The nitroxide spin-label MTSL (1-oxyl-2,2,5,5-tetramethyl-3-pyrroline-3-methylmethanethiosulfonate) (Toronto Research Chemicals Inc.) was attached to the introduced cysteine residue in each variant in a thiol-specific reaction. The cysteine variants were first reduced with 5 mM DTT, which was subsequently removed using a 20 mL HiTrap desalting column (Amersham-Pharmacia) connected to an Akta fast protein liquid chromatography instrument (Amersham-Pharmacia). Immediately following DTT removal, the protein solution was incubated overnight with a 10-fold molar excess of MTSL. After incubation, unreacted MTSL was removed with a HiTrap desalting column. Uniform labeling was confirmed using mass spectrometry. Analysis of the spin-labeled variants using circular dichroism showed no evidence of any conformational changes. Moreover, the amide proton and nitrogen chemical shifts in the HSQC spectra were not significantly altered, even for residues in the vicinity of the spin-label (Figures S1 and S2 of the Supporting Information).

NMR Spectroscopy

Two-dimensional gradient-enhanced ¹H–¹⁵N HSQC of βS and βS_HC was conducted following protocols described previously¹² at the EPSRC-supported biomolecular NMR facility (Department of Chemistry, University of Cambridge) on a Bruker Avance 700 MHz spectrometer operating at 10 °C. Experimental samples contained 100 μM uniformly ¹⁵N-labeled protein with MTSL attached in 10 mM sodium phosphate (pH 7.4), 100 mM NaCl, and 10% D₂O. Control samples contained 100 μM ¹⁵N-labeled protein and 100 μM spin-labeled protein. The uniformity of the I_ox/I_red calculated from the control spectra showed that there were no complications arising from the reduction method and that aggregation did not occur. Backbone NMR assignments for αS and βS were obtained by standard triple-resonance methods as previously described.^71,75 Assignment of βS_HC was obtained with truncated triple-resonance CBCA(CO)NH and HNCO experiments, and an overlay of the ¹H–¹⁵N HSQC spectra confirmed that the chemical shifts of the added and original residues conformed to the chemical shifts of these residues in αS and βS, respectively (Figure S3 of the Supporting Information). For each spin-labeled mutant, an HSQC spectrum was first acquired with the label in its oxidized state. A 5-fold molar excess of sodium ascorbate was then added from a concentrated stock solution to reduce the spin-label without altering significantly the sample volume or pH. After incubation for at least 20 h, a second HSQC spectrum was acquired with all parameters remaining unchanged. HSQC spectra were collected using 16 scans per increment, with 1024 complete points for the direct dimension and 128 complex points for the indirect dimension. NMR data were processed with NMRPipe⁹⁴ and analyzed with Sparky.⁹⁵ Harsh resolution enhancing functions were not used to avoid nonuniform effects on cross-peak intensities, and cross-peaks exhibiting severe overlap were omitted from further analysis.

Distance Calculations

The electron–proton distances were calculated from the intensity ratios (I_ox/I_red) as described previously,¹² including the modifications introduced by Allison et al.¹⁷ as detailed below. Residue-specific values of R₂ were used where available; otherwise, the average over all residues was used.

Examination of the effect of introducing uncertainty of up to 15% in I_ox/I_red on the calculated distance showed that variation of up to 10% in I_ox/I_red results in propagated uncertainties of less than −0.19 or 0.38 nm in the calculated distance, which is a tolerable level. Distances were therefore used as restraints only if the difference between each replicate value of I_ox/I_red and the average value was less than 10% of the average I_ox/I_red value. The fraction of the experimental data that was discarded in this way for each protein is listed in Table 3 along with the total number of distance restraints for each protein. For each protein, 20% of the distances were removed from the “working” data set to be used for independent cross-validation.

Table 3. Summary of the Experimental Restraints and How Well They Were Satisfied during the PRE-RMD Simulations^a.

	data				Q values
protein	NPRE	NwPRE	NfPRE	% discarded	QRh	QwPRE	QfPRE
αS	595	476	119	17	0.006	0.19	0.20
βS	635	508	127	17	0.005	0.20	0.19
βSHC	578	462	116	3	0.020	0.20	0.28

^aN_PRE is the total number of distances derived from the PRE–NMR experiment, and N_wPRE and N_fPRE are the numbers of distances in the working and free data sets, comprising 80 and 20% of the total data, respectively. The percentage of the experimental data that was discarded due to uncertainties of >10% is also shown. The Q values (eq 8) quantify how well the experimental ⟨R_h^–1⟩^–1 (Q_Rh) and the working (Q_wPRE) and free (Q_fPRE) distances were satisfied by the ensemble of structures obtained using PRE-RMD.

During ensemble-averaged simulations using PRE-derived distance restraints, the calculated distance, d_ij^calc(t), is allowed to vary freely within d_ij(t) – L and d_ij^exp(t) + U, where L and U are the distances to the lower and upper bounds, respectively, of the flat bottom of the harmonic square well. Detailed investigations using synthetic data have shown that the optimal choices for L and U to best reproduce the distribution of distances as well as the r^–6 average are 0.1 and 0.8 nm, respectively.^17,96

As a general rule, I_ox/I_red values of <0.15 are unreliable,³⁸ as any experimental uncertainty is large relative to the size of the measured I_ox/I_red. Distances calculated from experimental I_ox/I_red values of <0.15 were therefore assigned only an upper bound corresponding to d_ij^0.15 + U, where d_ij is the distance calculated from an I_ox/I_red value of 0.15. The nature of the equations used to calculate the distances means that for a high I_ox/I_red, a small change in I_ox/I_red results in a large change in the calculated distance. Thus, I_ox/I_red values of >0.85 were used as “negative” restraints by assigning only a lower bound corresponding to d_ij^0.85 – L, where d_ij is the distance calculated from an I_ox/I_red value of 0.85.

Molecular Dynamics Simulations

All simulations were conducted using an in-house version of the CHARMM biomolecular simulation package⁹⁷ that has been modified to allow restraints to be applied across multiple replicas. The Newtonian equations of motion were integrated using the Velocity Verlet algorithm,⁹⁸ and the Nose-Hoover thermostat^99,100 was employed so that a canonical ensemble was sampled. The CHARMM19 polar hydrogen representation¹⁰¹ was used, and bond lengths were constrained with the SHAKE algorithm,¹⁰² allowing for an integration time step of 2 fs. A set of unrelated, expanded starting structures for each protein were chosen from high-temperature (500 K) simulations with the EEF1¹⁰³ implicit solvent model. The final ensemble for each simulation was obtained by pooling together all of the structures obtained during the production phase; if multiple replicas were used, these were pooled, as well.

Random Coil Model

A reference random coil model for each protein was produced by truncating the nonbonded interactions so that only the repulsive part of the Lennard-Jones potential remained. Molecular dynamics simulations were run in vacuum with no electrostatic interactions. The temperature, T, was typically 500–600 K to enhance the rate of sampling, but the nature of the resulting ensemble was similar at lower values of T. The coordinates were saved every 20 ps for 200 ns, giving 10000 structures in total.

The intensity ratios expected for a purely random coil were computed by first calculating the r^–6-averaged distances between the Cα atoms of the spin-labeled residues and the amide hydrogens of all other residues. These distances were converted into intensity ratios by following the inverse of the procedure used to calculate distances from intensity ratios.

Molecular Dynamics Simulations with Replica-Averaged Distance Restraints

Restrained simulations were conducted using molecular dynamics with replica-averaged distance restraints derived from PRE–NMR measurements. In this approach,^{47,50,54,59,104−113} the restraints are applied to multiple independent replicas simulated in parallel. A restraint coordinate, ρ, is defined as the difference between the current average of each observable across all replicas, f_i^calc, and the experimentally derived restraint, f_i, averaged over all N^res restraints:

1

where f_i^exp refers to the r^–6-averaged distance d_ij derived from the experimental PRE–NMR data as detailed above and f_i^calc was calculated from the simulated structures according to

2

where r_ij,k(t) is the distance between residues i and j calculated from replica k of the restrained ensemble at time t and N^rep is the number of replicas. r_ij,k was defined as being between the Cα atom of spin-labeled residue i and the amide hydrogen of residue j. A flat bottom restraint potential was used, meaning that the contribution of a given distance d_ij to the restraint coordinate is zero if d_ij^exp(t) – L < d_ij(t) < d_ij^exp(t) + U.

An energy penalty of the form

3

is added to the potential energy if ρ(t) > ρ₀(t), where

4

and α is a force constant associated with the restraints. In this way, as the simulation proceeds, the ensemble of structures is progressively biased toward structures that, on average, satisfy the restraints.

The replica-averaged MD simulations were conducted using the SASA^114,115 implicit solvation model with default cutoff distances for nonbonded and electrostatic interactions and rectangular periodic boundary conditions. Following the protocol developed using synthetic data for αS,¹⁷ 24 replicas were simulated in parallel. The molecules were first heated to 700 K in 50 K increments (10 ps per temperature), and then α was increased from its starting value of 500 kcal mol^–1 Å^–2 to its final value of 364500 kcal mol^–1 Å^–2 by a factor of 3 every 10 ps. After a brief equilibration (200 ps), the coordinates were collected every 5 ps for 400 ps per replica, giving 1920 structures in total. The temperature, T, was then lowered by 25 K and the system re-equilibrated before 1920 structures were collected at the new T. Q values quantifying the agreement with the experimental data (see below) were calculated at each T so that the agreement with experiment could be monitored constantly. The cooling–equilibration–collection cycle was continued until the various Q values (Table 3) were simultaneously minimized. An additional 5760 structures (1.2 ns per replica) were collected at this optimal T for further analysis.

Analysis

Calculation of R_g and R_h

The geometric radius of gyration, R_g, was calculated from the heavy atoms of each structure using CHARMM analysis facilities. For comparison with experimental data, the hydrodynamic radius, R_h, of each ensemble was computed. For each protein, the R_h of 200 randomly selected structures of varying degrees of compactness was computed using HYDROPRO¹¹⁶ with default settings and six sizes of minibeads ranging from 0.18 to 0.28 nm. The molecular weight and partial specific volume were evaluated from the amino acid sequence. Relationships between R_g^–1 and R_h^–1 were then determined by linear regression (uncertainty represents standard error) (Table 1).

Table 1.

protein	relationship	correlation coefficient
αS	Rh–1 = 0.0148(±0.0003) + 0.4882(±0.0038)Rg–1	0.994
βS	Rh–1 = 0.0163(±0.0002) + 0.4537(±0.0042)Rg–1	0.991
βSHC	Rh–1 = 0.0151(±0.0002) + 0.4943(±0.0044)Rg–1	0.990

These equations were used to convert the calculated R_g of each structure into an R_h. The overall ⟨R_h^–1⟩^–1 was then computed according to

5

where N^struct is the number of structures in the ensemble, to reflect the averaging inherent in the experimental measurement.

Compaction Factors

Compaction factors, C_f, quantifying the degree of compaction relative to that of a fully unfolded (random coil) and natively folded state were calculated according to²⁷

6

where R_h^exp is the experimental R_h and R_h and R_h^U are the R_h values expected if the protein is natively folded (F) and fully unfolded (U), respectively:

7

Q Values

The agreement between the synthetic or experimental observables and those calculated from a calculated ensemble was quantified with a “quality factor”:¹¹⁷

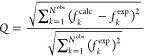8

where N^obs is the number of observables of that type (e.g., working or free PRE distances) and the f_k^calc values are the averages over the pooled ensemble.

Distance Comparison Maps

Distance comparison (DC) maps were created by plotting the root-mean-square (rms) distance between two residues, i and j, normalized by the rms distance predicted for a purely random coil:

9

The rms inter-residue distances for the calculated ensemble were calculated as

10

where N_struct is the number of structures in the calculated ensemble. The rms inter-residue distances for a random coil were calculated according to

11

which predicts the rms distance between two residues with sequence separation N^sep for a random flight chain with excluded volume and dihedral angles taken from a Protein Data Bank coil library.¹¹⁸ Similar results were obtained if ⟨(d_ij^rc)²⟩^1/2 was calculated from the random coil model of the protein in question. The normalization by ⟨(d_ij)²⟩^1/2 is important because it removes the dependence of the inter-residue distance on the sequence separation, allowing pairs of residues with different sequence separations and also proteins of different lengths to be compared.

³J Couplings

The ³J_HNHα couplings were calculated for each structure using the GROMACS¹¹⁹ program g_chi with default settings, values for the Karplus relation parameters of A = 6.4, B = −1.4, and C = 1.9,¹²⁰ and an offset of −60° and then averaged over all structures in an ensemble.

Residual Dipolar Couplings

Residual dipolar couplings were calculated for each structure using steric PALES¹²¹ with default settings and then averaged over all structures in an ensemble.

Solvent Accessible Surface Area

The solvent accessible surface area of each structure was calculated using the algorithm of Lee and Richards,¹²² as implemented in CHARMM, using default settings, including a probe radius of 0.16 nm.

Aggregation Propensity

Aggregation propensity profiles (Z_agg^prof) of αS, βS, and βS_HC were computed using an updated version of the Zyggregator algorithm,¹²³ which predicts the aggregation propensity of peptides and proteins in aqueous solution from the physicochemical properties of their constituent amino acids and compares this to the aggregation propensity of a set of randomly generated amino acid sequences of the same length.¹²⁴Z_agg indicates the regions that are most prone to aggregation.

Results and Discussion

Detection of Nonrandom Structure

PRE–NMR experiments combined with the calculation of ensembles of structures consistent with the NMR data have already been conducted for αS.^12,17 The ensemble of structures obtained was validated by comparison with independent experimental data. Here we describe similar experiments and calculations for βS, and for the artificial construct βS_HC. We note that in all cases, the nonacetylated form of the protein was studied, as this is the form of the heterologously expressed protein studied experimentally, and the simulations aimed to match the experiments as closely as possible.

In discussing these three proteins, we define the N-terminal and central regions as those regions that can form α-helical lipid-bound structure:¹²⁵ residues 1–98 in αS, residues 1–65 in βS, and, assuming the additional 11 residues from αS extend the helical region of βS, residues 1–76 in βS_HC, with the remainder of each protein being designated as the C-terminal region.

The backbone assignments of αS⁷⁵ and βS⁷¹ were previously described. For the βS_HC construct, the ¹H–¹⁵N HSQC spectrum overlaps with that of βS, and the additional 11 residues from αS exhibit chemical shifts in βS_HC that correspond closely to their resonances in αS (Figure S3 of the Supporting Information). This allowed a backbone assignment strategy in which the identification of individual amino acid resonances was confirmed by a combination of CBCA(CO)NH and HNCO triple-resonance experiments. The chemical shifts for βS_HC have been deposited in the BioMagResBank.

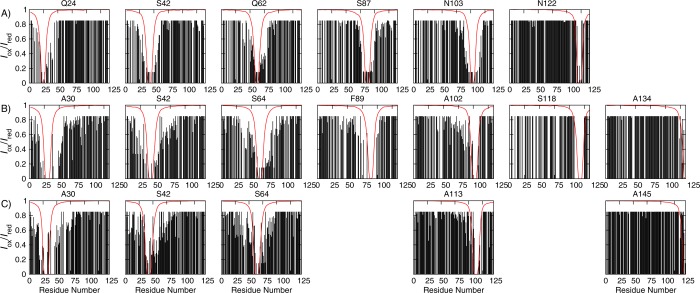
Seven distinct single-residue cysteine mutations were introduced into βS, and five into βS_HC, to which the MTSL spin-label was subsequently attached. The positions of the cysteine mutations were kept as consistent as possible among the three proteins (Table 3 and Figure 2) to facilitate comparisons. For each cysteine mutant of each protein, ¹H–¹⁵N HSQC spectra were collected with the spin-label in both its oxidized state and its reduced state. The heights of individual NMR resonances were then used to calculate the intensity ratios shown in Figure 2.

Figure 2.

Intensity ratios I_ox/I_red for each spin-label position for (A) αS,^12,17 (B) βS, and (C) βS_HC. The experimental data are shown as black bars, and the I_ox/I_red values calculated from the random coil ensemble are plotted as thick red lines. PRE–NMR experiments were conducted on 100 μM uniformly ¹⁵N-labeled protein with MTSL attached in 10 mM sodium phosphate (pH 7.4), 100 mM NaCl, and 10% D₂O at 10 °C. The experimental I_ox/I_red values are those processed for use in the simulations (see Methods); thus, any I_ox/I_red of <0.15 or >0.85 has been set to 0.15 or 0.85, respectively. If no bar is present, then either I_ox/I_red was not measured for this residue or it was discarded because of an uncertainty of >10%.

A decrease in the intensity ratio is expected for residues proximal in sequence to the spin-label attachment site. The predicted pattern of intensity ratios stemming from this effect is illustrated by the red lines in Figure 2, which show the intensity ratios calculated from random coil representations of each protein. Additional regions with intensity ratios lower than these values correspond to internuclear distances that are significantly shorter than in a random coil ensemble. All three proteins exhibit such long-range contact formation, indicative of nonrandom structure, suggesting that they are more compact than a random coil of the same sequence. Control experiments in which the HSQC spectra were collected for a mixture of isotopically labeled protein and spin-labeled protein confirmed that the observed intensity decreases were due to intramolecular contact formation, rather than from intermolecular contact formation due to aggregation (data not shown).

Examination of the intensity ratios in more detail reveals that the majority of the contact formation is between residues of intermediate (up to 30 residues apart) sequence separation, indicative of local structural collapse. In particular, the decreases in the intensity ratios for residues around spin-label positions Q24, A30, and A30 and Q62, S64, and S64 for αS, βS, and βS_HC, respectively, and S42 in βS and βS_HC extend further from the spin-label in both directions than what is predicted by the random coil model. However, when the spin-label is attached at position N103, A102, or A113 in αS, βS, or βS_HC, respectively, only residues located on the N-terminal side of the spin-label show decreased intensity ratios, suggestive of an extended C-terminus in all three proteins. In αS, attaching the spin-label at position S42 results in lower intensity ratios for C-terminal residues from position 110 onward, and some evidence of the reciprocal interaction can be seen for spin-label position N122. Neither of these effects is observed for βS or βS_HC, suggestive of fewer, or at least different, patterns of long-range contact formation for these proteins. Overall, the intensity ratios suggest some local compaction in the N-terminal and central regions of all three proteins, and more extended structure in the C-terminal regions, particularly for βS and βS_HC.

Generation of Ensembles of Structures

To determine the molecular details of the structures giving rise to the PRE–NMR data, ensembles of structures compatible with the PRE-derived distances were determined using replica-averaged restrained MD (PRE-RMD) simulations.^12,17,48 To account for the averaging inherent in the experimental data, the PRE-derived distance restraints were applied to multiple (24) independent replicas simulated in parallel. At each point in time, a restraint coordinate, ρ, was obtained by comparing the r^–6 average of each distance across all replicas to the experimental value (eq 1). An energy penalty, the magnitude of which depends on the magnitude of ρ, was applied only if the value of ρ at that time point was greater than the previous minimum (eq 3). In this way, the simulations were progressively biased toward structures that, on average, satisfy the restraints. The majority of the simulation parameters, including the number of replicas, were optimized previously so they would be suitable for reproducing disordered state ensembles.¹⁷ In particular, an asymmetric flat bottom harmonic potential was adopted to ensure that the structures generated are not overly compact, as can be the case for r^–6-averaged distance restraints like those used here. The only parameter that was changed in this work is the simulation temperature, which is used to tune the average dimensions of the structures that make up the ensemble, as quantified by the harmonic average of the hydrodynamic radius, ⟨R_h^–1⟩^–1, so that it matches the experimentally determined value. This tuning was shown greatly to improve the accuracy of the ensemble, measured in terms of the reproduction of distributions of structural properties.¹⁷ To provide further evidence that the ensembles of structures produced here are valid representations of the experimental ensembles, cross-validation, in which only 80% of the PRE-derived distance restraints were used in the PRE-RMD calculations (“working”) and the remaining 20% provide a “free” data set whose satisfaction is not preordained by their inclusion as restraints, was conducted. For all three proteins, the agreement with the “free” set of PRE-derived distances is almost as good as that of the “working” PRE-derived distances (Table 3).

Molecular Dimensions

Two different ensembles of αS restrained with PRE-derived distances have been obtained previously, one with an average R_h close to 2.7 nm,¹² consistent with the experimental R_h of 2.66 nm measured in unbuffered D₂O at 298 K (2.66 nm),⁷⁶ and one with an average R_h of 3.2 nm,¹⁷ to match the experimental R_h values of 3.20 and 3.19 nm measured in subsequent PFG-NMR experiments at 288 K in unbuffered D₂O¹²⁶ and in 20 mM phosphate buffer (pH 6.5) with 100 mM NaCl,¹³ respectively. The latter ensemble also made use of an additional 118 distance restraints obtained after determination of the first ensemble as well as the original 478 distance restraints. The R_h values of the βS and βS_HC ensembles were matched to experimental values measured under conditions as close as possible to those of the PRE–NMR experiments [pH 6.5 for αS and pH 7.4 for βS and βS_HC, 100 mM NaCl, 288 K (Table 2)] by tuning the simulation temperature.

Table 2. Predicted^aand Experimental^b,cR_h Values (nanometers) and Compaction Factors^d (C_f) for αS, βS, and βS_HC in Various States.

		U	F	NaClb	NaCl and SDSc
αS	Rh	3.70	1.99	3.19	2.46
	Cf		0.61	0.30	0.725
βS	Rh	3.60	1.97	3.24	3.22
	Cf		–	0.22	0.23
βSHC	Rh	3.77	2.01	–	2.97
	Cf		–	–	0.46

^aU and F refer to the R_h values predicted according to eq 7(27) for a fully unfolded and a compact folded polypeptide, respectively.

^bMeasured by PFG-NMR on 200 μM protein in D₂O and 20 mM phosphate buffer (pH 6.5) with 100 mM NaCl at 288 K.¹³ Note that the R_h measured by PFG-NMR for 100 μM αS in unbuffered D₂O at 288 K is almost identical (3.20 nm).¹²⁶

^cMeasured by PFG-NMR on 70 μM protein in 10 mM phosphate buffer (pH 7.7) with 100 mM NaCl and 0.5 mM SDS at 298 K.¹²⁹

^dCalculated according to eq 6.²⁷

Comparison of the R_h values of αS, βS, and βS_HC must take into account their different sequence lengths. The compaction factor²⁷ (see Methods), C_f, allows for this difference by comparing the experimental R_h to that expected if the polypeptide were to exist in a compact folded state or to be fully unfolded (i.e., random coil-like). A C_f of 1.0 indicates compaction typical of a natively folded protein, while a C_f of zero indicates random coil-like dimensions. According to this measure, the dimensions of βS (C_f = 0.45) and βS_HC (C_f = 0.23) resemble those of partially unfolded proteins that retain some nonlocal interactions, such as reduced hen egg white lysozyme at pH 2.0 or BPTI at pH 4.5 (C_f = 0.35),²⁷ with βS slightly more compact and βS_HC more unfolded. In contrast, αS (C_f = 0.72) is significantly more compact, exhibiting a degree of expansion similar to that of the low-pH molten globule state of myoglobin.²⁷

An alternative to the R_h value for quantifying the size of a molecule is the radius of gyration (R_g). It should be pointed out, however, that because the R_h is defined as the radius of a hard sphere with the observed diffusion rate, this parameter reflects only approximately the apparent size adopted by the solvated, tumbling molecule. R_g is defined as the mass-weighted average distance of each atom from the center of mass of the molecule, and therefore, calculating its value from the sets of coordinates obtained from an MD simulation is simple and fast. The R_h and R_g values are related to each other and can be interconverted by the approach described in Methods.

The broad distributions of the R_g values of the ensembles (Figure 3) reflect the wide variety of structures populated at least transiently by IDPs. Comparison with the R_g distributions of the random coil models of each protein, however, reveals that the range of structures accessible to each protein is restricted to conformations that are significantly more compact than those expected for a random coil, reflecting the non-zero C_f values. Also consistent with the trends observed for the compaction factors, the difference distribution of the R_g (Figure 3D) of βS_HC differs from those of αS and βS in a manner that indicates that the shift toward structures with smaller R_g values in the PRE-RMD simulations, compared to those expected for a random coil, is more pronounced for βS_HC than for the other two proteins. As with the R_h values, however, it is not appropriate to compare directly the R_g probability distributions of the three different synucleins because of their different sequence lengths.

Figure 3.

R_g probability distributions for (A) αS, (B) βS, and (C) βS_HC. The random coil ensembles (see the text for a definition) are colored black, and the ensembles calculated using PRE-RMD are colored red. Representative structures are shown for various values of R_g. The R_g distributions are shown rather than the R_h distributions because the former are faster to calculate, but the R_h distributions are similar. (D) Distributions of the difference between the random coil and PRE-RMD ensemble R_g probabilities [Δp(R_g) = p(R_g^random coil) – p(R_g)].

Comparison with Experimental Data Not Used as Restraints

The most stringent test of how well a simulation reproduces the actual ensemble of structures is a quantitative comparison with independent experimental data. As noted above, the agreement between the experimentally derived and calculated “free” PRE distances is almost as good as for the “working” PRE distances (Table 3), allowing a high level of confidence that the ensembles of structures provide a good representation of the long-range structural properties of αS, βS, and βS_HC.

While the primary aim of this work was to reproduce the long-range structure of the three proteins, NMR data reporting on more local structural properties, namely ³J_HNHα couplings and amide N–H RDCs, were calculated for αS and βS for comparison with experimental values.^11,13 Similar data are not available for βS_HC. The ³J_HNHα couplings calculated from the PRE-RMD ensembles of αS and βS structures are slightly greater than 5 Hz throughout the sequence, and those calculated from the random coil ensembles are slightly less than 5 Hz (Figure 4A,B). Neither set of calculated ³J_HNHa couplings for either protein bears a close resemblance to the experimentally measured values, which in general are larger and fluctuate more dramatically along the sequence. Although no experimental data are available for βS_HC, ³J_HNHa couplings were calculated from the PRE-RMD and random coil ensembles for comparison with those calculated from the αS and βS ensembles. The couplings calculated from the PRE-RMD ensemble are again close to 5 Hz, whereas those calculated from the random coil ensemble lie between 5 and 6 Hz and fluctuate somewhat throughout the sequence, an observation likely to be due to the more compact nature of the βS_HC structures inducing more local structure formation.

Figure 4.

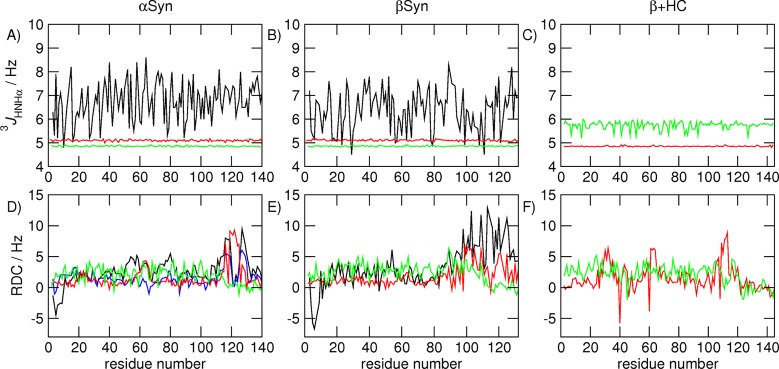
Comparison of experimentally measured^11,13 and calculated NMR observables for (A and D) αS, (B and E) βS, and (C and F) βS_HC. (A–C) ³J_HNHa couplings (black) measured experimentally, (red) calculated from the PRE-RMD ensembles, and (green) calculated from random coil ensembles. (D–F) Amide N–H RDCs measured experimentally in (black) C8E5/octanol or (blue) Pf1 bacteriophage, (red) calculated from the PRE-RMD ensembles, and (green) calculated from random coil ensembles.

The magnitudes of the RDCs calculated from both the PRE-RMD and random coil ensembles of αS and βS are more similar to those of the experimental RDCs (Figure 4D,E). The larger RDC values observed experimentally for the C-termini are not found in the values obtained from the random coil ensemble but are detectable in the RDCs calculated from the PRE-RMD ensemble. Again, however, the residue-specific variations in the experimental data are for the most part not accurately reproduced in either of the calculated ensembles.

Overall, the lack of agreement between the experimental ³J_HNHa couplings and those calculated from the PRE-RMD ensembles, coupled to the similarity between those calculated from the PRE-RMD and random coil ensembles, suggests that local residue-specific conformational preferences are not well reproduced in the PRE-RMD ensembles. This result is not surprising, given that the type of restraints used provides information about the long-range residual structures of the proteins under investigation, but not about their local conformations. Rather, it should serve as a warning that reproducing experimental data describing one structural aspect of a protein, particularly a disordered protein, does not imply that other structural properties will be accurately described. RDCs report on both local and global structure, so the improved agreement of the PRE-RMD ensemble with the experimental data for the C-termini is likely to reflect the fact that the long-range structure, in the form of the replica-averaged PRE distances, of this ensemble is in good agreement with that observed experimentally. However, the remaining discrepancies, as with the ³J_HNHa couplings, most likely result from the fact that the local structure is not well replicated in the calculated ensembles. A more accurate representation of such local conformations should be obtained by using additional restraints, such as ³J couplings and chemical shifts. These calculations were not performed here because the aspect of primary interest was the comparison of the long-range conformational behaviors of αS, βS, and βS_HC and whether any differences observed might be linked to their differing aggregation propensities.

Residual Structure Propensities

The nature of the structures comprising each ensemble is summarized in the distance comparison (DC) maps¹⁷ (Figure 5). In contrast to the residual contact probability (RCP) maps used previously to characterize disordered state ensembles,^12,48,49 which report on inter-residue distances of <0.85 nm, DC maps reflect the position of the center of the distance distribution relative to that of a random coil. DC values of <1.0 indicate compaction, and those >1.0 represent expansion relative to the random coil. DC maps were used here because unlike RCP maps, they report on aspects of the distribution not accessible experimentally.

Figure 5.

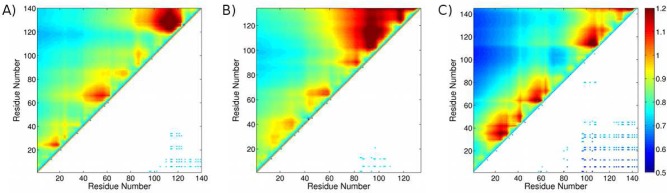
Distance comparison (DC) maps for the (A) αS, (B) βS, and (C) βS_HC ensembles determined by PRE-RMD. The top half shows the full DC map, whereas the bottom half shows only the scaled distances that are less than 75% of that expected for a random coil polymer and occur between pairs of oppositely charged residues. The same color scale is used for all the DC maps to aid comparisons.

For βS_HC, the scaled long-range distances are shorter than for either αS or βS, reflecting its larger compaction factor (Table 2). The DC maps for αS, βS, and βS_HC (Figure 5), however, all contain distinct regions of inter-residue distances that differ from those expected for a random coil, as indicated by DC values significantly less than or greater than 1.0, suggesting the presence of nonrandom residual structure. In both βS and βS_HC, the C-terminal residues exhibiting the shortest distances to residues 1–40 of the N-termini are broadened and include residues located closer to the N-termini compared to that in αS. In βS, the shortest distances are to residues 70–110, and in βS_HC, they are to residues 80–145; in αS, they are to residues 100–140. This observation may reflect additional shielding from intermolecular interaction of the central region in βS and βS_HC, in keeping with the lower aggregation propensity of both of these polypeptides.

Within the N-termini of all three proteins are clusters of residues close together in sequence separated by distances that are, on average, similar to those observed in a random coil. Such DC values could result from random coil or α-helical structure or some combination of the two, as the expected inter-residue distances are effectively the same for short sequence separations.¹²⁷ Additionally, all three proteins, and in particular βS, exhibit distances between residues within the C-terminal regions (residues 100–140 for αS, 100–134 for βS, and 110–145 for βS_HC) that are larger on average than in a random coil. This result could be indicative of either extended β-strand-like or PPII structure, each of which is characterized by rms inter-residue distances longer than those of a random flight chain.¹²⁷ For βS, PPII structure is most likely to be present, as the C-terminus of βS contains eight proline residues, which are known to disrupt β-sheet formation, and indeed, PPII structure has been observed experimentally.¹³ The experimental data for αS, in contrast, suggest a much lower PPII propensity,^13,75 indicating that DC values of >1.0 in the C-terminus of this protein are more likely to correspond to extended β-strand-like structure. Greater β-strand content in αS than in βS is in keeping with the recent observation that αS variants that populate β-strand structure more highly also aggregate faster.¹²⁸ There are fewer experimental data available for βS_HC, but the cross-peaks in the NMR HSQC spectra overlay with those of βS for a majority of the sequence (Figure S3 of the Supporting Information), indicating that the secondary structure preferences of the C-terminal region of βS_HC are likely to be similar to those of βS. Interestingly, the C-terminal region of βS_HC does not contain as many DC values greater than 1.0 as βS, suggesting that the insertion of the αS hydrophobic core may have an indirect effect on the structural propensities of this region of the protein.

Free Energy Landscapes

A more global perspective on the nature of the structures sampled by each of the three proteins can be gained by examining the free energy landscapes (Figure 6), which show the probability of the occurrence of different combinations of R_g and solvent accessible surface area (SASA). βS exhibits the narrowest range of SASA and βS_HC the widest; this pattern reflects the relationship between the C_f values of the three proteins (Table 2). In all cases, the structures with the lowest R_g values encompass a wide range of SASA values; similarly, there is a large range of R_g values corresponding to the largest SASA values. Thus, having a small R_g poses few restrictions on the fraction of the surface area that is exposed. This may facilitate the role of αS as a hub protein,¹³⁰ as a larger surface area allows for a diverse range of binding partners.² The greater similarity between the F(R_g,SASA) landscapes of αS and βS suggests that the insertion of the central NAC region into βS_HC causes it to behave more like αS in this respect.

Figure 6.

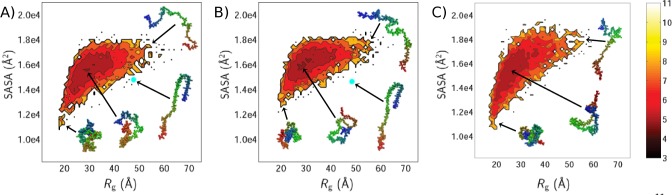
Free energy landscapes of structural ensembles determined for (A) αS, (B) βS, and (C) βS_HC ensembles. The free energy is defined as F(R_g,SASA) = −ln p(R_g,SASA). Examples of structures found at various points on each landscape are given, and the position of the experimental micelle-bound structure of αS¹³⁷ and a homology model of βS based on the αS structure are indicated by filled cyan circles.

Implications for Aggregation

The construction and study of βS_HC was initiated with the aim of understanding whether investigation of the transient long-range interactions can provide insight about why the aggregation rate of βS is lower than that of αS.⁷¹ It was originally thought that the fundamental cause of the different aggregation propensities of αS and βS was simply the absence of 11 residues (73–83) from the NAC region of βS^72,131 (Figure 1). Contrary to this expectation, however, βS_HC, which contains residues 73–83 of αS within the βS sequence following residue 72, was found to have aggregation properties similar to those of βS.¹²⁹ Further investigations, including analysis of the aggregation properties of two deletion mutants, αΔ73–83 and αΔ71–82, showed that the most likely reason for the similar aggregation behavior of βS and βS_HC is the inclusion of E83 in the βS_HC construct.⁷¹ This negatively charged residue is thought to disrupt the intermolecular interactions of the hydrophobic core and may therefore act as an aggregation “gatekeeper”.^72,73 It has also been shown that the aggregation properties of αS and βS can be effectively interchanged by swapping six residues among them (63–66, 71 and 72).⁷⁴ Further evidence of the role of residue E83 in αS aggregation comes from a study that showed that the interaction of dopamine and related derivatives with residues 125–129 of αS is mediated by electrostatic interactions between the ligand and E83, with replacement of glutamine by alanine preventing dopamine from inhibiting αS aggregation.¹³² Additionally, the incorporation of charged residues into the hydrophobic core of full-length αS decreases the rate of fibril formation, suggesting that the lower experimental and theoretical aggregation propensities of βS and βS_HC, both of which have a net charge greater than that of αS, may be due to intermolecular repulsion between charged residues.^72,73

The role of charge in preventing aggregation is not confined to the intermolecular interactions. While any contacts made by the C-terminus with the NAC region are thought to be hydrophobic in nature, interactions with the N-terminus are most likely to be electrostatic.¹⁰ The lower panels of the DC maps (Figure 5) indeed reveal that many of the inter-residue distances that are on average considerably shorter than would be expected for a random coil polymer occur between oppositely charged residues. The increased negative charge of the C-terminal regions of βS and βS_HC may therefore enhance these intramolecular electrostatic interactions. Correspondingly, comparison of the DC maps shows that the scaled distances between the N- and C-terminal regions of βS and βS_HC are shorter than those of αS (Figure 5), and the bottom panels show that many of the shortest scaled average inter-residue distances in βS_HC occur between oppositely charged residues. Moreover, the predicted aggregation propensities of the C-terminal regions of βS and βS_HC are even lower than that of αS (Figure 7). In addition to the effects of the long-range conformational properties on aggregation, contributions from the local secondary structure propensities can be expected.¹²⁸ The importance of electrostatic interactions between the N- and C-terminal regions in determining the aggregation properties is also supported by experimental data. C-Terminal truncation mutants of αS aggregate faster than the wild type only if the truncation removes the majority of the charged residues from the C-terminal region.¹³³ Additionally, the binding of positively charged polyamines such as spermine to the C-terminal region increases the aggregation rates of βS in SDS and αS in the absence of the addition of SDS.^{129,133−136} Thus, features apparent in the PRE-RMD ensembles correlate with the experimental data and provide further support for the suggestion that charge plays a key role in controlling the aggregation propensities of the synucleins.

Figure 7.

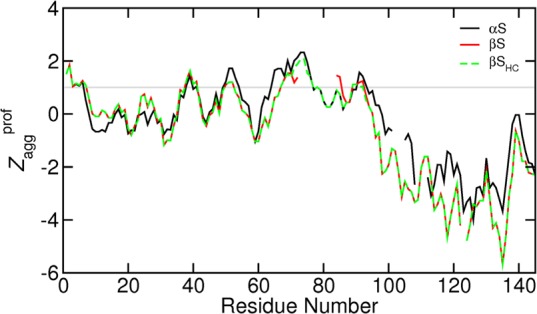
Aggregation propensity, Z_agg^prof, predicted using the Zyggregator algorithm¹²³ for (black, solid) αS, (red, solid) βS, and (green, dashed) βS_HC. The residue numbers and gaps correspond to the sequence alignment shown in Figure 1. The gray line at Z_agg = 1 indicates the threshold for classifying a sequence as being aggregation prone; regions exhibiting Z_agg^prof values greater than this are considered to be aggregation prone.

Conclusions

We have exploited the opportunities offered by the use of PRE-derived distances as replica-averaged structural restraints in MD simulations to increase the amount of information available from experimental measurements by providing atomic-level structural detail. Analysis of the transient long-range intramolecular interactions shows that the distances between the N- and C-terminal regions of all three proteins are shorter than expected for random coil structures, indicative of interactions between the two regions that may be electrostatic in nature. The resemblance between the structural propensities of βS_HC and βS echoes their similar aggregation propensities, with the main difference likely to be related to aggregation between these two proteins and being that αS and βS_HC exhibit a greater number of inter-residue distances between the N- and C-terminal regions that are shorter than expected for a random coil. As interactions between the N- and C-terminal regions are expected to be electrostatic in nature, this factor strengthens the case for charge playing a key role in modulating the aggregation properties of these polypeptides.

Supporting Information Available

Overlays of the ¹H–¹⁵N HSCQ spectra measured for S64C βS and βS_HC with the attached MTSL spin-label in its oxidized and reduced states, plots showing the change in the ¹⁵N and ¹H chemical shifts measured for each residue of S64C βS and βS_HC when the attached MTSL spin-label is in its oxidized and reduced forms, and the ¹H–¹⁵N HSCQ spectrum of βS_HC alone and overlaid with that of βS or of αS. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† J.R.A.: Centre for Theoretical Chemistry and Physics, Institute of Natural and Mathematical Sciences, Massey University, Albany Highway, Auckland 0632, New Zealand.

Author Present Address

^‡ R.C.R.: Office of Cancer Clinical Proteomics Research, National Cancer Institute, National Institutes of Health, Bethesda, MD 20892-2580.

Author Present Address

^§ J.C.C.: Institute of Structural and Molecular Biology, University College London and Birkbeck College, Gower Street, London WC1E 6BT, U.K.

The authors declare no competing financial interest.