Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Oct 27;30(46):14073–14078. doi: 10.1021/la503711g

Energetically Biased DNA Motor Containing a Thermodynamically Stable Partial Strand Displacement State

Preston B Landon †,‡,*, Joon Lee §, Michael Taeyoung Hwang §, Alexander H Mo §, Chen Zhang ∥, Anthony Neuberger †, Brian Meckes †, Jose J Gutierrez ⊥, Gennadi Glinsky ‡, Ratnesh Lal †,‡,§,*
PMCID: PMC4245991  PMID: 25347360

Abstract

graphic file with name la-2014-03711g_0004.jpg

Current work in tuning DNA kinetics has focused on changing toehold lengths and DNA concentrations. However, kinetics can also be improved by enhancing the completion probability of the strand displacement process. Here, we execute this strategy by creating a toehold DNA motor device with the inclusion of a synthetic nucleotide, inosine, at selected sites. Furthermore, we found that the energetic bias can be tuned such that the device can stay in a stable partially displaced state. This work demonstrates the utility of energetic biases to change DNA strand displacement kinetics and introduces a complementary strategy to the existing designs.

Introduction

Improvement in the kinetics of strand displacement reactions of conventional double helixes is highly desirable for building efficient DNA motors. Toehold-driven process, such as toehold-mediated strand displacement, has allowed for creating a multitude of functional DNA devices,1−17 including walkers,5,7−9 actuators,14,15 contractile machines,18 transporters,19 and assembly lines.20 Many of these devices have reversible reaction kinetics and are capable of performing successive cycles.2−4,7−9,13−15,20−22

Toeholds consist of complementary domains that allow strand f to be colocalized to g, even though g is already bound in a complex with j. Branch migration of the remaining domains then allows f to displace strand j away from g, resulting in a new complex formed by f and g (Figure 1a).23 The process of branch migration is isoenergetic and driven by chance. The process has been previously shown to be described by a simple one-dimensional random walk model.24−26

Figure 1.

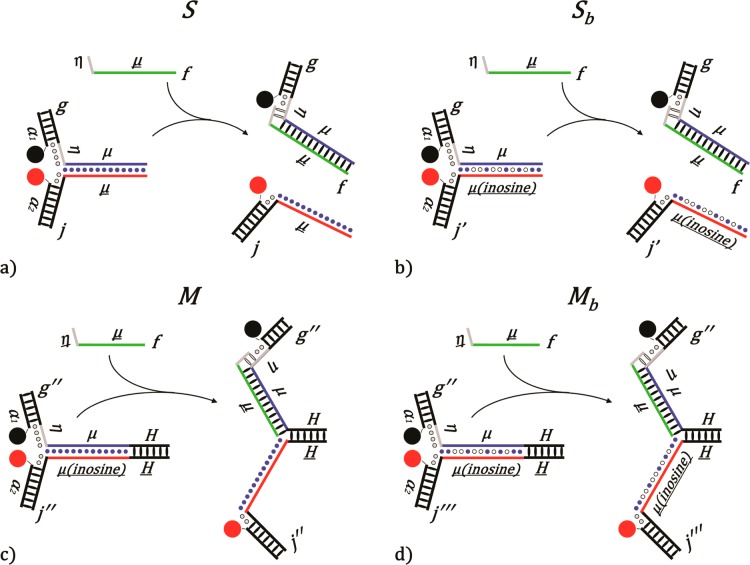
Figure 1

Open in a new tab

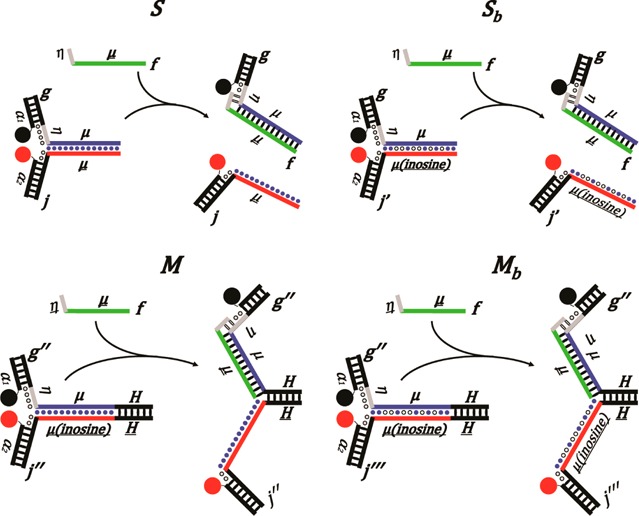
Illustrations of (a) S and (b) Sb are shown before (left) and after (right) invasion by the fuel strand f. The arms of the devices (α1 and α2) contain fluorescent labels, Iowa Black RQ (black circle) and FAM (red circle), respectively, that are quenched when the two sides are intact and fluorescent when they are separated. Toeholds (η) are depicted as gray, and the branch migration domain (μ) is depicted as blue. Depiction of the DNA motors with a hinge, (c) M and (d) Mb. A contracted motor (left) and an extended motor (right). The motor is held together by the hinge domain (H). The biased variants are created by replacing all of the guanines on the displaced side (red line) of the branch migration domain (μ) with inosine (inosines are depicted by hollow circles and natural bases by solid blue circles). The inosines were placed to create a forward-bias favoring branch migration to proceed from left to right.

DNA has been shown to produce a relatively strong force per molecule compared to naturally existing bimolecular motors.27,28 For example, kinesin has a stall force of ∼5 pN, whereas DNA has a stall force of ∼10–20 pN depending on its sequence.6,26,28−31 The calculated DNA stall force can be approximated by F = ΔG/Δx where Δx ≃ 0.34 nm per base separation.27,28 While DNA can produce a relatively large amount of force per molecule, the current reaction rates, reset times, and efficiencies of DNA devices are relatively poor compared to others from the bimolecular world. Increasing the kinetics of strand displacement reactions will result in the ability to create more robust functional devices and improve the chances for creating reliable and affordable DNA-based biomedical devices for a broad range of biomedical applications.

The complementary nature of Watson–Crick base pairing creates a challenging engineering problem for constructing reversible DNA-based devices.27,28 In order for a DNA motor to extend and contract like a motor that can be turned on or off on demand, there must be a thermodynamically stable energy state for the device to rest in when the DNA strands are in the extended position. Such a stable equilibrium point does not exist within the branch migration domain of traditional DNA-based devices.

One way to overcome this thermodynamic difficulty is by incorporating a small domain of several successively occurring unpaired bases (loop domain) positioned between the active domain and the hinge domain.2,18,32 This essentially creates a discontinuity separating the functional portion of the device from its structural portion.18 The discontinuity created by a loop domain results in creating a strand displacement device that is more likely to be in the open state. However, as a consequence, the device is incapable of maintaining tension in the open state. This inhibits its utility as a work-producing device. The insertion of the discontinuity is analogous to severing the elastic cable within a bungee cord, rendering it a lousy rope.

Here, we investigate the effect on the kinetics by introducing inosines in the branch migration domain and a hinge on one side of the device. The hinge keeps the two sides of the device from separating once it has been invaded. This resulted in producing a potential work-generating device with a continuous contractile transition separating the extended and contracted states of the device. The inosine-based motor was constructed using synthetic DNA bases to bias the branch migration domain to progress forward toward the extended state. This creates a thermodynamically stable partial strand displacement state by significantly shifting the thermodynamic stability of the device to favor the open state without introducing a loop. The bias of the branch migration domain can be controlled by location and frequency of inosine substitutions. The forward biasing also significantly increases the strand displacement reaction kinetics. To optimize the device’s performance, we compare the reaction kinetics of four variants of a single-strand displacement device with various toehold lengths (0 ≤ n ≤ 10). This work demonstrates the utility of energetic biases to change DNA strand displacement kinetics and introduces a complementary strategy to the existing designs.

Materials and Methods

Reagents

All chemicals and buffer solutions were obtained from Sigma-Aldrich (Saint Louis, MO) unless otherwise specified. All DNA constructs were obtained from IDT (Coralville, Iowa), DNA ladders from Promega (Madison, WI), and DNA gels from Lonza (Walkersville, MD). DNA constructs were suspended in DNAase-free 30 mM Tris and 0.16 M NaCl buffer solution at pH 8.0.

Gel Electrophoresis and Fluorescent Gel Imaging

DNA gel electrophoresis was performed with 4% agarose gels at 5 V/cm in TBE buffer while monitoring solution temperature to be less than 20 °C. All extending reactions were conducted by adding 10 times more extending fuel strands than devices. All contractions were conducted by adding 20 times more contracting fuel strands than devices to saturate the existing extending strands.

The positions of single- and double-stranded DNA within the gel were determined using fluorescent gel imaging and ethidium bromide (EtBr) staining. Gels were imaged with a Bio-Rad FX-Imager Pro Plus (Bio-Rad, Hercules, CA) and analyzed with the Quantity One software package (Bio-Rad). The only modifications made to presented gel images are cropping the image area, overlaying lines for reference, adding symbols for identification of the components, and adjusting the brightness and contrast. All quenchers were removed in the strands for gel imaging.

Time-Lapse Fluorescence and Strand Displacement Rate Constant Measurements

Time-lapse fluorescence measurements of the devices were visualized by tagging the strands with a fluorescent probe (FAM) and a fluorescent quencher (Iowa Black RQ). The excitation (Ex) and emission (Em) wavelengths for the FAM were 485/525 nm. Iowa Black RQ has an absorbance spectra ranging from 500 to 700 nm with a peak absorbance at 656 nm. Devices were initially quenched when the two sides of the arms were intact and fluorescent when they were separated. For strand displacement rate constant measurements, TexRed fluorophore (Ex 585/Em 625 nm) was used instead of FAM. Fluorescence measurements were conducted using a temperature-controlled Tecan Infinite 200 M plate reading spectrometer (San Jose, CA) at temperatures specified with an accuracy we estimate to be approximately ±1.5 °C. In all experiments, the device concentration was 3 nM, and the fuel strand concentration was 30 nM (unless otherwise specified). At the start of each cycle, the appropriate fuel strands were added. Addition of fuel strands between each cycle creates about 20–60 s of error in the measurements because of the time required to add the strands and restart the machine. This error was partially compensated by a stopwatch, timing the delay and adding the time back to the dataset. 10 to 30 times more extending or contracting strands (fc1 and fc2) were used for cycling experiments to reach reaction completion (saturation). The kf values were obtained from a second-order fit using MATLAB (details are in the Supporting Information).

Thermal Annealing

Thermally annealed DNA motors were self-assembled into their lowest energy configuration. A custom cycling program was run in a PCR thermocycler (Mastercycler Personal, Eppendorf, Westbury, NY) to accomplish this. The solution temperature was quickly increased to 94 °C, which is beyond the double-strand melting temperature and followed by a slow controlled cooling ramp at a rate of 1 °C every 2 min to a final temperature of 4 °C.

Results and Discussion

There were four different variants of the device investigated. Device S or Sb was disassociated once it was invaded by f, which produced two products. Devices M and Mb were constructed by placing a hinge domain (H) at one end of the device to keep the two sides from separating after being invaded. The biased variants of each device are represented by subscript b (Figure 1). All of the variants contained a branch migration domain with a length of 30 base pairs except Mb2 (constructed using sequences h, k, a3, and a4) with 38 base pairs. Exact sequences are listed in the Supporting Information.

Displacement Reaction Kinetics of the Unbiased Variants S and M

The two original sides of complex S were fully separated after invasion by f. The reaction rate constant (kf) from strand displacement reactions of S separated by f with various length toeholds (0 ≤ n ≤ 10) at two different temperatures (25 and 41 °C) are presented (Table 1). Reaction rates were increased by up to a factor of ∼2 after increasing the temperature from 25 to 41 °C. The original data are presented in the Supporting Information (Figures S1 and S2).

Table 1. Measured Strand Displacement Rate Constants of S by f (in units of M–1 s–1)a.

n kf of S (25 °C) kf of S (41 °C)
10 121000 228000
8 96100 188000
7 80600 148000
6 77100 102000
5 55200 60000
4 1790 2890
3 1210 1680
2 13.1 23.1
1 0.92 16.5
0b N/A 2.10b
Open in a new tab
a

The concentration of [S] = 3 nM, [f] = 30 nM (except for n = 4, [f] = 100 nM, n = 3, [f] = 1 μM, n = 2, [f] = 10 μM, and for n = 1, [f] = 100 μM).

b

The value for n = 0 was measured at 37 °C.

The unbiased variant M was extremely inefficient at extending, and hence its extending kinetics were not measured. At concentrations low enough to measure the reaction kinetics, the fold change in the fluorescence signal was significantly less than the noise in our system. Thus, the extending efficiency of M was measured at different temperatures and by using higher concentration (800–6400 times) of extending fuel strands. Change in the fluorescence intensity with temperatures was plotted (see Supporting Information Figure S3). Only the behavior of M with an extending fuel strand with a 6 nt toehold was examined (Figure S3). The 6 nt length toehold was chosen because, for the concentrations of the device (100 nM device, 800–6400 times fuel strand) at 41 °C, very few fuel strands are expected to be hybridized to the toehold on the device. However, at 4 °C, most of the toeholds on the devices are expected to be hybridized to a fuel with a 6 nt toehold (estimated using the IDT Biophysics calculator). The fraction of unbiased hinged variant M that was extended after invasion by f was found to be determined by the fraction bound to the toehold at thermodynamic equilibrium. This result is expected because there is not any energy driving the extending reaction of the unbiased variant M. Thus, the fraction of M that is extended is proportional to the fraction of fuel strands bound to the toehold at thermal equilibrium.

Displacement Reactions of the Biased Variants Sb and Mb

Both complex Sb and Mb were energetically biased variants created by replacing all of the guanines in the branch migration domain with inosines (Figure 1b,d). The incorporation of the inosine reduces the free energy associated with the two complementary sides. Inosine can only form two hydrogen bonds with cytosine, while cytosine can form three hydrogen bonds with guanine. This results in increased free energy favoring the biased variants to be invaded by f and shifts some of the energy driving the strand displacement reaction along the branch migration domain. Placing of inosines in the branch migration domain increases the likelihood that the invading strand hybridizes with the branch migration domain instead of resting only on the toehold. Rate constants of Sb were increased by up to a factor of 7500 when n = 1 compared to the rate constants of S. As the toehold length increases, the effect of introduction of inosine decreases, but the rate constants were still increased by at least 2-fold (Table 1 and Table 2).

Table 2. Measured Strand Displacement Rate Constants of Sb and Mb by f (units of M–1 s–1)a.

n kf of Sb (25 °C) kf of Mb (25 °C) Sb/Mb
10 219000 231000 1×
8 176000 176000 1×
7 168000 162000 1×
6 151000 154000 1×
5 122000 122000 1×
4 77000 70000 1.1×
3 56000 51000 1.1×
2 7700 2900 2.7×
1 6900 2300 3×
0 3800 950 4×
Open in a new tab
a

The concentration of [Sb] = [Mb] = 3 nM, [f] = 30 nM (except for n = 3, [f] = 1 μM, n = 1,2, [Sb] = [Mb] = 10 nM, [f] = 100 nM, and for n = 0, [Sb] = [Mb] = 3 nM, [f] = 300 nM).

The two sides of Mb remain connected after invasion by f because of the additional 26 base pairs on one side that function as a hinge. Also, the inosine bases result in both complexes being more energetically stable after being opened by f even when there is no toehold (n = 0). The incorporation of inosine bases into only one side of the complex can be envisioned as introducing a sporadically biased branch migration process. This is analogous to a random walk description of a drunkard heading toward a bar, located down successive flights of stairs. Stairways (inosine bases) favor forward migration toward the bar and inhibit backward migration up the stairs, while flat sections remain random (unbiased). Mathematically, a biased random walk is described with a forward step probability p > 1/2 and a backward step probability q = 1 – p.24 The use of inosine bases to bias branch migration is not unique, and any synthetic base analogue that decreases the hybridization energy could be used. Thus, synthetic nucleotide analogues for all four bases can potentially be employed.

Strand displacement rate constants of Sb and Mb by f with toehold lengths of 0 ≤ n ≤ 10 are presented in Table 2. The completion rate constants for Sb and Mb can be seen to be approximately the same for all f with a toehold length of n ≥ 3. When the toehold length was n = 2, Sb was experimentally observed to be 2.7 times faster than Mb and 4 times faster when there was no toehold (n = 0) (Table 2). This is possibly because Sb can be invaded at its ends from both sides while Mb can be invaded from only one side because of the hinge.

The above data (in Table 2) raise several questions which remain to be investigated. For example, what is the extent of the side attack pathway during the invasion of Mb by f from the major groove and what is the extent of the blunt end invasion by f. It is possible that Sb is significantly faster than Mb for short toeholds (n ≤ 2) because strand displacement can occur from both sides of Sb; however, strand displacement of Mb can only occur from one side of the device, and it also has an increased probability to close than Sb because of the hinge (Table 2). It is possible that the hinge alone lowers the probability of reaching completion enough to explain our data. However, none of these possibilities have been excluded. Further investigation of these systems is still required to quantitatively understand how the kinetics of the different variants relate to each other.

Systems with several unpaired bases separating a hinge domain from the biased domain have previously been investigated.32 However, a similar biased system with a thermodynamically stable displaced state (not separated by mismatched base pairs) has not been previously investigated. In the future, we expect the Mb system to be able to deliver a sustained contractile force when the device is switched to the contracted state.

Extension and Contraction Cycling of the Inosine-Based Motors

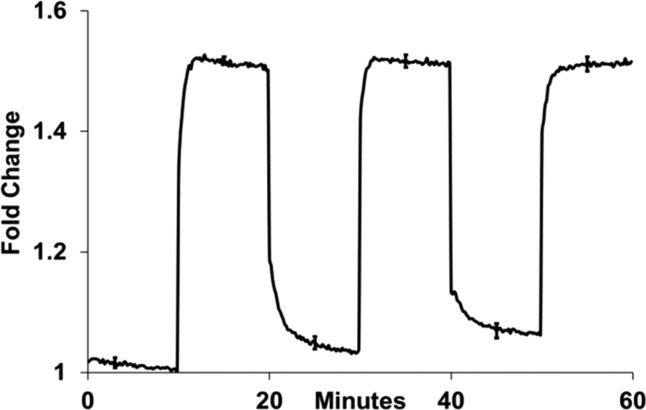
We expect the inosine-based DNA motors to function as “immortal” nanodevices continuously cycling between the extended and contracted states (excluding fuel strand poising of the system). The inosine-based motors were repeatedly extended and contracted using stepwise increasing concentrations of fuel strands for each cycle (Figure 2). The closing fuel strand fc1 is complementary to nearly half of the branch migration domain of the device, and fc2 is complementary to nearly the other half of the remaining bases in the branch migration domain. A small section of 8 base pairs must thermally decay from the device before fuel strand f2 can disassociate from the device after both closing strands are fully hybridized. This gap was introduced to minimize the interaction of the closing strands with the inosines in the device.

Figure 2.

Figure 2

Open in a new tab

Time-lapse fluorescence cycles from Mb2 at 37 °C. Initially, motors were contracted followed by successive extension and contraction using extending strands fuel f2 and contracting strands (fc1, fc2). The standard error from three successive experiments is included as error bars. The extension cycles used 10×, 30×, and 50× more f2 than Mb2, while contraction used 20× and 40× more (fc1, fc1) than Mb2. The concentration [Mb2] = 100 nM.

Gel Electrophoresis of the Initial and Final States from the Motor Reactions

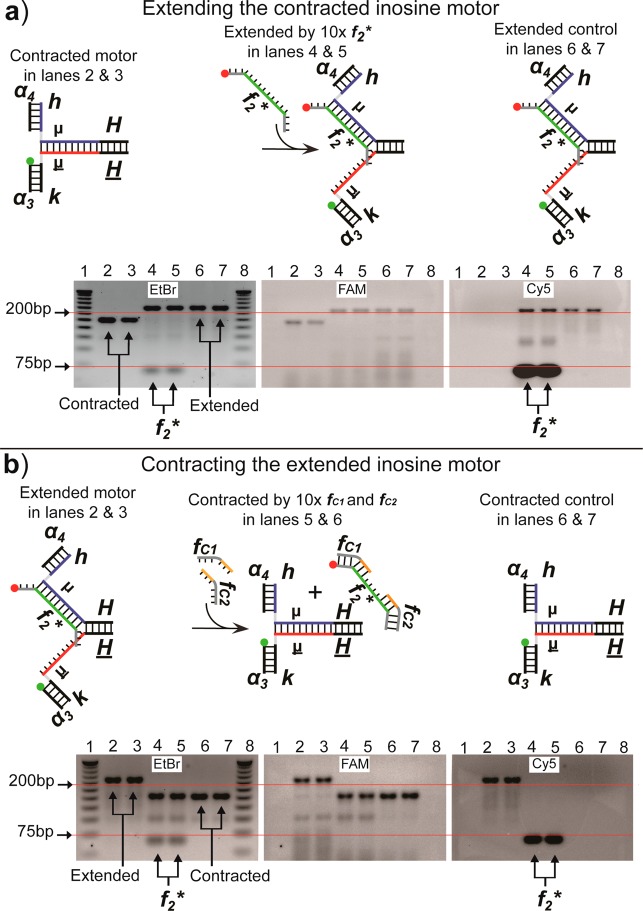
Gel electrophoresis was used for verification of the extension and contraction cycles of the inosine-containing Mb2 motor. The gels contained ethidium bromide for imaging duplexed DNA; a FAM fluorescent label was also attached to an arm of the device, and a Cy5 was attached to an extending fuel strand. The two fluorophores allowed simultaneous tracking of the device and the fuel strands in the gels (Figure 3a). The gel data demonstrated the extension process of the motors because the molecular weight of the motor device increased, and the two fluorophores were colocalized after the addition of the extending fuel strands. Likewise, the contraction process was confirmed because the molecular weight returned back to the closed value and the Cy5-labeled fuel strands were found to be pooled at the bottom of the gel (Figure 3b).

Figure 3.

Figure 3

Open in a new tab

Fluorescent gel imaging of the DNA motors. Fluorescence images of EtBr, FAM, and Cy5 were independently captured and are displayed side-by-side. (a) Extension of contracted motors. Lanes 4 and 5 contain motors extended with 10-fold excess of f2* strands. Unbound f2* strands were accumulated at the ∼60 bp position in the Cy5 image. FAM-labeled contracted motors are in lanes 2 and 3, and motors were extended by thermal annealing as a 1:1 ratio of f2* to the device (lanes 6 and 7). (b) Contraction of motors extended with equal ratio of f2*. Lanes 4 and 5 contain the motors with 10 times more closing strands (fc1, fc2) than the device. Removed f2* is at ∼60 bp position in the Cy5 image. For comparison, the motors extended by f2* (lanes 2 and 3) and contracted FAM-labeled motors (lanes 6 and 7) are included.

Conclusion

We studied two different DNA strand displacement devices with and without an inosine biased branch migration domain. One device contained a hinge that kept the two sides of the device from separating after invasion by a fuel strand, and the other did not (the two sides separated). The inclusion of inosines into the hinged device resulted in forming a thermodynamically stable partially displaced state, allowing the device to remain in the extended position after being invaded. The addition of inosines also resulted in increasing the strand displacement kinetics of both devices particularly when the toeholds were short. When the toehold was only 1 base, the strand displacement kinetics were increased by 7500 times. The use of an energetic bias to change DNA strand displacement kinetics and to create a thermally stable partially displaced state led to a strategy that can be used together with existing routes to create dynamic nucleic acid devices.

Acknowledgments

We extend our thanks to Dr. F. Arce for his help with the manuscript. We thank Prof. S. Subramaniam and Prof. X. Huang at UCSD for their constructive and insightful advice throughout the work and for their critical editing of the manuscript. The work is supported by grants from National Institute on Drug Abuse [5R01DA025296-04], and departmental development funds from the Dept. of Mechanical and Aerospace Engineering, UCSD.

Supporting Information Available

Additional experimental details. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

P.B.L. and J.L. contributed equally to this work.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

la503711g_si_001.pdf (799.1KB, pdf)

References

  1. Seeman N. C. DNA in a material world. Nature 2003, 4216921427–431. [DOI] [PubMed] [Google Scholar]
  2. Yin P.; Choi H. M. T.; Calvert C. R.; Pierce N. A. Programming biomolecular self-assembly pathways. Nature 2008, 4517176318-U4. [DOI] [PubMed] [Google Scholar]
  3. Benenson Y.; Paz-Elizur T.; Adar R.; Keinan E.; Livneh Z.; Shapiro E. Programmable and autonomous computing machine made of biomolecules. Nature 2001, 4146862430–434. [DOI] [PubMed] [Google Scholar]
  4. Elbaz J.; Moshe M.; Willner I. Coherent activation of DNA tweezers: A “SET-RESET” logic system. Angew. Chem., Int. Ed. 2009, 48213834–3837. [DOI] [PubMed] [Google Scholar]
  5. Lund K.; Manzo A. J.; Dabby N.; Michelotti N.; Johnson-Buck A.; Nangreave J.; Taylor S.; Pei R.; Stojanovic M. N.; Walter N. G.; Winfree E.; Yan H. Molecular robots guided by prescriptive landscapes. Nature 2010, 4657295206–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Mao C. D.; Sun W. Q.; Shen Z. Y.; Seeman N. C. A nanomechanical device based on the B-Z transition of DNA. Nature 1999, 3976715144–146. [DOI] [PubMed] [Google Scholar]
  7. Shin J. S.; Pierce N. A. A synthetic DNA walker for molecular transport. J. Am. Chem. Soc. 2004, 1263510834–10835. [DOI] [PubMed] [Google Scholar]
  8. Simmel F. C. Processive motion of bipedal DNA walkers. ChemPhysChem 2009, 10152593–2597. [DOI] [PubMed] [Google Scholar]
  9. Wickham S. F. J.; Bath J.; Katsuda Y.; Endo M.; Hidaka K.; Sugiyama H.; Turberfield A. J. A DNA-based molecular motor that can navigate a network of tracks. Nat. Nanotechnol. 2012, 73169–173. [DOI] [PubMed] [Google Scholar]
  10. Wang C.; Huang Z.; Lin Y.; Ren J.; Qu X. Artificial DNA nano-spring powered by protons. Adv. Mater. 2010, 22252792–2798. [DOI] [PubMed] [Google Scholar]
  11. Xia F.; Guo W.; Mao Y.; Hou X.; Xue J.; Xia H.; Wang L.; Song Y.; Ji H.; Ouyang Q.; Wang Y.; Jiang L. Gating of single synthetic nanopores by proton-driven DNA molecular motors. J. Am. Chem. Soc. 2008, 130268345–8350. [DOI] [PubMed] [Google Scholar]
  12. You M.; Chen Y.; Zhang X.; Liu H.; Wang R.; Wang K.; Williams K. R.; Tan W. An autonomous and controllable light-driven DNA walking device. Angew. Chem., Int. Ed. 2012, 51102457–2460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Yurke B.; Turberfield A. J.; Mills A. P.; Simmel F. C.; Neumann J. L. A DNA-fuelled molecular machine made of DNA. Nature 2000, 4066796605–608. [DOI] [PubMed] [Google Scholar]
  14. Goodman R. P.; Heilemann M.; Doose S.; Erben C. M.; Kapanidis A. N.; Turberfield A. J. Reconfigurable, braced, three-dimensional DNA nanostructures. Nat. Nanotechnol. 2008, 3293–96. [DOI] [PubMed] [Google Scholar]
  15. Zhang Z.; Olsen E. M.; Kryger M.; Voigt N. V.; Torring T.; Gultekin E.; Nielsen M.; MohammadZadegan R.; Andersen E. S.; Nielsen M. M.; Kjems J.; Birkedal V.; Gothelf K. V. A DNA tile actuator with eleven discrete states. Angew. Chem., Int. Ed. 2011, 50173983–3987. [DOI] [PubMed] [Google Scholar]
  16. Zhang Z.; Zeng D.; Ma H.; Feng G.; Hu J.; He L.; Li C.; Fan C. A DNA-origami chip platform for label-free SNP genotyping using toehold-mediated strand displacement. Small 2010, 6171854–1858. [DOI] [PubMed] [Google Scholar]
  17. Khodakov D. A.; Khodakova A. S.; Linacre A.; Ellis A. V. Toehold-mediated nonenzymatic DNA strand displacement as a platform for DNA genotyping. J. Am. Chem. Soc. 2013, 135155612–5619. [DOI] [PubMed] [Google Scholar]
  18. Lubrich D.; Lin J.; Yan J. A contractile DNA machine. Angew. Chem., Int. Ed. 2008, 47377026–7028. [DOI] [PubMed] [Google Scholar]
  19. Elbaz J.; Wang Z.-G.; Wang F.; Willner I. Programmed dynamic topologies in DNA catenanes. Angew. Chem., Int. Ed. 2012, 51102349–2353. [DOI] [PubMed] [Google Scholar]
  20. Gu H.; Chao J.; Xiao S.-J.; Seeman N. C. A proximity-based programmable DNA nanoscale assembly line. Nature 2010, 4657295202–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zhang D. Y.; Turberfield A. J.; Yurke B.; Winfree E. Engineering entropy-driven reactions and networks catalyzed by DNA. Science 2007, 31858531121–1125. [DOI] [PubMed] [Google Scholar]
  22. Zhang D. Y.; Winfree E. Dynamic allosteric control of noncovalent DNA catalysis reactions. J. Am. Chem. Soc. 2008, 1304213921–13926. [DOI] [PubMed] [Google Scholar]
  23. Zhang D. Y.; Winfree E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 2009, 1314717303–17314. [DOI] [PubMed] [Google Scholar]
  24. Feller W.an Introduction to Probability Theory and Its Applications, 3rd ed.; John Wiley & Sons: New York, 1968; p v. [Google Scholar]
  25. Radding C. M.; Beattie K. L.; Holloman W. K.; Wiegand R. C. Uptake of homologous single-stranded fragments by superhelical DNA. 4. Branch migration. J. Mol. Biol. 1977, 1164825–839. [DOI] [PubMed] [Google Scholar]
  26. Liphardt J.; Onoa B.; Smith S. B.; Tinoco I.; Bustamante C. Reversible unfolding of single RNA molecules by mechanical force. Science 2001, 2925517733–737. [DOI] [PubMed] [Google Scholar]
  27. Yurke B. DNA-based molecular motors. Abstr. Pap. Am. Chem. Soc. 2003, 226, U470–U471. [Google Scholar]
  28. Yurke B.Using DNA to power the nanoworld. In Controlled Nanoscale Motion; Linke H., Månsson A., Eds.; Springer: Berlin, 2007; Vol. 711, pp 331–347. [Google Scholar]
  29. EssevazRoulet B.; Bockelmann U.; Heslot F. Mechanical separation of the complementary strands of DNA. Proc. Natl. Acad. Sci. U.S.A. 1997, 942211935–11940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rief M.; Clausen-Schaumann H.; Gaub H. E. Sequence-dependent mechanics of single DNA molecules. Nat. Struct. Biol. 1999, 64346–349. [DOI] [PubMed] [Google Scholar]
  31. Visscher K.; Schnitzer M. J.; Block S. M. Single kinesin molecules studied with a molecular force clamp. Nature 1999, 4006740184–189. [DOI] [PubMed] [Google Scholar]
  32. Landon P. B.; Ramachandran S.; Gillman A.; Gidron T.; Yoon D.; Lal R. DNA zipper-based tweezers. Langmuir 2012, 281534–540. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la503711g_si_001.pdf (799.1KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES