Splitting, linking, knotting, and solitonic escape of topological defects in nematic drops with handles

Significance

There are few theoretical predictions of knotted, linked, solitonic, and other topologically nontrivial field configurations, which can be tested by experiments, due to the lack of experimentally accessible systems and techniques. This work presents an experimental realization and thorough theoretical analysis of interplay between topologies of the nematic field and closed confining surfaces with systematically varied genus. Handlebody-shaped nematic drops with normal boundary conditions reveal a large diversity of controlled field configurations, including ones with linked and knotted half-integer defect lines that are topologically distinct from predictions of mathematical theorems and that can exist only in nonpolar media. Our model system may become a testbed for probing a scale-invariant interplay of topologies of confining surfaces, fields, and defects.

Abstract

Topologically nontrivial field excitations, including solitonic, linked, and knotted structures, play important roles in physical systems ranging from classical fluids and liquid crystals, to electromagnetism, classic, and quantum field theories. These excitations can appear spontaneously during symmetry-breaking phase transitions. For example, in cosmological theories, cosmic strings may have formed knotted configurations influencing the Early Universe development, whereas in liquid crystals transient tangled defect lines were observed during isotropic–nematic transitions, eventually relaxing to defect-free states. Knotted and solitonic fields and defects were also obtained using optical manipulation, complex-shaped colloids, and frustrated cholesterics. Here we use confinement of nematic liquid crystal by closed surfaces with varied genus and perpendicular boundary conditions for a robust control of appearance and stability of such field excitations. Theoretical modeling and experiments reveal structure of defect lines as a function of the surface topology and material and geometric parameters, establishing a robust means of controlling solitonic, knotted, linked, and other field excitations.

Since the origins of the mathematical knot theory, development of which was prompted by early models of elementary building blocks of matter (1), knotted fields and structures arise in proteins (2), light (3–5), fluids (6–8), liquid crystals (LCs) (9–14), classic and quantum field theories (15, 16), topological insulators (17), and other physical systems (18). Such topologically nontrivial field configurations can be predicted from solutions of nonlinear field equations, but are rarely accessible to direct experimental visualization. On the other hand, LCs offer complexity in degrees of freedom and symmetries that allow for probing topologically analogous phenomena (19, 20) on completely different scales, such as kinetics of cosmic strings in the Early Universe (21). In this work, we develop polymer-dispersed nematic drops with nontrivial surface topology and perpendicular boundary conditions that prompt stable configurations of defect lines in forms of unknots, knots, links, 2D skyrmions, and other singular and solitonic structures that can be selected by controlling geometric and material parameters. This enables a robust control of defects in nematic drops of nonzero genus by shaping topology and varying geometric parameters of confining surfaces as well through the use of laser-guided temperature quenching of isotropic–nematic transition within the drops.

Our nematic drops in a polymer matrix have handlebody shapes with genus g varying from 1 to 5 and the corresponding Euler characteristics χ = 2(1 − g) from 0 to −8 (22). The closed confining surfaces impose strong homeotropic (normal) anchoring on the nematic director n(r) describing average local orientation of LC molecules, so that n(r) aligns along the inner normal to a bounding surface S. The surface topology and these boundary conditions dictate bulk defects of net topological hedgehog charge m = ±(1 − g) in the nematic domain, which, to assure the topological charge conservation, compensate the hedgehog charge of the field on the inner closed confining surface of the nematic drop given by the Gauss–Bonnet and Poincaré–Hopf theorems (23). One would therefore simply expect that the nematic interior of a single torus is topologically uncharged, g = 2 drop hosts a defect of m = ±1 topological charge, and so on, where the sign of m depends on the choice of vector field direction when decorating n(r) to determine the charge (24). However, the mathematical theorems prescribe no particular ways in which the topological constraints should be satisfied. Our study shows that this “flexibility” of satisfying topological constraints, combined with the nematic LCs nature and ability of hosting both half-integer line defects and point defects, leads to a large number of topologically nontrivial configurations that can be selected as stable and metastable structures by controlling material and geometric parameters. Importantly, some of these field and defect configurations, such as linked and knotted loops of half-integer defect lines, are topologically different from what topological theorems predict for vector fields under such confinement. Moreover, a combination of tuning topology (genus) and geometric parameters of confining surfaces as well as laser-guided spatially resolved isotropic–nematic temperature quench allow us to generate the precise desired defect and field configurations out of a host of topology-satisfying stable and metastable states.

Results

To deduce the structure of fields and defects, we combine numerical modeling based on minimization of the Landau–de Gennes free energy (25) with experimental 3D nonlinear optical imaging and holographic optical control (26) of n(r) and individual defects in the corresponding experimental systems. We investigate the structure and transformation of defects as a function of genus, temperature, material, and geometric parameters. The most common observed defects are loops of nematic line defects, dubbed “disclinations,” which are characterized by a winding number s counting the number of times n(r) rotates by 2π as one circumnavigates the defect once in a plane perpendicular to the line. For g = 1 surfaces, we observe a single disclination loop with s = 1, two s = 1/2 disclination loops, or nonsingular solitonic “escaped” director configurations containing no defects (Fig. 1). As the system is quenched from isotropic to nematic phase, we observe especially large structural richness of configurations with disclination rings, including links and knots. Drops of higher genus stabilize even larger combinations of multiple s = 1/2 loops and escaped configurations supplemented with additional topological point and disclination loop defects. Whereas constraints imposed by topological theorems are always met and hedgehog charges always add to m = ±χ/2, the particular defects that occur are highly dependent on geometric and material parameters, as well as on the laser-controlled temperature quench, allowing for a precise selection and control of desired field configurations.

Fig. 1.

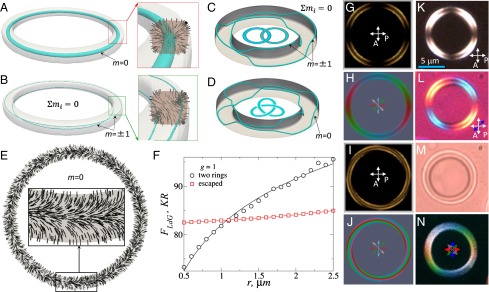
(A and B) Configurations with (A) a single s = 1 and (B) two s = 1/2 disclination rings, having isosurfaces of (A) $Q=0.2\hspace{0.17em}$ and (B) $Q=0.25$ shown in blue; $R=2.5\hspace{0.17em}\mu \text{m},\hspace{0.17em}r=0.1R,\hspace{0.17em}\alpha =10.$ (Insets) n(r) around the defects. (C) Hopf link and (D) trefoil T(3; 2) torus knot, known also as $3_1$ knot in the Alexander-Briggs notation, of half-integer disclination loops, with blue isosurfaces of $Q=0.3;\hspace{0.17em}R=1\hspace{0.17em}\mu \text{m},\hspace{0.17em}r=0.2\hspace{0.17em}\mu \text{m},\hspace{0.17em}\alpha =6$. (E) n(r) in a plane of a torus with an escaped n(r) for $R=10\hspace{0.5em}\mu \text{m},\hspace{0.17em}r=0.1R,\hspace{0.17em}\alpha =10$. (F) Landau–de Gennes free energy, Eq. 1 (in excess over the free energy of the uniform nematic) as a function of $r$ at $R=10r$ for the two structures. (G–J) Computer-simulated (G and I) POM and (H and J) 3PEF-PM textures of drops with (G and H) two defect rings and (I and J) escaped n(r). Linear polarizations of 3PEF-PM probing light (marked by red, blue, green, and pink double arrows) of four images used to obtain the superimposed textures shown in (H and J). (K–M) Optical micrographs obtained between crossed polarizer P and analyzer A, without (K) and with (L) an additional 530-nm phase retardation plate (blue double arrow depicts its low axis) and (M) without these optical elements. (N) Experimental 3PEF-PM texture obtained by overlaying images with polarizations of probing light at $0°$(red), $45°$(green), $90°$(blue), and $135°$(pink) and corresponding to H.

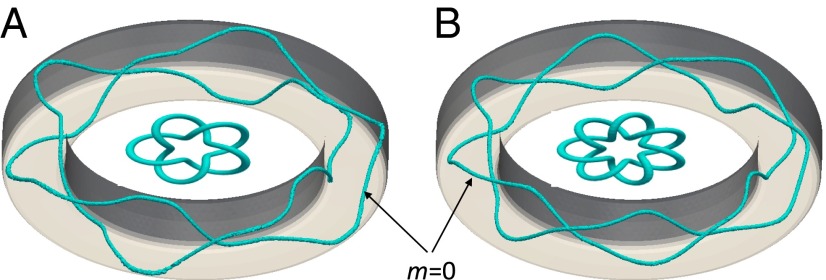
Fig. 1 summarizes experiments and numerical modeling of director configurations in g = 1 drops with rounded-square cross-sections. They are characterized by the torus major and minor radii $R$ and $r$, respectively, and by the exponent $\alpha \ge 2$ determining the tube’s cross-sectional rounded-square shape, with larger $\alpha$ giving larger deviations from a circle (SI Text). Fig. 1 A and B shows defect structures stable at small to intermediate values of $r$ (Table 1). The stability limit $r^{\ast }$ of the double rings depends on temperature and $R$, and is of the order of $r^{\ast }\sim 100\xi$, where $\xi$ ∼ 15 nm is the nematic correlation length (Table 1 and SI Text). Both the single s = 1 (Fig. 1A) and the pair of s = 1/2 disclination rings (Fig. 1B) carry topological charges m = 0. Such disclination rings are unstable in a nematic bulk, which is consistent with the topology of the order parameter manifold and free-energy minimization (27). However, they are energetically stabilized by the surface confinement and perpendicular boundary conditions in g = 1 drops. The configuration with a single s = 1 ring is relatively exotic and observed mainly only at very strong confinement with $r\sim \xi$. The threshold value of $r$ at which the s = 1 ring loses its stability grows with temperature, and for temperatures very close to the nematic–isotropic phase coexistence reaches values of the order of ∼10$\xi \hspace{0.17em}$ (Table 1). In practically realizable experimental systems, although bringing the system close to the isotropic–nematic-phase transition (while still in a nematic phase) increases stability of s = 1 lines, such structures still can be realized only for drops with $r$ in the submicrometer range and cannot be probed in detail due to limited resolution of optical imaging techniques. For $\xi \mathrm{\lesssim }\hspace{0.17em}r\mathrm{\lesssim }100\xi$, room-temperature field configurations with double rings of s = 1/2 disclinations appear (Fig. 1B). Because each of the rings has a winding number of the same sign, they mutually repel (18, 19) and tend to localize in the diagonal corners of rounded-square cross-section, maximizing their separation (Fig. 1B). This ground-state structure for drops with submicrometer- and micrometer-sized ring cross-sections can be realized along with many metastable configurations, including the ones with linked and knotted disclinations. As an example, Fig. 1C shows a Hopf link of two s = 1/2 defect loops and Fig. 1D depicts a trefoil knot of a single half-integer defect line. Two more examples out of a large number of confinement-stabilized structures are shown in Fig. 2, representing pentafoil and septafoil torus knots of the half-integer disclinations. It is interesting that the nonpolar nature of n(r) allows for so many topologically interesting field configurations to occur while satisfying boundary conditions and topological constrains that the net hedgehog charge m of all defects is zero. Moreover, for larger drops, a defect-free escaped director configuration becomes energetically favorable (Fig. 1 E and F), having the perpendicular boundary conditions met simply through nonsingular distortions of n(r). Single and double defect rings and the escape of singularity through continuous director distortions (Fig. 1 A, B, and E) are also hosted by nematics in cylindrical capillaries (28, 29), with the solitonic escaped field configuration also resembling the solitons dubbed “skyrmions” that recently received prominent attention in studies of chiral magnets (30). LC confinement in toroidal drops dramatically enriches this behavior by allowing linked, knotted, and other topological field and defect configurations (Figs. 1 and 2) that cannot be stabilized in cylindrical capillaries or in unconfined nematic samples.

Table 1.

Ground-state field and defect configurations and their corresponding r range of stability for genus g = 1 droplets

Configuration	Approximate r − range of stability
Single s = +1 ring	r ∼ ξ
	r ∼ 10ξ at τ = τNI
Two s = +1/2 rings	ξ ≲ r ≲ 100ξ
	Funknot < Flink < Fknot
Escaped director field	r ≳ 100ξ

Fig. 2.

(A) Pentafoil T(5,2) knot ($5_1$ in the Alexander-Briggs notation) of disclinations. (B) Septafoil T(7,2) knot ($7_1$ in the Alexander-Briggs notation) of disclinations. Blue surfaces of the knotted tubes depicting the defects correspond to $Q=0.3$; $R=1\hspace{0.17em}\mu \text{m},\hspace{0.17em}r=0.2\hspace{0.17em}\mu \text{m},\hspace{0.17em}\alpha =6.$

To directly compare experiments and results of numerical modeling, we have simulated three-photon excitation fluorescence polarizing microscopy (3PEF-PM) and polarizing optical microscopy (POM) micrographs of global and local minimum-energy nematic field and defect configurations while accounting for the finite resolution effects (Fig. 1 G–J) (26). The structures can be identified based on comparison of such images. For example, POM and superimposed 3PEF-PM micrographs of configurations with two disclination rings (Fig. 1 G and H) differ from images with escaped n(r) (Fig. 1 I and J). Furthermore, theoretical POM images, such as the one obtained for the drop with double disclination rings (Fig. 1G), are consistent with the experimental ones obtained with (Fig. 1K) and without (Fig. 1L) an additional phase retardation plate. Optical 3PEF-PM micrographs obtained through the superimposition of theoretically calculated 3PEF-PM fluorescence patterns using four different linear polarizations of excitation light (such as the one shown in Fig. 1H) also agree with the corresponding experiments (Fig. 1N).

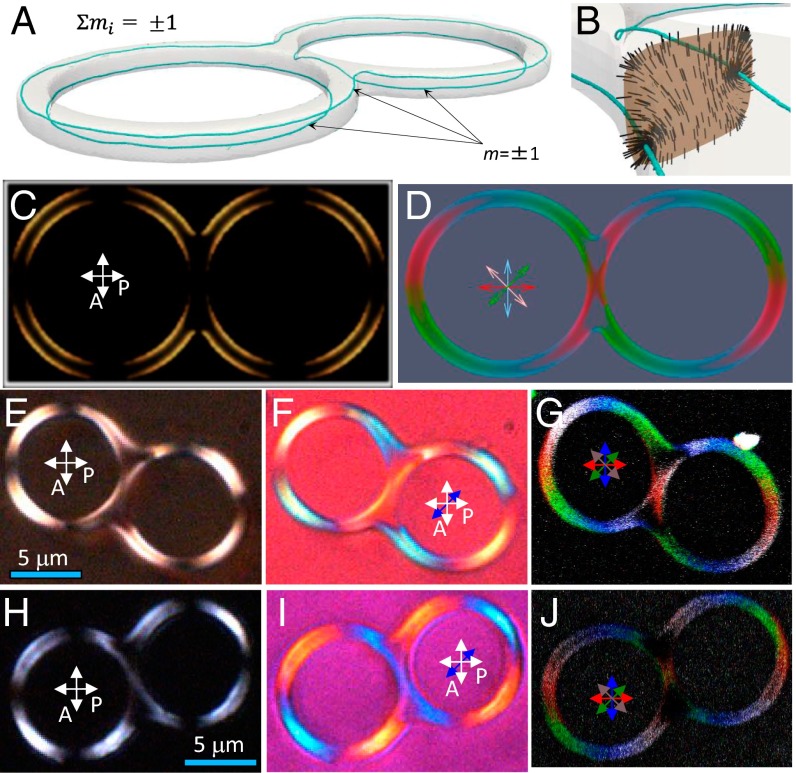
For drops with g > 1, defects of nonzero net charge are required by the Poincaré–Hopf index theorem (23), and we observe them in both experiments and numerical modeling. In contrast with g = 1 drops, in drops with small values of minor radius $r$, we do not observe the s = 1 disclination rings, which are unstable even at temperatures close to nematic–isotropic transition and tend to break into multiple (depending on g) s = 1/2 defect loops. Three half-integer disclination loops form in small drops of g = 2 (Fig. 3A), with one of them running along the whole drop perimeter, whereas two others encircle the two holes of the drop. Similar configurations, with one large disclination looping around the largest perimeter and g small circular loops encircling holes, are also observed for droplet of g > 2. Theoretical POM (Fig. 3C) and 3PEF-PM (Fig. 3D) textures match their experimental counterparts shown in Fig. 3 E and H and G and J, respectively. The net hedgehog charges of defect loops add to m = ± χ/2, such as m = ±1 for the configuration shown in Fig. 3A, although these topological charges are not localized in particular regions within the drop and charges due to individual defects often mutually compensate each other. Similar to genus g = 1 drops, a large number of linked and knotted configurations of such half-integer defect lines can be realized too and will be explored in detail elsewhere.

Fig. 3.

(A) g = 2 drop with defect rings depicted using blue isosurfaces of $Q=0.35$ and corresponding (B) cross-section of n(r) and (C) POM texture. (D) The 3PEF-PM texture obtained by superimposing simulated images acquired at four different linear polarizations of excitation light marked by red, blue, green, and pink double arrows; $R=2.5\hspace{0.5em}\mu \text{m},\hspace{0.5em}r=0.1R,\hspace{0.17em}\alpha =10.$ (E–J) Experimental micrographs obtained using POM between crossed polarizer P and analyzer A without (E and H) and with an additional 530-nm phase retardation plate (F and I) and using 3PEF-PM (G and J). Experimental 3PEF-PM texture was obtained by superimposing images with polarizations of probing light at $0°$(red), ${45}^{°}$(green), $90°$(blue), and $135°$(pink), corresponding to the simulated texture shown in D; note the dark areas in junctions, where n(r) is perpendicular to the images.

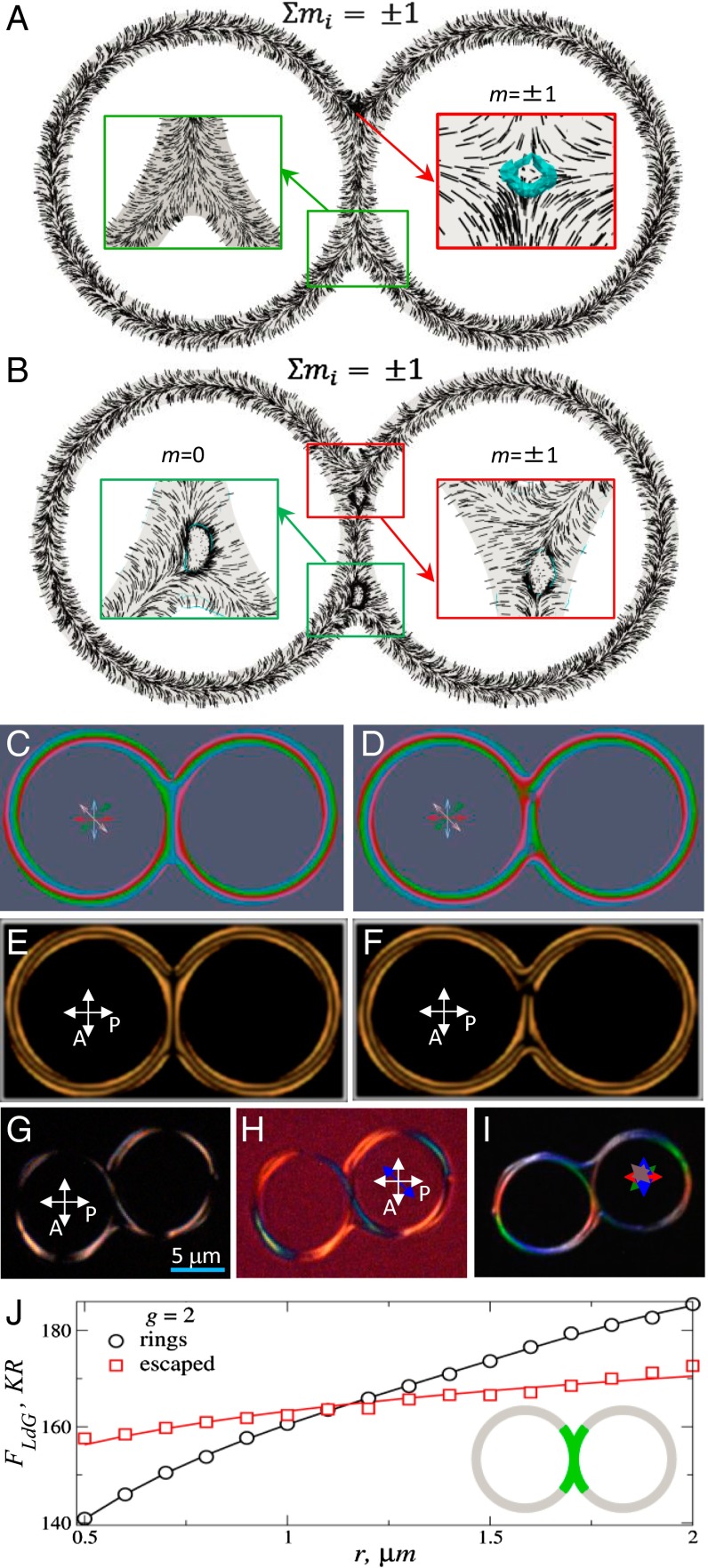
For larger drops with $r\mathrm{\gtrsim }100\xi$, the escaped director profiles fully replace the singular defect rings (Fig. 4), yielding point defects or small disclination loops localized in the junction regions (Figs. 4 A and B and 5 A and B). In the configuration depicted in Fig. 4A, a hyperbolic hedgehog of m = ±1 is found in the upper part of the junction, corresponding to the point where different colors in the 3PEF-PM image and dark brushes in the POM image meet (Fig. 4 C and E). The defect core is open into a ring shown in Fig. 4A, Inset (in the red frame). By varying initial conditions for minimization of the Landau–de Gennes functional and also by quenching the sample from isotropic to nematic phase in both experiments and in numerical modeling (including the laser-guided quenching described in the SI Text), other metastable escaped configurations can be realized too. One of them is shown in Fig. 4B, in which n(r) escapes in the same direction in both branches of the 2-tori, in contrast with that in Fig. 4A where n(r) escapes in the opposite directions. In the former case, each of the two junction regions hosts an extended half-integer disclination loop. The sum of their topological charges is still m = ±1. A close inspection of n(r) reveals that the upper loop has m = ±1 and the bottom one is topologically “neutral” (m = 0), occurring to minimize the free energy for a given mutual directionality of the n(r) escape in the two rings. The transformation of this configuration to the ground-state structure shown in Fig. 4A faces a formidable free-energy barrier, trapping the system in a metastable state. Defect loops in junctions encircle small nematic regions with n(r) perpendicular to the tori planes (Fig. 4B), appearing as dark areas in both simulated and experimental 3PEF-PM and POM textures (Figs. 4 C–I and 5 C–G). Far from the junctions, the corresponding theoretical and experimental 3PEF-PM (Fig. 4 C, D, and I) and POM images (Fig. 4 E–H) also show mutually consistent intensity patterns, indicating realization of the same field and defect configurations in experiments and theory. Interestingly, the threshold value of the minor tori radius r at which escaped configuration replaces the one with half-integer defect loops is slightly larger (by about 10%) for g = 2 drops than for g = 1 drops (Fig. 4J). This is caused by the free-energy contribution of the intertori region (shown in green in Fig. 4J, Inset), which is required to host at least one m = ±1 topological defect (Fig. 4A), increasing the free energy of the escaped configuration.

Fig. 4.

(A and B) Escaped n(r) structures depicted in the drop’s midplane for $R=10\hspace{0.17em}\mu \text{m},\hspace{0.17em}r=0.1R,\hspace{0.17em}\alpha =10$. (Insets) Junction regions and blue tubes depict isosurfaces of $Q=0.3$. Hyperbolic hedgehog defect core and disclination loops with zero (green-framed) and unit (red-framed) topological charges. (C and D) Corresponding 3PEF-PM textures obtained by superimposing simulated images at four different linear polarizations of excitation light marked by red, blue, green, and pink double arrows. (E and F) corresponding POM images between crossed polarizer P and analyzer A. (G and H) Experimental POM textures obtained (G) without and (H) with an inserted phase retardation plate having a slow axis along the blue double arrow. (I) Experimental 3PEF-PM texture obtained by superimposing images with polarizations of probing light at $0°$(red), $45°$(green), $90°$(blue), and $135°$(pink). (J) Landau–de Gennes free energy, Eq. 1, as a function $r$ at $R=10r$ for configuration with disclination rings (circles) and solitonic escape (squares) as shown in A. The green region of the droplet (Inset) marks the 3D minimization domain. In the gray region, the minimization is done by exploiting the symmetry of the confinement region and then the $\mathit{Q}$ tensor is fixed (see Materials and Methods for more details).

Fig. 5.

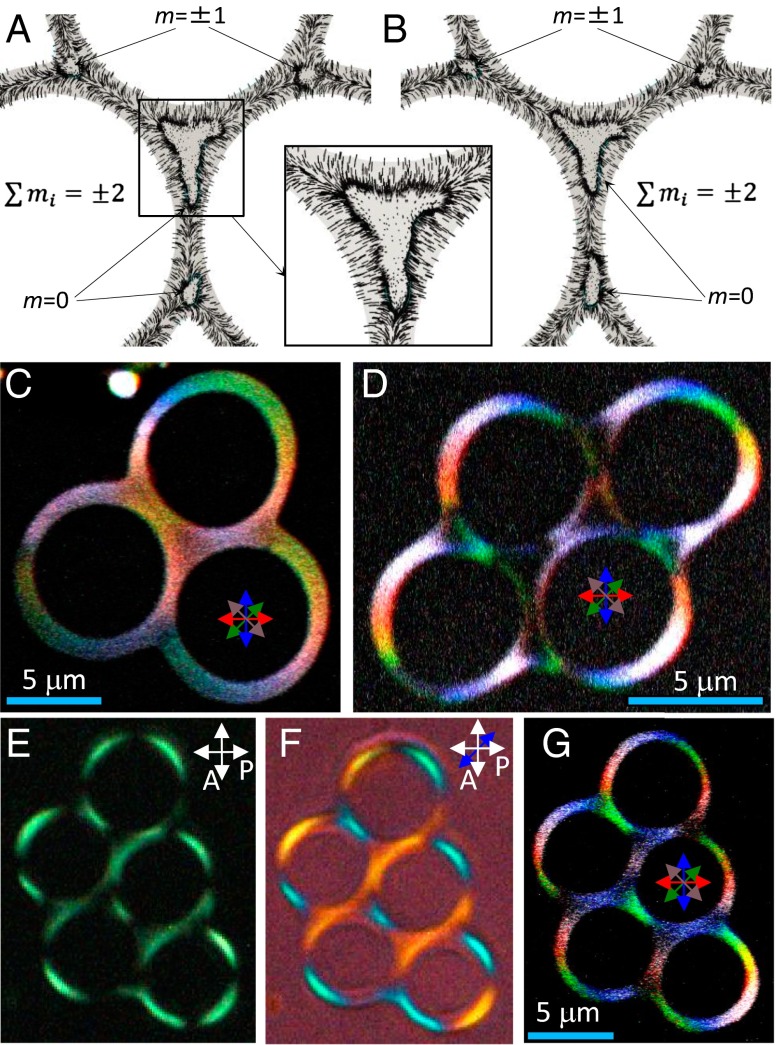
(A and B) Examples of numerically calculated escaped n(r) for $R=10\hspace{0.5em}\mu \text{m},\hspace{0.5em}r=1\hspace{0.5em}\mu \text{m},\hspace{0.17em}\alpha =10$. (C, D, and G) Experimental 3PEF-PM textures obtained by superimposing images of g = 3–5 drops for linear polarizations of probing light at $0°$(red), $45°$(green), $90°$(blue), and $135°$(pink). (E and F) Experimental POM images of a g = 5 drop obtained (E) without and (F) with an inserted 530-nm phase retardation plate having a slow axis along the blue double arrow.

Discussion

A spectacular property of our confined nematic system is the diversity of structures satisfying topological constraints imposed by mathematical theorems and perpendicular boundary conditions on the closed handlebody surfaces. This feature largely stems from the nonpolar nature of n(r). Indeed, all half-integer defect lines would be disallowed in polar systems, thus precluding appearance of knotted and linked defects and dramatically reducing the number of topologically admissible structures. From a large number of experimental and theoretical configurations seen in n(r), the structures that would still be allowed in a vector field include only ones with escaped director field hosting solely point defects at the intertori junctions and s = 1 disclination rings, substantially reducing the spectrum of possibilities of satisfying both boundary conditions and the topological theorems for drops of different g. The fact that the nonpolar nature of nematic fields diversifies the topology of allowed linked, knotted, and other configurations is important beyond our soft matter system, because defect lines in nonpolar fields in cosmology (cosmic strings) and in many other physical systems are topologically similar to nematic disclinations, although much less accessible experimentally. What is even more important is that our study shows a way of satisfying topological constraints that guide interactions between closed surfaces and nonpolar nematic director fields, which is topologically distinct from that predicted by mathematical theorems for vector fields. Indeed, although unknots of small defect loops at intertori junctions of large handlebody drops are topologically similar to point defects, the linked and knotted defect lines are not, and thus are topologically distinct from what can be realized in vector fields. It is surprising that, to the best of our knowledge, the issue of how the interplay of the topology of a closed surface and a nonpolar field confined by it may differ from that in the case of a confined vector field was never considered by mathematicians or physicists alike. Our study reveals the unexpected richness of possible nonpolar field and corresponding defect configurations under confinement by closed varying-genus surfaces, which includes all structures observed in vector fields and, additionally, a zoo of other topologically distinct configurations, such as the ones with knotted or linked defect lines.

Our system allows one not only to realize a large variety of topologically distinct field and defect configurations, but also to precisely control and select a particular configuration out of a large variety of stable and metastable ones (Table 1). Control capabilities at our disposal include (i) defining the total topological hedgehog charge m determined by the genus g of a confining surface; (ii) control of appearance of different types of defect structures (integer or half-integer disclinations spanning the whole droplet, versus various escaped solitonic configurations) through varying geometric parameters like the minor tori radius $r$. Our results also show that at each given g and $r$, there are different types of topology-satisfying stable and metastable nematic configurations (e.g., unknots, links, or knots), which cannot be selected by a random process of quenching the sample from isotropic to nematic state. Appearance of a particular variation of defect loops in this case is kinetically dominated during the temperature quench. However, even this fine selection between configurations with similar types of defects is possible through the laser-guided temperature quench (Fig. S1). Holographically or laser-scanning implemented knotted and linked distributions of high-intensity laser light (10) results in increased local heating of the LC along the knotted–linked tubes of high laser intensity, allowing for selection of the precise defect configuration of interest out of the zoo of stable and metastable structures that can exist at given g and $r$. In the larger drops with g > 1 and escaped director structures, the particular types of defects in the junction domains can also be selected by “combing” the director field in the desired direction within each ring of handlebody by linearly polarized laser light (Fig. S2) upon temperature quench from the isotropic state, which then defines the types of defects occurring at the tori junctions. Although the spontaneous temperature typically yields a large number of stable and metastable structures, the above two different types of laser-guided quench allow us to select precise individual defect configurations. In simple words, by using random temperature quench, we can first create a “menu” of defect configurations that can be realized for given genus and geometric parameters (of which $r$ is the most important), and then deliver the precise field–defect configuration by the use of laser-guided temperature quench.

To conclude, we realized experimentally and analyzed theoretically structural organization in nematic drops confined by closed handlebody surfaces with systematically varied genus. We show richness of topologically nontrivial field excitations when confining surfaces impose normal boundary conditions on the director. The topological interaction of the director field and surfaces generates linked, knotted, and other 3D field configurations which match theoretical predictions and may allow for insights into many topologically analogous phenomena in other branches of physics, ranging from particle physics to cosmology. Because few theoretical predictions of topological field configurations can be tested experimentally due to lack of experimentally accessible systems and techniques, our model system may become a testbed for probing a potentially scale-invariant interplay of topologies of confining surfaces, fields, and defects. Similar to probing the cosmological Kibble mechanism using LC phase transitions (19), it may enable new cosmology and particle physics relevant experiments. On the other hand, our experimental and theoretical findings demonstrate topologically distinct behavior of defect and field configurations in confined nematic nonpolar molecular alignment field that are different from well-known predictions of topological theorems applied for vector fields in contact with closed surfaces of nonzero genus. In addition to the richness of new fundamental behavior, our system may be of interest for realizing new types of multistate optically addressed topological memory devices that can allow for recording and reading information through optically changing different topology-satisfying field and defect configurations in the polymer-dispersed nematic drops of controlled genus.

Materials and Methods

Fabrication and 3D Imaging.

To create nematic drops with nonzero genus, we first fabricated handlebody-shaped silica microstructures by means of photolithography (24, 31). Desired polymer structures were obtained using replica molding and soft lithography (32). Norlin optical adhesive (NOA63) was placed between a glass plate and a substrate containing handlebody-shaped silica microstructures and then UV cured for 20 s using an OmniCure S2000 illumination system (Lumen Dynamics). The polymerized film was peeled off to leave the desired surface topography on one of its sides. We also fabricated flat polymer films of 5–10 μm in thickness needed to form closed handlebody-like surfaces by sandwiching the two films together. To realize homeotropic boundary conditions, we treated the polymer films and glass substrates by a 0.5 wt % aqueous solution of N,N-Dimethyl-N-octadecyl-3-aminopropyltrimethoxysilyl chloride or by a solution of lecithin in toluene (10). Additionally, some NOA63 films were heated to temperatures right beneath the isotropic nematic transition of the nematic LC E31 (from EM Chemicals). Nematic E31 was then filled between a microstructured polymer sheet and either a flat polymer film or coverslip, which were pressed together and sealed through additional NOA63 UV curing. The ensuing polymer films had LC drops of genus g = 1–5 with rounded-square cross-sections and homeotropic anchoring.

Nonlinear optical 3PEF-PM imaging used a setup built around an inverted microscope IX 81 (Olympus), a tunable Ti-sapphire oscillator (680–1,080 nm, Coherent) emitting 140-fs pulses at a repetition rate of 80 MHz, an oil-immersion 100× objective with numerical aperture of 1.4, and a photomultiplier tube detector H5784-20 (Hamamatsu) (24). Three-dimensional submicrometer resolution was enabled by the nonlinear optical excitation. The fluorescence intensity exhibited a strong ∝cos⁶θ dependence on the angle θ between n(r) and the linear polarization of the probing light; 3PEF-PM and POM imaging at different polarizations of probing light revealed 3D director field configurations (10). These images were then compared with the ones simulated numerically using the extended Jones matrix method described in detail elsewhere (33, 34) and the theoretical n(r) structures obtained as described below.

Theoretical Approach.

Landau–de Gennes free energy is formulated in terms of a traceless symmetric rank-3 tensor order parameter with five independent components $Q_{ij}\hspace{0.17em}(i,j=1,\mathrm{...},3)$. Free-energy density then is written as an expansion in powers of $\mathit{Q}$ and its spatial derivatives (25)

$$F_{LdG}=\underset{V}{{\displaystyle \int }}\left(a\left(T\right)Q_{ij}^2-b{Q}_{ij}{Q}_{jk}{Q}_{ki}+c{\left(Q_{ij}^2\right)}^2+\frac{L_1}{2}{\partial }_k{Q}_{ij}{\partial }_k{Q}_{ij}+\frac{L_2}{2}{\partial }_j{Q}_{ij}{\partial }_k{Q}_{ik}\right),\hspace{0.17em}$$ [1]

where $a\left(T\right)$ is a linear function of temperature T, and b, c are considered temperature-independent material constants, summation over repeated indexes is assumed, $L_1$ and $L_2$ are phenomenological parameters related to the Frank–Oseen elastic constants. The integral in Eq. 1 is over 3D domain $V$, with the first three terms describing bulk free-energy density and the last two gradient terms representing elastic free-energy density. We model homeotropic anchoring by using the following surface free energy:

$$F_s=W\underset{\partial V}{{\displaystyle \int }}{\left(Q_{ij}-Q_{ij}^s\right)}^{2}ds,$$ [2]

where $W>0$ is the anchoring strength, $Q_{ij}^s=3Q_b\hspace{0.17em}({\nu }_i{\nu }_j-{\delta }_{ij}/3)/2$ describes the preferred surface nematic ordering, with $\mathit{v}$ being the unit normal to the confining surface, ${\delta }_{ij}$ is the Kronecker delta symbol, and $Q_b$ is the bulk value of the scalar order parameter (SI Text). We numerically minimize the Landau–de Gennes free energy, Eq. 1, supplemented by the surface term given by Eq. 2, by using the adaptive finite elements method (35).

The free-energy profiles shown in Fig. 1F for g = 1 were calculated by taking advantage of the axial symmetry of the structures with double rings of disclinations and escaped director configurations. This reduces the initial 3D problem to an effective 2D one, which significantly increases the accuracy of the free energy calculation for the largest considered sizes of droplets. We also assume rigid normal boundary conditions in this case.

To obtain the free-energy profiles for a g = 2 drop shown in Fig. 4J, we first assumed that the nematic configurations in the regions away from the tori junctions do not significantly differ from the corresponding g = 1 configurations at the same r and R. Based on this assumption, the volume of a g = 2 droplet is divided into an “active” junction region, shown in Fig. 4J, Inset by green, and a “passive” off-junction one shown in gray in the aforementioned inset. Then, in the course of minimization only fields in the active region vary, whereas those within the passive one are kept fixed according to the solution of the associated g = 1 problem. The angular extent of the passive regions is given by their respective central angles, which were set to $8\pi /5$.