Criterion for stability of Goldstone modes and Fermi liquid behavior in a metal with broken symmetry

Significance

A remarkable feature of many particle systems is that although they are described by equations respecting various symmetries, they may spontaneously organize into a state that explicitly breaks symmetries. An example is a crystal that breaks the translation symmetry of space. In such cases, a celebrated theorem predicts an excitation, the Goldstone mode. In this paper we examine whether this continues to hold inside a metal, where electrons can collide with the Goldstone excitations. Our result is a one-equation criterion that specifies whether the interactions between electrons and Goldstone modes can be ignored or whether it completely changes their character. In the latter case, unusual phases of matter such as non-Fermi liquids or superconductors may arise.

Abstract

There are few general physical principles that protect the low-energy excitations of a quantum phase. Of these, Goldstone’s theorem and Landau–Fermi liquid theory are the most relevant to solids. We investigate the stability of the resulting gapless excitations—Nambu–Goldstone bosons (NGBs) and Landau quasiparticles—when coupled to one another, which is of direct relevance to metals with a broken continuous symmetry. Typically, the coupling between NGBs and Landau quasiparticles vanishes at low energies, leaving the gapless modes unaffected. If, however, the low-energy coupling is nonvanishing, non-Fermi liquid behavior and overdamped bosons are expected. Here we prove a general criterion that specifies when the coupling is nonvanishing. It is satisfied by the case of a nematic Fermi fluid, consistent with earlier microscopic calculations. In addition, the criterion identifies a new kind of symmetry breaking—of magnetic translations—where nonvanishing couplings should arise, opening a previously unidentified route to realizing non-Fermi liquid phases.

According to the Goldstone theorem, spontaneous breaking of a continuous symmetry leads to gapless Nambu–Goldstone bosons (NGBs). In a Lorentz invariant theory, these bosons are expected to be well-defined excitations, even in the presence of other gapless fields, such as massless Dirac fermions, providing a powerful general mechanism for low-energy excitation (1). A key ingredient leading to their stability is the fact that interactions with NGBs are strongly constrained by symmetry, leading to suppressed couplings at small momentum transfer.

In nonrelativistic systems, though, such general results are not applicable. A particularly important scenario is spontaneous symmetry breaking in a metallic environment, of which there are numerous examples such as magnetic order in a metal. Do the NGBs then survive as well-defined low-energy modes? Or does coupling to the high density of gapless fermionic excitations of the metal lead to overdamped excitations? In this work we establish a general criterion to answer this question based on the pattern of symmetry breaking.

A closely related question has to do with the stability of the Fermi liquid (FL) when coupled to gapless bosonic modes. Besides NGBs, gauge bosons can be gapless over an entire phase, i.e., photons of the electromagnetic field or emergent gauge bosons of spin liquids or quantum Hall states. Alternately, one can tune to a quantum critical point where gapless critical modes centered at wave vector $q=0$ interact with the FL. The latter two cases, of gauge bosons or $q=0$ quantum critical bosons coupled to a Fermi sea, have been studied in many works (2–18). These studies conclude that, for example in $d=2+1$ dimensions, the lifetime of excitations near the Fermi surface is significantly reduced, leading to an absence of well-defined quasiparticles and a breakdown of FL theory. Similarly, the bosonic modes get overdamped and can no longer be observed as well-defined particle-like excitations. In some cases, however, superconductivity intervenes at low energies (19).

In contrast, coupling electrons in a metal to NGBs typically leads to a much more benign outcome. We know, from examples of magnons in ferromagnets and phonons in crystals, that NGBs are typically underdamped even in a metallic environment and the FL theory remains valid. In other words, in these cases the coupling between NGBs and FLs is irrelevant, leading to effectively independent fermionic excitations and NGBs at low energies. This is because interactions involving NGBs are very strongly restricted by both broken and unbroken symmetries. In particular, for these cases the scattering amplitude of electrons off NGBs in the limit of small energy-momentum transfer must vanish. In contrast, quantum critical modes and gauge bosons couple directly to fermions, without derivatives acting on the bosonic field.

However, there is one known exception to this rule. When the continuous spatial rotation in $d=2+1$ dimensions is spontaneously broken by a Fermi surface distortion (20–22), the resulting orientational NGB strongly couples to electrons; i.e., their coupling does not vanish in the limit of small energy-momentum transfer. We refer to this type of coupling as nonvanishing coupling. In this context, Oganesyan et al. (20) discussed non-Fermi liquid (NFL) behavior and Landau damping of NGBs, in close analogy with the case of critical bosons or gauge bosons coupled to a FL. However, the deeper reason why this example violates the standard rule of vanishing NGB–electron couplings in the infrared has been left unclear. Also, whether this is the only pattern of symmetry breaking with nonvanishing coupling remains an open question.

In this article we formulate a simple criterion that allows one to diagnose the nature of the NGB–electron coupling. If the broken symmetry generator fails to commute with translations, the coupling is anomalous and is nonvanishing in the infrared. Furthermore, armed with this criterion we are able to identify a new physical setting, distinct from the spontaneous breaking of rotation symmetry, that also leads to nonvanishing couplings and thus, if we follow standard arguments, to a NFL and overdamped NGBs.

Results

General Criterion for Nonvanishing Couplings.

Let us assume that we are at zero temperature and we make no assumption about spatial dimensionality except that it allows for spontaneous symmetry breaking. NGBs can be associated with symmetry generators that are spontaneously broken, which we label $Q_a$. Furthermore, to sharply define a Fermi surface we assume the existence of a conserved momentum $\overrightarrow{P}$. This could be either the conserved momentum of continuous translation symmetry or crystal momentum (of discrete translation symmetry). Let

$$\left[Q_a,P_i\right]=i{\mathrm{\Lambda }}_{ai}.$$ [1]

We now state the general criterion. If ${\mathrm{\Lambda }}_{ai}=0$, this is the usual situation where the coupling does vanish. However, if ${\mathrm{\Lambda }}_{ai}\ne 0$, then the coupling between the NGB and electrons does not vanish in the limit of small energy-momentum transfer. Note that this criterion is very general and involves only the pattern of symmetry breaking. For any internal symmetry (e.g., spin rotation or number conservation), the commutator is zero. Thus, for nonvanishing couplings one must consider a space-dependent symmetry. The simple case of broken space translation symmetry has $Q_a=P_a$ and the commutator is again zero, which implies that the corresponding Goldstone modes, the phonons, have vanishing coupling to electrons at small momentum transfer, as is well known.

However, for the case of rotational symmetry breaking, $Q_a=L_z$, which satisfies $\left[L_z,P_i\right]=i{\mathit{ϵ}}_{ij}{P}_j\ne 0$, where $i,j\in \left\{x,y\right\}$. Thus, nonvanishing couplings are expected in this case, consistent with the results of Oganesyan and coworkers in the context of nematic order in a 2D Fermi fluid (20–22).

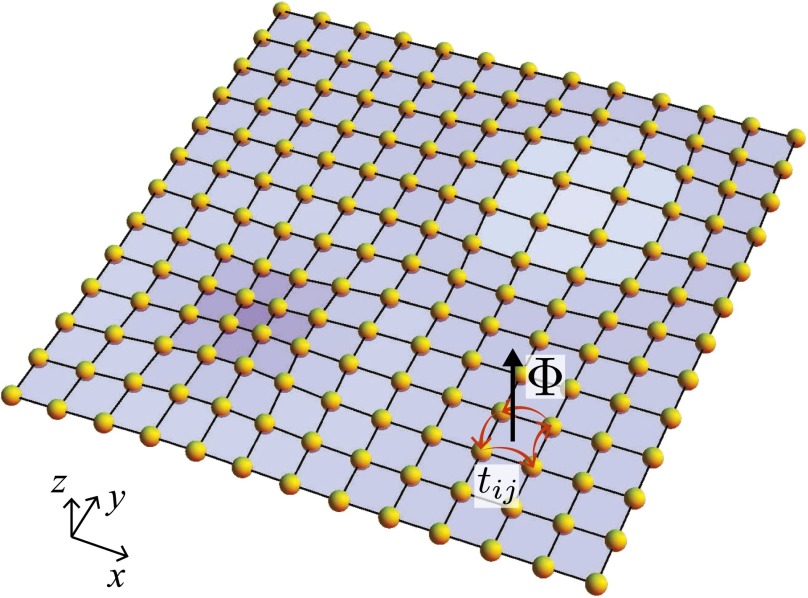
This general criterion allows us to identify an entirely new example of nonvanishing coupling. The criterion for nonvanishing coupling is also fulfilled by spontaneous breaking of magnetic translations. That is, begin with charged particles in a uniform magnetic field, with magnetic translation symmetry. Spontaneous formation of a crystal breaks this symmetry, resulting in phonons. Now, the magnetic translation operator $\overrightarrow{\mathcal{P}}$ generates NGBs (phonons) and satisfies the nonabelian algebra, $\left[{\mathcal{P}}_x,{\mathcal{P}}_y\right]=-ieBN$. Thus, electron–phonon interactions under a uniform magnetic field are predicted to have nonvanishing coupling as we verify by explicit calculation. This surprising conclusion may be rationalized by imagining the fermions to hop between sites of the corresponding tight-binding model. The external magnetic field affects the phase of the hopping matrix as $t_{ij}\to t_{ij}\exp \left(i{\displaystyle {\int }_{{\overrightarrow{x}}_i}^{{\overrightarrow{x}}_j}\overrightarrow{A}\left({\overrightarrow{x}}^{\prime },t\right)\cdot \text{d}{\overrightarrow{x}}^{\prime }}\right)$. However, a phonon fluctuation $\overrightarrow{u}$ that changes the local flux per unit cell produces a fluctuation of $t_{ij}$, as illustrated in Fig. 1. One can imagine this as resulting from a fluctuating gauge field $\delta B=B\nabla \cdot \overrightarrow{u}=\nabla \times \delta A$. Therefore, for electrons, some part of phonon fluctuation under a magnetic field is equivalent to that of a vector potential $\delta A=B\widehat{z}\times \overrightarrow{u}$ and the problem resembles that of NFL behavior arising from minimal coupling to a fluctuating gauge field.

Fig. 1.

A previously unidentified route to strongly coupling NGBs and quasiparticles—electron–phonon interaction in a uniform magnetic field. A lattice distortion (phonon fluctuation) with $\overrightarrow{\nabla }\cdot \overrightarrow{u}\ne 0$ changes the local flux threading each unit cell (darker blue indicates a larger flux), inducing fluctuations of the phase of the hopping matrix $t_{ij}$. The phonon therefore couples like a gauge field to the fermions, without spatial derivatives.

Proof of the General Criterion.

The total Hamiltonian of the system can be split into three pieces, ${\mathrm{\mathscr{H}}}_{\text{tot}}={\mathrm{\mathscr{H}}}_{\text{el}}+{\mathrm{\mathscr{H}}}_{\text{NGB}}+{\mathrm{\mathscr{H}}}_{\text{int}}$, and each of these terms commutes with symmetry generators. We are mainly concerned with ${\mathrm{\mathscr{H}}}_{\text{int}}$, which we expand as a series in the NGB fields ${\pi }^a$, ${\mathrm{\mathscr{H}}}_{\text{int}}={\mathrm{\mathscr{H}}}_{\text{int}}^{\left(0\right)}+{\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}+\cdots$. Note that ${\mathrm{\mathscr{H}}}_0\equiv {\mathrm{\mathscr{H}}}_{\text{el}}\left({\psi }^{†},\psi \right)+{\mathrm{\mathscr{H}}}_{\text{int}}^{\left(0\right)}\left({\psi }^{†},\psi \right)$ is the mean-field Hamiltonian that defines a one-electron problem by picking a symmetry-broken ground state. The interaction with NGBs is then determined by symmetry; e.g., the linear coupling for a constant ${\pi }^a$ is simply obtained by rotating the mean-field Hamiltonian by the corresponding symmetry generator $Q_a$ (SI Text):

$${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}=-\left[i{\pi }^a{Q}_a,{\mathrm{\mathscr{H}}}_0\right].$$ [2]

To set up the perturbation theory, we first solve the single-particle electron problem described by ${\mathrm{\mathscr{H}}}_0$ and obtain simultaneous eigenstates $|n\overrightarrow{k}\rangle$ of ${\mathrm{\mathscr{H}}}_0$ and the momentum $\overrightarrow{P}$,

$${\mathrm{\mathscr{H}}}_0|n\overrightarrow{k}\rangle ={\mathit{ϵ}}_{n\overrightarrow{k}}|n\overrightarrow{k}\rangle ,\hspace{1em}\overrightarrow{P}|n\overrightarrow{k}\rangle =\overrightarrow{k}|n\overrightarrow{k}\rangle ,$$ [3]

where n is the band index. When the translation symmetry is discrete, we replace the second relation with

$$T_i|n\overrightarrow{k}\rangle =e^{i\overrightarrow{k}\cdot {\overrightarrow{a}}_i}|n\overrightarrow{k}\rangle ,\hspace{1em}{T}_i=e^{i\overrightarrow{P}\cdot {\overrightarrow{a}}_i},$$ [4]

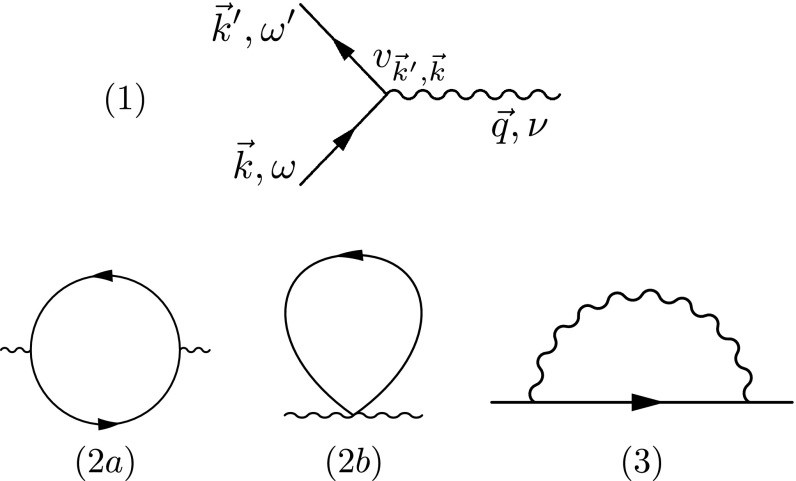
where ${\left\{{\overrightarrow{a}}_i\right\}}_{i=1,\dots ,d}$ are primitive lattice vectors. The interaction of electrons and NGBs to lowest order can then be written as (Fig. 2) (1)

$${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}={\displaystyle \sum _{n^{\prime },n,a}{\displaystyle \int \frac{{\text{d}}^{d}k{\text{d}}^d{k}^{\prime }}{{\left(2\pi \right)}^{2d}}{v}_{n^{\prime }{\overrightarrow{k}}^{\prime },n\overrightarrow{k}}^a{c}_{n^{\prime }{\overrightarrow{k}}^{\prime }}^{†}{c}_{n\overrightarrow{k}}{\pi }_{\overrightarrow{q}}^a}},$$ [5]

where $\overrightarrow{q}={\overrightarrow{k}}^{\prime }-\overrightarrow{k}$ and $v_{n^{\prime }{\overrightarrow{k}}^{\prime },n\overrightarrow{k}}^a$ is the (bare) vertex function, which is the matrix element of ${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}$. This can be written via Eq. 2 as

$$\begin{array}{c}{\pi }_{\overrightarrow{q}}^a{v}_{n^{\prime }{\overrightarrow{k}}^{\prime },n\overrightarrow{k}}^a=-i{\pi }_{\overrightarrow{q}}^a\langle n^{\prime }{\overrightarrow{k}}^{\prime }|\left[Q_a,{\mathrm{\mathscr{H}}}_0\right]|n\overrightarrow{k}\rangle \\ =i{\pi }_{\overrightarrow{q}}^a\langle n^{\prime }{\overrightarrow{k}}^{\prime }|Q_a|n\overrightarrow{k}\rangle \left({\mathit{ϵ}}_{n^{\prime }{\overrightarrow{k}}^{\prime }}-{\mathit{ϵ}}_{n\overrightarrow{k}}\right),\end{array}$$ [6]

which, for low energy scattering $n=n^{\prime }$ and $\overrightarrow{q}\to 0$, is

$$v_{n{\overrightarrow{k}}^{\prime },n\overrightarrow{k}}^a\approx i\langle n\overrightarrow{k}|Q_a|n\overrightarrow{k}\rangle \overrightarrow{q}\cdot {\overrightarrow{\nabla }}_{\overrightarrow{k}}{\mathit{ϵ}}_{n\overrightarrow{k}}.$$ [7]

Clearly, as long as $\langle n\overrightarrow{k}|Q_a|n\overrightarrow{k}\rangle$ is finite, the vertex vanishes as $\overrightarrow{q}\to 0$. This is why scatterings of electrons off NGBs usually vanish at $\overrightarrow{q}=0$, leaving behind well-defined NGBs and Fermi liquid quasiparticles.

Fig. 2.

(1) The bare vertex with one NG line. (2a and 2b) One-loop diagrams for the self-energy of the boson. (3) The same for electrons.

However, we can evade this conclusion if, and only if, the matrix element $\langle n{\overrightarrow{k}}^{\prime }|Q_a|n\overrightarrow{k}\rangle$ diverges as ${\overrightarrow{k}}^{\prime }\to \overrightarrow{k}$. To ensure an appropriate divergence, we will need $\left[Q_a,P_i\right]\ne 0$ as we now explain. If $\left[Q_a,P_i\right]=i{\mathrm{\Lambda }}_{ai}\ne 0$, then the matrix element is $\langle n{\overrightarrow{k}}^{\prime }|Q_a|n\overrightarrow{k}\rangle =-i\left(\langle n{\overrightarrow{k}}^{\prime }|{\mathrm{\Lambda }}_{ai}|n\overrightarrow{k}\rangle /\left({k^{\prime }}_i-k_i\right)\right)$ (SI Text). Substituting this in Eq. 7 and setting $\overrightarrow{q}\to 0$, we have the coupling

$$v_{n\overrightarrow{k},n\overrightarrow{k}}^a={\displaystyle \sum _i\langle n\overrightarrow{k}|{\mathrm{\Lambda }}_{ai}|n\overrightarrow{k}\rangle {\partial }_{k_i}{\mathit{ϵ}}_{n\overrightarrow{k}}},$$ [8]

which is generically nonvanishing. This proves our claim that when the symmetry generator corresponding to the NGB fails to commute with translations, nonvanishing couplings result. If the translation symmetry is discrete rather than continuous, we simply replace $P^i$ by the discrete translation operator $T_i$ and require $\left[Q_a,T_i\right]\ne 0$. Then the matrix element

$$\langle n{\overrightarrow{k}}^{\prime }|Q_a|n\overrightarrow{k}\rangle =-\frac{\langle n{\overrightarrow{k}}^{\prime }|\left[Q_a,T_i\right]|n\overrightarrow{k}\rangle }{e^{i{\overrightarrow{k}}^{\prime }\cdot {\overrightarrow{a}}_i}-e^{i\overrightarrow{k}\cdot {\overrightarrow{a}}_i}}$$ [9]

is inversely proportional to $\left({\overrightarrow{k}}^{\prime }-\overrightarrow{k}\right)\cdot {\overrightarrow{a}}_i$, leading again to a nonvanishing coupling in Eq. 7 even at ${\overrightarrow{k}}^{\prime }=\overrightarrow{k}$. Note that $\left[Q_a,T_i\right]\ne 0$ follows from $\left[Q_a,P_i\right]\ne 0$.

Before turning to specific examples we discuss consequences of the nonvanishing couplings.

Non-Fermi Liquid and Overdamped Goldstone Bosons.

A nonvanishing coupling connects our problem to well-studied problems of a Fermi surface interacting with gauge or critical bosons. The vertex ${\overrightarrow{v}}_{{\overrightarrow{k}}^{\prime },\overrightarrow{k}}=-e\left({\overrightarrow{k}}^{\prime }+\overrightarrow{k}\right)/2m$ of the gauge coupling $-e\overrightarrow{A}\cdot \overrightarrow{j}$ does not vanish at ${\overrightarrow{k}}^{\prime }=\overrightarrow{k}$. Similarly, the Yukawa interaction between $q=0$ critical bosons and electrons is not severely restricted by symmetries and nonvanishing couplings are expected (e.g., Yukawa couplings). We can readily argue, via the one-loop calculation below, that nonvanishing couplings destabilize the fixed point of free NGBs and a decoupled Fermi liquid. The actual fate of this strongly coupled problem—a non-Fermi liquid, a superconductor, or some other state—requires a case-by-case analysis and is currently under active investigation.

The boson self-energy correction ${\mathrm{\Pi }}_{ab}\left(\nu ,\overrightarrow{q}\right)$ from diagrams 2a and 2b of Fig. 2 is dominated by (SI Text)

$$\begin{array}{c}\underset{ab}{\mathrm{\Pi }}\left(\nu ,\overrightarrow{q}\right)=-i\pi \frac{\nu }{\left|\overrightarrow{q}\right|}{\gamma }^{ab}\left(\widehat{q}\right),\\ {\gamma }^{ab}\left(\widehat{q}\right)={\displaystyle \int \frac{{\text{d}}^{d}k}{{\left(2\pi \right)}^d}{v}_{\overrightarrow{k},\overrightarrow{k}}^a{v}_{\overrightarrow{k},\overrightarrow{k}}^b\delta \left({\mathit{ϵ}}_{\overrightarrow{k}}\right)\delta \left(\widehat{q}\cdot {\overrightarrow{\nabla }}_{\overrightarrow{k}}{\mathit{ϵ}}_{\overrightarrow{k}}\right)}.\end{array}$$ [10]

The first delta function puts the electron momentum $\overrightarrow{k}$ on the Fermi surface and the second one further restricts $\overrightarrow{k}$ into a subspace where $\overrightarrow{q}$ is tangential to the Fermi surface. Note that the correction in Eq. 10 vanishes if $v_{\overrightarrow{k},\overrightarrow{k}}^a=0$ (we have suppressed the band index n). The one-loop corrected boson propagator $D^{-1}=D_0^{-1}-\mathrm{\Pi }$ has overdamped poles $\nu \propto -i{q}^3$ due to the singularity in Eq. 10. Thus, the NGBs are destroyed (overdamped) by interaction with the Fermi surface at this order.

Now, one can study the lifetime of fermionic quasiparticles by evaluating diagram 3 of Fig. 2 with the corrected propagator D; the result is (23)

$${\tau }^{-1}\equiv -2\hspace{0.17em}\mathit{Im}\hspace{0.17em}\mathrm{\Sigma }\propto {\omega }^{d/3}.$$ [11]

Therefore, Landau’s criterion $\omega \tau \to \mathrm{\infty }$ as $\omega \to 0$ does not hold when $d\le 3$, implying the breakdown of the FL theory.

Thus, this one-loop treatment at least shows the instability of FLs and NGBs against infinitesimal couplings with ${\overrightarrow{v}}_{\overrightarrow{k},\overrightarrow{k}}\ne 0$. The ultimate fate of these interacting systems continues to be an active area of research (10, 12–14) and we do not expand further on that aspect here. We merely establish the condition when interactions with NGBs are relevant and render the decoupled fixed point unstable, similarly to other well-studied cases.

Below, we demonstrate our general criterion through examples.

Examples

Internal Symmetries—Conventional Coupling.

Let us first discuss interactions between electrons and magnons in ferromagnets (in the absence of spin-orbit interactions). The coupling between the ferromagnetic order parameter $\overrightarrow{n}$ and the electron spin $\overrightarrow{s}={\psi }^{†}\left(\overrightarrow{\sigma }/2\right)\psi$ ($\overrightarrow{\sigma }$ is the Pauli matrix) may not contain any derivatives; e.g.,

$${\mathrm{\mathscr{H}}}_{\text{el}-\text{magnon}}=J\overrightarrow{n}\cdot \overrightarrow{s}.$$ [12]

Hence it is not obvious that the electron–magnon vertex vanishes in the limit of small momentum transfer. However, we know it must from our general criterion, as the spin $\overrightarrow{S}$ and the momentum $\overrightarrow{P}$ commute.

To see this more explicitly, we perform a local $SU\left(2\right)$ rotation $U\left(\overrightarrow{x},t\right)$ defined by $U^{†}\left(\overrightarrow{x},t\right)\overrightarrow{n}\left(\overrightarrow{x},t\right)\cdot \overrightarrow{\sigma }U\left(\overrightarrow{x},t\right)={\sigma }_z$. Now, the spin–spin interaction becomes a Zeeman field along $s_z$, while electron–magnon interactions are included in derivatives of the rotated electron field ${\partial }_{\mu }\psi =U\left({\partial }_{\mu }+i{\mathcal{A}}_{\mu }\right){\psi }^{\prime }$ through ${\mathcal{A}}_{\mu }\equiv -i{U}^{†}{\partial }_{\mu }U$. If we expand ${\mathcal{A}}_{\mu }$ in series of NGB fields, each term contains one derivative acting on them. Therefore, electron–magnon interactions vanish in the limit of small energy-momentum transfer (more details in SI Text).

In general, generators $Q_a$ of internal symmetries commute with $\overrightarrow{P}$ and therefore we always obtain vanishing couplings.

Continuous Space Rotation—Nonvanishing Coupling.

Our first nontrivial example is the spontaneous breaking of continuous spatial rotation symmetry. For concreteness, consider nematic order in $2+1$ dimensions, in which a circular Fermi surface is distorted into an ellipse in the ordered phase. The generator of $SO\left(2\right)$ spatial rotations is $L_z$, which does not commute with the momentum operator, $\left[L_z,P_i\right]=i{\mathit{ϵ}}_{ij}{P}_j\ne 0$ (where $i,j\in \left\{x,y\right\}$). Hence, from Eq. 8, we expect a nonvanishing coupling

$$v_{\overrightarrow{k},\overrightarrow{k}}={\mathit{ϵ}}_{ij}\langle \overrightarrow{k}|p_j|\overrightarrow{k}\rangle {\partial }_{k_i}{\mathit{ϵ}}_{\overrightarrow{k}},$$ [13]

where we assume a single band and, for simplicity, ignore spin.

To see this from an explicit calculation, suppose that the spatial $SO\left(2\right)$ rotation is spontaneously broken by the order parameter $\langle \overrightarrow{n}\rangle ={\left(\mathrm{1,0}\right)}^T$. The Goldstone fluctuation θ of the order parameter $\overrightarrow{n}={\left(\cos \theta ,\sin \theta \right)}^T$ can couple to the spinless electron field ψ via, e.g., ${\mathrm{\mathscr{H}}}_{\text{int}}=\left(\chi /2m\right)|\overrightarrow{n}\cdot \overrightarrow{\nabla }\psi {|}^2$ as both $\nabla \psi$ and $\overrightarrow{n}$ are vectors. Expanding the interaction to first order in θ $\left[\overrightarrow{n}\sim {\left(1,\theta \right)}^T\right]$, we have

$${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(0\right)}=\chi \frac{{\nabla }_x{\psi }^{†}{\nabla }_x\psi }{2m},$$ [14]

$${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}=\chi \theta \frac{{\nabla }_x{\psi }^{†}{\nabla }_y\psi +{\nabla }_y{\psi }^{†}{\nabla }_x\psi }{2m}.$$ [15]

Hence, the single-particle electron Hamiltonian is given by

$${\mathrm{\mathscr{H}}}_0=\frac{{\overrightarrow{p}}^2}{2m}+\chi \frac{p_x^2}{2m},$$ [16]

leading to a single-particle dispersion ${\mathit{ϵ}}_{\overrightarrow{k}}=\left[\left(1+\chi \right)k_x^2+k_y^2\right]/2m$ for plane waves with wave vector k.

By directly evaluating the matrix element of Eq. 15 for plane waves, we get

$$v_{{\overrightarrow{k}}^{\prime },\overrightarrow{k}}=\frac{\chi }{2m}\left(k_x\prime k_y+k_x{k}_y\prime \right).$$ [17]

This is consistent with our criterion in Eq. 13. Indeed, using the above dispersion ${\mathit{ϵ}}_{\overrightarrow{k}}$ and $\langle n\overrightarrow{k}|p_j|n\overrightarrow{k}\rangle =k_j$ in Eq. 13, one gets $v_{\overrightarrow{k},\overrightarrow{k}}=\chi k_x{k}_y/m$, which agrees with Eq. 17 in the limit ${\overrightarrow{k}}^{\prime }\to \overrightarrow{k}$.

Note that the vertex does not vanish at ${\overrightarrow{k}}^{\prime }=\overrightarrow{k}$ for generic points on the Fermi surface, except for few high-symmetry points with $k_x=0$ or $k_y=0$. Therefore, at most of a part of the Fermi surface, the quasiparticle lifetime is heavily suppressed by the interaction with the NGB θ that originated from spontaneously broken continuous rotation. A nematic order of an elliptically distorted Fermi surface (20, 21) and a ferromagnetic order in the presence of a Rashba interaction (22, 24) are known examples of this mechanism.

Finally, let us remark on a subtlety regarding space–time symmetries. In certain cases, even if the spatial rotation is spontaneously broken, NGBs associated with the broken rotation may not appear. Suppose translations $p_{x,y}$ are spontaneously broken in $2+1$ dimensions. Although rotation symmetry is also broken, it does not lead to independent NGBs. Phonons originating from $p_{x,y}$ play the role of the NGB of ${\ell }_z$ as well, and the fluctuation θ associated with ${\ell }_z$ is related to displacement fields by $\theta ={\partial }_x{u}_y-{\partial }_y{u}_x$. Although the field θ can couple strongly to electrons, these additional derivatives annihilate the scattering in the limit of small energy-momentum transfer. Even when only $p_x$ or $p_y$ is broken, ${\ell }_z$ cannot produce an independent NGB. For example, helimagnets in $3+1$ dimensions with the spiral vector along the z axis break $p_z-{\ell }_z$ and ${\ell }_{x,y}$ but the phonon associated with $p_z$ plays the role of NGBs of ${\ell }_{x,y}$ and orientational NGBs are absent (25–28).

Magnetic Translation—Nonvanishing Coupling.

As a previously unidentified example of nonvanishing couplings, we discuss continuous translation under a uniform magnetic field in $2+1$ dimensions. Suppose that a crystalline order with lattice vectors ${\left\{{\overrightarrow{a}}_i\right\}}_{i=\mathrm{1,2}}$ is spontaneously formed, breaking the magnetic translation and giving birth to phonons (NGBs). We assume an integer flux quantum per unit cell for the commutativity of the lattice translations $T_i\equiv e^{i\overrightarrow{\mathcal{P}}\cdot {\overrightarrow{a}}_i}$, where $\left({\mathcal{P}}_x,{\mathcal{P}}_y\right)$ is given by $\left(-i{\partial }_x,-i{\partial }_y+eBx\right)$ in the Landau gauge $\overrightarrow{A}=-By\widehat{x}$. Due to an effective periodic potential, the electron band structure becomes dispersive (Fig. 3). We are interested in coupling the NGBs (phonons) to quasiparticle excitations near the Fermi surface of a partially filled band.

Fig. 3.

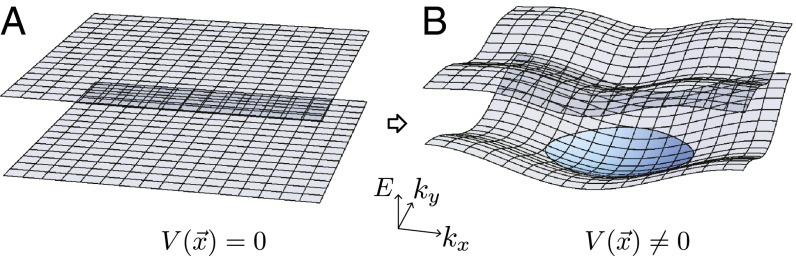
(A) Electron band structure under a uniform magnetic field (Landau levels). (B) A spontaneously generated periodic lattice potential $V\left(\overrightarrow{x}\right)$ produces dispersing bands. The quasiparticle excitation of the partially filled band (filled states shaded in blue) has a reduced lifetime due to the nonvanishing electron–phonon interaction.

In this case, the conserved (magnetic) momenta $\overrightarrow{\mathcal{P}}$ also play the role of broken generators $Q_a={\mathcal{P}}_a$ $\left(a=x,y\right)$ that produce phonons. Hence, we should look at the commutation relation $\left[{\mathcal{P}}_a,{\mathcal{P}}_b\right]=-i{\mathit{ϵ}}_{ab}eB\ne 0$. For discrete translations, we have $\left[\overrightarrow{\mathcal{P}},T_i\right]=-eB\widehat{z}\times {\overrightarrow{a}}_i{T}_i$ (no sum over i), and we expect nonvanishing coupling from Eqs. 7 and 9:

$${\overrightarrow{v}}_{n\overrightarrow{k},n\overrightarrow{k}}=eB\widehat{z}\times {\overrightarrow{a}}_i\left({\overrightarrow{b}}_i\cdot {\overrightarrow{\nabla }}_{\overrightarrow{k}}{\mathit{ϵ}}_{n\overrightarrow{k}}\right).$$ [18]

Here ${\left\{{\overrightarrow{b}}_i\right\}}_{i=\mathrm{1,2}}$ are reciprocal lattice vectors ${\overrightarrow{a}}_i\cdot {\overrightarrow{b}}_j={\delta }_{ij}$. Therefore, electrons may show NFL behaviors as a result of the nonvanishing interaction with phonons. As we know, in the absence of the magnetic field $B=0$, the electron–phonon coupling is conventional as one can see from Eq. 18.

Let us confirm the nonvanishing coupling in Eq. 18 from a direct calculation. For simplicity, we assume one flux quantum per square lattice unit cell and assume the mean-field lattice potential experienced by electrons is

$$V\left(\overrightarrow{x}\right)=-V_0\left[\cos \frac{2\pi x}{a}+\cos \frac{2\pi y}{a}\right].$$ [19]

The electrons and phonons interact with each other through the potential ${\mathrm{\mathscr{H}}}_{\text{int}}=V\left(\overrightarrow{x}-\overrightarrow{u}\right){\psi }^{†}\psi$. Expanding ${\mathrm{\mathscr{H}}}_{\text{int}}$ in series of $\overrightarrow{u}$, we have

$${\mathrm{\mathscr{H}}}_0=\frac{{\left(\overrightarrow{p}-e\overrightarrow{A}\right)}^2}{2m}+V\left(\overrightarrow{x}\right),$$ [20]

$${\mathrm{\mathscr{H}}}_{\text{int}}^{\left(1\right)}=-\overrightarrow{u}\cdot \overrightarrow{\nabla }V.$$ [21]

We diagonalize ${\mathrm{\mathscr{H}}}_0$ in the strong magnetic field limit, perturbatively taking into account the lattice potential to the lowest order in $m{V}_0/eB$. In the Landau gauge, the lowest Landau level wave functions that simultaneously diagonalize $T_i$ are given by ref. 29 (SI Text):

$${\mathrm{\Psi }}_{\overrightarrow{k}}\propto {\displaystyle \sum _{m\in \mathrm{\mathbb{Z}}}{e}^{-\left(1/2\right){\left(y/\ell +k_x\ell +\left(2\pi \ell /a\right)m\right)}^2+i\left(k_x+\left(2\pi /a\right)m\right)x-i{k}_{y}am}}.$$ [22]

Therefore, the lowest electron band to first order in perturbation theory is

$$\begin{array}{c}{\mathit{ϵ}}_{\overrightarrow{k}}=E_0+\langle \overrightarrow{k}|V|\overrightarrow{k}\rangle \\ =\frac{eB}{2m}-\tilde{V}\left[\cos \left(k_{y}a\right)+\cos \left(k_{x}a\right)\right]\end{array}$$ [23]

with $\tilde{V}\equiv V_0{e}^{-{\left(\pi \ell /a\right)}^2}$. Using our formula [18] and the dispersion above, we predict the nonvanishing coupling ${\overrightarrow{v}}_{\overrightarrow{k},\overrightarrow{k}}=eB\tilde{V}a\left(-\sin k_{y}a,\sin k_{x}a\right)$.

Now we directly compute the electron–phonon vertex by evaluating matrix elements of Eq. 21 with the zeroth-order wave function [22] and $u=u_{\overrightarrow{q}}{e}^{i\overrightarrow{q}\cdot \overrightarrow{x}}$, which gives

$${\overrightarrow{v}}_{\overrightarrow{k}\prime ,\overrightarrow{k}}=\mathit{e}\mathit{B}\tilde{V}a{\mathit{e}}^{-\frac{{\left(\mathit{q}\ell \right)}^2}{4}-\mathit{i}{\mathit{q}}_{\mathit{y}}\frac{{k\prime }_x+k_x}{2}{\ell }^2}\left(\begin{array}{c}-\sin \frac{\left({k\prime }_y+k_y+i{q}_x\right)a}{2}\\ \sin \frac{\left({k\prime }_x+k_x-i{q}_y\right)a}{2}\end{array}\right).$$ [24]

This indeed agrees with our formula when ${\overrightarrow{k}}^{\prime }\to \overrightarrow{k}$.

Let us now note some important physical consequences. For our results, it is important that spontaneous breaking of magnetic translation symmetry occurs in a system with a uniform magnetic field. On the other hand, if the underlying symmetry is regular translation, and magnetic flux is spontaneously generated in the symmetry-breaking process (as in a skyrmion lattice), this does not lead to nonvanishing coupling (30), and a Fermi liquid results. A different but equally valid viewpoint on our result is to consider the magnetic field being applied after breaking the translation symmetry (as in a crystal), which should modify the electron–phonon coupling. Therefore, in a clean metal, a magnetic field should induce a nonvanishing coupling between phonons and electrons. Although in principle this would have important consequences, in a typical solid, even at the highest available magnetic fields there is a wide separation $\ell \gg a$ between the magnetic length $\ell ={\left(eB\right)}^{-1/2}$ and lattice spacing a. The typical dispersion of the Landau levels induced by the lattice, and hence the coupling constant, is $e^{-C{\left(\ell /a\right)}^2}\ll 1$ (SI Text). Thus, although a nonvanishing coupling is expected, its absolute magnitude is extremely small. A more promising physical scenario is the quantum Hall regime, where $\ell \sim a$, and where translation symmetry breaking into stripe and bubble phases is predicted and may have been observed in higher Landau levels (31–34). We leave an analysis of this interesting possibility to future work.