Significance
Phylogenetic trees play a central role in biology, modeling evolutionary histories of taxa ranging from genes, to genomes, and to species. Although trees will continue to be an essential modeling tool in evolution, phenomena such as hybridization, or gene flow more generally, result in evolutionary histories that are best modeled by phylogenetic networks. Inference of such networks is complicated by the presence of other evolutionary events, such as incomplete lineage sorting (ILS). Here, we provide a maximum likelihood method for inferring reticulate evolutionary histories while accounting for ILS. The method enables new evolutionary analyses under more complex evolutionary scenarios than existing methods can handle.
Keywords: reticulate evolution, incomplete lineage sorting, phylogenetic networks, maximum likelihood
Abstract
Hybridization plays an important role in the evolution of certain groups of organisms, adaptation to their environments, and diversification of their genomes. The evolutionary histories of such groups are reticulate, and methods for reconstructing them are still in their infancy and have limited applicability. We present a maximum likelihood method for inferring reticulate evolutionary histories while accounting simultaneously for incomplete lineage sorting. Additionally, we propose methods for assessing confidence in the amount of reticulation and the topology of the inferred evolutionary history. Our method obtains accurate estimates of reticulate evolutionary histories on simulated datasets. Furthermore, our method provides support for a hypothesis of a reticulate evolutionary history inferred from a set of house mouse (Mus musculus) genomes. As evidence of hybridization in eukaryotic groups accumulates, it is essential to have methods that infer reticulate evolutionary histories. The work we present here allows for such inference and provides a significant step toward putting phylogenetic networks on par with phylogenetic trees as a model of capturing evolutionary relationships.
Phylogenetic trees have long been a mainstay of biology, providing an interpretive model of the evolution of molecules and characters and a backdrop against which comparative genomics and phenomics are conducted. Nevertheless, some evolutionary events, most notably horizontal gene transfer in prokaryotes and hybridization in eukaryotes, necessitate going beyond trees (1). These events result in reticulate evolutionary histories, which are best modeled by phylogenetic networks (2). The topology of a phylogenetic network is given by a rooted, directed, acyclic graph (rDAG) that is leaf-labeled by a set of taxa (Fig. 1; more details are provided in Model and SI Appendix). Reticulation events result in genomic regions with local genealogies that are incongruent with the speciation pattern. Several methods and heuristics use this incongruence as a signal for inferring reticulation events and reconstructing phylogenetic networks from local genealogies. These methods, which are surveyed elsewhere (2–4), assume that reticulation events are the sole cause of all incongruence among the gene trees and seek phylogenetic networks to explain all of the incongruence. A serious limitation of these methods is that they would grossly overestimate the amount of reticulation in a dataset when other causes of incongruence are at play. Indeed, several recent studies (5–9) have shown that detecting hybridization in practice can be complicated by the presence of incomplete lineage sorting (ILS) (Fig. 1).
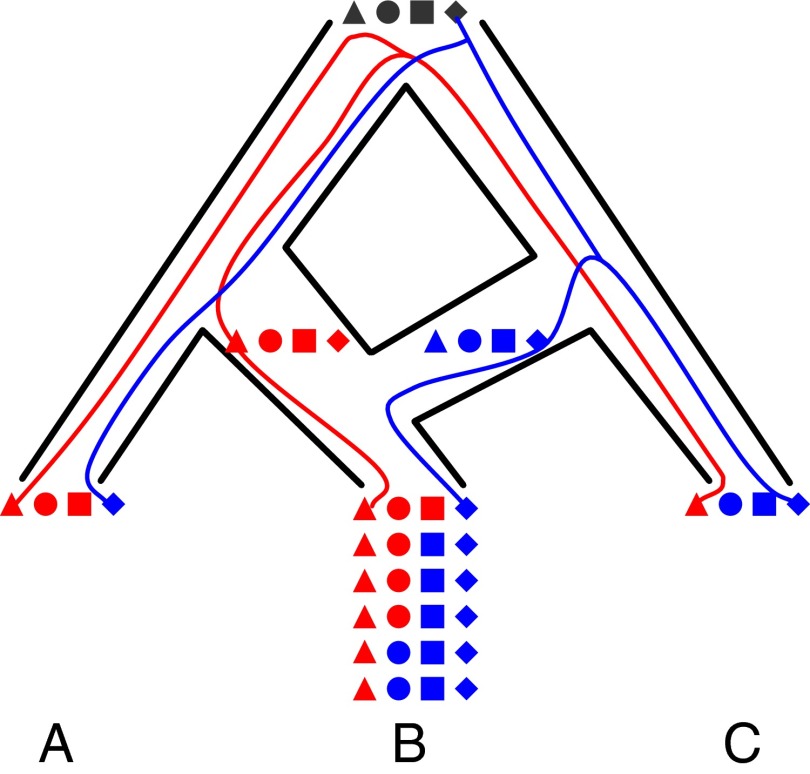
Fig. 1.
Phylogenetic networks. Here, the MRCA of A and B split from its MRCA with C, and some time after A and B split, hybridization occurred between B and C. Four independent loci, ▲, ●, ■, and ♦, are illustrated, for which a single individual is sampled from each of A and C and six individuals are sampled from B. Two gene trees are depicted for the ▲ and ♦ loci, and both trees agree in terms of their shapes. However, the disagreement of the species splitting pattern with the gene tree in red is due to ILS, whereas the disagreement with the gene tree in blue is due to hybridization. Furthermore, the ▲ locus exhibits no evidence of hybridization in B, the ♦ locus has lost all signal of vertical inheritance from the MRCA of B with A, and the other two loci exhibit varying degrees of hybridization signal in the population. Locus-specific inheritance probabilities are needed to capture such scenarios.
Recently, a set of methods was devised to analyze data where reticulation and ILS might both be simultaneously at play (10–15). However, these methods are all applicable to simple scenarios of species evolution and mostly assume a known hypothesis about the topology of the phylogenetic network. As reported (16, 17), we devised methods for computing the likelihood of a phylogenetic network, given a set of gene tree topologies. Still, these methods did not allow for inference of phylogenetic networks (they assume a given phylogenetic network topology and compute its likelihood). To the best of our knowledge, the first method to conduct a search of the phylogenetic network space in search of optimal phylogenies is described in a study by our group (18). However, this method is based on the maximum parsimony criterion: It seeks a phylogenetic network that minimizes the number of “extra lineages” resulting from embedding the set of gene tree topologies within its branches.
Progress with phylogenetic network inference notwithstanding, methods of inferring reticulate evolutionary histories while accounting for ILS are still considered to be in their infancy and inapplicable broadly (9). This inapplicability stems mainly from two major issues: the lack of a phylogenetic network inference method and the lack of a method to assess the confidence in the inference. Here, we develop methods that resolve both issues and carry phylogenetic networks into the realm of practical phylogenomic applications. For the inference, we propose operations for traversing the phylogenetic network space, as well as methods for assessing the complexity of a network. For measuring branch support of inferred networks, we use the bootstrap method. Furthermore, we derive, for the first time to our knowledge, the distribution (density) of gene trees with branch lengths, given a phylogenetic network, and use it in inference. Our methods provided very good results on simulated datasets. We also applied our methods to a dataset of thousands of loci from five house mouse (Mus musculus) genomes. The analysis yielded a well-supported evolutionary history with two hybridization events.
Model
We seek to infer a phylogenetic network Ψ that models the (potentially reticulate) evolutionary history of a set of species, where multiple individuals might be sampled per species. We use the phylogenetic network model given by Nakhleh (2). A phylogenetic -network, or -network for short, Ψ is an rDAG whose leaves are bijectively labeled by the set of taxa and whose every internal node (except the root) has in-degree 1 and out-degree greater than 1 (tree nodes) or in-degree 2 and out-degree 1 (reticulation nodes). We use and to denote the set of nodes and edges, respectively, of phylogenetic network Ψ. Every edge (or branch) b of Ψ has a length in coalescent units, where is the duration of edge b in generations and is the population size corresponding to branch b. A consequence of this setting is that the phylogenetic network does not have to be ultrametric. Furthermore, whereas the model does not require or necessitate a constant population size across all branches of the network, the population size and number of generations of each branch are dependent, given the branch’s length. In other words, the values of neither of these two parameters can be uniquely determined, given the length of a branch in our model (e.g., doubling both keeps the branch length unchanged). As is common in the literature in this area, we use a single composite parameter Ψ to denote the phylogenetic network topology and its branch lengths.
Tracing the evolution of a lineage from a leaf of the network back toward the root follows the multispecies coalescent model on trees, yet with one major difference: As a lineage encounters a reticulation node, it tracks one of the two parents of that node according to an inheritance probability. Because the probabilities of inheritance vary from one hybridization event to another in the network, and because different loci may provide different hybridization signals in the population (Fig. 1), the inheritance probabilities are given by a matrix Γ, where m is the number of independent loci (given the species phylogeny) in the dataset being analyzed and the entries of Γ satisfy three conditions for every : (i) for every , (ii) for every edge b incident into a tree node, and (iii) for every distinct pair such that b and are incident into the same reticulation node. For an edge b incident into node v in Ψ, the entry denotes the probability that a sample from locus i tracks branch b when “entering” the population represented by node v. It is important to note here that the topology and branch lengths of Ψ, as well as the matrix Γ, are to be inferred from the data; details are given below and in SI Appendix.
Likelihood Formulation Based on Sequence Data.
Consider m independent loci along with a set of sequence alignments, where corresponds to locus i. The number of sequences in each equals the total number of individuals from which a sequence is available for locus i, and this number can vary from one locus to another. Under the independence assumption, the likelihood of an evolutionary history Ψ and inheritance probabilities Γ is given by
| [1] |
where is the probability of the (sequence) data, given a particular gene genealogy g, and is the distribution (density) of gene genealogies (topologies and branch lengths), given the model parameters. The integral in the equation is taken over all possible values of g, where g represents a gene genealogy (topology and branch lengths). It is important to note here that for computing the probability , the genealogy’s branch lengths are in units of the expected number of nucleotide substitutions per site, whereas for computing , the genealogy’s branch lengths need to be converted to coalescent units. Given the population mutation rate , where is the effective population size and u is the per-site mutation rate, the conversion from units of the expected number of nucleotide substitutions per site to coalescent units can be done by multiplying every gene tree branch length by .
Likelihood Formulation Based on Estimated Genealogies.
Although the likelihood formulation given by Eq. 1 uses all of the information in the data, inference of the species phylogeny from estimated genealogies can significantly speed up the inference. In this case, the likelihood formulation becomes
| [2] |
where is the genealogy estimated for locus i and . Here, is the probability mass function (pmf) or probability density function (pdf), depending on whether the s are given by their topologies alone or by topologies and branch lengths, respectively. Indeed, for the case when the topology of Ψ is a tree, the Species Tree Estimating using Maximum Likelihood (STEM) method (19) and the Species Tree Inference with Likelihood for Lineage Sorting (STELLS) method (20) use this formulation for inference of Ψ, where the former makes use of the gene genealogies’ topologies and branch lengths and the latter makes use of only the genealogies’ topologies.
Inference of high-quality species phylogenies based on Eq. 2 requires accurate estimates of the individual gene genealogies. Because the methods are aimed at data from closely related species and potentially multiple individuals from populations, the signal in the sequence data might be too low for estimating accurate gene genealogies. Although inference from sequences (Eq. 1) accounts naturally for this issue, it is important to account for it explicitly when conducting inference from estimates of gene genealogies. Assume that for each locus i, the uncertainty in estimation is accounted for by having a collection of gene genealogies ; for example, these gene genealogies could be the trees inferred for locus i based on p bootstrap replicates. In this case, we have
| [3] |
where, once again, p is given by the pmf or pdf, depending on whether the individual genealogy estimates are given by their topologies alone or by their topologies and branch lengths, respectively. The likelihood model is now given by Eq. 2, with p from Eq. 3 being used instead of the pmf or pdf for individual binary genealogies. We demonstrate the performance of this formulation in Results.
Maximum Likelihood Inference.
Under maximum likelihood (ML), the inference problem amounts to computing the pair that maximizes the likelihood function based on sequence data using Eq. 1 or based on estimated gene genealogies using Eq. 2. Inference based on Eq. 1 requires computing the integral over all possible gene genealogies. Bryant et al. (21) provided an efficient algorithm for computing this integral when each independent locus is given by a biallelic marker. To enable ML inference based on Eq. 1, the algorithm of Bryant et al. (21) needs to be extended along three axes: allowing for sites with more than two states, allowing for the species history to have reticulations, and allowing for each marker to consist of more than a single site. Although extensions along all three axes are technically achievable, inference of even three-taxon networks with a single reticulation from a few sites is computationally prohibitive (Discussion). We therefore focus on inference based on Eq. 2 in this work. Using this formulation, the pmf , when is the gene genealogy’s topology alone, is computable using the algorithms of Yu et al. (16, 17). In Results, we derive the pdf of gene genealogies (with branch lengths), given a phylogenetic network.
Given all of these tools, the inference problem is still very hard computationally, because the optimal Ψ and Γ need to be computed. It is standard in the case of species tree inference to use heuristics that walk the tree space in search of optimal solution candidates. It makes sense, therefore, to devise techniques for walking the phylogenetic network space in search of optimal phylogenetic networks while optimizing branch lengths and the Γ matrix. However, extra caution must be taken when searching the network space. In the case of trees, all rooted, binary trees on a given number of taxa are essentially different models with the same number of parameters. In the case of networks, on the other hand, an arbitrarily large number of reticulation nodes can be added during the search, resulting in more complex models that, by definition, could fit the data at least as well as simpler models. Because the goal is to estimate the true amount of reticulation, rather than only fitting the data, we address this challenge in two ways. First, we devise a search heuristic that searches the phylogenetic network space in layers. Second, we explore the use of cross-validation as a method to ameliorate overfitting the data, which adds to the array of other methods (e.g., information criteria) that have already been used (12, 16). Finally, to assess the fit of the inferred phylogenetic network to the data, we devise a parametric bootstrap approach that allows us to quantify branch support for the phylogenetic network. We give details for all of these methods below and in SI Appendix.
Results
Probability Density of a Gene Tree.
Given a phylogenetic network Ψ and a gene genealogy for locus j (topology and branch lengths in both cases), we denote by the set of all coalescent histories of within the branches of Ψ. Then, the distribution (density) of gene trees is given by
| [4] |
where Γ is the inheritance probabilities matrix, as described above. For an edge , we define to be the vector of times (in increasing order) of coalescence events that occur on branch b under the coalescent history h and the time of node y (a formal definition is provided in SI Appendix). We denote by the ith element of the vector. Furthermore, we denote by the number of gene lineages entering edge b and by the number of gene lineages leaving edge b under h. Then, we have
| [5] |
where for edge is the time of node x in the phylogenetic network Ψ. A full derivation of the formula and a more efficient algorithm for computing it along the lines of Yu et al. (17), which avoid explicit summations over the possible coalescent histories, are given in SI Appendix.
Searching the Space of Phylogenetic Networks.
Letting denote the space of all phylogenetic networks on n taxa, we denote by the subspace of that contains all phylogenetic networks (rDAGs) with n leaves and k reticulation nodes. In particular, is the subspace that contains all phylogenetic trees. To search the phylogenetic network space in a layered fashion, we define two operations that allow for searching within for a given k: one operation that allows the search to ascend a layer from to and one operation that allows the search to descend a layer from to . For searching within a layer, the operations either relocate the destination of a reticulation edge or relocate the source of an edge (reticulation or not). For ascending a layer, the operation consists of adding a reticulation edge between two existing edges in the network, and for descending a layer, the operation removes a reticulation edge (more details are provided in SI Appendix). It is worth mentioning that although the space of all phylogenetic tree topologies on n taxa is finite, the space of all phylogenetic network topologies on n taxa is, in theory, infinite, because and k are unbounded. For example, consider the case of only two taxa. There is a unique, rooted tree in this case. However, because multiple hybridization events could happen between the same two sister taxa at different times, any number of horizontal edges can be added between these two taxa. Nevertheless, whether such repetitive hybridization scenarios are identifiable from typical genomic datasets is a different question.
A heuristic for estimating the optimal branch lengths for a fixed species tree topology, given gene tree topologies, that is based on repeated application of Brent’s method (22) was introduced by Wu (20). We use a similar heuristic for estimating the phylogenetic network branch lengths and inheritance probabilities (full details are given in SI Appendix). Coupling topological transformations and parameter estimation heuristics with the likelihood formulation above enables searching the space in a hill-climbing manner to infer an ML phylogenetic network. Given the existence of local optima within each layer, multiple, independent runs can be made.
Controlling for Model Complexity.
Because networks in provide more complex models than networks in , the approaches described above must handle the model selection problem. Information criteria have already been used in the context of phylogenetic networks (12, 16), and we use them here (instead of searching based on the likelihood score, the search proceeds based on the values of these criteria, which incorporate the likelihood scores). Another approach that we propose here, for the first time to our knowledge, is the use of K-fold cross-validation, whereby the input set of gene trees is partitioned into K subsets of equal sizes, the parameters of the model are inferred from subsets, and the model’s fit of the remaining subset is computed. This fit is computed by comparing the frequencies of the gene trees in the validation subset with the distribution of the gene trees produced by the inferred network. If the fit of the best network found in is not much better (we use a cutoff of 3% improvement, chosen based on empirical observations) than the fit of the best network found in , we declare k to be the correct estimate of the number of reticulation nodes and to be the optimal phylogenetic network. It is important to note here that this cross-validation idea works only for fully resolved gene tree topologies, because in the case of gene trees with branch lengths, the frequencies of the gene trees in the validation subset are not informative.
Finally, to assess the support of the phylogenetic networks we infer, we propose using parametric bootstrapping. Having inferred a network Ψ from the data , we use Ψ to generate datasets, from which we infer phylogenetic networks . We then estimate the support of each branch b in Ψ as the number of networks (out of the ) that have an equivalent branch. We say that two edges in two phylogenetic networks are equivalent if (i) either or both are reticulation edges or both are not and (ii) both define the same clusters (the cluster defined by a branch is the set of all taxa under that branch in the network).
Performance on Simulated Data.
We implemented all of the methods described above in the publicly available, open-source software package PhyloNet (23) and studied the performance of the methods on several simulated datasets. In the simulation study whose results are reported in Fig. 2, we used phylogenetic network as the model network, and for various numbers of loci, we evolved gene trees under the coalescent within the branches of the network and then simulated sequence evolution on these gene trees with varying sequence lengths. We then estimated for each sequence alignment 100 gene trees using ML with bootstrapping. Finally, we inferred networks using our ML method from (i) true gene tree topologies, (ii) estimated gene tree topologies, (iii) true gene tree topologies and branch lengths, and (iv) estimated gene tree topologies and branch lengths. The results of (i) and (ii) are shown in Fig. 2B, whereas the results of (iii) and (iv) are shown in Fig. 2C. For each setting of the number of loci and sequence length, we generated 30 datasets and conducted inferences on all of them.
Fig. 2.
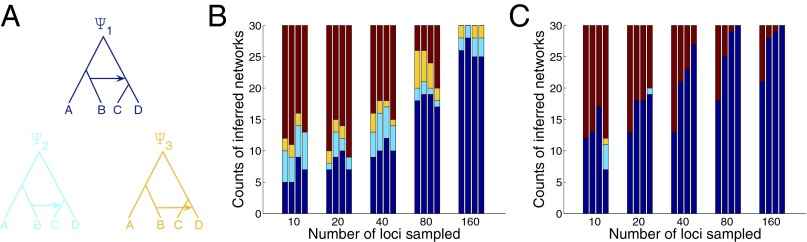
Accuracy of the method on simulated data. (A) Data were generated down the phylogenetic network (all internal branches, except for the horizontal edge, have lengths of 1 coalescent unit, and the inheritance probability is 0.1 for all loci). Results based on gene tree topology estimates (B) and gene tree topology and branch length estimates (C) are shown. For every number of loci, the rightmost bar corresponds to inference from the true gene genealogies and the other three bars, from left to right, correspond to gene genealogies estimated (using 100 bootstrap replicates and Eq. 3) from sequences of lengths of 250, 500, and 1,000, respectively. The dark blue, cyan, and yellow regions correspond to the number of times each of the networks , , and , respectively, in A was inferred. The maroon region corresponds to the number of times any other network with a single reticulation was inferred. Here, one individual was sampled per taxon for each of the loci.
Whereas the hybridization in the model network involves B and the most recent common ancestor (MRCA) of C and D, the length of the branch between the hybridization event and the divergence of C and D from their MRCA can have a big effect on distinguishing between the true hybridization scenarios and the two given by and in Fig. 2A. Therefore, for every dataset, we recorded whether the method inferred one of the three networks shown in Fig. 2A, as opposed to any other network with a single reticulation.
Several trends can be observed in Fig. 2A. First, using the true gene tree topologies with branch lengths results in more accurate inferences than using gene tree topologies alone. This finding is not surprising, because the former type of data contains more information than the latter. In particular, when using 80 or 160 loci, the inferred network from the true gene trees with branch lengths is always the true network. On the other hand, when using only the gene tree topologies for 160 loci, in five of the 30 cases, the inference returned one of the two alternative networks and . Second, the accuracy of the inferences improved as the number of loci increases and as the sequence length increases, although the increase in the number of loci had much more of a positive effect on the inference accuracy. Third, a very surprising result is that when using gene tree topologies alone, using the true gene trees almost never resulted in better accuracy than when using estimated gene tree topologies for a given number of loci. This result attests to the fact that when accounting carefully for uncertainty in the gene tree estimates, the method can obtain very good results. Even when using gene tree topologies and branch lengths, the gain in accuracy when using the true gene trees is very small compared with using the gene tree estimates with uncertainty taken into account. Fourth, the combination of a low value of inheritance probability (0.1 in this simulation) and a relatively short time between hybridization and subsequent speciation results in uncertainty in identifying the donor and recipient of the hybridization event. For example, when using gene tree topologies alone for 160 loci, the inferred network is always one of the three networks , , and , even thought it is mostly . We found that increasing the branch lengths or the inheritance probabilities would result in higher accuracies. Furthermore, in our simulations, we found that increasing the number of individuals sampled per taxon would result in improved accuracy, albeit rather slightly (SI Appendix). However, we expect that sampling more individuals would result in more significant improvements on larger or more complex datasets. In terms of the inferred inheritance probabilities, the true gene trees resulted in very accurate estimates, whereas estimated gene trees with branch lengths resulted, in general, in more accurate estimates of the probabilities. Finally, we found that cross-validation generally does better than information criteria at determining the number of hybridization events (including on the biological dataset, as discussed below). More extensive simulation results under scenarios that are easier for inference than the ones we discussed here are contained in SI Appendix.
Analysis of a Multilocus House Mouse Dataset.
We also used our method to analyze a multilocus dataset of house mouse (M. musculus) genomes, obtained from the studies of Staubach et al. (7), Didion et al. (24), and Yang et al. (25) (more details are provided in SI Appendix). Staubach et al. (7) found substantial genome-wide evidence of subspecific introgression in all four populations, amounting to 3% of the genome in the two M. m. domesticus populations (one from France and the other from Germany), 4% in an M. m. musculus population from Kazakhstan, and 18% in an M. m. musculus population from the Czech Republic. However, it is important to note that the HAPMIX method (26), which was used by Staubach et al. (7), does not explicitly account for ILS.
Our study included all of the samples in the study of Staubach et al. (7). Furthermore, our study included additional samples from an M. m. musculus population from China (25) that were not used in the study of Staubach et al. (7). In this analysis, we used estimated gene tree topologies alone. The reason for doing so is that the genomic sequences are obtained from very closely related individuals (these individuals are five individuals from the same species), and very little variation exists in the data to estimate branch lengths with any accuracy. Furthermore, this low variation does not allow for proper bootstrap analysis of gene trees for the individual loci. The powerful signal in this dataset comes from the very large number of loci. In our analysis, we found a significant improvement in a phylogenetic network with a single reticulation over no reticulations and a significant improvement in a phylogenetic network with two reticulations over a single reticulation. However, when we continued the search for the optimal network with three reticulations, we found that the improvement gained by considering a third reticulation event was insignificant based on the information criteria, and that there was no improvement at all based on cross-validation. We thus called the optimal phylogenetic network with two reticulations as our hypothesis for the evolutionary history of this set of genomes. This evolutionary history is shown in Fig. 3 (more details of the results and analyses are provided in SI Appendix). The phylogenetic network is not ultrametric, and it is worth emphasizing that the branch lengths are given in coalescent units. Thus, the lack of ultrametricity could be due to different population sizes or, to a lesser degree, different generation times.
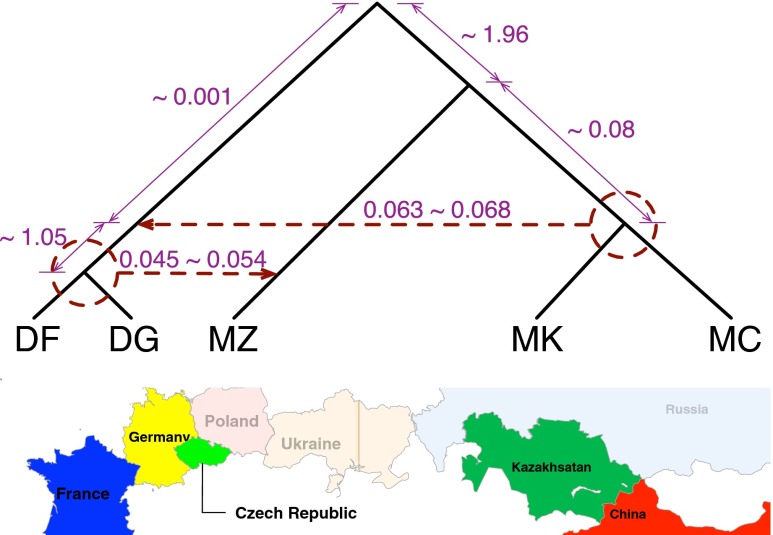
Fig. 3.
Optimal phylogenetic network inferred on the house mouse (M. musculus) dataset. A single individual was sampled from each of five populations: M. m. domesticus from France (DF), M. m. domesticus from Germany (DG), M. m. musculus from the Czech Republic (MZ), M. m. musculus from Kazakhstan (MK), and M. m. musculus from China (MC). The analysis found multiple, almost equally optimal, phylogenetic networks with two reticulation events. These multiple networks all agreed on the recipient populations but disagreed on the donor populations. One hybridization (the top dashed horizontal arrow) involves the MRCA of DF and DG as a recipient population, yet seems to have involved MK, MC, or their MRCA as the donor population. The second hybridization (the bottom dashed horizontal arrow) involves MZ as a recipient population, yet seems to have involved DF, DG, or their MRCA as the donor population. Branch lengths in coalescent units (on the tree branches) and inheritance probabilities (on the horizontal edges) are shown (full details of the data and results are provided in SI Appendix).
Our analysis of house mouse genomes produces an evolutionary history that differs from that reported by Staubach et al. (7) not only in terms of the number of populations involved but also by accounting for the evolutionary history of the populations involved. We consider the percentages of the genome with introgressed origin reported by Staubach et al. (7) to be overestimates, because introgression involving an ancestral population that later split into more than one extant population would be multiply reported for each extant population in the case of the study by Staubach et al. (7). On the other hand, the same percentages would be underestimated in the case where admixed populations were used in place of the nonadmixed reference populations required by HAPMIX, as Staubach et al. (7) did by using putatively introgressed mouse samples to construct the reference populations. Notably, our methodology does not require the use of nonadmixed reference populations.
We hypothesize that the more recent introgression event in Fig. 3 is due to gene flow from secondary contact, where the ranges of the two M. musculus subspecies overlapped, roughly at the border between Germany and the Czech Republic. The biological interpretation of the more ancient introgression event is less clear. We conjecture that the event is related to gene flow during and after subspecific divergence. Further study may provide important clues to the mechanistic basis of the evolution of subspecies in M. musculus and the process of speciation itself.
It is important to note that although we used a very large number of loci, there was still uncertainty in the inferred origins of the two hybridization events (as shown in Fig. 3), a similar pattern to the one observed in the simulation results and discussed above. This uncertainty is a reflection of the weak signal in these data, coupled with the low inheritance probability and short branch length between the hybridization and the MRCA of M. m. musculus from China and M. m. musculus from Kazakhstan and M. m. domesticus from France and M. m. domesticus from Germany, which is an issue that we discussed above in the context of the simulated data. The samples used are very closely related, resulting in genomes with a very small number of segregating sites, and hence a weaker signal for inference. Nonetheless, the uncertainty is localized in the sense that the potential donors of the genetic material of each hybridization event revolve around a single ancestral node. Because all five populations under analysis are closely related, most of the reconstructed gene trees were not binary, due to identical sequences of multiple alleles. Because bootstrapping is not useful in these scenarios (every locus has a handful of sites, most of which are monomorphic), we used the nonbinary gene tree topologies for the loci and considered the set of all resolutions as the set of gene tree estimates to use in Eq. 3.
Discussion
We have devised methods that enable revisiting existing evolutionary analyses and conducting new ones when both hybridization and ILS are either suspected or observed. Programs implementing all of these methods are publicly available in the open-source software package PhyloNet (23). We illustrated the power of our method in extensive simulations and demonstrated its utility on a dataset of mouse genomes. In our model, we abstract the notion of hybridization such that each reticulation edge can be viewed as a “tunnel” through which genetic material can flow repetitively and at different, yet close, times. In other words, the interpretation of a reticulation edge is not that it is a single event of mating between two individuals from two populations or species; rather, it encompasses an ongoing gene flow within a time interval that can be abstracted with one edge and one inheritance probability. This abstraction is a major difference between our model and the more detailed population genetic models that account explicitly for rates of gene flow, such as the isolation-with-migration model. A major direction for future research is scaling up our methods to larger datasets. Currently, it takes a few seconds to a few minutes to evaluate the likelihood of a phylogenetic network with 10–20 taxa (17). This running time can vary significantly even among networks with the same numbers of taxa and reticulation events, because the shape of the gene tree and the configuration of the reticulation nodes in the network (their locations and interdependencies) are the crucial factors (27). However, optimizing the branch lengths and inheritance probabilities, coupled with the phylogenetic network search, is the bottleneck for computation. Furthermore, as our analyses, both on simulated and biological data, demonstrated, it might often be the case that several evolutionary histories have similar likelihoods. This observation calls for Bayesian approaches to inference of phylogenetic networks, whereby a distribution of networks, rather than a point estimate, is computed. In this case, modern Markov chain Monte Carlo techniques can replace the traditional hill-climbing technique we used here.
Although we discussed the model above with respect to a single population mutation rate (θ), it is generalizable in a straightforward manner to allow for different rates across the branches of the phylogenetic network if the branch-specific population size is known. Furthermore, a rate can be specific for locus i to vary the mutation rates across loci (all gene tree branch lengths for locus i are multiplied by ). Similarly, the model can naturally incorporate a single set of inheritance probabilities for the various hybridization events and allow for rate parameters, one per locus, to vary the inheritance probabilities across loci.
A major assumption underlying our models and methods is free recombination between loci and no recombination within. This assumption is common to the majority of methods and tools that infer species phylogenies from multilocus data (even in the absence of hybridization). Relaxing this assumption requires introducing spatial dependence in the data, similar to a method we recently introduced (28). However, this extension only makes the model more complex and significantly increases the computational requirements of the inference methods. Currently, to use such inference methods, it is assumed that independent loci are sampled and that each locus is recombination-free. If a locus contains recombination, it can be partitioned into recombination-free regions, potentially at the expense of creating regions that are too short for reliable estimation of gene trees, further emphasizing the need to account carefully for uncertainty in gene tree estimates.
Although we focused on using gene trees, the ultimate goal is to enable inference directly from sequences (Eq. 1), because such an approach uses the full signal in the data and bypasses the issue of uncertainty in gene tree estimates and the need to deal with it carefully. As discussed above, the SNP (single nucleotide polymorphism) and AFLP (amplified fragment length polymorphism) Package for Phylogenetic analysis (SNAPP) method of Bryant et al. (21) enables such an inference from biallelic data in the case of phylogenetic trees (when no hybridization is allowed), even though the authors presented a Bayesian approach based on the likelihood function, rather than an ML approach. Extending the algorithms of SNAPP to allow for an ML inference based on Eq. 1 is doable, yet the application of such an extension is computationally prohibitive even for the smallest phylogenetic network (three taxa and a single reticulation), as we have observed from preliminary work.
Finally, although we varied the number of individuals sampled per species in our simulations, more thorough investigations need be conducted of the data requirements (more taxa, more loci, or more alleles) to tease apart introgression signals from those signals arising from population effects. These investigations would inform the data collection and help focus the efforts aimed at ameliorating the computational requirements. For example, in the mouse dataset we considered here, the five genomes are very closely related, giving a very weak signal for estimating gene tree branch lengths with any reasonable accuracy. In this case, the large number of loci provided a powerful signal for the network inference. The simulations, on the other hand, show that with stronger signal within the individual markers, fewer loci would be needed for accurate inferences.
Supplementary Material
Acknowledgments
L.N. was supported, in part, by National Science Foundation Grants DBI-1062463 and CCF-1302179, as well as by Grant R01LM009494 from the National Library of Medicine (NLM). K.J.L. was partially supported by a training fellowship from the Keck Center of the Gulf Coast Consortia, on the NLM Training Program in Biomedical Informatics (Grant T15LM007093).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1407950111/-/DCSupplemental.
References
- 1.Bapteste E, et al. Networks: Expanding evolutionary thinking. Trends Genet. 2013;29(8):439–441. doi: 10.1016/j.tig.2013.05.007. [DOI] [PubMed] [Google Scholar]
- 2.Nakhleh L. Evolutionary phylogenetic networks: Models and issues. In: Heath L, Ramakrishnan N, editors. The Problem Solving Handbook for Computational Biology and Bioinformatics. Springer; Berlin: 2010. pp. 125–158. [Google Scholar]
- 3.Huson D, Rupp R, Scornavacca C. Phylogenetic Networks: Concepts, Algorithms, and Applications. Cambridge Univ Press; New York: 2010. [Google Scholar]
- 4.Nakhleh L. Computational approaches to species phylogeny inference and gene tree reconciliation. Trends Ecol Evol. 2013;28(12):719–728. doi: 10.1016/j.tree.2013.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Green RE, et al. A draft sequence of the Neandertal genome. Science. 2010;328(5979):710–722. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Eriksson A, Manica A. Effect of ancient population structure on the degree of polymorphism shared between modern human populations and ancient hominins. Proc Natl Acad Sci USA. 2012;109(35):13956–13960. doi: 10.1073/pnas.1200567109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Staubach F, et al. Genome patterns of selection and introgression of haplotypes in natural populations of the house mouse (Mus musculus) PLoS Genet. 2012;8(8):e1002891. doi: 10.1371/journal.pgen.1002891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heliconius Genome Consortium Butterfly genome reveals promiscuous exchange of mimicry adaptations among species. Nature. 2012;487(7405):94–98. doi: 10.1038/nature11041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moody ML, Rieseberg LH. Sorting through the chaff, nDNA gene trees for phylogenetic inference and hybrid identification of annual sunflowers (Helianthus sect. Helianthus) Mol Phylogenet Evol. 2012;64(1):145–155. doi: 10.1016/j.ympev.2012.03.012. [DOI] [PubMed] [Google Scholar]
- 10.Huber KT, Oxelman B, Lott M, Moulton V. Reconstructing the evolutionary history of polyploids from multilabeled trees. Mol Biol Evol. 2006;23(9):1784–1791. doi: 10.1093/molbev/msl045. [DOI] [PubMed] [Google Scholar]
- 11.Meng C, Kubatko LS. Detecting hybrid speciation in the presence of incomplete lineage sorting using gene tree incongruence: A model. Theor Popul Biol. 2009;75(1):35–45. doi: 10.1016/j.tpb.2008.10.004. [DOI] [PubMed] [Google Scholar]
- 12.Kubatko LS. Identifying hybridization events in the presence of coalescence via model selection. Syst Biol. 2009;58(5):478–488. doi: 10.1093/sysbio/syp055. [DOI] [PubMed] [Google Scholar]
- 13.Joly S, McLenachan PA, Lockhart PJ. A statistical approach for distinguishing hybridization and incomplete lineage sorting. Am Nat. 2009;174(2):E54–E70. doi: 10.1086/600082. [DOI] [PubMed] [Google Scholar]
- 14.Yu Y, Than C, Degnan JH, Nakhleh L. Coalescent histories on phylogenetic networks and detection of hybridization despite incomplete lineage sorting. Syst Biol. 2011;60(2):138–149. doi: 10.1093/sysbio/syq084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jones G, Sagitov S, Oxelman B. Statistical inference of allopolyploid species networks in the presence of incomplete lineage sorting. Syst Biol. 2013;62(3):467–478. doi: 10.1093/sysbio/syt012. [DOI] [PubMed] [Google Scholar]
- 16.Yu Y, Degnan JH, Nakhleh L. The probability of a gene tree topology within a phylogenetic network with applications to hybridization detection. PLoS Genet. 2012;8(4):e1002660. doi: 10.1371/journal.pgen.1002660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yu Y, Ristic N, Nakhleh L. Fast algorithms and heuristics for phylogenomics under ILS and hybridization. BMC Bioinformatics. 2013;14(Suppl 15):S6. doi: 10.1186/1471-2105-14-S15-S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yu Y, Barnett RM, Nakhleh L. Parsimonious inference of hybridization in the presence of incomplete lineage sorting. Syst Biol. 2013;62(5):738–751. doi: 10.1093/sysbio/syt037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kubatko LS, Carstens BC, Knowles LL. STEM: Species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics. 2009;25(7):971–973. doi: 10.1093/bioinformatics/btp079. [DOI] [PubMed] [Google Scholar]
- 20.Wu Y. Coalescent-based species tree inference from gene tree topologies under incomplete lineage sorting by maximum likelihood. Evolution. 2012;66(3):763–775. doi: 10.1111/j.1558-5646.2011.01476.x. [DOI] [PubMed] [Google Scholar]
- 21.Bryant D, Bouckaert R, Felsenstein J, Rosenberg NA, RoyChoudhury A. Inferring species trees directly from biallelic genetic markers: Bypassing gene trees in a full coalescent analysis. Mol Biol Evol. 2012;29(8):1917–1932. doi: 10.1093/molbev/mss086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brent R. Algorithms for Minimization without Derivatives. Prentice Hall; Englewood Cliffs, NJ: 1973. [Google Scholar]
- 23.Than C, Ruths D, Nakhleh L. PhyloNet: A software package for analyzing and reconstructing reticulate evolutionary relationships. BMC Bioinformatics. 2008;9:322. doi: 10.1186/1471-2105-9-322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Didion JP, et al. Discovery of novel variants in genotyping arrays improves genotype retention and reduces ascertainment bias. BMC Genomics. 2012;13:34. doi: 10.1186/1471-2164-13-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yang H, et al. Subspecific origin and haplotype diversity in the laboratory mouse. Nat Genet. 2011;43(7):648–655. doi: 10.1038/ng.847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Price AL, et al. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5(6):e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yu Y. 2014. Models and methods for evolutionary histories involving hybridization and incomplete lineage sorting. PhD thesis (Rice University, Houston, TX)
- 28.Liu KJ, et al. An HMM-based comparative genomic framework for detecting introgression in eukaryotes. PLOS Comput Biol. 2014;10(6):e1003649. doi: 10.1371/journal.pcbi.1003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.