Genome Size, Quantitative Genetics and the Genomic Basis for Flower Size Evolution in Silene latifolia

Abstract

• Background and Aims The overall goal of this paper is to construct an overview of the genetic basis for flower size evolution in Silene latifolia. It aims to examine the relationship between the molecular bases for flower size and the underlying assumption of quantitative genetics theory that quantitative variation is ultimately due to the impact of a number of structural genes.

• Scope Previous work is reviewed on the quantitative genetics and potential for response to selection on flower size, and the relationship between flower size and nuclear DNA content in S. latifolia. These earlier findings provide a framework within which to consider more recent analyses of a joint quantitative trait loci (QTL) analysis of flower size and DNA content in this species.

• Key Results Flower size is a character that fits the classical quantitative genetics model of inheritance very nicely. However, an earlier finding that flower size is correlated with nuclear DNA content suggested that quantitative aspects of genome composition rather than allelic substitution at structural loci might play a major role in the evolution of flower size. The present results reported here show that QTL for flower size are correlated with QTL for DNA content, further corroborating an earlier result and providing additional support for the conclusion that localized variations in DNA content underlie evolutionary changes in flower size.

• Conclusions The search image for QTL should be broadened to include overall aspects of genome regulation. As we prepare to enter the much-heralded post-genomic era, we also need to revisit our overall models of the relationship between genotype and phenotype to encompass aspects of genome structure and composition beyond structural genes.

INTRODUCTION

The genetic basis for characters showing continuous variation has been a focus of ongoing controversy in evolutionary theory ever since the beginning of the last century (Bateson, 1894; Bulmer, 2003). One of Fisher's many contributions to evolutionary theory was to provide a statistical model for Mendelian inheritance that could account for continuous variation (Fisher, 1918), giving rise to the field of quantitative genetics (Bulmer, 1980; Falconer and Mackay, 1996). Under this model, continuous variation is reduced to statistical variance components, which can be analysed and interpreted in the context of response to selection without direct reference to specific genetic loci. However, an essential premise of quantitative genetics is that the ultimate causation of such variance components is segregating alleles at many underlying loci, each of which has a very small individual impact on the character in question: the infinitesimal model of quantitative genetics.

Recent advances in genomic methods have opened new possibilities for investigating the molecular basis for variation in quantitative traits. Extensive variation in genome size was perceived to be much greater than necessary to account for the corresponding range of organismic complexity, and this perception gave rise to the C-value enigma (Hartl, 2000; Gregory, 2001). However, as a result of modern genomic analysis, such variation is now known to be coupled with genome structure and organization. Specifically, much of the variation in DNA content observed between and within taxa is attributable to different categories of repetitive DNA (Kubis et al., 1998; Schmidt and Heslop-Harrison, 1998; Kumar and Bennetzen, 1999), some of which have been shown to have an impact on patterns of gene expression (Vinogradov, 1998; Zuckerkandl, 2002).

Another impact of genomic methods, the increased availability of large arrays of genetic markers and associated statistical methods for their analysis, has made it feasible to isolate and identify genomic regions that impact on variation in specific quantitative characters (Liu, 1997). Analysis of such quantitative trait loci (QTL) has become a growth industry and has raised expectations that a causal link between coding structural genes and quantitative variation can be established. However, methods of QTL analysis, while a considerable refinement on quantitative genetics, often still leave open to question the precise mechanism by which identified effects on a genetic map are influencing phenotypic variation (Kearsey and Farquhar, 1998; Flint and Mott, 2001; Remington and Purugganan, 2003). We propose here that, in addition to structural genes, some QTL could be made up of localized variations in repetitive DNA content, which in turn are effecting quantitative variation through impact of patterns of gene regulation.

In the present paper, we provide an overview of a range of investigations into a quantitative trait, flower size, in the dioecious plant Silene latifolia. We will consider this trait in terms of its genetic basis from a quantitative genetics perspective, in terms of its potential for ecological adaptation, and in terms of its relationship to genome size and genome organization. Our objective in so doing is to achieve a synthesis across these different levels of investigation as well as to provide insight into the molecular basis for QTL influencing this trait.

QUANTITATIVE GENETICS OF FLOWER SIZE

Flower size is an essential feature of floral display (Bell, 1985). Typically, flower size is a continuously varying character, and thus a reasonable candidate for analysis using the methods of quantitative genetics. In the case of a dioecious species, such as S. latifolia, there is an added dimension that there are two types of flowers, male and female, occurring on two types of plants. Indeed, our initial focus of investigation into flower size in S. latifolia was on sex differences in flower size: male flowers are smaller than female flowers (Meagher, 1992).

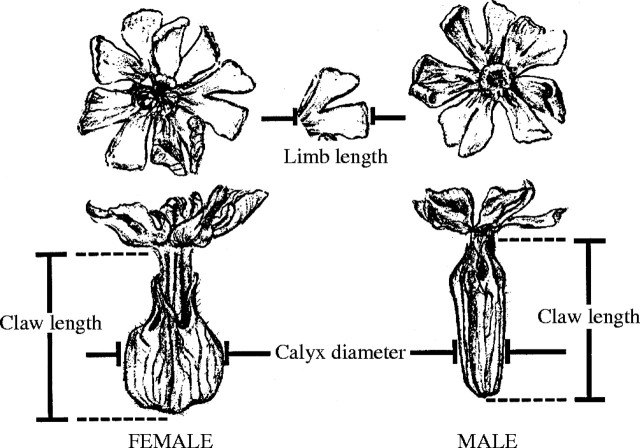
In order to assess the quantitative genetic basis for flower size, an analysis of three floral dimensions (petal claw length, petal limb length and calyx diameter; Fig. 1) was conducted using a four-generation dataset based on plants maintained under controlled growth conditions throughout (Meagher, 1999). These data were subjected to a REML analysis (Shaw, 1987; Groeneveld, 1993), taking into account the various covariances among relatives across generations, to estimate additive genetic variances and covariances among the three floral traits (Table 1). Results show high levels of additive genetic variance for flower size as well as strong genetic covariances between the sexes for the same traits and between characters more generally. The pattern that emerges is that there is considerable quantitative genetic variation for these traits; and, considering the patterns of covariance, there is considerable overlap between the sexes in the underlying factors influencing flower size, in spite of the size differences between the sexes.

Fig. 1.

Floral dimensions measured in males and females of Silenelatifolia (from Meagher and Costich, 1994, fig. 1).

Table 1.

Quantitative genetic variance/covariance structure of flower size and number in Silene latifolia. Maximum likelihood estimates of genetic variance/covariance matrix components were obtained using the VCE program package (Groeneveld, 1993). Statistical significance for difference from zero for variances (one-tailed t-tests) and covariances (two-tailed t-tests) are shown as footnotes (from Meagher, 1999, table 2)

	Male					Female
	Limb	Claw	Calyx	Limb	Claw	Calyx
1. Population 1
Male
Petal limb length	0·546	0·556	0·060	0·656	0·616	0·184
Petal claw length		1·256	0·216	0·456	1·376	0·276
Calyx diameter			0·216	0·060	0·206	0·316
Female
Limb length				1·006	0·516	0·255
Claw length					1·686	0·213
Calyx diameter						0·676
2. Population 2
Male
Limb length	0·546	0·266	0·166	0·356	0·336	0·101
Claw length		1·466	0·436	0·336	1·476	0·726
Calyx diameter			0·406	0·206	0·436	0·586
Female
Limb length				0·326	0·346	0·246
Claw length					1·996	0·686
Calyx diameter						1·076

⁰not significant

¹P < 0·05

²P < 0·01

³P < 0·005

⁴P < 0·001

⁵P < 0·0005

⁶P < 0·0001.

SELECTION ON FLOWER SIZE

Additive genetic variation and covariation provide the means by which plants respond to selection. In order to determine the significance of this variation in evolutionary response, there are two additional pieces of information required. On the one hand, the potential of such variation in responding to selection can be tested by applying selection to experimental populations. On the other hand, the strength of selection that might be operating on this variation in natural populations needs to be determined.

Experimental selection was applied to flower size and number over two generations (Meagher, 1994). Seed collected from two natural populations near Blacksburg, Virginia, USA, exhibiting contrasting life history characteristics were raised under controlled conditions, and the resulting plants were used in a series of random crosses to establish a base generation for a selection experiment. From this second generation, a series of selection lines and control lines were established. Selection was performed on flower number (male and female high lines and male and female low lines) and calyx diameter (four lines as for flower number), so that for each population of origin there were nine lineages established. The initial population, the second generation base population, and the two subsequent generations under selection constituted the four-generation dataset for the quantitative genetic analysis referenced above.

The present discussion will focus only on selection on calyx diameter. Of the selection lines established, there were two lines per population of origin that had been selected for an increase in calyx diameter, based on male flowers and female flowers separately in the two lines, and two lines that had been selected for a decrease in calyx diameter, again on male flowers in one line and females in the other. Following two generations of selection, lines that had been selected for an increase in calyx diameter showed an increase, and lines selected for decrease showed a decrease, both relative to each other and relative to an unselected control line (Fig. 2). This was true for selection applied to male or female calyx diameter, and selection on flowers of one sex resulted in a correlated response in the other sex. The net finding of this experiment was that calyx diameter responds to selection in a manner predictable from the observed pattern of additive genetic variance/covariance.

Fig. 2.

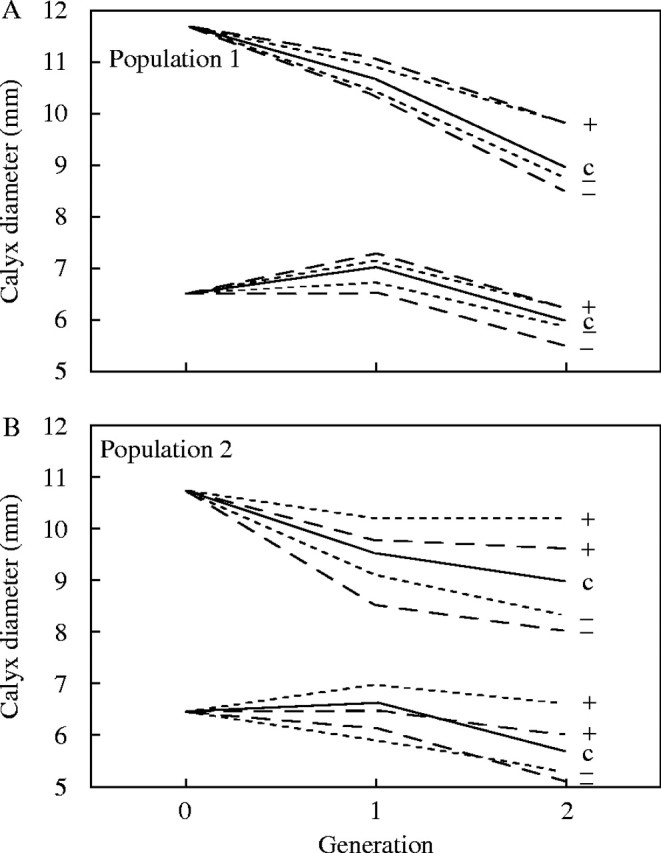
Response to selection on calyx diameter. The higher set of lines corresponds to females. For each sex within each panel, solid lines represent the control line (c), dashed lines represent female-based selection, and dotted lines represent male-based selection. Selection for increases or decreases in the character are indicated by ‘+’ and ‘−’ symbols (from Meagher, 1994, fig. 1).

The genetic capacity to respond to selection on flower size is only relevant if there is selection acting on flower size under field conditions. The sexual differences in flower size are one indication that such selection has acted on S. latifolia. Indeed, using quantitative genetic parameters in combination with the observed sexual dimorphism in flower size, a ‘retrospective’ selection gradient analysis showed that there must have been strong sex-specific selection in the past (Meagher, 1999). The strength of selection acting on flower size in contemporary populations of S. latifolia has also been measured (Wright and Meagher, 2004). In these latter cases, selection measures only took into account one or two field seasons, and as a consequence the patterns are more subtle than the long-term effects. In natural Spanish populations, which are presumed to manifest long-term ecological properties that impose selection on flower size, such as the association between S. latifolia and the noctuid moths that serve as pollinators and seed predators, there were contrasting patterns of selection on male and female plants (Fig. 3). Selection gradients show that decrease in both the magnitude (linear gradients) and variance (quadratic gradients) in calyx diameter should be favoured in males relative to females. Similar effects have also been noted in experimental populations of S. latifolia in New Jersey, USA (Meagher et al., in prep.).

Fig. 3.

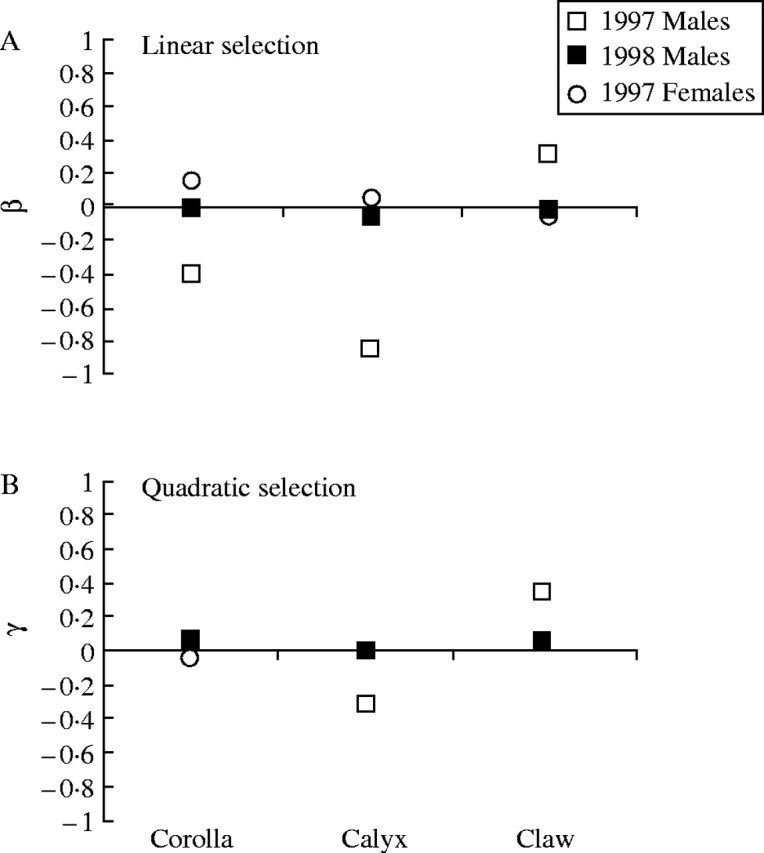
A comparison between (A) the linear selection gradients (β values), and (B) the quadratic selection gradients (γ values) for the male and female plants in a natural Spanish population (Guadalupe) in 1997 and 1998. The 1997 male γ value for calyx diameter was the only result found to be significant (from Wright and Meagher, 2004, fig. 4).

THE RELATIONSHIP BETWEEN GENOME SIZE AND FLOWER SIZE

There are many features of S. latifolia that have attracted scientific attention. Among these is presence of heteromorphic sex chromosomes (XX female, XY male) (Westergaard, 1958; Ciupercescu et al., 1990; Charlesworth, 2002; Grabowska-Joachimiak and Joachimiak, 2002; Lengerova et al., 2003). The extent of differentiation between the X and the Y chromosomes is such that there is a measurable difference between males and females in nuclear DNA content (Costich et al., 1991; Dolezel and Gohde, 1995), with males containing the enlarged Y chromosome, which in turn contributes to higher nuclear DNA content. As is evident in the pattern of sexual dimorphism, male plants have a higher DNA content and smaller flowers than do females. In a regional population survey to determine the generality of this relationship, a negative correlation was established between nuclear DNA content and flower size not only between the sexes, but also within the sexes (Meagher and Costich, 1994).

In a survey of natural populations, a correlation such as this could arise for any number of reasons. For example, such a correlation would occur if both genome size variation and flower size variation were responding to a third unmeasured variable. Another possibility is that there is a more direct causal relationship between DNA content and flower size. If this were the case, then the observed negative correlation should be robust to experimental testing. In order to test this robustness, nuclear DNA content was assessed among progeny from the final generation of the selection experiment discussed above. There were two measures of DNA content used: the first measured overall DNA content using the fluorescence of propidium iodide (PI) and the second provided an AT-biased assay of DNA content by measuring fluorescence of PI in the presence of chromomycin (PI+CA3), which preferentially binds to GC-rich sequences (Meagher and Costich, 1996). Results from this survey showed that lineages that had responded to selection for increase in flower size (in this case, calyx diameter) showed an inverse correlated change in nuclear DNA content (Meagher and Costich, 1996), particularly for the AT-biased assay.

Our interpretation of the correlated response to selection is that there is a causal basis for the negative correlation between DNA content and flower size. The stronger correlation in the AT-biased assay further suggests that this effect is likely due to repetitive DNA, which tends to be rich in AT in plants. This result is consistent with the overall finding that variation in DNA content is generally associated with repetitive DNA sequences. More recently, specific subsets of repetitive DNA, such as retrotransposons, have been shown to comprise a high percentage of the repetitive DNA of plants (Kumar and Bennetzen, 1999). Since many such elements express regulatory factors associated with gene expression for their own replication, they are also contributing to the overall regulatory environment, and thus could play a role in phenotypic expression for characters such as flower size.

We have now established that flower size in S. latifolia is well characterized by classical approaches of quantitative genetics. Moreover, there is a clear link between this character and variation in genome size, which in turn reflects variation in underlying genome organization. A next step toward understanding the genomic architecture of flower size is to localize quantitative trait loci (QTL) affecting this character within the genome. Moreover, a joint analysis of QTL for flower size and nuclear DNA content will provide another level of insight into the precise mechanism by which these two features of S. latifolia are causally related.

QTL ANALYSIS OF FLOWER SIZE AND GENOME SIZE

We report here a preliminary assessment of QTL for flower size and nuclear DNA content in S. latifolia. This includes an evaluation of the magnitude of QTL effects and the correlation between magnitudes of effect for the two characters as evaluated for segregating amplified fragment length polymorphisms (AFLP) (Vos et al., 1995) among 469 progeny from a single cross. A more detailed analysis involving placement of QTL onto a genetic map is still in progress.

Materials and Methods

Parental plants were identified from the experimental population involved in evaluating correlated changes in DNA content in response to selection on flower size. QTL can only be detected if they are segregating within the parents, i.e. if the parents are heterozygous for QTL effects. In order to maximize the number of segregating QTL, we chose parents of intermediate DNA content and calyx diameter from the plants available. Similarly, AFLP markers, which express dominance, are only useful if they are segregating in one parent and absent in the other, in which case all progeny expressing an allele can be assumed to be heterozygotes so that the loci can be treated as co-dominant. In order to maximize the number of loci that would show such a pattern, crosses were conducted between parents from different populations of origin in the field. The results below are from a single such cross consisting of 460 progeny that has been analysed in detail.

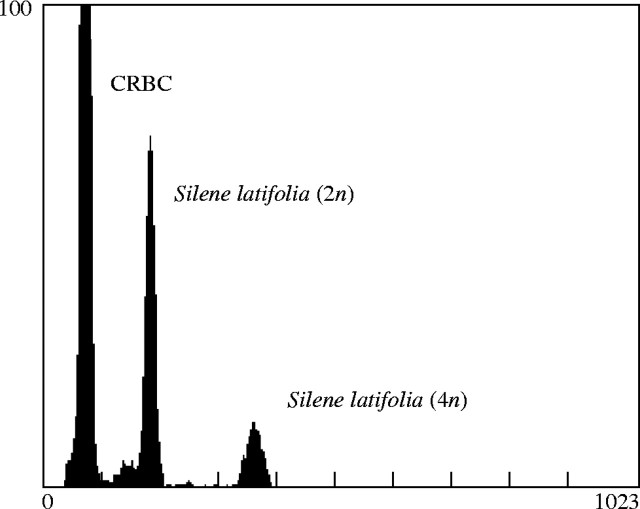
As plants reached flowering maturity, the gender was noted and flower measurements were taken on petal limb, petal claw and calyx diameter. Four flowers were measured, and the QTL analysis was based on the average dimensions for each plant. Plants were subsequently measured for DNA content as outlined in Costich et al. (1991). Two measures of DNA content were taken. First, isolated nuclei were stained with PI, resulting in a measure of overall DNA content. Second, isolated nuclei were stained with PI in the presence of CA3, resulting in an AT-biased assay of DNA content as CA3 preferentially binds to GC-rich sequences, thus excluding PI. For both assays, DNA content was estimated by taking the ratio of the average fluorescence of diploid S. latifolia nuclei against an internal standard of chicken red blood cells (CRBC) (Fig. 4) and then multiplying by 2·33, the 2C nuclear DNA content in picograms of CRBC.

Fig. 4.

Example flow cytometry output showing the frequency distribution of particle fluorescence in Silene latifolia nuclear DNA preparations. Chicken red blood cells (CRBC) were used as the internal calibration standard.

There has been some controversy over recent reports of intraspecific variation in DNA content (Doležel and Bartoš, 2005; Greilhuber, 2005). Specifically, in sunflowers it has been shown that PI staining can be influenced by secondary compounds that in turn are sensitive to environmental perturbation (Price and Johnston, 1996; Price et al., 2000). In order to ensure that our measures of DNA content reflect differences in DNA content as opposed to other aspects of cellular physiology, we have compared the fluorescence variance of our sample relative to the CRBC internal standard (Meagher and Costich, 2004). If there were a biochemical factor being released, it should affect both cells in the same solution. The variance ratio of CRBC/Silene was very high, ranging from 9·13 to 36·93 over different biological groupings by species, population and sex. These results show that the intraspecific variation being detected by our methods is in fact variation in DNA content and not artefactual.

DNA was isolated from leaf tissue using a standard CTAB extraction procedure (Doyle and Doyle, 1990). AFLP analysis was conducted as outlined in the Instruction Manual for AFLP Analysis System II (GibcoBRL part number 50661) using kits for AFLP provided by the same manufacturer. In summary, DNA samples were digested using two restriction enzymes: EcoRI and MseI. The resulting fragments were modified by ligation with primer sequences matched to the loose ends resulting from restriction digests. Modified fragments were then subjected to a non-selective PCR amplification based on the newly attached primer sequences, and then a subsequent series of selective amplifications using the primer sequences plus a three base sequence. Fragments resulting from the selective PCR were surveyed using a Beckman Coulter CEQ8000 DNA fragment analyzer.

The standard procedure for AFLP selective amplification entails a set of eight three-base sequences at the EcoRI end and eight at the MseI end of the DNA fragments, yielding 64 primer pair combinations. A subset of progeny was subjected to these 64 selective amplifications, and 15 primer pairs (Table 2) that yielded a reasonable number of fragments were identified for comprehensive screening of the entire progeny array. The CEQ8000 is very sensitive, so that many fragments that were picked up were specific to a relatively small number of DNA samples. Consequently, it was necessary to impose additional screening limits. Since our interest was primarily in segregating markers, such markers are expected to show a segregation probability of 50 %, so that subsequent analysis only included AFLP bands that showed a frequency of greater than 35 % but less that 65 % among the progeny. Among those, there were also a number of AFLP bands that showed sex-limited (Y chromosome transmitted and thus limited to male progeny) or sex-linked (X chromosome transmitted that, when derived from a male parent, will only appear in female progeny) inheritance. Altogether, there were 469 useful AFLP markers after these various criteria had been met, including among them five X-linked and 19 Y-linked markers (Table 2).

Table 2.

Primer pair combinations and numbers of scorable bands for the AFLP analysis

‘E’ primer	‘M’ primer	Dye	Total scored	X-linked	Y-linked
E-AAC	M-CAA	D2	8	0	0
E-AAC	M-CAG	D4	49	1	3
E-AAC	M-CAT	D4	33	1	2
E-AAC	M-CTC	D4	39	0	0
E-AAC	M-CTG	D2	26	0	0
E-AAC	M-CTT	D2	15	0	0
E-AAG	M-CAA	D3	41	0	0
E-AAG	M-CTA	D3	35	0	0
E-AAG	M-CTC	D3	22	0	1
E-ACC	M-CTA	D3	43	1	6
E-ACC	M-CTC	D3	39	0	1
E-AGC	M-CTA	D4	54	0	2
E-AGC	M-CTC	D4	40	2	4
E-AGC	M-CTG	D2	14	0	0
E-AGC	M-CTT	D2	11	0	0
Totals			469	5	19

Because all of the characters involved in this study are known to exhibit sexual dimorphism, QTL analyses were calculated separately for male and female progeny traits. Sex-specific floral dimensions and DNA content measurements were standardized for QTL analysis by subtracting the mean for each sex and dividing by the standard deviation, yielding group distributions for each character with a mean of zero and a variance of one. The purpose of this was to place all of the measurements on the same standardized scale so that the relative magnitudes of QTL effects could be compared across different characters. For each of the 469 markers, mean values for the standardized floral dimensions and DNA content were obtained for male and female progeny either with or without the band present. From these, sex-specific QTL effects were obtained by subtracting the mean for plants with the band absent from the mean for plants with the band present.

Results

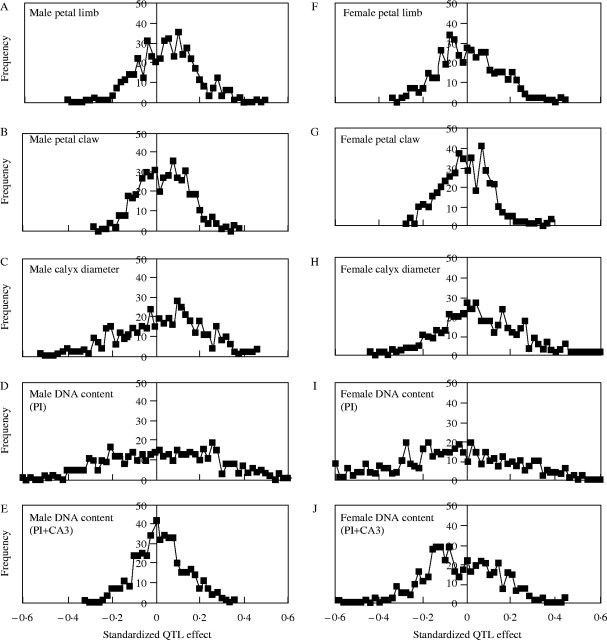
There were a wide range of QTL effects for all characters measured (Fig. 5, Table 3). Among the morphological traits, calyx diameter stands out as having the greatest range of QTL effects. Since intermediate calyx diameter measures were one of the criteria used to identify parents for this cross, on the grounds that this would increase the likelihood of segregating QTL effects, it is not surprising that this character would show more extreme QTL. Similarly, overall DNA content (PI) showed a very high range of QTL effects, and again, this was one of the two traits used to identify potential parents for the initial cross.

Fig. 5.

Frequency distributions of standardized QTL effects over the 469 AFLP loci.

Table 3.

Summary statistics for estimated QTL effects

	N	Mean	s.d.	Minimum	Maximum
Male QTL
Limb	469	0·0424	0·1333	−0·4077	0·4989
Claw	469	0·0307	0·1139	−0·2802	0·3612
Calyx	469	0·0233	0·1839	−0·5341	0·4584
pDNA	469	0·0290	0·2413	−0·6155	0·6473
cDNA	469	0·0158	0·1114	−0·3359	0·3474
Female QTL
Limb	469	−0·0053	0·1391	−0·3537	0·4303
Claw	469	−0·0177	0·1145	−0·2826	0·3784
Calyx	469	0·0369	0·1687	−0·4529	0·8517
pDNA	469	−0·0578	0·2577	−0·7568	0·6681
cDNA	469	−0·0389	0·1579	−0·5865	0·4288

Correlations among QTL effects for flower size and DNA content (Table 4) show patterns that are consistent with earlier studies. QTL among floral traits within males and females are all positive, QTL correlations between the sexes, where significant, are positive. QTL correlations between floral traits and DNA content are negative for some combinations, consistent with earlier studies, but then positive for others. Looking more closely at calyx diameter in particular, there is a strong negative correlation between calyx and DNA (PI) QTL in males, and a negative correlation between male-based DNA (PI) and female-based calyx diameter QTL, but no apparent correlation within females. The difference here could be that the genetic factors segregating in the male and female parents of this cross are having different effects. The ‘male’ pattern is more in line with the negative correlation we have observed in other studies.

Table 4.

Correlations among QTL effects over 469 AFLP loci scored. Statistical significance for difference from zero are shown as footnotes

	Males							Females
	Claw	Calyx	pDNA	cDNA	Limb	Claw	Calyx	pDNA	cDNA
Males
Limb	0·122	0·476	−0·336	0·070	0·154	−0·090	0·050	−0·153	0·050
Claw		0·060	0·216	0·000	−0·070	−0·080	−0·040	0·143	−0·020
Calyx			−0·476	0·030	−0·175	−0·050	−0·080	0·196	−0·070
pDNA				0·226	−0·186	0·256	−0·256	0·416	0·050
cDNA					0·101	−0·050	0·185	−0·186	0·060
Females
Limb						0·386	0·164	−0·070	0·080
Claw							0·456	0·111	−0·020
Calyx								0·030	−0·175
pDNA									0·020

⁰not significant

¹P < 0·05

²P < 0·01

³P < 0·005

⁴P < 0·001

⁵P < 0·0005

⁶P < 0·0001.

DISCUSSION AND CONCLUSION

We have entered what many are confidently referring to as the ‘post-genomic’ era. There is an abundance of information on DNA sequences for a growing number of genes, and the number of species for which mostly complete sequence data exists is growing as well. This has generated a feeling that we have conquered the genome and that the remaining chore is to sort out the pieces. However, in spite of this wealth of information, many efforts to locate a structural gene underlying a QTL effect still fall short of their goal. The results discussed here suggest that we should broaden our search image to include other aspects of genome organization as possible bases for QTL effects.

Relationships between DNA content and various aspects of ecology and life history have been found for a wide range of species (Grime, 1998). These have largely been attributed to impacts of DNA content on nuclear volume, cell volume and cell reproduction rates: e.g. the nucleotype theory. At the same time, genomic analyses of development have shown that localized variation within the genome in DNA content and composition can have very broad regulatory impacts. These regulatory impacts, in turn, provide a more subtle mechanism whereby variation in DNA content might impact on morphology, as indeed appears to be the case for S. latifolia.

The correlations we have reported between QTL for flower size and QTL for nuclear DNA content suggest that there is a causal relationship between the two. It would appear that the QTL for flower size are likely to be found in the form of generic regulatory effects arising from localized accumulation or loss of repetitive DNA sequences. We are currently exploring various possibilities as to what the more precise nature of such sequences might be. For example, they may be trans-acting regulatory effects generated by retroviruses or physicochemical impacts of a local abundance of AT-rich DNA.

The ‘pre-genomic’ era was dominated by the central dogma of genetics, which emphasized the role of structural genes and their products as the primary basis for phenotypes. As a consequence, the bulk of the genome was dismissed as non-coding DNA whose presence was labelled the C-value paradox. We submit that biology has now entered a ‘mid-genomics’ era in which fundamental models for the relationship between genotype and phenotype need to be revisited. At the end of this process, we may recognize that there is actually considerably more hereditary information in the genome than is found in the relatively small number of structural genes.