Three-dimensional cell body shape dictates the onset of traction force generation and growth of focal adhesions

Significance

Living cells interact with their environment through surface receptors. In particular, adhesion molecules form complexes that anchor cells to each other and to the extracellular matrix. These complexes ensure mechanical integrity of tissues and control cell function through specific biochemical signaling. This dual role is due to the ability of adhesion complexes to grow and change their composition and activity in response to mechanical forces. Here, we show how cell spreading, by modifying cell shape, controls the distribution of internal tension over adhesion complexes, inducing their growth above a well-defined spread area. Because such a threshold area was reported for many cell functions, our findings shed a new light on the possible mechanisms behind the geometric control of cell fate.

Abstract

Cell shape affects proliferation and differentiation, which are processes known to depend on integrin-based focal adhesion (FA) signaling. Because shape results from force balance and FAs are mechanosensitive complexes transmitting tension from the cell structure to its mechanical environment, we investigated the interplay between 3D cell shape, traction forces generated through the cell body, and FA growth during early spreading. Combining measurements of cell-scale normal traction forces with FA monitoring, we show that the cell body contact angle controls the onset of force generation and, subsequently, the initiation of FA growth at the leading edge of the lamella. This suggests that, when the cell body switches from convex to concave, tension in the apical cortex is transmitted to the lamella where force-sensitive FAs start to grow. Along this line, increasing the stiffness resisting cell body contraction led to a decrease of the lag time between force generation and FA growth, indicating mechanical continuity of the cell structure and force transmission from the cell body to the leading edge. Remarkably, the overall normal force per unit area of FA increased with stiffness, and its values were similar to those reported for local tangential forces acting on individual FAs. These results reveal how the 3D cell shape feeds back on its internal organization and how it may control cell fate through FA-based signaling.

When cells are cultured on flat substrates, their functions and fate can be modulated by the size and shape of the surface they are allowed to spread on (1–6). In particular, the cell spread area was shown to control the balance between proliferation and apoptosis (1), DNA synthesis (3), and histone acetylation (6). Although the mechanisms behind these phenomena remain to be defined, focal adhesions (FAs) and actomyosin-dependent contractility are clearly involved. For instance, constitutively active focal adhesion kinase (FAK) restores proliferation in nonadherent cells (7, 8). Indeed, FAs are assemblies of multiple proteins among which many are part of fundamental networks of regulation of cell functions (9, 10). Moreover, FAs are mechanosensitive anchors that resist the tension developed in the cell architecture. They are known to grow under the application of an external force, and to shrink when internal tension is decreased (11–13). Thus, many recent studies investigated the correlation between local traction forces and maturation of individual FAs using 2D deformable substrates (14–18).

However, to understand how the cell spread area could control cell fate, a description of the link between the overall cell shape and FA dynamics is still missing. Noteworthily, cell traction forces (19, 20) and cell signaling (1, 3, 6) were shown to be nonlinear functions of the cell spread area. In other words, the magnitude of traction forces, the fraction of apoptotic cells, or the level of histone acetylation present a switch from a low to a high value at a defined cell spread area. Thus, the spread area by itself cannot explain such a switch. We reasoned that the existence of such a threshold area could originate from the 3D (out-of-plane) cell shape that undergoes a huge change when the cell, initially spheric, flattens out during spreading. Moreover, because cell shape results from a force balance inside its mechanical structure, it seems reasonable to hypothesize that 3D cell shape could control FA growth by modulating the level of forces transmitted to the cell environment.

To test this hypothesis, we characterized force generation and adhesion dynamics at the cell scale when cells were experiencing important shape changes. We analyzed the early spreading of Ref-52 fibroblasts by using a novel setup combining parallel-plates single-cell traction force measurements (21–23) and total internal reflection fluorescence (TIRF) monitoring of cell adhesions. In contrast to previous studies that focused on individual FAs and local tangential traction forces, we investigated the interplay between the 3D cell shape, the out-of-plane cell-scale traction forces generated in the cell body, and the growth and spatial distribution of FAs over the whole cell–substrate contact area.

We show, for the first time (to our knowledge), that FAs start to grow at a well-defined spread area independently of spreading kinetics or myosin II-based contractility, suggesting a geometrical control of FA growth. Confocal analysis of the 3D cell shape revealed that the cell body contact angle dictates the onset of FA growth: not until the spreading cell makes a 90° contact angle with the substrate do visible FA-like clusters start to form. Using the parallel-plates technique, we found that this 90° contact angle also corresponds to the onset of cell traction in between the plates, i.e., through the cell body. Remarkably, the lag time between the onset of these normal forces and FA growth at the leading edge decreased with the stiffness of the plate the cell was pulling on. These observations demonstrate the mechanical continuity of the cell structure and the transmission, beyond 90°, of cell body forces to the flat lamella where mechanosensitive FAs start to grow. Consistently, the force per unit area of FA, as retrieved here from normal cell body forces, increased with the normal stiffness, and its values were similar to those reported from measurements of local tangential forces acting on individual FAs. Eventually, comparing cell spreading on a flat substrate with that in-between parallel plates, we show that the onset of FA growth happens at 90° in both cases, whereas the threshold cell–substrate contact area depends on the spreading geometry, indicating that the cell body contact angle is indeed the control parameter.

Results

Paxillin Clusters Exhibit Two Distinct Organizations Corresponding to Two Phases of Cell Spreading.

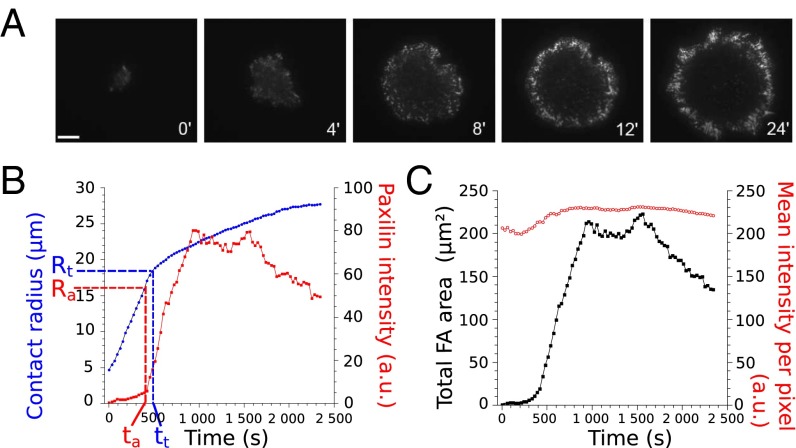
We let Ref-52 fibroblasts spread on glass plates coated with fibronectin and used TIRF microscopy (TIRFM) to determine the time evolution of the cell–substrate contact area A, as well as that of the paxillin distribution (details in SI Text, sections 1 and 2 and Fig. S1). We recorded only the early isotropic spreading (Fig. 1A) and defined the effective contact radius as $R=\sqrt{A/\pi }$. We observed two different paxillin organizations during spreading. At first, small paxillin dots were randomly distributed over the contact area. In a second phase, we observed the buildup of a ring of intense and radially elongated structures of paxillin (Fig. 1A and Movie S1). The shape and size of these bright structures of paxillin were similar to those reported for FAs (24). Quantifying the evolution of the paxillin intensity in adhesion clusters (SI Text, section 1), we found that the two phases of paxillin organization corresponded to two regimes of spreading (Fig. 1B and Fig. S2A) described previously as P1, characterized by a rapid increase of the contact radius R, and P2, with slower spreading (25–27). Statistical analysis revealed that adhesion clusters started to grow at a characteristic radius R_a = 14.8 ± 0.4 μm and time t_a = 290 ± 30 s, whereas the transition between P1 and P2 occurred at R_t = 18.4 ± 0.7 μm, after t_t = 450 ± 50 s (mean values ± SE over 37 cells). This observation is confirmed on a cell-by-cell basis when representing t_t as a function of t_a for the 37 tested cells (Fig. S2B). Thus, FAs appear statistically before the slowdown of spreading, i.e., before the end of P1 (P value = 1.4 × 10⁻³, Wilcoxon test).

Fig. 1.

Correlation between FA growth and slowdown of cell spreading. (A) TIRFM image sequence showing the distribution of paxillin-YFP during the early spreading of a Ref-52 fibroblast. Initially, small dots of paxillin are randomly distributed over the cell–substrate contact area. After ∼5 min, a ring of FA-like paxillin clusters starts to build up at the periphery of the spread area. (Scale bar: 10 μm.) See also Movie S1. (B) The cell–substrate contact radius (blue) and the total intensity in paxillin clusters (red) as functions of time. The onset of FA growth (increase in intensity at time t_a and radius R_a) correlated with the slowdown of spreading (time t_t and radius R_t). (C) Time evolution of the total area and the mean intensity in FAs. The mean intensity was almost constant over time (mean increase of 15% over 23 cells), whereas the total area of FAs increased by orders of magnitude. (Scale bar: 10 μm.)

FAs Appear at a Defined Spread Area, Independently of Spreading Kinetics.

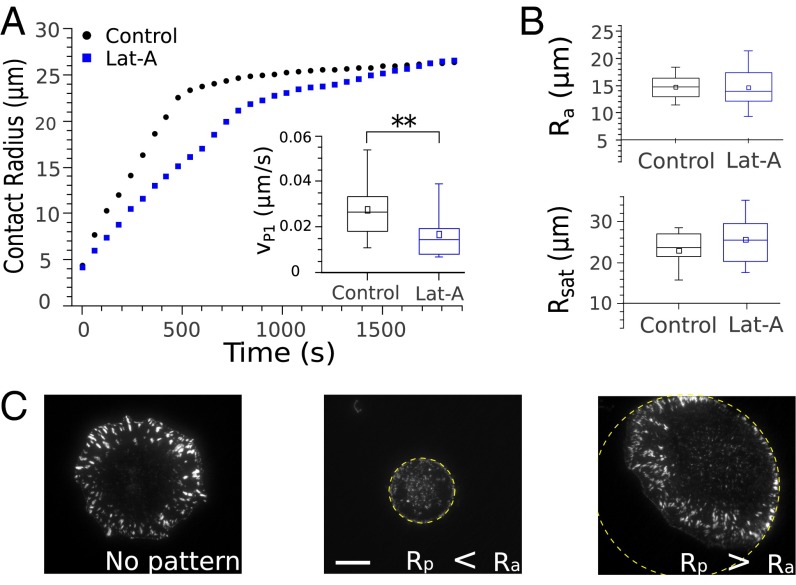
To determine whether the onset of FA growth was time or geometry dependent, we next carried out experiments where the overall kinetics of cell spreading was slowed down. Cells were treated with latrunculin A (Lat-A) to reduce the rate of actin polymerization. A systematic study of the effect of increasing amounts of Lat-A (SI Text, section 3 and Fig. S3) showed that a concentration of 0.05 μM was enough to significantly slow down the kinetics of cell spreading (Fig. 2A) without modifying its geometric features (Fig. 2B) nor the distribution of adhesion complexes (Fig. S3D). Indeed, whereas the rate of cell spreading in P1 was almost divided by 2 (V_p1–control = 0.030 ± 0.002 μm/s over 37 cells, V_p1–LatA = 0.016 ± 0.003 μm/s over 16 cells), the cell radius R_a at the onset of adhesion complexes formation, its radius R_sat at saturation, as well as the fraction $A_{adh}/A$ of the cell–substrate contact area covered by FAs remained unchanged. Remarkably, the contact radius R_t at the transition between P1 and P2 was also unaffected by Lat-A (R_t–control = 18.4 ± 0.7 μm over 37 cells, R_t–LatA = 21.7 ± 2.3 μm over 16 cells), whereas the time at transition almost doubled (t_t–control = 450 ± 50 s over 37 cells, t_t–LatA = 870 ± 160 s over 16 cells). In conclusion, it appears that the steps of cell spreading and the growth of FAs occur at well-defined spread area, whatever the time needed for the cell structure to reorganize. In particular, the fact that R_a was not affected by spreading kinetics suggests that cell shape could indeed control the onset of FA growth. Consistently, preventing cell spreading beyond R_a by using adhesive patterns of limited area inhibited FA formation (Fig. 2C).

Fig. 2.

Geometrical control of FA growth. (A and B) Lat-A slows down the kinetics of cell spreading without modifying its geometric features. (A) Contact radius R as a function of the time t for control cells (black) and cells treated with 0.05 μM Lat-A (blue). (Inset) The slope of R(t)—i.e., the rate of spreading V_p1 = dR/dt—was almost divided by 2 (P value = 5.5 × 10⁻³, Wilcoxon test). (B) In contrast, the radius R_a at the onset of FA growth, and the radius R_sat at saturation were not modified by Lat-A. (C) Paxillin distributions imaged after 20 min of spreading on fibronectin patterns of various sizes. FAs did not form on patterns of radius R_p = 10 μm, smaller than the threshold contact radius R_a = 14.8 ± 0.4 μm at which adhesion clusters start to form on substrates of unlimited area. On large patterns (R_p = 35 μm > R_a), a peripheral ring of FAs was clearly visible, just as for unlimited substrates. Interestingly, cells plated on the edge of large patterns showed asymmetric paxillin distributions. FAs developed well in the center of the pattern where the cells were allowed to spread, whereas no adhesions could form on the edge where spreading was prevented. (Scale bar: 10 μm.)

FAs Start to Grow at a 90° Cell Body Contact Angle.

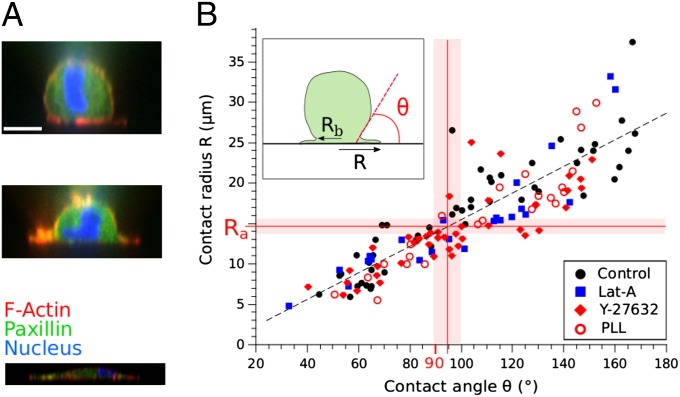
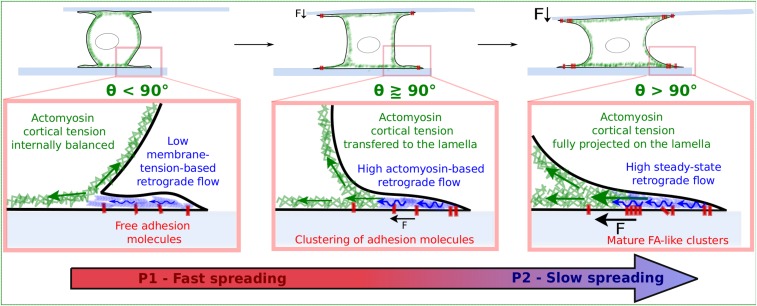
To understand how cell shape evolution could explain the existence of a well-defined radius R_a triggering the onset of FA growth, we visualized, using confocal microscopy, the internal structure of cells fixed at different times of spreading (Fig. 3A). We represented, for each fixed cell, the contact radius R as a function of the contact angle θ between the cell body and the substrate (Fig. 3B). The contact angle is a parameter commonly used in fluid mechanics to quantify the spreading of a liquid droplet on a solid substrate. It reflects the balance between antagonistic surface tension forces that promote/resist spreading and determine the final droplet shape (30). Remarkably, it appeared that the mean contact radius at the onset of FA growth (R_a = 14.8 ± 0.4 μm) corresponded to a contact angle θ slightly higher than 90°. In other words, FAs start to form when the apparent curvature of the cell body switches from convex to concave. This is an important observation because the cell body cortex starts to align with the lamella when the contact angle exceeds 90°.

Fig. 3.

Relationship between the cell body contact angle and the spread radius. (A) Confocal side views of cells at different times of spreading (Actin in red, paxillin in green, and nucleus in blue). Note the continuity of the actin cortex at the cell body–lamella junction (see also refs. 28 and 29 for superresolution imaging). (Scale bar: 10 μm.) (B) The spread radius R on fibronectin-coated substrates as a function of the cell body contact angle θ for control (black circles), 0.05 μm Lat-A (blue squares), and 8 μM Y-27632 (red diamonds). The radius R_a at which FAs start to grow corresponds to θ ≳ 90°, independently from actin polymerization or contractile myosin II activities, underlining the geometric triggering of FA growth. Consistently, the relationship between R and θ is maintained when cells are spreading on polylysine-coated substrates (red open circles), indicating that integrin signaling is not required. The pink stripes correspond to the SE on R_a.

Thus, one can hypothesize that, beyond 90°, the out-of-plane tension generated in the apical cortex (at least its centripetal component, parallel to the substrate) could be transferred to the lamella as tangential forces, thus inducing FA growth.

Consistently, decreasing myosin II contractililty by treatment with 8 μM ROCK kinase inhibitor Y-27632 did not modify the relationship between R and θ, nor the contact radius R_a at which paxillin clusters start to grow (Fig. 3B and Fig. S4 E, G, H, and I), but led to a decreased area of these clusters (Fig. S4F and Movie S2). This supports the idea that the onset of FA growth and the transition in spreading are geometric in nature, with no effect of contractility.

To further test the physical origin of the transition at θ = 90°, we analyzed cell spreading on polylysine (PLL)-coated substrates with no specific integrin engagement. In the absence of FAs (Fig. S5), the relationship between R and θ was conserved (Fig. 3B), underlining its geometric nature. Moreover, although the spreading rate in P1 was not modified (V_p1–PLL = 0.029 ± 0.004 μm/s over 16 cells), the slowing down of spreading, i.e., the transition between P1 and P2, happened at a smaller radius (R_t–PLL = 15.8 ± 1.0 μm, instead of 18.4 ± 0.7 μm on fibronectin coating) corresponding to θ ≳ 90°, and the spread radius after 20 min was also decreased (R_sat–PLL = 19.9 ± 1.0 μm over 16 cells, instead of 23.8 ± 0.7 μm). Thus, in the absence of FAs, the kinetics of cell spreading are only affected beyond 90°, supporting our hypothesis of a rearward tension transmitted to the lamella when the cell body switches from convex to concave.

The Cell Body Contact Angle Controls the Onset of Normal Force Generation.

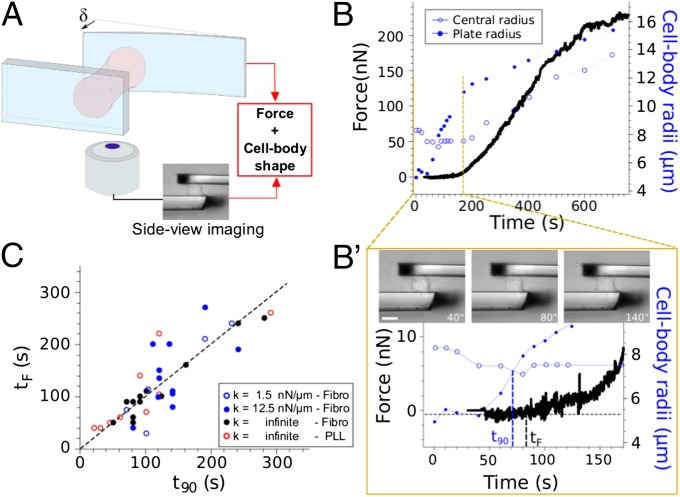
To directly test this hypothesis of traction force generation at 90°, we carried out single-cell traction force measurements in a parallel-plates setup allowing simultaneous visualization of the 3D cell body shape (Fig. 4A). It turned out that the onset of force generation correlated with the switch in cell body curvature during spreading (Fig. 4B and zoom of Fig. 4B′). Force became significantly different from zero when cells, initially spherical, adopted a cylindrical shape with a 90° contact angle with the plates. We reported, for each cell tested, the time t_F corresponding to the onset of force generation as a function of the time t₉₀ at which the cell body contact angle reached 90° (Fig. 4C). The data appeared symmetrically distributed around the line t_F = t₉₀, indicating that the change in cell shape from convex to concave and the onset of traction force generation were statistically simultaneous. This correlation between the cell body shape and the onset of traction force was conserved for nonspecific cell plates adhesion through polylysine coating (Fig. 4C), showing that integrin engagement is not required, and supporting the geometric origin of the relationship.

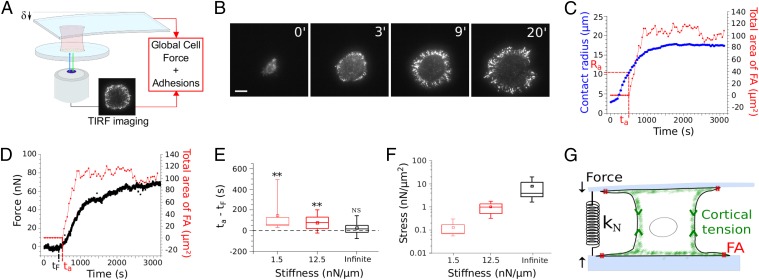
Fig. 4.

The onset of force generation corresponds to a 90° cell body contact angle. (A) Principle of traction force measurements with side view. A cell is pulling on two parallel microplates, one stiff, and the other flexible with calibrated stiffness k. The force is retrieved from the flexible plate deflection δ, F = kδ. (B, B′, and C) Correlation between cell shape and force generation. (B) Time evolution of the cell traction force F (black), the cell body contact radius R_b (blue solid circles), and the central radius R_c (blue open circles). (B′) Zoom on short times showing that the onset of traction (F > 0) correlates with R_b = R_c, i.e., a 90° contact angle (cylindrical cell body shape). (Scale bar: 10 μm.) (C) Time t_F at the onset of force generation as a function of the time t₉₀ at which the cell body reaches 90° for various conditions [fibronectin coating with infinite stiffness (black circles), k = 12.5 nN/μm (blue solid circles), and k = 1.5 nN/μm (blue open circles); polylysine coating and infinite stiffness (red open circles)]. The data are symmetrically distributed around the line t_F = t₉₀, indicating that the change in cell shape from convex to concave and the onset of traction force generation were statistically simultaneous, independently from the rigidity of the plates the cells were pulling on, or from integrin engagement.

Traction Force Generation Precedes the Onset of FA Growth.

Having shown that traction force generation on the one hand, and FA growth on the other hand, could only occur for a cell body contact angle higher than 90°, we decided to directly test the relationship between force generation through the cell body and the onset of FA growth. We designed a novel setup combining parallel-plates single-cell traction force measurements with TIRFM (Fig. 5A; details in SI Text, section 5 and Fig. S6). Cell spreading between parallel plates was qualitatively similar to that on a single flat substrate: at first no FAs and fast spreading, and then FA growth and slower spreading (Fig. 5 B and C and Movie S3). However, the contact radius R_a at the onset of FA growth was smaller (R_a = 10.3 ± 0.3 μm over 40 cells) than the one found for a single substrate (R_a = 14.8 ± 0.4 μm over 37 cells). This is consistent with the fact that the cell body contact radius R_b at 90° was smaller in the parallel-plates geometry [R_b(90°) = 7.6 ± 0.4 μm over 33 cells; Fig. 4] than for spreading on a single substrate [R_b(90°) = 10.5 ± 0.4 μm over 49 cells; confocal analysis]. Consequently, the fact that R_b(90°) and R_a display different values for spreading on a single substrate and between parallel plates, confirms that the contact angle is indeed the parameter controlling FA growth, and not R_b nor R_a.

Fig. 5.

Force generation precedes FA growth. (A) Principle of the new setup combining single-cell traction force measurements and TIRFM monitoring of adhesions dynamics (details in SI Text). (B) TIRFM image sequence showing the distribution of paxillin-YFP during early spreading between parallel microplates (Movie S3). (Scale bar: 10 μm.) (C) Time evolution of the contact radius R (blue), and FA area (red). Spreading between parallel plates is qualitatively similar to that on a single substrate (Fig. 1), but transitions occur at smaller contact radii. (D) Traction force F (black) and FA area (red) measured for the same cell. Note that the slight increase of the overall cell force after FA saturation is similar to the one previously reported for individual FAs and local tangential forces (14). (E) The lag time [t_a − t_F] between force generation and FA growth decreases with the normal stiffness k_N, which resists the contraction of the cell body (light red: k_N = 1.5 nN/μm; bold red: k_N = 12.5 nN/μm; black: infinite stiffness). In particular, although [t_a − t_F] > 0 for 1.5 and 12.5 nN/μm (n = 14 and 13 cells; P values = 3.7 × 10⁻³ and 7.8 × 10⁻³, respectively; Wilcoxon test), there is no measurable lag time for infinite stiffness (t_a = t_F; n = 15 cells; P value = 0.34; Wilcoxon test). (F) The force per unit FA area increases with k_N, and its values at spreading saturation (1,200 s) are comparable to those reported for local tangential force measurements (15). (G) Schematic drawing summarizing the results. The measured normal forces reflect the tension generated in the cell body. The normal stiffness k_N impacts the growth of FAs at the edge of the flat lamella, underlining the mechanical continuity of the cell structure and the role of apical tension in FA growth.

Monitoring the traction force F(t) generated by the cell in-between the plates simultaneously with the total area A_adh(t) of adhesion clusters (Fig. 5D), we found that F(t) and A_adh(t) exhibited similar time evolutions with a first phase of latency, followed by an increase after a few minutes, and eventually saturation. We reported, for each tested cell, the time t_a at which FAs appeared, and the time t_F corresponding to the onset of force generation. FAs statistically appeared after the onset of force generation (t_a − t_F > 0; Fig. 5E).

This suggests that adhesion complexes could be sensitive to long-range forces propagated through the cell body, here from one plate to the other. Because FAs are known to adapt to the rigidity of 2D substrates (15, 24, 31), we tested this hypothesis by changing the normal stiffness k_N, which resists cell body contraction (ref. 23; Fig. 5G and Fig. S7). Remarkably, we found that the lag time Δt = t_a − t_F between the onset of force generation and the formation of adhesion complexes decreased when k_N was increased. In particular, the onset of FA growth and force generation were simultaneous at infinite stiffness, whereas Δt_1.5 = 141 ± 52 s for k_N = 1.5 nN/μm (mean value ± SE over 14 cells). This finding is consistent with the fact that rigid 2D substrates tend to stabilize FAs better than soft ones (31). Moreover, the force per unit area of FAs increased with the normal stiffness (Fig. 5F), and its values were comparable to those reported for individual FAs and local tangential forces (15). Thus, FAs that form at the edge of the lamella, a very flat cell compartment where forces are essentially tangential to the substrate, appear to be sensitive to forces and stiffness acting in the normal direction, orthogonally to the plates the cells are spreading on (Fig. 5G). This observation supports the idea that the cortical actomyosin tension is transmitted to the lamella (Fig. 6). It is only when the cell body curvature changes and the cell cortex align with the two lamellas spreading on the opposite parallel plates (contact angle > 90°) that force is generated on the plates and FAs start to grow. This idea of a direct relationship between tension in the cortex and tangential forces acting on FAs in the lamella is reinforced by the fact that the total area of FAs and the orthogonal traction force (22) are similarly reduced by increasing amounts of myosin inhibitor blebbistatin (SI Text, section 4 and Fig. S4C).

Fig. 6.

Summary of the results emphasizing the interplay between 3D cell shape evolution, traction force generation, and growth of FAs during early cell spreading. In the first phase, the cell is rounded, the spreading rate is high, and there is no force, nor FAs. The transition toward the second phase of spreading is initiated when the cell body contact angle θ reaches 90°. At this point, the cell starts to generate traction forces on the substrate. Force generation is followed by the onset of FA growth. Eventually, ruffling in the lamella is damped and the rate of spreading decreases. Remarkably, above 90°, FAs start to grow at the edge of the lamella, and not along the contact line between the cell body and the lamella. This observation suggests that the apical cell body cortical tension may be transmitted as tangential rearward forces in the lamella, triggering a coordinated cell-scale retrograde flow and FA growth in the lamella. This scenario is strongly supported by the fact that, in the parallel-plates geometry, FA growth is sensitive to the normal stiffness resisting the cell body contraction (Fig. 5 E–G), both the normal force and FA area being proportional to myosin II activity (SI Text and ref. 22).

Discussion

Cell spreading and migration are fundamental phenomena involving the regulation and the coordination—at the overall cell scale—of many processes such as remodeling of the cytoskeleton, force generation, and dynamical control of the adhesion to the extracellular matrix. Our aim was to reveal the role of 3D cell shape and mechanical interactions in the coordination and control of cell spreading. Combining various imaging techniques and micromechanical measurements, and using specific drugs inhibiting alternatively actin or myosin activity, we could dissect the different contributions to, and crucial steps of, early spreading. In particular, we show how the 3D cell shape, which is modified by the actin polymerization-powered extension of the cell–substrate contact area, feeds back on the spreading dynamics and triggers the growth of mechanosensitive adhesion complexes by controlling the amount of cortical actomyosin tension transmitted to the lamella.

These findings are important by many aspects. First, the transmission of rearward tension to the lamella at 90° is a simple explanation for the well-documented transition in spreading dynamics when the cell body contact radius R_b reaches approximately the initial cell radius R₀ (26, 27). Without FA growth, this tension would lead to retraction of the lamella and decreased spreading. FAs, by increasing friction with the substrate, probably avoid lamella slippage (32), thus allowing the cell to pursue spreading even with a reduced rate.

This scenario is consistent with the sharp increase in tangential traction forces already observed at the onset of P2 (20), as well as with the fact that, for cells spread on different areas Ap of 2D arrays of microposts, the force per post increases nonlinearly with Ap (19). In particular, this force is almost zero for nonspread cells (Ap = 440 μm²), whereas it is high for spread cells (Ap = 900 and 1,520 μm²) (19) in quantitative agreement with the threshold spread area ∼700 μm² we observed for θ = 90°. More fundamentally, this threshold area is also in agreement with the typical values reported for the switch between proliferation and apoptosis in endothelial cells [∼500 μm² (1)], for the transition in DNA synthesis in lung human endothelial cells [∼900 μm² (3)], and the switch in histone acetylation in NIH 3T3 fibroblasts [∼500 μm² (6)]. Because FAs are important cell-signaling centers, maintaining the cell spread area below the critical value for tension projection and FA formation (θ < 90°), could lead to impaired signaling and cell death. Note that spreading and tension projection could also control cell fate through direct compression of the nucleus (5, 33). For instance, it has been shown that ciliogenesis in human retinal pigment epithelial cells is regulated by the spread area, cilium growth being repressed by the apical actomyosin tension, above a threshold area of 750 μm² (28).

Eventually, we show that spreading, although initiated by specific integrin-based signaling [mainly Rac-dependent lamellipodial extension (34)], induces the generation of traction forces that modify, in turn, cell signaling (FA growth) and spreading itself (slower rate). This self-organization through feedback between chemical signaling and 3D shape-dependent mechanical forces is conceptually similar to what has been reported in development at the scale of the organism (35, 36).

Along this line, in both morphogenesis and early cell spreading, feedback between chemical signaling and mechanics could take place in part through membrane tension (37). Indeed, we observed that ruffling and protrusions from the top of the lamella were damped at the onset of P2 (Fig. S8 and Movie S4), in agreement with the results of Gauthier et al. (38) showing that spreading in P2 correlates with increased membrane tension and exocytosis. Remarkably, it has been recently shown that enhanced cell–substrate adhesion leads to increased membrane tension (39). Future investigations should thus focus on the link between transmission of cortical tension to the lamella and adhesion growth on the one hand, and increase of membrane tension on the other hand.

Materials and Methods

Cell Culture.

Rat embryonic fibroblasts (Ref-52) were grown using DMEM supplemented with 10% (vol/vol) heat-inactivated FCS, 2 mM glutamin, 50 units/mL penicillin, and 50 g/mL streptomycin. All cultures were maintained at 37 °C under humidified 5% CO₂ atmosphere.

Spreading Assay.

Cover glasses were incubated with 5 μg/mL fibronectin (F1141; Sigma-Aldrich) in DMEM, or with poly-l-lysine (0.01%; molecular weight, 70–150 kDa; Sigma-Aldrich), at 37 °C for 30 min and rinsed before the experiment. Cells were trypsinized, centrifuged at 90 × g for 3 min, resuspended in culture medium (only DMEM was changed: we used DMEM without Phenol red to avoid self-fluorescence) supplemented with 15 mM Hepes, and maintained under smooth agitation for at least 2 h at 37 °C before the experiment. Cells were then released in the same medium and imaged using a TIRF setup with a laser emitting at 488 nm, coupled to a IX-71 stage from Olympus (Olympus). To inhibit actin polymerization, cells were treated with various concentrations of Lat-A (Sigma) during 1 h before the experiments. To inhibit their contractility, cells were put in the presence of various concentrations of blebbistatin (Sigma-Aldrich) and Y-27632 (Sigma-Aldrich) 20 and 30 min before the beginning of the experiments, respectively.

TIRF Imaging.

We used a monochromatic (GFP, 450–480 nm) TIRF setup from Olympus, with a PlanApo 100×/1.45 oil objective and a F-View 1.4 MP (6.45 × 6.45 μm²) CCD camera (Olympus) leading to an overall resolution of 65 × 65 nm²/pixel. Image acquisition was performed at a rate of two pictures per minute. We carefully checked that TIRF imaging itself did not affect the intensity profiles (no photobleaching), nor cell spreading (no phototoxicity; SI Text and Table S1).

Confocal Imaging.

Cells were fixed at different stages of spreading using paraformaldehyde (15 min; 3% in PBS), then permeabilized with Triton X-100 (15 min; 0.2% in PBS), put in the presence of ammonium chloride (30 min; 50 mM in PBS), and BSA (30 min; 1% in PBS) to prevent nonspecific staining. For actin staining, cells were incubated with fluorescent phalloidin from Fluoprobes (30 min; 0.1% in PBS). For nucleus staining, cells were incubated with DAPI (30 min; 0.1% in PBS). Cells were imaged using a confocal spinning disk from Andor Technology coupled to an Olympus IX-81 microscope with a 60× oil objective. Cell contact radius and contact angles were determined manually after reconstruction of the 3D image.

Traction Force Experiments.

Both traction force setups (coupled to bright-field side view or to TIRFM) are based on the same principle. Before experiments, glass plates are pulled using a micropipette puller (PB-7; Narishige) and shaped with a microforge (MF-900; Narishige). Then, the stiffness k of the flexible plates is calibrated (21). During the experiments, the flexible glass plate is illuminated through bright light and its deflection δ is optically detected in real time by a position sensitive detector (Hamamatsu) used in inverted-contrast mode (21). The traction force F exerted by the cell is then given by the following: F = kδ. Details about the deflection detection in the regular side-view setup can be found in ref. 21. For the new setup coupling force measurements with TIRFM, we had to design a specific position detection module with adapted optical path and synchronous fluorescence imaging (Fig. S6). Concerning the effective stiffness protocol, see ref. 23.