Significance
Mechanisms are zero-energy motions that are key to the operation of mechanical devices, from windshield wipers to robotic arms. We built and studied chain-like mechanisms of coupled rigid rotors that are topologically protected, which means that they are not affected by smooth changes in material parameters like their quantum analogues. These prototypes are examples of mechanical structures that we dub topological metamaterials. Their mechanical excitations are nonlinear solitary waves which are topologically protected and yet tunable by changing the geometry of the unit cell. Although the left and right edges of the sample are equivalent in terms of local constraint counting, the solitary waves can start propagating only from the edge singled out by the topological polarization of the chain.
Keywords: topological matter, origami, isostaticity, jamming, active matter
Abstract
Networks of rigid bars connected by joints, termed linkages, provide a minimal framework to design robotic arms and mechanical metamaterials built of folding components. Here, we investigate a chain-like linkage that, according to linear elasticity, behaves like a topological mechanical insulator whose zero-energy modes are localized at the edge. Simple experiments we performed using prototypes of the chain vividly illustrate how the soft motion, initially localized at the edge, can in fact propagate unobstructed all of the way to the opposite end. Using real prototypes, simulations, and analytical models, we demonstrate that the chain is a mechanical conductor, whose carriers are nonlinear solitary waves, not captured within linear elasticity. Indeed, the linkage prototype can be regarded as the simplest example of a topological metamaterial whose protected mechanical excitations are solitons, moving domain walls between distinct topological mechanical phases. More practically, we have built a topologically protected mechanism that can perform basic tasks such as transporting a mechanical state from one location to another. Our work paves the way toward adopting the principle of topological robustness in the design of robots assembled from activated linkages as well as in the fabrication of complex molecular nanostructures.
Mechanical structures composed of folding components, such as bars or plates rotating around pivots or hinges, are ubiquitous in engineering, materials science, and biology (1). For example, complex origami-like structures can be created by folding a paper sheet along suitably chosen creases around which two nearby faces can freely rotate (2–4). Similarly, linkages can be viewed as 1D versions of origami where rigid bars (links) are joined at their ends by joints (vertices) that permit full rotation of the bars (Fig. 1 A–C). Some of the joints can be pinned to the plane while the remaining ones rotate relative to each other under the constraints imposed by the network structure of the linkage (5). Familiar examples include the windshield wiper, robotic arms, biological linkages in the jaw and knee, and toys like the Jacob’s ladder (6) and the Hoberman sphere. Moreover, linkages and origami can be used in the design of microscopic and structural metamaterials whose peculiar properties are controlled by the geometry of the unit cell (7, 8).
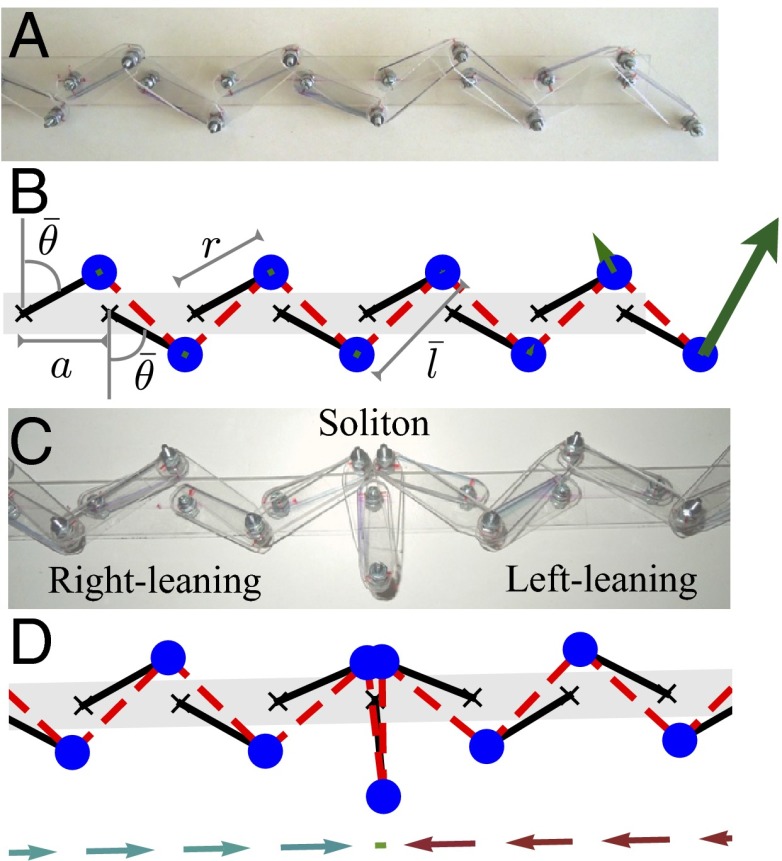
Fig. 1.
The chain of rotors in the flipper phase. (A) The translation symmetric system with constant. We show a linkage made from plastic and metal screws. (B) A computer sketch of the elastic chain (11): The masses are blue, rigid rotors are black, and springs are dashed red lines. The green arrows depict the amplitude of displacement of each mass of the edge-localized zero mode of the system. (C) A configuration of the linkage showing a soliton as a domain wall between right-leaning and left-leaning states. (D) A computer-simulated static configuration. The arrows beneath show the x projections of each rotor.
Many of these examples are instances of what mechanical engineers call mechanisms: structures where the degrees of freedom are nearly balanced by carefully chosen constraints so that the allowed free motions encode a desired mechanical function. However, as the number of components increases, more can go wrong: lack of precision machining or undesired perturbations. Robustness in this sense is a concern relevant to the design of complex mechanical structures from the microscopic to the architectural scale, typically addressed at the cost of higher manufacturing tolerances or active feedback.
Here, we take an alternative approach inspired by recent developments in the design of fault tolerant quantum devices (9). Consider, as an example, the quantized Hall conductivity of a 2D electron gas that is topologically protected in the sense that it cannot change when the Hamiltonian is smoothly varied (10). In this article, we present a topologically protected classical mechanism that can transport a mechanical state across a chain-like linkage without being affected by changes in material parameters or smooth deformations of the underlying structure, very much like its quantum counterparts.
Kane and Lubensky (11) recently took an important step toward establishing a dictionary between the quantum and classical problems. Their starting point, which seems at first disconnected from the linkages we study here, was to analyze the phonons in elastic systems composed of stretchable springs. In particular they derived a mathematical mapping between electronic states in topological insulators and superconductors (10) and the mechanical zero modes in certain elastic lattices (12). The simplest is the 1D elastic chain, shown in Fig. 1B, inspired by the Su–Schrieffer–Heeger (SSH) model for polyacetylene (13), a linear polymer chain with topologically protected electronic states at its free boundaries. In the mechanical chain, the electronic modes map onto zero-energy vibrational modes with a nontrivial topological index, whose eigenvectors represented as green arrows in Fig. 1B are localized at one of the edges (11). An intriguing question then arises: Could these zero-energy edge modes propagate through the system in the form of finite deformations?
We address this question by building and analyzing a linkage of rigid bars as an extreme limit of the 1D lattice of springs. This linkage allows no stretching deformations, yet it still displays the distinctive zero-energy mode localized at the edges (Fig. 1 and Movie S1). By nudging the rotors along the direction of the zero-energy mode (Fig. 1B and Movie S2), we provide a vivid demonstration of how the initially localized edge mode can indeed propagate and be moved around the chain at an arbitrarily small energy cost. We then show analytically and numerically that the mechanism underlying the mechanical conduction is in fact an evolution of the edge mode into a nonlinear topological soliton, which is the only mode of propagation in the chain of linkages that costs zero potential energy. The soliton or domain wall interpolates between two distinct topological mechanical phases of the chain and derives its robustness from the presence of a band gap within linear elasticity and the boundary conditions imposed at the edges of the chain. Although the topological protection ensures the existence of a domain wall, the dynamical nature of the soliton falls into two distinct classes that can ultimately be traced to the geometry of the unit cell. The prototypes we built therefore provide simple examples of structures that we dub topological metamaterials whose excitations are topologically protected zero-energy solitons (9).
Topological Band Theory of Phonons
The application of topological band theory to mechanics is most easily demonstrated in the context of the 1D elastic chain (11) (Fig. 1B). The model consists of a periodic arrangement of alternating massless rigid rotors of length r (black bars), constrained to rotate about fixed pivot points (black crosses), around an equilibrium angle at odd-numbered sites and at even-numbered sites. Here, the blue circles denote point masses M, a is the lattice spacing, and is the equilibrium (unstretched) length of the Hookean spring (with spring constant ke) connecting the masses. Because the 1D mechanical system has Ns = N lattice points and Nb = N − 1 bonds, there is (at least) one zero-energy vibrational mode as required by constraint counting; i.e., N0 = dNs − Nb, where N0 is the number of zero modes and d is the number of spatial dimensions.
The rigidity matrix (1, 14) for the lattice in Fig. 1, denoted R, is obtained by linearizing the change in length of the spring that connects masses {n, n + 1} in terms of small angular displacements δθn,n+1 from the equilibrium value ; i.e., δln,n+1 = Rniδθi (the authors of ref. 11 work with a matrix Q = RT). The phonon modes are readily obtained from the Fourier-transformed rigidity matrix R(k) (considering the chain as a periodic arrangement of two-particle unit cells),
| [1] |
where . In this notation, the (Fourier-transformed) dynamical matrix reads D(k) = R†(k)R(k). The eigenvalues of D are the squared vibrational frequencies (in units of ) of the normal modes of the lattice, given by ω(k) = |q+ ± q−eika|, where the ± belongs to the acoustic (+) and optical (−) branches of the dispersion curve, respectively.
For small k (and q+ > 0, q− < 0), the vibrational spectrum of the acoustic branch is gapped, and , where
| [2] |
is the gap frequency and
| [3] |
is the squared speed of sound. Owing to the gap, no propagating modes (with real k) can be excited for ω < ω0. Nevertheless, there is a zero-energy mode, which corresponds to the specific value of for which ω = 0, i.e., the value of k for which there are no changes in the spring length δln,n+1 = 0 for all n. Because k is complex, the zero-energy mode is nonpropagating and thus Im k yields an inverse penetration depth ℓ−1 that evaluates to
| [4] |
where the last relation is valid for small . As shown in Fig. 1B, the eigenvectors of the dynamical matrix (shown as green arrows) have appreciable magnitude only on the rightmost two particles, illustrating the exponential localization of the zero-energy mode at the boundary.
Eq. 4 shows that for , ℓ diverges and the zero-energy end mode becomes an ordinary infinite-wavelength acoustic phonon—the chain is no longer gapped. At the phonon spectrum collapses entirely to 0. This demonstrates the topological robustness of the zero-energy edge modes: Unless the chain is prepared with the specific values of for which the gap closes, their presence is insensitive to changes in material parameters.
Whether the zero-energy mode is localized at the right or the left edge is determined by the topological polarization introduced in ref. 11; here, it is simply the winding number of the complex phase of det R(k). As k goes from −π/(2a) to π/(2a), the path of det R(k) in the complex plane is a circle centered on the real axis at with radius , provided that . [If , the path of det R(k) passes through 0, making the phase undefined.] Thus, the winding number n is 1 if and zero if , indicating that the mode is localized respectively to the left (ℓ > 0 in Eq. 4) or the right (ℓ < 0) edge of the chain. The physical meaning of this classification is apparent when considering the symmetry classes of the uniform ground states: The black rotors in Fig. 1 can be either left (n = 1) or right leaning (n = 0).
Because the zero potential energy motion does not involve stretching or compression of the spring, it can be studied in the hybrid spring–strut system introduced by Kane and Lubensky as well as in the chain of linkages shown in Fig. 1 A and C. In these prototypes, the plastic rotors rotate around bolts attached to a longer piece of plastic that serves as the rigid background and are attached at their ends by other plastic pieces. Self-intersections are avoided by arranging alternating bars at different heights in the transverse direction.
Beyond Phonons: Solitons in Systems of Linkages
The linear elastic theory reviewed in the previous section predicts that there are no bulk low-energy phonons below the gap frequency and that the zero-energy mode is exponentially localized at the edge—i.e., the chain is a topological mechanical insulator (Movie S1). However, this conclusion is manifestly at odds with the simple experiments we performed using prototypes of the SSH chain with rigid constraints, as shown in Fig. 1.
By tilting the chain, a soft mode initially localized at the edge of the chain propagates under the effect of gravity all of the way to the opposite end, as shown vividly in Movie S2. This simple experiment demonstrates that the chain is in fact a mechanical conductor whose carriers are nonlinear solitary wave excitations not captured within linear elasticity. The nonlinear mechanism of conduction is the central result of our work and relies on a key difference between vibrational and electronic states: Phonons are infinitesimal physical displacements that can be integrated to finite deformations of the underlying mechanical structure, whereas electronic states live in an abstract Hilbert space.
The SSH chain is a paradigmatic and analytically tractable representative from a broader class of floppy mechanical systems that share a common feature—the infinitesimal zero-energy motion described by the localized topological modes extends to a finite zero-energy motion that propagates freely through the bulk. We expect similar behavior to occur in 2D and 3D structures involving linkages or other general mechanical structures that could be of considerable interest for robotic manipulations and design of metamaterials (15).
What types of nonlinear waves does this type of system support? Are there different phases of motion? To answer these questions we performed Newtonian dynamics simulations of the chain for different values of the geometrical parameters and the spring constant, ke. Newton’s laws are numerically integrated with the initial condition set by the zero-energy mode: , where is the initial velocity of the ith particle, is the component corresponding to the ith particle in the zero-energy eigenvector of the dynamical matrix, and v0 is a factor determining the initial speed. As seen in Fig. 2 and Movie S3, because the zero-energy mode is initially localized at the edge, the above procedure amounts to imparting an initial kick to the first few particles. We discuss below how this initial impulse evolves and propagates through the chain as well as the rich phenomenology that emerges as we vary the geometrical parameters of the chain.
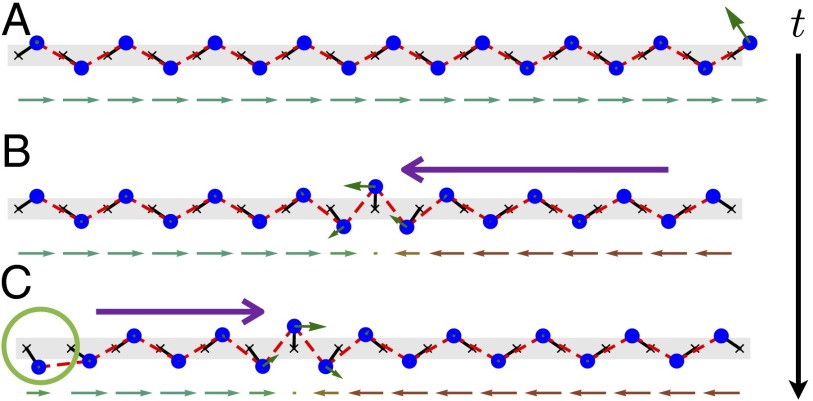
Fig. 2.
The evolution of a flipper soliton arising from integrating the zero mode of a finite chain , with x projections of the rotors underneath each snapshot (Movie S3 and S4). The system evolves from (A) right leaning to (B) left leaning and then back to (C) right leaning. The green arrows attached to the rotors depict the amplitude of the zero mode on each mass; note that it is always localized to the domain wall. In the flipper phase, the angle of a rotor flips between and each time the soliton passes through, except for the rotors on the ends, which also toggle between up pointing and down pointing. Hence in a full cycle the soliton goes from right to left and back twice.
In Fig. 2A, we show a chain with the rotors initially in the right-leaning mechanical state. As the rotors at the right end rotate following the zero-energy eigenmode (marked with small green arrows), their angles soon reach and they enter the left-leaning state and halt. However, rotors farther to the left now begin to rotate, generating a moving, localized region of motion. At the far left of the chain, the rotors remain in the right-leaning state until that region reaches them. The dynamics thus generate a domain wall interpolating between the right- and left-leaning states. Fig. 2B shows a snapshot of the chain where the domain wall is halfway to the left end. Because the passage of the domain wall flips the direction of the rotors from to (measured with respect to the positive y axis on the odd-numbered sites), we label this the flipper phase of motion. Once the domain wall has reflected off the left edge of the chain, the edge rotor now points down (Fig. 2C). Only when the domain wall has traversed the chain back and forth twice does the entire chain return to its initial right-leaning state. Upon varying the geometrical parameters of the chain, in particular after increasing the ratio r/a, we find that the rotors in the flipper can also overshoot their equilibrium positions and the profile exhibits oscillations, although the final effect of the soliton is still to flip the rotors between the two states. We call this variant the wobbling flipper (Movie S4).
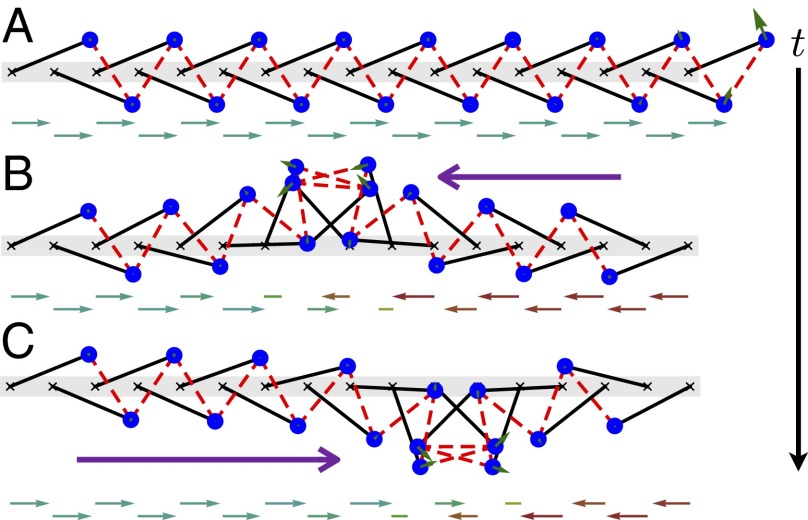
After further increasing r/a, a strikingly different behavior emerges (Fig. 3 and Movie S5). Although a domain wall interpolating between the right- and left-leaning mechanical states is still observed (Fig. 3B), the rotors now rotate counterclockwise by an angle of π each time a domain wall passes by. We refer to this as the spinner phase of motion. As the domain wall reflects off the ends of the chain, the edge rotors rotate by 2π and complete a full circle. In contrast to the flipper phase, the initial state of the chain is restored after the domain wall has completed one cycle around the chain.
Fig. 3.
The evolution of a spinner soliton arising from integrating the zero mode of a finite chain , with x projections of the rotors underneath each snapshot (Movie S5). The system evolves from (A) right leaning to (B) left leaning and then back to (C) right leaning. The green arrows attached to the rotors depict the amplitude of the zero mode on each mass; note that it is always localized to the domain wall. In the spinner phase, the angle of each rotor advances by +π each time the soliton passes.
Phase Diagram of Nonlinear Excitations
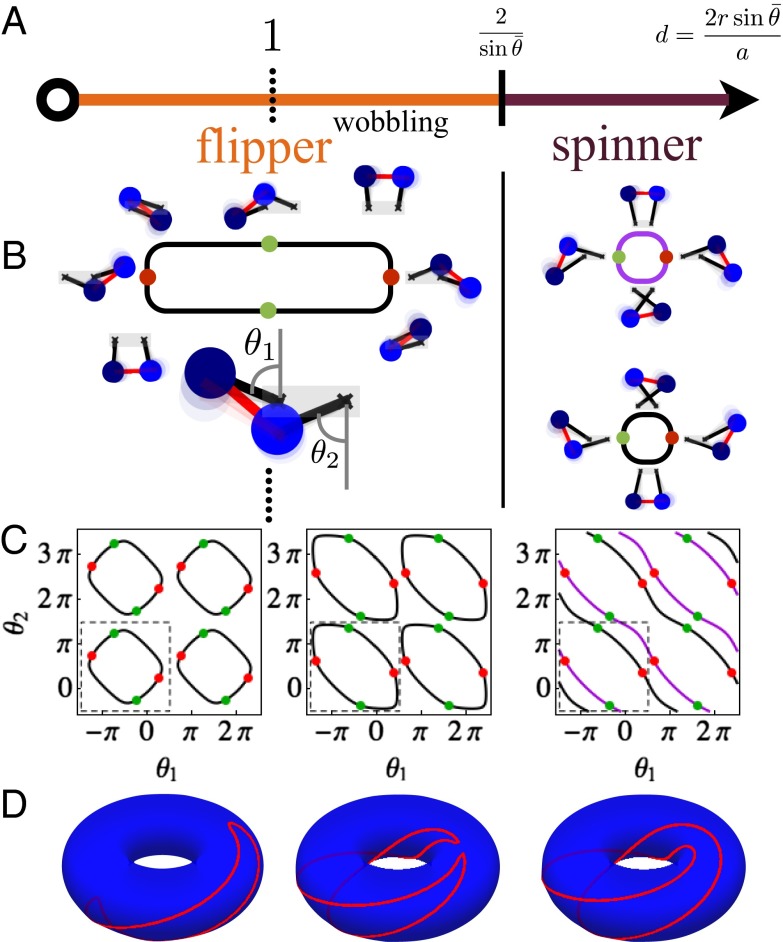
To understand the transitions and differences between these phases of motion, we can treat the chain as a 1D metamaterial and explain the nonlinear dynamics in terms of the geometry of the unit cell, parameterized by the dimensionless number . Consider the zero-energy configuration space of the four-bar linkage that is the unit cell of the chain. This space is defined by the zero-stretching constraint δln,n+1 = 0 (for the spring connecting rotors n and n + 1) and hence we replace the spring by a strut in what follows. In Fig. 4B, we show snapshots of the unit cell parameterized by the angles (θ1, θ2), whereas in Fig. 4C we show the corresponding configuration spaces for flippers (Fig. 4C, Left), wobblers (Fig. 4C, Center), and spinners (Fig. 4C, Right), respectively (Movies S6–S8 show full cycles of motion for the unit cells in all three cases, alongside animations of the unit cell configuration spaces). The red (right-leaning) and green (left-leaning) circles in Fig. 4 B and C represent four special configurations for which and correspond to the four spatially periodic ground states that are related to each other by reflection symmetries.
Fig. 4.
(A) Phases of the soliton as a function of . (B) The unit cell (four-bar linkage) configuration spaces in the flipper and spinner phases (four copies of each). The translation-symmetric points are marked in red (right leaning) and green (left leaning). There are two connected components in the spinner phase and just one in the flipper phase. (C) Pictures of the unit cell configuration space in the torus of θ1, θ2 angles (defined by δl1,2 = 0). (D) The topology of the configuration spaces depicted on 3D tori. In going from flipper to spinner, one circle splits into two linked Villarceau-like rings.
In going from Left to Right in Fig. 4C (increasing d), the configuration space evolves from one connected circle bounding a disk on a torus [parameterized by the coordinates (θ1, θ2)] to two diagonal circles “linked” on that torus. This happens precisely when decreases below 2r − a, equivalently , thus marking the transition from the flipper to the spinner phase. In Fig. 4D, we show sketches of the phase portrait on a 3D torus to emphasize this doubly periodic configuration space. Thus, the boundary that separates the flipper phase from the spinner phase is in fact a topological change in the configuration space of the four-bar linkage (16).
To understand this change, observe that when r ≪ a we can smoothly access all of the possible configurations of a linkage of four bars (Fig. 4B, Left). However, as r/a increases, the four-bar linkage approaches a triangle that is pinned at one vertex. Because it is impossible to transform a triangle to its mirror image via translations and rotations in the plane, the set of configurations becomes disconnected (Fig. 4B, Right). Thus, for d > dc (spinners) the unit cell configuration space consists of two components, each containing a single pair of ground states and . A period of the motion of the four-bar linkage reveals how the soliton propagates through the chain—all rotors rotate in the same direction, from to , say. By contrast, for d < dc (flippers), a full cycle of the unit cell visits all four ground state configurations. The transition between flipper and spinner states appears to be discontinuous, as we show when we discuss the continuum description of the solutions.
To understand the transition between the nonwobbling flipper and the wobbling flipper phases, note that as a flipper soliton passes through, the rotors must eventually rotate from to , passing through θ = 0. Suppose the first and second masses at the edge initially both rotate counterclockwise. By virtue of the flipper motion, the second mass must eventually rotate clockwise; thus it will appear to wobble. This is visible in Fig. 4C as the change in sign of the slope dθ2/dθ1 at all of the red and green circles, and the threshold for this can be derived from the point at which the penetration depth ℓ in Eq. 4 vanishes: or d = 1.
The existence of these rich phases of motion illustrates the fact that the uniform ground states and localized zero-energy edge mode are best viewed as snapshots of a periodic nonlinear motion and its velocity field.
Continuum Theory: Flipper Solitons
In this section and the next we discuss how the flipper and spinner motions discussed qualitatively in the previous section emerge as topological soliton solutions to the very equation that within the linear approximation predicts a localized edge mode: the constraint equation δln,n+1 = 0. These solitons are described by solutions to the ϕ4 and sine-Gordon equations, but have the key additional feature that they cost precisely zero potential energy.
We begin by deriving the equation of motion of the flipper solitons in the limit d ≪ 1. In terms of the angles of the rotors in a unit cell θn and π − θn+1 (measured clockwise with respect to the +y axis), the constraint equation reads
| [5] |
To take the continuum limit of Eq. 5, we define a slowly varying angular field θ(x) by letting a → dx, , (using a Taylor series expansion centered at x = n + 1/2). We obtain
| [6] |
Note that this choice preserves the underlying reflection symmetry (x, θ) → (−x, −θ).
In terms of the field u(x) = r sin θ(x) (the x component of the position of the mass), Eq. 6 reads
| [7] |
where . Besides the uniform left- and right-leaning solutions , Eq. 7 admits only one zero-energy solution (for ) given by the kink
| [8] |
where is the width of the static domain wall that interpolates between left-leaning (u < 0 as x → −∞) and right-leaning (u > 0 as x → +∞) states. Note that w0 is proportional to the penetration length ℓ derived in Eq. 4 for small and diverges when the gap closes. This is analogous to the divergence of domain wall widths at the critical point in the Landau theory of second-order phase transitions.
In SI Appendix, we derive the continuum Lagrangian for the chain in the flipper phase in the limit and , which reads
| [9] |
In addition to the ordinary ϕ4 potential, ℒ has an additional boundary term linear in ∂xu. This extra term ensures that the static kink has zero energy because the last three terms in Eq. 9 can be written as a perfect square that vanishes for the static kink solution in Eq. 7 (17, 18). It also breaks the ∂xu → −∂xu symmetry of the ordinary ϕ4 theory. As a result, the antikink solution of Eq. 9 (with left- and right-leaning states reversed in space) costs a finite stretching energy. Hence, the antikink is forbidden in the linkage limit, where ke → ∞ and only solutions of Eq. 7 are admitted. We can define the topological charge Q as the difference in the number of kinks and antikinks:
| [10] |
For a system with periodic boundary conditions, Q = 0, and no solitons exist. For a system that has a left- and right-leaning edge, Q = 1, and the linkage must support one and only one kink that is therefore topologically protected. The topological index is thus a measure of the number of solitons in the system and is consistent with the number of zero modes from constraint counting.
Because the ϕ4 theory is Lorentz invariant, the dynamical solution is simply obtained by a Lorentz boost
| [11] |
where v is the speed at which the kink propagates (set by the initial kinetic energy in the system) and c is the linear speed of sound. From Eq. 3, the speed of linear sound (defined from the linear part of the dispersion curves above the gap) for r ≪ a is valid for small . In the comoving frame, Eq. 11 is equivalent to Eq. 8, provided that the static width w0 is replaced by the Lorentz contracted width . For linkages c diverges, and hence w = w0.
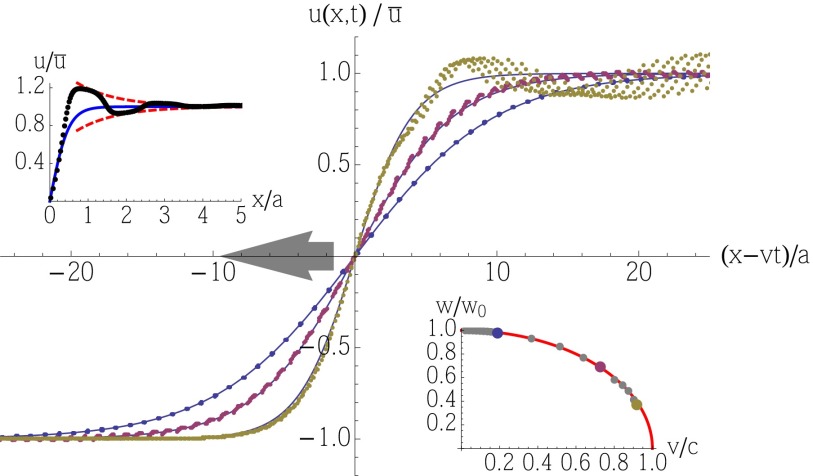
To test our continuum approximation for the domain wall in the discrete mechanical chain, we numerically obtain the displacement field u(x, t) of the rotors for a range of initial energies imparted to the chain. In Fig. 5, we show that the displacements (dotted curves) in the flipper phase compare favorably with the continuum ϕ4 predictions in Eq. 11 (solid lines). The predicted Lorentz contraction is evident in the profiles in Fig. 5 as a decrease in the width of the profiles when the speed of propagation v is increased (Fig. 5, Lower Right Inset). Note the presence of a large wake behind the moving domain wall, exhibited in the profile with the highest energy (gold symbols). We leave a more detailed analysis of the wake and higher-order nonlinearities for future work.
Fig. 5.
A comparison of the numerically generated displacement field u(x − vt) (symbols) with the continuum profiles in Eq. 11 (solid lines) in the flipper phase. The numerical results are for a chain of 150 rotors with and ke = 1, M = 1. Colors denote different propagation speeds, increasing from blue to gold circles. The speed of propagation v used in Eq. 11 was measured by tracking the motion of the center of mass of the domain wall [obtained by interpolating the data points (j, θj) and choosing the value of x where the line passes through θ = 0]. The curves correspond to 10 time snapshots of a single chain, each translated so that the center of the soliton is at x − vt = 0. Lower Right Inset shows the numerically extracted width of the kinks (data points obtained from the inverse of the slope of for the recentered profiles) compared with the Lorentz contraction factor (red line). Upper Left Inset shows data from a wobbling flipper profile with (black circles) compared with a tanh profile (blue) with the flipper width and an exponential decay envelope (red) with the spinner width. See SI Appendix and Figs. S1 and S2 for a more detailed look at the wobbling flipper profiles.
The wobbling flipper phase is more challenging to treat analytically. As shown in Fig. 5, Upper Left Inset, the profile exhibits oscillations around the values . Numerically, the slope at the kink center seems to follow the prediction coming from the inverse width of the continuum flipper solution (blue curve). However, the oscillations in the profile decay exponentially with a decay length of approximately (red dashed envelope). As we shall see in the next section, this length scale is associated with the width of the spinner. In SI Appendix, we derive a linearized approximation for the wobbling flipper that recovers the oscillations qualitatively and recovers precisely this decay length (Figs. S1 and S2), shedding light on how the transition between flipper and spinner phases occurs.
Continuum Theory: Spinner Solitons
The solution presented for the flipper phase assumes that u never exceeds , a condition that is certainly violated by the spinner solitons in which the rotors rotate by π. Moreover, in the spinner phase where r ≫ a, pairs of neighboring rotors in a unit cell seem to move nearly in phase like adjacent sides of a rigid triangle (Movie S5). To describe the motion in this phase, we thus construct a description for the dynamics of spinner solitons by integrating out the motion of every other rotor (say, the even sites).
Let ln,n+1 be the length of the springs between nodes {n, n + 1}. Then, the constraint equation can again be expressed in terms of the geometrical parameters r, a and the angles {θn, θn+1, θn+2} as before. We next “integrate out” θn+1, by using the constraint equation . Expressing this second constraint equation in terms of the angles , we find (in the limit a ≪ r) that . (We explicitly tested the validity of this approximate relation in classical dynamics simulations.)
Taking the continuum limit, θn → θ(x) and θn+2 → θ(x + 2a) = θ + 2aθ′ (where f′ ≡ df/dx), and retaining terms to leading order in a, we obtain the following differential equation for the static profile valid in the spinner phase
| [12] |
that can be easily integrated with the result
| [13] |
Thus, the static spinner profile at alternate sites is described by a sine-Gordon soliton of the form in Eq. 13 whose width is . This is in contrast to the flipper phase of motion where the width of the soliton scales inversely with d (Eq. 8). Indeed, the basic continuum field in the spinner phase lives on only half the rotors, compared with the flipper phase where the field lives on all of the rotors. Thus, at a very basic level, the transition between flippers and spinners cannot be described as a smooth transition between two profile shapes.
The dynamical solution is again obtained by a Lorentz boost
| [14] |
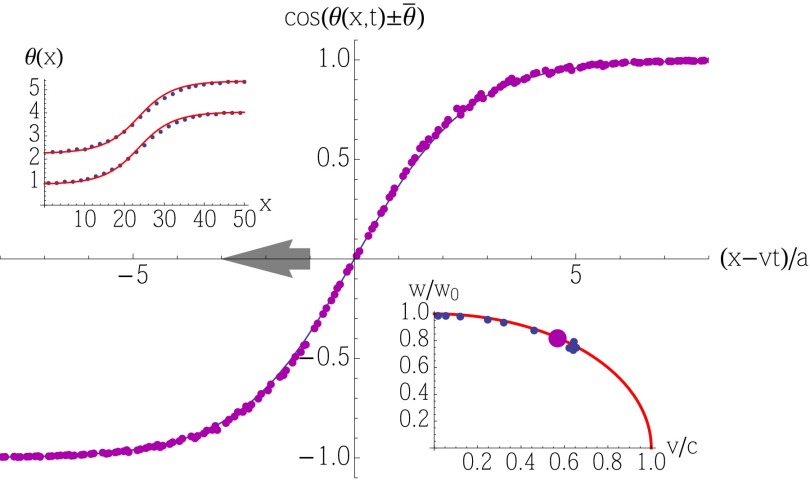
where ± correspond to the solutions for even (odd) sites, respectively, and from Eq. 3, the speed of sound in the spinner phase (r ≪ a) is . In SI Appendix, we rederive the sine-Gordon solution starting from the discrete Lagrangian for our mechanical chain, valid in the spinner phase. In Fig. 6 we compare the continuum sine-Gordon predictions (solid line) to numerical solutions (symbols) and find good agreement in the dynamical width as well (Fig. 6, Lower Right Inset).
Fig. 6.
A comparison of the numerically generated field (symbols) with the continuum profiles in Eq. 14 (solid line) in the spinner phase. The numerical results are for a chain of 50 rotors with and ke = 1, M = 1. Profiles and speeds were obtained as in Fig. 5, except that the even and odd sites are first shifted appropriately to yield continuous profiles. Upper Left Inset shows θ(x) for one snapshot showing how the even and odd angles are offset by the constant . Lower Right Inset shows the numerically extracted width of the kink (as in Fig. 5) compared with the Lorentz contraction factor.
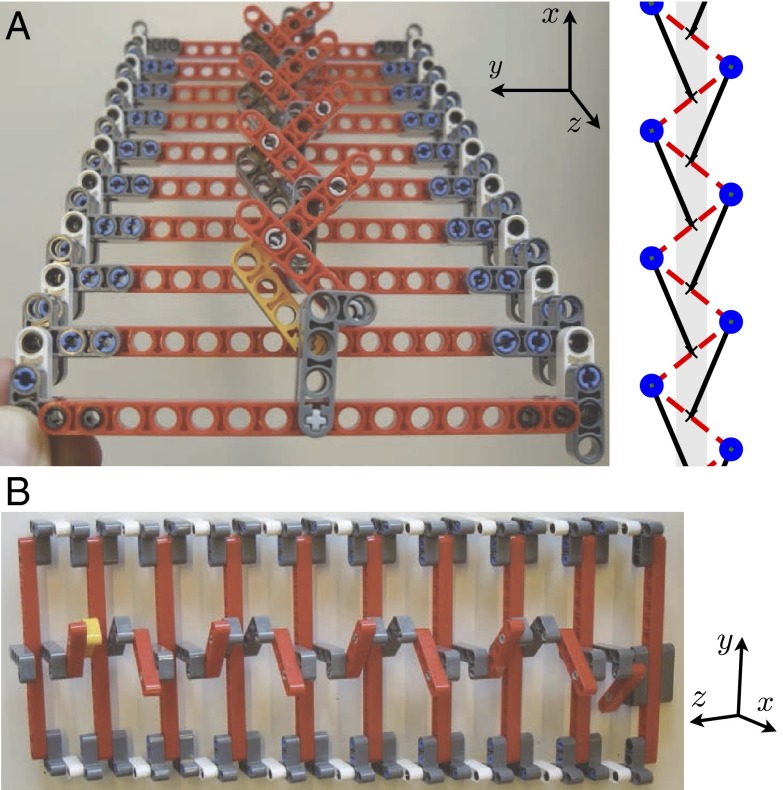
To build a spinner prototype, the 3D embedding must avoid the many self-intersections visible in Fig. 3. A model made from LEGO pieces is shown in Fig. 7 and Movie S9. The crucial point is that the rotors are staggered in the transverse direction, causing the transverse width to be proportional to the number of rotors; see the z axis in Fig. 7.
Fig. 7.
A LEGO realization of a chain admitting a spinner soliton (Movie S9). (A) A view of the realization alongside a computer graphics sketch. The “L”-shaped pieces are the rotors, the shorter red bars connecting their ends are the springs, and the long red bars serve as supports for the pinning. The “T”-shaped pieces connect the red bars to a single rigid background frame. (B) Another view showing the staggering of the rotors in the transverse (z) direction.
To sum up, the zero-energy moving domain walls in simple model chains are basic examples of a generic physical process that we expect to exist in more complex man-made and natural structures relevant to robotics and mechanical metamaterials. The protected excitations of topological mechanical metamaterials that appear as zero-energy vibrational modes within the linear approximation may integrate to finite deformations capable of transporting a mechanical state across the system. Our work raises the question of whether the principle of topological robustness can be adopted in the design of robotic manipulators composed of activated linkages as well as in the fabrication of complex molecular nanostructures.
Supplementary Material
Acknowledgments
We thank J. C. Y. Teo, A. Turner, J. Paulose, and Y. Zhou for helpful discussions and are grateful to T.-s. Chen for assistance in constructing the flipper. We acknowledge financial support from the Foundation for Fundamental Research on Matter (FOM) and the Netherlands Organisation for Scientific Research (NWO).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1405969111/-/DCSupplemental.
References
- 1.Demaine E, O’Rourke J. 2007. Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Cambridge Univ Press, Cambridge, UK), pp 9–16, 50–52.
- 2.Wei ZY, Guo ZV, Dudte L, Liang HY, Mahadevan L. Geometric mechanics of periodic pleated origami. Phys Rev Lett. 2013;110(21):215501. doi: 10.1103/PhysRevLett.110.215501. [DOI] [PubMed] [Google Scholar]
- 3.Dias MA, Dudte LH, Mahadevan L, Santangelo CD. Geometric mechanics of curved crease origami. Phys Rev Lett. 2012;109(11):114301. doi: 10.1103/PhysRevLett.109.114301. [DOI] [PubMed] [Google Scholar]
- 4.Schenk M, Guest SD. Geometry of Miura-folded metamaterials. Proc Natl Acad Sci USA. 2013;110(9):3276–3281. doi: 10.1073/pnas.1217998110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Thorpe MF. Continuous deformations in random networks. J Non-Cryst Solids. 1983;57:355–370. [Google Scholar]
- 6.Edge R. Solitons. Phys Teach. 1998;36:483–485. [Google Scholar]
- 7.Kang SH, et al. Complex ordered patterns in mechanical instability induced geometrically frustrated triangular cellular structures. Phys Rev Lett. 2014;112(9):098701. doi: 10.1103/PhysRevLett.112.098701. [DOI] [PubMed] [Google Scholar]
- 8.Milton GW, Cherkaev AV. Which elasticity tensors are realizable? J Eng Mater Technol. 1995;117(4):483–493. [Google Scholar]
- 9.Vitelli V. Topological soft matter: Kagome lattices with a twist. Proc Natl Acad Sci USA. 2012;109(31):12266–12267. doi: 10.1073/pnas.1209950109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hasan MZ, Kane CL. Topological insulators. Rev Mod Phys. 2010;82:3045–3067. [Google Scholar]
- 11.Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys. 2014;10(1):39–45. [Google Scholar]
- 12.Sun K, Souslov A, Mao X, Lubensky TC. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc Natl Acad Sci USA. 2012;109(31):12369–12374. doi: 10.1073/pnas.1119941109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Su WP, Schrieffer JR, Heeger AJ. Solitons in polyacetylene. Phys Rev Lett. 1979;42(25):1698. [Google Scholar]
- 14.Calladine CR. Buckminster Fuller’s “Tensegrity” structures and Clerk Maxwell’s rules for the construction of stiff frames. Int J Solids Struct. 1978;14(2):161–172. [Google Scholar]
- 15.Hawkes E, et al. Programmable matter by folding. Proc Natl Acad Sci USA. 2010;107(28):12441–12445. doi: 10.1073/pnas.0914069107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kapovich M, Millson J. On the moduli spaces of polygons in the Euclidean plane. J Differ Geom. 1995;42(1):430–464. [Google Scholar]
- 17.Bogomolnyi E. The stability of classical solutions. Sov J Nucl Phys. 1976;24(4):449–454. [Google Scholar]
- 18.Prasad MK, Sommerfield CH. Exact classical solution for the ’t Hooft monopole and the Julia-Zee dyon. Phys Rev Lett. 1975;35(12):760–762. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.