Hypothesis Testing for an Extended Cox Model with Time-Varying Coefficients

Summary

The log-rank test has been widely used to test treatment effects under the Cox model for censored time-to-event outcomes, though it may lose power substantially when the model’s proportional hazards assumption does not hold. In this paper, we consider an extended Cox model that uses B-splines or smoothing splines to model a time-varying treatment effect and propose score test statistics for the treatment effect. Our proposed new tests combine statistical evidence from both the magnitude and the shape of the time-varying hazard ratio function, and thus are omnibus and powerful against various types of alternatives. In addition, the new testing framework is applicable to any choice of spline basis functions, including B-splines and smoothing splines. Simulation studies confirm that the proposed tests performed well in finite samples and were frequently more powerful than conventional tests alone in many settings. The new methods were applied to the HIVNET 012 Study, a randomized clinical trial to assess the efficacy of single-dose Nevirapine against mother-to-child HIV transmission conducted by the HIV Prevention Trial Network.

1. Introduction

The HIVNET 012 Study is a randomized clinical trial conducted by the HIV Prevention Trial Network (HPTN) between 1997 and 2001 (The HIVNET/HPTN Group, 2003). It showed an astounding prevention benefit for a short course of nevirapine (NVP) versus zidovudine (AZT) among HIV infected pregnant women in Uganda: NVP was associated with a 41% reduction in relative risk of mother-to-child transmission (MTCT) of HIV-1 through to the age of 18 months (Jackson et al., 2003).

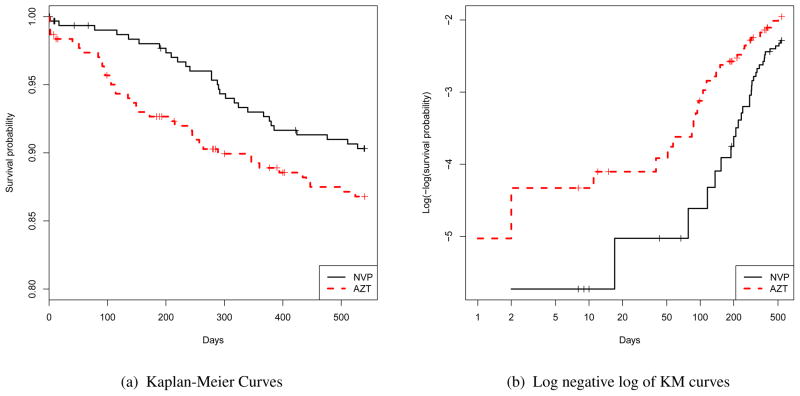
Besides the prevention benefit, it was also important for this study to assess whether or not the NVP would eventually improve the newborn’s 18-month survival. As shown in Figure 1(a), Kaplan-Meier curves indicate that the NVP group appears to have better infant survival. However, the log-rank test does not show statistical significance (p-value: 0.147). Although the lack of significance could be due to insufficient sample size, the power of the log-rank test may also be compromised if the proportional hazards assumption does not hold. We plot the log-log-transformed estimated cumulative hazard functions in Figure 1(b), which demonstrates that the two Kaplan-Meier curves indeed appear to get closer as time progresses. This suggests that the hazard ratio is not constant over time.

Figure 1.

The HIVNET 012 Study: estimated Kaplan-Meier curves for two treatment arms and their transformation by log negative log.

In the HIVNET 012 Study, NVP was only given once to the mothers at labor onset and once to the babies within 72 hours of birth, while AZT was given to the mothers from labor onset to delivery and to the babies twice daily for 7 days after birth. It was not expected that the NVP effect would sustain throughout the 18 months of follow-up. In addition, even if the babies were born uninfected, they could be infected after birth via breastmilk because the ratio of HIV-susceptible cells to total breastmilk cells increases over time. Therefore, one would predict the risk reduction of 18-month infant mortality to vary over time. If so, it is important to develop appropriate statistics to test whether there is any infant survival benefit from NVP while allowing for nonproportional hazards.

As alluded to above, the power of log-rank test, or the score test based on the partial likelihood for the Cox proportional hazards model (Cox, 1972), depends on the alternative assumption of proportional hazards. They may lose power if the assumption does not hold, as in the HIVNET 012 Study example. This paper aims to develop flexible testing procedures for potentially time-varying treatment effects for censored time-to-event data.

To be specific, we consider an extended Cox proportional hazards model as follows:

$$\lambda (t\mid X,Z)={\lambda }_0(t)exp\{X^{\mathrm{T}}\beta +Z\theta (t)\}.$$ (1)

Here, λ(·|X, Z) is the hazard function for the p-dimensional covariate vector X ∈ 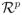and the treatment indicator Z ∈ 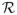, and λ₀(·) is the baseline hazard function. The superscript T is for vector (matrix) transpose. Moreover, β is the time-independent regression parameter of the same p-dimension for X, and θ(·) is the time-varying coefficient for Z that is assumed to be a smooth function of time. When θ(t) is constant, model (1) reduces to the usual Cox model. Under model (1), we are interested in testing the null hypothesis that Z has effect at any time while adjusting for X, i.e., H₀: θ(t) = 0 for any t ≥ 0.

There have been several approaches in the statistical literature for hypothesis testing involving θ(·) in (1). For example, Self (1991) and Wu and Gilbert (2002) considered adaptively weighted log-rank tests, assuming parametric forms of θ(·) to be polynomial functions. For nonparametric or semiparametric approaches, Gray (1994) applied B-spline bases to approximate θ(·) with a careful manual choice of tuning parameters, such as degrees of freedom and number of knots. Nevertheless, the choice of tuning parameters would depend on the functional shape of true θ(·) and was generally unknown; different choices of tuning parameters could affect power considerably and lead to different p-values. Other approaches may resort to direct nonparametric estimation of θ(·), as seen in O’Sullivan (1988), Hastie and Tibshirani (1990), Zucker and Karr (1990), Sleeper and Harrington (1990), Kooperberg et al. (1995), Brown et al. (2007), and references therein. This work is useful in understanding the overall shape of θ(·). Although asymptotic properties are developed for an estimated θ̂(t) at a specific time t, they are usually not intended for testing the global null H₀: θ(t) = 0 for any t ≥ 0.

The null hypothesis of interest is related to but fundamentally different from H_0,PH: θ(t) = c for some constant c ∈ 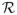. In fact, H_0,PH is exactly equivalent to the proportional hazards assumption, with testing procedures including Pettitt and Bin Daud (1990), Gray (1994) and Lin et al. (2006). Specifically in Lin et al. (2006), θ(·) was approximated by smoothing spline bases, and the authors proposed a score test for H_0,PH that does not involve tuning parameters. Nevertheless, we would like to emphasize that these approaches test a different null hypothesis from the proposed test, and are thus not comparable with our work. The differences between our work and other previous literature are further clarified in Section 3.5.

In this article, we aim to develop proper testing methods specifically for the null hypothesis H₀: θ(t) = 0 for any t ≥ 0 under model (1), based on spline representation of the hazard ratio θ(t). The rest of the paper is organized as follows. In Section 3, we study the extended Cox model and derive the proposed statistics. Extensive Monte-Carlo simulations studies are presented in Section 4 with various choices of θ(t) to evaluate a finite sample performance of our score statistics. We also apply our proposed statistics to compare the 18-month infant survival rates of the HIVNET 012 Study. We conclude in Section 5 by summarizing our results and discussing relevant issues and future directions.

2. The extended Cox model

Throughout this paper, we assume the extended Cox model as in (1). Our aim is to develop powerful and omnibus hypothesis testing procedures for H₀: θ(t) = 0 for any t ≥ 0. When θ(·) is constant, model (1) reduces to the usual Cox proportional hazards model. Nevertheless, θ(t) can be quite flexible. It allows the hazard ratio between two treatment groups to change over time for any given X. Some properties regarding this model are summarized as follows:

Property

Denote the cumulative hazard function by $\mathrm{\Lambda }(t)={\int }_0^t\lambda (s)ds$. Let θ(0) = θ₀ and assume that lim_t→∞ θ(t) = θ₁ < ∞. Then

1. lim_t→0 log{Λ(t | X, Z)/Λ₀(t)} = X^Tβ + Zθ₀, and

2. lim_t→∞ log{Λ(t | X, Z)/Λ₀(t)} = X^Tβ + Zθ₁.

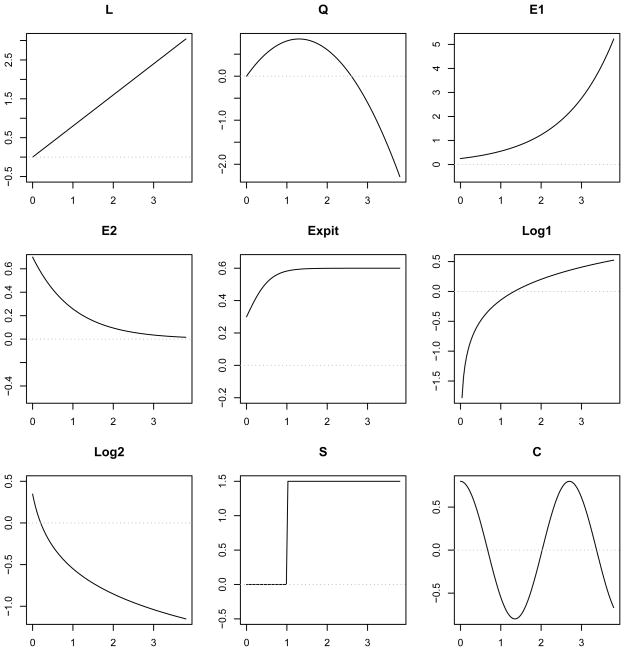
Proof of this property is straightforward. Based on this, when θ(·) is monotone, θ₀ and θ₁ define the lower and upper boundaries of the relative risk in cumulative hazard functions adjusted for X. For example, when θ(t) = 0.7 exp(−t), the hazard ratio for Z is 0.7 at t = 0, but gradually reduces to zero as time progresses. More examples of θ(·) are shown in Figure 2. Self (1991) and Wu and Gilbert (2002) considered special parametric submodels, where the shape θ(·) is represented by a family of polynomial functions indexed by a few parameters to account for early or late effects.

Figure 2.

Functional shapes of hazard ratio θ(t) that were used in simulations. We considered nine hazard functions, including linear (L), quadratic (Q), exponential (E1, E2), inverse-logistic (Expit), logarithm (Log1, Log2), step (S) and cosine (C) functions. Their specific functional forms are specified in Table 1.

2.1 Spline representations of θ(t)

We assume that the collected data consist of n independent and identically distributed (iid) copies of (Y, Δ, X, Z), where Y is the minimum of time to event T and censoring time C, i.e., Y = min(T, C), Δ = I(T ≤ C) is the event indicator, X is the vector of covariates other than the treatment indicator Z, namely {(Y_i, Δ_i, X_i, Z_i), i = 1, 2, …, n}. Let $t_1^o\le t_2^o\le \cdots \le t_r^o$ denote the ordered observed failure times, i.e., ordered statistics of {Y_i: i = 1, 2, ···, n, and Δ_i = 1}, where $r={\sum }_{i=1}^n{\mathrm{\Delta }}_i$ is the number of observed failure time points.

To model the time-varying treatment effect flexibly, we consider representing θ(t) by fixed knots B-splines or smoothing splines, i.e.,

$$\theta (t)={\theta }_0+\sum _{k=1}^K{\theta }_k{B}_k(t),$$ (2)

where B_k(t) forms a set of basis functions. Note that the methods development below works for both B-spline or smoothing spline approaches, and our experience is that the performance of the two approaches are comparable as long as the number of knots are reasonably dense. If one is using fixed knots B-splines, the number of basis function K is fixed and depends on the number of knots and the order of polynomials. For the smoothing spline approach, on the other hand, the number of basis functions depends on the sample size and the order of polynomials, i.e., K = r + m − 1.

Since the partial likelihood involves θ(t) evaluated at the observed failure time $t_1^o,\dots ,t_r^o$ only, we define $\gamma ={\{\theta (t_1^o),\dots ,\theta (t_r^o)\}}^T=\mathbf{1}{\theta }_0+B\underset{\_}{\theta }$, where 1 ∈ ℝ^r is a vector whose elements are all 1, θ = (θ₁, …, θ_K)^T ∈ Θ ⊂ ℝ^r and B is a r × K matrix whose (i, j) element is $B_i(t_j^o)$.

2.2 Penalized likelihood

The spline representation introduces K parameters (θ₁, ···, θ_K) for the hazard ratio function to allow flexibility. However, with a large degree of freedom, the model could overfit and the power to detect deviations from the null may be low. One strategy to avoid overfitting is to introduce a penalized partial likelihood function by penalizing the roughness of θ(t), e.g., in the form of ∫ {θ′(t)}²dt. It can be shown that the penalty term is a quadratic function of θ,

$$\int {\{{\theta }^{\prime }(t)\}}^{2}dt=\int {\{{\sum }_k{\theta }_k{B}_k^{\prime }(t)\}}^{2}dt={\underset{\_}{\theta }}^T\mathrm{\sum }\underset{\_}{\theta },$$

where Σ is a K × K matrix whose (i, j) element is $\int B_i^{\prime }(t)B_j^{\prime }(t)dt$, which is fully determined by the choice of splines. Thus, the penalized partial log likelihood function is defined by

$$\begin{array}{l}\ell \{\beta ,\theta (·),\tau \}\equiv {\ell }_P\{\beta ,\theta (·)\}-\frac{1}{2\tau }\int {\{{\theta }^{\prime }(t)\}}^{2}dt\\ ={\ell }_P(\beta ,{\theta }_0,\underset{\_}{\theta })-\frac{1}{2\tau }{\underset{\_}{\theta }}^T\mathrm{\sum }\underset{\_}{\theta },\end{array}$$ (3)

where τ is a tuning parameter that controls smoothness of θ(t), and ℓ_P is the partial likelihood corresponding to hazard ratio function θ(t),

$${\ell }_P(\beta ,\theta (·))=\sum _{i=1}^n{\mathrm{\Delta }}_i\left[X_i^T\beta +S_i\theta (Y_i)-log\left\{\sum _{j=1}^{n}exp\{X_j^T\beta +S_j\theta (Y_i)\}I(Y_j\ge Y_i)\right\}\right].$$

Note that τ controls the level of smoothness of θ(t) and thus the effective degree of freedom. When τ is small, the penalized partial likelihood encourages solutions that are close to the Cox proportional model with df = 1 for treatment effect. When τ is large, the effect of penalty is negligible and the model involves K + 1 parameters for the treatment effect, e.g., df = K + 1. Under this model, the null hypothesis can be represented as H₀: θ_k = 0, , k ∈ {0, 1, ···, K}. Gray (1994) used B-splines and studied asymptotic properties of Wald, score and likelihood ratio tests for fixed tuning parameter τ. For the choice of tuning parameter, they suggested choosing a suitable degree of freedom (henceforth denoted df) and finding τ to achieve the desired df. However, in practice, the choice of suitable df is subjective, and the power performance depends on the tuning parameter.

To construct tests that do not depend on tuning parameters, one can exploit the connection between the penalized splines and random effects models (Ruppert et al., 2003). Note that the second term of (3) is proportional to the logarithm of a multivariate normal density with mean zero and the covariance matrix τΣ⁻¹. Hence, one can treat θ as “random effects,” and integrate θ out with respect to the multivariate normal density to obtain the marginal partial log likelihood

$${\ell }_m(\beta ,{\theta }_0,\tau )={\int }_{\theta \in \mathrm{\Theta }}exp\{{\ell }_P(\beta ,{\theta }_0,\underset{\_}{\theta })\}exp\left(-\frac{1}{2\tau }{\underset{\_}{\theta }}^T\mathrm{\sum }\underset{\_}{\theta }\right)d\underset{\_}{\theta }.$$ (4)

We use this marginal likelihood as our objective function to derive the score statistics. In fact, since τ is the variance component for the random effects, setting τ = 0 shall lead to θ = 0. As a result, testing H₀ is equivalent to H₀: θ₀ = 0, τ = 0. Note that this mixed effect model representation holds for both B-splines and smoothing splines.

Remark 1

Lin et al. (2006) considered a smoothing splines approach, where the log hazard ratio θ(t) can be represented by

$$\theta (t)={\theta }_0+\sum _{j=1}^{m-1}{\delta }_j{t}^j+\sum _{k=1}^r{\theta }_{k}R(t,t_k^o),$$

where δ_j and θ_k are spline coefficients, {1, t, ···, t^m−1} is a set of basis functions for (m − 1)^th order polynomials, and $R(t,s)={\int }_0^1{(t-u)}_{+}^{m-1}{(s-u)}_{+}^{m-1}/{\{(m-1)!\}}^{2}du$, where x₊ = x ∨ 0 = max{x, 0}. The choice of m in (2) depends on a pre-specified level of smoothness. If one chooses m = 1, the time-varying coefficient (2) is simplified as $\theta (t)={\theta }_0+{\sum }_{k=1}^r{\theta }_{k}R(t,t_k^o)$, where R(t, s) = min{t, s}. It can be shown that matrix B is exactly the same as Σ in this case.

Remark 2

There are several key differences between Lin et al. (2006) and our work. First, they are interested in testing the proportional hazards assumption, $H_0^{PH}:\tau =0$, which is a different null hypothesis. Thus, our approach and theirs are not directly comparable. Second, their null hypothesis involves the variance component parameter only, where ours involves an additional fixed effects parameter θ₀. Statistically, as will be seen later, our work involves addressing challenges to combine score tests for both θ₀ and τ, due to some non-standard properties for the variance component τ. Third, our approach here is not limited to the smoothing splines approach, and it works for other choices of basis functions such as B-splines.

3. Proposed test statistics

The aim of this paper is to propose “omnibus” testing procedures for potentially time-varying treatment effects, without making parametric assumptions on the shape of the hazard ratio. The idea is to combine evidence from both the average magnitude and shape of the hazard ratio function and construct test statistics that are powerful under both proportional hazards (henceforth denoted PH) and various non-PH alternatives.

3.1 A two-stage test

In the literature, there were developments on hypothesis testing procedures for the proportional hazards assumption, e.g., Lin et al. (2006), denoted by T_LZD. If one aims to test treatment effect H₀ while accounting for potential non-proportionality, a natural strategy is to construct a two-stage procedure as follows (henceforth denoted T^2stg),

• S1apply the test T_LZD for the PH assumption. Reject H₀, if the p-value is less than a pre-determined significance level α₁; otherwise, go to the second stage;
• S2apply the standard log-rank test for treatment effect. Reject H₀ if the p-value is less than another pre-determined significance level α₂.

This procedure is a straightforward extension of the log-rank test and T_LZD. Note that S1 tests the proportional hazards assumption, while S2 tests treatment effect given the proportional hazards assumption is plausible. The overall null hypothesis is rejected if either stage rejects the null. The overall type I error rate of this two-stage procedure depends on the correlation of two tests, but is bounded by α₁ + α₂ from above according to the Bonferroni inequality. The parameters α₁ and α₂ control how much type I error was assigned to the two tests. In practice, one can choose α₁ = α₂ = α/2 without prior information on the plausibility of proportional hazards, where α is the targeted overall significance level. The performance of this simple two-stage procedure will be compared with the standard log-rank test as well as other proposed methods discussed below.

3.2 Score statistics

Next, we construct a few test statistics based on combining score statistics for θ₀ and τ. Taking the derivatives of (4) with respect to θ₀ and τ, one obtains

$$U_{{\theta }_0}={\frac{\partial {\ell }_m(\beta ,{\theta }_0,\tau )}{\partial {\theta }_0}|}_{\beta =\widehat{\beta },{\theta }_0=0,\tau =0}={\mathbf{1}}^T\frac{\partial {\ell }_P(\widehat{\beta },{\theta }_0=0,\underset{\_}{\theta }=\mathbf{0})}{\partial \gamma },$$

and

$$U_{\tau }={\frac{\partial {\ell }_m(\beta ,{\theta }_0,\tau )}{\partial \tau }|}_{\beta =\widehat{\beta },{\theta }_0=0,\tau =0}=\frac{1}{2}\frac{\partial {\ell }_P(\widehat{\beta },{\theta }_0=0,\underset{\_}{\theta }=\mathbf{0})}{\partial {\gamma }^T}B{\mathrm{\sum }}^{-1}{B}^T\frac{\partial {\ell }_P(\widehat{\beta },{\theta }_0=0,\underset{\_}{\theta }=\mathbf{0})}{\partial \gamma }+\frac{1}{2}\text{tr}\left[\frac{{\partial }^2{\ell }_P(\widehat{\beta },{\theta }_{0}0,\underset{\_}{\theta }=\mathbf{0})}{\partial \gamma \partial {\gamma }^T}B{\mathrm{\sum }}^{-1}{B}^T\right],$$ (5)

where β̂ is the maximum partial likelihood estimate of the Cox model without treatment effect, i.e., the maximizer of the partial likelihood ℓ_P (β, θ₀ = 0, θ = 0). First, we look at the derivative with respect to θ₀. Denote S(β, θ₀, θ) = (∂/∂γ)ℓ_P (β, θ₀, θ), the k^th element of S(β̂, 0, 0) is then ${\sum }_{i}I(Y_i=t_k^o){\mathrm{\Delta }}_i\{S_i-{\sum }_j{S}_{j}exp({\widehat{\beta }}^T{X}_j)I(Y_j\ge t_k^o)/{\sum }_{j}exp({\widehat{\beta }}^T{X}_j)I(Y_j\ge t_k^o)\}$. It can be shown that the covariance matrix of S(β, θ₀, θ) is given by $V=I_{\gamma \gamma }-I_{\gamma \beta }{I}_{\beta \beta }^{-1}{I}_{\beta \gamma }$, where the Fisher information matrices are evaluated under the true parameter values. Thus, 1^TS(β̂, 0, 0) is in fact the usual partial likelihood score function evaluated under the null. The standard score test statistic for θ₀ can be written as

$$T_{LR}={\{{\mathbf{1}}^{T}S(\widehat{\beta },0,0)\}}^2/var\{{\mathbf{1}}^{T}S(\widehat{\beta },0,0)\}={I_0}^{-1}S{(\widehat{\beta },0,0)}^T\mathbf{1}{\mathbf{1}}^{T}S(\widehat{\beta },0,0),$$

which is a quadratic form of S(β̂, 0, 0) and converges to ${\chi }_1^2$ due to rank(11^T) = 1. Note here I₀ = var{1^TS(β̂, 0, 0)} = 1^TV 1 is exactly the efficient Fisher information for θ₀ under the Cox model. Thus, the standardized score test statistic T_LR converges to a ${\chi }_1^2$ distribution under the null hypothesis. Next, we look at the derivative with respect to τ. It has been shown that the variation of second term of (5) is negligible relative to the first term (Lin et al., 2006). The first term of (5) is a quadratic form of S(β̂, 0, 0). According to quadratic form theory, its limiting distribution is weighted sum of χ²’s, with weights determined by the eigenvalues of Σ. This suggests that the asymptotic behavior of the score function for τ is non-standard.

Remark 3

For the smoothing splines approach with first-order polynomials (Lin et al., 2006), the term BΣ⁻¹B^T simplifies to Σ as B = Σ = B^T in this case. They evaluated the score for τ at (β = β̃, θ₀ = θ̃₀, θ = 0) instead, where β̃ and θ̃₀ are their maximum likelihood estimates under the Cox model, because they are testing a different null hypothesis $H_0^{PH}$.

3.3 Combine scores for θ₀ and τ

To test H₀: θ₀ = 0, τ = 0, since the null hypothesis involves both θ₀ and τ, one needs to combine score functions with respect to θ₀ and τ (denoted as U_θ0 and U_τ, respectively), which reflect information from the average magnitude and shape of the hazard ratio function, respectively. Under regularity conditions, score functions for multiple parameters follow multivariate normal distribution asymptotically, and the standard approach is constructing linear combination of U_θ0 and U_τ weighted by the square root of the joint Fisher information matrix. However, this procedure does not work here, due to non-standard properties in testing variance components.

As discussed above, the parameter τ = 0 is on the boundary of its parameter space under the null. The dominating term of the score function with respect to τ converges to a weighted sum of ${\chi }_1^2$’s, instead of a Gaussian distribution. To overcome these challenges, we propose methods of combing two score functions to construct test statistics. Note that U_θ0 and U_τ are linear and quadratic forms of S(β̂, 0, 0), respectively. We propose combinations of them that are quadratic forms of S(β̂, 0, 0), whose asymptotic distribution can be derived conveniently.

The first test statistic T₁ is constructed by taking the sum of U_τ and $U_{{\theta }_0}^2$,

$$\begin{array}{l}{T}_1\equiv S^T(\widehat{\beta },0,0)B{\mathrm{\sum }}^{-1}{B}^{T}S(\widehat{\beta },0,0)+{({\widehat{I}}_0)}^{-1}{S}^T(\widehat{\beta },0,0)\mathbf{1}{\mathbf{1}}^{T}S(\widehat{\beta },0,0)\\ =S^T(\widehat{\beta },0,0)\left\{B{\mathrm{\sum }}^{-1}{B}^T+{({\widehat{I}}_0)}^{-1}\mathbf{1}{\mathbf{1}}^T\right\}S(\widehat{\beta },0,0),\end{array}$$ (6)

where Î₀ is an estimate of the efficient information for θ₀ in the usual Cox model. Note that T₁ is also a quadratic form of S(β̂, 0, 0), and thus its limiting distribution can be easily calculated. It converges to a weighted sum of ${\chi }_1^2$’s, with weights determined by eigenvalues of the matrix M₁=BΣ⁻¹B^T + (Î₀)⁻¹11^T. Using the Satterthwaite approximation, the limiting distribution can be further simplified. Our score statistic rejects the null hypothesis H₀ at the nominal level α if $T_1\ge k_1{\chi }_{\alpha ,v_1}^2$ where ${\chi }_{\alpha ,v}^2$ is a 100(1 − α) percentile of the ${\chi }_v^2$ random variable with degree of freedom v. Here, k₁ = tr(M₁V M₁V)/tr(M₁V), and v₁ = {tr(M₁V)}²/tr(M₁V M₁V), where V = ∂²ℓ_P {β̂, (θ₀, θ^T) = 0}/∂γ∂γ^T. The details on deriving the limiting distribution and its approximations are discussed in Appendix A.

The test statistic T₁ is a sum of two quadratic forms. However, these two parts are not independent, and taking the sum directly may not be optimal in terms of power, with potential power loss depending their correlation. We propose to remove the projection of S_τ on S_θ0, so that the modified score statistics for τ (denoted by subscript “mPH”, i.e., modified test for PH) is asymptotically independent to the score statistics for θ₀. Let

$$T_{\mathit{mPH}}\equiv S^T(\widehat{\beta },0,0)W^{T}B{\mathrm{\sum }}^{-1}{B}^{T}WS(\widehat{\beta },0,0),$$ (7)

where W = I_r×r−V 11^T/{1^TV 1}. The matrix W is constructed so that WS(β̂, 0, 0) and 1^TS(β̂, 0, 0) are asymptotically independent (see Appendix C). Note that T_mPH is also a quadratic form of S(β̂, 0, 0) that reflects evidence on proportionality, on the direction that is orthogonal to the average magnitude of hazard ratio. The degree of freedom of T_mPH depends on realizations of the data, and can be calculated by tr(V⁻¹W^TBΣ⁻¹B^TW).

We now construct the second test statistic by taking the sum of T_LR and T_mPH,

$$T_2\equiv T_{LR}+T_{\mathit{mPH}}=S^T(\widehat{\beta },0,0)\left\{W^{T}B{\mathrm{\sum }}^{-1}{B}^{T}W+{({\widehat{I}}_0)}^{-1}\mathbf{1}{\mathbf{1}}^T\right\}S(\widehat{\beta },0,0),$$ (8)

The test statistic T₂ is also a quadratic form, and we can obtain the approximate asymptotic distribution according to Appendix A. Our score statistic T₂ rejects the null hypothesis H₀ at the nominal level α if $T_2\ge k_2{\chi }_{\alpha ,v_2}^2$ where k₂ = tr(M₂V M₂V)/tr(M₂V), v₂ = {tr(M₂V)}²/tr(M₂V M₂V), and M₂ = W^TBΣ^{− 1}B^TW + (Î₀)⁻¹11^T.

Remark 4

More generally, one can consider the family of linear combinations of T_LR and T_mPH, e.g., using test statistics

$$T(\rho )=\rho T_{LR}+(1-\rho )T_{\mathit{mPH}},\text{where}0\le \rho \le 1,$$ (9)

where ρ determines the weights from two parts. The test statistic T(ρ) becomes the standard log-rank test when ρ = 0, and the modified test for proportionality when ρ = 1. The proposed test T₂ corresponds to ρ = 0.5. The optimal choice of tuning parameter ρ is not clear and we plan to investigate this family of test statistics in the future. Our simulation studies suggest that T₂ performs well in terms of power in finite samples.

3.4 Combination procedures based on p-values

We also explored a few other methods to combine information, e.g., Koziol and Perlman (1978), taking advantage of the fact that T_LR and T_mPH are asymptotically independent. For example, two commonly used procedures for combining independent tests are based on p-values, Fisher’s and Tippett’s procedures. Specifically, let P_LR and P_mPH denote p-values from T_LR and T_mPH respectively. The test statistics for Fisher’s procedure is

$$T_3=-2log{P}_{LR}-2log{P}_{\mathit{mPH}}.$$

Under H₀, it can be shown that T₃ follows ${\chi }_4^2$, and thus p-values can be calculated by $P_3=1-F_{{\chi }_4^2}(T_3)$, where $F_{{\chi }_4^2}$ is the cumulative distribution function of ${\chi }_4^2$. We reject the null when $T_3>{\chi }_{4,1-\alpha }^2$ at significance level α. On the other hand, Tippett’s procedure rejects the null when either P_LR or P_mPH is small, i.e., the test statistic is the minimum of two p-values

$$T_4=\mathit{min}(P_{LR},P_{\mathit{mPH}}).$$

Under (asymptotic) independence of two tests, one can show that the formula for p-values for the combined test is P₄ = 1 − (1 − T₄)². At significance level α, the rejection region is given by T₄ < 1 − (1 − α)^1/2.

Note that the two-stage test T^2stg described in Section 3.1 can also be viewed as a combination procedure based on p-values. However, the proposed T₃ and T₄ combines two test statistics that are asymptotically independent, while the two statistics of T_2stg are possibly correlated. The finite sample performance of these procedures will be evaluated in simulation studies.

3.5 Connection with previous literature

In the literature, there are two existing approaches most relevant to our proposed methods: Gray (1994) and Lin et al. (2006). However, there are substantial differences between their work and our proposed tests.

First, Gray (1994) used B-splines to model θ(t) and proposed Wald, score and likelihood ratio statistics based on penalized partial likelihood for fixed values of tuning parameter. Their approach is applicable to several hypothesis testing problems, including testing time-varying treatment effect H₀ (see Section 4 of their paper). However, it depends on a tuning parameter that controls the effective degree of freedom of splines. The tuning parameter affects the power of these tests substantially and is often difficult to choose in practice. If we use the same B-spline approach, our work can be viewed as extensions of Gray (1994) through a mixed effects model framework. In contrast, our proposed tests are automatic procedures that do not depend on tuning parameters, and are shown to be as or more powerful in finite samples (see the next section).

Second, Lin et al. (2006) proposed smoothing spline based score tests in extended Cox models. They discussed several hypothesis testing problems, including testing the proportional hazards null H_0,PH : θ(t) = θ₀ versus an alternative model with a time-varying hazard function. From a random effects model perspective, their null hypothesis can be represented via the variance component, i.e., H_0,PH : τ = 0. Although our development adapts some technical arguments from Lin et al. (2006), we target a different null hypothesis H₀ : θ(t) = 0, or equivalently H₀ : θ₀ = 0, τ = 0. Their approach is applicable only when the null hypothesis is represented via the variance component τ only, thus excluding the problem of testing H₀. Other than the fundamental differences in the null hypotheses of interest, the primary challenge of extending their approach to our problem is how to combine information from θ₀ and τ, and this is not straightforward given the non-standard nature of variance components. We proposed a few approaches to combine score statistics for θ₀ and τ, and this is one of the main contributions of this paper from a methodological perspective.

4. Numerical Studies

4.1 Simulations

To study the finite sample performance of the proposed tests, survival data of sample sizes n = 100 and n = 500 were generated from the extended Cox model (1) with a binary treatment indicator and no additional covariates. The baseline hazard function was a constant function, i.e., λ₀(t) = 1. The censoring distribution was the uniform distribution on [0, c] where c was chosen to yield censoring probability 30% for each scenario. We conducted extensive simulation studies with various choices of θ(t), corresponding to different shapes of hazard ratio functions. The shapes of θ(t) are shown in Figure 2, most of which were considered by Gray (1994) and Lin et al. (2006) up to scale changes.

For each simulated dataset, we compared our methods with the log-rank test (denoted T_LR), the two stage procedure with α₁ = α₂ = 0.025% as described in Section 3.1 (denoted T^2stg), and the score statistic of Gray (1994) with pre-selected degree of freedom (denoted $G_{S,df}^K$ with K knots and degree of freedom df). For the score statistic of Gray (1994), we considered four choices, with the number of knots K = 10 and 20, and degrees of freedom df = 1.5 and 5. The performances of the likelihood ratio and Wald statistics of Gray (1994) are similar to the score statistic, and thus we only reported results for their score statistics. We also reported power from the modified test for proportionality, T_mPH, since it is a valid test for H₀ with a correct type I error. However, we do not mean to compare its performance with other tests directly, as T_mPH summarizes evidence from non-constant shape of the hazard ratio only; rather our intention is to gain insights of how each method combines information from the magnitude and shape of the hazard ratio. We implemented the proposed test statistics T₁, T₂, T₃, T₄ using both B-splines with K = 20 knots and smoothing splines. The results were similar, and we only report the latter.

Table 1 summarizes results from our simulations. In terms of type I error, all test statistics maintained the nominal level of size (α = 0.05) approximately under the null hypothesis H₀. In terms of power, none of the test statistics is optimal in detecting all types of alternatives. It is well known that the log-rank test is most powerful for treatment effect under the PH assumption, but may lose power otherwise. The aim of our work is to propose new “omnibus” tests that do not lose much power compared to log-rank under the PH assumption and also have decent power to detect non-PH alternatives.

Table 1.

Type I error rates and power for the proposed tests versus alternatives in simulations. The testing procedures include standard log-rank test (T_LR), modified test for proportionality (T_mPH), the two-stage test (T^2stg), Gray’s score tests ( $G_{S,df}^K$ with K knots and degree of freedom df) and the proposed test statistics (T₁, T₂, T₃ and T₄).

θ(t)	n	TLR	TmPH	T2stg	$G_{S,1.5}^{10}$	$G_{S,5}^{10}$	$G_{S,1.5}^{20}$	$G_{S,5}^{20}$	T1	T2	T3	T4
H0: 0	100	0.058	0.049	0.059	0.056	0.051	0.057	0.061	0.056	0.052	0.055	0.059
	500	0.042	0.063	0.060	0.056	0.058	0.059	0.053	0.054	0.062	0.059	0.060
H0,PH: log 1.5	100	0.363	0.042	0.292	0.369	0.258	0.418	0.271	0.329	0.323	0.278	0.298
	500	0.971	0.053	0.933	0.966	0.905	0.964	0.912	0.943	0.946	0.932	0.934
L: 0.8t	100	0.350	0.221	0.369	0.421	0.373	0.444	0.424	0.491	0.428	0.407	0.373
	500	0.968	0.843	0.986	0.994	0.988	0.990	0.994	0.998	0.995	0.992	0.986
Q: −0. 5t(t − 2.6)	100	0.423	0.163	0.409	0.499	0.390	0.494	0.446	0.534	0.466	0.429	0.414
	500	0.990	0.636	0.987	0.995	0.991	0.993	0.991	0.996	0.993	0.992	0.987
E1: 0.25 exp(0.8t)	100	0.352	0.082	0.296	0.382	0.279	0.401	0.306	0.393	0.334	0.293	0.305
	500	0.968	0.316	0.954	0.980	0.950	0.971	0.954	0.981	0.971	0.969	0.956
E2: 0.7 exp(−t)	100	0.493	0.095	0.414	0.508	0.368	0.530	0.380	0.368	0.468	0.444	0.420
	500	0.990	0.285	0.991	0.997	0.988	0.994	0.981	0.975	0.995	0.993	0.991
$\text{Expit}:\frac{0.6exp(3.5t)}{1+exp(3.5t)}$	100	0.503	0.064	0.413	0.520	0.398	0.528	0.432	0.505	0.457	0.406	0.422
	500	0.995	0.151	0.993	1.000	0.983	0.991	0.987	0.995	0.993	0.991	0.993
Log1: 0.5 log(.75t)	100	0.449	0.393	0.557	0.525	0.549	0.518	0.550	0.231	0.614	0.619	0.561
	500	0.978	0.976	0.999	0.997	0.999	0.997	1.000	0.835	1.000	1.000	0.999
Log2: $\text{Log}2:0.5log\frac{2}{1+5t}$	100	0.165	0.263	0.275	0.234	0.255	0.223	0.279	0.348	0.314	0.300	0.283
	500	0.652	0.862	0.911	0.882	0.922	0.871	0.946	0.952	0.941	0.940	0.912
S: 1.5I (t < 1.0)	100	0.187	0.439	0.413	0.297	0.494	0.307	0.514	0.372	0.441	0.449	0.417
	500	0.760	0.996	0.997	0.996	0.998	0.987	0.999	0.990	0.998	0.998	0.997
C: 0.8 cos(2πt=2.7)	100	0.354	0.440	0.545	0.475	0.501	0.484	0.499	0.245	0.576	0.606	0.549
	500	0.949	0.981	0.999	0.998	0.999	0.994	0.997	0.933	0.999	0.999	0.999

We now compare power of various test statistics under both PH alternatives and a wide variety of non-PH alternatives. When the PH assumption holds and the true model is the Cox model (H_0,PH), the log-rank test was the most powerful as expected. Gray’s score tests performed well, particularly with low degree of freedom (df = 1.5), but lost power substantially with higher degree of freedom (df = 5). The proposed linear combination statistics T₁ and T₂ have slightly lower power compared to the log-rank test, but the differences are small. The proposed p-value based statistics T₃ and T₄ are less powerful than the linear combination tests from simulations.

Under non-PH alternatives, there is no universally best test according to Table 1. First, we compare power performance between two proposed statistics T₁ and T₂. Under several scenarios (L, Q, E1, Expit, Log2), T₁ has slightly higher power than T₂ by around 2% and 6%. On the other hand, T₂ outperforms T₁ in other settings (E2, Log1, S, C), but generally with a more substantial power gain that varies between 7% to as high as 38% (Log1). Thus, the statistic T₂ is considered “omnibus” in the sense that it has decent power against all types of alternatives and is our preferred choice, while T₁ is prone to very low power to detect certain types of alternatives. The substantial power gain of T₂ is likely due to the fact that the latter exploits orthogonality between information on the magnitude and shape of the hazard ratio function.

Next, we compare the proposed score statistic T₂ versus the log-rank test (T_LR), the modified PH test (T_mPH) and the two-stage procedure (T^2stg) under non-PH alternatives. Under many settings, T₂ outperforms both T_LR and T_two−stg. For example, under alternative curve Log2 and a sample size of 500, the power for T₂ is 61.4%, much higher than both T_LR (44.9%) and T^2stg (55.7%). Under some alternatives (E1, E2, Expit), the power of T₂ is lower than the log-rank test T_LR but only by very slight margins. Thus, the proposed test T₂ is generally comparable to or more powerful than T_LR, since it combines information from the shape of hazard functions. The proposed test can potentially pick up evidence of treatment effects even if both T_LR and TwoStg fail to suggest so. We also compared T₂ versus Gray’s score tests. The power of Gray’s score tests varies with tuning parameters, especially with the degree of freedom, which needs to be prespecified and can affect power performance considerably. Their score tests with low df ( $G_{S,1.5}^{10}$ and $G_{S,1.5}^{20}$) perform well when the hazard function is close to a constant or linear function but poorly otherwise, while the opposite holds for the tests with high df ( $G_{S,5}^{10}$ and $G_{S,5}^{20}$). The proposed test T₂ is often comparable or close to Gray’s statistics with the “better” choice of df in terms of power, and sometimes outperform all of them under certain alternatives (Log1 and C).

To summarize, the proposed test statistics, especially the preferred T₂, demonstrate decent power performances under various alternative hypotheses in simulations. Other testing procedures, such as the log-rank test, the two-stage procedure and Gray (1994)’s score tests, are often powerful against certain alternatives but may lose power substantially against others. In addition, T₂ does not depend on tuning parameters, making it an omnibus and desirable testing procedure to use in practice.

4.2 Application to HIVNET 012 Study

We demonstrate our proposed methods by analyzing our motivating example of infant survival in the HIVNET 012 Study mentioned in Section 1. In our data set, 310 women were assigned to the NVP group and 306 women to the AZT group. We exclude the second twins or more and stillbirth babies from the analysis. Mean CD4+ counts at the baseline for mothers in both groups were 482 and 465 (p = .41); mean log RNA viral copies with base 10 at visit 101 were 4.35 and 4.39 (p = .59); mean birth weights were 3080 kg and 3197 kg (p = 0.001), respectively. The total follow-up time is 18 months. The HIV-1 transmission risk and risk of death at the end of the study is 14.9 % and 23.5% (p = 0.007), and 9.3% and 12.7% (p = .18).

As we discussed in Section 1, the log-rank test does not show significance (p = 0.145), with estimated hazard ratio 0.701 (95 % CI: 0.43–1.13). However, the lack of statistical significance may be due to the fact that the log-rank test is not powerful when the PH assumption does not hold, which seemed to be the case in this application (Figure 6).

Next, we applied alternative tests, including weighted log-rank test, Gray’s test and the proposed tests. For weighted log-rank tests, we used weights corresponding to the Peto-Peto modification of the Wilcoxon statistic (Peto and Peto, 1972) considering the drug effect gradually disappeared over time, but the result is not significant (p = 0.125). We also tried weights from the G^ρ family (Harrington and Fleming, 1982) with different ρ’s, but the usual choice of ρ between 0 and 1 did not yield a significant result. Gray’s score tests yielded different results depending on tuning parameters such as degrees of freedom and numbers of knots. Specifically, p-values corresponding to df = 1.5, 3 and 5 are 0.073, 0.032 and 0.057, respectively, with K = 10 knots, and are 0.069, 0.032 and 0.053, respectively, with K = 20 knots. These results may be confusing to practitioners since different df led to different p-values, and it is not clear which df one should choose for this specific application. The proposed test T₂ suggested significant treatment effects (p = 0.015). To confirm the proportionality of the hazard ratio, we also applied the test and obtained p-value (p = 0.013), which suggested that the hazard ratio is time-varying and that the log-rank test is not optimal in this setting.

5. Discussion

We developed spline based score tests for time-varying treatment effects in an extended Cox model. The proposed approach is designed to test treatment effects when the proportional hazards assumption may not hold. These test statistics do not depend on tuning parameters and are easy to compute since they only require fitting the null model (Cox model). Simulation studies suggested that our methods gained power substantially compared to the log-rank test when the proportional hazards assumption does not hold.

There are some connections between the proposed tests and the widely used weighted log-rank test. As shown in Appendix B, the family of quadratic form tests Q = S^TUS, which include the weighted log-rank test, Lin et al.’s proportionality test and the proposed tests, are equivalent to a linear combination of several weighted log-rank tests with weights determined by the eigenvectors of the matrix U. The weighted log-rank test (when U has rank 1) is powerful when the chosen weights are close to the true hazard ratio functions, but may lose power substantially otherwise. In contrast, the proposed tests combine several plausible weighted log-rank tests, some of which reflect information on the smoothness of the hazard ratio function, and thus provide omnibus testing procedures that are powerful to detect a variety of alternatives.

There are a few areas for future research. As discussed in Section 2.2, one main challenge is how to combine scores for parameters θ₀ and τ, given the non-standard nature of variance components testing. While the two proposed statistics are natural choices, they are not necessarily optimal in terms of power. There may be other ways to combine the score statistics. For example, one may explore the family of linear combinations and find an optimal weight within this family, or even identify the optimal statistics among nonlinear combinations if possible. The proposed methods can also be applied to other models and setting to detect a nonlinear trend. Although we focused on an extended Cox model, our method can be extended to other models such as an additive hazards models. Finally, one could also consider generalized Wald or partial likelihood ratio type approaches, as suggested by the reviewers. These approaches require first obtaining an estimate θ̂(t), which depends on the choice of the smoothing parameter τ. The tuning parameters are often chosen by adaptive approaches such as cross validation, and it is challenging to account for the uncertainty of choosing τ in the inference for θ(t). The (generalized) likelihood ratio test has been developed for linear mixed models (Fan et al., 2001; Crainiceanu and Ruppert, 2004), but not on generalized linear mixed models for discrete outcomes and mixed models for censored time-to-event data. Actually this is one of the main reasons that score tests are more popular in hypothesis testing for nonlinear mixed models.

One reviewer raised an interesting question of deriving a method to differentiate three hypotheses: the null, constant or truly time-varying effect of treatment. Two step procedures will be needed to accomplish this, as standard hypothesis testing is designed to distinguish two hypotheses only. For example, one can first apply the test of Lin et al. (2006), which differentiates “null or constant effect” vs. time-varying effect. If the null was not rejected in the first step, then apply the log-rank test to further differentiate null vs. constant effect. Alternatively, one can first apply the proposed test statistics, which differentiates null vs. “constant or time-varying effect.” If the null was rejected, then apply the test of Lin et al. (2006) to further differentiate constant vs. time-varying effect.