Combining Biomarkers to Optimize Patient Treatment Recommendations

Summary

Markers that predict treatment effect have the potential to improve patient outcomes. For example, the Oncotype DX ^® Recurrence Score^® has some ability to predict the benefit of adjuvant chemotherapy over and above hormone therapy for the treatment of estrogen-receptor-positive breast cancer, facilitating the provision of chemotherapy to women most likely to benefit from it. Given that the score was originally developed for predicting outcome given hormone therapy alone, it is of interest to develop alternative combinations of the genes comprising the score that are optimized for treatment selection. However most methodology for combining markers is useful when predicting outcome under a single treatment. We propose a method for combining markers for treatment selection which requires modeling the treatment effect as a function of markers. Multiple models of treatment effect are fit iteratively by upweighting or “boosting” subjects potentially misclassified according to treatment benefit at the previous stage. The boosting approach is compared to existing methods in a simulation study based on the change in expected outcome under marker-based treatment. The approach improves upon methods in some settings and has comparable performance in others. Our simulation study also provides insights as to the relative merits of the existing methods. Application of the boosting approach to the breast cancer data, using scaled versions of the original markers, produces marker combinations that may have improved performance for treatment selection.

1. Introduction

Discovering and describing heterogeneity in treatment effects across patient subgroups has emerged as a key objective in clinical trials and drug development. If the treatment effect can be predicted given marker values such as biological measurements and clinical characteristics, providing patients and clinicians with these marker values can help them make more informed treatment decisions. For example, the Oncotype DX Recurrence Score is a leading marker for predicting the benefit of adjuvant chemotherapy over and above tamoxifen among breast cancer patients with estrogen receptor-positive (ER-positive) tumors (Albain al., 2010a). The Recurrence Score is a proprietary combination of expression levels of 21 genes (16 cancer-related and 5 reference) measured in breast cancer tumor tissue, and is used to identify a subgroup of patients for whom the likelihood of benefitting from adjuvant chemotherapy is small. These patients can therefore avoid unnecessary and potentially toxic treatment.

There is a large literature on statistical methods for combining markers, but the vast majority of them have focused on combining markers for predicting outcome under a single treatment (for example, Etzioni et al. (2003); Pepe et al. (2005); Zhao et al. (2011)). However, combinations of markers for risk prediction or classification under a single treatment are not optimized for treatment selection. Being at high risk for the outcome does not necessarily imply a larger benefit from a particular treatment (Henry and Hayes (2006); Janes et al. (2011, 2013a)). In particular, the Recurrence Score was originally developed for predicting the risk of disease recurrence or death given treatment with tamoxifen alone (Paik et al., 2004), and was later shown to have value for predicting chemotherapy benefit (Paik et al. (2006); Albain at al. (2010a, b)). Therefore, it is of interest to explore alternative combinations of gene expression measures that are optimized for treatment selection.

Statistical methods for combining markers for treatment selection are being developed (see Gunter et al. (2007); Brinkley et al. (2010); Cai et al. (2011); Claggett et al. (2011); Lu et al. (2011); Foster et al. (2011); Gunter et al. (2011a); Zhang et al. (2012); Zhao et al. (2012)). A simple approach uses generalized linear regression to model the expected disease outcome as a function of treatment and markers, including an interaction between each marker and treatment (Gunter et al. (2007); Cai et al. (2011); Lu et al. (2011); Janes et al. (2013b)). This model is difficult to specify, particulary with multiple markers as in the breast cancer example, and hence an approach that is robust to model mis-specification is warranted. This is a key motivation for our approach to combining markers for treatment selection. We call our approach “boosting” since it is a natural generalization of the Adaboost (Adaptive boosting) method used to predict disease outcome under a single treatment (Freund and Schapire (1997); Friedman et al. (2000)).

Candidate approaches for combining markers should be compared with respect to a clinically relevant performance measure, and yet a few of the existing studies have performed such comparisons. In a simulation study and in our analysis of the breast cancer data, we evaluate methods for combining markers using the cardinal measure of model performance: the improvement in expected outcome under marker-based treatment (Song and Pepe (2004); Brinkley et al. (2010); Gunter et al. (2011b); Zhang et al. (2012); Janes et al. (2013a, b)). To the best of our knowledge, only two other papers (Qian and Murphy (2011); Zhang et al. (2012)) have used this approach for evaluating new methodology.

The structure of the paper is as follows. In Section 2, we introduce our approach to evaluating marker combinations for treatment selection and describe the boosting method. A simulation study used to evaluate the boosting approach in comparison to other candidate approaches is described in Section 3. Section 4 describes our application of the boosting approach to the breast cancer data. We conclude with a discussion of our findings and further research topics to pursue.

2. Methods

2.1 Context and notation

Let D be a binary indicator of an adverse outcome following treatment which we refer to as “disease”. In the breast cancer example, D indicates death or cancer recurrence within 5 years of study enrollment. We assume that D captures all the consequences of treatment, such as subsequent toxicity, morbidity, and mortality; more general settings are addressed in Section 5. Suppose that the task is to decide, for each individual patient, between two treatment options denoted by T, where we call T = 1 “treatment” and T = 0 “no treatment”. We assume that the default treatment strategy is to treat all patients. The marker, Y ∈ ℝ^p, may be useful for identifying a subgroup of patients who can avoid treatment. This setup is motivated by the breast cancer context, wherein adjuvant chemotherapy in addition to hormone therapy (T = 1) is the standard of care and markers are used to identify women who can forego adjuvant chemotherapy (T = 0). The setting where T = 0 is the default and Y is used to identify a subgroup to treat can be handled by simply switching treatment labels (T = 0 for treatment and 1 for no treatment). We assume that the data ${\{D_i,T_i,Y_i\}}_{i=1}^n$ come from the ideal setting for evaluating treatment efficacy, a randomized clinical trial comparing T = 0 to T = 1 where Y is measured at baseline and D is a clinical outcome observed for all subjects.

2.2 Measures for evaluating marker performance

Let Δ(Y) ≡ P(D = 1|T = 0, Y) − P(D = 1|T = 1, Y) denote the marker-specific treatment effect. Given marker values Y for all subjects, the treatment policy that minimizes the population disease rate is to recommend no treatment if ϕ(Y) = 1{Δ(Y) ≤ 0} = 1, where 1(·) is the indicator function (Vickers et al. (2007); Brinkley et al. (2010); Lu et al. (2011); Zhang et al. (2012)). In the breast cancer example, this policy would recommend hormone therapy alone to patients with negative treatment effects and adjuvant chemotherapy to patients with positive treatment effects. The function Δ(Y) is therefore the combination of markers that we seek, and ϕ(Y) is the associated treatment rule. Given data {D_i, T_i, Y_i} for i = 1, …, n subjects, we estimate the marker-specific treatment effect by fitting a model for P(D = 1|T, Y), termed the “risk model”, and calculate Δ̂(Y) = P̂(D = 1|T = 0, Y) − P̂(D = 1|T = 1, Y) and ϕ̂(Y) = 1{Δ̂(Y) ≤ 0}.

We characterize the performance of an arbitrary estimated treatment rule ϕ̂(Y) by evaluating the benefit of marker-based treatment (Song and Pepe (2004); Brinkley et al. (2010); Gunter et al. (2011b); Zhang et al. (2012); Janes et al. (2013a, b)). This is measured by the difference in the disease rate under marker-based treatment assignment versus the default strategy of providing treatment to all patients:

$$\begin{array}{l}\theta \{\widehat{\varphi }(Y)\}\equiv P(D=1\mid T=1)\\ -[P\{D=1\mid T=0,\widehat{\varphi }(Y)=1\}P\{\widehat{\varphi }(Y)=1\}+P\{D=1\mid T=1,\widehat{\varphi }(Y)=0\}P\{\widehat{\varphi }(Y)=0\}]\\ =[P\{D=1\mid T=1,\widehat{\varphi }(Y)=1\}-P\{D=1\mid T=0,\widehat{\varphi }(Y)=1\}]\times P\{\widehat{\varphi }(Y)=1\}.\end{array}$$

In the breast cancer example, θ denotes the reduction in the 5-year death or recurrence rate under marker-based treatment; in general, a higher value of θ indicates greater marker value. Using the standard empirical measure ${\mathbb{P}}_n(\delta )\equiv {\displaystyle \sum _{i=1}^n}{n}^{-1}{\delta }_i$, θ is estimated empirically as follows:

$$\widehat{\theta }\{\widehat{\varphi }(Y)\}=\left[\frac{{\mathbb{P}}_n\mathbf{1}\{D=1,T=1,\widehat{\varphi }(Y)=1\}}{{\mathbb{P}}_n\mathbf{1}\{T=1,\widehat{\varphi }(Y)=1\}}-\frac{{\mathbb{P}}_n\mathbf{1}\{D=1,T=0,\widehat{\varphi }(Y)=1\}}{{\mathbb{P}}_n\mathbf{1}\{T=0,\widehat{\varphi }(Y)=1\}}\right]\times {\mathbb{P}}_n\mathbf{1}\{\widehat{\varphi }(Y)=1\}.$$

Another important measure of the population performance of the marker is the rate of incorrect treatment recommendations, which we call the misclassification rate of treatment benefit, MCR_TB{ϕ̂(Y)} ≡ P{ϕ(Y) ≠ ϕ̂(Y)}, and estimate by ${\widehat{\text{MCR}}}_{\text{TB}}\{\varphi (Y)\}={\mathbb{P}}_n\mathbf{1}\{\varphi (Y)\ne \widehat{\varphi }(Y)\}$. Similar measures have been used by Foster et al. (2011) and Lu et al. (2011). Although this measure can not be evaluated in practice since Δ(Y) is unknown, it can be evaluated in simulated data where Δ(Y) is known.

2.3 The boosting method of combining markers for treatment selection

A simple approach for estimating Δ(Y) is to use a generalized linear model for the outcome, D, as a function of markers, Y, and treatment, T, including interactions between each marker and treatment. That is, to stipulate that

$$h\{P(D=1\mid T,Y)\}=\eta (T,Y),$$ (1)

where the linear predictor η(T, Y) = Ỹβ₁ + TỸβ₂, Ỹ = (1^T, Y^T)^T, β₁ and β₂ are (p + 1)-dimensional vectors of regression coefficients for the markers’ main effects and interactions with treatment, respectively, and h is a link function. The logit link is the most common choice for a binary outcome. This risk model, if correctly specified, produces the combination of markers, Δ(Y), with optimal performance, that is, θ{ϕ(Y)}. However if the risk model is mis-specified, it will produce a biased estimate of treatment effect, resulting in a suboptimal combination of markers and rule for assigning treatment. With multiple markers, the likelihood of risk model mis-specification is increased. Our method seeks to improve upon logistic regression by providing an estimate of treatment effect, and a combination of markers, that is more robust to risk model mis-specification.

To achieve this goal, we adopt the idea of Adaboost, which iteratively fits classifiers, at each stage assigning higher weights to subjects whose outcomes are misclassified at the previous stage in order to minimize classification error. Analogously, we repeatedly fit a “working model” for P(D = 1|T, Y), and at each stage give more weight to subjects who lie close to the decision boundary, Δ(Y) = 0, who have greater potential to be recommended the incorrect treatment. In other words, we extend Adaboost from the classification setting, where the outcome to be predicted is D, to the treatment selection setting, where the outcome is 1{Δ(Y) ≤ 0}. The added complexity is that 1{Δ(Y) ≤ 0} is not directly observable. Details of the boosting algorithm are given below.

Boosting algorithm

1. With initial weight $w_i^{(0)}=w^{(0)}(Y_i)$ for subject i, i = 1, …, n, fit the working risk model and calculate P̃⁽⁰⁾(D = 1|T = t, Y), t = 0, 1 and Δ̃⁽⁰⁾(Y) = P̃⁽⁰⁾(D = 1|T = 0, Y) − P̃⁽⁰⁾(D = 1|T = 1, Y).

2. Update weights according to $w_i^{(1)}=w_i^{\ast (1)}/{\displaystyle \sum _{i=1}^n}{w}_i^{\ast (1)}$, where $w_i^{\ast (1)}=min[\stackrel{\sim }{w}\{{\stackrel{\sim }{\mathrm{\Delta }}}^{(0)}(Y_i)\},{\mathrm{C}}_{\mathrm{M}}]$, for w̃(u) decreasing in |u| and a specified maximum weight C_M. In our simulations, we use $\stackrel{\sim }{w}\{{\stackrel{\sim }{\mathrm{\Delta }}}^{(0)}(Y_i)\}={\mid {\stackrel{\sim }{\mathrm{\Delta }}}^{(0)}(Y_i)\mid }^{-\frac{1}{3}}$ and C_M = 500. This upweights subjects with small |Δ̃⁽⁰⁾(Y)| and limits the maximum size of the weights.

3. Re-fit the working model with updated weights $w_i^{(1)}$ to obtain P̃⁽¹⁾(D = 1|T = t, Y), t = 0, 1 and Δ̃⁽¹⁾(Y_i) = P̃⁽¹⁾(D = 1|T = 0, Y_i) − P̃⁽¹⁾(D = 1|T = 1, Y_i) for all subjects.

4. Repeat steps (2)–(3) until either a pre-specified convergence criterion is satisfied or a specified maximum number of iterations (M_max) is reached. In our simulations, we set M_max = 500 as an upper limit on the number of iterations that would be necessary.

5. After the last iteration, denoted by M ≤ M_max, we have {P̃⁽¹⁾(D = 1|T = t, Y_i), …, P̃^(M)(D = 1|T = t, Y_i)}, t = 0, 1 and {Δ̃⁽¹⁾(Y_i), …, Δ̃^(M)(Y_i)} for i = 1, …, n. The estimated disease rate and treatment effect for subject i are $\widehat{P}(D_i=1\mid T_i=t,Y_i)=M^{-1}{\displaystyle \sum _{m=1}^M}{\stackrel{\sim }{P}}^{(m)}(D_i=1\mid T_i=t,Y_i)$ for t = 0, 1, and $\widehat{\mathrm{\Delta }}(Y_i)=M^{-1}{\displaystyle \sum _{m=1}^M}{\stackrel{\sim }{\mathrm{\Delta }}}^{(m)}(Y_i)$, and the estimated treatment rule is ϕ̂(Y_i) = 1{Δ̂Y_i) ≤ 0}.

6. Given a new subject with covariate Y⁰, say in an independent test data set, we apply the set of working risk models in (5) and calculate Δ̃^(m)(Y⁰) for m = 1, …, M. The estimated treatment effect is $\widehat{\mathrm{\Delta }}(Y^0)=M^{-1}{\displaystyle \sum _{m=1}^M}{\stackrel{\sim }{\mathrm{\Delta }}}^{(m)}(Y^0)$ and ϕ̂(Y⁰) = 1{Δ̂(Y⁰) ≤ 0}.

We explore use of the linear logistic regression model (1) and a binary classification tree (Breiman et al., 1984) as working models. However, the boosting method applies to any arbitrary model for P(D = 1|T, Y). Choice of the weight function, w̃(u), maximum weight, C_M, and algorithm stopping rule are discussed in Web appendix A. With the logistic working model, we stop the iterations when ||β̃^(k) − β̃^(k−1)|| ≤ 10⁻⁷, where β̃^(k) is the vector of estimated regression coefficients at the k^th iteration, or when M = M_max; and with the classification tree working model, we stop the iterations when M = M_max.

3. Simulation study

A simulation study was performed to compare the boosting method to existing approaches for combining markers for treatment selection. The boosting method is compared to four comparator approaches: 1) using Adaboost (Friedman et al. (2000)) to combine classification trees for predicting disease outcome under each treatment separately; 2) fitting a classification tree to both treatment groups including all marker-by-treatment interactions as predictors; 3) the classic logistic regression approach which fits model (1) using maximum likelihood; and 4) the approaches of Zhang et al. (2012) that maximize the Inverse Probability Weighted (IPW) or Augmented Inverse Probability (AIPW) estimators of θ.

3.1 Comparator methods for combining markers

3.1.1 Applying Adaboost separately to each treatment group

A natural approach is to use a risk model to combine markers to predict outcome under each treatment separately. We consider the Adaboost algorithm (Freund and Schapire (1997); Friedman et al. (2000)) which combines predictions across multiple binary classification trees (Breiman et al., 1984) (“base trees” (Hastie et al., 2001)). Hereafter this is referred to as the “Adaboost trees” method. Each base tree is built by assigning higher weights to subjects that are misclassified at the previous stage. The associated risk model for each treatment group is a function of individual markers and, potentially, interactions between markers. We use Friedman et al.’s method (Friedman et al., 2000) for estimating P(D = 1|T, Y). Adaboost trees is implemented by the R function ada (R package ada (Culp et al., 2012)) using the following default settings: exponential loss function, discrete boosting algorithm, and 500 base trees. Since Adaboost trees is a non-parametric approach, the obtained combination of markers is expected to be more robust than logistic regression. However, fitting a separate classifier to each treatment group may not yield the optimal marker combination for treatment selection.

3.1.2 A single classification tree with marker-by-treatment interactions

An alternative nonparametric approach is to fit a single classification tree to both treatment groups including {T, TY₁, …, TY_p, (1 − T)Y₁, …, (1 − T)Y_p} as predictors. Using this classification tree, P(D = 1|T, Y) can be estimated using the empirical proportion of D = 1 observations in each terminal node. We use the R function rpart (R package rpart (Therneau et al., 2012)) with default settings: the minimal number of observations required to split is 20, the minimum number of observations in any terminal node is 7, and the maximal number of nodes prior to terminal node is 30. We do not prune the tree to stabilize the probability estimates (Provost and Domingos (2003); Chu et al. (2011)), but these estimates are improved by averaging across multiple tree classifiers (Chu et al., 2011).

3.1.3 Maximizing the IPW or AIPW estimators of θ

Recently, Zhang et al. (2012) proposed an approach that finds a combination of markers by directly maximizing the mean outcome (in our context, minimizing the disease rate) under marker-based treatment. This is equivalent to maximizing θ̂, the estimated decrease in disease rate under marker-based treatment. Zhang et al. (2012) consider maximizing both IPW and AIPW estimators.

Briefly, let D(t) denote the potential disease outcome under treatment t. For arbitrary treatment rule g : Y ↦ {0, 1} (in our context, assigning no treatment), the goal is to estimate the optimal treatment rule defined by $g^{\text{opt}}(Y)=\underset{g\in \mathcal{G}}{argmin}E\{D(g)\}=\mathbf{1}\{\mathrm{\Delta }(Y)\le 0\}$, where D(g) ≡ D(1){1 − g(Y)} + D(0)g(Y). Given a parametric working risk model P(D = 1|T, Y ; β) parameterized by finite-dimensional parameter β, let η = η(β) denote a scaled version of β satisfying ||η|| = 1 with ||·|| denoting the ℓ₂-norm. Treatment rules in this class of risk models are written g(Y, η). The scaling is used to ensure that the solution ${\eta }^{\text{opt}}\equiv \underset{\eta }{argmin}Q(\eta )$, where Q(η) ≡ E[D{g(Y, η)}], is unique. Specifically, η^opt is estimated by minimizing the IPW or AIPW estimators of Q(η) as follows:

$$\text{IPWE}(\eta )={\mathbb{P}}_n\{\frac{C_{\eta }D}{{\pi }_c(Y;\eta ,\widehat{\gamma })}\},$$ (2)

$$\text{AIPWE}(\eta )={\mathbb{P}}_n\{\frac{C_{\eta }D}{{\pi }_c(Y;\eta ,\widehat{\gamma })}-\frac{C_{\eta }-{\pi }_c(Y;\eta ,\widehat{\gamma })}{{\pi }_c(Y;\eta ,\widehat{\gamma })}m(Y;\eta ,\widehat{\beta })\},$$ (3)

where Ỹ.= (1,Y), $\pi (Y;\gamma )=P(T=1\mid Y;\gamma )=\frac{e^{\stackrel{\sim }{Y}\gamma }}{1+e^{\stackrel{\sim }{Y}\gamma }}$ is a known or estimated probability of treatment (the “propensity score”), π_c(Y ; η, γ̂) = π(Y ; γ̂)^T + {1 − π(Y ; γ̂)}^1−T, C_η = T {1 − g(Y, η)} + (1 − T)g(Y, η) is the treatment recommend by the rule g(Y, η), and m(Y ; η, β̂) = P(D = 1|T = 1, Y ; β̂){1 − g(Y, η)} + P(D = 1|T = 0, Y ; β̂)g(Y, η) is the model-estimated disease rate under g(Y, η). In our randomized trial setting, the propensity score model is known by design. The IPW estimator (2) thus reduces to the empirical disease rate under marker-based treatment. The AIPW estimator (3) is more efficient in large samples. Maximizing (2) or (3) therefore yields the marker combination with the highest IPW or AIPW θ̂{ϕ̂(Y)} in the training data within the class of the working risk model. However, when the working model is mis-specified, this combination may perform poorly, and it is in this setting where the boosting approach may generate marker combinations with closer-to-optimal performance.

To implement the approach, we find η̂^opt that minimizes IPWE(η) or AIPWE(η) under the linear logistic working model (1) where η = β/||β||. Under this model, 1{Δ(Y) ≤ 0} is equivalent to 1{Ỹη ≤ 0}, and so the class of treatment rules is 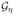= {g(Ỹ ; η) = 1{Ỹη ≤ 0}, ||η|| = 1, Ỹ = (1, Y₁, …, Y_p)}. Following Zhang et al. (2012), the R function genoud (R package rgenoud (Mebane, Jr. and Sekhon, 2011)) is utilized to minimize IPWE(η) (2) or AIPWE(η) (3) using the genetic algorithm (Sekhon and Mebane, Jr., 1998).

3.2 Simulation set-up

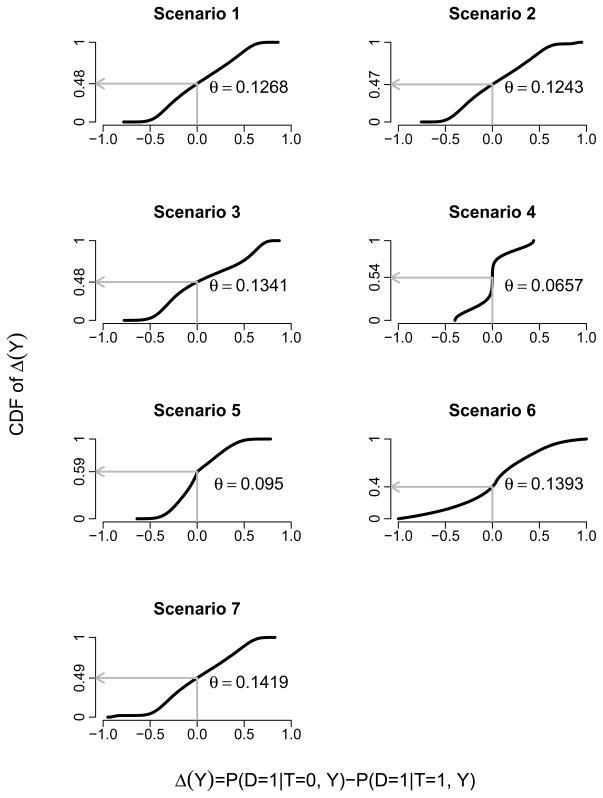
We generate simulated data sets with 500 or 5,000 observations in the following fashion. Binary treatment indicators T ~ Bernoulli (0.5). In most scenarios we generate three independent continuous markers Y₁, Y₂, and Y₃ (Y = (Y₁, Y₂, Y₃)) each following a standard normal distribution; exceptions are noted below. The binary outcome D ~ Bernoulli {P(D = 1|T, Y)}. The risk model P(D = 1|T, Y) varies among the seven scenarios as shown in Table 1 and described below. Figure 1 displays the distribution of Δ(Y) for each scenario. The linear logistic regression model (1) and the classification tree including {T, TY, (1 − T)Y} as predictors are used as working models for the boosting method.

Table 1.

True risk models and marker distributions for the seven simulation scenarios. The linear logistic regression model logitP(D = 1|T, Y) = Ỹβ₁ + TỸβ₂, with Ỹ = (1, Y), and the classification tree including {T, TY, (1 − T)Y} as predictors are evaluated as working models in all scenarios.

Scenario		True risk model	Marker distribution
The linear logistic working model is correctly specified.	1	logit P(D = 1|T, Y) = 0.3 + 0.2Y1 − 0.2Y2 − 0.2Y3 + T(−0.1 − 2Y1 − 0.7Y2 − 0.1Y3)	Y1, Y2, and Y3 are independent N(0, 1)
	2	logit P(D = 1|T, Y) = 0.3 + 0.2Y1 − 0.2Y2 − 0.2Y3 + T(−0.1 − 2Y1 − 0.7Y2 − 0.1Y3)	Same as Scenario 1 except for 2% of high leverage observations where Y1 ~ Uniform (8, 9)
Link function in the linear logistic working model is incorrectly specified.	3	log{−logP(D = 1|T, Y)} = −0.7 − 0.2Y1 − 0.2Y2 + 0.1Y3 + T(0.1 + 2Y1 − Y2 − 0.3Y3)	Same as Scenario 1
Link function and main effects in the linear logistic working model are incorrectly specified.	4	$log\{-\text{log}P(D=1\mid T,Y)\}=2-1.5Y_1^2-1.5Y_2^2+3Y_1{Y}_2+T(-0.1-Y_1+Y_2)$	Y1, and Y2 are independent Uniform (−1.5, 1.5)
Main effects and interactions are incorrectly specified in the linear logistic working model.	5	$\text{logit}P(D=1\mid T,Y)=-0.1-0.2Y_1+0.2Y_2-0.1Y_3+Y_1^2+T(-0.5-2Y_1-Y_2-0.1Y_3+2Y_1^2)$	Same as Scenario 1
	6	logit P(D = 1|T, Y) = 0.1 − 0.2Y1 + 0.2Y2 − Y1Y2 + T(−0.5 − Y1 + Y2 + 3Y1Y2)
Linear logistic working model is mis-specified for outlying observations.	7	$P(D=1\mid T,Y)=\mathbf{1}\{Y_1<8\}\frac{1}{1+e^{-\eta }}+\mathbf{1}\{Y_1\ge 8\}\left(1-\frac{1}{1+e^{-\eta }}\right)$, where η = 0.3 + 0.2Y1 − 0.2Y2 − 0.2Y3 + T(−0.1 − 2Y1 − 0.7Y2 − 0.1Y2)	Same as Scenario 2

Figure 1.

Distribution of the marker-specific treatment effect, Δ(Y) = P(D = 1|T = 0, Y)−P(D = 1|T = 1, Y), for each of the seven simulation scenarios. The proportion of individuals with negative treatment effects is indicated on the Y-axis, and θ = [P{D = 1|T = 1, ϕ(Y) = 1} − P{D = 1|T = 0, ϕ(Y) = 1}] × P{ϕ(Y) = 1}, measuring the impact of marker-based treatment assignment, is shown.

Simulation scenarios

• Scenario 1. The true risk model is linear logistic where Y₁, Y₂, and Y₃ have strong, intermediate, and weak interactions with treatment: logit P(D = 1|T, Y) = 0.3 + 0.2Y₁ − 0.2Y₂ −0.2Y₃ + T(−0.1 − 2Y₁ − 0.7Y₂ − 0.1Y₃). The marker combination obtained by fitting the linear logistic working model with maximum likelihood estimation (MLE) is expected to achieve the best performance. However, it is of interest to determine the extent to which other methods produce comparable results.

• Scenario 2. The true risk model is the same as in Scenario 1, but now Y₁ has high leverage points. Specifically, a random 2% of Y₁ values are replaced with draws from a Uniform (8, 9) distribution. This scenario is used to compare the performance of the approaches that use the correct linear logistic working model in the context of high leverage observations.

• Scenario 3. The true risk model is log{−log P(D = 1|T, Y)} = −0.7 − 0.2Y₁ − 0.2Y₂ + 0.1Y₃ + T(0.1 + 2Y₁ − Y₂ − 0.3Y₃), where Y₁, Y₂, and Y₃ have strong, intermediate, and weak interactions with treatment. The linear predictor of the linear logistic working model is correct but the link function is incorrect. This scenario is used to compare the robustness of the boosting approach to other approaches in the context of minor working model mis-specification.

• Scenario 4. The true risk model is $log\{-logP(D=1\mid T,Y)\}=2-1.5Y_1^2-1.5Y_2^2+3Y_1{Y}_2+T(-0.1-Y_1+Y_2)$. Y₁ and Y₂ follow a Uniform (−1.5, 1.5) distribution. The link function and main effects of the linear logistic working model are incorrectly specified, the latter due to omission of quadratic and marker-by-marker interaction terms, but the interaction terms are correct. This scenario is chosen for its similarity to the first scenario in Zhang et al. (2012) who found that, in a continuous outcome setting, maximizing the IPW or AIPW estimators of θ yielded substantial improvement over standard linear regression.

• Scenario 5. The true risk model is $\text{logit}P(D=1\mid T,Y)=-0.1-0.2Y_1+0.2Y_2-0.1Y_3+Y_1^2+T(-0.5-2Y_1-Y_2-0.1Y_3+2Y_1^2)$ including a non-linear main effect and interaction of Y₁ with treatment. The linear logistic working model mis-specifies these Y₁ effects, but the classification tree working model should be able to detect them.

• Scenario 6. The true risk model is a logistic regression model including an interaction between Y₁ and Y₂ where Y₁, Y₂ and Y₁Y₂ have intermediate, intermediate, and strong interactions with treatment: logit P(D = 1|T, Y) = 0.1 − 0.2Y₁ + 0.2Y₂ − Y₁Y₂ + T(−0.5 − Y₁ + Y₂ + 3Y₁Y₂). The linear logistic working model does not include Y₁Y₂ and TY₁Y₂ interaction terms whereas a classification tree working model does allow for them.

• Scenario 7. The true risk model is the same linear logistic model as in Scenario 1 except for the presence of 2% outlying observations. Specifically, for a random 2% sample, Y₁ is replaced with a draw from a Uniform (8, 9) distribution and D is replaced with 1 − D.

For each scenario, 1000 data sets are generated and used as training data to build a prediction model and treatment assignment rule, ϕ̂(Y) = 1{Δ̂(Y) ≤ 0}. To avoid overoptimism associated with fitting and evaluating the risk model using the same data, a single large independent test data set with n = 10⁵ observations is generated and used to evaluate the performance of the fitted treatment rule, θ{ϕ̂(Y)}. Mean and Monte-carlo standard deviation (SD) of θ{ϕ̂(Y)} and mean MCR_TB{ϕ̂(Y)} are reported. The performance of the true treatment rule, θ{ϕ(Y)}, is calculated as an average of θ̂{ϕ(Y)} over 100 Monte-carlo simulations where each θ̂{ϕ(Y)} is obtained using n = 3 × 10⁷ observations.

3.3 Results of the simulation study

Tables 2 and 3 summarize the simulation results for sample sizes n = 500 and n = 5000, respectively. The performances of marker combinations obtained using the following methods are compared: Logistic regression with maximum likelihood estimation (hereafter “linear logistic MLE”), the boosting method described in Section 2.3 with linear logistic working model (“linear logistic boosting”), maximizing the IPW or AIPW estimators of θ as proposed by Zhang et al. (2012) (“maximizing IPWE or AIPWE of θ”), a single classification tree with marker-by-treatment interactions (“single classification tree”), the boosting method with a classification tree working model including marker-by-treatment interactions (“classification tree boosting”), and applying Adaboost trees to each treatment group separately (“separate Adaboost”). For each scenario, the method with the highest mean θ is marked in bold.

Table 2.

Results of the simulation study with sample size n = 500. Marker combinations obtained using the following methods are compared: Logistic regression with maximum likelihood estimation (MLE), the boosting method of Section 2.3 with linear logistic working model, maximizing the IPW and AIPW estimators of θ as described by Zhang et al. (2012), a single classification tree with interactions between markers and treatment, the boosting method with classification tree working model, and applying Adaboost trees to each treatment group separately. Mean and Monte Carlo standard deviation (SD) of θ are shown, along with the mean misclassification rate for treatment benefit (MCR_TB). For each scenario, the method with the highest mean θ is marked in bold.

Scenario	True θ			Working model	Linear logistic				Classification tree with interactions		Separate Adaboost
				Fitting algorithm	MLE	Boosting	Max θ̂ (IPWE)	Max θ̂ (AIPWE)	Single tree	Boosting
The linear logistic working model is correctly specified.	1	0.1268	θ	Mean	0.1199	0.1195	0.1076	0.1134	0.0971	0.1083	0.0854
				SD	0.00218	0.00258	0.01273	0.00728	0.01206	0.00649	0.00907
			MCRTB	Mean	0.0517	0.0555	0.1261	0.0996	0.2351	0.1294	0.2111
	2	0.1243	θ	Mean	0.1232	0.1229	0.1099	0.1158	0.1004	0.1104	0.0876
				SD	0.01306	0.01156	0.01292	0.00760	0.01306	0.00740	0.00852
			MCRTB	Mean	0.0512	0.0526	0.1240	0.0973	0.2372	0.1269	0.2053
Link function in the linear logistic working model is incorrectly specified.	3	0.1341	θ	Mean	0.1302	0.1299	0.1176	0.1234	0.1056	0.1162	0.1038
				SD	0.00204	0.00224	0.01245	0.00712	0.01110	0.00654	0.00667
			MCRTB	Mean	0.0418	0.0444	0.1045	0.0824	0.2072	0.1124	0.1539
Link function and main effects in the linear logistic working model are incorrectly specified.	4	0.0657	θ	Mean	0.0574	0.0607	0.0561	0.0567	0.0221	0.0378	0.0352
				SD	0.01267	0.00986	0.01296	0.01482	0.01143	0.00867	0.00718
			MCRTB	Mean	0.1511	0.1206	0.1719	0.1653	0.5397	0.3251	0.5304
Main effects and interactions are incorrectly specified in the linear logistic working model.	5	0.0950	θ	Mean	0.0681	0.0702	0.0668	0.0694	0.0615	0.0735	0.0590
				SD	0.00703	0.00737	0.01303	0.01098	0.01359	0.00813	0.00854
			MCRTB	Mean	0.2667	0.2540	0.2588	0.2503	0.2737	0.1838	0.2478
	6	0.1393	θ	Mean	0.0236	0.0438	0.0498	0.0544	0.0978	0.1186	0.1010
				SD	0.01875	0.01276	0.01238	0.00893	0.01996	0.01057	0.00807
			MCRTB	Mean	0.3865	0.3542	0.3452	0.3330	0.2697	0.1762	0.2433
Linear logistic working model is mis-specified for outlying observations.	7	0.1419	θ	Mean	0.0879	0.1140	0.1099	0.1153	0.1042	0.1151	0.0856
				SD	0.02370	0.01183	0.01294	0.00816	0.01657	0.00944	0.00944
			MCRTB	Mean	0.2163	0.1207	0.1436	0.1198	0.2399	0.1394	0.2339

Table 3.

Results of the simulation study with sample size n = 5000. Marker combinations obtained using the following methods are compared: Logistic regression with maximum likelihood estimation (MLE), the boosting method of Section 2.3 with linear logistic working model, maximizing the IPW and AIPW estimators of θ as described by Zhang et al. (2012), a single classification tree with interactions between markers and treatment, the boosting method with classification tree working model, and applying Adaboost trees to each treatment group separately. Mean and Monte Carlo standard deviation (SD) of θ are shown, along with the mean misclassification rate for treatment benefit (MCR_TB). For each scenario, the method with the highest mean θ is marked in bold.

Scenario	True θ			Working model	Linear logistic				Classification tree with interactions		Separate Adaboost
				Fitting algorithm	MLE	Boosting	Max θ̂ (IPWE)	Max θ̂ (AIPWE)	Single tree	Boosting
The linear logistic working model is correctly specified.	1	0.1268	θ	Mean	0.1258	0.1257	0.1198	0.1206	0.1114	0.1143	0.0990
				SD	0.00038	0.00043	0.00216	0.00149	0.00523	0.00434	0.00237
			MCRTB	Mean	0.0165	0.0182	0.0527	0.0443	0.3222	0.2099	0.1664
	2	0.1243	θ	Mean	0.1252	0.1252	0.1227	0.1236	0.1140	0.1165	0.1003
				SD	0.00038	0.00043	0.00239	0.00170	0.00513	0.00473	0.00245
			MCRTB	Mean	0.0160	0.0173	0.0530	0.0430	0.3182	0.2251	0.1635
Link function in the linear logistic working model is incorrectly specified.	3	0.1341	θ	Mean	0.1316	0.1319	0.1299	0.1308	0.1130	0.1215	0.1120
				SD	0.00046	0.00046	0.00228	0.00151	0.00644	0.00328	0.00194
			MCRTB	Mean	0.0222	0.0188	0.0436	0.0355	0.2092	0.1148	0.1290
Link function and main effects in the linear logistic working model are incorrectly specified.	4	0.0657	θ	Mean	0.0640	0.0640	0.0625	0.0636	0.0259	0.0549	0.0436
				SD	0.00041	0.00036	0.00218	0.00077	0.01029	0.00412	0.00270
			MCRTB	Mean	0.0633	0.0544	0.1252	0.1034	0.4949	0.2041	0.2694
Main effects and interactions are incorrectly specified in the linear logistic working model.	5	0.0950	θ	Mean	0.0772	0.0804	0.0787	0.0797	0.0766	0.0839	0.0703
				SD	0.00210	0.00238	0.00280	0.00222	0.00458	0.00617	0.00231
			MCRTB	Mean	0.2485	0.2326	0.2008	0.1941	0.3287	0.1357	0.1829
	6	0.1393	θ	Mean	0.0218	0.0496	0.0570	0.0582	0.1143	0.1290	0.1200
				SD	0.00834	0.00485	0.00403	0.00345	0.01494	0.00846	0.00247
			MCRTB	Mean	0.3851	0.3490	0.3460	0.3472	0.2212	0.1231	0.1804
Linear logistic working model is mis-specified for outlying observations.	7	0.1419	θ	Mean	0.1019	0.1215	0.1226	0.1236	0.1315	0.1355	0.1179
				SD	0.00824	0.00167	0.00247	0.00172	0.00537	0.00436	0.00246
			MCRTB	Mean	0.1684	0.0668	0.0742	0.0635	0.3285	0.1459	0.1632

When the linear logistic working model was correctly specified (Scenario 1), as expected the combination of markers obtained using linear logistic MLE had the highest mean θ, smallest SD of θ, and smallest MCR_TB. Linear logistic boosting produced almost identical results, whereas all other methods produced modestly lower mean θ and substantially higher SD of θ and MCR_TB.

In the presence of high leverage points (Scenario 2), linear logistic MLE continued to produce the highest mean θ and smallest MCR_TB. However, the SD of θ was slightly lower with linear logistic boosting and substantially lower when maximizing the AIPWE of θ, or employing classification tree boosting, even while the associated mean θ’s were close to optimal. This suggests that, as expected, linear logistic MLE yields variable estimates in the presence of high leverage points; this effect disappears with large n (Table 3). Another observation is that only linear logistic boosting produced MCR_TB near that of linear logistic MLE; all other methods produced substantially higher classification error.

Mis-specifying the link function of the logistic working model (Scenario 3) had minimal impact on θ and both linear logistic MLE and linear logistic boosting produced nearly optimal mean θ and similarly low SD of θ and MCR_TB. All other methods yielded slightly lower mean θ and substantially higher SD of θ and MCR_TB. The superiority of the linear logistic regression methods persisted with larger n (Table 3). When both the link function and main effects were mis-specified (Scenario 4), methods with linear logistic working models produced similar mean θ (close to the optimal value) but linear logistic boosting had some advantage in terms of lower SD of θ and MCR_TB. Differences among methods were smaller again for larger n (Table 3).

Scenarios 5 and 6 explore substantial mis-specification of the linear logistic working model; the mean θ for linear logistic MLE is far from the optimal value. In these scenarios, boosting improved upon linear logistic MLE. Classification tree boosting yielded the best performance with the most dramatic improvement over logistic regression in the highly nonlinear setting of Scenario 6. These results persisted for large n (Table 3).

When the risk model mis-specification was due to outlying observations (Scenario 7), maximizing the AIPWE of θ and boosting provided marker combinations with improved performance over those generated by linear logistic MLE.

In summary, these simulation results demonstrate that the boosting method can improve upon existing methods for combining markers in certain settings. Under a substantially mis-specified working model, boosting can dramatically improve model performance. When the working model is mis-specified but not far from the true risk model, boosting may slightly improve performance. When high leverage points exist, boosting reduces variability without compromising mean performance. Boosting can perform better than direct maximization of the IPWE and AIPWE of θ, under mild or substantial working model mis-specification. As expected, linear logistic boosting performs best with minor mis-specification of the logistic risk function while classification tree boosting better captures nonlinear main effects and interactions with treatment.

4. Breast cancer data

The boosting method was then applied to the breast cancer data. The performance of the On-cotype DX Recurrence Score was most recently evaluated in the Southwest Oncology Group (SWOG)-SS8814 trial (Albain al., 2010a), which randomized women with node-positive, ER-positive breast cancer to tamoxifen plus adjuvant chemotherapy (cyclophosphamide, doxorubicin, and fluorouracil before or concurrent with tamoxifen) or tamoxifen alone. For 367 women (219 on tamoxifen plus adjuvant chemotherapy sequentially (T=1) and 148 on tamoxifen alone (T=0)), expression levels of 16 breast cancer-related and 5 reference genes were measured on tumor samples obtained at surgery (before adjuvant chemotherapy), and the Recurrence Score was calculated.

We use the SS8814 data to explore alternative combinations of the 16 breast cancer related genes that are optimized for treatment selection. In these data, there were 80 deaths or breast cancer recurrences by 5 years (35 given T = 0 and 45 given T = 1). There was little censoring; for 9 subjects censored before 5 years, we assume D = 0. Because the data are not currently available for public use, we modified the gene values but preserved the basic underlying structure of the data. Specifically, we use scaled versions of the markers (mean centered with unit variance) and un-labeled genes. A modified version of the original Recurrence Score was used. Combinations of the following marker sets were considered for their potential to guide treatment decisions: 1) The modified risk score (MRS); 2) three genes, G₁, G₂, and G₃, that showed evidence of marker-by-treatment interactions in a multivariate linear logistic regression model; and 3) two genes, G₄ and G₅, that exhibited a significant three-way interaction TG₄G₅ in a linear logistic regression model.

We implement the following approaches: Linear logistic MLE, linear logistic boosting, maximization of the IPWE or AIPWE of θ described by Zhang et al. (2012), a single classification tree with marker-by-treatment interactions, and classification tree boosting. The tuning parameters M_max and w̃{Δ(Y)} varied across marker sets and were determined using cross-validation (see Web Appendix A); C_max was set to 500 (See Web Appendix A). To assess model performance, we calculate the apparent performance (θ̂{ϕ̂(Y)}) using the original (training) data and use the percentile bootstrap to calculate a 95% confidence interval. A bootstrap-bias-corrected estimate of model performance (θ̂_c{ϕ̂_b(Y)}) (Efron and Tibshirani, 1993) is also calculated along with a 95% confidence interval obtained using the double-bootstrap (see Web Appendix B).

Performance measures of the various marker combinations are shown in Table 4. For every set of markers, maximizing the AIPWE of θ, linear logistic boosting, a single classification tree, or classification tree boosting yields a combination of markers with better performance (higher θ̂) than that obtained using linear logistic MLE. For example, for the models including G₄, G₅, and G₄G₅, classification tree boosting yields a marker combination associated with a 9% decrease in 5-year recurrence or death (95% CI: 8% to 18%) and the marker combination maximizing the AIPWE of θ yields a 3% decrease (95% CI: 2% to 11%). In contrast, the combination derived using linear logistic MLE yields a 0.3% decrease (95% CI: −2% to 8%). These new combinations of markers may have improved ability to identify a subgroup of women who can avoid adjuvant chemotherapy, in terms of providing a lower population rate of 5-year death or recurrence. For example, the best function of the MRS is estimated to yield a 5% reduction in 5-year death or recurrence (95% CI 4% to 13%), while allowing 64% women to avoid adjuvant chemotherapy.

Table 4.

Performance of marker combinations in the breast cancer data. Models including the modified risk score (MRS); genes G₁, G₂ and G₃; and genes G₄, G₅ and G₄ × G₅ are shown. The following methods are used to obtain marker combinations: Logistic regression with maximum likelihood estimation (MLE), the boosting method with linear logistic working model, maximizing the IPW or AIPW estimator of θ as described by Zhang et al. (2012), a single classification tree with interactions between markers and treatment, and the boosting method with classification tree working model. For each method the apparent model performance (θ̂{ϕ̂(Y)}) and corresponding bootstrap-based 95% confidence interval; and bootstrap-bias-corrected estimate of model performance (θ̂_c{ϕ̂_b(Y)}) and corresponding bootstrap-based 95% confidence interval, are shown.

Marker set (Y)	Working model	Linear logistic				Classification tree with interactions
	Fitting algorithm	MLE	Boosting	Max θ̂		Single tree	Boosting
				(IPWE)	(AIPWE)
MRS	θ̂{ϕ̂(Y)}	0.026	0.034	−0.012	0.044	0.052	0.074
	95% CI	(−0.017, 0.068)	(−0.015, 0.072)	(−0.062, 0.073)	(0.005, 0.092)	(−0.011, 0.153)	(0.027, 0.159)
	θ̂c{ϕ̂b(Y)}	0.002	0.008	−0.009	0.033	0.040	0.051
	95% CI	(−0.010, 0.060)	(−0.014, 0.062)	(−0.042, 0.072)	(−0.001, 0.087)	(0.025, 0.127)	(0.037, 0.133)
(G1, G2, G3)	θ̂{ϕ̂(Y)}	0.052	0.060	0.063	0.080	0.075	0.095
	95% CI	(−0.012, 0.110)	(0.013, 0.121)	(−0.034, 0.115)	(0.053, 0.146)	(0.031, 0.169)	(0.074, 0.206)
	θ̂c{ϕ̂b(Y)}	0.037	0.048	0.028	0.063	0.054	0.081
	95% CI	(−0.009, 0.102)	(0.000, 0.117)	(−0.010, 0.086)	(0.000, 0.137)	(0.000, 0.132)	(0.000, 0.159)
(G4, G5, G4 × G5)	θ̂{ϕ̂(Y)}	0.011	0.049	0.050	0.057	0.053	0.125
	95% CI	(−0.027, 0.095)	(−0.013, 0.102)	(−0.013, 0.094)	(0.028, 0.126)	(0.025, 0.159)	(0.087, 0.240)
	θ̂c{ϕ̂b(Y)}	0.003	0.015	0.022	0.034	0.042	0.089
	95% CI	(−0.016, 0.075)	(−0.013, 0.087)	(−0.018, 0.076)	(0.018, 0.110)	(0.032, 0.124)	(0.080, 0.175)

Observe in Table 5 that the differences in performance between models are due to a large proportion of subjects being differently classified according to treatment benefit using linear logistic MLE versus the other approaches. The results also suggest that the linear logistic model may not hold for the modified risk score since maximizing the AIPWE of and classification tree boosting produce substantially higher θ̂ than linear logistic MLE.

Table 5.

Estimated treatment rules in the breast cancer data obtained using the following methods: Logistic regression with maximum likelihood estimation (MLE), the boosting method with linear logistic working model, maximizing the IPW or AIPW estimator of θ as described by Zhang et al. (2012), a single classification tree with interactions between markers and treatment, and the boosting method with classification tree working model. Cells show the number (%) of subjects in the data set cross-classified by treatment rules from linear logistic MLE and other marker combination approaches. Subjects with Δ̂(Y) ≤ 0 are recommended tamoxifen alone (T = 0) and those satisfying Δ̂(Y) > 0 are recommended adjuvant chemotherapy (T = 1).

Marker set (Y)	Linear logistic MLE	Linear logistic						Classification tree with interactions
		Boosting		Max θ̂				Single tree		Boosting
				(IPWE)		(AIPWE)
		Δ̂(Y) ≤ 0	Δ̂(Y) > 0	Δ̂(Y) ≤ 0	Δ̂(Y) > 0	Δ̂(Y) ≤ 0	Δ̂(Y) > 0	Δ̂(Y) ≤ 0	Δ̂(Y) > 0	Δ̂(Y) ≤ 0	Δ̂(Y) > 0
MRS	Δ̂(Y) ≤ 0	169 (46)	0 (0)	169 (46)	0 (0)	169 (46)	0 (0)	169 (46)	0 (0)	169 (46)	0 (0)	169 (46)
	Δ̂(Y) > 0	9 (2)	189 (51)	155 (42)	43 (12)	17 (5)	181 (49)	107 (29)	91 (25)	67 (18)	131 (36)	198 (54)
		178 (49)	189 (51)	324 (88)	43 (12)	186 (51)	181 (49)	276 (75)	91 (25)	236 (64)	131 (36)	367 (100)
(G1, G2, G3)	Δ̂(Y) ≤ 0	171 (47)	13 (4)	109 (30)	75 (20)	73 (36)	111 (14)	160 (44)	24 (7)	138 (38)	46 (13)	184 (50)
	Δ̂(Y) > 0	12 (3)	171 (47)	19 (4)	164 (46)	13 (2)	170 (48)	103 (28)	80 (22)	79 (22)	104 (28)	183 (50)
		183 (50)	184 (50)	128 (35)	239 (65)	86 (23)	281 (77)	263 (72)	104 (28)	217 (59)	150 (41)	367 (100)
(G4, G5, G4 × G5)	Δ̂(Y) ≤ 0	88 (24)	26 (7)	50 (14)	64 (17)	98 (27)	16 (4)	98 (27)	16 (4)	42 (11)	72 (20)	114 (31)
	Δ̂(Y) > 0	69 (19)	184 (50)	68 (19)	185 (50)	75 (20)	178 (49)	173 (47)	80 (22)	77 (21)	176 (48)	253 (69)
		157 (43)	210 (57)	118 (32)	249 (68)	173 (47)	194 (53)	271 (74)	96 (26)	119 (32)	248 (68)	367 (100)

These results must be interpreted with caution, however, since even our bootstrap-bias-corrected estimates of model performance may be overoptimistic. With the small sample size, cross-validation did not produce satisfactory estimates of test data performance; results were highly dependent on the random seed used to split the data. Other bias correction approaches such as the .632 bootstrap method (Efron and Tibshirani, 1993) do not appear to apply to the measure θ. Obtaining sufficiently large data sets to validate marker combinations is a pervasive challenge for the treatment selection field.

5. Discussion

This paper describes a novel application of boosting to combining markers for predicting treatment effect. The approach is intended to build in robustness to risk model mis-specification, by averaging across risk models fit by iteratively upweighting subjects potentially misclassified according to treatment benefit at the previous stage. We evaluate the performance of the approach using clinically relevant measures and find several settings in which the boosting method results in combinations of markers that have closer-to-optimal performance than combinations derived using less-robust existing approaches. Specifically, boosting appears advantageous under substantial risk model mis-specification and in settings with high leverage points. Our analysis of the breast cancer data suggests that, in these data, boosting can yield new marker combinations that may have superior ability to identify women who do not benefit from adjuvant chemotherapy.

A simple approach to combining markers for treatment selection is to apply one of the plethora of methods available for combining markers for classification separately to each treatment group. As discussed by Claggett et al. (2011), however, the two best performing risk models for each treatment group do not necessarily produce the best model for treatment effect. This strategy risks missing markers that are strongly associated with treatment effect but which have modest main effects, and risks including markers which have strong main effects but modest interactions with treatment. For example, human epidermal growth factor receptor 2 (HER-2) is not considered a significant predictor of cancer recurrence in breast cancer patients while it is an important predictor of the effects of some adjuvant chemotherapies and hormone therapies (Clark (1995); Henry and Hayes (2006)). In our simulations, fitting a risk model to each treatment group separately tended to produce marker combinations with inferior performance compared to those that simultaneously considered both treatment groups, such as the novel boosting method.

When evaluating candidate approaches for combining markers, it is important that methods be compared with respect to compelling and clinically relevant measures of model performance. Measures such as the frequency of correct variables selected (Gunter et al. (2007); Lu et al. (2011)), the area under the receiver operating characteristic curve (AUC) for each treatment group (Claggett et al., 2011) and the Mean Squared Error (MSE) of model coefficients (Lu et al., 2011) suffer from lack of clinical interpretation and do not characterize the benefit of the marker combination. The rate of incorrect treatment recommendation, MCR_TB, is appealing and useful for simulation studies evaluating new methods. The decrease in the disease rate under marker-based treatment, measured by θ, has clear relevance. This measure, or a variation on it, has been advocated in several recent papers on evaluating treatment selection markers (Song and Pepe (2004); Gunter et al. (2007, 2011b); Brinkley et al. (2010); Qian and Murphy (2011); Janes et al. (2011, 2013a, b); Zhang et al. (2012)). θ is comprised of the proportion of subjects who are marker-negative and the treatment effect in the marker-negative subgroup. While these constituents inform about the nature of markers’ effect, neither can serve as the sole basis for comparing combinations of markers.

The relative performance of the different approaches to combining markers for treatment selection depends on the scale of the outcome. While many of the methods to-date have focused on the continuous outcome setting, this paper compares approaches given a binary outcome. In particular, we present results on the IPWE or AIPWE of θ maximization approach compared to logistic regression MLE, whereas the original paper (Zhang et al., 2012) focused on a continuous outcome and linear regression. In our simulation study, improving upon logistic regression proved difficult. Even under risk model mis-specification, maximizing the IPWE or AIPWE of θ only resulted in moderately higher mean θ in most scenarios. In Scenario 4, constructed to be similar to the first simulation scenario of Zhang et al. (2012), maximizing the IPWE or AIPWE of θ did not yield a marker combination with superior performance to that associated with logistic regression MLE. Based on these results, it appears more difficult to improve upon logistic regression for binary outcomes than it is to improve upon linear regression for continuous outcomes. Pepe et al. (2005) also found logistic regression to be remarkably robust in the classification context.

The boosting method described here warrants further research along several avenues. The method can be generalized naturally to settings where the outcome does not capture all consequences of treatment and therefore the optimal treatment rule is Δ(Y) ≤ δ for some δ > 0 (Vickers et al. (2007); Janes et al. (2013a)). Continuous outcomes and time-to-event outcomes could be also accommodated. Further investigation of the optimal weight function for the boosting method is of interest. The method could be extended to settings with marker values missing at random, multiple treatment options, or to the observational study setting. Another challenge is doing variable selection in the treatment selection context. Application of boosting with a penalized regression working model is one potential approach that would accommodate high dimensional makers.