Modeling the Timing of Antilatency Drug Administration during HIV Treatment

ABSTRACT

Latently infected cells are considered a major barrier to the cure of HIV infection, since they are long-lived under antiretroviral therapy (ART) and cause viral replication to restart soon after stopping ART. In the last decade, different types of antilatency drugs have been explored with the aim of reactivating and purging this latent reservoir and the hope of achieving a cure. Because of toxicity and safety considerations, antilatency drugs can only be given for a short time to patients on long-term ART, with little effect. We recently investigated the turnover of latently infected cells during active infection and have found that it was strongly correlated with viral load. This implies that although latently infected cells had long life spans in a setting of a low viral load (such as during ART), they turned over quickly under a high viral load. Possible reasons for this could be that an increased viral load causes increased activation or death of CD4⁺ T cells, including those that are latently infected. Taking these results into account, we developed a mathematical model to study the most appropriate timing of antilatency drugs in relationship to the initiation of ART. We found that the best timing of a short-term antilatency drug would be the start of ART, when viral load, CD4⁺ T cell activation, and latent cell turnover are all high. These results have important implications for the design of HIV cure-related clinical trials.

IMPORTANCE The antiretroviral therapy (ART) of HIV-infected patients currently needs to be lifelong, because the cells latently infected with HIV start new rounds of infection as soon as the treatment is stopped. In the last decade, a number of different types of antilatency drugs have been explored with the aim of “reactivating” and “purging” this latent reservoir and thus achieving a cure. These drugs have thus far been tested on patients only after long-term ART and have demonstrated little or no effect. We use mathematical modeling to show that the most efficacious timing of a short-term antilatency treatment may be the start of ART because of possible interactions of antilatency drugs with natural activation pathways.

INTRODUCTION

Human immunodeficiency virus (HIV) remains a major cause of morbidity and mortality worldwide. Antiretroviral treatment (ART) can successfully maintain an undetectable viral load in infected individuals and thus limit transmission and drastically improve the duration and quality of life of patients, but ART cannot cure the disease. Current antiretroviral drugs block new cycles of infection but leave the cells with already integrated provirus intact. The main barrier to curing HIV infection is the existence of a reservoir of latently infected cells that harbor integrated virus without expressing it (1–3), which is very long-lived in the setting of long-term ART (2–4). Since these cells are not affected by antiretroviral drugs (4), they reactivate and start a new round of infection within weeks after ART is stopped (5). ART is therefore currently lifelong and is associated with significant cost and side effects. As the number of people living with HIV grows beyond 40 million despite the decrease in cost and increase in availability of ART medications, providing lifelong therapy is becoming a huge public health burden.

Reducing the number of latently infected cells that remain after long-term ART is designed to increase the average time to reemergence of infection after ART interruption and to possibly eradicate the virus. In recent years, different pharmacological approaches have been tried in attempts to reduce the latent HIV reservoir, each addressing a different possible mechanism that may cause HIV-infected cells to stably integrate transcriptionally silent HIV DNA (6). These include (i) drugs that trigger the NF-κB activation pathway by different targeting mechanisms, such as interleukin-2 (7, 8), prostratin and analogues (9), or bryostatin and analogues (10), (ii) drugs that enhance the binding of the viral transactivator Tat protein to the HIV TAR element, such as JQ1 and the other BET inhibitors (11), and (iii) epigenetic modifiers such as histone deacetylase inhibitors (HDACi), including valproic acid (12, 13), vorinostat (14), and panobinostat. The HDACi were considered among the most promising because several studies have suggested that they may activate a proportion of latently infected cells in vitro and in vivo. However, one detailed recent study (15) found many of these promising drugs ineffective in reversing HIV latency in vitro.

As the search for HIV cure continues, new activating/antilatency drugs will be developed and tested, with the overall effect of reactivating latently infected cells to express HIV and either die or be cleared by the immune system. Such interventions are studied for short durations (2 weeks or less) because of toxicity concerns and usually in patients on long-term ART. We discuss here the possibility that administering antilatency drugs at the initiation of ART may in some circumstances enhance the ability of these drugs to purge the latent reservoir (16).

The life span of latently infected cells has usually been measured in the setting of long-term ART and has been found to be very long (months to years). However, there have been only a few studies attempting to measure how long-lived latently infected cells are during active infection in the absence of ART. In a recent study (17), we measured the turnover of SIV DNA in resting infected CD4⁺ T cells in vivo in simian immunodeficiency virus (SIV)-infected pigtail macaques not on ART. We found that this reservoir turned over slowly (with a half-life on the order of years) in animals that had a low chronic viral load (<10⁴ RNA copies/ml), consistent with the findings in humans on ART. However, we found that SIV DNA within resting CD4 T cells turned over with a half-life of 0.8 day⁻¹ or less in the animals with high viral loads (>10⁶ RNA copies/ml). A possible reason for this could be that an increased viral load may cause increased activation (18) or death (19) of CD4⁺ T cells, including those that are latently infected. In other words, a high viral load could provide a natural mechanism for purging the latent reservoir during active infection, and the antilatency drugs may be interacting with this mechanism in different ways. We model here how to optimize the reduction of the latent reservoir for two types of such interaction by choosing the best timing of antilatency drug administration during ART.

MATERIALS AND METHODS

In order to better understand the implications of the hypothesized virus-mediated activation or death for the possible dynamics of the latent pool during antilatency drug administration, we developed a simple model of HIV infection (Fig. 1A). The model is the extension of the standard model of viral dynamics (20, 21). In this model, the uninfected susceptible CD4⁺ T cells (T) are replaced at the rate λ and die at the rate d_T. They are infected by free virus (V) according to the mass action law with infectivity β. A large fraction f becomes productively infected (I) and short-lived, producing virus at the rate p and dying at the death rate δ. A small fraction (1 – f) becomes latently infected (L) and does not produce virus. In the model we assume that these fractions remain constant throughout the infection. The latently infected cells are activated at the rate α, upon which they become productive and short-lived, and die at the rate ω:

$$\begin{array}{c}dT/dt=\lambda -d_{T}T-\beta VT\\ dI/dt=f\beta VT-\delta I+\alpha L\\ dL/dt=\left(1-f\right)\beta VT-\left(\alpha +\omega \right)L\\ dV/dt=pI-cV\end{array}$$ (1)

FIG 1.

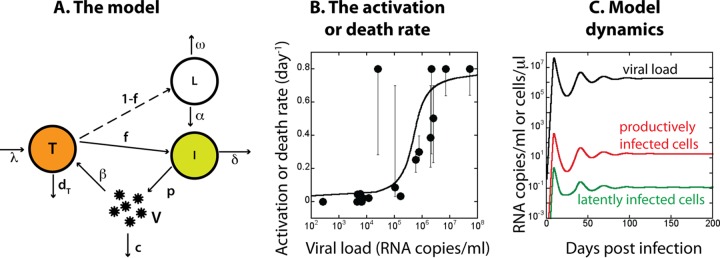
Model of the dynamics of the latent reservoir in HIV infection. (A) Simple model of infection. Uninfected CD4⁺ T cells (T) are replaced at the rate λ and die at the rate d_T. They have susceptibility β to infection by virus (V). A large fraction f is productively infected (I); they produce virus at the rate p and die at the rate δ. The remaining small fraction 1 − f is latently infected (L). They do not produce virus but are activated by virus at the rate α and die at the rate ω. (B) Dependence of activation or death rate on viral load. Full circles indicate results from reference 16; the full line shows the fit to experimental results used in modeling. (C) Dynamics of viral load (black line), productively infected cells (red line), and latently infected cells (green line) obtained from the model.

The death rate of productively infected cells, assumed constant during infection, includes the averaged influence of immune control components, as do the other infection parameters (infectivity, virus production rate, and clearance). An implicit assumption of the model is that the reactivated latently infected cells behave the same as the productively infected cells, most importantly that they die at the same rate, which may not be true for reactivation with currently investigated antilatency drugs (22) but should be the outcome of a successful latency-reversing agent. This simple model is essentially the same as a model used earlier (23), the only difference being that the activation rate α and/or the death rate ω of latently infected cells in our model may increase with viral load V (Fig. 1B). The correlation of viral load with latent cell turnover is consistent with our previous experimental observations (17). However, we do not imply that this relationship is causative (i.e., that viral load itself drives activation). Instead, viral load may be a proxy correlating with a number of other potential stimuli, such as antigenic stimulation, proinflammatory cytokines, and homeostatic cytokines.

Using the conventions of the standard model (20, 21), we follow the cell and virion frequencies in peripheral blood, i.e., T, I, and L are expressed in numbers per microliter, and V is expressed in RNA copies per milliliter. These are also the quantities most easily measured in vivo. However, we assume that similar dynamics of turnover would be found in tissues, where viral load would follow the same dynamics as in plasma.

We used our earlier results (17) (full circles in Fig. 1B) to define the dependence of the activation or death rate on viral load. We found that the shifted arctan(logV) function is a good approximation for the observed dependence (full line, Fig. 1B):

$$\alpha +\omega =0.8\{0.5+\arctan \hspace{0.17em}[3(\log \hspace{0.17em}V-\log \hspace{0.17em}5\cdot {10}^5)]/\pi \}{\text{day}}^{-1}$$ (2)

where viral load V is expressed in RNA copies/ml. We used the arctan function because it changes between two limiting values within an adjustable interval like the data points in Fig. 1B and is easier to use in a simulation than a more conventional spline fit. Some general predictions of the model are discussed in the supplemental material. The relationship between the steady states of the viral load and the size of the latent reservoir for different variations of parameters are shown in Fig. S1 in the supplemental material.

In an earlier study (17), we measured the turnover rate of the latent reservoir in SIV-infected macaques by comparing the replacement of the wild-type strain of the virus by an escape mutant in plasma and in the latently infected cells over time. We obtained the results by fitting of one overall turnover rate for each animal and correlating it with the chronic viral load for this animal. Therefore, Fig. 1B shows the results that are essentially cross-sectional (in “chronic infection”), although they were obtained by fitting longitudinal data for each animal. The results showed a strong positive correlation of this overall turnover rate and chronic viral load. In the present study we used this cross-sectional data to model the longitudinal dependence of the turnover rate on the current viral load. In Fig. S2 in the supplemental material we show that instantaneous dependence of the turnover on viral load as in equation 2 could produce the overall correlation observed in Fig. 1B if a wide range of parameter variations in equation 1 cause the differences in the chronic viral load in different individuals. The results are not at all sensitive to the choice of the turnover function in equation 2 as long as it has similar saturation properties as the data, i.e., as long as it is similarly S-shaped.

Irrespective of whether the activation or the death rate of latently infected cells or both depend on viral load as in equation 2, the model predicts qualitatively similar dynamics of the latent cell reservoir (Fig. 1C). We used a model in which only the activation rate is virus dependent and the death rate of latently infected cells is constant (ω = 2 × 10⁻⁴ day⁻¹) to generate the dynamics of viral load and latently infected cells in Fig. 1 and 2. For the infection parameters δ, c, p, and β, we used the values from the literature (24–28), and the disease-free parameters were chosen so that the disease-free concentration of target cells T₀ = λ/d_T is 1,000 cells/μl and λ is small compared to T₀ (20). The values and sources for the parameters are listed in Table 1.

FIG 2.

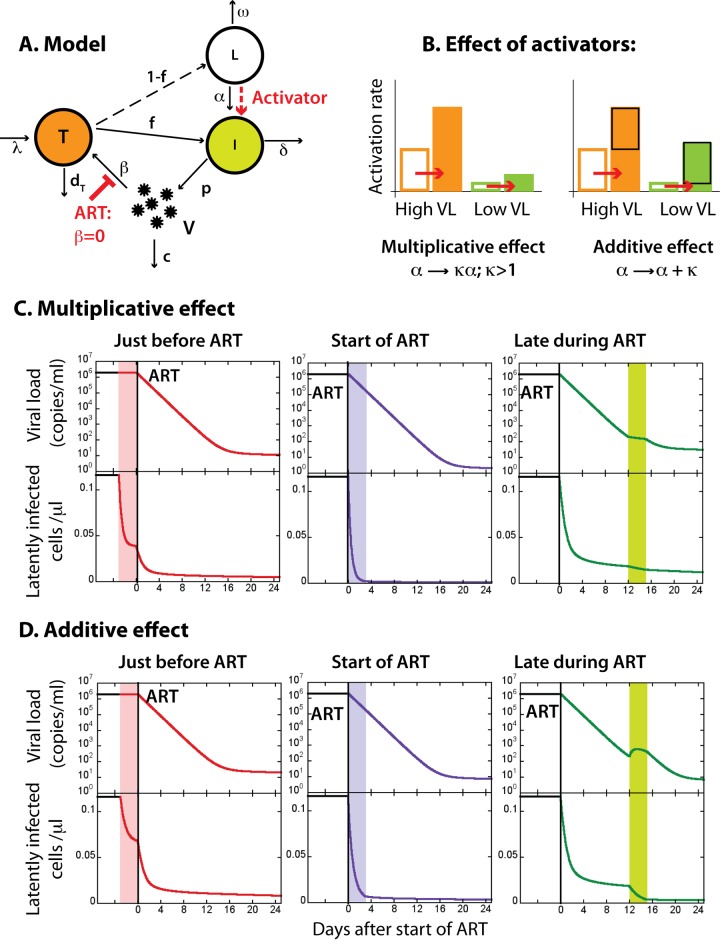
Effect of timing of antilatency drug treatment relative to ART. (A) We assume that antilatency drugs increase the rate of activation of latently infected cells. (B) The effect of antilatency drugs on the activation rate can be either multiplicative (activation rate is multiplied by a dose-dependent factor) or additive (activation rate increases by a dose-dependent amount). (C and D) ART starts at time = 0 (black vertical line). Antilatency drugs are given for 3 days either just before ART (pink interval), at the start of ART (purple interval), or after more than a week of ART when the viral load is close to undetectable (green interval). A black line represents the set point viral load (upper panel) and the stable latently infected cell pool (lower panel) in the untreated infection. A red line shows the effect of an activator given just before the start of ART. A purple line shows the effect of activator given at the start of ART. A green line represents ART with the activator given late during ART. The parameters for the untreated infection were the same as in Fig. 1. During ART, β = 0; multiplicative effect, κ = 3; additive effect, κ = 0.5.

TABLE 1.

Parameters used in Fig. 1 and 2

Parameter	Value	Reference(s)
λ (cells μl−1 day−1)	20	20
dT (day−1)	0.02
δ (day−1)	0.8	24–27
c (day−1)	20	26, 27
β (μl copy−1 day−1)	3.6 × 10−5	28
p (copies cell−1 day−1)	2,000	26
f	0.995
ω (day−1)	10−4

RESULTS

Levels of latently infected cells in the absence of ART.

We first modeled the size of the latent reservoir in the absence of ART. Early in infection the model (Fig. 1C) predicts that the size of the latent reservoir would grow and reach a peak before the peak viral load because the subsequent growth to the peak viral load would cause the rise in the turnover rate of the latent reservoir to its highest level during the infection. Therefore, the early peak in latently infected cells would be followed by a trough (around the peak viral load) caused by this high turnover rate. The size of the latent reservoir may subsequently vary depending on variations in the viral load. In the chronic phase of infection (at the viral set point) the viral load and the latently infected cell levels would be generally lower than at the peak viral load. In this chronic stage, latently infected cells accumulate to reach a steady state where their slower accumulation from new infections is balanced by slower activation due to lower viral load. In the acute phase of infection the latent reservoir obtained from the model may be highly variable, varying from the large peak before the peak viral load to low levels just after the peak but would later stabilize at higher levels for higher viral loads. Apart from the early peak, the acute-phase level of latently infected cells would on average be lower than in the chronic phase. The experimental estimates of the latent pool in untreated patients in different stages of HIV infection indicate that it could indeed be smaller in the acute phase (29) and that later it positively correlates with the chronic viral load (23). Our model reproduces these known features of the latently infected cell accumulation. An important caveat is that we have not explicitly modeled the impact of CD8⁺ T lymphocyte control in acute infection. Depending on the dynamics of CD8⁺ T cells and the mechanisms by which they suppress virus (which are controversial [30–32]), this may also have effects on the size of the latent reservoir during acute infection.

Timing of the antilatency drugs with respect to ART.

We then modeled how the initiation of ART and treatment with antilatency drugs may alter levels of latently infected cells. In the model we assumed that ART is 100% effective in preventing new infection events and that antilatency drugs increase the natural activation rate of latently infected cells (Fig. 2A). Each type of these drugs may interact differently with the specific combination of natural activation mechanisms already present in each host and specifically with the virus-mediated activation. The interaction could be of two types (Fig. 2B). One is additive, where latency-reversing agents activate a fixed proportion of the latent pool, independent of the baseline level of host cell activation. We consider this an additive effect. The second type of effect of the latency-reversing drugs may be multiplicative, where they amplify the existing activation level by a dose-dependent factor. This type of interaction would occur if the activation processes induced by the latency-reversing drug partially overlapped with the global activation processes such as virus-associated activation. The mechanisms of current latency-reversing agents appear to induce global gene expression (15, 33), suggesting that they may have a multiplicative effect. In this case, at high viral loads an already high activation rate would become even higher (e.g., twice as high for a doubling dose), while at a low viral load a low activation rate may increase (e.g., double) but would still stay relatively low.

The antilatency drugs with multiplicative effects would have the highest impact on activation rate when it is already high (Fig. 2B). The possible results of 3-day administration of such drugs at different times relative to the initiation of ART are illustrated in Fig. 2C. Antilatency drugs would be the most effective if given when the viral load and the natural activation rate are still high. However, if given before the start of ART, the virus produced by the reactivated latently infected cells could infect new cells, some of which could become latent. Thus, the effectiveness of antilatency activation would be somewhat impaired by reseeding of the latent pool by the enhanced viral load. Therefore, we predict that the optimal timing of the antilatency treatment would be just at the start of ART, when any increase in viral production is blocked by ART from forming new latently infected cells. This model predicts that the antilatency drugs would have minimal effect when given after long-term ART when the viral load (and consequently the level of virus-induced immune activation) was low.

If instead of increasing activation by a multiplicative factor, the effect of the antilatency drug were simply additive, we would have a different scenario. The antilatency drugs with the additive effect on the natural activation rate (Fig. 2D) would also be less effective if given before starting ART because of reseeding. However, it would make no difference at which point during ART they were given, because the effect on the latent reservoir would be the same at all times, since the additive effect implies a constant boost of activation independent of endogenous level of activation. In all cases there may be a slightly slower decay or a blip of virus during antilatency treatment because of the rise in the number of latently infected cells becoming productive.

In our interpretation of the reduced life span of the latently infected cells under high viral load (Fig. 1B), we have assumed that increased viral load causes an increased rate at which latently infected cells reactivate and produce virus and that they die at the same rate as the other activated, productively infected cells. An alternative interpretation would be that virus causes the latently infected cells to reactivate and die before starting virus production. It is not clear whether and how the antilatency drugs would interact with this killing mechanism, but the results of an additive or multiplicative effect would be similar to reactivation, although without the increase in viral load.

DISCUSSION

In our understanding of HIV latency, major questions remain as to when and how the latent reservoir is formed during infection, how the natural turnover of latently infected cells changes during active infection and treatment, and what are the natural mechanisms and dynamics of reactivation of latently infected cells on therapy. The recently investigated antilatency drugs and interventions seem to show less promise than initially hoped and anticipated (15). This is partly due to the limited understanding of their mechanisms of action. The most important thing we need to know about a potentially successful latency-reversing agent is whether it can drive a lasting activation of latently infected cells that leads to faster cell death (3, 34) in vivo. If the cells reactivated by antilatency drugs fail to die or revert to latency as soon as the drug is removed, such a drug would have no benefit. The second question, essential for designing strategies for use of antilatency drugs during ART, concerns the interactions of these activators with the natural activation mechanisms. Do they amplify the natural activation rate by a dose-dependent factor (multiplicative mechanism), or do they act independently of these natural pathways by adding a dose-dependent boost (additive mechanism)?

Using antilatency drugs at a time when they would be most efficient in purging the latent pool is important because of the concerns about their toxicity, which limit the duration of treatment. Here we have analyzed the possible outcomes of treatment with antilatency drugs in the light of our recent discovery that high viremia increases the turnover of the latent reservoir. We have not explicitly modeled the possible mechanisms that may cause this type of correlation (for example, antigen-driven activation, homeostatic activation or the effects of virus binding to CD4⁺ T cells), all of which may predict somewhat different dynamics. We have also assumed that the treatment with antilatency drugs acts by driving the latently infected cells to reactivate, produce virus, and die rapidly, which would be the desired effect of successful latency-reversing agents.

However, using this simple model we found that, if the antilatency activators act multiplicatively, they are best given at the start of ART when the viral load and the natural activation rate are still high. Their effect after long-term ART would be negligible. On the other hand, if the antilatency drugs act independently of the natural activation pathways (that is, act additively), their effect would be the same irrespective of their time of administration during ART. Giving activators without ART would decrease their effect because of reseeding of the latent pool by the increased viral load.

In the absence of knowing precisely how the activating drugs interact with the natural activation pathways of latent virus (multiplicatively or additively) and to what extent the reactivated latently infected cells produce virus or die, our model suggests that giving these drugs at the initiation of ART may be more effective, and should not be less effective, than giving them after long-term ART. Current trials of antilatency drugs have been on patients who have been suppressed for extended periods of time so that a baseline reservoir size can be established, and any reduction from that measured as an outcome. However, trials to test the efficacy of latency-reversing drugs during ART induction do not have this stable reservoir size, as HIV DNA levels decline rapidly during early ART (35). Thus, we predict that antilatency drugs administration in early ART will lead to a greater decline in reservoir size from active infection to treatment. Thus, trials comparing the drop in HIV-DNA levels from pre-ART to 6 months in the presence or absence or latency-reversing drugs would directly test this prediction.

The limited data from the few current antilatency drug studies show no impact on reservoir size (14, 36–38). This lack of effect on reservoir size likely occurs because too few latent cells are activated during chronic ART (39). However, great efforts are being made worldwide to discover new, less toxic, and more effective antilatency treatments (34, 39). As new drugs are being investigated in an urgent race to approach at least a functional cure, we point to the importance of testing them for their interaction with the natural activation mechanisms in order to optimize their effectiveness in treatment. In the meantime, their administration at the start of ART seems a better option than after long-time ART. Under long-term ART, latent virus is quiescent and may be hard to reactivate, whereas during active infection and early ART it may be turning over much faster. Attempting to purge the latent virus in this more active early stage may be more effective and cannot be less effective, than doing it later.