The utility of data-driven feature selection: Re: Chu et al. 2012

Abstract

The recent Chu et al. (2012) manuscript discusses two key findings regarding feature selection (FS): (1) data driven FS was no better than using whole brain voxel data and (2) a priori biological knowledge was effective to guide FS. Use of FS is highly relevant in neuroimaging-based machine learning, as the number of attributes can greatly exceed the number of exemplars. We strongly endorse their demonstration of both of these findings, and we provide additional important practical and theoretical arguments as to why, in their case, the data-driven FS methods they implemented did not result in improved accuracy. Further, we emphasize that the data-driven FS methods they tested performed approximately as well as the all-voxel case. We discuss why a sparse model may be favored over a complex one with similar performance. We caution readers that the findings in the Chu et al. report should not be generalized to all data-driven FS methods.

Comment

Recently, Chu et al. (2012) assessed how feature selection (FS) affected classification accuracy on a series of two class problems using gray matter voxel features. FS techniques are categorized typically as filter based, embedded, or wrapper based methods (Tuv et al., 2009). Within the neuroimaging community, data-driven FS (DD-FS) methods have been used commonly because they are generally effective: univariate t-test filtering (e.g. Esterman et al., 2009; Johnson et al., 2009 and wrapper-based SVM recursive feature elimination (RFE) approaches (established in Guyon et al., 2002; effective in De Martino et al., 2008; Ecker et al., 2010; Dai et al., 2012).

Chu et al. (2012) presented a principled analysis that compared the performance of these two DD-FS approaches with voxelized features from a region of interest (ROI) based on a biological hypothesis, t-test in combination within an ROI constraint, and in the absence of any first stage FS. Their analysis revealed that the DD-FS methods tested were unable to outperform simply using all ∼300,000 voxel features for discrimination, similar to results published by Cuingnet et al. (2011) who tested a series of FS methods. While Chu et al. clearly discuss that these results are data specific, their findings nonetheless highlight the essential importance for further analysis of FS methods in neuroimaging applications where the data is both noisy and vast. We emphasize that their findings that DD-FS did not improve accuracies should be limited to a certain class of FS methods, for a limited set of parameter choices and kernels. The sensitivity of SVM accuracy to DD-FS methods with respect to changing kernels was discussed by Song et al. (2011), so we focus on the specific DD-FS methods implemented by Chu et al. We caution readers that their results should not be generalized to other DD-FS methods.

We first discuss the two DD-FS methods that were tested, and point out certain theoretical constraints that are common across both techniques. These limitations are well established in the machine learning (ML) literature, and have been discussed by the primary author of the fundamental RFE manuscript (Guyon and Elisseeff, 2003). Both t-test filtering and RFE favor selection of features that maximize accuracy individually, assuming that these will provide the highest discrimination accuracy when used in aggregate (Guyon et al., 2002). Consider however, examples where multiple features provide largely redundant, yet highly diagnostic, information (i.e., spatially adjacent neuroimaging voxels), while other features with lower margins and t statistics hold unique information (Haxby et al., 2001). Within this framework, the redundant features will be retained, while the features that provide unique information that could improve performance will be discarded. Both of these factors contribute to a decrease in classification accuracy, rather than an increase, as discussed for neuroimaging data by Kriegeskorte et al. (2006), Pereira and Botvinick (2010) and Björnsdotter et al. (2011).

Further, features that are not themselves diagnostic, but which control for nuisance factors (e.g. age-associated atrophy; Farid et al., 2012) are expected to have extremely low univariate |t| values and reduced margins. To determine the utility of each feature in RFE, the multivariate separability vector, w, is projected onto each feature-dimension to get a univariate margin, w_j. In RFE, features with the smallest univariate margin, ‖w_j‖, are excluded iteratively until the desired number of features is achieved. We expect that the margin of nuisance-controlling factors would be greater than noise but smaller than the margin of the diagnostic feature. In this case, the smallest margin and |t| statistic features would be excluded before the diagnostic features by these DD-FS methods because the stopping criterion used by Chu et al. was the number of selected input features. The stopping criterion is defined by the criteria used to determine exactly how many features are included in the final model. If one had used the observed training or testing accuracy (as in backward or forward selection) or an arbitrary fixed criterion for ‖w_j‖ or |t| to determine the stopping criterion, we would expect that these nuisance features may be included in the final model learned using RFE, but not using t-statistic filtering.

In contrast, the least-squares (ℓ₂) regularization in SVM, itself a multivariate DD-FS method, likely includes these nuisance factors: in regularization, features are selected based on the degree to which they maximize classification accuracy instead of reducing the number of input features using an indirect proxy for classification accuracy. The RFE model is mathematically equivalent to the ℓ₂ SVM model in which the smallest SVM margins are set to be identically zero instead of their small estimated value. Similarly, t statistics assumes that the margins of low |t|-statistic features should be zero. This assumption is identical to the sparsity assumption of an ℓ₁ regularized SVM. However, ℓ₁ SVMs only outperform ℓ₂ SVMs when the underlying solution itself is sparse (Liu et al., 2007). By extension, we believe that RFE and t statistic filtering will only outperform ℓ₂ SVM if the best diagnostic model is sparse.

As shown by Chu et al., RFE and t-statistics did not improve performance, suggesting that these assumptions of non-redundancy and sparsity may have been violated. These shortcomings suggest that, while t-statistics and RFE have practical value, they are not general panaceas.

The limited efficacy of RFE, or univariate t statistics, does not predict that alternate unsupervised DD-FS algorithms will, or will not, outperform regularization. Independent and Principal Component Analysis (ICA and PCA), for example, can both in effect project multiple linearly correlated, or redundant, features onto a reduced number of features (Comon, 1994; Hyvarinen, 1999; Jutten and Herault, 1991; Wold et al., 1987). In contrast to RFE and t-statistics, these methods that combine highly correlated and, frequently, spatially continuous voxels into regional features improve generalization substantially (e.g. Douglas et al., 2010; Franke et al., 2010, 2012; Hinrichs et al., 2009; McKeown et al., 1997). Both ICA and PCA can control for the variation in highly diagnostic independent or principal components due to nuisance factors. Other DD-FS methods such as information criteria (Ding and Peng, 2005; Peng et al., 2005), genetic algorithms (Yang and Honavar, 1998), and Markov Chain Monte Carlo methods (Green, 1995) select a single representative of each set of redundant diagnostic features. This perspective on DD-FS does not modify the original input features; instead it aims to more efficiently select the minimum subset of non-redundant features that maximizes performance. Numerous other DD-FS approaches employ clever algorithms that overcome some of the limitations of RFE and t statistics (i.e. Dietterich, 2000; Freund and Schapire, 1997; Friedman et al., 2000; Kwak and Choi, 2002; Leiva-Murillo and Artes-Rodriguez, 2007; Liu and Setiono, 1997; Setiono and Liu, 1997; Sindhwani et al., 2004; Zhang and Sun, 2002; for a review see Saeys et al., 2007). Therefore, we emphasize again that the findings for RFE and t statistics should not be generalized to all DD-FS methods.

As a second practical point, we consider the conclusion that DD-FS performed worse than the feature selection inherent to SVM. We direct attention to Fig. 9E of the original manuscript, which shows how accuracy changes with decreasing values of the SVM regularization parameter, C, as a function of the DD-FS method employed for the largest sample size. We remind the reader of the original soft margin SVM formulation presented famously by Cortes and Vapnik (1995) that presents the Lagrange functional for the two-class problem as:

$$L(w,b,R,\xi )=\frac{1}{2}{\Vert w\Vert }^2-\sum _{i=1}^n{\alpha }_i[y_i(x_i\cdot w+b)-1+{\xi }_i]-\sum _{i=1}^n{r}_i{\xi }_i+C\sum _{i=1}^n{\xi }_i$$ (1)

where n, i, w, b, Y, X, α, r, and ξ, are the total number of exemplars, exemplar index, margin, intercept, output class vector, input data matrix, support vector Lagrange parameter, soft margin Lagrange parameter and soft margin misclassification penalty, respectively. The linear decision function in the feature space takes the form:

$$I(z)=\text{sign}(\sum _{\text{Support Vectors}}{\alpha }_i{x}_i\cdot z+b)$$ (2)

where z is the hyperplane perpendicular to w. If α_i = 0, then the corresponding sample was classified correctly and is irrelevant to the final solution. If α_i = C, then the sample was misclassified, and if 0 < α_i < C, then the sample is located on the margin. If α_i > 0, the sample is called a support vector (Biggio et al., 2011). When solving for very large values of C, the problem tends towards the hard margin solution that can be solved using quadratic programming. With smaller C, the soft margin functional can be optimized through its dual formulation with quadratic programming.

Within their analysis, Chu et al. assessed their accuracy with several parameter choices of C without cross-validation. The global optimum accuracy was obtained in the absence of FS. However, we would like to emphasize that even for the optimum C case (indicated by C*), the performance of the other FS algorithms were all within the 95% confidence interval of the no FS approach (Fig. 1). For moderate to small choices of C, FS methods systematically outperformed no FS, and were overall less sensitive and more robust to the choice of C. As discussed by Chu et al., the selection of this C is computationally intense therefore it is frequently simply selected a priori.

Fig. 1.

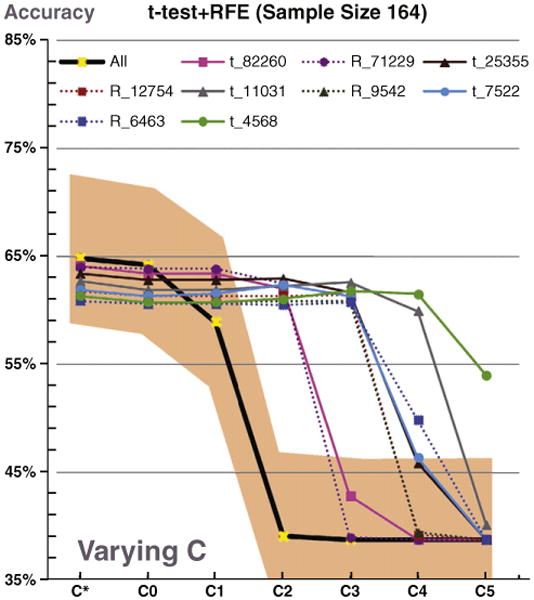
A reproduction of Chu et al.'s Fig. 9E where the added shading indicates the 95% confidence interval for the no feature selection accuracy using the normal approximation of the binomial distribution. Accuracy using all voxelized features was not significantly higher than data-driven feature selection accuracy at the optimum C, C*. At multiple non-optimum C values, the accuracy using data-driven feature selection was significantly higher than using all voxelized features.

While we agree that DD-FS does not always improve classification accuracy, it may nevertheless help elucidate the pathology or physiology of the system under study, and can reduce the sensitivity of performance to tuning parameters when applied to the data in a principled manner. Overall, a parsimonious model made possible by DD-FS allows models to be more transparent, and thereby more useful for neuroscientific interpretation (Hanke et al., 2010). This sparsity can be implemented through separate FS methods, or within the SVM itself. While ℓ₂ regularization already applies a degree of sparsity (Cortes and Vapnik, 1995), ℓ₀ regularization imposes a stricter penalty and has been used to interpret dynamic causal modeling features (Brodersen et al., 2011).

In the ML literature, it is common to evaluate methods primarily, or solely, on their classification accuracy. For typical cases, this is entirely appropriate: the goal is to classify, and not to explain. In investigative research, however, the needs are broader and more nuanced. In our own work, we use ML to aid in our understanding of brain function and dysfunction. We have shown previously that in some cases high classification accuracy can be obtained either from nuisance factors (Anderson et al., 2011), or from factors in the data, such as demographics, unrelated to neuroimaging (Colby et al., 2012). While these have the potential to generate clinically meaningful accuracies, they provide limited neurophysiological insight. If, on the other hand, the feature space is selected to project onto well-defined, neurally-oriented subspaces, it is possible to jointly achieve excellent accuracy and explanatory power to aid in neuroscientific discovery. For example, independent components identified from functional MRI data frequently identify the default mode network (Greicius et al., 2004) and have been used for classification (Douglas et al., 2010) as well as the generation of meaningful feature dictionaries (Anderson et al., 2011; Zibulevsky and Pearlmutter, 2001). Although these dictionary elements would vary across subjects and scans, we and others have shown that they are consistent enough to have an identifiable manifestation, an assumption underlying group-ICA methods (Franco et al., in press; Sui et al., 2009). Therefore, these methods accomplish the tasks of feature ‘identification’ and ‘selection’ simultaneously.

The goal of feature selection is to minimize the number of estimated parameters in the final machine-learning model to improve performance and generalizability. The concept of balancing the empirical performance of the model to the data with the number of estimated parameters is well established in conventional statistics. For generalized linear models, the pervasive F test explicitly divides the explained variance of a model by the number of estimated parameters in the model to calculate the mean squared error. Additionally, the reference F distribution for determining significance is wider for models with more estimated parameters. Similarly, the Akaike and Bayesian information criteria (AIC and BIC) explicitly penalize the observed log likelihood of models using a function of the number of estimated parameters. While these criteria cannot formally be applied directly to cross-validation accuracy, our perspective is that the concept behind these criteria is applicable to machine-learning models. Based on that idea, machine-learning models that achieve similar accuracy by operating on a selected set of features are preferred in investigative research over machine-learning models that are saturated with input features. We recognize that, unlike the likelihood or explained variance, cross-validation accuracies do not monotonically increase with the number of estimated parameters. We believe that DD-FS methods, in some situations, can be used effectively to accomplish this dual goal of model simplicity and high empirical cross-validation accuracy.

Despite the shortcomings of the methods tested mentioned herein, we also find it interesting that removal of a vast number of potentially irrelevant features with FS did not offer improvement, despite the theoretical caveats we detail above. It is possible that this lack of improvement is informative in and of itself. We suggest that pre/post FS accuracy should be reported more often, as these results may be helpful in conceptualizing how feature interactions are related to information representation in neural systems.

Because of this improvement in interpretability, we emphasize that FS methods are valuable beyond improving classification accuracy; just as a picture is a thousand words, an interpretable model is oftentimes immensely more valuable than a marginally superior yet uninstructive classification tool.