Identifying Splicing Regulatory Elements with de Bruijn Graphs

Abstract

Splicing regulatory elements (SREs) are short, degenerate sequences on pre-mRNA molecules that enhance or inhibit the splicing process via the binding of splicing factors, proteins that regulate the functioning of the spliceosome. Existing methods for identifying SREs in a genome are either experimental or computational. Here, we propose a formalism based on de Bruijn graphs that combines genomic structure, word count enrichment analysis, and experimental evidence to identify SREs found in exons. In our approach, SREs are not restricted to a fixed length (i.e., k-mers, for a fixed k). As a result, we identify 2001 putative exonic enhancers and 3080 putative exonic silencers for human genes, with lengths varying from 6 to 15 nucleotides. Many of the predicted SREs overlap with experimentally verified binding sites. Our model provides a novel method to predict variable length putative regulatory elements computationally for further experimental investigation.

1. Introduction

Alternative splicing is a process for regulating gene expression and promoting proteomic diversity in eukaryotes. It is the process whereby a pre-mRNA from a eukaryotic gene can be spliced in different ways to produce different mRNA isoforms with potentially different functions (Eichner et al., 2011). Recent studies indicate that more than 95% of human genes undergo alternative splicing (E et al., 2013; Lv et al., 2013; Wen et al., 2010). The RNA splicing process depends on the recognition of specific sequence elements in pre-mRNAs called splicing signals. They include conserved sequences, called the core splicing signals, that act as the corresponding signals to the spliceosome to splice out the intronic regions, such as the 5′ splice site, the 3′ splice site, and the branch point sequence. In addition to these core splicing signals, other short sequences on the pre-mRNA, called splicing regulatory elements (SREs), are pivotal to ensure that splicing events occur accurately and efficiently (Matlin et al., 2005). Splicing factors, such as SR proteins and hnRNPs, which are specific proteins that regulate alternative splicing, bind to these SREs (Wang and Burge, 2008). Therefore, identifying SREs is crucial to the understanding of alternative splicing.

The SREs are classified as exonic/intronic splicing enhancers/silencers (ESE, ESS, ISE, or ISS) based on where they reside (exon or intron) and whether they promote or inhibit the inclusion of the exons (Buendia et al., 2012; Wang and Burge, 2008; Wen et al., 2010). Accurate splicing is crucial. It is believed that up to 50% of human genetic diseases are the result of mutations either in the core splicing signals or in the SREs (Barash et al., 2010a; Ferreira et al., 2007; Keren et al., 2010; Lv et al., 2013; Matlin et al., 2005). For instance, alternative splicing is involved in familial isolated GH deficiency type II (IGHD II) (Kim et al., 2009), Frasier syndrome disease (Kim et al., 2009), neurodegenerative diseases (Garcia-Blanco et al., 2004), and frontotemporal dementia with parkinsonism-17 (FTFP-17) (E et al., 2013).

There have been several large-scale experimental studies of alternative splicing. Experimental techniques utilized to identify SREs include systematic evolution of ligands by exponential enrichment (SELEX) (Chasin, 2007), UV crosslinking and immunoprecipitation (CLIP) (Ule et al., 2003), and minigene-based systems (Wang et al., 2004). SELEX experiments have been carried out with a number of SR proteins and hnRNPs (Djordjevic, 2007; Matlin et al., 2005). CLIP has allowed the identification of the binding sites in vivo of several splicing factors, such as NOVA (Ule et al., 2003), SRSF1 (ASF/SF2) (Sanford et al., 2008), hnRNP A1 (Guil and Cáceres, 2007), and TDP-43 (Tollervey et al., 2011). There are at least 655 human splicing factor binding sites that are experimentally verified currently (Giulietti et al., 2013). The minigene-based technology utilizes the natural transcriptional and splicing machinery but concentrates only on a genomic segment of interest (Warner and Chamberlain, 2006). Several studies have exploited minigene technology for identifying SREs (Barash et al., 2010b; Ke and Chasin, 2010; Zhang et al., 2005; Zhang and Chasin, 2004).

On the other hand, there are various computational approaches that have been utilized to identify SREs. The word count enrichment approach is a widely used technique. It identifies SREs as short nucleotide sequences (typically 6-mers) that are statistically enriched in a thoughtfully selected set of exons with respect to a background or negative data set. For example, in the RESCUE-ESE approach, Fairbrother et al. (2002) identified 6-mers in constitutive human exons by sequence enrichment in exons versus introns and by sequence enrichment in exons with weak splice sites versus exons with strong splice sites. Using strict cutoffs, 238 distinct 6-mers were identified as possible ESEs, which were clustered into ten motifs. Zhang and Chasin (2004) utilized noncoding exons (exons that are not involved in protein synthesis although they exist in the pre-mRNA) instead of protein-coding exons and identified 2096 enhancers and 974 silencers.

Wen et al. (2010) employed the same approach to identify tissue-specific SREs in mouse genes. Mouse RNA-seq data for three tissues (brain, liver, and skeletal muscle) were utilized. Using a z-score, they identified any 6-mer that is over-represented in one tissue but not in the other two tissues as a tissue-specific SRE. The authors identified 456 putative enhancers and silencers. Among these, 45 were common to all tissues. Fedorov et al. (2001) compared the frequencies of 4-mers and 5-mers in exons to those in intronless genes. They identified 23 sequences that were significantly more abundant in exons. Pertea et al. (2007) introduced another computational approach to identifying ESE motifs in the model plant Arabidopsis thaliana. First, they utilized an approach similar to RESCUE-ESE to identify putative ESE 6-mers; 84 potential ESE 6-mers were identified. Then, they applied Gibbs sampling to the 5′ and 3′ flanking ends of the internal exons to identify the most common motifs, where the previously identified ESEs were used as input seeds.

Instead of employing statistical analyses, Zhang et al. (2003) exploited support vector machine (SVM) classifiers to define specific sequence information that distinguishes true exons from pseudo-exons. Pseudo-exons are intronic sequences that, although flanked by obvious consensus splice sites, they are not observed in spliced mRNAs. The authors identified 256 splicing elements. Zhang et al. (2012) employed a varying effect regression model on splicing elements (VERSE) to predict genome-wide intronic SREs. RNA-seq data for 16 human tissues were used. The authors incorporated non-motif-based biological features (e.g., phyloP conservation scores) into the model as the baseline binding preference of splicing factors. More than half of the SREs (55.68%) were found to be significant only in one tissue.

In all the previously stated studies, a predefined length for SREs is assumed, and the frequency of occurrence of these SREs is taken into account. What is known is that the motifs recognized by SR proteins are short and degenerate (Pertea et al., 2007). Their lengths range from 4 to 18 nucleotides (Goren et al., 2006), but most SRE studies have focused on 6-mers (Alexandre et al., 2004; Buendia et al., 2012; Pertea et al., 2007; Ramalho et al., 2013; Sakabe and De Souza, 2007; Wen et al., 2013). Some utilized 7-mers (Kim et al., 2009; Szcześniak et al., 2013; Zhang and Chasin, 2004) or 5-mers (Zhang et al., 2003) instead. As experimental evidence indicates, SREs should not be restricted to a fixed length. SpliceAid-F (Giulietti et al., 2013) is a recent comprehensive database that includes all known splicing factors and their experimentally determined binding sites, from which it is clear that the experimentally verified SREs vary in length. SpliceAid-F contains binding site sequences for different organisms. That includes human, mouse, chicken, rat, and rabbit. Therefore, assuming a predefined size beforehand can lead to inaccurate results, especially when the SRE frequency is a key part in the analysis, as SRE length affects frequency.

Here, we propose a de Bruijn graph-based model to identify exonic splicing elements of variable length that entails word count enrichment analysis. The proposed model combines different data sources to accurately identify SREs. We utilize data from Ke et al. (2011), who used a minigene approach to insert random 6-mers into the central exon. Based on their results, an enrichment index is calculated for all possible 6-mers, which is considered a measure of central exon inclusion ability. Utilizing these scores in our graph model, we can identify longer k-mers. We apply our model on a data set of all known human coding exons and their flanking intronic regions to find exonic enhancers and silencers. The discovered ESEs and ESSs overlap with many of the experimentally verified splicing elements in the SpliceAid-F database (Giulietti et al., 2013), as well as several computationally predicted data sets.

2. Preliminaries

We use terminology from formal language theory (Hopcroft and Ullman, 1979). Let Σ be an alphabet, a finite set of symbols such as the DNA alphabet {A, C, G, T}. For k ≥ 1, the k-dimensional de Bruijn graph G = (V, E) over Σ is a directed graph with vertex set V = Σ^k, all length-k strings over Σ, and edge set

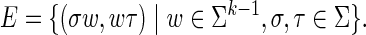In other words, an ordered pair of length-k strings (u, v) 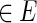if the length-(k − 1) suffix of u equals the length-(k − 1) prefix of v (Rosenberg and Heath, 2000). Clearly, |V | = |Σ|^k, |E| = |Σ|^k+1, and the indegree and outdegree of each vertex is |Σ|.

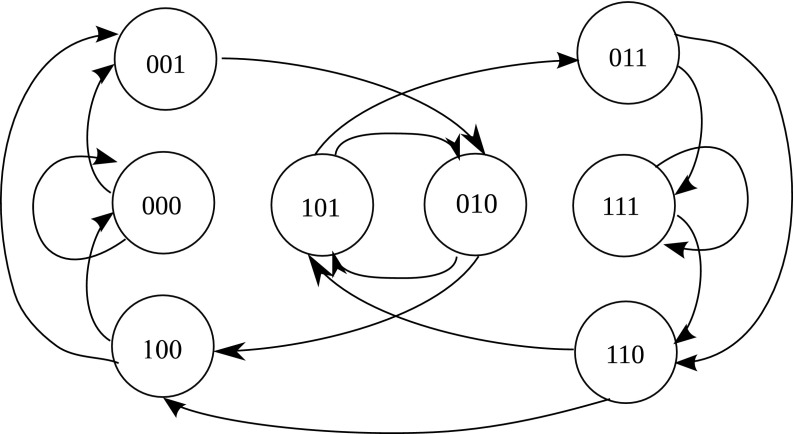
For example, the three-dimensional (3D) de Bruijn graph over the binary alphabet Σ = {0, 1} has 2³ = 8 vertices, that is V = {000, 001, 010, 011, 100, 101, 110, 111}. This de Bruijn graph is depicted in Figure 1. Similarly, the two-dimensional (2D) de Bruijn graph over the DNA alphabet Σ = {A, C, G, T} has vertex set

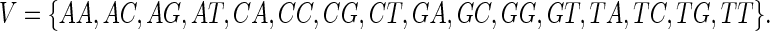FIG. 1.

The three-dimensional (3D) de Bruijn graph over alphabet Σ = {0, 1}.

Let G = (V, E) be any de Bruijn graph, and let U ⊆ V. The SRE graph G_U = (U, E′) for G and U is the vertex-induced subgraph of G with edge set

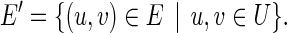A weakly connected component in a directed graph G = (V, E) is a maximal, nonempty set of vertices C ⊆ V such that, for every pair of vertices 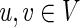, there is path in the underlying undirected graph from u to v (Pemmaraju and Skiena, 2003). The set of weakly connected components of G clearly partition V.

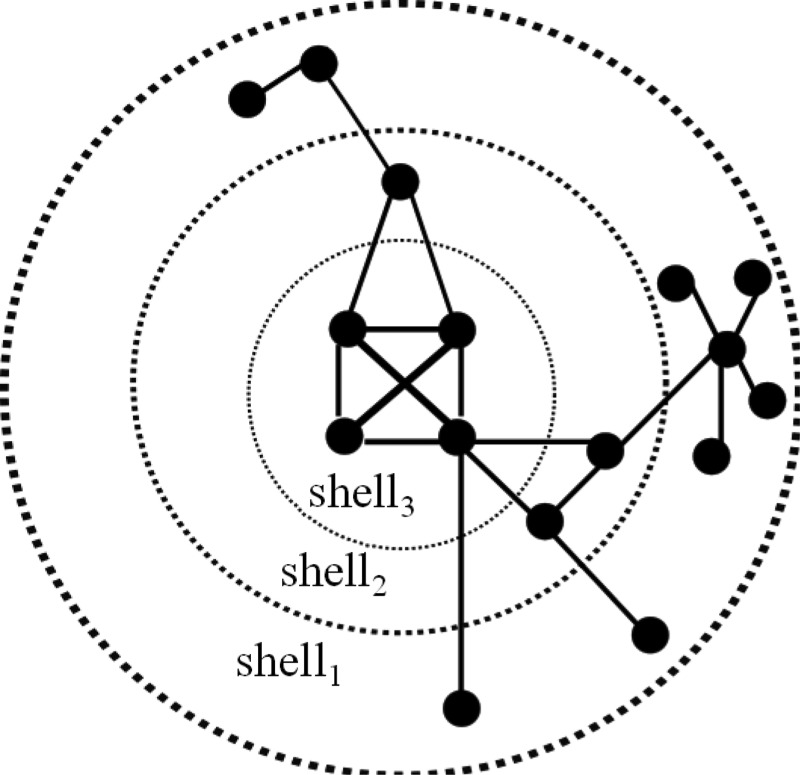
A j-core (or j-shell) decomposition analysis is a method to identify the most connected or important nodes in a graph (Kitsak et al., 2010). Using j-core analysis, the graph is described in a layered structure as illustrated in Figure 2, where the innermost nodes are the most important ones and the other nodes will be positioned in the outer layers according to their importance, revealing a hierarchy for the graph. Therefore, finding the position of the node relative to the organization of the network can determine its influence better than utilizing a local property of nodes such as its degree (Batagelj and Zaversnik, 2003). The j-core of a graph is obtained by recursively removing all nodes with degree < j and their incident edges; the remaining nodes and edges form the j-core graph.

FIG. 2.

An example of j-core analysis where three shells are identified (adapted from Kitsak et al., 2010).

3. Methods

3.1. Data Sets

LEIsc (log of the enrichment index, scaled) scores from Ke et al. (2011) are used. Utilizing the minigene approach, they placed all 4096 6-mers at five different sites in two model exons. For each 6-mer, an LEIsc value was calculated. It represents a relative measure of central exon inclusion for each pre-mRNA molecule, with higher values representing greater inclusion.

A library of variant minigenes was constructed to include random 6-mers and then sequenced using an Illumina Genome Analyzer. A relative concentration was assigned to all 6-mers based on millions of high-confidence reads. The library was then transfected into human embryonic kidney cells (HEK293), and 24 hours after the transfection, the mRNA molecules that had successfully included the central exon were isolated and converted to cDNA. The output molecules were then similarly sequenced. For each 6-mer, an enrichment of output proportion over input proportion (enrichment index, or EI) was calculated. The EI value represents the splicing efficiency of the central exon.

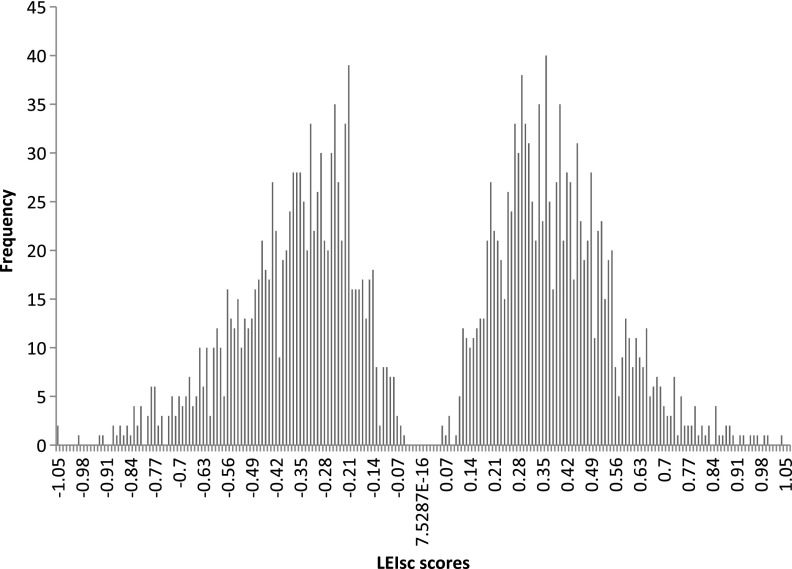
The spectra of activities of the 6-mers often differed among the five chosen sites. Much of this context effect was due to the creation of different overlapping sequences at each site. The 6-mer scores were identified based on the average of LEIsc values of a specific 6-mer in all five sites and all different places within a 16-nucleotide region of each site. In this way, LEIsc values can determine potential SREs that are generally used. Using a t-test to compare each LEIsc value of a specific 6-mer with the average of the LEIsc values of molecules that do not contain this 6-mer, Ke et al. (2011) identified 1182 potential ESEs and 1090 potential ESSs. The LEIsc scores range from 0.0534 to 1.034 in the ESE case. In the ESS case, they range from −0.0596 to −1.061. Figure 3 shows the distribution for both ESE values and ESS values.

FIG. 3.

Distribution of the LEIsc scores. The x-axis represents LEIsc scores and the y-axis represents their frequencies. On the left, ESS values range from −0.0596 to −1.061, while on the right, the ESE values range from 0.0534 to 1.034. LEIsc, log of the enrichment index, scaled; ESS, exonic splicing silencers; ESE, exonic splicing enhancers.

Another data source is all the available unique coding exons for known human genes from the ENCODE project (Karolchik et al., 2004), which reports 205,163 exons from 29,179 genes. Data was acquired from the RefSeq Genes track, where known human protein-coding and non-protein-coding genes are recorded. The December 2013 human genome assembly (GRCh38/hg38) is used. The 200 intronic nucleotides upstream and the 200 intronic nucleotides downstream of each exon are also retrieved.

For comparing our results with previously published results, several databases are utilized. SpliceAid-F (Giulietti et al., 2013) is a recent comprehensive database that includes all the experimentally verified splicing factors and their binding sites. It contains 71 splicing factors and 655 binding sites for human. We also used AEdb (Stamm et al., 2006), which is a database for alternative exons and their properties from various species; it is the manually curated component of the Alternative Splicing Database (ASD). The exon data in AEdb have been experimentally verified.

In addition, we compared our ESE list with four other computational data sets. The RESCUE-ESE (Fairbrother et al., 2002) data set contains 238 6-mers for human exons. Another data set is PESE (Zhang and Chasin, 2004), where 2096 8-mers were identified. The third data set is from Fedorov et al. (2001) and contains 4- and 5-mers as potential ESEs. Finally, in the data set from Zhang et al. (2003), the authors concentrated on 5-mer putative ESEs.

For ESSs, we compared our results with FAS-ESS (Wang et al., 2004) and PESS (Zhang and Chasin, 2004). The FAS-ESS data set contains 130 10-mer sequences that were identified utilizing the mini-gene approach. PESS is another data set in which the authors compared the frequencies of 8-mers (allowing one mismatch) in constitutively spliced noncoding exons with those in pseudo-exons and the 5′ untranslated regions (UTRs) of intronless genes.

3.2. Outline of our computational strategy

A de Bruijn graph–based model followed by word count enrichment analysis is applied. Our hypothesis is that SREs can be detected through both their effect on splicing (inclusion ratio and LEIsc scores) and their frequency in a specific data set (exons) with respect to a background data set (flanking introns). In particular, utilizing a de Bruijn graph allows us to detect potential SREs of different lengths based on the experimental data from Ke et al. (2011). The assumption that all SREs are of the same length can lead to inaccurate results as the actual length of an SRE is usually unknown. Therefore, developing a computational method to produce SREs that vary in length based on experimental data can achieve more accurate results.

If there are two 6-mers that overlap in five nucleotides and both of them have high LEIsc values, there is a greater probability that they form a potential 7-mer SRE. For example, if the two 6-mers ACGTCA and CGTCAT both have high LEIsc scores, there is a good chance of having one 7-mer SRE with the sequence ACGTCAT. The same applies with m consecutive 6-mers in the de Bruijn graph; if they all have high LEIsc values, then they can form one potential (m + 5)-mer SRE.

The processing in our model consists of six steps. First, we construct the six-dimensional de Bruijn graph G = (V, E) over the DNA alphabet Σ = {A, C, G, T} and associate each vertex with its rank based on LEIsc scores from Ke et al. (2011). Second, depending on whether we are searching for ESEs or ESSs, we select a subset U ⊆ V; for example, if we are looking for ESEs, then we might select U to be the 400 6-mers with the highest LEIsc values. Third, we construct the SRE graph G_U. Fourth, we determine the weakly connected components in G_U. Fifth, we apply the algorithm GenSRE to each weakly connected component to determine a set of potential SREs (see section 3.3). Sixth, these sequences are submitted to word count enrichment analysis accompanied by all known human coding exons with their intronic flanks (see section 3.4).

3.3. Identifying variable length SREs

The six-dimensional de Bruijn graph G = (V, E) over the DNA alphabet Σ = {A, C, G, T} is constructed. Each vertex v is a 6-mer. G represents all the possible one-character overlaps between pairs of 6-mers. It has 4096 vertices and 16,384 edges.

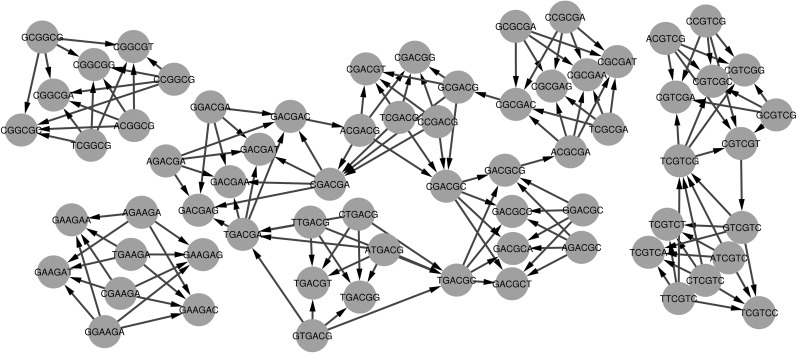
As stated before, each 6-mer has an LEIsc value that represents a relative splicing strength score for that 6-mer (Ke et al., 2011). The higher the LEIsc value, the greater the potential enhancing effect of that 6-mer on splicing. Similarly, the lower the LEIsc value, the greater the potential silencing effect of that 6-mer (Fig. 3). We utilize the findings in Ke et al. (2011) of potential exonic enhancers and silencers. If a specific 6-mer was found to be an enhancer or silencer, we use its associated LEIsc score. If it is defined as neutral, we consider its LEIsc value to be zero. Then, we order all the scores in descending order and associate each vertex v in the G graph with its rank. The rank is suggestive of the strength of a 6-mer on splicing. As a result, the graph can capture hot spots where many connected vertices have high ranks (for enhancers) or low ranks (for silencers). Supplementary Table S1 (Supplementary Data are available online at www.liebertonline.com/cmb) contains all possible 6-mers in descending order according to their LEIsc scores. Let R be a predefined number of ranks. A set U is constructed by choosing the top R vertices by rank in the case of searching for ESEs, and the lowest R vertices by rank in the case of ESSs. The SRE graph G_U = (U, E′) is constructed. Weakly connected components 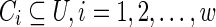, where w is the number of weakly connected components in G_U, are then extracted. Supplementary Figure S1 is an example of one of the weakly connected components for ESEs, where R = 100.

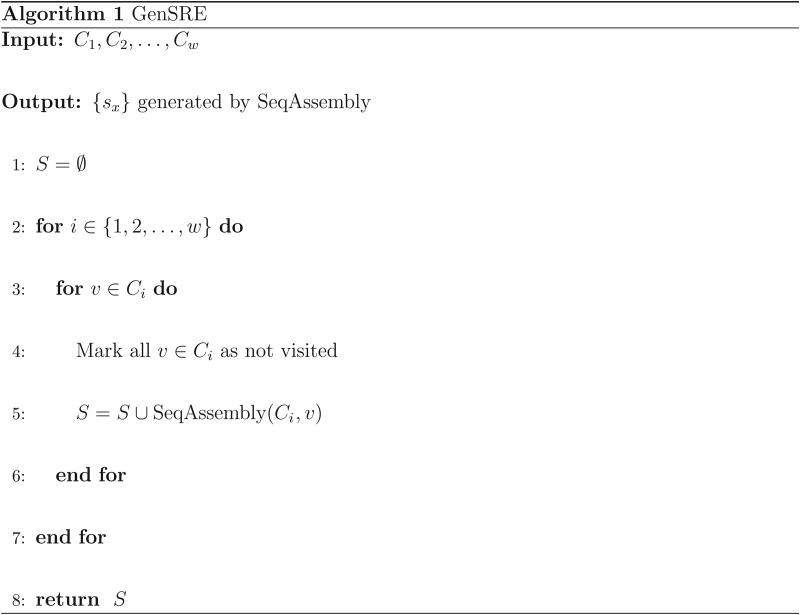
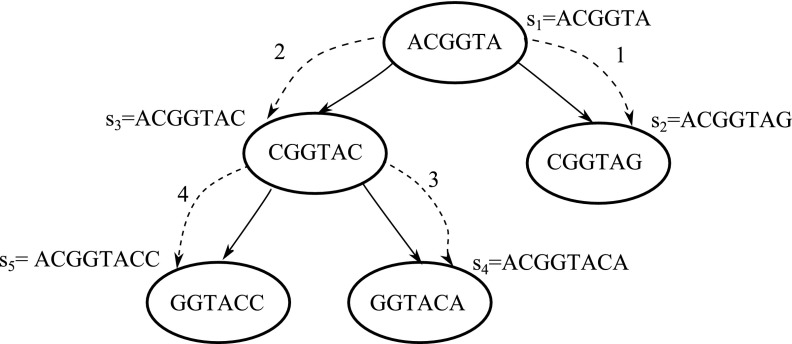
We developed the GenSRE algorithm to generate all potential SREs. The pseudocode for GenSRE can be found in Figure 4. For each C_i, the SeqAssembly algorithm is applied as illustrated in Figure 5. Starting from each vertex 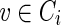, a modified depth-first traversal is performed. At each vertex x, a sequence s_x will be produced, representing the sequence going from v to x. Clearly, the sequence length |s_x| depends on what level the traversal reaches. This process is repeated with each vertex in C_i as the starting vertex for the traversal, as given in the GenSRE algorithm. The result is all potential sequences with length six or more. As stated before, the idea is that, if there are two 6-mers that are overlapping in five nucleotides and both of them have high ranks, there is a greater probability that they form a 7-mer potential ESE. Figure 6 illustrates an example of the traversal and the output sequences. Consequently, the output sequences represent k-mers that can serve as potential SREs.

FIG. 4.

GenSRE algorithm: Generating all possible sequences from the weakly connected components.

FIG. 5.

SeqAssembly: Sequence assembling algorithm. A subroutine to traverse a weakly connected component starting from a specific vertex. Each vertex x is associated with a sequence s_x, which is extended as the traversal goes deeper.

FIG. 6.

An illustration of GenSRE algorithm. The depth-first traversal starts at vertex ACGGTA where the dotted lines with its associated number represent order of the traversal. The resulting sequences are labeled by the order they were produced. The output sequences in order are: s₁ = ACGGTA, s₂ = ACGGTAG, s₃ = ACGGTAC, s₄ = ACGGTACA, s₅ = ACGGTACC.

As illustrated in line 10 of the SeqAssembly algorithm, we mark the vertices we encounter in the traversal as visited. Therefore, these vertices will not be visited again. We do not allow such revisits, because the existence of directed cycles will result in an infinite loop. The main drawback is that a vertex may be reached multiple times because two initially parallel paths from v intersect at some vertex x. Fortunately, these paths will rarely be shorter than length 6, so the algorithm does retrieve most SREs of length ≤ 12.

Theorem 1. The GenSRE algorithm has time complexity O(|U|(|U| + |E′|)), where |U| is the number of nodes in the SRE graph and |E′| is the number of edges.

Proof. The SeqAssembly algorithm will be repeated for each weakly connected component and each vertex in each component. Having |U| nodes in all the components, this operation will be repeated |U| times. The time complexity of the depth-first traversal is O(|V_Ci| + |E_Ci|), where |V_Ci| is the number of vertices in a weakly connected component C_i and |E_Ci| is the number of its edges. Therefore the time complexity for the traversal on all components is O(|U| + |E′|). Consequently, the time complexity of the algorithm is O(|U|(|U| + |E′|)).     ■

3.4. Word count enrichment analysis

As mentioned before, word count enrichment analysis is a computational technique that is widely used for identifying SREs. It searches for short nucleotide sequences that are statistically overrepresented or underrepresented through the comparison of foreground and background sequences (Wen et al., 2010; Zhang et al., 2012). The same approach is followed here on the set S of sequences produced from the GenSRE algorithm. A data set consisting of the human coding exons and of their flanking intronic regions is utilized as well.

Consider any sequence 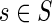; let j = |s| be its length. Its frequency f_E(s) in the first and last 50 nucleotides of all the exons is calculated. Its frequency f_I(s) in the intronic flanking regions is calculated as well. Let N_E and N_I be the total number of j-mers in the exonic and intronic regions, respectively. Note that N_E and N_I change with each j-mer based on its length. The two-sample proportion z-score (Fairbrother et al., 2002; Wen et al., 2010; Zhang and Chasin, 2004) of s is then given by

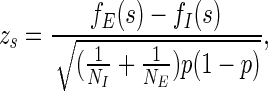where

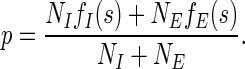We use pooled sample proportion p, as our null hypothesis states that f_E = f_I (Weiss, 2005). Potential SREs are defined as overrepresented j-mers in exonic regions but not in intronic regions. To test the statistical significance under the null hypothesis f_E = f_I, j-mers with z ≥ 1.64 (p < 0.05, two-tail test) are identified as being overrepresented. A false discovery rate (FDR) is calculated for each overrepresented j-mer, and j-mer with FDR corrected p-value that is less than 0.05 are reported (Benjamini and Hochberg, 1995).

3.5. Analysis of the functional characteristics of predicted SREs

To assess the significance of our predicted SREs and whether they are good candidates for ESEs or ESSs, we utilized the command-line version of Ontologizer (Bauer et al., 2008), with the goal of determining the enriched GO annotations for the experimentally verified SREs from SpliceAid-F (Giulietti et al., 2013) and checking whether our predicted SREs share the same enriched GO terms. This can be interpreted, as both sets of SREs affect the regulation of similar pathways.

The genes that contain all the human coding exons that we use in our analysis are utilized as a background data set. For each exonic splicing element in SpliceAid-F, the exon data set is searched to allocate each splicing element, and the corresponding gene set is identified to form the study set. GO annotation files gene_ontology_edit.obo and gene_association.goa_human were downloaded. GO enrichment analysis is performed using the Topology-Elim algorithm. Westfall-Young Single Step multiple testing correction procedure is then applied. The same approach is applied on our predicted splicing elements.

We are interested in the biological process annotations. Therefore, for the previously known splicing elements, we choose the biological process category with the minimum adjusted p-value, where we consider only terms with p < 0.05 to be significant. Then, we categorize the known splicing elements according to their biological processes, and we did the same procedure for our set of putative splicing elements.

4. Results

For predicting potential ESEs, we chose the highest 400 6-mers by LEIsc values. In other words, the SRE graph was extracted with R = 400. We chose the value of R to be 400 as most of the analysis done by Ke et al. (2011) on their produced LEIsc scores, which we utilize, was on the highest or the lowest 400 LEIsc scores. However, R can be chosen to be any value based on the utilized data. Applying our model, 36 weakly connected components are produced with most of the 6-mers located in one large component. This component consists of 352 6-mers out of the 400. Table 1 provides the sizes of all the weakly connected components. Certainly, a weakly connected component of size 1 can produce only one ESE, a 6-mer, while most of the potential ESEs are harvested from the one of size 352.

Table 1.

Distribution of the 400 6-mers on the Weakly Connected Components in Case of Extracting Potential Exonic Splicing Enhancers

Number of 6-mer ESEs	352	5	2	1
Number of weakly connected components	1	2	5	28

ESE, exonic splicing enhancers.

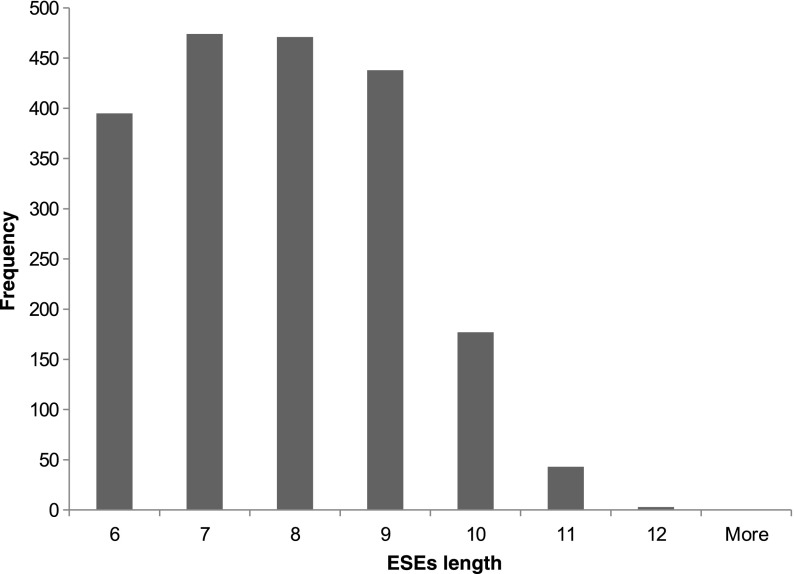
The GenSRE algorithm recovered 53,984 potential ESEs. Their lengths range from 6 to 87 nucleotides, with an average length of 48 nucleotides. Having one large weakly connected component is the reason that there are many potential ESEs that are quite long. Applying word count enrichment analysis, we obtained about 1500 to 2000 ESEs based on how many nucleotides are taken into account from the start and the end of all the exons (exonic flanks), as shown in Table 2. We started with n = 50, where n is the size of the exonic flanks. Extending this to n = 100 nucleotides did not change the results significantly, as many of the resulting ESEs are overlapping, as illustrated in Table 3. Different experiments were done utilizing different exonic flank lengths. These included 50, 100, 150, and 200 nucleotides. Supplementary Tables S2, S3, S4, and S5 contain the details of each experiment, including: a list of predicted ESEs, the frequency of each ESE in the exonic and intronic regions, its z-score, its associated p-value, and its FDR corrected p-value. In case of 50 nucleotide exonic flanks, we identified 2001 potential ESEs where their lengths range from 6 to 12 nucleotides. Figure 7 depicts the predicted ESE length distribution.

Table 2.

Number of Resulted ESEs Using Different Exonic Flank Sizes

Exon flank size (n)	50	100	150	200
Number of utilized exons	134596	34595	14970	10634
Number of putative ESEs	2001	1806	1595	1575

Table 3.

Number of Common ESEs Between Different Experiments

n (Number of ESEs)	50 (2001)	100 (1806)	150 (1595)	200 (1575)
50 (2001)	2001	1704	1514	1467
100 (1806)	—	1806	1528	1475
150 (1595)	—	—	1595	1460
200 (1575)	—	—	—	1575

FIG. 7.

Distribution of the ESE lengths. The x-axis represents ESE length and the y-axis represents the frequency of occurrence.

We compared our results, where the exonic flanks are 50 nucleotides, with exonic binding sites from SpliceAid-F (Giulietti et al., 2013). Removing duplicate binding sites, SpliceAid-F includes 330 different sequences for humans. Among those, 112 are exonic binding sites. We removed all sites that bind to members of the extended family of heterogeneous nuclear ribonucleoproteins (hnRNPs) and other splicing factors that are considered silencers according to the literature. The remaining 59 sequences are considered ESEs, as they bind to splicing factors that are involved in enhancing activities. Since our predicted ESEs are of variable length, as are SpliceAid-F binding sites, we calculated the overlap between the two sets by finding whether each sequence in the first list is totally contained in at least one sequence in the second list and vice versa. The total number of overlapped sequences is 105.

Another data set is AEdb (Stamm et al., 2006). It contains 294 splicing regulatory motifs. Among those, 124 are ESEs. We considered only the 64 ESEs that belong to humans.

In addition, we compared our ESE list with four other computational data sets, such as the RESCUE-ESE (Fairbrother et al., 2002) data set where the total overlap was 54 6-mers. The RESCUE-ESE approach is focused on exon skipping events (Chasin, 2007), which may explain the low overlapping percentage. Another data set is PESE (Zhang and Chasin, 2004), where the overlap is 454 sequences. That includes 44 exact sequences (of length 8). The third data set is from Fedorov et al. (2001). As it contains only 4- and 5-mers as potential ESEs, we could only test if our data set includes any of these sequences. This also applies to the data set from Zhang et al. (2003). Table 4 summarizes the overlapping results.

Table 4.

Number of Overlapped ESEs with Previously Published Data Sets

Data set	SpliceAid-F 2001/69	AEdb 2001/64	RESCUE-ESE 2001/238	PESE 2001/2060	Fedrove 2001/42	Zhang 2001/42
Approximate	103/9	62/6	54/54	447/51	—/16	—/12
Exact	7	5	54	44	—	—
Total	105	63	54	454	42	12

To verify the ability of word count enrichment analysis to filter the potential splicing elements, we applied this analysis to the 112 exonic and 87 intronic binding sites from SpliceAid-F (Giulietti et al., 2013). Table 5 illustrates that 70.3% of the exonic binding sites were overrepresented in the human coding exons and about 74% of the intronic binding sites were overrepresented in the flanking intronic regions, which indicates the ability of this analysis to identify potential regulatory elements. The total number of exonic binding sites is 112 sequences. However, we are searching for overrepresented sequences in the exonic flanks of length 50 nucleotides. Therefore, we limited the search for sequences with length less than or equal to 50 nucleotides (104 sequences). Many of the sequences were not found in our data set of all human coding exons (40 sequences). The remaining sequences (64 sequences) were tested for overrepresentation by calculating their z-scores. Using the same cutoffs, k-mers with z ≥ 1.64 (P < 0.05, two-tail test) are identified as being overrepresented. A false discovery rate (FDR) is calculated for each overrepresented k-mer, and k-mers with FDR corrected p-value that is less than 0.05 are reported. The same approach is applied on the intronic binding sites.

Table 5.

OverPresented Binding Site Statistics from the SpliceAid-F Data Set Utilizing Word Count Enrichment Analysis

Binding sites	Exonic	Intronic
Total number	112	87
Total number with length ≤ 50 nucleotides	104	77
Number of sequences found in our data set	64	50
Number of overrepresented sequences	45 (70.3%)	37 (74%)

For the exonic splicing silencers, we chose the lowest 400 6-mers in LEIsc values by rank. Applying our model, 18 weakly connected components are produced with most of the 6-mer silencers connected in one component, as in the case of 6-mer enhancers. The largest component consists of 369 6-mer ESSs out of the 400 silencers. Table 6 indicates the size of all the produced components.

Table 6.

Distribution of the 400 6-mers on the Weakly Connected Components in Case of Extracting Potential ESSs

Number of 6-mer ESSs	369	6	4	3	2	1
Number of weakly connected components	1	1	1	2	2	11

ESS, exonic splicing silencers.

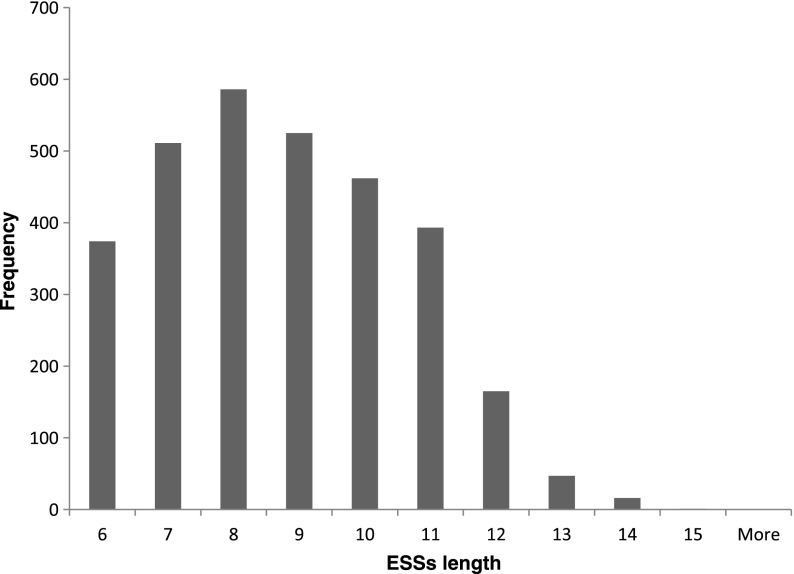
The GenSRE algorithm resulted in 63,780 potential ESSs, with lengths ranging from 6 to 88 nucleotides and an average length of 47 nucleotides. For word count enrichment analysis, we chose the exonic flank size to be 50 nucleotides as in the case of ESEs. This resulted in 3080 ESSs with length ranges from 6 to 15 nucleotides. Figure 8 illustrates the ESS length distribution. Supplementary Table S6 contains the ESS related information, including: a list of predicted ESSs, the frequency of each ESS in the exonic and intronic regions, its z-score, associated p-value, and its FDR corrected p-value.

FIG. 8.

Distribution of the ESS lengths. The x-axis represents ESS lengths and the y-axis represents their frequencies.

Our ESSs are compared with other data sets as illustrated in Table 7, such as SpliceAid-F (Giulietti et al., 2013), AEdb (Stamm et al., 2006), FAS-ESS (Wang et al., 2004), and PESS (Zhang and Chasin, 2004).

Table 7.

Number of Overlapped Potential ESSs with Previously Published Data Sets

Data set	SpliceAid-F 3080/53	AEdb 3080/24	FAS 3080/130	PESS 3080/1019
Approximate	88/10	22/3	190/—	338/35
Exact	3	3	—	34
Total	95	23	190	339

We used Ontologizer to analyze the functional similarities between the known splicing elements from SpliceAid-F data set and our predicted SREs. Table 8 depicts the different biological process categories for both ESEs from SpliceAid-F and our predicted ESEs. Out of 19 categories for the known ESEs, 14 are shared with our ESEs with the largest p-value as 0.00271. Supplementary Table S7 contains the complete list of the biological processes in which the predicted ESEs are involved. Supplementary Tables S8 and S9 depict the common biological process categories for ESSs and the biological processes for the predicted ESSs, respectively. Our remaining ESEs have more functional categories; some of them are listed in Table 9.

Table 8.

Common Biological Process Categories of Our ESE List and ESE from SpliceAid-F Based on GO Term Enrichment Analysis

GO ID	Name	SpliceAid-F ESEs	Predicted ESEs
GO:0007250	Actin filament capping	1	1
GO:0006200	ATP catabolic process	1	5
GO:0007411	Axon guidance	11	178
GO:0030574	Collagen catabolic process	1	39
GO:0032508	DNA duplex unwinding	1	6
GO:0022617	Extracellular matrix disassembly	5	191
GO:0046037	GMP metabolic process	1	1
GO:0071044	Histone mRNA catabolic process	1	4
GO:0086010	Membrane depolarization during action potential	1	11
GO:0007018	Microtubule-based movement	2	26
GO:0007528	Neuromuscular junction development	1	7
GO:0090292	Nuclear matrix anchoring at nuclear membrane	4	1
GO:0021860	Pyramidal neuron development	1	1
GO:0060372	Regulation of atrial cardiac muscle cell membrane repolarization	1	1

Table 9.

Example of Some Biological Process Categories of the Predicted ESEs Based on GO Term Enrichment Analysis

ID	Annotation	Number of predicted ESEs
GO:0031532	Actin cytoskeleton reorganization	3
GO:0008154	Actin polymerization or depolymerization	2
GO:0070358	Actin polymerization-dependent cell motility	2
GO:0007190	Activation of adenylate cyclase activity	2
GO:0006919	Activation of cysteine-type endopeptidase activity involved in apoptotic process	2
GO:0009060	Aerobic respiration	3
GO:0097055	Agmatine biosynthetic process	3
GO:0021960	Anterior commissure morphogenesis	2
GO:0019885	Antigen processing and presentation of endogenous peptide antigen via MHC class I	5
GO:0015991	ATP hydrolysis coupled proton transport	5
GO:0007409	Axonogenesis	3
GO:0051016	Barbed-end actin filament capping	4
GO:0006699	Bile acid biosynthetic process	3
GO:0015878	Biotin transport	11
GO:0007596	Blood coagulation	3

5. Discussion

We introduce a de Bruijn graph formalism to identify exonic splicing elements of variable length. Utilizing this approach leads to the identification of new potential ESEs and ESSs. One of the advantages of our model is its scalability. This model allows building the de Bruijn from any k-mer (based on the available data). The number of k-mers that are taken into consideration (R) can be changed according to the available data as well. In our case, we utilized the LEIsc scores as a measurement for ranking 6-mers. The rank can be based on other criteria such as conservation scores. Deciding on the significance of the produced k-mers may depend not only on the rank values and frequency but also on other data sources. For example, having a list of all protein binding sequences that are experimentally verified can increase the probability of having a certain k-mer as a putative SRE if a part of the sequence is in the verified list. Another possibility is utilizing the conservation score of the sequence of interest.

Another advantage of our model is its flexibility. We applied our model on a list of all known human coding exons and its flanking intronic regions to find potential ESEs. The same approach is also applied for finding ESSs. To do so, instead of selecting the highest 400 6-mers, we selected the lowest 400 6-mer in the LEIsc scores. Potentially, our model can also be utilized to find ISEs and ISSs by searching for the sequences of interest to be overrepresented in the intronic regions and underrepresented in the exonic flanks.

Using the parameter values of R = 400 and exonic flank size of 50 nucleotides, we identified 2001 potential ESEs. This includes some of the well-known ESEs such as GAAGAA, which is verified experimentally in the RESCUE-ESE data set (Fairbrother et al., 2002). It is noticed that this 6-mer is part of the consensus sequences RGAAGAAC (R = A or G) that has been verified as a SELEX binding motif to the ASF/SF2 splicing factor (Tacke and Manley, 1995). ASF/SF2 is one of the highly conserved proteins that affects alternative splicing (Tacke and Manley, 1995). Our method could accurately identify this binding site as GGAAGAAC with p-value 1.07 × 10⁻⁵⁵. Moreover, there are some other possibilities that contain the same sequence such as GGAAGAACG and GAAGAACG with p-values 2.01 × 10⁻⁹ and 2.43 × 10⁻⁴¹, respectively.

Another consensus motif for the ASF/SF2 splicing factor is GARGARGAR (Selvakumar and Helfman, 1999), which we have in our results as GAAGAAGAG with p-value 9.58 × 10⁻²³, in addition to longer k-mers that contain this sequence (see Supplementary Table S3).

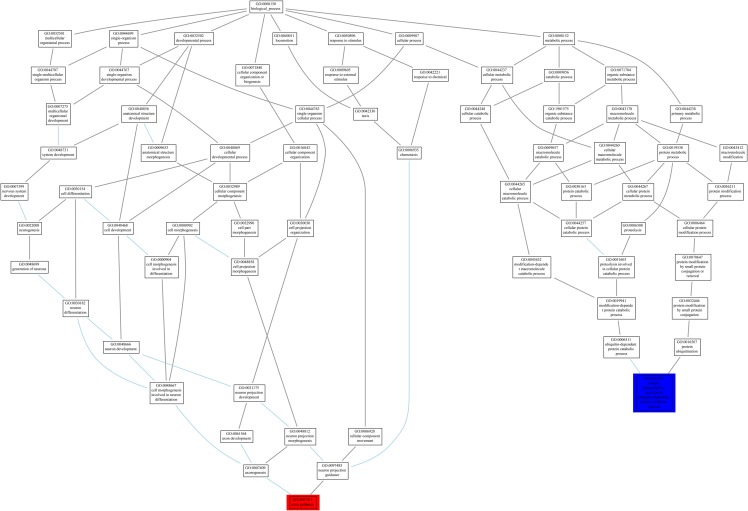
Utilizing the results obtained from Ontologizer, we investigated the effect of having similar binding sites on the biological processes in which they are involved. In other words, we wanted to know if the genes that contain the binding site GAAGAA are involved in the same biological process of the genes that contain the longer binding site GGAAGAAC. The answer is “no.” For GAAGAA; the most enriched biological process is “axon guidance” while, for GGAAGAAC, it is “protein ubiquitination involved in ubiquitin-dependent protein catabolic process.” It is obvious from Figure 9 that they are unrelated processes.

FIG. 9.

A tree map of gene ontology to illustrate the biological processes in which the genes of the two binding sites GAAGAA and GGAAGAAC are involved. GAAGAA biological process “axon guidance” is highlighted in red, while the other one “ubiquitin-dependent protein catabolic process” is highlighted in blue.

Axon guidance or axon path finding is a critical and complicated process for nervous system wiring, where there are certain tracts the axons should follow to reach specific targets (Nugent et al., 2012). Defects in this process can lead to various human disorders such as HGPPS (Nugent et al., 2012; Engle, 2010), congenital mirror movements, and congenital fibrosis of the extraocular muscles (Nugent et al., 2012), L1 syndrome, and albinism (Engle, 2010). Some of these disorders, such as HGPPS and L1 syndrome, are caused from missense, splice site, and frameshift mutations of the ROBO3 and L1CAM genes, respectively.

On the other hand, ubiquitin is a small regulatory protein that resides in eukaryotic cells and attaches to other proteins. This attachment can signal protein degradation (Burnett et al., 2008). It has been shown that ubiquitin has a controlling role in the splicing pathway and hence affects spliceosome assembly (Bellare et al., 2008). Moreover, according to Burnett et al. (2008), ubiquitin influences the stability and degradation of the SMN protein. In humans, SMN is encoded by two genes, SMN1 and SMN2. Mutations in SMN1 cause spinal muscular atrophy (SMA) disease. SMN stability is affected by its ability to oligomerize. Therefore, SMN mutations that prevent oligomerization lead to rapid degradation, and this may be the reason that it causes SMA (Burnett et al., 2008). It is also worth mentioning that the SMN protein is part of a large multiprotein complex (the SMN complex), which is essential for the biogenesis of small nuclear ribonucleoprotein particles (snRNPs). These snRNPs are major components of the spliceosome machinery.

It is clear that, although both of the these binding sites are overlapping on most of their sequences, the biological processes of the genes they reside in are highly different and alternative splicing is involved in both of the processes in different ways. The ability to determine a specific biological process can make it easier to investigate the actual effect the alternative splicing has in different contexts. Mutations in these binding sites can also affect the alternative splicing role. Therefore, having the ability to predict variable length SREs, instead of having a prefixed size before applying our analysis, gives the opportunity to discover new biological processes that alternative splicing may affect and gives an insight into how alternative splicing may work. Although we have a large number of biological processes in our analysis (947 categories), we see it as an opportunity for investigating specific contexts in which alternative splicing may play a role.

One of the ESSs that we have in our results and that is validated experimentally is TAGTTAG, a 7-mer ESS, which binds to the splicing repressor hnRNP A1 (Millevoi et al., 2010). Another 7-mer exon silencer is TTAAGGT (Baris et al., 2003), which is involved in optic atrophy disease.

Having one large weakly connected component that contains most of the SREs, whether for enhancers or silencers, indicates that there is much overlapping among the known SREs and confirms our hypothesis that longer k-mers can be a better and more accurate representation of SREs than shorter ones. As stated before, having an edge between two vertices means they overlap in five nucleotides and perhaps they form one 7-mer SRE. Analyzing the largest component further using j-core analysis (Batagelj and Zaversnik, 2003), Figure 10 illustrates the most influential nodes in the ESE case. In other words, these nodes are the most central and highly connected nodes. As a result, the 6-mers that these nodes represent are the most repeated 6-mers in our ESE list.

FIG. 10.

The most influential nodes in the largest weakly connected component for ESEs.

These sequences are found to be GC enriched with GC content about 68% (Table 10, column 1), which is analogous to many data sets that are experimentally verified (Table 2 in Chasin, 2007). This is also consistent with the fact that the regions around the splice sites are GC-enriched, which is considered one characteristic of having a stable pre-mRNA secondary structure (Zhang et al., 2011). Conserved and stable pre-mRNA secondary structures are thought to play an important role in splicing, as in Hiller et al. (2007), some of the experimentally verified SREs were found to be enriched near the splice sites in the regions of a single-stranded local secondary structure.

Table 10.

Base Compositions of Core Sequences in the Case of Exonic Enhancers and Silencers

Data	ESEs	ESSs
A%	21	23
C%	30	6
G%	38	33
T%	11	38

On the other hand, performing the same analysis on the silencers list, core sequences are found to be T-rich and C-poor just as in the PESS data set (Zhang and Chasin, 2004). Supplementary Figure S2 indicates the core nodes in the ESS case.

6. Conclusion

We have presented a new de Bruijn graph formalism to identify exonic splicing elements of variable length. Utilizing this approach leads to the identification of new potential ESEs and ESSs. Genomic structure, word count enrichment analysis, and experimental evidence were all utilized in our model to increase the accuracy of our results. We have developed GenSRE algorithm to produce potential variable length SREs. To demonstrate the usefulness of our approach, we compared our results with experimentally verified data sets and computational data sets as well. Our results overlap with many of the experimental and computational results. We also analyzed the effect of having similar binding sites on the biological processes in which they are involved. We indicated that although the binding sites may overlap on most of their sequences, the biological processes of the genes they reside in can be highly different. Thus, the SRE's length is a key part in the analysis where it cannot be assumed to be fixed. Our approach can open new directions to study SREs and the roles they play in alternative splicing.

Acknowledgments

We express appreciation for the support of NSF grant DBI-1062472. We also thank Dr. Ruth Grene for helpful discussions. This work is supported in part by the VT-MENA program of Egypt.

Author Disclosure Statement

The authors declare that no competing financial interests exist.