Characterization of structural variants with single molecule and hybrid sequencing approaches

Abstract

Motivation: Structural variation is common in human and cancer genomes. High-throughput DNA sequencing has enabled genome-scale surveys of structural variation. However, the short reads produced by these technologies limit the study of complex variants, particularly those involving repetitive regions. Recent ‘third-generation’ sequencing technologies provide single-molecule templates and longer sequencing reads, but at the cost of higher per-nucleotide error rates.

Results: We present MultiBreak-SV, an algorithm to detect structural variants (SVs) from single molecule sequencing data, paired read sequencing data, or a combination of sequencing data from different platforms. We demonstrate that combining low-coverage third-generation data from Pacific Biosciences (PacBio) with high-coverage paired read data is advantageous on simulated chromosomes. We apply MultiBreak-SV to PacBio data from four human fosmids and show that it detects known SVs with high sensitivity and specificity. Finally, we perform a whole-genome analysis on PacBio data from a complete hydatidiform mole cell line and predict 1002 high-probability SVs, over half of which are confirmed by an Illumina-based assembly.

Availability and implementation: MultiBreak-SV is available at http://compbio.cs.brown.edu/software/.

Contact: annaritz@vt.edu or braphael@cs.brown.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Structural variation—including duplications, deletions, insertions and translocations of genomic segments—are an important source of variation in human and cancer genomes. Human genomes differ by thousands of inherited structural variants (SVs) (Quinlan and Hall, 2012), many of which have been associated with genetic disorders and diseases (Hurles et al., 2008; Mills et al., 2011; Xi et al., 2010). SVs have long been recognized as a form of somatic mutations that drive the development and progression of cancer (Choy et al., 2010; Mardis, 2012). The continuing decline in sequencing costs for next-generation DNA sequencing has made it the standard technique for structural variation detection, largely replacing microarrays and earlier cytogenetic techniques (Alkan et al., 2011).

Most structural variation studies conducted on highly repetitive mammalian genomes use a resequencing approach, where reads from an individual genome are independently aligned to a reference genome. Discrepancies between the expected and observed alignments or the number of aligned reads suggest potential SVs in the individual genome compared with the reference. Identifying SVs from short-read paired-end sequencing data is complicated by a number of factors, including sequencing and alignment errors, as well as repetitive sequences near SV boundaries (Korbel et al., 2007; Kidd et al., 2008).

To handle these obstacles, most methods detect structural variation by clustering fragments and assigning a higher confidence or score to the cluster if many fragments support the variant. Early approaches for paired-end data simplified the issue of repeats by either ignoring fragments that align to multiple locations in the reference or choosing a single ‘best’ alignment, breaking ties arbitrarily (Chen et al., 2009; Korbel et al., 2009; Sindi et al., 2009). Methods that incorporate ambiguous alignments for paired reads improved SV detection (Hormozdiari et al., 2009, 2010; Lee et al., 2008; Quinlan et al., 2010); however, these methods report a single set of predictions that usually involves minimizing the total number of SVs. More recently, GASVPro (Sindi et al., 2012) demonstrated the effectiveness of a probabilistic model that considers many possible read mappings and incorporates both a paired-end and a read-depth signal to refine variant predictions. Additionally, some tools have the capacity to analyze ‘split-reads’—correctly mapping the read subsequences for reads spanning breakpoint junctions—usually in the context of deletions or transcriptomic data (Jiang et al., 2012; Kim and Salzberg, 2011; Rausch et al., 2012; Stromberg, 2010; Trapnell et al., 2009). Despite these improvements, existing methods are inherently limited by the underlying sequencing technology; i.e. they often rely on explicit assumptions about fragment length, error rate, and the number of SVs that fragments imply.

Emerging single-molecule sequencing technologies—coined ‘third-generation’ technologies—from companies such as Pacific Biosciences (PacBio) and Oxford Nanopore are capable of sequencing longer fragments than current sequencing technologies. For example, PacBio’s Single Molecule Real Time (SMRT) sequencing generates reads greater than 7 kb on average, with some reads exceeding 40Kb (Eid et al., 2009; Korlach et al., 2010; Roberts et al., 2013). The benefits of longer reads come at a cost; per-base error rates of such technologies are higher than next-generation sequencing technologies (∼15% for PacBio). While Oxford Nanopore has not yet launched a commercial machine, early indications are that error rates will be higher than the 1–2% rates of current short-read technologies.

The properties of third-generation technologies provide unique opportunities and challenges for SV detection. A single read may span multiple SVs in the sequenced genome, generalizing the concept of split reads. Thus, standard assumptions of observing a single breakpoint from a single read must be relaxed as SVs are no longer independent from one another. Additionally, protocols such as strobe sequencing which produced multiply-linked reads from a single fragment of DNA (Turner, 2009), generalize the concept of paired-end sequencing. Both long reads and multiply-linked reads provide increased power to detect complex rearrangements with multiple nearby SVs. However, higher error rates create ambiguity in assessing an optimal alignment, making it necessary to consider a large set of possible alignments. Accounting for both higher error rates and multiple SVs leads to more subtle algorithmic concerns.

Previous work on SV prediction from single-molecule sequencing data (in the context of strobe sequencing data) formulated an optimization problem that aimed to minimize the number of predicted SVs (Ritz et al., 2010). While strobes showed increased specificity in SV predictions compared to paired-end sequencing, the method suffered from a large false positive rate and was never tested on real sequencing data. We propose a new algorithm, MultiBreak-SV, which directly addresses the challenges of high error rates and multiple SVs reported by a single read. Rather than trying to find a single solution and assignment for the data, MultiBreak-SV employs a probabilistic approach that considers all possible solutions. MultiBreak-SV is capable of predicting variants from paired-end sequencing data, third-generation data, and data from a combination of sequencing platforms. We benchmark MultiBreak-SV on simulated, highly-repetitive chromosomes using long read sequencing, strobe sequencing, paired-end sequencing and a mixture of strobe and paired-end data. We then demonstrate the accuracy of MultiBreak-SV on PacBio strobe sequencing data from four fosmids containing known SVs. Finally, we perform a genome-wide analysis on PacBio long read data to predict SVs from a cell line derived from a complete hydatidiform mole.

2 METHODS

We model an individual genome generated from a reference genome by independently deleting, duplicating and rearranging segments of the reference genome. We define a novel adjacency to be a pair of adjacent coordinates in the individual genome that are not adjacent in the reference genome. The number of novel adjacencies in the individual genome is related to the number of SVs: some variants, such as deletions, create one adjacency whereas other variants, such as inversions, create two adjacencies.

Sequenced fragments from the individual genome can be described as a τ-multi-reads consisting of an ordered list $S=(R_1,R_2,\dots ,R_{\tau })$ of τ contiguous substrings, or reads, from the individual genome. τ = 1 corresponds to single (long) reads, τ = 2 to paired-reads, and $\tau \ge 2$ to strobes or multi-linked reads (Supplementary Section 1.1). When $\tau \ge 2$, the reads are separated by regions of unknown sequences called advances.

To identify novel adjacencies, we align a set S of τ-multi-reads from an individual genome to a reference genome (Figure 1, Step 1). Aligning a single read R_i to the reference may result in full length alignments or, in the case of split reads, alignments of substrings of R_i. We define a t-multi-breakpoint-mapping to be a multi-read that aligns to the reference genome in t pieces, the pieces being non-overlapping substrings of the reads R_i (Supplementary Section 1.1). Generally, a multi-read S gives a multi-breakpoint-mapping by selecting an alignment for each read. If the alignment of each R_i is full length, then a τ-multi-read gives a τ-multi-breakpoint-mapping. However, in the case of long read fragments we may have $t\ge \tau$. In this case, we split the fragment into t-multi-breakpoint-mappings with advance length 0.

Fig. 1.

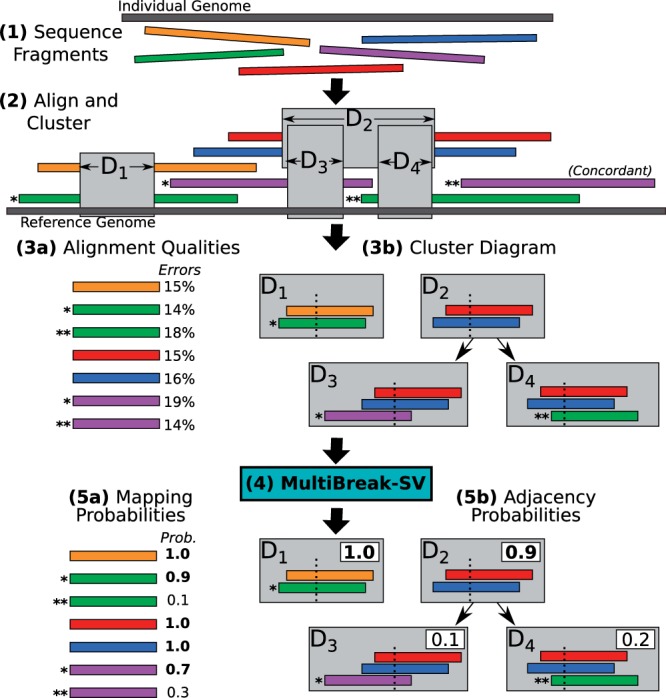
Overview of MultiBreak-SV. (1) Five long reads are sequenced from an individual genome. (2) The reads are aligned to the reference genome, producing seven distinct multi-breakpoint-mappings. When clustered, the multi-breakpoint-mappings indicate four novel adjacencies ($D_1,D_2,D_3,D_4$). (3a) The quality of the read alignments (e.g. the edit distance) is noted for each multi-breakpoint-mapping. (3b) The set of all possible novel adjacencies $\{D_1,D_2,D_3,D_4\}$ is represented as a cluster diagram G, where the nodes are novel adjacencies and the directed edges represent overlapping novel adjacencies. (4) The cluster diagram and alignment qualities are input to MultiBreak-SV. (5a) MultiBreak-SV assigns probabilities to each multi-breakpoint-mapping. (5b) From these mappings, the probability of each novel adjacency is computed. A solution to the Multi-Read Mapping Problem is a selection of at most one alignment for each multi read and a selection of at most one novel adjacency for each connected component in G (bold)

Each fragment corresponds to a single segment of the individual genome; we assume that this portion of the individual genome maps to at most a single location in the reference. Thus, for multi-read S there is at most one correct multi-breakpoint-mapping. Let A(S) be the set of all multi-breakpoint-mappings for multi-read S, along with the empty set (which indicates that the correct alignment is not present). The correct multi-breakpoint-mapping for multi-read S is thus an element in A(S). Selecting one element from A(S) for each multi-read in S produces a candidate mapping M that describes the placement of every multi-read in S. The goal of this work is to solve the following problem:

• Multi-Read Mapping Problem. Given a set S of multi-reads and their corresponding multi-breakpoint-mappings, find (1) an optimal mapping M*; that is, a selection of one element from A(S) for each $S\in S$, and (2) the set of novel adjacencies implied by M*.

When there are more than two reads (t > 2), there is a dependence between pairs of consecutive reads, and thus direct application of paired-read methods will not necessary yield a valid solution to the Multi-Read Mapping Problem. For example, for a 3-multi-read $(R_1,R_2,R_3)$, the alignments of the pairs (R₁, R₂) and (R₂, R₃), cannot be selected independently: a single alignment of R₂ must be chosen. MultiBreak-SV finds highly-probable mappings and novel adjacencies to solve the Multi-Read Mapping Problem (Fig. 1).

2.1 Implied adjacencies and the cluster diagram

For each read R_i, every read alignment a provides (i) the interval $[x_a,y_a]$ in the reference genome corresponding to the alignment location, (ii) the orientation sign_a of the alignment, (iii) and the edit distance ${\in }_a$ of the alignment. Let $\mathcal{P}$ be all pairs of alignments from adjacent reads in each multi-read, or the consecutive read pairs (Supplementary Section 1.2.1). A consecutive read pair $(a_1,a_2)\in \mathcal{P}$ is concordant if the aligned distance and orientation of the pair is expected given the sequencing platform and parameters (Supplementary Sections 1.2–1.2.1). If (a₁, a₂) is not concordant, then it is discordant and implies a novel adjacency in the individual genome. Let $P_{\text{discord}}\subseteq \mathcal{P}$ be the set of discordant consecutive read pairs (which we will call discordant pairs when the context is clear). When τ = 1 (in the case of long reads), $P_{\text{discord}}=\mathcal{P}$ because full alignments are considered concordant (Figure 1).

To accurately predict SVs, we must first identify all possible candidate novel adjacencies that arise from the set $P_{\text{discord}}$ of discordant pairs. Let $\mathcal{N}$ be the set of possible novel adjacencies determined from the discordant pairs $P_{\text{discord}}$. $\mathcal{N}$ is determined by clustering discordant pairs whose alignments are consistent with the same novel adjacency (Fig. 1, Step 2). We cluster discordant pairs using Geometric Analysis of Structural Variants (GASV) (Sindi et al., 2009), an algorithm which identifies candidate novel adjacencies and provides a geometric representation of how the discordant pairs contribute to each novel adjacency prediction (Supplementary Section 1.3).

To solve the Multi-Read Mapping Problem, we must ensure that the novel adjacencies implied by M do not conflict; that is, each discordant pair supports at most one novel adjacency. We capture the organization of these ‘conflicting’ novel adjacency predictions using a directed graph G called a cluster diagram (Figure 1, Step 3b). Nodes in G represent candidate novel adjacencies and edges represent pairs of candidate adjacencies that have one or more discordant pairs in common. A solution of the Multi-Read Mapping Problem includes at most one node from each connected component in the cluster diagram. G is computed as a preprocessing step using an efficient line-sweep algorithm (Supplementary Section 1.3).

2.2 Probabilistic model

We will now describe a probabilistic model for a mapping M given the data D which consists of (i) the multi-breakpoint-mappings $A(S)={\cup }_{S\in S}A(S)$ and (ii) the cluster diagram G. We provide a high-level description here; refer to Supplementary Section 1.4 for the full model. Our goal is to compute $P(M|D)$, the probability of a mapping M given the data. After applying Bayes’ Rule, the probability of D given M includes the conditional probability of the selected multi-breakpoint-mappings $A(S)$ and the conditional probability of the novel adjacencies G (the cluster diagram).

$$P(M|D)=\frac{P(D|M)P(M)}{P(D)}=\frac{P(A(S)|M)P(G|M)P(M)}{P(D)}.$$ (1)

A mapping M can be partitioned into the set A(M) of read alignments in M and the number e_M of missing alignments (empty sets):

$$P(A(S)|M)=P(A(M),e_M)=P(A(M))P(e_M).$$

The probability $P(A(M))$ of the read alignments depends on the error rates and fragment lengths of the sequencing technology. For a mapping M, let $\mathrm{ϵ}(M)$ be the total edit distance and $\ell (M)$ be the total length of all read alignments in M. We use a binomial distribution to model the probability of observing $\mathrm{ϵ}(M)$ errors in a string of length $\ell (M)$ when the sequencing error is $p_{\text{seq}}$. We assume the missed alignments occur independently with a fixed probability $p_{\text{err}}$. To compute $P(G|M)$, we find the smallest number of nodes in the cluster diagram G that cover the discordant pairs in M (Supplementary Section 1.3). The alignments in M are partitioned into the selected novel adjacencies; the number of mappings for each node is called the support. Let the non-zero supports be a vector $\Phi (M)$. We model the expected support of a novel adjacency as a Poisson process with parameter ${\lambda }_d=\lambda L_{\text{avg}}(t-1)$ where λ is the sequence coverage, t is the number of reads in the multi-read, and $L_{\text{avg}}$ is the average advance length. $P(M|D)$ in Equation (1) now becomes

$$\frac{[\text{Bin}\left(\mathrm{ϵ}(M);\ell (M),p_{\text{seq}}\right)p_{\text{err}}^{e_M}][{\displaystyle \prod _{k\in \Phi (M)}\text{Poiss}}(k;{\lambda }_d)]P(M)}{P(D)}$$ (2)

with hyperparameters $p_{\text{seq}},p_{\text{err}}$, and λ_d, and a uniform prior P(M) over all mappings. The hyperparameters can be prespecified or inferred from the read alignments. We have generalized the model to include multiple sequencing technologies (e.g. strobes and pairs), allowing for multiple hyperparameters (Supplementary Section 1.7).

2.3 Markov chain Monte Carlo method

The probability in Equation (2) is prohibitive to compute due to the large number of possible mappings M. However, we still want to consider the distribution of mapping probabilities for the data rather than simply finding a mapping M that maximizes $P(M|D)$. To achieve this, MultiBreak-SV employs a Metropolis–Hastings algorithm to sample mappings M with probability proportional to $P(M|D)$ (Figure 1, Step 4). MultiBreak-SV takes the set $A(S)$ of alignments and a cluster diagram G and samples mappings M for z iterations with probability asymptotically proportional to $P(M|D)$. MultiBreak-SV explores the solution space via two types of moves: a local move that changes the assignment of a single multi-read and a ‘jump’ move that changes the assignment of many multi-reads at one time (Supplementary Section 1.5).

Since the number of possible mappings grows exponentially with the number of multi-breakpoint-mappings, the Markov chain may take an extremely long time to converge. Fortunately, since novel adjacencies are independent, we divide S into independent subproblems for which MultiBreak-SV can be run in parallel (Supplementary Section 1.5.3). This independence observation was made by (Sindi et al., 2012) to make the problem tractable for GASVPro on paired-end data. We run each problem from 2 to 20 million iterations depending on the subproblem size.

2.3.1 Computing adjacency probabilities

To solve the Multi-Read Mapping Problem, we predict novel adjacencies (nodes in the cluster diagram G) from the mapping probabilities. We calculate the probability of the multi-breakpoint-mappings in order to derive an adjacency probability for each node in the cluster diagram G (Figure 1, Step 5). First, for every multi-read S we compute the probability of each multi-breakpoint-mapping $a\in A(S)$ by summing over probabilities of the mappings M that contain a (Supplementary Section 1.6). Then, for every node in G we compute the probability that the node is supported by k or more multi-breakpoint-mappings for a fixed value of k (Supplementary Section 1.6). Finally, we choose the node with the highest probability in each connected component of G as a predicted novel adjacency.

2.4 Datasets and algorithms for comparison

2.4.1 Simulated datasets

Following other methods (Chen et al., 2009; Ritz et al., 2010; Sindi et al., 2012), we constructed an individual chromosome, Venter, by including ∼17 000 adjacencies (including deletions, insertions and inversions) from HuRef into hg18 chr17 (Levy et al., 2007). From these rearrangements, we evaluated 124 deletions greater than 120 bp (detectable deletions) and four inversions. We focused on deletions greater than 120 bp to account for uncertainty (±60 bp) in fragment lengths for multi-reads with $\tau \ge 2$ (Ritz et al., 2010). We also constructed a chromosome with hundreds of novel adjacencies inserted from individuals from the 1000 Genomes project individuals into chr1 (1000 Genomes Project Consortium, 2010) and evaluated 511 deletions greater than 120 bp. We found notable differences in performance between the two simulations; see Supplementary Section 2.2 for a detailed discussion of 1000 Genomes simulation.

To simulate PacBio’s strobe platform, we generated 3-multi-reads with normally distributed read lengths (mean ± SD 322 ± 134, 360 ± 130, 359 ± 142) and advance lengths (1214 ± 40, 1171 ± 40) determined from the fosmid sequencing data described below, and inserted 15% error using Alchemy (Chaisson, 2012). To simulate short-read Illumina-like platforms, we generated two multi-reads with exactly 100 bp reads and normally distributed advance lengths (mean 400), inserted 1% error into the reads using wgsim (Li et al., 2009). We call the simulated strobe datasets Strobes, the simulated paired datasets Pairs. We also combined Strobes with Pairs datasets to produce Hybrid datasets.

We aligned all Pairs data with BWA version 0.6.2 (Li and Durbin, 2009) and all Strobes data with BLASR (Chaisson and Tesler, 2012) using default values, taking full alignments for each read and determining discordant pairs from the resulting multi-breakpoint-mappings. BWA retains a single, unique alignment for each paired-read; we found that including multiple alignments for a read in the paired dataset decreased performance (Supplementary Section 2.3). We fixed $p_{\text{seq}}=0.15$ for PacBio data, $p_{\text{seq}}=0.01$ for Pairs data, and $p_{\text{err}}=0.01$ for all datasets. The choice of λ_d depends on the sequencing coverage (Supplementary Table 1).

To simulate PacBio’s long read sequencing platform, we generated one-multi-reads whose lengths were exponentially distributed with mean 3.4 kb (approximating PacBio performance at the time of data generation), inserted 15% error using Alchemy, and aligned the reads using BLASR. We processed the alignments in two ways.

1. Determine multi-breakpoint-mappings from partial alignments. We construct a set of t-multi-breakpoint-mappings (for $t\ge 2$) from the alignments to the reference. We do this by building a directed acyclic graph with vertices corresponding to the alignments and edges corresponding to allowed discordant pairs between alignments (according to the coordinates in the long read). Traversing this graph in a depth-first manner produces potential multi-breakpoint-mappings; we retain multi-breakpoint-mappings that include at least 80% of the original long read. This construction is analogous to split read alignment approaches (Abyzov and Gerstein, 2011; Jiang et al., 2012; Wang et al., 2011); however here we permit the read to split into more than two pieces and do not require that the pieces partition the entire read. The latter is important as repetitive sequences at the breakpoint sometimes lead to overlapping and/or incomplete partial alignments.

2. Determine potential deletion coordinates within full alignments. We observed that BLASR often aligned across deletion coordinates in the reference with a gap. Further, the BLASR-reported coordinates of the gaps did not accurately reflect the deletion novel adjacencies. Thus, we refined the multi-read mapping coordinates reported by BLASR using a three-state (deletion, match/mismatch, insertion) hidden Markov model (HMM). For the match state emission probabilities, we fit a 20% error (symmetrically for insertions and deletions), thus 0.8 probability of emitting a match state. For insertions and deletions, we used a 0.9 probability of emitting their respective states. We allowed a 0.01 probability of transition from insertion and deletion states to a match state and a strict $1\times {10}^{-10}$ probability to transition from a match state to either insertion or deletion states. Initialization and termination states were both enforced to be match states, and the Viterbi path was selected to identify potential insertions and deletions. We found that deletion coordinates called in this manner were more accurate than the original BLASR gap coordinates. Each deletion greater than 200 bp called in this manner was considered a two multi-breakpoint-mapping.

We also ignored multi-breakpoint-mappings near telomeres/centromeres, and converted multi-breakpoint-mappings to discordant pairs by taking the outer coordinates in the case that the BLASR alignments aligned across the breakpoint (which occurs in highly repetitive regions). More details about the two steps above and the filtering are in the Supplementary Section 1.8.1. We call the simulated long read dataset Long.

2.4.2 PacBio Data

We sequenced four human fosmids (two harboring a deletion, two harboring an inversion) from individual NA15510 (Kidd et al., 2008) (Supplementary Section 2.4). The fosmids were sequenced using an early prototype PacBio machine; two SMRT cells were used for each inversion compared with one SMRT cell for each deletion. We performed a robustness analysis by varying $p_{\text{err}}$ and λ_d.

We also obtained 10 × coverage of publicly-available long read data of the human CHM1TERT cell line from PacBio (Pacific Biosciences, 2013). We used the Long processing pipeline described above with one pre-processing step before executing Step 1: we ignored any long read where 80% of the read aligned contiguously to the reference. We also ensured that the alignment did not contain a large deletion by requiring that the coordinates in the reference must be within 20% of the long read length. We used the same $p_{\text{err}}$ and $p_{\text{seq}}$ as in the simulations. To estimate λ_d, we determined the coverage of long read alignments to chr20. There are 78 121 long reads that have over 80% aligning to chr20; the average length of these long reads is about 6500. Dividing the total number of bases in these reads by the size of chr20 yields a λ_d of 8.06 (Supplementary Table 1).

2.4.3 Illumina assembly

We compare CHM1TERT to a reference-guided CHM1TERT assembly (NCBI BioProject PRJNA178030). An initial assembly was generated from 38 × coverage Illumina HiSeq2000 aligned to hg19; the assembly was then refined using 400 BAC clones for CHM1TERT. We mapped the coordinates in the reference (hg19) to the CHM1TERT assembly by aligning each chromosome assembly to the corresponding chromosome in hg19 using nucmer (Delcher et al., 2002). We retained alignments greater than 7 kb and alignments that had a one-to-one query-to-reference mapping. This was achieved with the delta-filter ‘−1’ option, which maps each position of the query to the best hit in the reference and vice versa. We use the alignments to map novel adjacency coordinates to the assembly.

2.4.4 Algorithms for comparison

We compared MultiBreak-SV to GASV version 2.0 (Sindi et al., 2009), Hydra version 0.5.3 (Quinlan et al., 2010), VariationHunter version 3.0 (Hormozdiari et al., 2009), Delly version 0.5.6 (Rausch et al., 2012), and a parsimony based method for multi-reads (Ritz et al., 2010).

3 RESULTS

3.1 Venter simulation

We evaluated the ability of MultiBreak-SV to predict SVs from the Venter simulated chromosome and compared MultiBreak-SV predictions to other state-of-the-art variant-calling methods. We first assessed the accuracy in recovering deletions and inversions, and then assessed the accuracy of selecting the correct multi-breakpoint-mapping for each multi-read.

3.1.1 Deletion calling accuracy

A predicted novel adjacency is a true positive (TP) variant that reflects deletion (x, y) if there exists a pair of novel adjacency coordinates (a, b) such that a is within $L_{\text{max}}/2$ of x and b is within $L_{\text{max}}/2$ of y (‘double-uncertainty metric’ (Sindi et al., 2009)); otherwise it is a false positive (FP). For each method applied to each dataset, varied a parameter that thresholds the number of predictions (Supplementary Table 3) to produce a ranked list of predicted novel adjacencies. From this ranked list, we computed a receiver operating characteristic (ROC) curve to evaluate the algorithm’s performance on 124 deletions from the Venter simulation (Figure 2 Left). Of the 124 deletions, 112 (90.32%) have repetitive sequence spanning both of the novel adjacency coordinates; this set is a good representative of variants that lie in repetitive regions. Further, multi-breakpoint-mappings that span these deletions are not necessarily the best BLASR hit (Supplementary Section 2.1). MultiBreak-SV on 5× Strobes predicts more TP variants than any other dataset up to six false positives; after this point MultiBreak-SV on 2×/30× Hybrid is comparable to 5× Strobes MultiBreak-SV. Notably, all methods applied to the Strobes datasets improve over all methods applied to 30× Pairs, where predictions from 30× Pairs incur four times the number of false positives to find 70 detectable deletions. Further, MultiBreak-SV on 5× Strobes over the previously-published parsimony method at all values of specificity, predicting an additional 8–28 TP variants. MultiBreak-SV applied to 5× Long data has increased sensitivity compared to 30× Pairs up to 17 false positives, at which point GASVPro on 30× Pairs is comparable.

Fig. 2.

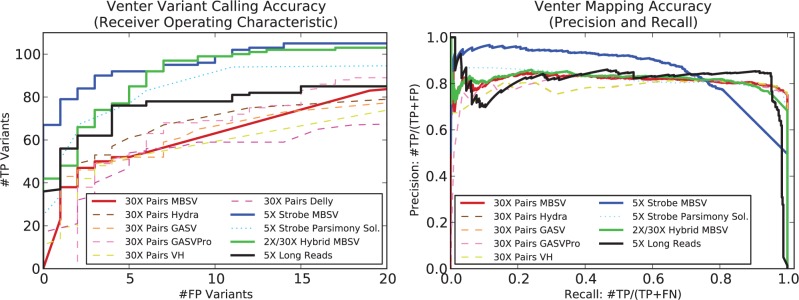
(Left) ROC curve of the variant calling accuracy and (Right) precision-recall curve of the mapping accuracy for the Venter simulation. For both plots, solid lines are MultiBreak-SV predictions (denoted MBSV), the dotted line is a an algorithm designed for multi-breakpoint reads (Ritz et al., 2010), and dashed lines are algorithms designed for paired-end reads: Hydra (Quinlan et al., 2010), GASV (Sindi et al., 2009), GASVPro (Sindi et al., 2012),VariationHunter (VH) (Hormozdiari et al., 2009), and Delly (Rausch et al., 2012)

3.1.2 Inversion calling accuracy

Inversions in human genomes are often difficult to identify from sequencing data because their adjacency coordinates tend to lie in repetitive regions (Antonacci et al., 2009). There are four inversions in the Venter simulation, which were evaluated using the double-uncertainty metric as above. MultiBreak-SV on the Strobes and Hybrid dataset predicts all four inversions, while MultiBreak-SV on 30× Pairs detects only two (Table 1). Inversions 1 and 4 were each supported by only a single strobe in the dataset. Thus, MultiBreak-SV incurs 50 false positives when predicting Inversion 4 due to the poor alignment quality of the supported mapping (error rate of 23%). Inversion 1 is predicted with only 6 false positives because the alignment quality of this supported mapping is higher (error rate of 17%).

Table 1.

Four inversions predicted by MultiBreak-SV on simulated data from Venter

	Inversion 1			Inversion 2
	Sup.	Prob	FPs	Sup.	Prob	FPs
2X Strobes	1	2e−3	6	7	1.0	0
5X Strobes	4	1.0	0	16	1.0	0
30X Pairs	0	—	—	50	1.0	0
2X/30X Hybrid	1	1e-3	6	57	1.0	0
	Inversion 3			Inversion 4
	Sup.	Prob	FPs	Sup.	Prob	FPs
2X Strobes	10	0.921	1	1	0.0	50
5X Strobes	24	1.0	0	4	0.365	3
30X Pairs	0	—	—	60	1.0	0
2X/30X Hybrid	10	0.479	1	61	0.5	0

Note: Sup. is the number of reads with a correct mapping in the dataset, Prob is the MultiBreak-SV probability of the correct inversion, and FPs are the number of false positives incorrect to detect the inversion.

3.1.3 Mapping accuracy

We called a predicted multi-read mapping a TP if there is at least an 80% overlap between the reported alignment to the reference genome and the true location. Since there are a different number of TP mappings for each dataset, we compute the precision and recall for each method rather than the ROC curve (Fig. 2 Right). Strikingly, MultiBreak-SV on 5X Strobes has mapping precision of 0.9 between recall of 0.05 and 0.5, where it gradually drops to 0.77. All other methods maintain a precision of about 0.8 after a recall of 0.2. This suggests that MultiBreak-SV on 5× Strobes enriches for a larger proportion of TP mappings than other methods. Note that MultiBreak-SV on Hybrid is comparable to MultiBreak-SV on 30× pairs due to the larger fraction of Hybrid mappings from paired-read data.

3.2 Sequenced fosmids from NA15510

Motivated by the promising performance of MultiBreak-SV in detecting variants on simulated data sets, we generated strobe sequencing data for four fosmids from individual NA15510 that were previously reported to contain SVs (Kidd et al., 2008). Before selecting fosmids from individual NA15510 for sequencing, we evaluated the detectability of the reported variants for the 63 fully sequenced fosmids (44 deletions and 19 inversions) from this study (Kidd et al., 2008). To identify candidates for strobe sequencing, we simulated 30× Strobes and 30× Pairs datasets and selected two deletions supported by $\ge 5$ strobes and $\ge 5$ pairs (D1 and D2). Additionally, we selected two inversions that were supported by $\ge 5$ strobes but not pairs (I1 and I2) (Supplementary Section 2.4).

MultiBreak-SV predicts the correct adjacency for all parameter choices in both deletions (Table 2; Supplementary Section 2.4). Deletions in D1 were predicted with no false positives for all parameter choices and similarly one false positive for D2. While both inversions were predicted using MultiBreak-SV, a number of false positives were also predicted. This was not surprising, since the breakpoints of the inversions lie in segmental duplications and the majority of the multi-breakpoint-mappings were ambiguous alignments (95% for I1 and 90% for I2 and Supplementary Section 2.4). Interestingly, although I2 has higher sequence similarity near the breakpoints than I1 (99% vs. 95%), the prediction of I2 incurs fewer false positives than I1 (Table 2).

Table 2.

Results on Sequenced Fosmids

			${\lambda }_d=10,$		${\lambda }_d=\{5,10,15,20\}$
			$p_{err}=.01$		$p_{err}=0.005-0.15$
	Accession	Cov.	TP	FP	TP	FP
D1	AC158335	18X	1	0	1 ± 0.00	0 ± 0.00
D2	AC153483	9X	1	0	1 ± 0.00	0.25 ± 0.44
I1	AC195776	31X	1	4	0.45 ± 0.51	3.7 ± 2.45
I2	AC193137	33X	1	1	1 ± 0.00	0.65 ± 0.67

Note: For each fosmid (D1, D2, I1 and I2) multiple values of λ and p_err were simulated. The steps for p_err in the last column are $\{0.005,0.01,0.05,0.1,0.15\}$. Values represent mean ± standard deviation.

3.3 Sequenced CHM1TERT genome

We applied MultiBreak-SV to third-generation sequencing data of CHM1TERT, a haploid cell line derived from a complete hydatidiform mole (Pacific Biosciences, 2013). CHM1TERT was sequenced to 10× coverage, producing over 300 000 multi-breakpoint-mappings for input to MultiBreak-SV (Supplementary Table 2).

3.3.1 Running time of MultiBreak-SV

There were nearly 250 000 GASV clusters from the multi-breakpoint-mappings, orders of magnitude larger than the number of SVs one would expect from a human genome compared to HuRef hg19. Nearly 90% of the are clusters supported by only one long read, indicating a spurious alignment. The GASV clusters could be divided into 131 594 independent subproblems, allowing for parallelization. About 122 294 (93%) of the subproblems contained six or fewer discordant pairs; we explicitly computed the probability for every possible solution, which took at most 10 s. Most of the remaining 9300 subproblems took about a minute to run (Supplementary Figure 15). The largest subproblem took ∼4.75 days, and included 535 clusters of all types (deletions, inversions and translocations). All 1962 fragments in this subproblem contained a multi-breakpoint-mapping to a highly rearranged region of chr16 q11.2; this region is responsible for the dependence of all fragments in the subproblem. We have removed this subproblem from the subsequent analysis.

3.3.2 Novel adjacencies predicted by MultiBreak-SV

MultiBreak-SV returns the posterior probability of every multi-breakpoint-mapping; we use these probabilities to compute the probability than an adjacency is supported by k or more multi-breakpoint-mappings (see Methods and Supplementary Section 1.6). When we compute the probability that an adjacency is supported by any multi-breakpoint-mapping (k = 1), 242 395 (98%) of the GASV clusters have an adjacency probability of less than 0.01. These clusters consist of multi-reads that are more often assigned an error rather than a mapping, and are consistent with the observation of spurious alignments in the GASV clusters. The remaining adjacency probabilities $\ge$ 0.01 are shown in Figure 3. Most of the high-probability (P $\ge$ 0.9) predicted adjacencies are deletions, while more inversions and translocations appear with lower probabilities. Since we used two methods to determine deletion breakpoints, the deletions are better characterized than the other types of novel adjacencies in our analysis. When we compute the probability of adjacencies supported by k = 5 or more mappings, there are 1034 adjacencies with a probability $\ge$0.01; 1002 with a probability $\ge$0.9 (Fig. 3). Again, there are more deletions than other types of adjacencies; however we do identify high-probability translocations (k = 5) and high-probability inversions (k = 1) (Fig. 4(A)).

Fig. 3.

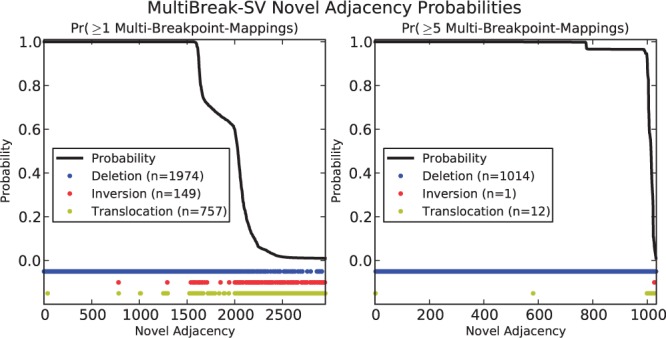
Distribution of CHM1TERT novel adjacencies predicted by MultiBreak-SV. (Left) Novel adjacency probabilities supported by at least one multi-breakpoint-mapping. Horizontal colored bands show the distribution of novel adjacencies by SV type. (Right) Novel adjacency probabilities supported by at least five multi-breakpoint-mappings

Fig. 4.

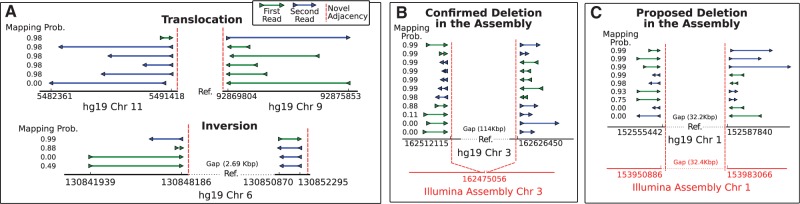
Examples of CHM1TERT novel adjacencies predicted by MultiBreak-SV. (A) Example of a high-probability translocation (prob=1.0 for k = 5) and an inversion (P = 0.999 for k = 1). Multi-breakpoint-mapping probabilities from MultiBreak-SV are shown next to each multi-breakpoint-mapping. (B) Confirmed deletion in the Illumina assembly. (C) Proposed deletion in the Illumina assembly

3.3.3 Comparison of predicted deletions to Illumina-based assembly

We compared the 997 deletions with adjacency probability greater than 0.9 for k = 5 to a CHM1TERT reference-guided assembly using Illumina data (see Methods). A predicted deletion in the reference with coordinates (a, b) is confirmed if there is an assembly-to-reference alignment within 100 bp of a, an assembly-to-reference alignment within 100 bp of b, and the two alignments are within 10 bp of each other in the assembly (Supplementary Section 2.5.1). Otherwise, we map a and b to the assembly using the assembly alignments, producing coordinates $a\prime$ and $b\prime$. A predicted deletion in the reference with coordinates (a, b) is proposed if the length b – a in the reference is within 80% of the length $b\prime -a\prime$ in the assembly (Supplementary Section 2.5.1).

About 552 (55%) of the deletions are confirmed by the assembly; this number increases to 581 when the coordinates a and b are within 100 bp of each other. An example of a confirmed deletion is shown in Figure 4(B). The large proportion of confirmed deletions is striking due to the differences between the two analyses in terms of sequencing platforms (PacBio versus Illumina) and the means of variant detection (resequencing versus genome assembly). Of the remaining 445 deletions, 128 (29%) are proposed deletions in the assembly (Figure 4(C) and Supplementary Tables 7–9). These predicted deletions suggest that the novel adjacency coordinates should be next to each other in the assembly, similar to Figure 4(B).

4 DISCUSSION

As long read technologies become more practical for large-scale genome sequencing, there is a clear need for methods that take advantage of these reads while allowing for the higher single-nucleotide error rates in current long read technologies. In addition, methods that integrate these datasets with existing short read data are also a priority. MultiBreak-SV helps address this need using a probabilistic model that considers many possible alternative alignments for each read. MultiBreak-SV additionally provides a natural framework for identifying SVs across multiple platforms. We have benchmarked MultiBreak-SV on multiple types of simulated sequencing data and compared it to other state-of-the-art variant detection algorithms designed for paired read and multi-read data. We have put forth a pipeline for identifying multi-breakpoint-mappings from long reads, enabling novel adjacency prediction from long read data. Here, we have shown that MultiBreak-SV not only outperforms current approaches using data from a single platform, but also enables hybrid approaches that combine data from multiple sequencing platforms.

We applied MultiBreak-SV to whole-genome sequencing data from CHM1TERT, a human cell line derived from a complete hydatidiform mole, which a target for a high-quality ‘platinum’ genome assembly (Pacific Biosciences, 2013). While probabilistic approaches such as MultiBreak-SV are powerful, they are more time-consuming than the parsimony-based methods we compare to (Hormozdiari et al., 2009; Quinlan et al., 2010; Ritz et al., 2010; Rausch et al., 2012). We have demonstrated that parallel processing of the data makes MultiBreak-SV feasible the CHM1TERT analysis. To evaluate our resulting predictions, we compare them to novel adjacencies found in an Illumina-based CHM1TERT assembly. We acknowledge that this assembly may be incorrect and incomplete, thus we do not treat it as a gold standard. Identifying a subset of the high-probability novel adjacencies that may be used to augment the existing assembly remains future work. Finally, since CHM1TERT is haploid, we suspect that it is considerably easier to identify variants since there should be no heterozygous events. It will be important to evaluate MultiBreak-SV on PacBio long read data generated from a diploid human genome when the data becomes available.

One of the challenges in single-molecule sequencing technologies is dealing with a higher per-nucleotide error rate. By considering many possible alignments for each read and constructing a model which incorporates the error rate, as well as the expected support for an adjacency, we are able to take advantage of the length of the read while mitigating false positives due to high error rates. This trade-off appears to be inherent to single molecule technologies. Upcoming technologies, such as Oxford Nanopore, have suggested they can achieve read lengths greater than 10 kb with per-base costs similar to short read technologies (Brown, 2012; Jaffe, 2014), and read lengths from PacBio continue to increase while maintaining similar error profiles.

Detecting multiple breakpoints from the same DNA fragment is not a strategy limited to single-molecule sequencing platforms. Recent advances, such as long fragment read (LFR) technology, allow short read sequencing platforms to mimic long reads (Peters et al., 2012). The ‘Infinipair’ technique holds the potential of obtaining multiple linked short reads from a single sequence fragment by inducing an electrical field over Illumina flow cells (Schwartz, 2012). These advances in short read platforms further motivate the need for designing algorithms for fragments with more than two sequenced reads (τ-multi-reads with $\tau >2$).

Sensitive alignment procedures to find ambiguous alignments from long reads and multi-reads are important for discovering high-quality predictions. Many structural variation methods propose tiered alignment strategies to find ambiguous alignments (Sindi et al., 2012; Quinlan et al., 2010; Hormozdiari et al., 2009); however we found that these strategies drastically increased the total number of ambiguous alignments to consider, effectively “drowning out” the signal from true variants (Supplementary Section 2.3). Ultimately, more sensitive alignment pipelines will improve SV prediction from multi-breakpoint reads. The HMM for identifying breakpoints within completely-spanning BLASR alignments is one step towards this goal.

Complex SVs with multiple, co-located breakpoints have been observed in both normal and cancer genomes (Sharp et al., 2006; Malhotra et al., 2013). Given the complexity of structural variation observed in humans, the ability to detect multiple breakpoints on a single read is becoming increasingly critical. In 2–3% of all cancer genomes (and up to 25% in some cancers) specific chromosomal regions are seen to be greatly enriched for nearby rearrangements via a process known as chromothripsis (Korbel and Campbell, 2013). As researchers delve into increasingly complex regions of the genome (with multiple co-located rearrangements and/or dense repeat structure), probabilistic methods that can assign confidence to each call, while integrating orthogonal sequencing platforms, will become a necessity. Our method, MultiBreak-SV, provides a generalized framework for such approaches.