Conformational dynamics and aggregation behavior of piezoelectric diphenylalanine peptides in an external electric field

Abstract

Aromatic peptides such as diphenylalanine (FF) have the characteristic capacity to self-assemble into ordered nanostructures such as peptide nanotubes, which are biocompatible, thermally and chemically stable, and have strong piezoelectric activity and high mechanical strength. The physical properties of FF aggregates open up a variety of potential biomedical applications. Electric fields are commonly applied to align FF nanotubes, yet little is known about the effect of the electric field on the assembly process. Using all-atom molecular dynamics with explicit water molecules, we probe the conformational dynamics of individual, solvated FF molecules with both charged and neutral ends, to account for different possible pH conditions. With charged ends, the FF molecules show more complex dynamics, experiencing three main conformational states (cis, trans and extended). We first examine the structural response of FF monomers to the application of a constant external electric field over a range of intensities. We also probe the aggregation mechanism of FF peptides, both with and without an externally applied electric field, and find that the presence of even relatively weak fields can accelerate the formation of ordered FF aggregates, primarily by facilitating the alignment of individual molecular dipole moments. The correlation between the strength of the external electric field and the local dipolar interactions is modulated both by the conformational response of individual FF peptides (e.g. backbone stretching, hydrogen bonds and relative alignment of aromatic sidechains) and by the response of neighboring FF and water molecules. These field-dependent observations may facilitate future studies on the controlled formation of nano-structured aggregates of piezoelectric peptides and the understanding of their specific electromechanical properties.

Introduction

Aromatic peptides have the intrinsic ability to self-assemble into highly-ordered nanostructures such as nanospheres, nanotubes, nanofibrils, nanoplates, etc. [1–3]. These structures form by conformational packing and linkage between the amino acid sequence, stabilized by non-covalent weak interactions (hydrogen bonds, van der Waals, electrostatic interactions), aromatic interactions and π-π stacking [4–6]. Such nanostructures possess high stiffness and excellent thermal and chemical stability [7, 8]. Self-assembly facilitates opportunities for economical and environmentally propitious production of these nanomaterials. In addition, these materials are naturally biocompatible and easily chemically modified, resulting in their application to many areas including bio-sensing, drug delivery, tissue engineering, kinase activity measurements and pathogen detection [9–11]. Diphenylalanine (FF) is a common peptide occurring naturally as the core derivative of the amyloid beta (Aβ) protein. FF self-assembles, forming nanotubes through thermodynamic folding of the β-sheet [1, 2]. FF nanotubes are intrinsically biocompatible, strong materials, with favorable thermal and chemical properties [7, 9, 11]. Furthermore, they are easily functionalized with receptor molecules and for this reason are the subjects of intense research [11, 12]. Kholkin et al. have demonstrated these nanotubes exhibit a strong piezoresponse using (piezoresponse force microscopy) PFM [13]. Piezoelectricity is a characteristic of non-centrosymmetric materials, whereby the material will undergo a mechanical stress/strain when placed under an electric field, or conversely, the material will generate an electric charge under a mechanical stress. FF nanotubes display a shear piezoelectric deformation due to the polarization orientation along the axis of the tubes and a piezoelectric coefficient d₁₅ ≈ 60 pm/V [13, 14]. Therefore, FF peptide nanotubes could function as both the sensitive biological element and the transducer/detector element in an electromechanical biosensor, thus eliminating inorganic elements and complicated fabrication steps, and reducing costs. Materials exploiting electromechanical coupling could also potentially be used as energy generating devices in vivo, for example replacing batteries in medical devices such as pacemakers [13]. Lee et al. have shown that virus-based piezoelectric energy generation is possible [15], which is further motivation for exploiting electromechanical coupling using peptide nanostructures.

The source of this response is thought to be a result of the non-centrosymmetric nature of the beta sheet [13]. Piezoelectricity arises in a non-centrosymmetric material when it is placed under a mechanical stress, which distorts the atomic structure of the crystal, such that ions in the structure separate, and a dipole moment is formed. For a net polarization to develop, the dipole formed must not be cancelled out by other dipoles in the unit cell. Therefore, to understand the source of this response in the nanotubes, it is important to understand the behavior of the dipole moments within the FF molecules during self-assembly.

Experimentally, Reches and Gazit were the first to report the spontaneous self-assembly of FF molecules into ordered semi-crystalline structures [5]. Since then Görbitz et al. have shown using X-ray diffraction that the FF molecule has an unusual conformation, promoting the crystallographic hexagonal symmetry of hydrogen-bonded head-to-tail chains in the shape of helices with four to six peptide molecules per turn [1]. The side chains appear to emanate from the channel core and the resulting structures have chiral hydrophilic channels with a van der Waals diameter up to 10 Å [1]. Bystrov et al. have performed MD simulations investigating the piezoelectricity and related changes in the dipole moments and polarization of an isolated ring with six dipeptides, as well the parallel stacking of two rings [16]. Computational studies using coarse-grained models [17, 18] have also illustrated both the role of solvation and of the specific side chain-side chain interactions in the self-assembly of FF peptides [19–22].

Directed self-assembly occurs when such a system is placed under the influence of an external stimulus, i.e., mechanical vibration, pH, etc. This enables the tuning of desired interactions, structure and properties of the final assembly. The main challenge with directed self-assembly is the need for rigorous predictive models. An example of directed assembly is applying an electric field to the FF molecule, and measuring the effect on the position of the dipole. Methods of self-assembly such as dielectrophoresis exert this kind of stimulus on the whole nanostructure and have been used to influence the alignment of FF nanotubes [23–29].

It remains unclear, however, how an electric field affects a single FF monomer dipole, and how it would affect the initial conditions for self-assembly. Therefore, the objective of this work is to provide a predictive model of the behavior of a single FF molecule when placed in an electric field and simulate the effect when the molecules begin to aggregate/self-assemble.

Methods

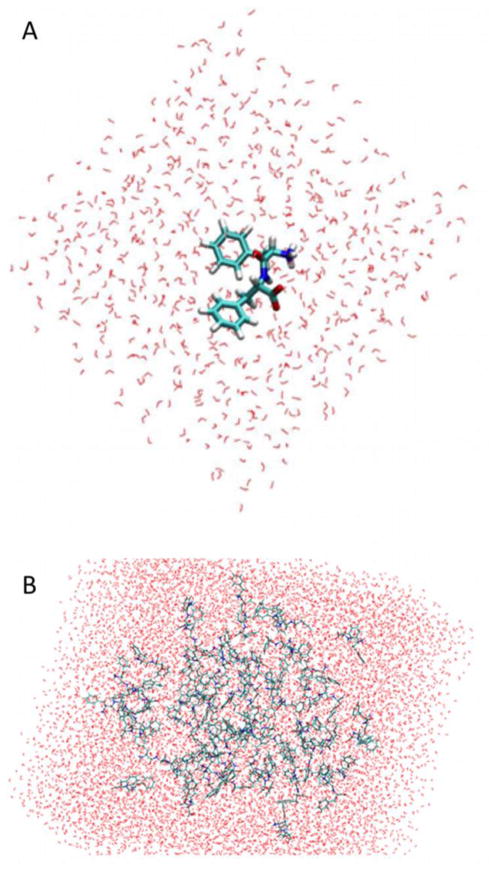
Two simple FF peptide models were constructed and studied using molecular dynamics (MD) simulations: one with neutral termini and one with charged termini. For neutral termini, NNEU (NH₂) and CNEU (COOH) caps were applied. For charged termini, NTER (NH₃⁺) and CTER (COO⁻) caps were applied. In a first stage, the FF monomer conformational dynamics was studied (Fig. 1A). In a second stage, using the model with charged termini, a 64-FF system was also created by randomly placing FF molecules with an overall concentration of approximately 16 FFs per 100,000 ų (Fig. 1B). This relatively high concentration allows for faster aggregation and shorter simulation times.

Figure 1.

Atomistic representations of the initial model of an FF monomer (A), and the 64-FF system (B) surrounded by explicit water molecules.

MD simulations (see Table 1 for a summary) were performed with the NAMD 2.8 software [30] using the CHARMM27 force field [31, 32]. All simulations were performed in the isothermal-isobaric ensemble (i.e., NPT, constant number of atoms, pressure and temperature), using periodic boundary conditions. We used the modified Nosé-Hoover Langevin piston method implemented in NAMD [33, 34] with a damping time of 0.1 ps, while maintaining a pressure of 1 atm. The temperature was set to 310 K and controlled using a Langevin thermostat with a damping coefficient of 1 ps⁻¹. Long-range electrostatic interactions were calculated using the particle-mesh Ewald (PME) method [35]. The switching distance for non-bonded electrostatics and van der Waals interactions was 10 Å with a cutoff distance of 10 Å. The integration time step was 1 fs.

Table 1.

Summary of the MD simulation trajectories and the corresponding parameters used in this study.

Simulation No.	No. of FF molecules	Charged termini	Water molecules	Total atoms	Electric field (kcal/(mol Å e))	Simulation time (ns)
1	1	No	665	2038	0	68.1
2	1	Yes	665	2038	0	91.3
3	1	Yes	665	2038	10	85.9
4	1	Yes	665	2038	20	76.3
5	1	Yes	665	2038	40	83.9
6	1	Yes	665	2038	60	79.8
7	1	Yes	665	2038	80	75.7
8	1	Yes	665	2038	100	81.2
9	64	Yes	11582	37498	0	9.44
10	64	Yes	11582	37498	10	10.00

Each system was solvated with explicit TIP3P water molecules [36] prior to minimization, heating and equilibration. The TIP3P water model [36] has been broadly tested and used in biomolecular atomistic MD simulations using the NAMD 2.8 software [30] particularly in conjunction with the CHARMM27 force field [31, 32]. Here, the TIP3P model is expected to generate a realistic ensemble of confirmations for the FF peptides, which are the focus of our study. However, for a more accurate (yet slower to compute) representation of the dielectric properties as well as of the water conformational dynamics, a newer higher-order model (e.g., TIP4P or TIP5P) or polarizable versions of the non-polarizable models could be used, but at a significantly increased computational cost.[37] While an improved, more detailed water model is expected to react better than TIP3P to an external electric field, it may not affect significantly the conformational dynamics of the solvated peptides.[37]

For the momomeric FF systems (Fig. 1A), the box size was approx. 22,500 ų (or 30 × 30 × 25 Å). For the 64-FF systems (Fig. 1B), the box size was approx. 400,000 ų (or 77 × 87 × 60 Å). Total atom numbers for each system including water molecules are reported in Table 1. Systems were prepared for MD simulation as described in our previous papers using also similar NPT MD studies [38–40] of larger amyloid peptides such as Alzheimer’s amyloid-beta (Aβ, [41–43]) or human amylin (hIAPP, [44]).

Single-FF systems were minimized for 1,000 steps with the backbone fixed in place, and then 1,000 steps with the entire system free to move. The system was heated to 310 K over 3 ps. This was followed by 5 ps of equilibration with the backbone restrained, and then 10 ps of equilibration with no restraints.

64-FF systems were minimized for 10,000 steps with the backbone fixed in place, and then 10,000 steps with the entire system free to move. The system was heated to 310 K over 30 ps. This was followed by 50 ps of equilibration with the backbone restrained, and then 100 ps of equilibration with no restraints.

For the single-FF system with charged termini, a range of simulations was run with constant electric fields of 0, 10, 20, 40, 60, 80 and 100 kcal/(mol Å e) for times varying between 68 ns and 91 ns (where 1 kcal/(mol Å e) = 4.336 * 10⁸ V/m). For the 64-FF system, a 9.4 ns simulation was run with no applied electric field, and a 10 ns simulation was run with a constant electric field of 10 kcal/(mol Å e).

VMD [45] and PyMOL [46] were used for analysis and visualization.

Results & Discussion

Single-FF systems with no applied electric field

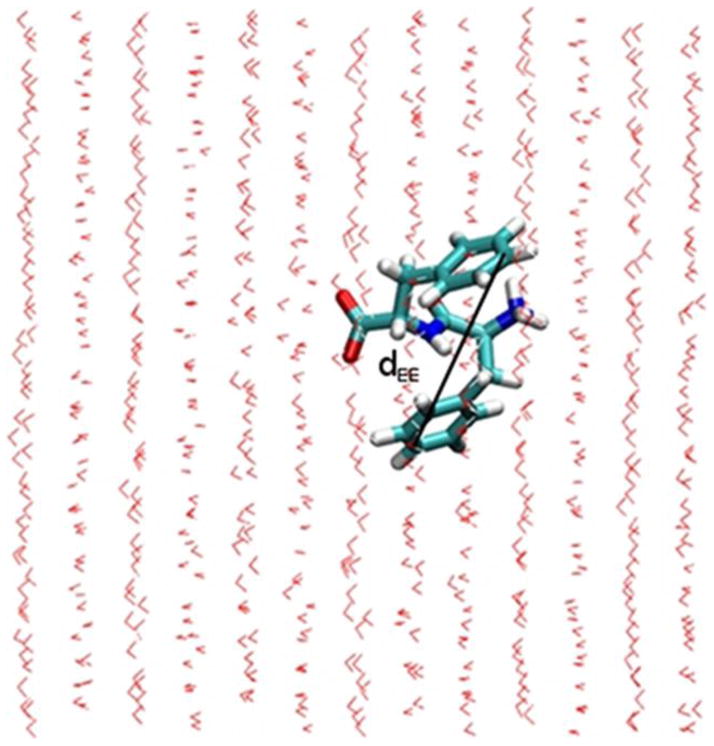
For single-FF monomer molecules, we define the end-to-end distance (d_EE) as the distance between the end carbons (carbon- ζ) of each phenyl ring of FF (see Fig. 2).

Figure 2.

Atomistic representation of a representative FF monomer conformation in an MD simulation with explicit water molecules, in an external electric field of magnitude 20 kcal/(mol Å e) applied from left to right. The FF end-to-end distance, d_EE, is indicated between the carbon-ζ atoms in each phenyl ring of FF.

Interestingly, the single-FF system with charged termini and no applied electric field experiences three distinct conformational states during the 91.3 ns MD simulation (Fig. 3). This is characterized well by the end-to-end distance, d_EE, values of the FF molecule (see Figs. 2 and 3). The convergence of our simulations for estimating the distribution FF d_EE values is achieved after only about 50 ns (as shown in Fig. S1), a value smaller than the typical length of our simulation monomeric runs (Table. 1).

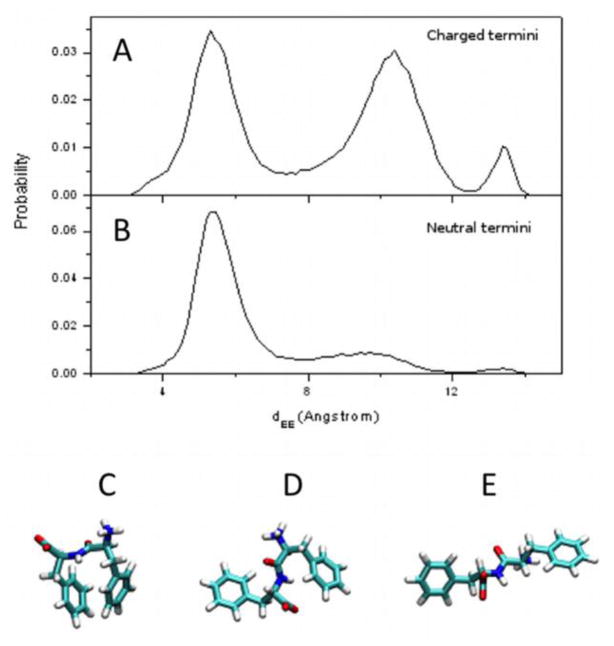
Figure 3.

Probability distributions of d_EE for single FF with charged termini (A) and single FF with neutral termini (B), showing representative conformations of FF for each peak, i.e. a closed or cis state (C), an intermediate or trans state (D), and a fully extended state (E) respectively.

Here, we are using for analysis as well additional parameters characteristic to our FF systems such as the root mean square deviation (RMSD) values (i.e., calculated along the MD trajectories) and the molecular dipole moments (see below and Fig. S2).

The d_EE values of the (i) charged-termini and (ii) neutral-termini FF systems vary from 3.0 Å to 14.3 Å. The overall average d_EE is 8.2 ± 2.7 Å for charged termini (though their distribution is tri-modal, see below), and 6.4 ± 1.9 Å for neutral termini. Overall, the d_EE of the neutral-termini system is lower on average than that of the charged-termini system, indicating that it spends more time in a folded or closed state (see Fig. S2-A(ii)). The d_EE of the charged-termini system is higher on average, with a higher standard deviation. This indicates that it spends more time in open states, and that these states are further from the average state than in the case of the neutral-termini system. (Fig. 3)

Periodicity can be seen in the d_EE values. While the neutral-termini system spends most of the trajectory with d_EE ≈ 5.5 Å (Fig. S2-A(ii)), the d_EE of the charged-termini system alternates between values of approximately 6 Å and approximately 10 Å (Fig. S2-A(i)). This periodicity reveals the rate at which FF changes states. These state transitions are more regular (approximately every 3 ns) for the charged-termini system. This is another indication that the charged-termini system fluctuates more between various states. The population distribution of the d_EE of the charged-termini system (Fig. 3A) shows three distinct peaks, each corresponding to a conformational state: (i) a closed cis state, with d_EE ≈ 5.5Å (Fig. 3C), an intermediate or trans state, with d_EE ≈ 10.5Å (Fig. 3D), and (iii) an extended state, with d_EE ≈ 13.5Å (Fig. 3E). Representative images for each of the three states are shown in Fig. 3A. The population distribution for the neutral-termini system (Fig. 3B) shows that it spends most of the simulation in a closed cis state with d_EE ≈ 5.5Å. The other states still appear, but with very small populations. It is clear that charged termini play an important role in folding and unfolding, or state transitions, for small peptides such as FF.

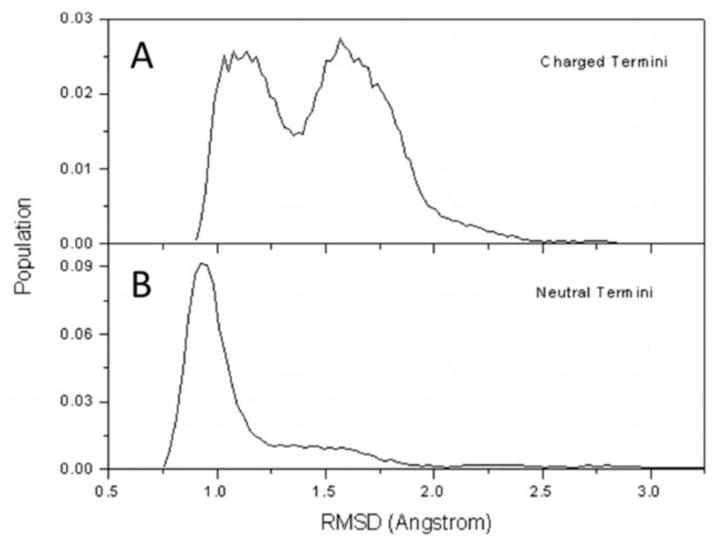
It is also possible to use the root mean square deviation (RMSD) in order to identify metastable conformational states associated with the molecule. RMSD values calculated with respect to the average position are shown in Fig. S2-B. In this paper, RMSD is always taken with respect to the average position of the atoms.

This average atomic position or average conformational state is very well represented by the end-to-end distance of the molecule. That is the state with d_EE ≈ 8.2 ± 2.7 Å in the charged termini case, and with d_EE ≈ 6.4 ± 1.9 Å for the neutral termini case. High values of RMSD (~3 Å) correspond to a state which is far from this average. This means a state which is either highly folded or highly unfolded, i.e. has either d_EE ≈ 3 Å or d_EE ≈ 14 Å. Low RMSD values (~0.25 Å) represent states which are close to the average atomic conformation, and by previous reasoning, close to the average d_EE in each case. The average RMSDs in each case are 1.5 ± 0.3 Å and 1.2 ± 0.5 Å for charged and neutral termini respectively. The higher value for charged termini compared to neutral represents a larger deviation from its average conformational state. There are two distinct peaks in the corresponding population distribution (Fig. 4A) for FF molecules with charged termini. They are another manifestation of the intermediate state, and the folded or unfolded states. Thus, a distinct d_EE-defined state has similar atomic deviations from the average position of atoms compared to another d_EE-defined state and cannot be identified properly by RMSD values alone. The difference in d_EE between the intermediate state and folded state is ~5 Å, which compares to the difference between intermediate and unfolded states (~3 Å). The neutral-termini system only shows one distinct population peak (Fig. 4B). Again, this shows that it rarely deviates from its average, more compact state.

Figure 4.

Probability distribution for root mean square distance (RMSD) values for the of non-hydrogen atoms of single FF with charged (A) and neutral termini (B) with respect to the average conformation in each case.

The dipole moment of FF molecules was calculated using the standard measuring facility available in the VMD software [45], as $\overrightarrow{\mu }={\sum }_{i=1}^N(q_i-q_0)r_i$, where q_i are the charges and r_i are the positions of the atoms in the protein, and q₀ is the monopole component: $q_0=\frac{1}{N}{\sum }_{i=1}^N{q}_i$. We note that the direct calculation using the above formula makes the dipole moment estimation independent of the choice of origin.

The dipole magnitude for the single-FF system with charged termini (Fig. S2-C(i)) varies over an interval of 18.7–33.6 debye (D). There is a difference in dipole moment of 14.9 D between one state and another. These two states may not exactly correspond to the highly populated d_EE-defined or RMSD states. Nonetheless, there exist two conformational states with lowest and highest dipole magnitude, and it is apparent that the folded and unfolded states have considerably different dipoles. The dipole moment is much lower for the neutral-termini system (Fig. S2-C(ii)). The average magnitudes in each case are 27.7 ± 2.1 D and 4.5 ± 1.3 D for charged and neutral termini respectively. Thus, the main contribution (approx. 86%) of the total dipole moment of the FF monomer at normal pH is due to the charged termini.

Systems of solvated FF molecules with an applied electric field

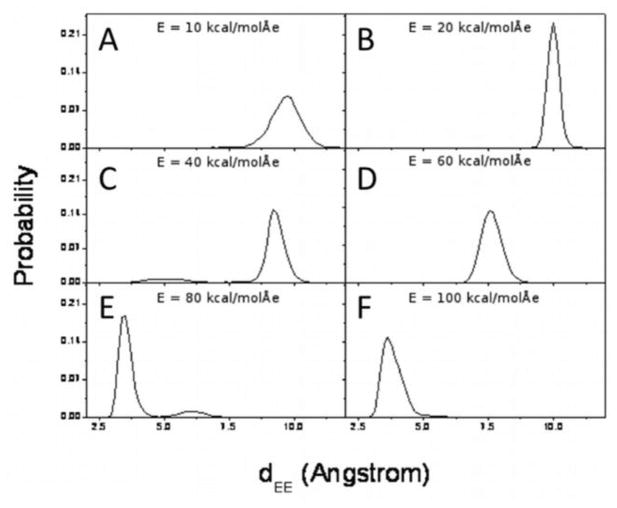
The application of an electric field drastically changes the conformational state populations. Rather than presenting three distinct conformational states, as seen for the charged-termini FF molecules with no applied electric field, FF is forced into essentially one state (see Figs. 5 and S3). For low field strengths, this conformation is similar to the zero field intermediate state with d_EE values of approximately 9 to 10 Å.

Figure 5.

Probability distributions of d_EE for each electric field magnitude: E = 10 kcal/(mol Å e) (A), 20 kcal/(mol Å e) (B), 40 kcal/(mol Å e) (C), 60 kcal/(mol Å e) (D), 80 kcal/(mol Å e) (E), and 100 kcal/(mol Å e) (F).

High-magnitude fields separate the polar end groups (COO⁻ and NH₃⁺) by a further average distance, and thus they stretch the backbone forming a conformational state with very close side chains (in this case phenyl groups) and therefore a low d_EE (approx. 3.5 Å).

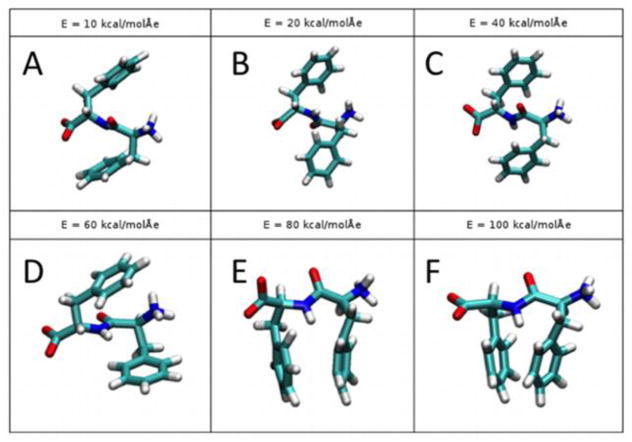
Representative images of average conformational states caused by the electric field in each case are shown in Fig. 6.

Figure 6.

Representative images of average conformational states for each electric field magnitude: E = 10 kcal/(mol Å e) (A), 20 kcal/(mol Å e) (B), 40 kcal/(mol Å e) (C), 60 kcal/(mol Å e) (D), 80 kcal/(mol Å e) (E), and 100 kcal/(mol Å e) (F).

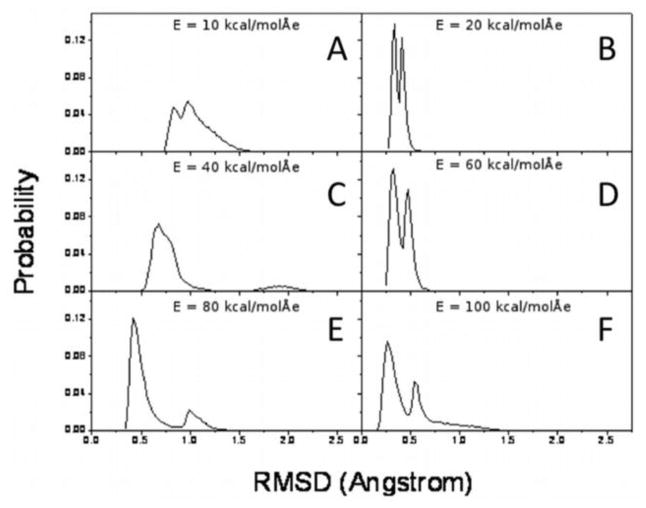
RMSD values, calculated again with respect to the average conformation, generally decrease with field strength (see Figs. 7 and S4).

Figure 7.

RMSD probability distributions of non-hydrogen FF atoms with respect to the average atomic position of the charged-termini single-FF system, for each electric field magnitude: E = 10 kcal/(mol Å e) (A), 20 kcal/(mol Å e) (B), 40 kcal/(mol Å e) (C), 60 kcal/(mol Å e) (D), 80 kcal/(mol Å e) (E), and 100 kcal/(mol Å e) (F).

As a general observation, the backbone becomes less flexible due to the external electric field. Higher-magnitude fields decrease the movement of the backbone. There are certain field values which result in sharper peaks in both the d_EE (Fig. 5) and the RMSD (Fig. 7) probability distributions. For example, this occurs for E = 20, 60, 80 kcal/(mol Å e). These field magnitudes give rise to more populated conformational states than at the other field magnitudes in our simulations. This is especially true for E = 20 kcal/(mol Å e), which gives the highest peaks in the d_EE and the RMSD probability distributions. This conformational state corresponds to the highly populated intermediate state (d_EE ≈ 10.5 Å) from the simulation of the charged-termini single-FF system with no applied electric field. Similarly, an applied external field of E = 80 kcal/(mol Å e) gives rise to a state which corresponds to the closed state (d_EE ≈ 3.5 Å) from the E = 0 simulation. These field-induced conformational states are more stable than other conformational states which do not have corresponding E = 0 states.

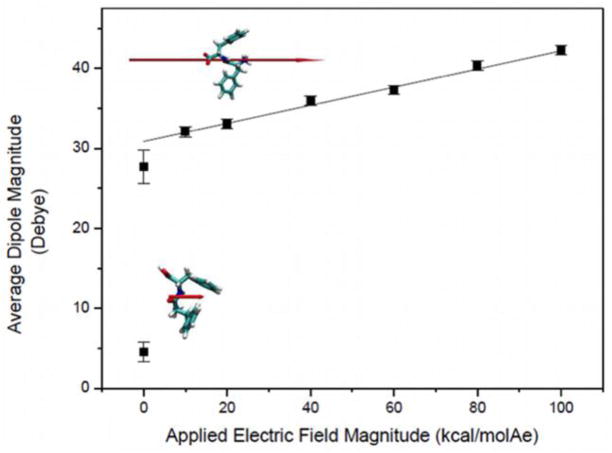
As previously stated, approx. 86% of the contribution to the molecular dipole moment in FF molecules can be due to their charged termini. Thus, the primary effect of an external electric field upon FF with charged termini is the further separation of the charged termini from each another, and thus the increase of its dipole moment. This can be seen in Figs. S5 and 8. This further separation of the end groups causes the backbone to stretch significantly. Thus, an external electric field applied to FF molecules in aqueous solution appears to be acting primarily by stretching their peptide backbone. Due to the geometry of the backbone, this causes the side chains, in this case phenyl groups, to become closer to each-other and to experience additional favorable pi-stacking interactions (i.e., for FF molecules, d_EE generally decreases with field).

Figure 8.

Average dipole magnitude over an increasing applied electric field magnitude for FF, including zero field with neutral termini (not included in linear fit), with representative images of FF and its dipole moment (red arrow) corresponding to a zero field with neutral termini (lower left) and with charged termini (upper left). Slope of linear fit: 0.12 ± 0.01 (mol Å e D)/kcal.

Simulations of aggregation in systems of 64 FF molecules

Our model for an aggregate FF system consists of 64 FF molecules arranged in a random starting configuration in the simulation box. A comparison is made between normal conditions (E = 0) and the addition of a constant electric field (E = 10 kcal/(mol Å e)) across the system.

An atomistic representation of the positions of each FF at the beginning, middle and end of each simulation is illustrated in Fig. 9. The dipoles align with the applied field and each FF assumes a state similar to the single-FF case with E = 10 kcal/(mol Å e) (that is, a state with d_EE ≈ 10.5 Å).

Figure 9.

Atomistic representations of the 64-FF system for initial, intermediate, and final states. Systems with no applied electric field are shown in the top row, and systems with an applied electric field of magnitude 10 kcal/(mol Å e) are shown in the bottom row.

The RMSD is plotted in Fig. 10A with respect to the average position of the non-hydrogen atoms of the peptide. Similarly to the single-peptide system, the RMSD is on average much lower when there is an applied constant electric field. It is apparent from the single-peptide case that an applied field causes the peptide to have much higher probability to remain in one state, rather than to be fluctuating between various conformational states, as is the case with no applied electric field. This is also true in the 64-FF system, although the state of the entire system is considered. The system has a higher probability to remain in a single conformational state with an applied external field. This results in a low RMSD, as the system has less displacement from its average position when it prefers to adopt mainly one conformational state (i.e., when there is an applied electric field).

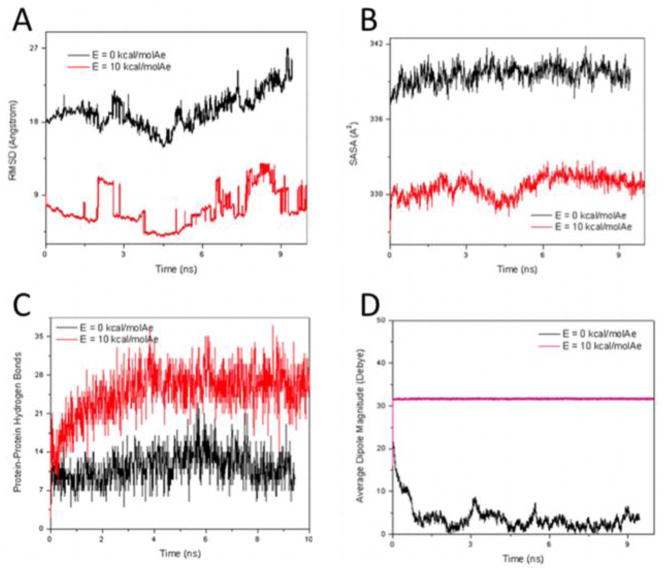
Figure 10.

RMSD with respect to the average positions of the non-hydrogen atoms of the 64-FF system for electric field magnitudes of 0 and 10 kcal/(mol Å e) (A). Solvent-accessible surface area for the 64-FF system with a solvent radius 1.4 Å and electric field magnitudes of 0 and 10 kcal/(mol Å e) (B). Number of hydrogen bonds between polar atoms (N, O) of the protein with maximum donor-acceptor distance 3 Å and cutoff angle 20° (C). Average dipole magnitude for each FF over time in the 64-FF system, with and without an applied electric field (D).

We also note that the 64-FF system remains more aggregated when there is an applied field, as shown in Fig. 9. The lower RMSD values as calculated from the average position with an applied electric field compared to the E = 0 case is a clear indication of this observation (Fig. 10A). The average position of all the atomic coordinates would be approximately an average between the initial, middle and end states as shown in Fig. 9E. The initial state is close to a single aggregated cluster and it takes significant time (i.e., more than the 10 ns simulation time) to observe its partial dissociation. Thus, it appears that the average state of the 64-FF system will be closer to an aggregate than to a dissociated ensemble, and a lower RMSD represents less deviation from an aggregated cluster.

This can be shown even more convincingly by the average solvent-accessible surface area (SASA) for each FF in the aggregate (Fig. 10B). The SASA values are lower when an electric field is applied due to the 64-FF system being more aggregated compared to the E = 0 case (see Fig. 10B).

The number of peptide-peptide hydrogen bonds may also be used as an indicator of aggregation. This is illustrated for E = 0 and E = 10 kcal/(mol Å e) in Fig. 10C. The higher the number of peptide-peptide hydrogen bonds, the closer the peptides are to one another, and the more aggregated the system is.

The average dipole magnitude of the monomers in the aggregate with an applied electric field is much higher compared to when there is no applied field (Fig. 10D). This is because the dipole moments of each FF line up with the applied field. When there is no applied field, the dipoles adopt random orientations and somewhat cancel each other out. Compared with the single FF system without applied field, the average FF monomer in the aggregate system has a much lower dipole moment (3.8 ± 2.9 D) than the single peptide (27.7 ± 2.1 D). This is also due to the random orientations of the dipoles in the aggregate, and the dipole cancellations that occur. With the application of an electric field of magnitude 10 kcal/(mol Å e), the average dipole moment for a monomer in the aggregate is 31.7 ± 0.2 D, compared to 32.0 ± 0.7 D for FF in the single monomer system (Fig. 10D). These values are very similar, which shows that interactions between monomers in the aggregate do not alter their individual dipole moments. The strongest contribution to the dipole moment is from the charged termini. The charge of these termini remains constant so the distance between them is the only variable. Interactions between monomers do not appear to affect the distance between termini (i.e., the effective length of the FF peptide backbone), and thus interactions between FF monomers in an aggregate do not strongly alter their d_EE values. The conformational states of the FF monomers depend strongest mainly on the magnitude of the applied electric field.

Conclusions

Under near-physiological conditions (emulated in our atomistic MD simulations), FF monomers can self-assemble into peptide nanotubes, a process that can be modulated by the presence of an external electric field.

In the absence of the external field, individual FF monomers are shown to experience three distinct conformations (i.e., cis, trans, and extended states) characterized by increasing degrees of peptide backbone extension length. The populations of these conformational states are strongly dependent on the charged states of the peptide termini, and can thus depend on the solution pH and the presence of ions and other factors that may affect the partially charged states of FF peptides. With neutral termini, the FF system remains essentially in its closed state, with state transitions occurring much less frequently than in the model with charged termini.

The application of an external electric field has several effects, the most prominent of which is the stretching of the FF peptide backbone. As the external field magnitude increases, the FF monomer moves through a sequence of different conformational states - a stable intermediate (E=10–20 kcal/(mol Å e)), an unstable intermediate (E=40–60 kcal/(mol Å e)), and a stretched conformation (E=80–100 kcal/(mol Å e)) where the phenyl rings are adjacent and aligned to each other, using pi-stacking as an additional stabilizing factor.

Our simulations of an FF ensemble of 64 peptides show that more strongly aggregated conformations are adopted when an external electric field is applied. FF peptide-peptide interactions appear to have little effect on the length of the peptide backbone, which seems to be almost entirely dependent on the magnitude of the applied electric field. Our study suggests that the application of an electric field to an ensemble of FF molecules may accelerate their self-assembly process in a controlled manner.

Nanostructures are made from periodic lattices of FF monomers. In particular, FF nanotubes are made from a cyclic lattice of FF monomers [1–3, 6, 13, 26]. We expect that the application of an electric field across an FF nanotube would distort and rigidify its lattice, with direct effects on the elongation or contraction of the nanotube length, leading to the piezoelectric properties of aggregated FF structures. Any physical factor (e.g., temperature change, pH, etc.) that significantly alters the probabilities of the FF conformational states, could also be able to distort the FF aggregate lattice and result in a change in tube length, though external electric fields are likely to offer one of the most sensitive ways to modulate and control this process.

We note that the facilitation by an external electric field of self-assembly in the piezoelectric FF peptide system is different from generic aggregation processes as it results in specific ordered, aligned structures of the diphenylalanine assemblies. The electric field-induced alignment appears to preferentially bias the FF assembly towards structures with different propensities to form backbone hydrogen bonds by extending the dipeptide backbone (Figs. 6 and 8), and simultaneously increasing the steric possibility of pi-pi stacking interactions between the phenylalanine aromatic rings. Future computational and experimental studies could quantitatively explore this effect and its consequences on the physical properties of materials such as FF nanotubes. Moreover, future computational and experimental studies could further explore the extent to which the FF molecular alignment in nanomaterials modulates its interactions with surfaces with various properties (e.g., hydrophobic/hydrophilic, charged, carbon nanotubes or graphene oxide layers) and, in particular, with the surface associated interfacial layers of water molecules.

Highlights.

• Molecular dynamics simulations of FF peptides in external electric fields.

• FF peptides with charged termini have a more complex conformational space.

• Electric fields induce extended FF conformations with larger dipole moments.

• Electric fields increase the self-assembly propensity of FF peptides in nanomaterials.

Abbreviations

FF

diphenylalanine

MD

molecular dynamics

RMSD

root mean square deviation

d_EE

end-to-end distance

SASA

solvent accessible surface area