Association Rates of Membrane-Coupled Cell Adhesion Molecules

Abstract

Thus far, understanding how the confined cellular environment affects the lifetime of bonds, as well as the extraction of complexation rates, has been a major challenge in studies of cell adhesion. Based on a theoretical description of the growth curves of adhesion domains, we present a new (to our knowledge) method to measure the association rate k_on of ligand-receptor pairs incorporated into lipid membranes. As a proof of principle, we apply this method to several systems. We find that the k_on for the interaction of biotin with neutravidin is larger than that for integrin binding to RGD or sialyl Lewis^x to E-selectin. Furthermore, we find k_on to be enhanced by membrane fluctuations that increase the probability for encounters between the binders. The opposite effect on k_on could be attributed to the presence of repulsive polymers that mimic the glycocalyx, which points to two potential mechanisms for controlling the speed of protein complexation during the cell recognition process.

Chemical reaction kinetics in the confined environment of fluctuating membranes can be very different from those in an unconstrained situation. For example, it is well established that the enthalpy for ligand-receptor binding differs significantly for events occurring in two and three dimensions (1–3). This is particularly important in the context of cell adhesion, where membrane-bound ligands react with receptors on another surface. Furthermore, although 2D dissociation rates have been extensively modeled (4–7) and measured with reasonable confidence, often in single-molecule experiments (8,9), determining the association rate seems to be more challenging (10–15). For instance, when one of the reactants is bound to a membrane (16) or the tip of a polymer (17), the thermal fluctuations of the membrane (or polymer) will determine how often the binding partners come into the interaction range, thus influencing the association rate k_on. Similarly, repellent polymers on one or both of the interacting surfaces will hinder the reactant encounters (14,18), thus reducing k_on.

We measure k_on for three ligand-receptor pairs in different environments: 1), the strong biotin-neutravidin pair (3D binding energy $E_b^{3D}\approx 35k_{\text{B}}T$) (16), which is often used as a model but has no known physiological relevance; 2), the Arg-Gly-Asp (RGD)-α_IIbβ₃ integrin pair, which is considered strong in the context of cell adhesion ($E_b^{3D}\approx 10k_{\text{B}}T$) (19); and 3), the weaker sialyl Lewis^x binding to E-selectin ($E_b^{3D}\approx 5k_{\text{B}}T$) (20).

As cell models, we use giant unilamellar vesicles (GUVs) (21,22) that are functionalized with lipid-anchored ligands (biotin, RGD, or sialyl Lewis^x) of size a at an initial concentration (see Supporting Material for details). Due to the fluidity of the GUV membrane, the ligands can explore their surface with a diffusion constant D ≈ 10 μm²/s. The corresponding receptors are fixed on a 2D planar substrate at density ρ_r. E-selectin and integrin are deposited by physisorption, whereas the neutravidin is incorporated into a solid supported bilayer, where it is nevertheless immobile at the considered densities due to crowding (23). We modulate the rate of ligand-receptor encounters by adding polymers (polyethyleneglycol (PEG)) to the GUV membrane or by increasing the membrane fluctuations after the osmotic deflation of vesicles.

In the early stages of the experiment, vesicles sediment onto the substrate and form a strongly fluctuating contact zone, which when visualized by reflection interference contrast microscopy (RICM) (24) appears as a patch of variable intensity surrounded by a few quasi-circular fringes against a gray background (Fig. 1, top). Experimental details can be found in the Supporting Material and Fig. S3. At some point, an adhesion domain rich in bonds nucleates (as shown by a dark, homogeneous patch with strongly reduced fluctuations in RICM) and begins to grow radially outward (16,19,20). After a certain time, its area saturates due to the finite size of the vesicle (Fig. 1, bottom). In the case of weaker bonds, multiple seeds may form; however, such cases are not considered here because interactions between the domains could make a quantitative analysis unreliable.

Figure 1.

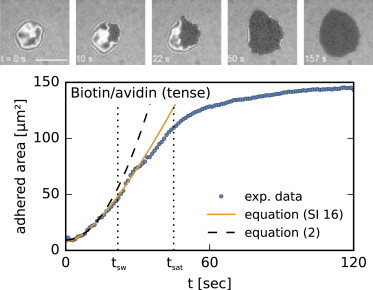
Top: RICM snapshots of a growing adhesion domain (dark area) mediated by biotin-avidin bonds. The scale bar is 10 μm. Bottom: experimental growth curve including fits to our theoretical results.

Qualitatively, the same behavior was observed in a few systems with different binding pairs (20,25,26), and depending on the relative importance of viscous dissipation, membrane elasticity, and bond density and strength, several mechanisms were theoretically suggested to be responsible for the dynamics (27,28). Furthermore, two qualitatively different regimes were identified depending on the relative density of receptors and ligands. Specifically, for ${\rho }_l^0/{\rho }_r>1$, the growth of the adhesion area was quadratic in time, as expected for reaction-limited kinetics (19,29). Alternatively, for ${\rho }_l^0/{\rho }_r<1$, the area of a domain displayed a linear time dependence (19), which is consistent with the solution of the Stefan problem (29–31). By inspection of our own and previously published data (19) for which ${\rho }_l^0/{\rho }_r<1$, we notice deviations from the linear behavior at short timescales (Fig. 1). We explain this effect by reformulating the Stefan problem (see Fig. S1 and Supporting Material for details) to account for a k_on-dependent radiation boundary condition (Eq. S2). The full solution (Eq. S16) of this diffusion problem shows that the growth of a domain is always reaction limited in the initial stages. At later times, the growth becomes diffusion limited because the contact zone becomes depleted of ligands, which then have to be transported from the bulk of the vesicle. The crossover time, from which we can also obtain the reaction rate, is estimated from the full solution to be

$$t_{\text{sw}}=\frac{D}{{\left(k_{\text{on}}a\right)}^2},$$ (1)

Consequently, if ${\rho }_l^0/{\rho }_r<1$ for t < t_sw/4, the time evolution of the area is quadratic (see Fig. S2 and Supporting Material for the derivation) and given by

$$A\left(t\right)=\pi {\left(\frac{{\rho }_l^0}{{\rho }_r}\right)}^2{k}_{\text{on}}^2{a}^2{t}^2.$$ (2)

Interestingly, Eq. 2 also emerges from the solution for the reaction-limited kinetics and can be applied for ${\rho }_l^0/{\rho }_r>1$.

Due to the finite size of the vesicle, however, the growth will saturate as the system approaches a thermodynamic equilibrium (18). Actually, from t_sat (Eq. S26), the concentration of free ligands in the entire vesicle will begin to drop. This will affect the dynamics of growth in a way that is not accounted for in modeling (29–31), where one typically assumes the constant binder density (Eq. S2) at the rim. Actually, the smaller the number of ligands in the vesicle compared with the number of receptors (and formed bonds), the shorter is the reaction-limited regime and the quicker is the expansion of the depletion zone over the area of the entire vesicle. Hence, the finiteness will more strongly affect the diffusion-limited regime, which therefore should not be used to directly extract the diffusion constant of the ligand.

The crossover from the quadratic to the linear regime is clearly seen in our fastest neutravidin-biotin system (Fig. 1), as well as for the slower integrin-RGD binding (Fig. S4). The binding rate is obtained from both Eq. 1 and Eq. 2, as shown in Table 1. In principle, the two approaches provide relatively similar k_on-values. However, the results obtained with Eq. 2 may underestimate the rate by up to 50%. This is because the fits are extended to t_sw, which for fast processes may still be beneficial due to the limited time resolution of sampling. On the other hand, k_on obtained from the Eq. 1 agrees excellently with the values obtained from the fits of the full solution of the diffusion problem (Eq. S16). This is despite relatively large uncertainties in determining t_sw, and is due to the square-root dependency of the rate on this typical time.

Table 1.

Association rate k_on in units of s⁻¹ from experiments

	${\rho }_l^0/{\rho }_b$	Eq. 1	Eq. 2
Biotin (floppy)	0.4	(1.8 ± 0.2)⋅103	(1.5 ± 0.03)⋅103
Biotin (tense)	0.4	(1.2 ± 0.1)⋅103	(0.6 ± 0.02)⋅103
RGD (1% PEG)	5.9		(7.9 ± 0.2)⋅101
RGD (3% PEG)	5.9		(6.0 ± 0.1)⋅100
sLex	59		(4.1 ± 0.1)⋅10−1

See Supporting Material for details and calculation of the error bars.

Regardless of the abovementioned uncertainties, it is interesting that the difference in the binding rates between floppy and tense vesicles (neutravidin-biotin system) is significant. As was previously predicted theoretically (32,33), larger fluctuations of vesicle membrane increase the association rate k_on because encounters between ligands and receptors are more frequent.

Even more prominent is the change in the binding rate due to the presence of repelling polymers (PEG) mimicking the cellular glycocalyx. We incorporated these polymers at concentrations of 1 mol% and 3 mol% into vesicles carrying RGDs binding to integrins and found that k_on was one order of magnitude lower for vesicles with more PEG (Table 1). This clearly demonstrates that repelling molecules affect not only the thermodynamic equilibrium but also the rates for bond formation. In addition, the reported rate (1% PEG) is in full agreement with the rates extracted from the set of growth curves (19) where the concentration of RGD in the vesicles was varied systematically to induce the change from the diffusion-limited regime to the reaction-limited one (see Fig. S5 and Table S1 in the Supporting Material).

The condition for reaction-limited growth (second column in Table 1) is also very well satisfied for the slowest sialyl Lewis^x binding to E-selectin (20). As expected, the growth curves are well fitted with the parabola (for an example, see Supporting Material) corresponding to Eq. 2. This rate is of the same order of magnitude as the previously reported binding rates of membrane-bound P and L selectins (11) measured by the micropipette technique (10).

Here, we have presented a new (to our knowledge) strategy to measure the association constant k_on from adhesion growth curves. We used well-controlled cell models with three different kinds of ligand-receptor pairs to demonstrate proof of principle. We obtained the highest k_on-values for the energetically strongest bonds. The results suggest a mechanism that could be relevant for the control of cell adhesion dynamics, namely, the membrane shape fluctuations, which increase the association rate (32,33) when enhanced. On a similar note, we find that repelling polymer cushions, which were previously used to modulate unspecific GUV adhesion (20,34) as well as to influence bond formation in the context of surface-surface interactions (14,20), directly influence the association rate. This result is also interesting in the context of cells, as it suggests that bonds between binding pairs with long extracellular domains (e.g., as selectin-PSLG links) could form rapidly. In contrast, the links with integrins (hidden in the glycocalyx) should be very slow. These hypotheses are further supported by the fact that cells regulate both the membrane fluctuations and the thickness of the glycocalyx (22).

Interestingly, although they differ by at least an order of magnitude, the association rates for the integrin-RGD binding and the recognition of sialyl Lewis^x motifs by E-selectin are relatively low. This suggests that at physiological concentrations, the reaction-limited regimes could extend for a very long time before entering the diffusive regime. For example, for the sialyl Lewis^x binding to E-selectin, this time is on the order of 10⁵ s, which is beyond the timescale of a cell or a vesicle. This suggests that a diffusion-limited behavior could not be relevant for cell adhesion with these two binding pairs unless extreme crowding effects would affect the recruitment of proteins to adhesion patches, which does not seem to be the case.