A Magic-Angle Spinning NMR Method for the Site-Specific Measurement of Proton Chemical-Shift Anisotropy in Biological and Organic Solids

Abstract

Proton chemical shifts are a rich probe of structure and hydrogen bonding environments in organic and biological molecules. Until recently, measurements of ¹H chemical shift tensors have been restricted to either solid systems with sparse proton sites or were based on the indirect determination of anisotropic tensor components from cross-relaxation and liquid-crystal experiments. We have introduced an MAS approach that permits site-resolved determination of CSA tensors of protons forming chemical bonds with labeled spin-1/2 nuclei in fully protonated solids with multiple sites, including organic molecules and proteins. This approach, originally introduced for the measurements of chemical shift tensors of amide protons, is based on three RN-symmetry based experiments, from which the principal components of the ¹H CS tensor can be reliably extracted by simultaneous triple fit of the data. In this article, we expand our approach to a much more challenging system involving aliphatic and aromatic protons. We start with a review of the prior work on experimental-NMR and computational-quantum-chemical approaches for the measurements of ¹H chemical shift tensors and for relating these to the electronic structures. We then present our experimental results on U-¹³C,¹⁵N-labeled histdine demonstrating that ¹H chemical shift tensors can be reliably determined for the ¹H¹⁵N and ¹H¹³C spin pairs in cationic and neutral forms of histidine. Finally, we demonstrate that the experimental ¹H(C) and ¹H(N) chemical shift tensors are in agreement with Density Functional Theory calculations, therefore establishing the usefulness of our method for characterization of structure and hydrogen bonding environment in organic and biological solids.

1. INTRODUCTION

The NMR literature has displayed great interest in the relationship between the full properties of chemical-shift tensors of nuclei like ¹³C, ¹⁵N, ¹⁹F, ³¹P and local molecular structures.^[1–3] The same can be said about protons. For instance, correlations between experimentally determined principal values and hydrogen-bond lengths have been reported.^[4–12] Numerous ab initio and Density Functional Theory (DFT) calculations have, besides supporting this relationship, indicated that accurate predictions of proton chemical shifts require detailed knowledge of molecular structure including the hydrogen bonding and the crystal packing (the latter particularly important for small molecules). The following few examples illustrate the significance of the molecular environment. Concerning amide protons it was found that tensor components in addition to depending very strongly on the hydrogen bond length also exhibit a weaker dependence on the hydrogen bond angle.^[13] From DFT calculations it was concluded that, while the hydrogen bond geometry is the most important shift-tensor determinant, longerrange cooperative effects of extended hydrogen networks make significant contributions.^[14] Other calculations showed that the origin of isotropic chemical-shift differences among protein amide protons is predominantly the magnetic anisotropy effect from the C=O acceptor.^[15] In liquid water, the proton chemical-shift tensor was shown to be strongly dependent on the hydrogen-bond distances and angles, a relationship that allowed the temperature-dependent geometry to be derived from experimental chemical-shift tensor results.^[16–17] In benzene the tensor was shown to differ greatly between the individual molecule and the crystal.^[18] Recently, a quantum chemistry study of dichloroacetic acid attributed a partial covalent character to the OH…O hydrogen bond and demonstrated a strong correlation with the proton chemical-shift tensor.^[19]

A more complete understanding of the effects of molecular structure on the anisotropy of the proton chemical shift will undoubtedly be served by a broad database of experimental results and will be instrumental in extracting structural information from the measurements. Unfortunately, this database has remained rather limited in size, mainly because the measurement of proton chemical shift by solid-state NMR methods is challenging due to the small magnitude of the chemical-shift interactions of the protons in the presence of the much stronger ¹H-¹H homonuclear dipolar interactions. The only conventional proton CW experiments we know to have produced proton shift-tensor results are single-crystal measurements of trichloroacetic acid by Haddix and Lauterbur in 1969^[20] and powder measurements of HF in a solid composite by Moroz in 1983.^[21] We are also aware of one proton CSA result that was obtained by single-pulse-excitation ¹H FTNMR at slow magic-anglespinning (MAS) of a crystal hydrate (see below).^[22] On the other hand, numerous more sophisticated approaches have been introduced over the years to obtain quantitative information of proton shielding tensors in solids, liquids, and even in the gas phase. One of such methods, recently proposed by us,^[12] is the subject of this contribution. It involves magic-angle spinning and symmetry-based pulse sequences. Before describing it in detail, we begin with presenting a short overview of a wide variety of other experimental approaches, thereby concentrating on the capabilities and limitations regarding their ability to obtain full information of the proton chemical-shift tensor characteristics while leaving out their sometimes exceptional achievements related to other spin interactions. While we made an attempt to review the key reports in the field we recognize that we might have inadvertently left out important contributions that we are not aware of.

All measurements to be reviewed relate to the symmetric part of the chemical-shift tensor. Since the antisymmetric part of the tensor is known not to yield measurable contributions to the resonance frequencies, it can in general be ignored.^[23] However, in the fast-motion limit it can make a sizable contribution to relaxation rates in liquids^[24–25] and should, in principle, be taken into account when relaxation measurements are used for the determination of proton shift tensors. The size of this effect on cross-correlated relaxation rates (see below) was estimated by Sharma et al. based on DFT calculations of amide-proton shift tensors in a protein and was found to be negligible.^[13] Following the generally encountered practice of disregarding the antisymmetric part of the tensor, we will in this article ignore the three tensor components that quantify its size. The six remaining quantities that define the symmetric part are usually represented in the form of its three principal components δ_XX, δ_YY, δ_ZZ, and the three angles that define the orientations of the principal axes X, Y, Z with respect to the molecular structure. The chemical-shift tensor is often seen as the combination of an isotropic shift δ_iso = (δ_XX + δ_YY + δ_ZZ)/3 and a traceless chemical-shift-anisotropy (CSA) tensor having as its principal components δ_ii − δ_iso, i = X, Y, Z. The two independent parameters defining the CSA principal components are usually presented in the form of two parameters, one quantifying its size, expressed either as the anisotropy Δδ=δ_ZZ − (δ_XX + δ_YY)/2, or as the reduced anisotropy δ = δ_ZZ − δ_iso, or as the span Ω = δ₁₁ − δ₃₃; and one quantifying its deviation from axial symmetry, expressed as the asymmetry parameter η = (δ_YY − δ_XX)/δ or as the skew 3(δ₂₂ − δ_iso)/(δ₁₁ − δ₃₃), whereby δ₃₃ ≤ δ₂₂ ≤ δ₁₁. Many of the experimental approaches that have been introduced for measuring the proton chemical-shift tensor are not able to determine all six variables that are needed to fully define the tensor.

The introduction in the late 1960's of multiple-pulse sequences for decoupling of the homonuclear dipolar interaction revolutionized high-resolution NMR in solids and led to the publication of the first three multiple-pulse measurements of proton CSA in 1973.^[26–28] These experiments were performed on powder samples, providing the three principal tensor components. In the same year, at the First Specialized Colloque Ampère, three groups reported proton multiple-pulse studies of single crystals,^[29–31] which, in addition, allowed the three angles that define the CSA tensor orientation with respect to the molecular structure to be determined. The following decade saw the measurements of the anisotropies of over sixty molecular systems. These are reviewed in detail by Haeberlen^[32] and Mehring.^[33] Most of these measurements were done by multiple-pulse NMR on single crystals, many of them by Haeberlen and coworkers. A collection of known chemical shift anisotropies compiled by Duncan in 1990 contains about eighty proton entries,^[34] a very modest number when compared with ¹³C. Since then only a few single crystals have been measured by proton multiple-pulse techniques.^[35–37] Presumably it reflects a number of difficulties when working with single crystals. The sample preparation is challenging and so are accurate sample alignment in the magnet, peak assignment when the unit cell contains many protons, and taking care of peak shifts arising from the magnetic susceptibility of the sample.

In a powder, a plain measurement of the shift tensor does not reveal information about its orientation in the molecular structure. However, by monitoring the correlation of the chemical shift interaction and the dipolar interaction with a neighboring nucleus, the direction of the internuclear vector with respect to the CSA tensor can be determined. This was employed in 1978 by Stoll et al. on a proton pair by applying a so-called separated local field (SLF) method^[38] in the form of a 2D dipolar/multiple-pulse experiment;^[39] in 1995 and 1997 by Opella and coworkers on ¹⁵N-¹H groups by 3D SLF and 2D PISEMA;^[40–41] in 1997 by Tekely et al. on hydrate crystals by analysis of an asymmetric side-band pattern in a single-pulse-excitation slow- MAS spectrum that was dominated by the ¹H-¹H dipolar interaction;^[22] in 1998 by Wu et al. on a ¹H-²H spin pair by measuring spectra of crystalline hydrates at two different fields;^[42] and in 1999 by Rasmussen et al. on a ³¹P-¹H-³¹P triad by applying combined rotation and multiple pulse (CRAMPS) at low spinning speed with and without ³¹P decoupling while deriving the information from the side-band patterns.^[43] In single crystals, the measurement of dipolar splittings also helps confirm the sample orientation with respect to the magnetic field.^{[20, 44]} In fact, correlations between CSA and dipolar interactions play an important role in most of the experimental approaches to be presented below.

Another way of overcoming the problem of homonuclear dipolar interactions is to work with deuterated samples, by measuring either ²H or diluted ¹H. A completely novel approach was introduced in 1976 by Pines, Ruben, Vega, and Mehring who measured the ¹H spectrum of low-concentration ¹H in a deuterated solid while decoupling the heteronuclear ²H-¹H dipolar interaction by double-quantum irradiation of the m = −1 → 1 transition the deuterons.^[45–46] They reported the first proton CS tensor components of ice. Vega et al. utilized the same irradiation concept by exciting the double-quantum transition of ²H in a single crystal and monitoring its signal evolution, which is exclusively determined by the resonance offset and not by quadrupolar interaction, such that the shift tensor could be measured.^[47] In 1977 Van Willigen et al. applied conventional ²H FTNMR to a deuterated single crystal to obtain quadrupolar-split deuterium doublets, the centers of which represent the chemical shift.^[48] Achlama and others applied this method to fully determine ²H chemical-shift tensors.^[49–52] Measuring ¹H spectra in a heavily deuterated liquid obviously does not require ²H decoupling but its dynamic spin interactions are nevertheless dominated by the ¹H-²H spin coupling and by the proton shift tensor. It allowed the proton CSA in water to be derived by measuring ¹H T₁ as a function of the magnetic field.^[16–17]

As mentioned above, CSA contributes to spin relaxation in liquids.^[24] Of special interest is the relaxation mechanism caused by the correlated stochastic dynamics of a nuclear CSA and of a neighboring homo- or heteronuclear dipole-dipole interaction. A theoretical description of this so-called cross-correlation-relaxation contribution to the relaxation rate was presented by Goldman in 1984^[53] and since then a variety of experimental approaches has been applied to measure this relaxation rate and to derive from it a measure of the proton CSA.^[54] The cross-correlation relaxation rate due to a particular CSA-dipole-dipole combination depends on a single variable related to the CSA tensor. For instance, in the case of isotropic tumbling and an axially symmetric chemical-shift tensor, the relaxation rate is proportional to Δσ(3cos²θ – 1)/2, where θ is the angle between the unique CSA axis and the internuclear vector of the dipolar interaction.^[53] More elaborate expressions have been formulated for asymmetric CSA,^[53] CSA-CSA cross-correlated relaxation,^[55] and systems consisting of more than two spins.^[56–59] When the molecular structure implies that η = 0 and θ = 0, then one measurement quantifies the complete CSA tensor.^[60–63] Otherwise, simplifying assumptions are regularly made about the symmetry and/or direction of the CSA tensor in order to arrive at a full tensor description. However, in several instances multiple cross-correlation relaxation rates were measured leading to a highly defined set of principal components and directions.^{[9, 11, 59]}

Different methods were introduced to extract the cross-correlation relaxation rate from the combination of concurrent processes that control the spin relaxation. While autocorrelation is instrumental in thermalization/dissipation processes associated with longitudinal, transverse, and cross-relaxation, cross-correlation distinguishes itself by initiating the buildup of multiple-spin polarizations and coherences and the transfer among them.^{[53, 58]} The majority of relaxation studies developed for the determination of CSAs are aimed at the measurements of the rates of these processes. Major contributions to these approaches were made by Bodenhausen and coworkers. As far as we know, cross-correlation relaxation experiments led to about fifteen publications reporting quantitative proton CSA results.^{[5–6, 8–9, 11, 55, 59–67]} Of particular interest are the measurements made since 1997 of multiple sites of amide protons in proteins^{[5–6, 9, 11, 67]} and of hydrogen bonds in RNA kissing complexes.^[59] None of the solid-state methods mentioned above has achieved multiple site analysis to this extent.

The mid-1970's also saw the appearance of reliable high-resolution proton CSA measurements of molecules dissolved in liquid crystals (LC).^[68–69] The so-called residual CSA (RCSA) shift between an LC and an isotropic phase provides information on the magnitude and orientation of the chemical shielding tensor relative to the molecule’s alignment frame. For the interpretation of the RCSA, the orientation and the order parameter of the molecular alignment are determined based on the effects of dipolar interactions on the spectra.^[70] Like in the case of cross-correlation relaxation, one such measurement quantifies a single CSA tensor component. For instance, in the case of a molecule with threefold symmetry axis, such as CH₃CN, the RCSA is given by ΔσS (3cos²θ – 1)/3, where S is the order parameter and θ is the angle between the average orientation of the molecular axis and the magnetic field, with S being obtained from experimental dipole-dipole couplings.^[70] In molecules of lower symmetry two or more order parameters are needed to describe the molecular alignment. To obtain values of more than one CSA tensor component measurements of multiple LC alignments are needed.^[11] Various experimental approaches, using temperature dependence or combinations of nematic solvents or smectic LCs are applied to determine the RCSA and the order parameters from which Δσ can readily be extracted. However, contributions arising from intermolecular interactions with the solvent molecules, as well as thermal motions, can have a substantial effect on the results. Unfortunately, uncertainties concerning these effects have at times put the reliability of these measurements into question.^{[33, 70–72]} Improved experimental methods have been developed over the years, mainly by Jokisaari and coworkers, greatly increasing the reliability by demonstrating good agreement with theoretical ab initio predictions.^[73] The great majority of ¹H CSA determinations by LC NMR were performed before the turn of the century on small symmetric molecules, such as methyl halides,^{[68, 71, 73–75]} CH₃CCl₃, CH₃SiCl₃, (CH₃)₄Si, and (CH₃)₄C,^[69] CH₃NC,^[76] ethane, ethene, and ethyne,^[77] benzene,^[76] and 1,3,5-trichlorobenzene.^[78]

Notable exceptions are two proton CSA determinations in LC-dissolved proteins performed by Bax and coworkers.^{[7, 11]} In 2000, Cornilescu and Bax dissolved perdeuterated ubiquitin in a medium containing phospholipid bicelles, where ¹H-¹⁵N dipolar couplings of reprotonated amide groups provided a reference to determine the protein alignment tensor. Assuming that all atoms of a given type had the same CSA tensor, the average principal CSA components of α-helix and β-sheet amide protons, as well as the tensor orientation for each residue could be determined. The approximation of an axially symmetric shielding tensor, commonly assumed for amide protons until that time, was found to be invalid. Instead, the tensors deviated strongly from axial symmetry, with the most shielded tensor component roughly parallel to the NH vector, and the least shielded component orthogonal to the peptide plane.^[7] More recently, Yao et al. measured the RCSAs of six mutants of the protein domain GB3 that align differently relative to the static magnetic field when dissolved in a liquid crystalline suspension, and combined the results with transverse cross-correlated relaxation rates between the amide-proton CSAs and four different dipolar couplings, taking into account an anisotropic diffusion tensor. It led to a highly accurate set of fully defined amide-proton CSA tensors.^[11]

In a completely different approach Kukolich determined in 1975 the spin-rotation tensors of ¹H in gaseous formaldehyde and NH₃ by beam maser measurements. From these they derived the paramagnetic shieldings, which are related to electron contributions to the spin-rotation tensor by a numerical constant, and combined them with molecular orbital calculations of the diamagnetic shieldings to obtain total absolute shielding tensor elements.^[79]

In view of the apparent great interest in proton CSA and the tremendous advancements having been made in the development of sophisticated MAS NMR experiments, it is surprising that until recently no MAS method had been applied for the measurement of proton CSA other than the slow-spinning experiments mentioned above, where the CSA could be derived from spinning-side-band patterns.^{[22, 43]} The first MAS experiment at higher spinning rates was reported in 2007 by Brouwer and Ripmeester,^[10] who applied the symmetry-based sequence R18₂⁵, which decouples homonuclear dipolar interactions and recouples CSA interaction,^[80–81] to maleic acid and citric acid. In a similar approach, Duma et al.^[82] applied rotary resonance to recouple proton CSA of hydrogen-bonded SiOH, COOH, and PO₂OH groups. Very recently, Miah et al.^[83] used the $R{16}_3^2$ symmetry sequence at spinning frequencies around 60 kHz to measure ¹H CSA in tyrosine and citric acid. These MAS methods were 2D experiments where the proton signal was detected in the direct dimension, either under free evolution^{[10, 82–83]} or under resolution enhancement by wPMLG5,^[10] a multiple-pulse method developed by Vega and coworkers for measurement of isotropic proton chemical shift by effective decoupling of homonuclear dipolar interactions.^[84] In these experiments, different proton sites could be measured individually thanks to the fact that the samples had relatively sparse hydroxyl proton spectra. Since no dipolar interactions with other nuclei were involved, the results provided principal tensor components without orientational information. The method introduced by us earlier this year^[12] also utilizes symmetry-based RN sequences under MAS and applies them to ¹HX spin pairs, X being a spin-1/2 nucleus like ¹⁵N or ¹³C. It detects both the ¹H CSA and the heteronuclear ¹HX dipolar interaction, while also taking advantage of the dipolar coupling through short-contact-time cross-polarization (CP) for well-resolved site-selective X-signal detection. Since the isotropic proton chemical shift is decoupled by the RN sequence, the measurements are restricted to the anisotropic tensor parameters δ and η, and due to the nature of the recoupling process, the sign of δ remains undetermined. Like in cases of other CSA-determining experimental methods mentioned above, additional experiments can be conducted independently to extract the isotropic shifts as well. When dealing with HX spin pairs in solid samples, this can readily be accomplished with HX HETCOR measurements.^[85–86] The incorporation of the dipolar interaction lets the RN experiment, in addition to the two principal-component CSA values, also provide two polar angles defining the internuclear vector with respect to the CSA tensor. A third Euler angle for complete tensor-component determination cannot be derived from the results. Like in the preceding modern MAS approaches, the interaction parameters are found by curve fitting of the lineshapes. We found that the accuracy of the results is greatly improved if a simultaneous fit of the lineshapes of three experiments is performed.^[12] One of these experiments, designated as RN-¹H(X_dec), follows the evolution of the ¹H spin state under CSA interaction while the interaction with X is decoupled; the second experiment, RN-¹H(X_und), is identical but X stays undecoupled; and the third one, RN-X, follows the evolution of the X spin state under dipolar and ¹H CSA interaction.^[12] In particular, it was found that the RN-¹H(Xdec) experiment, which is most similar to the other CSA-decoupling experiments^{[10, 82–83]} and is expected to provide data for the principal CSA components, does not lead to high-accuracy values unless it is combined with the other two experiments.

In our recent application we introduced the method in the context of the multidimensional experiments for site-resolved measurements of amide proton CSA. It allowed reasonably well-defined CSA tensors to be extracted for 42 amide proteins in the 89-residue protein CAP-Gly domain of dynactin.^[12] In the present contribution, we extend the applications of our method and report measurements of ¹H¹⁵N and ¹H¹³C spin pairs in histidine, thereby demonstrating that our approach is well suited for recording of ¹H CSA tensors for aliphatic and aromatic protons, which is a more challenging task due to the significantly smaller ¹H CSA interaction in these cases. We demonstrate that the ¹H CSA tensors differ significantly for the cationic and neutral forms of histidine. These experimental findings are in remarkable quantitative agreement with results of DFT calculations.

2. METHOD

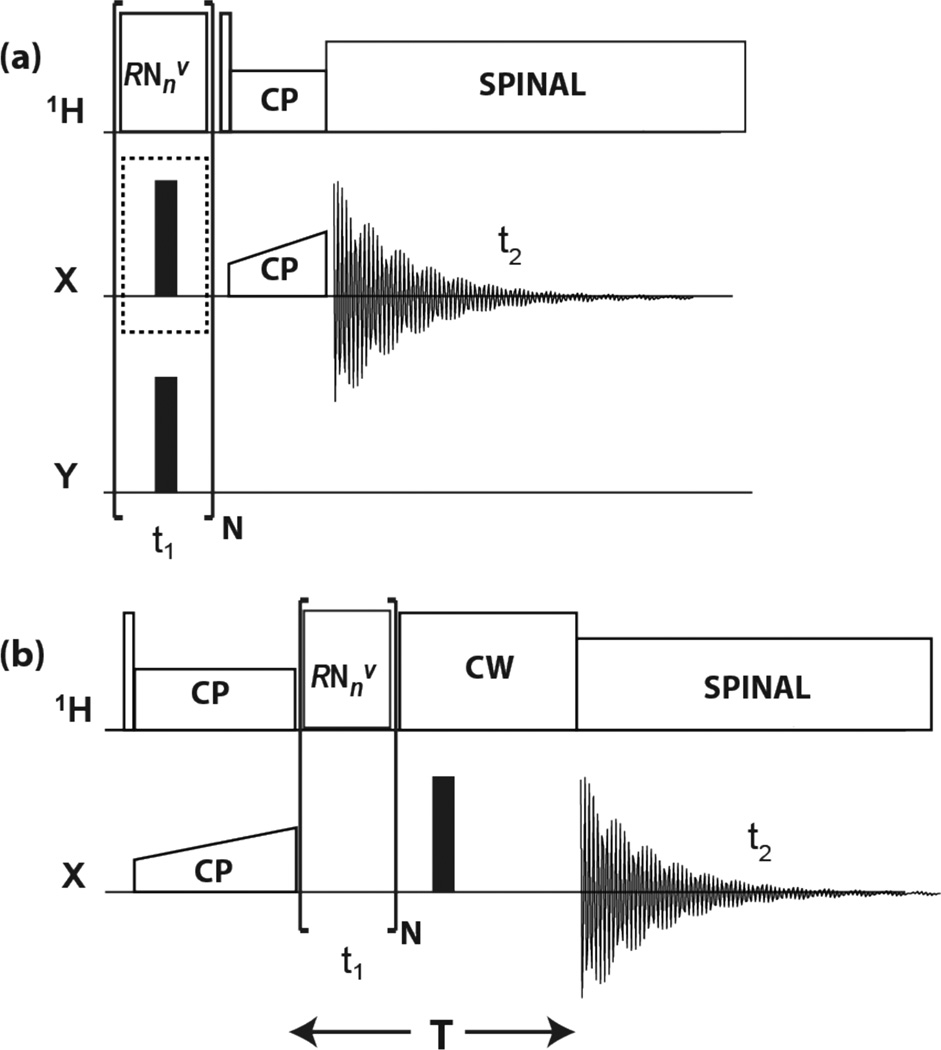
The three pulse sequences applied in this work for detection of ¹HX (X = ¹³C or ¹⁵N) spin-pair interactions are schematically shown in Figure 1. Y denotes the channel of the nonobserved, to be decoupled nucleus (¹⁵N or ¹³C, respectively). To describe the spin dynamics we assign the symbols I and S to the ¹H and X spins, respectively. The RN-¹H spectra are obtained with the sequence shown in Figure 1(a). In these experiments the beginning spin state is I_z, and the evolution of the expectation value of I_z is monitored. The π pulses on the X channel, that decouple the I-S interaction, are employed for the RN-¹H(X_dec) experiment and are omitted for the RN-¹H(X_und) experiment. The RN-X spectrum is measured with the sequence shown in Figure 1(b), which is identical to earlier R18_n^v experiments for obtaining heteronuclear dipolar spectra.^[87–91] In this pulse sequence, the spin state is prepared in the S_x state, and the evolution of the S_x coherence is monitored. The π pulse on the X channel in Figure 1(b) refocuses precessions due to chemical shift of S and enables constant-interval detection.^[87]

Figure 1.

Pulse sequences for (a) RN-¹H(X_und) and RN-¹H(X_dec), and (b) RN-X 2D experiments. In the present applications, X and Y represent ¹⁵N and ¹³C, or ¹³C and ¹⁵N, respectively. Rotor synchronized RN_n^v symmetry rf pulses are applied during t₁ evolution time to reintroduce ¹H CSA and ¹H−X dipolar interactions under MAS conditions. Empty and solid rectangles denote π/2 and π pulses, respectively. In (a), the time dependence of ¹H z-magnetization is monitored, either with application of the X decoupling π pulses for RN-¹H(X_dec), or without for RN-¹H(X_und). This optional decoupling pulse is marked by a dotted-line enclosure. Y is decoupled by π pulses during t₁. Site-selective ¹H detection is accomplished by short-contact-time CP to X. In (b), the time evolution of X x-magnetization is monitored with refocusing of the chemical shift over a constant evolution period T.

The $R{N}_n^v$ pulse sequences^[80–81] applicable to our experiments are those with the symmetry properties designed for recoupling of CSA and heteronuclear dipolar interactions while they suppress isotropic shift and homonuclear dipolar interactions.^{[10, 83, 87, 92–93]} Under this irradiation the first-order average Hamiltonian of the proton CSA interaction is^[12]

$$H_{av}^{\mathit{\text{CSA}}}=\frac{1}{6}{\kappa }_{2211}{\omega }_0\delta \left[\right\{-{\text{sin}}^2{\beta }_{\mathit{\text{CSA}}}+\eta ({\text{cos}}^2{\beta }_{\mathit{\text{CSA}}}+1)\text{cos}2{\alpha }_{\mathit{\text{CSA}}}\}(I_x\text{cos}2{\gamma }_{\mathit{\text{CSA}}}+I_y\text{sin}2{\gamma }_{\mathit{\text{CSA}}})+2\eta \text{cos}{\beta }_{\mathit{\text{CSA}}}\text{sin}2{\alpha }_{\mathit{\text{CSA}}}(I_x\text{sin}2{\gamma }_{\mathit{\text{CSA}}}-I_y\text{cos}2{\gamma }_{\mathit{\text{CSA}}})]$$ (1)

where κ₂₂₁₁ is a scaling factor, ω₀ is the Larmor frequency, δ = δ_ZZ – δ_iso is the size of the CSA, η is its asymmetry parameter, α_CSA and β_CSA are the polar angles of the rotor axis with respect to the X, Y, Z principal axis system of the CSA, and γ_CSA is the rotation angle of the sample at the beginning of the RN sequence (t₁ = 0) defined such that γ_CSA = 0 when the CSA Z axis, the magnetic field B₀, and the rotor axis are coplanar with the Z axis making an angle with B₀ that equals β_CSA plus the magic angle. The scaling factor κ₂₂₁₁ depends on the symmetry numbers of the RN_n^v sequence; for R12₁⁴ it is 0.3101. A detailed discussion of significant features of the effective Hamiltonian when applied to ¹HX spin pairs, including effects of the presence of additional nuclei, and relaxation, will be presented in a forthcoming publication. The average Hamiltonian for the heteronuclear XH interaction under this type of RN_n^v irradiation is^[12]

$$H_{av}^D=-{\kappa }_{2211}{b}_{IS}{\text{sin}}^2{\beta }_D(I_x{S}_z\text{cos}2{\gamma }_D+I_y{S}_z\text{sin}2{\gamma }_D)$$ (2)

where β_D is the angle between the HX bond direction and the rotor axis, γ_D is the sample rotation angle at t₁ = 0 defined such that γ_CSA = 0 when the angle between B₀ and the XH bond equals β_D plus the magic angle, and b_IS = D/2π is the dipolar coupling constant (DCC) determined by the XH internuclear distance r,

$$b_{IS}=-\frac{{\mu }_0{\gamma }_I{\gamma }_S\hslash }{4\pi r^3}$$ (3)

When applied to a powder sample, the spectral lineshapes will depend on the CSA parameters δ and η, the DCC, and the polar angles θ, ϕ of the direction of the XH bond direction with respect to the CSA principal axis system. As mentioned in the Introduction, no additional spin interaction is present that would cause spectral dependence on a third angle of CSA rotation about XH.^[12] The RN-¹H spectra, which are detected via CP to the neighboring X nucleus, are also affected by the orientational dependence of CP dynamics. The signal formation during the CP contact time τ_ct is to a good approximation described by the equation^[12]

$$\langle S_x({\tau }_{ct})\rangle =\langle I_x(0)\rangle {\text{sin}}^2(\frac{1}{4}{\tau }_{ct}\sqrt{2}{b}_{IS}\text{sin}2{\beta }_D/2),$$ (4)

where <I_x(0)> and <S_x(τ_ct)> are the expectation values of the I_z coherence emerging from the RN irradiation and of the to-be-detected S_x coherence, respectively. Under our experimental conditions the spectral lineshapes simulated according to these expressions are fairly good approximations of the spectra simulated based on the full time-dependent Hamiltonian but they are not accurate enough to precisely represent the interaction parameters. In the simultaneous curve fittings of the three experimental spectra RN-¹H(X_und), RN-¹H(X_dec), and RN-X we utilized the high speed of the average-Hamiltonian computer simulations to obtain approximate values of the to-be-fitted parameters and subsequently refined them with full-Hamiltonian calculations. Parameters to be fitted are the DCC, the CSA components δ and η, and the polar angles θ and ϕ. Relaxation during the RN irradiation also needs to be taken into account, which we do by assuming a uniform exponential decay corresponding to individual Lorentzian broadenings of the three spectra, leading to a total of eight parameters to be fitted.

3. RESULTS AND DISCUSSION

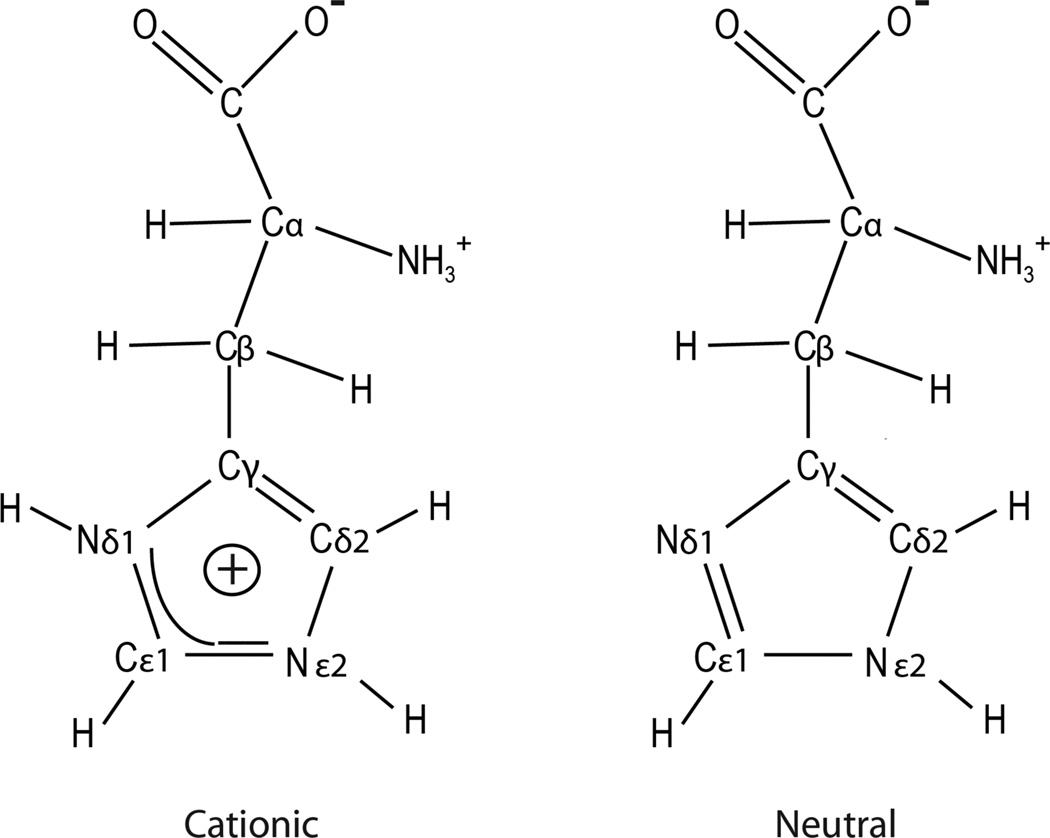
The method was applied to histidine. A number of NMR investigations of the chemical structure and dynamics of histidine in proteins and of chemical-shift and bond-length measurements of small-molecule histidine and imidazole in various protonation states have been reported in the past. These publications were reviewed by Li and Hong in 2011, who measured a complete set of ¹⁵N, ¹³C, and ¹H chemical shifts of histidine and its H-bonding properties and rotameric conformations over a wide range of pH values.^[94] These results included CSA of ¹⁵N and ¹³C but not of ¹H. When crystallized from an aqueous solution, the protonation level of the histidine molecule and its crystal structure depend on the pH of the solution. Our sample was precipitated from a solution containing HCl at a pH of 6.0. It led to a mixture of two types of crystallites, one made up of cationic biprotonated L-histidine·HCl·H₂O and the other of the neutral τtautomer of L-histidine.^[94] The corresponding two molecular structures^[94] are shown in Figure 2, and the ¹³C and ¹⁵N CPMAS spectra are presented in the Supporting Information. The chemical shifts closely agree with those reported by Li and Hong,^[94] (see Table S1 of the Supporting Information) ensuring that our crystal structures are most probably identical to theirs and enabling us to make the proper peak assignments.

Figure 2.

Molecular structures of histidine in the biprotonated cationic and neutral forms.

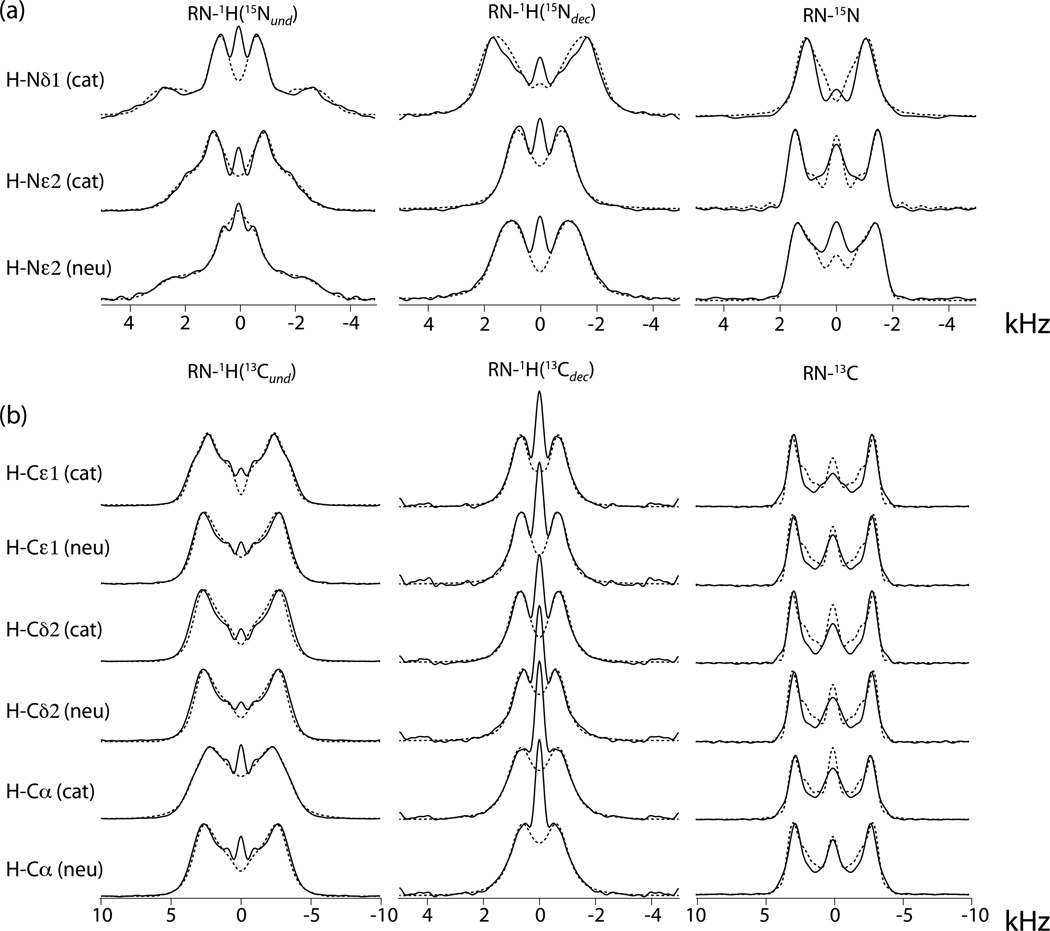
The R12₁⁴ experiments were performed at a proton frequency of 850 MHz and an MAS speed of 20 kHz. Figure 3 shows the ¹H¹⁵N and ¹H¹³C RN lineshapes extracted from the 2D spectra together with the full-Hamiltonian-simulated lineshapes resulting from triple curve fitting by the simplex method. Since there are conditions not represented by the two-spin Hamiltonian that cause the central region of the spectrum to deviate from the theoretical predictions,^[12] often in the form of a zero-frequency peak, we excluded the central region from the to-be-fitted line shapes. The fitted parameters are listed in Table 1, together with uncertainty ranges that were estimated from a Monte-Carlo error analysis.^[12] The table includes a column showing the span, Ω = |δ_XX – δ_ZZ|, of the tensor. As we observed before,^[12] the span represents a property of the CSA that has smaller relative uncertainty than the individual components. Furthermore, presenting the span avoids the difficulty of having to assign a sign to the δ parameter that, as we mentioned, remains undetermined by our method (see below).

Figure 3.

RN lineshapes of H-¹⁵N and H-¹³C spin pairs in cationic and neutral histidine extracted from experimental 2D spectra (full lines) and best-fit simulations (broken lines).

Table 1.

Spin-interaction parameters of NH and CH hydrogens in two protonation states of histidine, as derived from triple fits of the R12₁⁴ spectra.

		δXX – δiso (ppm)	δYY – δiso (ppm)	δZZ – δiso (ppm)	Ω (ppm)	DCC (kHz)	θ (°)	ϕ (°)
H-Nδ1,	cationic	11.4 ± 1.5	6.0 ± 1.8	−17.4 ± 0.6	28.8 ± 1.4	8.4 ± 0.2	1 ± 4	---
H-Nε2,	cationic	7.8 ± 0.3	−2.0 ± 0.4	−5.7 ± 0.4	13.5 ± 0.5	10.5 ± 0.1	1 ± 12	---
	neutral	8.9 ± 0.5	3.0 ± 0.5	−11.9 ± 0.3	20.8 ± 0.5	10.1 ± 0.1	12 ± 1	88 ± 15
H-Cε1,	cationic	5.1 ± 0.7	0.0 ± 1.0	−5.1 ± 0.7	10.2 ± 0.7	20.6 ± 0.5	26 ± 10	87 ± 40
	neutral	4.3 ± 0.6	0.7 ± 1.3	−5.0 ± 1.0	9.2 ± 1.1	20.4 ± 0.4	52 ± 12	42 ± 20
H-Cδ2,	cationic	5.1 ± 0.7	0.1 ± 0.8	−5.2 ± 0.6	10.3 ± 1.0	20.4 ± 0.7	57 ± 26	50 ± 40
	neutral	4.0 ± 0.7	0.1 ± 1.1	−4.2 ± 0.7	8.2 ± 0.9	20.3 ± 0.6	57 ± 12	51 ± 30
H-Cα,	cationic	4.4 ± 0.8	1.2 ± 1.3	−5.6 ± 0.6	10.0 ± 0.6	19.7 ± 0.5	28 ± 10	87 ± 30
	neutral	4.0 ± 1.2	0.4 ± 1.8	−4.4 ± 0.9	8.4 ± 1.1	20.3 ± 0.3	51 ± 30	72 ± 35

In order to be able to judge the reliability of these results we performed DFT calculations of the proton CSAs. Since the proton CSA values are known to be strongly dependent on the molecular structure and its environment, we could perform the calculations only on a molecule for which the crystal structure has been solved. For this we used the results of a neutron-diffraction study of L-histidine·HCl·H₂O,^[95] which was referred to by Zhao et al.,^[88] who determined the DCC of the ¹⁵N ¹H spin pairs by application of the R18₂⁵ symmetry sequence. Not having access to a neutral-histidine crystal structure, we did not perform a DFT calculation of that sample. To verify that our sample conforms with the crystal structure, we compare in Table 2 the neutron-diffraction bond lengths with the NH distances derived from DCC's obtained by Zhao et al., Li and Hong, and this work. As is generally the case, the NMR-derived bond lengths are somewhat longer than those determined by crystallography due to a reduction of the DCC caused by librational motions. Taking this into account, we observe a consistent elongation of the NH bond at Nδ1 in comparison to Nε2, which can be explained by a stronger hydrogen bond at Nδ1, in agreement with the shorter distance of the nitrogen to the oxygen acceptor of a neighboring carboxyl group (1.58 vs. 1.94 Å).^[95] In our results the NH bond at Nδ1 is also longer than at Nε2, indicating that it may be assumed that our sample has essentially the same crystal structure. Nevertheless, there appears to be stronger NH-bond stretching in our sample (see Table 2). This observation will be addressed later in the discussion, where it will be shown that artificially shortening of the NH bond to 1.09 Å can be accommodated with simulated lineshapes that do not deviate very much from the experimental spectra.

Table 2.

NH bond distances (Å) in cationic histidine as determined by neutron diffraction and as derived from three NMR experiments.

	H-Nδ1	H-Nε2
n-diffraction[95]	1.070 ± 0.004	1.026 ± 0.004
NMR, Zhao et al.[88]	1.09 ± 0.05	1.05 ± 0.05
NMR, Li and Hong[94]	1.09 ± 0.01	1.06 ± 0.01
NMR, present work	1.13 ± 0.01	1.05 ± 0.01

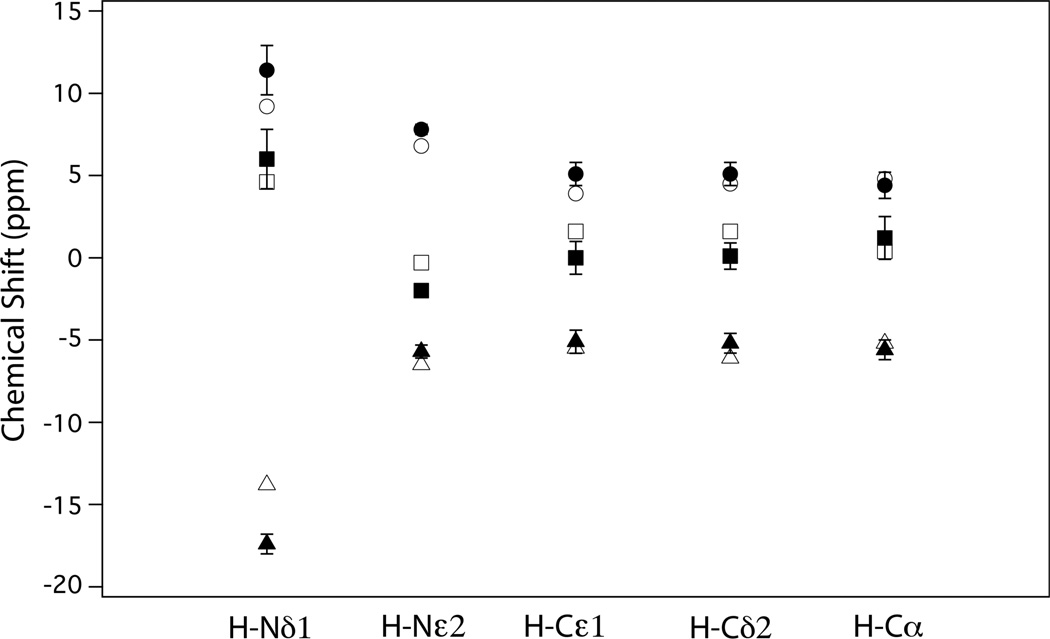
The results of the DFT calculations are shown in Table 3. The isotropic and CSA components of the tensor are listed separately to facilitate comparison with the NMR data in Table 1. With regard to the spans, Ω, the quality of the agreement with our CSA results can be readily assessed by comparing their values listed in Tables 1 and 3. For H-Nε2, H-Cε1, H-Cδ2, and H-Cα the deviations are within experimental error (≤ 8%), while for the strongly hydrogen-bonded H-Nδ1 the discrepancy is somewhat larger at 20%. The agreement of the individual principal CSA components is also quite reasonable as can be seen in Figure 4, where their values as determined by NMR and by DFT are plotted together. Furthermore, Table S2 of the Supporting Information, shows that the calculated isotropic shifts do not deviate more than 1 or 2 ppm from the shifts reported by Li and Hong.^[94] The large difference between tensor components of Nδ1 and Nε2 is in accordance with the well-established tendency of the CSA of hydrogen-bonded protons to be larger when the donor-acceptor distance is shorter.

Table 3.

Principal components of proton chemical-shift tensors and polar angles θ, ϕ of the XH bond direction for NH and CH groups in cationic histidine calculated using Density Functional Theory.

	δiso (ppm)	δXX – δiso (ppm)	δYY – δiso (ppm)	δZZ – δiso (ppm)	Ω (ppm)	θ (°)	ϕ (°)
H-Nδ1	15.8	9.2	4.6	−13.8	23.0	59	43
H-Nε2	11.7	6.8	−0.3	−6.5	13.3	67	6
H-Cε1	7.8	3.9	1.6	−5.5	9.4	17	62
H-Cδ2	7.4	4.5	1.6	−6.1	10.6	73	88
H-Cα,	3.4	4.8	0.4	−5.2	10.0	7	64

Figure 4.

Proton CSA principal components, δ_ii – δ_iso, i = X, Y, Z, of five XH spin pairs in cationic histidine as determined by DFT calculations (open symbols) and RN spectra (closed symbols).

Concerning the assignment of a positive or negative sign to the CSA parameter δ, we made our choices based on the following considerations. As can be seen in Table 1, we designated the X and Z axes to the highest and lowest CSA components, respectively. Had we chosen a set derived from an opposite sign of δ, the X and Z designations would have been interchanged. Such an inverse assignment must be accompanied by a corresponding reevaluation of the polar angles θ and ϕ, because they are defined in the X, Y, Z system. For the three listed NH sites we assumed, based on earlier results of hydrogen-bonded NH groups, that the NH bond makes a small angle with the direction of the most shielded CSA component. In most of the CH cases the δ_YY value happens to be zero within the uncertainty limits, i. e., η ~ 1, meaning that changing the signs does not significantly impact the values of δ_XX and δ_ZZ. Unfortunately, in the case of CH protons we have no conventional guideline that would help us finalize the axis designations. In particular, we have no guarantee that the CH bond direction is close to a particular axis, as is evident from the three DFT results listed in Table 3, where the CH bonds do point within 20° along one of the axes, but with two (Cε1 and C α) along Z and the other (Cδ2) along Y. However, in the cationic form we were able to make some choices based on the DFT results of the individual carbon sites as follows. At Cε1 and cationic C α the CH direction falls within 30° of one of the axes, a situation that prompted us to make the sign designation in accordance with the orientational DFT results. For these two sites it led to CH bond directions with respect to the CSA frame that point about 25° away from the DFT-determined directions. In the case of Cδ2 it was impossible to decide which axis choice accommodates the DFT direction most closely, because the best-fit CH is essentially parallel to the body diagonal of the CSA tensor (θ, ϕ = 57°, 50° vs. 54.7°, 45°). However, considering the large uncertainties of the polar angles reported in Table 1 for this site, the disagreement between NMR and DFT results could be unimportant. In the neutral molecule the CH bonds also have polar angles corresponding to directions that are not close to any of the principal axes. As a result, we are left with arbitrary component signs for most of the CH principal components

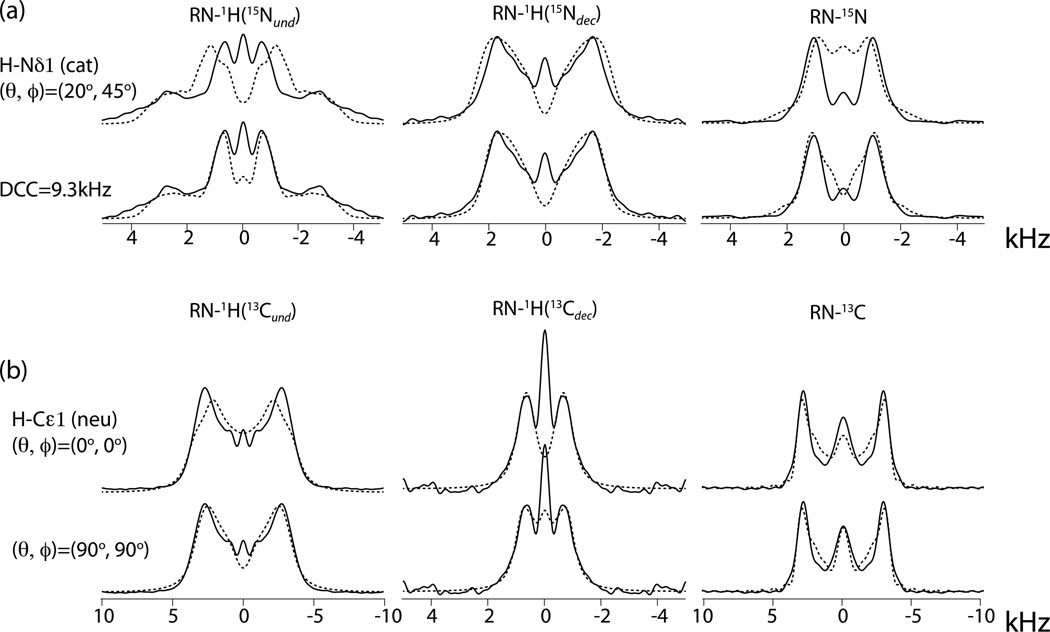
The severe disparity between the NH directions found by NMR and by DFT for the strongly cationic Nδ1 and Nε2 protons cannot be explained away by ascribing it to experimental uncertainties. This is confirmed in the top row of Figure 5, which shows a simulation of the cationic H-Nδ1 spectrum where the NH direction was taken to be half way between the orientations resulting from spectral curve fitting and DFT calculations. All other best-fit parameters were left unchanged. The misfit clearly demonstrates the strong dependence of the lineshapes on the NH orientation. On the other hand, the unusually long NH bond length derived from the lineshapes for this site can be accommodated by performing the triple fit with a fixed DCC value of 9.3 kHz corresponding to a bond length of 1.09 Å. It results in the simulated spectra shown in the second row of Figure 5 and in CSA components (10.4, 5.9, -16.3 ppm) that are slightly closer to the DFT results.

Figure 5.

Experimental RN lineshapes (full lines) of (a) cationic H-Nδ1 and (b) neutral H-Cε1 spin pairs and corresponding lineshapes (broken lines) simulated with indicated deviations from the best-fit parameters. In the top row of (a), (θ, ϕ) are changed to (20°, 45°) while all other parameters are kept equal to the best-fit values. All other simulations are fit results with the DCC or (θ, ϕ) kept fixed at the indicated values.

Another surprising orientation result is that in most cases the CH direction does not come out closely parallel to one of the axes. It is possible that this can also be attributed to experimental error. This is illustrated in the two bottom rows of Figure 5, where the simulations of the spectra of neutral H-Cε1 are displayed with the CH direction redirected along the Z axis and along the Y axis. Because the absolute values of δ_XX and δ_ZZ don't differ much, the spectra with CH parallel to X are nearly identical to those with CH // Z (not shown). The simulated spectra suggest that CH // Y could be the case. We must conclude that, while the agreement of the principal tensor components with DFT results is quite satisfactory, we are left with some uncertainty regarding the tensor orientations. In this context we note that our recent measurements of amide proton CSA in a protein using RN sequences showed consistently small angles between the CSA-Z axis and the NH direction, completely conforming with conventional expectations.^[12]

4. EXPERIMENTAL SECTION

Materials

U-¹³C, ¹⁵N]-L-histidine was purchased from Cambridge Isotope Laboratories. The histidine was recrystallized from an aqueous HCl-containing solution at a pH of 6.0, then packed into MAS rotor.

Solid-State NMR Spectroscopy

All NMR experiments were carried out on a 19.9 T Bruker Avance III narrow bore solid-state NMR spectrometer, operating at a Larmor frequency of 850.4 MHz for ¹H, 213.8 MHz for ¹³C and 86.2 MHz for ¹⁵N. A 1.9 mm Bruker MAS triple-resonance T3 probe was used. Approximately 9 mg of histidine were packed into the rotor over a length of 7.5 mm. The spectra were recorded with a MAS frequency of 20 kHz, controlled to within ± 0.005 kHz. To reduce the sample heating during MAS, nitrogen gas was used for cooling, resulting in a final sample temperature of 20°C. The temperature was calibrated for different MAS frequencies using a KBr temperature sensor, and the actual temperature at the sample was maintained to within ±0.5°C throughout the experiments using a Bruker temperature controller.

The pulse sequences for ¹H CSA measurements were shown above in Figure 1. R12₁⁴ symmetry-based pulses were applied during t₁ dimension for recoupling ¹H CSA, and ¹H-¹⁵N or ¹H-¹³C dipolar interactions. An R12₁⁴ cycle consists of one rotor period and contains 12 proton π pulses having rf amplitude 6 times the MAS frequency and phases alternating between 60° and - 60°. For NH proton CSA measurements, a π pulse with rf field strength of 50 kHz was applied on the ¹⁵N channel at the center of each R cycle to decouple the ¹H-¹⁵N heteronuclear dipolar interactions in the RN-¹H(¹⁵N_dec) experiment, and no ¹⁵N π pulse for RN-¹H(¹⁵N_und) experiment. A decoupling ¹³C π pulse with rf field strength of 70 kHz was applied at the center of each R cycle in both RN-¹H(¹⁵N_dec) and RN-¹H(¹⁵N_und) experiments. For CH proton CSA measurements, a π pulse with rf field strength of 70 kHz was applied on the ¹³C channel at the center of each R cycle to decouple the ¹H-¹³C heteronuclear dipolar interactions in the RN-¹H(¹³C_dec) experiment, and no ¹³C π pulse for RN-¹H(¹³Cund) experiment. A decoupling ¹⁵N π pulse with rf field strength of 50 kHz was applied at the center of each R cycle in both RN-¹H(¹³C_dec) and RN-¹H(¹³C_und) experiments. For the RN-¹⁵N (RN-¹³C) experiment, a ¹⁵N (¹³C) π pulse was applied at the center of a constant evolution period (T) to refocus ¹⁵N (¹³C) chemical shift and decouple ¹H-¹⁵N (¹H-¹³C) J-couplings. ¹H CW decoupling (same rf field strength as R irradiation) was applied between the end of the R12₁⁴ evolution time and the beginning of the detection. SPINAL64 decoupling was used in the direct dimension with rf field strength of 100 kHz in all cases. The ¹H-X CP contact time for the RN-¹H(X_und) and RN-¹H(X_dec) (X = ¹³C, ¹⁵N) lineshape measurement was set equal to two rotor periods, 100 µs. The optimized contact times were 1.6 and 1.0 ms for RN-¹⁵N and RN-¹³C spectra, respectively. ¹H-X cross polarization was achieved by applying a linearly ramped rf field from 90-110% of the first-sideband Hartmann-Hahn match on the X nuclei and constant-amplitude ¹H rf fields of 70 kHz and 90 kHz for X = ¹³C and ¹⁵N, respectively. The pulse delay was 15 s for all NMR experiments.

For NH proton CSA measurements, the dwell time in indirect dimensions was set equal to two rotor periods for all RN-¹H(¹⁵Ndec), RN-¹H(¹⁵N_und) and RN-¹⁵N experiments, and with 24, 24, 16 t₁ points were collected, respectively. For CH proton CSA measurements, the dwell time in indirect dimensions was set equal to two rotor periods for RN-¹H(¹³Cdec) experiment, and one rotor period for RN-¹H(¹³Cund) and RN-¹³C experiments, and 32, 32, 24 t₁ points were collected for RN-¹H(¹³Cdec), RN-¹H(¹³Cund) and RN-¹³C experiments, respectively.

Spectral Processing and Simulations

The RN_n^v spectra are evaluated as the real-FT of the corresponding indirect-dimension time-domain signals, following zero filling to 256 points. Narrow center peaks that are regularly observed in experimental RN-¹H spectra due to nonideal conditions are represented in the time domain signal as a nondecaying DC offset^{[12, 83]} and were suppressed by subtracting the last point of the time-domain spectrum from the entire spectrum prior to zero-filling. Numerical simulations were executed in a Fortran-95 program, details of which are described in Ref. ^[12] The central regions excluded from the to-be-fitted frequency region were bounded by ±0.5, ±0.5, and ±0.7 kHz in the RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_und), and RN-¹⁵N experiments, and by ±0.7, ±0.5, and ±1.5 kHz in the RN- ¹H(¹³C_und), RN-¹H(¹³C_und), and RN-¹³C experiments, respectively. Since we established that fit results obtained with time-consuming full-Hamiltonian calculation of the CP process barely differed from those evaluated using the short-cut expression of Equation (4), all curve fittings were performed based on this expression.

Density Functional Theory Calculations

The DFT calculations were performed using the hybrid functional B3LYP and the basis set 6-311G provided by Gaussian 03 (Revision E.01) software package.^[96] The calculation of the NMR parameters was done using the coordinates of the neutron-diffraction structure of the L-histidine·HCl·H₂O complex^[95] (CSD entry HISTCM12). Single point calculation using the GIAO method with no geometry optimization was performed on a cluster of 25 histidine molecules and surrounding chloride ions and water molecules of the crystal structure to take into account hydrogen bonding interactions up to 6 Å.

5. CONCLUSIONS

Proton chemical shift tensors are of interest to chemists, biochemists and structural biologists as a probe of structure and hydrogen bonding environments in a wide variety of organic and biological systems. While multiple NMR approaches have been developed over the past several decades for the measurement of proton chemical shift tensors in solids and in solution, until 2013 these have been restricted to either solid systems with sparse proton sites or were based on the indirect determination of anisotropic tensor components from cross-relaxation and liquid-crystal experiments. We have recently introduced an MAS approach that permits site-resolved measurement of CSA tensors of protons forming chemical bonds with labeled spin-1/2 nuclei such as ¹³C, ¹⁵N, and possibly ³¹P in fully protonated solids with multiple sites, including organic molecules and proteins. We have demonstrated that, using three RN-symmetry based experiments, the principal components of the ¹H CS tensor can be reliably extracted by simultaneous triple fit of the data. These RN-symmetry sequences can be readily incorporated in 2D and 3D experiments, permitting the introduction of isotropic chemical shift detections to enable the measurements for multiple sites simultaneously. In this work, we have expanded this approach to the measurement of ¹H chemical shift anisotropies of small magnitude, such as those for aliphatic and aromatic protons. Using histidine, we have shown that the experimental ¹H(C) and ¹H(N) chemical shift tensors are in agreement with Density Functional Theory calculations, therefore establishing the usefulness of our method for characterization of structure and hydrogen bonding environment in organic and biological solids.