Bayesian Inference of Shared Recombination Hotspots Between Humans and Chimpanzees

Abstract

Recombination generates variation and facilitates evolution. Recombination (or lack thereof) also contributes to human genetic disease. Methods for mapping genes influencing complex genetic diseases via association rely on linkage disequilibrium (LD) in human populations, which is influenced by rates of recombination across the genome. Comparative population genomic analyses of recombination using related primate species can identify factors influencing rates of recombination in humans. Such studies can indicate how variable hotspots for recombination may be both among individuals (or populations) and over evolutionary timescales. Previous studies have suggested that locations of recombination hotspots are not conserved between humans and chimpanzees. We made use of the data sets from recent resequencing projects and applied a Bayesian method for identifying hotspots and estimating recombination rates. We also reanalyzed SNP data sets for regions with known hotspots in humans using samples from the human and chimpanzee. The Bayes factors (BF) of shared recombination hotspots between human and chimpanzee across regions were obtained. Based on the analysis of the aligned regions of human chromosome 21, locations where the two species show evidence of shared recombination hotspots (with high BFs) were identified. Interestingly, previous comparative studies of human and chimpanzee that focused on the known human recombination hotspots within the β-globin and HLA regions did not find overlapping of hotspots. Our results show high BFs of shared hotspots at locations within both regions, and the estimated locations of shared hotspots overlap with the locations of human recombination hotspots obtained from sperm-typing studies.

RECOMBINATION plays an essential role during meiosis, ensuring proper chromosomal segregation; improper recombination and/or segregation may cause serious diseases (Lynn et al. 2004; Arnheim et al. 2007). By exchanging genetic material between chromosomes, recombination also influences natural selection (Coop and Przeworski 2007) and is an important factor shaping the patterns of linkage disequilibrium, which have a fundamental role in disease association analysis (Pritchard and Przeworski 2001; Slatkin 2008). Moreover, studies have suggested that nonallelic homologous recombination (NAHR) may be related to allelic homologous recombination (De Raedt et al. 2006; Lindsay et al. 2006). NAHR can result in chromosomal rearrangements, which are responsible for many diseases in humans (Lupski 2004). Despite the importance of recombination, many aspects of recombination are still unknown, although the recent discovery of PRDM9 has furthered understanding of the regulation of recombination (Paigen and Petkov 2010; Baudat et al. 2013). Studying the evolution of recombination hotspots among related species could potentially aid in our understanding about the mechanisms of recombination.

In recent years, our understanding of the rates of homologous recombination across the human genome has been advanced by high-resolution pedigree analyses (Kong et al. 2002; Coop et al. 2008), sperm-typing studies (reviewed in Kauppi et al. 2004; Arnheim et al. 2007), and statistical inference based on population genomic data (Crawford et al. 2004; Myers et al. 2005). Such studies have been facilitated by recent advances in genotyping technologies and statistical inference methods. Pedigree analyses have provided insights concerning recombination rates over broad scales across the human genome, but the resolution of such analyses is limited by the number of meioses in pedigrees. Sperm-typing studies have provided insights regarding fine-scale recombination rates for several genomic regions, but such methods are laborious and expensive and are currently difficult to scale up to the whole genome. In addition, only male recombination rates can be inferred. Genome-scale analyses of fine-scale recombination rates and comparative studies of recombination hotspots among primates more generally are currently being pursued by applying statistical methods to population genomic data.

Comparative studies of recombination hotspot locations between closely related species can provide insights concerning shared sequence features that may be involved in regulating recombination. Several comparative analyses have been carried out on the basis of population genomic data, mostly between human and chimpanzee (Ptak et al. 2004, 2005; Winckler et al. 2005; Myers et al. 2010; Auton et al. 2012), with one study considering human, chimpanzee, and macaque (Wall et al. 2003). In general, these studies have concluded that few hotspots are shared between the two species, including both regions for which prior information about human recombination hotspots is available, such as the β-globin and the human leukocyte antigen (HLA) regions, and regions for which no such prior knowledge is available (e.g., comparative analyses that are not focused to regions with known human recombination hotspots). These results raise many interesting questions regarding the evolution of recombination hotspots and the biological factors influencing recombination rates, given that human and chimpanzee possess highly similar DNA sequences (Coop and Przeworski 2007). One possible explanation is that shared hotspots exist but the statistical methodologies perform differently due to various approximations applied. The computational complexity of population genomic inference of fine-scale recombination rates has led to the use of statistical methods that rely on various approximations and it is therefore possible that methodology may play a role in generating the observed dissimilarities between species. Another possibility is that the nature of the mechanism of recombination differs even between closely related species. Previous studies (Myers et al. 2008, 2010) show that a sequence motif is associated with a certain percentage of human recombination hotspots and a zinc finger protein PRDM9 binds to the motif, but the motif is not active in chimpanzees. This might be due to trans-acting factors regulating recombination in chimpanzees that differ from humans.

To explore these questions, we applied our Bayesian Markov chain Monte Carlo method for simultaneously estimating recombination rates and detecting recombination hotspots (Wang and Rannala 2008, 2009) to the data from two recent resequencing projects (Abecasis et al. 2010; Prado-Martinez et al. 2013) and to the data sets from a previous study concerning known human recombination hotspots (Winckler et al. 2005). A full-likelihood method is used if the sampled genomic regions are not large; otherwise a composite-likelihood method is used by splitting the larger regions into subregions. The full-likelihood method is feasible for use in analyzing moderate-size intervals through the use of a SNP genealogy in which the ancestral markers are efficiently modeled by marker ancestry vectors (Wang and Rannala 2008). A composite-likelihood method applied to larger regions takes advantage of additional information in the larger subintervals, providing improved performance over methods that use small number of SNPs. Moreover, the population mutation rate parameter θ and the expected background recombination rates are integrated (or estimated) in the Markov chain, so that the estimated recombination rates are not influenced by prespecified values of these parameters, which are usually unknown, especially for species other than human. Currently, a Jukes–Cantor (JC69) DNA substitution model is assumed, although it is straightforward to use other models. Empirical data analyses using the JC69 and the F81 substitution models (Felsenstein 1981) suggest that estimated hotspots and recombination rates are not influenced by the substitution model. This is often the case for closely related sequences. By incorporating a realistic model of recombination hotspots and background rates, estimates of these parameters are expected to be improved. Both simulation studies and analyses of population human genomic data for regions that have been studied previously by sperm typing suggest that our method performs well and that the results are consistent over different scenarios (Wang and Rannala 2009). In the present study, we extended our analysis framework so that it can be used for estimating, at any location, the Bayes factors (BFs) that the location is within a hotspot for both species, in this case human and chimpanzee. In other words, we are interested in obtaining the BFs of shared hotspots between the two species across aligned regions.

Material and Methods

Syntenic region

We made use of the existing human–chimpanzee two-way alignment (hg19–panTro3), available from the Uuniversity of California—Santa Cruz (UCSC) genome browser, to obtain fine-scale syntenic regions. First, all syntenic regions that were ≥100 bp were noted. The overlapping regions were identified and only the largest regions were retained. For those regions that aligned to minus strands of the human genome, the coordinates for the regions were converted to coordinates on plus strands. The reference sequences for these regions were then obtained, and the human–chimpanzee sequence divergence d (percentage of bases that differ between reference sequences of human and chimpanzee) for each region was calculated. Only regions with d ≤ 10% were retained so that 1319 regions on chromosome 21 were removed and 46092 regions remained. The distance (percentage of different bases) and size distributions of the syntenic regions located on chromosome 21 are illustrated in Supporting Information, Figure S1 and Figure S2. The average distance was 1.98%.

Recombination hotspots are defined as genomic regions with elevated recombination rates compared with surrounding regions. It is impossible to identify hotspots if the regions are too small or if there is not enough data (polymorphic ites) to distinguish hotspot rates and background rates. To identify hotspots based on the sytenic regions, we merged regions into “syntenic blocks” if the gap between the two adjacent regions was <20 bp. Finally only those blocks that were larger than (or equal to) 10 kb and contained at least 20 SNPs from both species were retained. There were 653 such blocks identified on human chromosome 21, spanning 9,828,471 bp, and ranging from 10,000–38809 bp in size. The size distribution of the syntenic blocks is illustrated in Figure S3. The blocks covered 20.4% of the genome on chr21.

Polymorphism data for humans and chimpanzees

We used the human polymorphism data from the 1000 genomes project (Abecasis et al. 2010). Variant calls from release v. 3.20101123 were downloaded. Only SNPs with two alleles were retained. We chose 10 YRI individuals in our analysis. Their sample IDs are NA18486, NA18487, NA18489, NA18498, NA18499, NA18501, NA18502, NA18504, NA18505, and NA18508. For chimpanzees, we used the SNP data from Prado-Martinez et al. (2013). The chimpanzee samples in their study included individuals from four subspecies, including 10 Nigeria–Cameroon, 6 Eastern, 4 Central, and 4 Western chimpanzees, and only SNPs from the 10 Nigeria–Cameroon individuals were used in our analysis, since it may violate the assumption of the model if combining individuals from different subspecies. Note that these SNPs were identified by mapping reads to the human genome build 36 (hg18). The SNP positions were converted to hg19 using the liftover tool from the UCSC genome browser. For this study, we focused on human chromosome 21. Given the coordinates for the syntenic blocks, SNPs for human and chimpanzee that fall into these regions were identified and used in the recombination hotspot analyses. There are in total 37,118 SNPs for human and 42,403 SNPs for chimpanzee.

For the studies concerning the known human recombination hotspots, including the β-globin hotspot and the several hotspots at the HLA region, we analyzed the data set from a previous study (Winckler et al. 2005). The data are summarized in Table S1.

Bayesian inference of recombination hotspots

We applied our method to the data sets described above to identify recombination hotspots and studied the degree of sharing in hotspot usage. Our analysis framework is described elsewhere (Wang and Rannala 2008, 2009), so here we only briefly outline the method. We used a Markov chain Monte Carlo (MCMC) method to estimate the posterior distributions of recombination hotspots and recombination rates across regions. The haplotype phase, missing data (if they exist), ancestral haplotypes, genealogy relating the sample, background recombination rates, and mutation rate parameters are integrated over in the MCMC. Two main models were assumed: one is for the genealogy and the other is for the distribution of recombination hotspots. The genealogy of the sample is described using the coalescent with recombination, and the hotspot distribution is described by a model consisting of two exponential distributions for the waiting distance and duration distance of the hotspot and a log-normal distribution for the intensity of the hotspot.

Let x denote data and G denote the genealogy underlying the data, ρ = {ρ_H, ρ_B} be recombination rates consisting of the hotspot rate (ρ_H) and background rate (ρ_B), and θ be the mutation rate. Let λ₁ denote the expected waiting distance between hotspots and λ₂ denote the expected width of the hotspot. Note that based on the current knowledge about these two values, λ₁ and λ₂ were fixed to be 1/50,000 and 1/1000 (Jeffreys et al. 2001). The height (intensity) of the hotspot is log-normal distributed with parameters μ and σ. Parameters μ and σ were fixed to be 9 and 1, respectively, so the 95% interval is ∼(1141, 57532). Each hotspot is described by three variables: X₁, X₂, Z, representing the start and end positions, and the height of the hotspot. So the prior on ρ_H is p(ρ_H|λ₁, λ₂, μ, σ). The prior on ρ_B is an exponential distribution with parameter λ_B. The prior on θ is a Gamma distribution with shape parameter equal to 0.25 and scale parameter equal to 2. The priors were chosen to be diffuse with the 95% interval to be (5.3 × 10⁻⁷, 3.4). The posterior probability of hotspots at location i is

$$p\left(H_i|x\right)={\displaystyle \sum _G{\displaystyle \iint {\displaystyle \iint p\left(x|G,\theta \right)p\left(G|{\rho }_{\text{H}},{\rho }_{\text{B}}\right)p\left({\rho }_{\text{H}}\right)p\left({\rho }_{\text{B}}\right)p\left(\theta \right)p\left({\lambda }_{\text{B}}\right)\text{d}{\rho }_{\text{H}}\text{d}{\rho }_{\text{B}}}\hspace{0.17em}\text{d}\theta \hspace{0.17em}\text{d}{\lambda }_{\text{B}}}}.$$ (1)

Let $x_{S_1}$ and $x_{S_2}$ denote the data from species S₁ and S₂ respectively. The BF of shared hotspot between S₁ and S₂ is

$$\frac{p\left(H_i|x_{S_1}\right)p\left(H_i|x_{S_2}\right)/\left(1-p\left(H_i|x_{S_1}\right)p\left(H_i|x_{S_2}\right)\right)}{p{\left(H_i\right)}^2/\left(1-p{\left(H_i\right)}^2\right)},$$ (2)

where p(H_i) is defined by the recombination hotspot model in the analysis framework and is based on the values of λ₁ and λ₂. Since in our model, a hotspot that spans the beginning of the interval is not allowed, the prior probability of a hotspot across the region is thus not uniform, with the probability smaller toward the start of the interval. The prior probability of hotspots across the region were obtained by simulation and is plotted in Figure S4 for a region with size 1,000,000 bp.

Simulation studies

Since the current data set for chr21 contains only 10 YRI individuals and 10 chimpanzee individuals, to obtain a rough idea of the interpretations of different values of BFs of shared hotspots, we first conducted two simulation studies using the same parameters as those in our previous analysis (Wang and Rannala 2009). The data were simulated using msHOT (Hudson 2002; Hellenthal and Stephens 2007). The parameters used in the simulation are given in Wang and Rannala (2009). The data sets used here were labeled S1 and S2 and are the same as those used in Wang and Rannala (2009) except that 20 haplotypes were used (as 10 genotypes). Data sets S1 and S2 each includes 100 simulated replicates. The interval was 30 kb long with 0 as the starting point. The true hotspot was located between 15 and 16.5 kb. The hotspot intensity ρ_H was set to be 40/kb for S1 and 10/kb for S2. We added two additional simulated data sets illustrating two different cases: in the first case the hotspot is present only in one species, and in the second case, hotspots from two species are partially overlapped. The two data sets were labeled as S0 and S3. The location and hotspot intensities for the four simulated data sets are listed in Table 1. In summary, we considered six scenarios including a completely shared hotspot, no sharing of a hotspot, and partially overlapped hotspots between species. The six combinations are listed in Table 2.

Table 1. The location and intensity of the hotspots that were considered for generating the 4 simulated data sets in the simulation study.

Data set	Hotspot location (bp)	Hotspot intensity (ρ/kb)
S0	—	—
S1	15,000–16,500	40
S2	15,000–16,500	10
S3	15,700–17,200	10

The interval starts from 0 bp with a size of 30,000 bp. Each data set includes 100 replicates. For ρ = 40/kb, if assuming an effective population size (N_e) of 10⁴ (for example, for human; Morton, 1982), the recombination rate is 100 cM/Mb and is 25 cM/Mb for ρ = 10/kb.

Table 2. Six analysis scenarios that were considered for examining the performance of the method for detecting shared hotspots between species in the simulation studies.

Set	Data sets	No. pairs	Note
1	S1	4950	Hotspots are the same between two species with ρ = 40/kb
2	S2	4950	Hotspots are the same between two species with ρ = 10/kb
3	S0/S1	10000	One species has a hotspot with ρ = 40/kb and the other species lacks a hotspot
4	S0/S2	10000	One species has a hotspot with ρ = 10/kb and the other species lacks a hotspot
5	S1/S3	10000	Hotspots are partially overlapped with intensities of ρ = 40/kb for one species and ρ = 10 per kb for the other species
6	S2/S3	10000	Hotspots are partially overlapped with intensities of ρ = 10/kb for both species

The distribution of the hotspots for simulated data set S0–3 are listed in Table 1. The number of pairs that were used in each set are given in the table. For sets 1 and 2, since only 1 simulated data set was used and all possible pairs were considered, the number of pairs is 4950. For set 3–6, two different simulated data sets were used, and the number of pairs is 10,000.

First, for each simulated data set, we obtain the posterior probability of a hotspot across the region. The region was divided into 200-bp nonoverlapping windows. So we have a posterior probability of a hotspot for each window. We then calculated the BF of shared hotspots for each pair of simulated data sets for each set. Sets 1 and 2 contain 4950 pairs and sets 3–6 each contain 10,000 pairs. For each set, we calculated power and false-positive rate for each window across the regions. Power is defined as the probability that the window is correctly identified as a shared hotspot (when overlapped with a shared hotspot). False-positive rate is defined as the probability that the window is identified as a shared hotspot when it is not. We explored several BF thresholds for identifying shared hotspots. In the plots (Figure S8, Figure S9, and Figure S10), we used a BF threshold of 100 for calculating power and false-positive rate. The distributions of the BFs, power, and false-positive rate for locations across the regions were plotted in Figure S8, Figure S9, and Figure S10.

Since the hotspot locations are estimated on the basis of SNPs, the estimated locations of hotspots are usually not precise (it is affected by SNP density, location, etc.). The false-positive rate is relatively high around the shared hotspots and decreases rapidly while moving away from the shared hotspots (Figure S8 and Figure S10, right ). This is true for both completely shared hotspots (Figure S8) and partially overlapped hotspots (Figure S10). When there is no overlapped hotspots, the false-positive rate is very low and the maximum false-positive rate across the region is 0.0037 from 15,900 to 16,100 bp, which is within the hotspot of one species (Figure S9). Based on the simulation studies, a BF threshold of 100 was used for inferring shared hotspot in the following data analysis.

MCMC analyses

For the chr21 data sets, we analyzed all regions using two independent runs. For each run, four chains were used. The number of burn-in and sample iterations were set to be 100,000 and 100,000, respectively. The temperature parameter for the parallel chains was set to be 1.2. The tuning parameters for changing λ_B and ρ_B are 170 and 300. For other tuning parameters, default values of the program were used. Usually the tuning parameters are chosen on the basis of the percentage of accepted moves (swapping chains or parameter changes). We usually start some testing runs first to examine the percentage of accepted moves and then adjust the tuning parameters before running the entire MCMC. To assess the consistency between the two independent runs, we first calculated the BF of shared hotspots between YRI and chimpanzees across regions for all 653 syntenic regions from the two runs. We then calculate the correlation of BFs from the two independent runs; the correlation is 0.979.

For β-globin data set, we analyzed the data set from three populations, including BEN, CEU, and Chimp, using four independent runs. Again, four parallel chains were used for each run. The number of burn-in and sample iterations were set to be 80,000 and 120,000, respectively. The temperature parameter was set to be 1.1 for Chimp and CEPH data sets and 1.05 for BEN data set. The tuning parameters for changing λ_B and ρ_B were set to be 250 and 250 for all three data sets. The default values were used for other tuning parameters. The results from the four independent runs are largely consistent (Figure S11).

Convergence of the MCMC is sometimes problematic for the HLA region in chimpanzee. One possible explanation is that more heterogeneity of hotspots exists in chimpanzee. For the analyses across regions of chr21 and the β-globin region, the interval sizes are small enough that they can be analyzed using the full-likelihood method implemented in InferRho (IR). The HLA data sets were first split into 20-SNP intervals and were analyzed using the composite-likelihood method implemented in the program. The parameters were specified as follows: the number of burn-in iterations was 80,000, the number of sampling iterations was 120,000, the tuning parameter for λ_B was 150, the tuning parameter for ρ_B was 300, the temperature was 1.03, and the number of parallel chains was eight. We analyzed the data sets from three populations using five different runs. Due to the existence of slight inconsistencies between runs, we calculated the BFs of shared hotspots using the runs with the highest sum of log priors and log likelihood (which indicates a better mixing) for all thee data sets.

Results

Chromosome 21

We first identified syntenic regions of the genomes in humans and chimpanzees. In this analysis, we focus on regions located on human chromosome 21. We used the 1000 genomes project data for 10 Yoruban (YRI) samples (Abecasis et al. 2010) and the data from a recent ape resequencing project for 10 chimpanzee individuals (Prado-Martinez et al. 2013) for inferring recombination hotspots and estimating recombination rates. The YRI sample was chosen because it has a very ancient population history, which can be expected to increase the power for identifying hotspots. The coordinates of syntenic regions were obtained on the basis of the two-way alignment of human and chimpanzee. The regions were verified by calculating the distances (percentage of different bases) for each region to ensure synteny. There are 653 such syntenic blocks identified for human chromosome 21, spanning 9,828,471 bp and ranging in size from 10,000 to 38,809 bp (see Figure S3). The SNPs in these regions from the 1000 genomes project and the ape resequencing project were used for the recombination rate analyses. The posterior probabilities of recombination hotspots across regions were obtained using our program IR (Wang and Rannala 2009). The BF of shared hotspots between the two species was then calculated on the basis of the prior and posterior probabilities of hotspot in each species across locations, with the assumption that the posterior and prior probabilities of a recombination hotspot in the two species are independent.

To evaluate the validity of our method for detecting shared hotspots in two species we conducted six simulation analyses that explore the distribution of the BFs of shared hotspots for regions with (or without) a hotspot and that assessed how the locations of hotspots affect the distribution of the BFs. The simulation studies provide a reference for interpreting the estimated BFs obtained using the real data. Although the 95% credible interval of the BFs for locations within a hotspot is large, the BF decreases rapidly as one moves away from the hotspot along a chromosome. For regions that do not contain a common hotspot, the BF of a shared hotspot is uniformly low. For example, if we sample one location of 3900 bp over the 30-kb region and the location is relatively far away from the shared hotspot, which is located between 15 and 16.5 kb, the 95% interval of the BF is (0.000, 0.263) for data set S1 and is (0.000, 0.321) for data set S2. The simulation study results suggest that even a moderate BF (>10) can indicate a shared hotspot with high confidence.

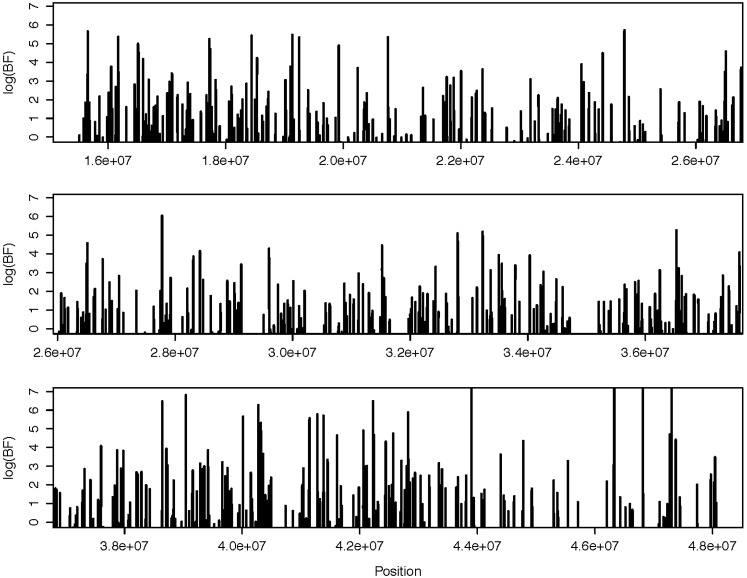
Across chr21 over all aligned blocks, the BFs of shared recombination hotspots between YRI and chimpanzee samples were plotted across the chromosome and are illustrated in Figure 1. The plot suggests that numerous hotspots that are shared between the two species with high confidence exist (BF ≥ 100). The estimated recombination rates for YRI and chimpanzee are presented in Figures S5, A–C. The locations with BF of shared hotspot ≥100 for chromosome 21 are given in Table S3, A–D.

Figure 1.

Log BF of shared recombination hotspots between humans and chimpanzees as a function of location for the 653 aligned syntenic regions across chromosome 21 estimated using 10 YRI samples and 10 chimpanzee samples. The coordinates are for the hg19 reference genome.

β-Globin and HLA regions

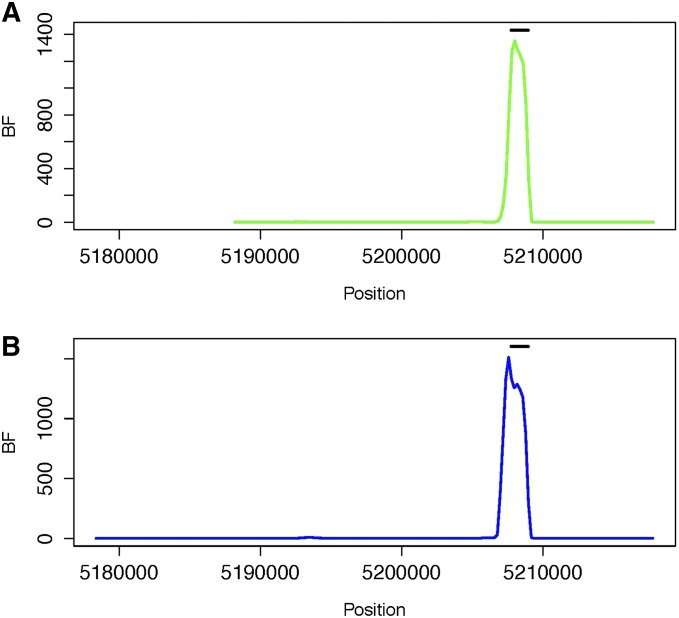
We also examined regions that contain well-established human recombination hotspots and examined whether these hotspots also exist in chimpanzee. The data sets that were analyzed are from Winckler et al. (2005). The hotspots include the β-globin hotspot and the several hotspots in the HLA region. In total, 48 individuals from the CEPH resource (CEU), 47 individuals from the Beni population sampled from Nigeria (BEN) and 37 individuals from the western African chimpanzee (Chimp) were sampled. The samples were genotyped at 26, 30, and 39 SNP loci, respectively. BFs of shared recombination hotspots between BEN and Chimp, and between CEU and Chimp, across the region were estimated. The results are shown in Figure 2. The human β-globin recombination hotspot obtained from a sperm-typing study overlaps with the interval showing high BFs of a shared hotspot. Our findings differ from those of previous analyses in suggesting that the well-established human β-globin hotspot is also present in chimpanzee. The estimated recombination rates across the region using samples of Beni, CEPH, and Chimp are plotted in Figure S6. The locations with BF of shared hotspot ≥100 for the β-globin region are given in Table S4 and Table S5.

Figure 2.

BF of shared recombination hotspots between (A) BEN and Chimp and between (B) CEU and Chimp as a function of location for the β-globin region. The coordinates are given on the basis of coordinates in the original data set (Winckler et al. 2005), which used the hg15 reference genome. The human β-globin recombination hotspot estimated from sperm-typing studies (Holloway et al. 2006) is illustrated with the horizontal bar.

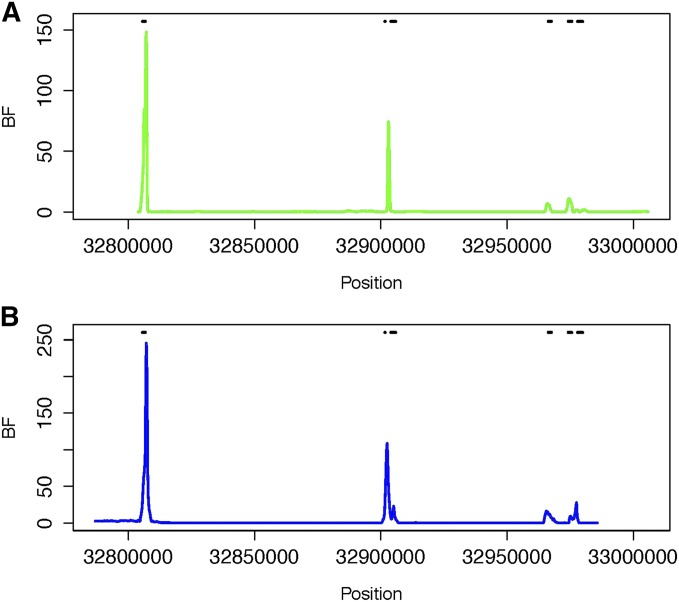
Sperm-typing studies have previously revealed six recombination hotspots in the human HLA region, including three hotspots in the DNA1-3 cluster, two hotspots in the DMB1-2 cluster, and a TAP2 hotspot Jeffreys et al. (2001). Winckler et al. (2005) examined the HLA regions spanning all six human recombination hotspots using the same sample of human and chimpanzee individuals as were used for the β-globin region study described above, genotyping 114, 111, and 98 SNP loci for Chimp, CEU, and BEN, respectively. The results based on a reanalysis of their data using IR are presented in Figure 3. The locations with higher BFs of sharing overlap with the locations of the human recombination hotspots identified from sperm-typing studies, although the BFs are smaller than those within the β-globin region. Thus, there is evidence that the TAP2 hotspot is shared between human and chimpanzee and weaker evidence of sharing for the two DMB hotspots. The estimated recombination rates across the region using samples of Beni, CEPH, and Chimp are plotted in Figure S7. The locations with BF of shared hotspot ≥100 for the HLA region are given in Table S6 and Table S7.

Figure 3.

BF of shared recombination hotspots between (A) BEN and Chimp and between (B) CEU and Chimp as a function of location for the HLA region. The coordinates are based on the coordinates in the original data set (Winckler et al. 2005), which used the hg15 reference genome. Six human recombination hotspots within the region, including DNA1, DNA2, DNA3, DMB1, DMB2, and TAP2, estimated from sperm-typing studies (Jeffreys et al. 2001), are illustrated with the horizontal bars.

Discussion

Our results partially support the findings of several previous studies that sharing of hotspots between humans and chimpanzees does not appear to be universal, but differ from these studies in that we identified a fraction of human recombination hotspots that are clearly present in both humans and chimpanzees. This difference may be due to methodology, for example the statistical power of different methods or parameter handling of different models. Conversely, the difference may be due to the existence of a higher degree of population heterogeneity in chimpanzee than in human. Especially based on our results, for example, the hotspot at the β-globin region is shared between the two species, but the recombination rates within the hotspot are much higher than the surrounding regions for human, and it is not that obvious for chimpanzees (Figure S6).

It may also be suspected that the degree of sharing is due to random effects (i.e., that independently arising hotspots in the two species overlap purely by chance). We conducted a simulation study to roughly examine how often the hotspots are shared if locations of hotspots are determined independently in each of the two species. Assuming that the length of the shared chromosome region is 9,828,471 bp (the size of the syntenic regions from human and chimpanzee based on above analysis of human chromosome 21), we simulated 1000 regions using our model of hotspot distribution with parameters as estimated from our empirical analysis (described in the above section). There are 499,500 pairs of regions. The simulated hotspots were examined for each pair to calculate the percentage of hotspots overlapping with the other species. On average the percentage of sharing is 0.039 if an overlap of at least 1 bp was considered as sharing and is 0.012 if a 1000-bp overlap was the criterion for sharing. The histograms in Figure S12 show the distribution of the percentages of sharing from the simulation. Based on our rough analysis, the expected degree of sharing is quite small if the distributions of hotspots from the two species arise by independent processes rather than being due to shared (homologous) genomic features. Given the evidence for shared hotspots, it may be useful to examine whether shared sequences are associated with the conserved hotspots and, if so, whether there are factors that are common in humans and chimpanzees that interact with certain sequences and regulate recombination activity. The program inferRho is available for download from http://rannala.org.