Synthesizing data and models for the spread of MERS-CoV, 2013: Key role of index cases and hospital transmission

Highlights

• •Transmission models for the MERS-CoV outbreak during April–October 2013.
• •MERS-CoV transmission models with index and secondary cases.
• •MERS-CoV transmission models with community and hospital compartments.
• •Calibration of MERS-CoV transmission models using MCMC methods.
• •Data indicate a strong support for R  < 1 in the first stage of the outbreak in 2013.

Abstract

The outbreak of Middle East respiratory syndrome coronavirus (MERS-CoV) has caused 209 deaths and 699 laboratory-confirmed cases in the Arabian Peninsula as of June 11, 2014. Preparedness efforts are hampered by considerable uncertainty about the nature and intensity of human-to-human transmission, with previous reproduction number estimates ranging from 0.4 to 1.5. Here we synthesize epidemiological data and transmission models for the MERS-CoV outbreak during April–October 2013 to resolve uncertainties in epidemic risk, while considering the impact of observation bias. We match the progression of MERS-CoV cases in 2013 to a dynamic transmission model that incorporates community and hospital compartments, and distinguishes transmission by zoonotic (index) cases and secondary cases. When observation bias is assumed to account for the fact that all reported zoonotic cases are severe, but only ∼57% of secondary cases are symptomatic, the average reproduction number of MERS-CoV is estimated to be 0.45 (95% CI:0.29–0.61). Alternatively, if these epidemiological observations are taken at face value, index cases are estimated to transmit substantially more effectively than secondary cases, (R_i = 0.84 (0.58-1.20) vs R_s = 0.36 (0.24–0.51)). In both scenarios the relative contribution of hospital-based transmission is over four times higher than that of community transmission, indicating that disease control should be focused on hospitalized patients.

Adjusting previously published estimates for observation bias confirms a strong support for the average R < 1 in the first stage of the outbreak in 2013 and thus, transmissibility of secondary cases of MERS-CoV remained well below the epidemic threshold. More information on the observation process is needed to clarify whether MERS-CoV is intrinsically weakly transmissible between people or whether existing control measures have contributed meaningfully to reducing the transmissibility of secondary cases. Our results could help evaluate the progression of MERS-CoV in recent months in response to changes in disease surveillance, control interventions, or viral adaptation.

Introduction

An outbreak of novel Middle East respiratory syndrome coronavirus (MERS-CoV) is ongoing in the Arabian Peninsula, with the first case identified in Jeddah, Saudi Arabia, in June 2012 (Zaki et al., 2012). Phylogenetic analyses have indicated that the novel virus emerged in July 2011, with broad uncertainty range, and that the outbreak results from multiple introductions of a weakly transmissible virus that is geographically dispersed (Cotten et al., 2013). A total of 699 laboratory-confirmed cases of infection with MERS-CoV, including 209 deaths, have been reported as of June 11, 2014 (The World Health Organization, 2014). Sporadic cases have been imported to Europe, Africa, Asia and North America via returning travelers from the Middle East, but no sustained transmission has been reported in those regions.

Sporadic introductions of MERS-CoV into humans are suspected to involve bats (Ithete et al., 2013) and/or camels (Reusken et al., 2013, Haagmans et al., 2014) with camels implicated as the likely source of most zoonotic infections of MERS-CoV in Saudi Arabia (Alagaili et al., 2014). Meanwhile, there is considerable uncertainty about the extent of human-to-human transmission and it is unclear whether MERS-CoV has the potential for epidemic spread. Transmission appears limited among family members but may be amplified in health care settings (Cotten et al., 2013, Breban et al., 2013). An understanding of the MERS-CoV epidemiology and transmission pathways are critically needed to devise effective surveillance, prevention and control strategies.

The reproduction number, R, which measures the average number of secondary cases from each infected person, is a useful metric for assessing the transmission potential of an emerging pathogen such as MERS-CoV (Lloyd-Smith et al., 2009, Wolfe et al., 2007). If R  < 1 then infections occur in isolated clusters as self-limited chains of transmission, and persistence of the disease requires continued animal-to-human infections (Anderson and May, 1991). When averaged over all reported cases, two recent studies have estimated an overall R (denoted R _overall) to be in a range of 0.42–0.92 (Breban et al., 2013, Cauchemez et al., 2014), thus diminishing the concern of MERS-CoV epidemic spread. In contrast, when R is evaluated for just the index cases originating from animal-to-human transmission, estimates (denoted R _i) can be as high as 1.5 (Cauchemez et al., 2014), suggesting that epidemic spread is possible.

In order to implement effective surveillance and control measures, it is important to understand the reason for the difference in inferred values of R _overall and R _i. One possibility is that secondary (human-to-human) cases transmit less than index cases, either because of intrinsic biological differences, or because of less effective control measures for index cases relative to secondary cases. A second possibility is that the transmission potential of index and secondary cases is similar, but many weakly transmitting index cases are unobserved. The tendency to identify and report larger clusters (whose index case cause a higher than average number of new cases) would lead to an overestimation of R _i (Ferguson et al., 2004, Blumberg and Lloyd-Smith, 2013a, Blumberg and Lloyd-Smith, 2013b, Farrington et al., 2003, Rimoin et al., 2010). It is important to evaluate both possibilities, because the optimal utilization of public health resources depends on the relative transmission potential of primary and secondary cases.

To gain perspective on the troublesome wide range of R estimates straddling the epidemic threshold of 1 associated with the 2013 outbreak of MERS-CoV, we develop a stochastic transmission model that distinguishes the transmission of index cases from secondary cases and incorporates different reporting scenarios for index cases. In order to relate case observation to disease severity we also distinguish cases that are sick enough to become hospitalized from those who are treated entirely in the community. We use a Markov-Chain-Monte-Carlo estimation technique to match our model with observed MERS-CoV 2013 case data, provide estimates of the reproduction number, and revisit earlier estimates (Breban et al., 2013, Cauchemez et al., 2014) through the lens of reporting bias. Finally, we highlight residual data gaps that would be particularly useful to clarify the transmission process in 2014 and beyond.

Materials and methods

Data sources

Our analysis focuses on the progression of the MERS-CoV outbreak in April–October 2013, a period when pro-active surveillance was in place in Saudi Arabia (Memish et al., 2014), the country where most cases have been reported thus far. The beginning of our study period coincides with the onset of a large hospital outbreak on April 8, 2013 (Assiri et al., 2013a), which prompted an increase in the incidence of MERS-CoV case reports in the country (Cauchemez et al., 2014, Penttinen et al., 2013), resulting in a steady case detection rate (Memish et al., 2014) and a balanced male-female ratio. Our study period ends in October 2013 so that our estimates can be compared with earlier studies focused on the early phase of the MERS-CoV outbreak (Breban et al., 2013, Cauchemez et al., 2014); in particular we do not consider the resurgence of cases reported in Spring 2014 (The World Health Organization, 2014).

We analyzed a line list of laboratory-confirmed and probable MERS-CoV cases from various sources including WHO bulletins and media reports, obtained through passive epidemiological surveillance and case contact tracing (Rambaut, 2013). For each of the 122 cases with symptoms reported during April 8 and October 31, 2013, we obtained the dates of symptom onset and hospital admission, reporting date, disease severity (asymptomatic, mild, and severe) and transmission category (i.e., index case, secondary case, as assessed by health authorities) (Rambaut, 2013).

MERS-CoV index cases were those with no identified exposure to other cases prior to disease onset and were considered to be zoonotic cases (i.e. arising from animal-to-human transmission). We also distinguished between transmission occurring in the hospital and in the community, based on surveillance reports.

Asymptomatic cases were defined as patients who did not exhibit symptoms but had laboratory confirmation of MERS-CoV infection (World Health Organization, 2013) while severe cases included all hospitalized cases, with possible admission to intensive care unit.

Epidemiological scenarios

To reflect uncertainty in the observation process of MERS-CoV cases, we considered two epidemiological scenarios. In a ‘surveillance bias’ scenario (scenario A), we assume that index and secondary cases have similar transmission properties, but only the hospitalized index cases are detected (Fig. 1 ). This scenario assumes the reason all observed index cases required hospitalization is that the observation process is flawed and can only detect severe index cases. In a ‘differential-transmission’ scenario (scenario B), we assume that all index cases develop severe disease, require hospitalization, and thus contribute more to the overall transmission process than a typical secondary case (Cauchemez et al., 2014). In both scenarios, secondary cases can either be asymptomatic, mild or severe and thus have zero, weak or strong transmissibility, respectively.

Fig. 1.

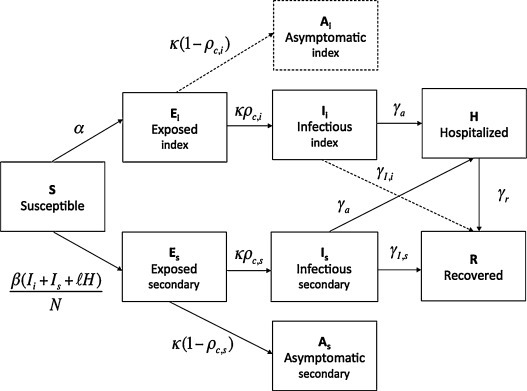
Schematic representation of the transition of cases (indicated by arrows) among the different epidemiological states in our model (Text S1).

Under ‘surveillance bias’ scenario A, index (zoonotic) and secondary cases follow a similar epidemiological progression (full model).

Under ‘transmission bias’ scenario B, index and secondary cases follow a different epidemiological progression: all index cases are symptomatic, develop severe disease, and require hospitalization (i.e., compartmental model in which the dashed arrows and compartment are removed).

We assume that only the symptomatic cases are observed. The description and corresponding estimates of the epidemiological parameters are given in Table 1.

Stochastic SEIR transmission model

We employed a stochastic SEIR-type compartmental transmission model (e.g., Anderson and May, 1991, Chowell et al., 2003, Riley et al., 2003, Lipsitch et al., 2003, Diekmann and Heesterbeek, 2000, Gumel et al., 2004) that incorporates key epidemiological features of the MERS-CoV outbreak (WHO MERS, 2013), including zoonotic transmission from an unspecified animal reservoir, and human-to-human transmission in the community and hospital (Fig. 1, Text S1). The model is stochastic, which is particularly important to consider when overall disease incidence is low. In our main analysis, we fit the model to observed outbreak size data at the end of the study period in each of the 3 transmission settings (reservoir, community, hospital), and run sensitivity analyses by trajectory matching the daily progression of cumulative cases.

In this model, the population is divided into 9 categories (Fig. 1): Susceptible individuals (S); Individuals exposed to the zoonotic reservoir (E _i) or to infectious humans (E _s), Infectious and symptomatic individuals arising from reservoir (I _i), or from human-to-human transmission (I _s); Asymptomatic and non-infectious individuals arising from environmental/animal exposure (A _i) or arising from human-to-human transmission (A _s); hospitalized individuals (H); and removed individuals after recovery or disease-induced death (R). The total population size (N) of Saudi Arabia is ∼29 million and assumed to be initially completely susceptible, in line with serosurveys (Tefanie Gierer et al., 2013, Aburizaiza et al., 2013).

The system of nonlinear differential equations that describe the full transmission model is given in supporting Text S1. Susceptible individuals are infected uniformly at random from the zoonotic reservoir at rate α, generating index cases⋅ Susceptible individuals infected through contact with infectious individuals (secondary cases) enter the latent period at rate β(I _i  +  I _s  +  lH)/N where β is the mean human-to-human transmission rate per day and l quantifies the relative transmissibility of hospitalized patients compared to symptomatic patients in the community. Thus 0 <  l  < 1 would represent partially effective hospital isolation measures that decrease MERS-CoV transmission probability below that seen in the community, and l  > 1 denotes increased transmission in the hospital relative to the community, potentially due to biologic or epidemiologic reasons. We make the simplifying assumption that asymptomatic individuals do not contribute to the transmission process (Leung et al., 2006, Ksiazek et al., 2003, Lee et al., 2003).

A proportion ρ _c,i of latent index cases individuals in E _i progress to the symptomatic infectious class I _i at the rate κ while the rest (1 −  ρ _c,i) progress to asymptomatic and non-infectious class A _i at the same rate κ. Only the symptomatic cases are observed. Symptomatic index infectious individuals I _i are hospitalized at the average rate γ _a or recover without being hospitalized at the average rate γ _I,i Similarly, a fraction ρ _c,s of secondary cases in E _s progress to the symptomatic class I _s at the rate κ while the rest (1 −  ρ _c,s) progress to asymptomatic and non-infectious class A_s at the same rate κ. Symptomatic secondary infectious I _s-individuals are hospitalized at average rate γ _a or recover without being hospitalized at average rate γ _I,s. Individuals in the “removed” class do not contribute to the transmission process.

We fit simulations to three types of observed MERS-CoV epidemiological data. First, we use the cumulative number of index cases reported during the Apr-Oct 2013 study period, which is the number of cases progressing to the I _i compartment in our model and follows equation C _i(t) (Text S1). Second, we use the cumulative number of secondary symptomatic community cases, which is the number of cases progressing to the I _s compartment in our model and follows equations C _s(t). Lastly, we consider the cumulative number of symptomatic secondary cases that are generated by hospitalized patients, including inpatients, health care workers, and visitors of hospital patients, which is given by equation C _IH(t) in our model.

Under the ‘surveillance bias’ scenario (A), the proportion of exposed (latent) individuals progressing to the infectious class and the proportion of symptomatic cases that are hospitalized are the same for both index and secondary cases (i.e., ρ _c,i  =  ρ _c,s and γ _I,i  =  γ _I,s). Under the ‘differential transmission’ scenario (B), all index cases develop symptomatic disease (ρ _c,i  = 1) and require hospitalization (γ _I,i  = 0).

MERS-CoV epidemiological parameters

The incubation period (1/k) was fixed at 5.2 days according to data from a hospital outbreak in Saudi Arabia (Assiri et al., 2013a), and in line with information from travel-related cases (Cauchemez et al., 2014). Based on 38 secondary cases with disease severity information in our dataset, the proportion of exposed individuals progressing to the symptomatic stage (ρ _c,s) was estimated at 55.3% while the fraction of symptomatic cases that were hospitalized (ρ _h) was estimated at 76.2%. The recovery rate for cases in the community (γ _I,s) was set at 1/5 days, which is in line with SARS epidemiology (Lipsitch et al., 2003). The average time from symptom onset to hospital admission (γ _a) was estimated based on ρ _h  =  γ _a/(γ _a  +  γ _I,s). Baseline parameter values and ranges used for sensitivity analysis are shown in Table 1 .

Table 1.

Epidemiological parameter estimates, ranges, and their sources. Prior distributions, posterior means and corresponding confidence intervals, and the Geweke index are provided for estimated epidemiological parameters (shaded cells) using the delayed rejection adaptive Metropolis-Hastings (DRAM) algorithm in a Markov-Chain Monte-Carlo (MCMC) framework.

Parameter	Scenario	Symbol	Initial/baseline	Range	Mean and 95% CI	Average Geweke index	Source
The average daily rate of new infections arising from exposure to environmental/animal source	A	α	0.5	(0, 5)	0.5 (0.36, 0.63)	0.99	Estimated
The mean human-human transmission rate per day	A	β	0.2	(0, 2)	0.10 (0.02, 0.21)	0.97	Estimated
Relative transmissibility of hospitalized cases	A	l	1.0	(0, 6)	2.0 (0.57,5.0)	0.98	Estimated
The average daily rate of new infections arising from exposure to environmental/animal source	B	α	0.5	(0, 5)	0.29 (0.22, 0.37)	0.99	Estimated
The mean human-human transmission rate per day	B	β	0.2	(0, 2)	0.08 (0.02, 0.17)	0.97	Estimated
Relative transmissibility of hospitalized cases	B	l	1.0	(0, 6)	1.9 (0.60, 5.0)	0.98	Estimated
Mean latent period (days)	A, B	1/k	5.2	(3, 8)	–	–	Assiri et al. (2013a), Lessler et al. (2009) & SA
Proportion of symptomatic and infectious cases among index cases	A B	ρc,i ρc,i ≣ 1	0.585	(0.3, 0.6)	–	–	Primary data & SA
Proportion of symptomatic and infectious cases among secondary cases	A, B	ρc,s〈βρ〉	0.585	(0.3, 0.6)	–	–	Primary data & SA
Proportion of hospitalized individuals among symptomatic and infectious index cases	A B	ρh,i ρh,i = 1	0.708	(0.4, 0.8)	–	–
Proportion of hospitalized individuals among symptomatic and infectious secondary cases	A, B	ρh,s	0.708	(0.4, 0.8)	–	–	Primary data & SA
Mean infectious period among primary cases (days)	A B	1/γI,I γI,i = 0	5.0	(3, 7)	–	–	Assiri et al. (2013a), Donnelly et al. (2003), Lessler et al. (2009) & SA
Mean infectious period among secondary cases (days)	A, B	1/γI,s	5.0	(3, 7)	–	–	Assiri et al. (2013a), Donnelly et al. (2003), Lessler et al. (2009) & SA
Mean time from symptom onset to hospital admission (days)	A, B	1/γa	γa = γIρh/(1 − ρh)	–	–	–	SA
Mean length of hospital stay (days)	A, B	1/γr	7.0	(5,10)	–	–	SA

SA = Sensitivity analysis.

The transmissibility of index and secondary cases, R_i and R_s, and their relationship to R_overall

Classically, the basic reproduction number, denoted by R ₀ (Anderson and May, 1991, Diekmann and Heesterbeek, 2000) quantifies the average number of secondary cases generated by infectious individuals in the absence of control interventions in a completely susceptible population and at the beginning of an epidemic. In order to compare our results to previous estimates of the reproduction number for MERS-CoV (Breban et al., 2013, Cauchemez et al., 2014), we define reproduction numbers R _i and R _s, as the average number of cases generated by a typical index and secondary case, respectively, and R _overall as the reproduction number averaged over all the cases. Extension of classic branching process results (Harris, 2002, Lange, 2010), provides the following relationship between the 3 transmission parameters (see supporting Text S2 for details):

$$R_{\text{overall}}=\frac{R_i}{1-R_s+R_i}$$

We note that R _i  > 1 does not imply endemic spread the way that R ₀  > 1 does. Indeed, the epidemic may die out if R_i  > 1 but R _s  < 1 and hence R _overall remains below 1. Further, these parameters integrate the impact of public health interventions (e.g. contact precautions, isolation in hospital wards) on transmission.

Under the ‘surveillance bias’ scenario A (ρ _c,i  =  ρ _c,s and γ _I,i  =  γ _I,s), the average transmissibility of index and secondary cases is the same, following:

$$R_i=R_s=\beta \left[{\rho }_{c,i}\left(\frac{1}{\left({\gamma }_a+{\gamma }_{I,i}\right)}\right)+l\left(\frac{1}{{\gamma }_r}\right)\left(\frac{{\gamma }_a}{\left({\gamma }_a+{\gamma }_{I,i}\right)}\right)\right]\text{.}$$

where (1/(γ _a  +  γ _I,i) is the mean infectious period of community cases, γ _a/(γ _a  +  γ _I,i) is the fraction symptomatic cases that are hospitalized, and 1/γ_r is the mean infectious period of hospitalized cases (see Chowell et al., 2006). This expression can be written as the sum of the contributions of infectious individuals in the community and the hospital as follows:

$$\begin{array}{l}{R}_i=R_{\_\text{comm,}i}+R_{\_\text{hosp},i}\\ R_s=R_{\_\text{comm,}s}+R_{\_\text{hosp},s}\end{array}$$

where R _{_comm,i}  =  R _{_comm,s}  =  β(ρ _c,i/(γ _a  +  γ _I,i)) and,

$$R_{\_\text{hosp},i}=R_{\_\text{hosp},s}=\beta l\left({\rho }_{c,i}\left(\frac{1}{{\gamma }_r}\right)\right)\left(\frac{{\gamma }_a}{\left({\gamma }_a+{\gamma }_{I,i}\right)}\right)\text{.}$$

Under the ‘differential transmission’ scenario B, the transmissibility of index cases is allowed to differ. Even if the reproduction number of index cases was greater than 1 in this scenario, subcritical transmission among secondary cases would still ensure the eventual extinction of all transmission chains. Under this scenario, the reproduction number of secondary cases is given by:

$$R_s=\beta \left[{\rho }_{c,s}\left(\frac{1}{\left({\gamma }_a+{\gamma }_{I,s}\right)}+l\left(\frac{1}{{\gamma }_r}\right)\left(\frac{{\gamma }_a}{\left({\gamma }_a+{\gamma }_{I,s}\right)}\right)\right)\right]\text{,}$$

whereas the reproduction number of index cases is given by:

$$R_i=\beta \left[\frac{1}{{\gamma }_a}+\frac{l}{{\gamma }_r}\right]$$

where R _{_comm,i}  = (β(1/γ _a)) and R _{_hosp,i}  = (β(l/γ_r)) are the contributions of community index cases and hospitalized index cases to transmission, respectively. Similarly, the contributions of community and hospital-based transmission to the reproduction number of secondary cases are given by:

$$\begin{array}{l}{R}_{\_\text{comm},s}=\beta \left(\frac{{\rho }_{c,i}}{\left({\gamma }_a+{\gamma }_{I,i}\right)}\right)\text{and,}\\ R_{\_\text{hosp},s}=\beta l\left({\rho }_{c,i}\left(\frac{1}{{\gamma }_r}\right)\left(\frac{{\gamma }_a}{\left({\gamma }_a+{\gamma }_{I,i}\right)}\right)\right).\end{array}$$

Parameter estimation

Since the date of symptom onset is lacking for a majority of cases, our main analysis relies on fitting our model to the total number of MERS-CoV cases (“outbreak size”) for the study period Apr–Oct 2013. As a sensitivity analysis, we also impute the missing dates of symptom onset for visualization purposes and to attempt to trajectory-match the cumulative number of daily cases (Text S1).

We estimated three parameters (daily rate of zoonotic infection, α; the human-human transmission rate, β; and the relative transmissibility of hospitalized cases, l) by fitting our transmission model predictions of C _i(t), C _s(t) and C _IH(t) to the total observed numbers of index, secondary and hospital-based secondary cases at the end of our study period. We minimized the “sum of square errors” between the corresponding model outputs and observed case counts for each of the three transmission settings (reservoir, community, hospital). We used a delayed rejection adaptive Metropolis-Hastings (DRAM) algorithm in a Markov-Chain Monte-Carlo (MCMC) framework which has been previously described in ref. (Haario et al., 2006) (Matlab package available from: http://helios.fmi.fi/∼lainema/mcmc/). We assumed uniform prior distributions for α, β and l with broad ranges (Table 1). We allowed the algorithm to run for 10,000 iterations with an initial burn-in of 5000 iterations to allow runs to reach a stationary regime. The Geweke diagnostic method was employed to assess convergence of chains (Geweke, 1992), with values close to 1 deemed satisfactory. Posterior distributions for each parameter were obtained from the underlying joint posterior distribution of resulting Markov chains. Since our study period starts with a large hospital outbreak, the outbreak simulation was initialized with one initial spillover case (i.e., I _i(0) = 1) and also included a low number of exposed secondary cases (i.e. E _s(0) = 5). Parameter estimates were not sensitive to these initial conditions.

Sensitivity analyses were performed by varying parameters defining the natural history of the disease (Table 1) and by fitting cumulative numbers of daily cases using interpolated onset dates, instead of final outbreak size data.

Quantifying stochastic uncertainty in outbreak progression

We reconstructed the stochastic uncertainty in the outbreak progression (number of spillover and human-to-human transmission events) by parametric bootstrapping in order to generate conservative uncertainty bounds for parameters. Specifically we simulated 200 epidemic realizations of our best-fit MERS-CoV transmission model (Table 1) through a Poisson simulation approach (Gustafsson and Sternad, 2007). We then estimated model parameters for each of the 200 stochastic outbreak realizations by the MCMC approach described above and used the distribution of estimated parameter values to construct 95% confidence intervals. Parameter convergence for each of the 200 runs was assessed by the Geweke diagnostic method (Geweke, 1992). This “hybrid” estimation approach allowed us to accomplish two goals: (1) estimate conservative parameter uncertainty bounds and (2) assess identifiability of model parameters.

Implications of surveillance bias on previous estimates of reproduction number

In order to model how previous estimates of R _i and R _overall (Breban et al., 2013, Cauchemez et al., 2014) could be influenced by surveillance bias, we assume that (1 −  ρ _c,i) of the MERS CoV cases are asymptomatic, unobserved index cases that do not transmit any infection. We then adjust previously reported estimates of R _i and R _overall (Breban et al., 2013, Cauchemez et al., 2014) to incorporate the negligible transmission of unobserved cases (see supporting Text S2 for details). In this framework, setting ρ _c,i  = 1, corresponds to taking the previous results at face value and is most similar to our differential transmission model (scenario B). Meanwhile setting ρ _c,i  = 0.585 (per Table 1) is similar to our surveillance-bias model (scenario A). This approach provides a synthesis of existing R estimates derived by different statistical methods and for different levels of underreporting.

Results

Epidemiological data

The course of the MERS-CoV outbreak in Saudi Arabia from April-8 to October-31, 2013, can be reconstructed from reported and imputed dates of symptom onset (Fig. 2 ). Of the 122 reported MERS-CoV cases during this period, 58 cases were putatively associated with exposure from a yet to be identified MERS-CoV reservoir source, and hence considered ‘index cases’. The remaining 64 cases were epidemiologically linked to an earlier case and hence classified as secondary cases. Of the 64 secondary cases, 47 were symptomatic and 17 did not exhibit symptoms. Of the 47 secondary symptomatic cases, 35 were linked to nosocomial transmission (hospital-based secondary cases in our terminology).

Fig. 2.

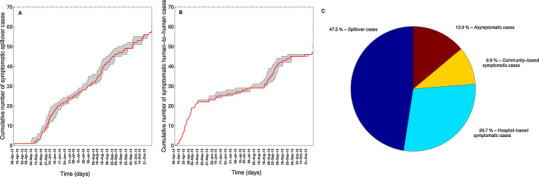
Temporal progression of MERS-CoV symptomatic cases according to exposure history by date of symptom onset, 08-April 2013 to 27-October 2013, Saudi Arabia (A and B). The gray shading shows the range of 500 cumulative curves obtained from the imputation strategy because the date of symptom onset was not available for all cases. The red solid line is the mean of the ensemble of curves. The overall percentage contribution of index cases, hospital-based symptomatic cases, community-based symptomatic cases, and asymptomatic cases to the total number of reported cases are also shown (C).

Model fitting

Convergence of our MERS-CoV transmission model fit was excellent for both the surveillance bias and differential transmission scenarios, as indicated by the corresponding Geweke indices (Table 1). The average daily rate of MERS–CoV spillover events was estimated at 0.5 (95% CI: 0.36, 0.63) cases a day for the ‘surveillance-bias’ scenario A. The spillover rate estimate was somewhat lower under the ‘differential transmission’ scenario B, with α   ≣  0.29 (95% CI: 0.22, 0.37) cases a day. Our estimates for the human-to-human transmission rate and the relative transmissibility of hospitalized cases vs community cases were consistent for both scenarios (See β and l values in Table 1). However, our simulation study revealed a significant negative correlation between these parameters (Spearman rho = −0.96, P  < 0.001), which precluded a reliable identification of these two parameters from data. Nevertheless, we were able to find reasonably well-bounded estimates of R as detailed below.

Reproduction number estimates

Despite potential correlation between 2 of the estimated parameters (β and l), reproduction numbers were estimated with good precision (Fig. 3 ). Both epidemiological scenarios indicated that the average transmissibility of secondary MERS-CoV cases remains below the critical threshold of 1.0 and underscored the importance of hospital-based transmission, estimated to be over 4-fold higher than community-based transmission for both index and secondary cases (Table 2 ).

Fig. 3.

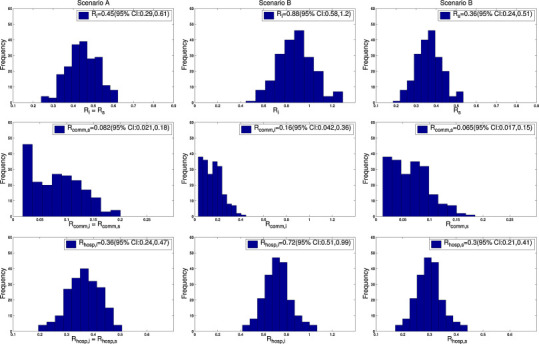
Distributions of the reproduction numbers for index and secondary cases and the relative contributions of community and hospitalized cases according to each epidemiological scenario. Scenario A: ‘Surveillance bias”. Scenario B: ‘Transmission bias’ (see text).

Table 2.

Reproduction number estimates and corresponding 95% confidence intervals derived from the uncertainty analysis described in the text for index (spillover) and secondary cases and the corresponding contributions of community and hospitalized cases to the reproduction number.

Surveillance bias scenario (Scenario A)
Index cases			Secondary cases
Ri	R_hosp,i	R_comm,i	Rs	R_hosp,s	R_comm,s
0.45 (0.29, 0.61)	0.36 (0.24, 0.47)	0.08 (0.02, 0.18)	0.45 (0.29, 0.61)	0.36 (0.24, 0.47)	0.08 (0.02, 0.18)
Differential-transmissibility scenario (Scenario B)
Index cases			Secondary cases
Ri	R_hosp,i	R_comm,i	Rs	R_hosp,s	R_comm,s
0.88 (0.58, 1.20)	0.72 (0.51, 0.99)	0.16 (0.04, 0.36)	0.36 (0.24, 0.51)	0.30 (0.21, 0.41)	0.07 (0.02, 0.15)

Under the ‘surveillance-bias’ scenario A, we estimated that the transmission potential of both index and secondary cases was well below 1.0, with R _i  =  R _s  = 0.45 (95% CI: 0.29, 0.61). Hospital-based transmission was estimated to be a major contributor to the outbreak, with R _{_hosp,i}  =  R _{_hosp,s}  = 0.36 (95% CI: 0.24, 0.47), which is about 4.5-times higher than the contribution of community-based transmission (R _{_comm,i}  =  R _{_comm,s}  = 0.08 (95% CI: 0.02, 0.18), Table 2). In other words, the contribution of hospital-based transmission to the reproduction number (R _i  =  R _s) was 82.0% (95% CI: 65.8, 94.3) (Fig. 4 ).

Fig. 4.

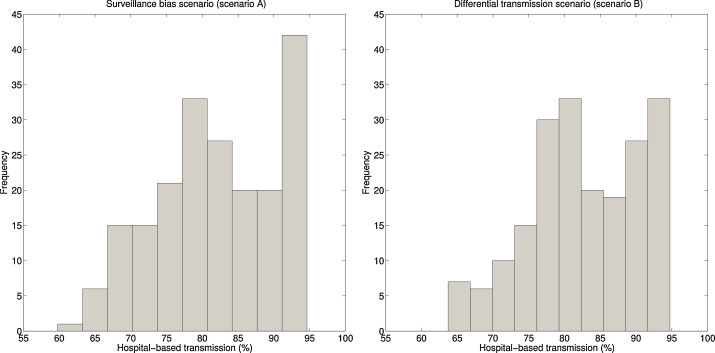
The percentage contribution of hospital-based transmission to the reproduction number of secondary cases for the surveillance bias and the transmission bias scenarios. Similar hospital-based contributions were obtained for index cases for both epidemiological scenarios (not shown).

Under the ‘differential-transmissibility’ scenario B, the reproduction number of index cases was substantially higher than that of secondary cases, with R _i  = 0.88 (95% CI: 0.58, 1.20), and R _s  = 0.36 (95% CI: 0.24, 0.51). The contribution of hospital-based transmission to the reproduction number of index cases was 82.7% (95% CI: 66.3, 94.4). Hospital-based transmission contributed similarly to the reproduction number of index and secondary cases (Fig. 4).

Based on our model, we estimate that a 20% reduction in the transmissibility of hospitalized cases would decrease the total number of secondary cases by 27%, and an 80% reduction in hospital transmission would decrease the number of secondary cases by 72%. By contrast, a 20% and 80% reduction in community transmission would only lead to a 12% and 28% reduction in numbers of secondary cases, respectively.

Outbreak simulations and sensitivity analyses

Overall, the extrapolated daily curves of cumulative symptomatic cases followed closely the surveillance bias model's predicted uncertainty bounds except for the early part of the study period when a substantial number of secondary cases were reported, in association with the large hospital outbreak (Fig. 5 ). Based on the ‘surveillance bias’ scenario, we estimated that a total of 98 spillover cases (95% CI: 81–119) and 86 secondary cases (95% CI: 42–132) occurred during our study period, so that only 59% of index cases and 55% of secondary cases were symptomatic cases reported through active surveillance. These results are in line with the original assumption of unbalanced detection probability between index and secondary cases. For illustration, Fig. 6 shows the predicted effects of control interventions (targeting community-based or hospital-based transmission, via parameter l), pathogen adaptation to humans (i.e, increase in baseline transmission rate, β), and potential increases in reservoir spillover rate (via parameter α), relative to the baseline ‘surveillance bias’ scenario A.

Fig. 5.

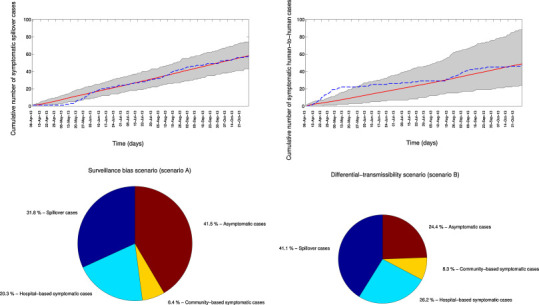
Temporal variation in MERS symptomatic cases associated with index (zoonotic) events and secondary (human-to-human) transmission as predicted from the model fit to the data according to epidemiological scenario A (‘Surveillance bias’, top). The mean (red solid line) and 95% uncertainty bounds (gray shading) generated from stochastic simulation as described in the text are shown. The blue dashed line is the approximate observed progression of symptomatic MERS-CoV cases by date of symptom onset (onset dates imputed as in Fig. 2). The overall percentage contribution of index cases, hospital-based symptomatic cases, community-based symptomatic cases, and asymptomatic cases to the total number of cases according for each epidemiological scenario are also shown (bottom). The radius of the pie chart for scenario B (‘transmission bias’) was scaled proportionally according to the total number of cases predicted from scenario A. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

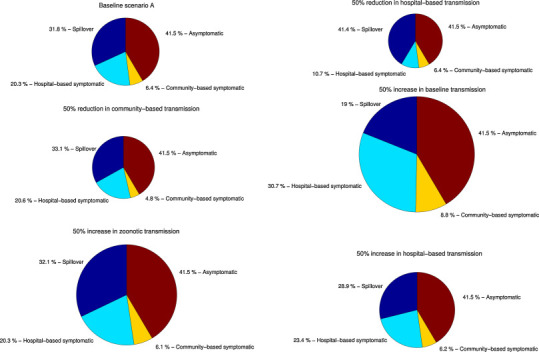
The effect of control interventions relatively to ‘surveillance bias’ scenario A (targeting hospital or community-based transmission) as well as the effect of potential pathogen adaptation to humans (increase in baseline transmission rate), and geographic spread with potential increases in reservoir spillover rate (via parameter alpha) or hospital-based transmission (via parameter l). The percentage contribution of index cases, hospital-based symptomatic cases, community-based symptomatic cases, and asymptomatic cases to the total number of cases according for each epidemiological scenario are shown. The radiuses of the pie charts were scaled proportionally according to the total number of cases predicted from the baseline scenario A.

Under the ‘surveillance bias’ scenario, average reproduction number estimates remained well below the epidemic threshold of R  = 1 under various sensitivity analyses for natural history parameters (Table 1). Mean estimates of the reproduction number for index and secondary cases (R _i  =  R _s) ranged from 0.43 to 0.51 while the ratio of the contribution of hospital-based to community-based transmission to the reproduction number ranged from 2.66 to 7.75 in sensitivity analyses. Moreover, the contribution of hospital-based transmission to the reproduction number ranged from 71.7% to 82.5%.

Under the ‘differential transmission’ scenario, although reproduction number estimates were more dependent on various assumptions about the natural history of disease, endemic transmission remained improbable since R _s was consistently less than one and ranged from 0.21 to 0.43. In contrast, the reproduction number of index cases R _i ranged from 0.72 to 2.46. For index cases the ratio of the contribution of hospital-based to community-based transmission to the reproduction number ranged from 2.4 to 4.4 while the percentage contribution of hospital-based transmission ranged from 69.4% to 84.0%. A similar contribution of hospital-based transmission to the reproduction number of secondary cases was obtained. Geweke convergence statistics showed excellent convergence for all estimated parameters in sensitivity analyses (average >0.95).

Synthesis of estimates of MERS-CoV transmission potential, 2013 outbreak

Our results provide perspective on two previous studies that have quantified the transmission potential of MERS-CoV (Breban et al., 2013, Cauchemez et al., 2014) (Fig. 7 ). Breban et al. (2013) use an inference method that assumes the transmission of index cases is similar to the transmission of secondary cases to produce two estimates of R _overall. Two separate estimates for R _overall (0.60 and 0.69) are reported based on whether ambiguously classified cases are favored to be primary or secondary cases. When these estimates are combined, the 95% confidence interval for these reproduction numbers spans 0.42–0.92. In their model, the inferred value for R _i is also 0.42–0.92, because no distinction between R _i and R _overall is made.

Fig. 7.

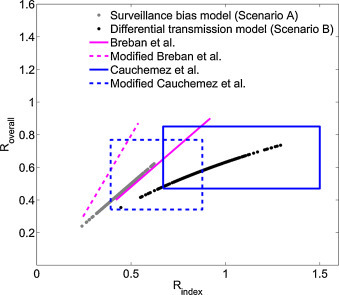
Synthesizing available estimates for the reproduction number of MERS CoV. The 95% confidence intervals for the reproduction number averaged over all cases (R_overall) and averaged over index cases (R_i) are shown. Besides the two transmission scenarios considered in this study (black and gray dots), the plot includes results of Breban et al. (2013) and Cauchemez et al. (2014). The key distinction among the models are that Breban et al. (2013) modeled primary and secondary transmission as being similar; Cauchemez et al. (2014) used the timing of cases to estimate R_i; our differential transmission model accounts for the higher observed disease severity of index cases; and our surveillance bias model considers the possibility that all weakly transmitting and asymptomatic index cases are unobserved. A modified version of Breban et al. and Cauchemez et al. are also shown in the plot that compensate for the possibility of unobserved index cases and thus allow direct comparison to our surveillance bias model. Cauchemez et al.’s results are presented as a confidence region because their inference of R_overall was separate from their inference of R_i. All the other models contain an intrinsic dependence between R_overall and R_i and so these results are presented as a curve.

Cauchemez et al. (2014) use a similar method, but more data, to produce a 95% confidence interval of 0.47–0.85 for R _overall. However, they also utilize an additional technique that incorporates data on the specific timing of cases (but assumes perfect observation of cases) to infer two separate 95% confidence intervals for R _i that span 0.67–1.50. Based on the approach of taking the observed data at face-value these prior results are best compared to our differential transmission scenario.

We can also adjust these prior results based on the assumption that asymptomatic index cases occur in the same proportion as in our surveillance bias scenario, but they escape surveillance. The adjusted 95% confidence intervals for Breban et al.’s model are 0.25–0.54 for R _i and 0.30–0.87 for R _overall. The adjusted 95% confidence intervals for Cauchemez et al.’s model are 0.39–0.88 for R _i and 0.34–0.77 for R _overall. These adjusted values are best compared to our surveillance bias results.

Key trends emerge from comparing reproduction number estimates across studies (Fig. 7). First, although some of the models include the possibility that R _i  > 1, none of them suggest that R _overall  > 1. This argues against the possibility that MERS-CoV is self-sustaining in humans. Rather, continual introduction from a non-human reservoir is needed for persistence. However, because some models predict R _i  > 1, it is unclear whether the lack of endemic spread is due to effective control interventions or intrinsically weak human-to-human transmissibility. Second, when observation bias is incorporated into parameter estimation, the range of possible values for both R _i and R _overall shift to smaller values. This may appear counter-intuitive because the existence of unobserved cases might suggest that transmission was under-estimated previously. This apparent paradox is a result of our assumption that asymptomatic index cases (rather than secondary cases) are the least likely to be observed.

Discussion

We have used dynamic epidemic modeling and branching processes to analyze epidemiological data on the progression of the MERS-CoV outbreak in Apr-Oct 2013 in Saudi Arabia (Cotten et al., 2013, Cauchemez et al., 2014, Assiri et al., 2013a, Assiri et al., 2013b, Penttinen et al., 2013, WHO MERS, 2013, Tefanie Gierer et al., 2013). Our analysis has focused on resolving uncertainty surrounding the transmissibility of MERS-CoV in its early dissemination phase, and quantifying the specific contributions of index, secondary, community and hospitalized cases, as well as surveillance bias, to the overall level of transmission. In the process we have provided perspective on the broad ranges of reproduction number estimates presented in two recent studies of the MERS-CoV outbreak (Breban et al., 2013, Cauchemez et al., 2014). All of the models consistently suggest that human-to-human transmission of MERS-CoV remained subcritical in 2013, arguing against the possibility that the outbreak was self-sustaining in humans. However, some models predict that the reproduction number of zoonotic cases may be higher than 1, which may support the effectiveness of control measures applied among contacts of identified cases, and could signal a potential acceleration of the epidemic if these measures were to be relaxed.

Prior studies of MERS-CoV have acknowledged that surveillance bias can complicate the inference of transmission parameters (Breban et al., 2013, Cauchemez et al., 2014). However, rather than accepting the possibility of surveillance bias as a limitation of our study, our analysis has explicitly incorporated its potential impact, while also considering an alternative ‘transmission bias’ scenario where observations are taken at face value. When we incorporate the possibility that less severe index cases are unobserved, the range of possible reproduction numbers in our study and previously published models (Breban et al., 2013, Cauchemez et al., 2014) shifts to smaller values (Fig. 7). Since convergence of our model to data is high in both the ‘surveillance bias’ scenario and ‘differential transmission’ scenarios, further information is needed to tease out the extent to which observation bias operated in 2013 and beyond. For example, targeted serological studies in communities where index cases have been reported could shed light on the fraction of index cases that may be unobserved. Further, it would be helpful to know more about the MERS-CoV surveillance process in Saudi Arabia, and determine whether individual cases were detected because they self-reported to a health center or were actively discovered via contact tracing of a severe case. More information on standards of clinical practice would also be helpful, such as the probability that a patient who presents with milder symptoms to a health care facility would be diagnosed with MERS-CoV. Ancillary data from laboratories would also be helpful such as the overall number of samples that were tested for MERS-CoV and their spatio-temporal distribution.

A particular concern for the epidemic potential of MERS-CoV is that the virus shares features of the related coronavirus that caused outbreaks of severe acute respiratory syndrome (SARS) in 2003, spanning several countries and continents (Ksiazek et al., 2003). Both MERS-CoV and SARS viruses can invade the lower respiratory tract and cause severe pneumonia (de Wit et al., 2013, Franks et al., 2003). Both infections are considered severe, especially among older adults with underlying medical conditions (Assiri et al., 2013b, Donnelly et al., 2003). Our findings indicate that the transmissibility MERS-CoV in secondary cases remained well below the epidemic threshold in Saudi Arabia in 2013, ensuring that all human-to-human transmission chains go extinct (Ferguson et al., 2004). At the time of this writing, there was not enough resolution in MERS-CoV phylogenetic data to assess whether transmission was only endemic in the animal reservoir or could persist in humans (Cauchemez et al., 2014). Based on our synthesis of epidemiological data and existing models, we argue that the transmission potential of MERS-CoV is currently low based on the progression of the 2013 outbreak, and on the same order as that of other stage III viral zoonoses such as influenza A/H5N1, monkeypox or Nipah virus, although much higher than that of influenza A/H7N9 (Blumberg and Lloyd-Smith, 2013a, Blumberg and Lloyd-Smith, 2013b, Chowell et al., 2013). In contrast, the reproduction number for SARS was estimated to be ∼2–3 during the pre-intervention period (Riley et al., 2003, Lipsitch et al., 2003). Although our study cannot speak to the dynamics of the recent resurgence of cases in Spring 2014, it is reassuring that disease transmission remained limited to the Arabian Peninsula throughout June 2014. Indeed, chains of transmission initiated by infected travelers returning to Europe, Africa, Asia and North America have remained extremely short (Cauchemez et al., 2014).

Despite these reassuring findings of weak secondary transmission based on 2013 MERS-CoV cases, we cannot rule out that transmissibility of index cases R _i, was substantially higher, with a 95% CI ranging from 0.6 to 1.2 (‘transmission bias’ scenario). If R _i happened to be greater than one, it is then essential to understand why R _s was less than one. One possibility is that control interventions around identified secondary cases were particularly effective in 2013. If this were the case, it is imperative to identify which of these interventions were most effective so that they can be rapidly implemented in the event that MERS-CoV spreads to a new geographic region. A similar situation arose in the last days of smallpox eradication, as stringent control measures were put in place once cases were identified, limiting the transmission of secondary cases (Fenner et al., 1988). Alternatively, it may be that there is an intrinsically biological phenomenon in which humans infected by a zoonotic reservoir experience more clinically severe disease, and in turn a higher transmission potential than those infected by humans. In this case, further adaptation of MERS-CoV to humans would be required for sustainable transmission to occur. A definite identification of the reservoir for MERS-CoV would help to shed light on potential variation in doses and route of exposure between index and secondary cases, which may account for the observed differences in onward transmission.

Because any increase in R _s leads to a greater than linear increase in size of transmission chains (Blumberg and Lloyd-Smith, 2013a), and the rate of MERS-CoV reports appears to increase (Cauchemez et al., 2014), there is strong motivation to ascertain the potential impact of control interventions. A key finding of our analysis was that the number of MERS-CoV cases caused by hospital-based transmission was 4.3 to 4.6-fold higher than community-based transmission and estimates were robust to a variety of sensitivity analysis. These findings are reminiscent of SARS (Varia et al., 2003, Lau et al., 2004, Tambyah et al., 2003) and indicate that more stringent hospital control measures would be particularly effecting at reducing transmission. The reasons for increased hospital transmission could include increased intensity and duration of viral shedding, or increased contacts with particularly vulnerable patients (Seto et al., 2003, Chowell et al., 2004). Understanding the MERS-CoV transmission process in the hospital is particularly important in light of recent reports of widespread infection among camels in North Africa (Chu et al., 2014), where low-resources could make surveillance and hospital control measures far harder to implement.

Our study is prone to limitations, as we made important simplifying assumptions to safeguard tractable inference. First, we assumed that the rate of zoonotic introductions into the human populations was constant. This assumption may be reasonable if MERS-CoV prevalence level in the zoonotic reservoir has reached an endemic state and the rate of animal-to-human contacts was stable throughout our study period. Similarly, we have not attempted to quantify changes in the baseline transmission rate or the relative transmissibility of hospitalized cases over time, but we fit our model solely to cases that occurred when pro-active surveillance was implemented in Saudi Arabia (Memish et al., 2014). Further, we assume that asymptomatic cases do not transmit infection. However, given that MERS-CoV secondary cases have typically been traceable to an index case it seems unlikely that there can be much asymptomatic transmission as this would lead to difficulty in reconstructing transmission chains. Another limitation of our model is that parameters β and l were not uniquely identified, although we were able to find reasonably well-bounded estimates of R. This is not entirely surprising, as a similar phenomenon occurs when a simple SIR model is fitted to the early exponential phase of an epidemic. In such a simple model, both β (the transmission rate) and γ (the recovery rate) are not identifiable. Yet, the ratio beta/gamma =  R ₀ is often identifiable in practice.

More elaborate models either based on dynamic systems or branching processes could be developed for MERS-CoV to incorporate more realistic mixing structures and possibly refine the spillover transmission dynamics. Although our model assumes homogeneous mixing within community and hospital populations, our results did not warrant further model heterogeneity given limited available data. As more data become available, these assumptions could be refined particularly if the pathogen's intrinsic transmissibility increases or if the virus spreads to poor areas where nosocomial transmission may be amplified. An important issue in modeling outbreaks in the Arabian Peninsula is the lack of information on age- and gender-specific contact rate patterns, as it has been done for European countries (Lee et al., 2003). Finally, we did not consider the progression of more recent cases of MERS-CoV reported after October 2013, to maintain comparability with previous transmission studies (Breban et al., 2013, Cauchemez et al., 2014).

In conclusion, modeling of available MERS-CoV case data reported during Apr–Oct 2013 in Saudi Arabia found robust support for the lack of persistence of the infection in humans without continued reintroduction from the reservoir. However, as with all emerging zoonoses, the potential for viral adaptation towards increased transmissibility is a real threat that needs careful monitoring. We have highlighted how observation bias (particularly the difficulty in observing asymptomatic and less severe index cases) can skew the inference and interpretation of transmission parameters. In particular, more data on the surveillance process is needed so that the transmission potential of index cases can be more rigorously ascertained both retrospectively and in the on-going 2014 outbreak. The relative transmissibility of primary and secondary cases has important implications for the efficacy of current control measures and the potential for spread in other regions that are more resource-limited. As a focal point of control, we have found that over 80% of transmission events are likely occurring in a hospital setting. We hope that future surveillance efforts can elucidate specific mechanisms of hospital-based transmission and effective control so that targeted interventions can be rapidly implemented if MERS-CoV spreads globally or adapts to humans.

Funding information

This research was conducted in the context of the Multinational Influenza Seasonal Mortality Study (MISMS), an on-going international collaborative effort to understand influenza epidemiological and evolutionary patterns, led by the Fogarty International Center, National Institutes of Health (http://www.origem.info/misms/index.php). Funding for this project comes in part (LS) from the RAPIDD program of the Science & Technology Directorate, Department of Homeland Security, and from the Office of Global Affairs’ International Influenza Unit in the Office of the Secretary of the Department of Health and Human Services. SB acknowledges financial support from RAPIDD program of the Science and Technology Directorate, Department of Homeland Security, the Fogarty International Center, National Institutes of Health, and the National Institute of Health MIDAS program (Modeling Infectious Disease Agent Study, grant number NIH NIGMS 1-U01-GM08778].

Appendix A. Supplementary data

Text S1 System of equations that describe the transmission model.

Text S2 Mathematical derivations for (1) Relating the overall reproduction number to the reproduction numbers of index and secondary cases and (2) Adjusting observed reproduction numbers of index cases and overall cases for the proportion of asymptomatic index cases that are unobserved.

The following are the supplementary data to this article: