LOCAL CASE-CONTROL SAMPLING: EFFICIENT SUBSAMPLING IN IMBALANCED DATA SETS

Abstract

For classification problems with significant class imbalance, subsampling can reduce computational costs at the price of inflated variance in estimating model parameters. We propose a method for subsampling efficiently for logistic regression by adjusting the class balance locally in feature space via an accept–reject scheme. Our method generalizes standard case-control sampling, using a pilot estimate to preferentially select examples whose responses are conditionally rare given their features. The biased subsampling is corrected by a post-hoc analytic adjustment to the parameters. The method is simple and requires one parallelizable scan over the full data set.

Standard case-control sampling is inconsistent under model misspecification for the population risk-minimizing coefficients θ*. By contrast, our estimator is consistent for θ* provided that the pilot estimate is. Moreover, under correct specification and with a consistent, independent pilot estimate, our estimator has exactly twice the asymptotic variance of the full-sample MLE—even if the selected subsample comprises a miniscule fraction of the full data set, as happens when the original data are severely imbalanced. The factor of two improves to $1+\frac{1}{c}$ if we multiply the baseline acceptance probabilities by c > 1 (and weight points with acceptance probability greater than 1), taking roughly $\frac{1+c}{2}$ times as many data points into the subsample. Experiments on simulated and real data show that our method can substantially outperform standard case-control subsampling.

1. Introduction

In recent years, statisticians, scientists and engineers are increasingly analyzing enormous data sets. When data sets grow sufficiently large, computational costs may play a major role in the analysis, potentially constraining our choice of methodology or the number of data points we can afford to process. Computational savings can translate directly to statistical gains if they:

1. enable us to experiment with and prototype a variety of models, instead of trying only one or two,

2. allow us to refit our models more often to adapt to changing conditions,

3. allow for cross-validation, bagging, boosting, bootstrapping or other computationally intensive statistical procedures or

4. open the door to using more sophisticated statistical techniques on a compressed data set.

Bottou and Bousquet (2008) discuss the tradeoffs arising when we adopt this point of view. One simple manifestation of these tradeoffs is that we may run out of computing resources before we run out of data, in effect making the sample size n a function of the efficiency of our fitting method.

1.1. Imbalanced data sets

Class imbalance is pervasive in modern classification problems and has received a great deal of attention in the machine learning literature [Chawla, Japkowicz and Kotcz (2004)]. It can come in two forms:

• Marginal imbalance. One of the classes is quite rare; for instance, ℙ(Y = 1) ≈ 0. Such imbalance typically occurs in data sets for predicting click-through rates in online advertising, detecting fraud or diagnosing rare diseases.

• Conditional imbalance. For most values of the features X, the response Y is very easy to predict; for instance, ℙ(Y = 1|X = 0) ≈ 0 but ℙ(Y = 1|X = 1) ≈ 1. For example, such imbalance might arise in the context of email spam filtering, where well-trained classifiers typically make very few mistakes.

Both or neither of the above may occur in any given data set. The machine learning literature on class imbalance usually focuses on the first type, but the second type is also common.

If, for example, our data set contains one thousand or one million negative examples for each positive example, then many of the negative data points are in some sense redundant. Typically in such problems, the statistical noise is primarily driven by the number of representatives of the rare class, whereas the total size of the sample determines the computational cost. If so, we might hope to finesse our computational constraints by subsampling the original data set in a way that enriches for the rare class. Such a strategy must be implemented with care if our ultimate inferences are to be valid for the full data set.

This article proposes one such data reduction scheme, local case-control sampling, for use in fitting logistic regression models. The method requires one parallelizable scan over the full data set and yields a potentially much smaller subsample containing roughly half of the information found in the original data set.

1.2. Subsampling

The simplest way to reduce the computational cost of a procedure is to subsample the data before doing anything else. However, uniform subsampling from an imbalanced data set is inefficient since it fails to exploit the unequal importance of the data points.

Case-control sampling—sampling uniformly from each class but adjusting the mixture of the classes—is a more promising approach. This procedure originated in epidemiology, where the positive examples (cases) are typically diseased patients and negative examples (controls) are disease-free [Mantel and Haenszel (1959)]. Often, an equal number of cases and controls are sampled, resulting in a subsample with no marginal imbalance, and costly measurements of predictor variables are only made for selected patients [Breslow, Day et al. (1980)]. This method is useful in our context as well, since a logistic regression model fitted on the subsample can be converted to a valid model for the original population via a simple adjustment to the intercept [Anderson (1972), Prentice and Pyke (1979)].

However, standard case-control sampling still may not make most efficient use of the data. For instance, it does nothing to exploit conditional imbalance in a data set that is marginally balanced. Even with some marginal imbalance, a control that looks similar to the cases is often more useful for discrimination purposes than one that is obviously not a case.

We propose a method, local case-control sampling, which attempts to remedy imbalance locally throughout the feature space. Given a pilot estimate (α̃, β̃) of the logistic regression parameters, local case-control sampling preferentially keeps data points for which Y is surprising given X. Specifically, if $\mathrm{p̃}(x)=\frac{e^{\mathrm{\alpha ̃}+\mathrm{\beta ̃}\prime x}}{1+e^{\mathrm{\alpha ̃}+\mathrm{\beta ̃}\prime x}}$, we accept (x_i, y_i) with probability |y_i − p̃(x_i)|, the ℓ₁ residual of the pilot model. In the presence of extreme marginal or conditional imbalance, these errors will generally be quite small and the subsample can be many orders of magnitude smaller than the full data set.

Just as with case-control sampling, we can fit our model to the subsample and make an equally simple correction to obtain an estimate for the original data set. When the logistic regression model is correctly specified and the pilot is consistent and independent of the data, the asymptotic variance of the local case-control estimate is exactly twice the variance of a logistic regression fit on the (potentially much larger) full data set. This factor of two improves to $1+\frac{1}{c}$ if we accept with probability c|y_i − p̃(x_i)| ∧ 1 and weight accepted points by a factor of c|y_i − p̃(x_i)| ∨ 1. For example, if c = 5 then the variance of the subsampled estimate is only 20% greater than the variance of the full-sample MLE. The subsample we take with c > 1 is no more than c times larger than the subsample for c = 1, and for data sets with large imbalance is roughly $\frac{1+c}{2}$ times as large.

Local case-control sampling also improves on the bias of standard case-control sampling. When the logistic regression model is misspecified, case-control sampling is in general inconsistent for the risk minimizer in the original population. By contrast, local case-control sampling is always consistent given a consistent pilot, and is also asymptotically unbiased when the pilot is. Sections 5 and 6 present empirical results demonstrating the advantages of our approach in simulations and on the Yahoo! webspam data set.

1.3. Notation and problem setting

Our setting is that of predictive classification: we are given n independent and identically distributed observations, each consisting of predictors x_i ∈ 𝒳 and a binary response y_i ∈ {0, 1}, with joint probability measure ℙ. For our purposes, we assume the predictors are mapped into some real covariate vector space, so that 𝒳 ⊆ ℝ^p Our aim is to learn the function

$$p(x)=\mathbb{P}(Y=1|X=x)$$ (1)

or equivalently to learn

$$f(x)=\text{logit}(p(x))=\text{log}\frac{p(x)}{1-p(x)}$$ (2)

which could be infinite for some x.

A linear logistic regression model assumes f is linear in x; that is,

$$f_{\theta }(x)=f_{\alpha ,\beta }(x)=\alpha +\beta \prime x,$$ (3)

where θ = (α, β) ∈ ℝ^p+1. This is less of a restriction than it might seem, since x may represent a very large basis expansion of some smaller set of “raw” features.

Nevertheless, in the real world, f is unlikely to satisfy our parametric model for any given basis x. When the model is misspecified, we can still view logistic regression as an M-estimator with convex loss equal to the negative log-likelihood for a single data set:

$$\rho (\theta ;x,y)=-y(\alpha +\beta \prime x)+\text{log}(1+e^{\alpha +\beta \prime x}).$$ (4)

As an M-estimator, under general conditions logistic regression in large samples will converge to the minimizer of the population risk R(θ) = 𝔼ρ(θ; X, Y) [Huber (2011)]. That is, θ converges to the population maximizer of the expected log-likelihood

$${\theta }^{*}=\text{arg}\underset{\theta }{\text{min}}𝔼\rho (\theta ;X,Y)$$ (5)

$$=\text{arg}\underset{\theta }{\text{min}}𝔼[-Y(\alpha +\beta \prime X)+\text{log}(1+e^{\alpha +\beta \prime X})].$$ (6)

If f = f_θ0 for some θ₀, then θ* = θ₀; otherwise f_θ* is the best linear approximation to f in the sense of (5). For a misspecified model, f_θ̂ cannot possibly converge to f no matter what sampling scheme or estimation procedure we use, or how much data we obtain. Consistency, then, will mean that $\mathrm{\theta ̂}\stackrel{p}{\to }{\theta }^{*}$.

Model misspecification is ubiquitous in real-world applications of regression methods. For reasons of exposition, the misspecification always takes a simple form in our simulations, for example, in Example 1 there are two binary predictors, and we would have correct specification if only we added one interaction—but in the real world it usually is neither possible nor even desirable to expand the feature basis until the model is correctly specified. For instance, if p = 1000, then there are $\left(\begin{array}{c}\hfill p+1\hfill \\ \hfill 2\hfill \end{array}\right)=500,500$ quadratic terms. Even if we included all those terms as features, we would still be missing cubic terms, quartic terms, and so on.

Some kinds of misspecification are milder than others, and some are easier to find and fix than others. Seeking better-specified models (without adding too much model complexity) is a worthy goal, but realistically perfect specification is unattainable.

Our goal, then, is to speed up computation while still obtaining a good estimate of θ*, the population logistic regression parameters. As we will see, standard case-control sampling achieves the first goal, but may fail at the second.

1.4. Related work

Recent years have seen substantial work on classification in imbalanced data sets. See Chawla, Japkowicz and Kotcz (2004) and He and Garcia (2009) for surveys of machine learning efforts on this problem. Many of the methods proposed involve some form of undersampling the majority class, oversampling the minority class, or both. Owen (2007) examined the limit of marginally imbalanced logistic regression and proved it is equivalent to fitting an exponential family model to the minority class.

One recurring theme is to preferentially sample negative examples that lie near positive examples in feature space. For example, Mani and Zhang (2003) propose selecting majority-class examples whose average distance to its three nearest minority examples is smallest. Our method has a similar flavor since the probability of sampling a negative example (x, 0) is p̃(x), which is large when the features x are similar to those characteristic of positive examples.

Our proposal lies more in the tradition of the epidemiological case-control sampling literature. In particular, case-control sampling within several categorical strata has been studied by Fears and Brown (1986), Breslow and Cain (1988), Weinberg and Wacholder (1990), Scott and Wild (1991). Typically, the strata are based on easy-to-measure screening variables available for a wide population, with more laborious-to-collect variables being measured on the sampled subjects. Lumley, Shaw and Dai (2011) discuss survey calibration methods for efficient regression in two-stage sampling schemes, which are interesting but too computationally intensive for our purposes here.

2. Case-control subsampling

Case-control sampling is commonly carried out by taking all the cases and exactly c times as many controls for some fixed c (e.g., c = 1, 2, 5). However, for our purposes it will be simpler to consider a nearly equivalent procedure based on accept–reject sampling.

Define some acceptance probability function a(y) and let $b=\text{log}\frac{a\left(1\right)}{a\left(0\right)}$, the log-selection bias. Consider the following algorithm:

1. Generate independent z_i ~ Bernoulli(a(y_i)).

2. Fit a logistic regression to the subsample S = {(x_i, y_i) : z_i = 1}, obtaining unadjusted estimates θ̂_S = (α̂_S, β̂_S).

3. Assign α̂ ← α̂_S − b and β̂ ← β̂_S.

Specifically, we could generate the z_i by first generating u_i ~ U(0, 1) mutually independent of the pilot, the data, and each other, then taking z_i = 1_ui≤a(yi). Note that steps (2)–(3) are equivalent to logistic regression with offset b for each data point.

This variant is convenient to analyze because the subsample thus obtained is an i.i.d. sample from a new population:

$${\mathbb{P}}_S(X,Y)=\mathbb{P}(X,Y|Z=1)=\frac{a(Y)\mathbb{P}(X,Y)}{ā}$$ (7)

with ā = a(1)ℙ(Y = 1) + a(0)ℙ(Y = 0), the marginal probability of Z = 1.

The estimate (α̂, β̂) is motivated by a simple application of Bayes’ rule relating the odds of Y = 1 in ℙ and ℙ_S. If g(x) is the true conditional log-odds function for ℙ_S, we have

$$g(x)=\text{log}\frac{\mathbb{P}(Y=1|X=x,Z=1)}{\mathbb{P}(Y=0|X=x,Z=1)}$$ (8)

$$=\text{log}\frac{\mathbb{P}(Y=1|X=x)}{\mathbb{P}(Y=0|X=x)}+\text{log}\frac{\mathbb{P}(Z=1|Y=1,X=x)}{\mathbb{P}(Z=1|Y=0,X=x)}$$ (9)

$$=f(x)+b.$$ (10)

That is, the log-odds g(x) in our biased population is simply a vertical shift by b of the log-odds f(x) in the original population, so given an estimate of g we can subtract b to estimate f. If the model is correctly specified, logistic regression on the subsample yields a consistent estimate for the function g(x), so the estimate for f(x) is also consistent.

Note that the derivation (8)–(10) is equally valid if the sampling bias b depends on x, in which case we have g(x) = f(x) + b(x). Local case-control sampling exploits this more general identity.

2.1. Conditional probability and the logit loss

If X is integrable, then upon differentiating the population risk (5) with respect to θ we obtain the population score criterion:

$$0=𝔼\left[\right(Y-\frac{e^{f_{\theta }(X)}}{1+e^{f_{\theta }(X)}}\left)\right(\begin{array}{c}\hfill 1\hfill \\ \hfill X\hfill \end{array}\left)\right]=\int (p(x)-p_{\theta }(x))\left(\begin{array}{c}\hfill 1\hfill \\ \hfill x\hfill \end{array}\right)d\mathbb{P}(x).$$ (11)

Informally, the best linear predictor is the one that gets the conditional probabilities right on average. Note this is not the same as a predictor that gets the conditional log-odds right on average.

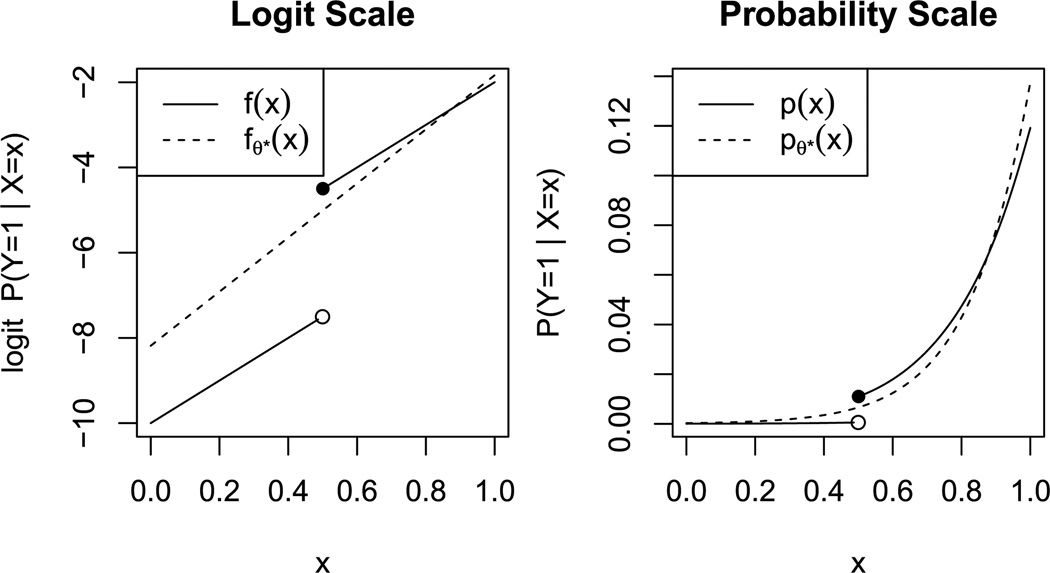
To illustrate the difference between approximating probabilities and approximating logits, suppose that X ~ U(0, 1) and f(x) = −10 + 5x + 3 · 1_x>0.5. The left panel of Figure 1 shows f(x) as a solid line and its best linear approximation as a dashed line. On the logit scale, the dashed line appears to be a very poor fit to the black curve. It fits reasonably well for large x, but it appears more or less to ignore the smaller values of x.

Fig. 1.

The best linear fit f_θ* (x) approximates the true log-odds f(x) in the sense of matching its implied conditional probabilities, not logits.

The right panel of Figure 1 shows why. When we transform both curves to the probability scale, the fit looks much more reasonable. f_θ*(x) need not approximate f(x) particularly well for small x, because in that range even a large change in the log-odds produces a negligible change in the conditional probability p(x). By contrast, f_θ*(x) needs to approximate f(x) well for larger x, where p(x) changes more rapidly.

In general, logistic regression places highest priority on fitting f where $\frac{dp\left(x\right)}{df\left(x\right)}$ is largest: where f(x) ≈ 0 and p(x) ≈ 0.5. In this example, with its strong marginal imbalance, the regions that matter most are those where p(x) is largest. This often makes sense in applications such as medical screening or advertising click-through rate prediction, where accuracy is most important when the probability of disease or click-through is nonnegligible. In Section 7, we consider how to modify the method to obtain classifiers that prioritize correctness near some other, user-defined level curve of p(x).

Finally, note that Figure 1 suggests the case-control sampling estimate is unlikely to be consistent for θ* in general. The nature of our linear approximation in the left panel is intimately related to the fact that f(x) < 0 everywhere in the sample space. If f(x) were shifted upward by some constant, the response of the dashed curve would be more complicated than a simple constant shift by b, since the relative importance of the two segments would change. Therefore, estimating f(x) + b and then subtracting b may not be a successful strategy.

2.2. Inconsistency of case-control under misspecification

If the linear model is misspecified, the case-control estimate is generically not consistent for the best linear predictor θ* as n → ∞ [Xie and Manski (1989), Manski and Thompson (1989)]. The unadjusted estimate will instead converge to the best linear predictor of g for the distribution ℙ_S, which solves the score criterion

$$0=\int (\frac{e^{f(x)+b}}{1+e^{f(x)+b}}-\frac{e^{f_{\theta }(x)}}{1+e^{f_{\theta }(x)}})\left(\begin{array}{c}\hfill 1\hfill \\ \hfill x\hfill \end{array}\right)d{\mathbb{P}}_S(x).$$ (12)

Let ${\theta }_{\mathrm{C}\mathrm{C}}^{*}\left(b\right)$ be the large-sample limit of the adjusted case-control sampling estimate with bias b. Then ${\theta }_{\mathrm{C}\mathrm{C}}^{*}\left(b\right)$ solves the population score criterion

$$0=\int (\frac{e^{f(x)+b}}{1+e^{f(x)+b}}-\frac{e^{f_{\theta }(x)+b}}{1+e^{f_{\theta }(x)+b}})\left(\begin{array}{c}\hfill 1\hfill \\ \hfill x\hfill \end{array}\right)d{\mathbb{P}}_S(x)$$ (13)

which differs from (11) in two ways. First, the integral is taken over a different distribution for X. Second, and more importantly, the integrand is different. We are now approximating f(x) in a different sense than we were.

In general under misspecification, ${\theta }_{\mathrm{C}\mathrm{C}}^{*}\left(b\right)$ is different for every b. If we sample cases and controls equally, in the limit we will get a different answer than if we sample twice as many controls; and in either case we will get a different answer than if we use the entire data set or subsample uniformly.

These differences can be quite consequential for our inferences about β or the predictive performance of our model, as we see next.

Example 1 (Oatmeal and disease risk). In this fictitious example, we consider estimating the effect of exposure to oatmeal on a person’s risk of developing some rare disease. Suppose that 10% of the population has a family history of the disease, half the population eats oatmeal (independently of family history), and that both exposure and family history are binary predictors. Suppose further that the true conditional log-odds function f(x) is given by the top-left panel of Table 1.

Table 1.

Disease risk in the full population, and in the population created by case-control sampling with equal numbers in each class

Original population (ℙ)			Case-control population (ℙS)
Conditional log-odds (f)			Conditional log-odds (g)
	History −	History +		History −	History +
Oatmeal −	−5	−4	Oatmeal −	−1.2	−0.2
Oatmeal +	−10	−1	Oatmeal +	−6.2	2.8
Conditional probabilities			Conditional probabilities
	History −	History +		History −	History +
Oatmeal −	0.007	0.02	Oatmeal −	0.24	0.46
Oatmeal +	5E−5	0.37	Oatmeal +	0.002	0.94

The corresponding conditional probabilities p(x) are given in the lower-left panel of Table 1. Notice that oatmeal increases the risk for people who are already at risk by virtue of their family history, but has a protective effect for everyone else. This interaction means that the additive logistic regression model is misspecified.

Because only the probabilities in the “History +” column are large enough to matter, the fitted model for f(x) pays more attention to the at-risk population, for whom oatmeal elevates the risk of disease. A logistic regression on a large sample from this population estimates the coefficient for oatmeal as ${\beta }_{\text{Oatmeal}}^{*}=1.4$, implying an odds ratio of about 4.0. This is close to the marginal odds ratio of roughly 4.3 that we would obtain if we did not control for family history.

Suppose, however, that we sampled an equal number of cases and controls. Then the conditional log-odds of disease in our sample would reflect the top-right panel of Table 1, with all cells increased by the same amount.

For large samples, the case-control estimate is ${\beta }_{\mathrm{C}\mathrm{C},\text{Oatmeal}}^{*}=-0.83$, implying an odds ratio of about 0.44. Using case-control sampling has reversed our inference about the effect of oatmeal exposure, because after shifting the log-odds the left column becomes much more important.

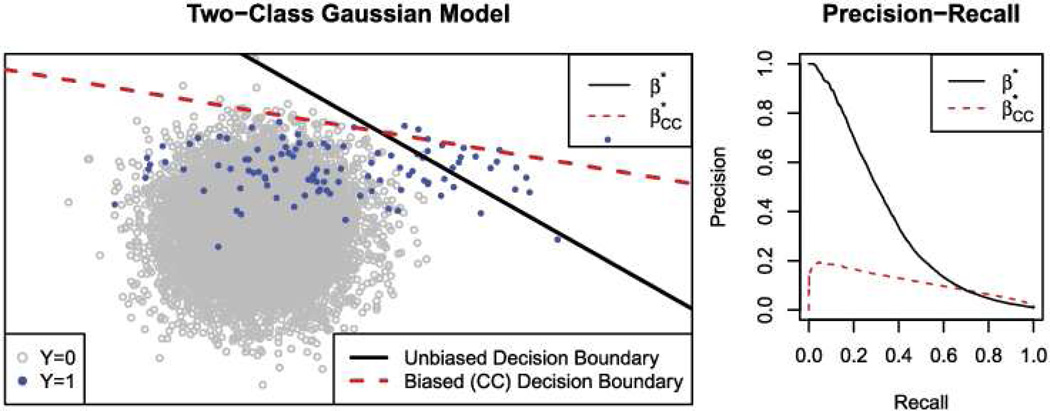
Example 2 (Two-class Gaussian model). Suppose that ℙ(Y = 1) = 1%, and that X|Y ~ N(μ_Y, Σ_Y). Let

$${\mu }_0=(0,0),{\mathrm{\Sigma }}_0=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),$$ (14)

$${\mu }_1=(1.5,1.5),{\mathrm{\Sigma }}_1=\left(\begin{array}{cc}\hfill 0.3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 5\hfill \end{array}\right).$$ (15)

Data simulated from this model are shown in the left panel of Figure 2. In this example, the true log-odds f(x) is an additive quadratic function of the two coordinates X₁ and X₂.

Fig. 2.

At left, biased (case-control) and unbiased decision boundaries for the bivariate Gaussian mixture model. At right, precision–recall curves for β* and ${\beta }_{\mathrm{C}\mathrm{C}}^{*}$.

In this example as in the previous one, the population-optimal case-control parameters differ substantially from the optimal parameters in the original population, with dramatic effects for the predictive performance of the model. The decision boundaries for the two estimates are overlayed on the left panel of Figure 2. In the right panel, we plot the precision–recall curves resulting from each set of parameters on a large test set.

2.3. Weighted case-control sampling

A simple alternative to standard case-control sampling is to weight the subsampled data points by the inverse of their probability of being sampled. We include weighted case-control sampling as a competitor in our simulation studies in Section 5. Because it is a Horvitz–Thompson estimator with positive sampling probabilities for any (x, y) pair, this method is $\sqrt{n}-\text{consistent}$, and asymptotically normal and unbiased under general conditions [Horvitz and Thompson (1952)].

Although weighting succeeds in removing the bias induced by the case-control sampling, this consistency comes at a cost of increasing the variance, since the effective sample size is reduced [Scott and Wild (1986, 2002)].

Despite its inefficiency, the weighted case-control method can be an attractive means of obtaining a consistent pilot if another good pilot is not immediately available, and we later will use it to that end in our experiments.

3. Local case-control subsampling

In this section, we describe local case-control subsampling, a generalization of standard case-control sampling that both improves on its efficiency and resolves its problem of inconsistency. To achieve these benefits, we require a pilot estimate, that is, a good guess θ̃ = (α̃, β̃) for the population-optimal θ*.

3.1. The local case-control sampling algorithm

Local case-control sampling differs from case-control sampling only in that the acceptance probability a is allowed to depend on x as well as y. Our criterion for selection will be the degree of “surprise” we experience upon observing y_i given x_i:

$$a(x,y)=|y-\mathrm{p̃}(x)|=\{\begin{array}{cc}1-\mathrm{p̃}(x),\hfill & y=1,\hfill \\ \mathrm{p̃}(x),\hfill & y=0,\hfill \end{array}$$ (16)

where $\mathrm{p̃}(x)=\frac{e^{\mathrm{\alpha ̃}+\mathrm{\beta ̃}\prime x}}{1+e^{\mathrm{\alpha ̃}+\mathrm{\beta ̃}\prime x}}$ is the pilot estimate of ℙ(Y = 1|X = x). The algorithm is:

1. Generate independent z_i ~ Bernoulli(a(x_i, y_i)).

2. Fit a logistic regression to the sample S = {(x_i, y_i) : z_i = 1} to obtain unadjusted estimates θ̂_S = (α̂_S, β̂_S).

3. Assign α̂ ← α̂_S + α̃ and β̂ ← β̂_S + β̃.

As before, steps (2)–(3) are equivalent to fitting a logistic regression in the subsample with offsets −α̃ − β̃′x_i. The z_i are generated as in Section 2, and the adjustment is again justified by (8)–(10), only now with the constant b replaced by

$$b(x)=\text{log}\left(\frac{a(x,1)}{a(x,0)}\right)=-\mathrm{\alpha ̃}-\mathrm{\beta ̃}\prime x.$$ (17)

In other words, the subsample is drawn from a measure with

$$g(x)=f(x)-\mathrm{\alpha ̃}-\mathrm{\beta ̃}\prime x.$$ (18)

If f(x) is well approximated by the pilot estimate, then g(x) ≈ 0 throughout feature space. That is, conditional on selection into S, y_i given x_i is nearly a fair coin toss.

To motivate this choice heuristically, recall that the Fisher information for the log-odds of a Bernoulli random variable is maximized when the probability is $\frac{1}{2}$: fair coin tosses are more informative than heavily biased ones. In effect, local case-control sampling tilts the conditional distribution of Y given X = x to make each y_i in the subsample more informative. We then fit a logistic regression in the more favorable sampling measure, and “tilt back” to obtain a valid estimate for the original population.

In marginally imbalanced data sets where ℙ(Y = 1|X = x) is small everywhere in the predictor space, a good pilot has p̃(x) ≈ 0 for all x, and the number of cases discarded by this algorithm will be quite small. If we wish to avoid discarding any cases, we can always modify the algorithm so that instead of keeping (x, 1) with probability a(x, 1), we keep it with probability 1 and assign weight a(x, 1).

3.2. Choosing the pilot fit

In many applications, there may be a natural choice of pilot fit θ̃; for instance, if we are refitting a classification model every day to adapt to a changing world, then yesterday’s fit is a natural choice for today’s pilot.

If no pilot fit is available from such a source, we recommend an initial pass of weighted case-control sampling (described in Section 2.3) to obtain the pilot. Weighted case-control sampling using a fixed fraction of the original sample is itself $\sqrt{n}-\text{consistent}$ and asymptotically unbiased for the true parameters. Consequently, if the pilot were fit using an independent data set the second-stage estimate would enjoy consistency and asymptotic unbiasedness per the results in Section 4.

Our experiments suggest that mild inaccuracy in the pilot estimate, and using a data-dependent pilot, do not unduly degrade the performance of the local case-control algorithm. For example, is Simulation 2 of Section 5.2, the pilot is fifty times less efficient than the final local case-control estimate. The main role of the pilot fit is to guide us in discarding most of the data points for which y_i is obvious given x_i while keeping those for which y_i is conditionally surprising.

In our example and simulations, we use a pilot sample about the same size as the local case-control subsample, on the principle that we can afford to spend about as much time computing the pilot as computing the second-stage estimate. When ℙ(Y = 1|X) is small throughout 𝒳, this rule amounts roughly to weighted case-control sampling using all the cases and one control per case. Although the above rule has worked reasonably well for us, at this time we can offer no finite-sample guarantees that any given pilot sample size is large enough.

Because standard case-control sampling amounts to local case-control sampling with a constant-only pilot fit, we might expect that the pilot fit need not be perfect to improve upon case-control sampling. Our experiments in Sections 5 and 6 support this intuition.

3.3. Taking a larger or smaller sample

As we will see in Section 4.3, under correct model specification, and with an independent and consistent pilot, the baseline procedure described above has exactly twice the asymptotic variance as a logistic regression estimated with the full sample, despite using a potentially very small subset of the data. We can improve upon this factor of two by increasing the size of the subsample.

One simple way to achieve this is to multiply all acceptance probabilities by some constant c, for example, c = 5. When deciding whether to sample the point (x_i, y_i), we would then generate z_i ~ Bernoulli(ca(x_i, y_i) ∧ 1) and assign weight w_i = ca(x_i, y_i) ∨ 1 to each sampled point. This amounts to a larger, weighted subsample from ℙ_S, and we can make the same correction to the estimates from the subsample. We see in Section 4.4 that for c > 1 the factor of two is replaced by a factor of $1+\frac{1}{c}$.

In the case of large imbalance, most of the p̃(x_i) are near 0 or 1. For c > 1, the marginal acceptance probability at x_i becomes

$$\mathbb{P}(z_i=1|x_i=x)=p(x)(c(1-\mathrm{p̃}(x))\wedge 1)+(1-p(x))(c\mathrm{p̃}(x)\wedge 1)$$ (19)

$$\approx (1+c)p(x)(1-p(x)),$$ (20)

where the approximation holds for p(x) ≈ p̃(x) ≈ 0 or 1. For c = 1, the marginal acceptance probability is p(x)(1 − p̃(x)) + (1 − p(x))p̃(x) ≈ 2p(x)(1 − p(x)), so for c > 1 we take roughly $\frac{1+c}{2}$ times as many data points as for c = 1. For example, if c = 5, the subsample accepted is roughly 3 times as large, and the relative efficiency improves from 1/2 to 5/6.

Alternatively, if n is extremely large, even a small fraction of the full data set may still be more than we want. In that case, we can proceed as above with c < 1, or simply sample any desired number n_s of data points uniformly from the local case-control subsample.

4. Asymptotics of the local case-control estimate

We now turn to examining the asymptotic behavior of the local case-control estimate. We first establish consistency, assuming a consistent pilot estimate θ̃. We expressly do not assume that the pilot estimate is independent of the data, since in some cases we may recycle into the subsample some of the data we used to calculate the pilot.

By assuming independence of θ̃ and the data, we can obtain finer results about the asymptotic distribution of θ̂. We show it is asymptotically unbiased when θ̃ is, and derive the asymptotic variance of the estimate. When the logistic regression model is correctly specified, the local case-control estimate has exactly twice the asymptotic variance of the MLE for the full data set.

4.1. Preliminaries

For better clarity of notation in this section, we will use the letter λ in place of θ̃ to denote pilot estimates. Additionally, we drop the notation $\left(\begin{array}{c}\hfill 1\hfill \\ \hfill x\hfill \end{array}\right)$ and absorb the constant term into x, so that f_θ(x) = θ′x. To avoid trivialities, assume without loss of generality that there is no υ ∈ ℝ^p for which 𝔼|υ′X| = 0 (if not, we can discard redundant features).

For π ∈ [0, 1] define the “soft hinge” function

$$h(\eta ;\pi )=-\pi \eta +\text{log}(1+e^{\eta }),$$ (21)

and note that

$$𝔼[\rho (\theta ;X,Y)|X=x]=h(\theta \prime x;p(x)).$$ (22)

As a function of η, h is positive and strictly convex, its magnitude is bounded by 1 + |η|, and it has Lipschitz constant max(π, 1 − π) ≤ 1. If π < 1, h diverges as η → ∞, and if π > 0 h diverges as η → −∞.

As a function of λ, $a_{\lambda }(x,y)=|y-\frac{e^{\lambda \prime x}}{1+e^{\lambda \prime x}}|\in (0,1)$ has Lipschitz constant ≤ ‖x‖. Hence, ā(λ) = 𝔼a_λ(X, Y) ∈ (0, 1) with Lipschitz constant ≤ 𝔼‖X‖. The marginal acceptance probability given x is

$${â}_{\lambda }(x)=\mathrm{p̃}(x)(1-p(x))+(1-\mathrm{p̃}(x))p(x)\in (0,1).$$ (23)

Given pilot λ, the local case-control subsampling scheme effectively samples from the probability measure ℙ_λ, where

$$d{\mathbb{P}}_{\lambda }(x,y)=\frac{a_{\lambda }(x,y)d\mathbb{P}(x,y)}{ā(\lambda )},$$ (24)

and ā(λ) = ∫ a_λ(x, y) dℙ(x, y) is the marginal probability of acceptance. Under this measure,

$$\text{logit}{\mathbb{P}}_{\lambda }(Y=1|X=x)=f(x)-\lambda \prime x.$$ (25)

Because a_λ(x, y) ≤ 1, if g(X, Y) is integrable under ℙ it is also integrable under any ℙ_λ.

Conditioning on X, we can write the population risk of the logistic regression parameters θ with respect to sampling measure ℙ_λ as

$$R_{\lambda }(\theta )=\frac{-1}{ā(\lambda )}\int h(\theta \prime x;\frac{e^{f(x)-\lambda \prime x}}{1+e^{f(x)-\lambda \prime x}}){â}_{\lambda }(x)d\mathbb{P}(x).$$ (26)

By Cauchy–Schwarz, the integrand in (26) is bounded by 2(1 + ‖θ‖‖x‖). If 𝔼‖X‖ < ∞, then, we may appeal to dominated convergence and take limits with respect to θ and λ inside the integral.

R_λ(θ) is strictly convex because the integrand is, and always has a unique population minimizer if there is no separating hyperplane in the population.

Lemma 1. Assume there is no υ for which

$$\mathbb{P}(Y=0,\upsilon \prime X>0)=\mathbb{P}(Y=1,\upsilon \prime X<0)=0.$$ (27)

Henceforth, we refer to this assumption as nonseparability. Then R_λ(θ) attains a unique minimum for every λ ∈ ℝ^p.

Denote by ${\mathrm{R̂}}_{\lambda }^{(0)}(\theta )$ the empirical risk on a local case-control subsample taken using the pilot estimate λ. Then

$${\mathrm{R̂}}_{\lambda }^{(0)}(\theta )=-{\left(\sum _{i=1}^n{z}_i\right)}^{-1}\sum _{i=1}^n{z}_i[y_i\theta \prime x_i-\text{log}(1+e^{\theta \prime x_i})].$$ (28)

It will be somewhat simpler to replace the random subsample size ${\sum }_{i=1}^n{z}_i$ with its expectation nā(λ). Define

$${\mathrm{R̂}}_{\lambda }(\theta )=-\frac{1}{nā(\lambda )}\sum _{i=1}^n{z}_i[y_i\theta \prime x_i-\text{log}(1+e^{\theta \prime x_i})].$$ (29)

Since minimizing (28) with respect to θ is equivalent to minimizing (29), the two are equivalent for our purposes.

If the unadjusted parameters θ̂_S minimize R̂_λ, the local case-control estimate θ̂ = θ̂_S + λ is an M-estimator minimizing Q̂_λ(θ) = R̂_λ(θ − λ). We use analogous notation for the population version:

$$Q_{\lambda }(\theta )=R_{\lambda }(\theta -\lambda ).$$ (30)

For any given pilot estimate λ and large n, we expect

$$\mathrm{\theta ̂}\approx \text{arg}\underset{\theta }{\text{min}}{Q}_{\lambda }(\theta ).$$ (31)

Define the right-hand side of (31) to be θ̄(λ), the large-sample limit of local case-control sampling with pilot estimate fixed at λ. The best linear predictor for the original population corresponds to the case λ = 0 (uniform subsampling), that is, θ* = θ̄(0). Consistency means that for large n, $\mathrm{\theta ̂}\stackrel{p}{\to }{\theta }^{*}$.

Recall that if the model is correctly specified with true parameters θ₀, then θ̄(λ) = θ₀ for any fixed pilot estimate λ. Minimizing Q̂_λ therefore yields a consistent estimate. Unfortunately, in the misspecified case θ̄(λ) ≠ θ̄(0) = θ*. In this sense, local case-control sampling with the pilot λ held fixed is in general not consistent for θ*. However, we see below that it is consistent if λ = θ*.

Proposition 2. Assume 𝔼‖X‖ < ∞, that the classes are nonseparable, and that θ* = θ̄(0) is the best linear predictor for the original measure ℙ. Then

$${\theta }^{*}=\text{arg}\underset{\theta }{\text{min}}{Q}_{{\theta }^{*}}(\theta )=\mathrm{\theta ̄}({\theta }^{*}).$$ (32)

In other words, if we could only choose our pilot perfectly, then the local case-control estimate would converge to θ* as n → ∞.

Proof of Proposition 2. Write $p^{*}(x)=\frac{e^{{\theta }^{*}\prime x}}{1+e^{{\theta }^{*}\prime x}}$. The population optimality criterion for LCC with pilot λ is

$$0=-ā(\lambda ){\mathrm{\nabla }}_{\theta }{R}_{\lambda }(\theta -\lambda )$$ (33)

$$=-𝔼[X\rho \prime ((\theta -\lambda )\prime X;X,Y)a_{\lambda }(X,Y)].$$ (34)

Noting that $-\rho \prime (0;x,y)=y-\frac{1}{2}$, if we evaluate the above at λ = θ = θ*, we obtain

$$𝔼[X(Y-\frac{1}{2})a_{\lambda }(X,Y)]=\frac{1}{2}𝔼[X(p(X)(1-p^{*}(X))-(1-p(X))p^{*}(X))]$$ (35)

$$\frac{1}{2}𝔼[X(Y-p^{*}(X))]$$ (36)

which is exactly half the population score (11) for the original population. Since θ* optimizes the risk for the original population, this value is 0.

There is an intuitive explanation of this result: in ℙ_θ*, the acceptance probabilities are p*(X) if Y = 0 and 1 − p*(X) if Y = 1; hence they play the same role as the pseudoresiduals Y − p*(X) did in the original measure ℙ. For example, the point (x, 0) would contribute p*(x)x to the gradient if we evaluated the full-sample score at θ*. Evaluating the subsample score at 0, the same point now contributes $\frac{1}{2}x$ to the score—but only if it is accepted, which occurs with probability exactly p* (x). So, in essence, the subsampling stands in for the reweighting that we otherwise would have done when fitting our logistic regression to the full sample.

Of course, in practice we never have a perfect pilot—if we did we would not need to estimate θ*—but Proposition 2 suggests that if λ is near θ*, minimizing Q̂_λ yields a good estimate. In fact, we will see that if $\lambda \stackrel{p}{\to }{\theta }^{*}$ then $\mathrm{\theta ̂}\stackrel{p}{\to }{\theta }^{*}$ as well.

4.2. Consistency

For our asymptotic results, assume we have an infinite reservoir (x₁, y₁), (x₂, y₂), … of i.i.d. pairs, a sequence of i.i.d. U(0, 1) variables u₁, u₂, … for making accept–reject decisions, and a sequence of pilot estimates λ₁, λ₂, …. The λ_n are possibly dependent upon the data, but the u_i are assumed to be independent of everything else.

θ̂_n is the local case-control estimate, computed using pilot λ_n, data ${\{(x_i,y_i)\}}_{i=1}^n$, and accept–reject decisions z_i = 1_{ui≤aλn(xi, yi)}.

The main result of this section is that if the pilot estimate λ_n is consistent for θ*, then so is θ̂_n. The details are somewhat technical, especially the proof of Proposition 3, but the main idea is that if ${\lambda }_n\stackrel{p}{\to }{\theta }^{*}$, then for large n

$${\mathrm{Q̂}}_{{\lambda }_n}\approx Q_{{\theta }^{*}}$$ (37)

in the appropriate sense. Q̂_λn is what the local case-control estimate actually minimizes, whereas the last function is minimized by θ*, our ultimate target.

First, we establish pointwise convergence.

Proposition 3. If 𝔼‖X‖ < ∞ and ${\lambda }_n\stackrel{p}{\to }{\lambda }_{\infty }$, then for each θ ∈ ℝ^p,

$${\mathrm{Q̂}}_{{\lambda }_n}(\theta )\stackrel{p}{\to }{Q}_{{\lambda }_{\infty }}(\theta ).$$ (38)

Because we avoid assuming independence between the pilot λ_n and the data (x_i, y_i), the proof is technical and is deferred to the Appendix. The proof relies on the coupling of the acceptance decisions z_i for different pilot estimates through u_i. With this coupling, two nearby pilot estimates will differ on very few accept–reject decisions.

Because neither Q̂_λn(θ) nor Q_λ∞(θ) changes very fast, pointwise convergence also implies uniform convergence on compacts.

Proposition 4. If 𝔼‖X‖ < ∞ and ${\lambda }_n\stackrel{p}{\to }{\lambda }_{\infty }$, then for compact Θ ⊆ ℝ^p,

$$\underset{\theta \in \mathrm{\Theta }}{\text{sup}}|{\mathrm{Q̂}}_{{\lambda }_n}(\theta )-Q_{{\lambda }_{\infty }}(\theta )|\stackrel{p}{\to }0.$$ (39)

Proof. Define

$$F_n(\theta )={\mathrm{Q̂}}_{{\lambda }_n}(\theta )-Q_{{\lambda }_{\infty }}(\theta ).$$ (40)

By Proposition 3, $F_n(\theta )\stackrel{p}{\to }0$ pointwise. Next, we show it is Lipschitz. The integrand in (35) is x times two factors each bounded by ±1, hence

$$\Vert ā({\lambda }_{\infty }){\mathrm{\nabla }}_{\theta }{Q}_{{\lambda }_{\infty }}\Vert \le \int \Vert x\Vert d\mathbb{P}(x)=𝔼\Vert x\Vert .$$ (41)

Similarly for Q̂_λn, we have

$${\nabla }_{\theta }{\mathrm{Q̂}}_{{\lambda }_n}=-\frac{1}{nā({\lambda }_n)}\sum _{i=1}^n{z}_i(y_i-\frac{e^{(\theta -{\lambda }_n)\prime x_i}}{1+e^{(\theta -{\lambda }_n)\prime x_i}})x_i$$ (42)

so that

$$\underset{\theta }{\text{sup}}\Vert {\nabla }_{\theta }{\mathrm{Q̂}}_{{\lambda }_n}\Vert \le ā{({\lambda }_n)}^{-1}\frac{1}{n}\sum _{i=1}^n\Vert x_i\Vert \stackrel{p}{\to }ā{({\lambda }_{\infty })}^{-1}𝔼\Vert X\Vert .$$ (43)

It follows that, with probability tending to 1, F_n(θ) has Lipschitz constant less than c = 3ā(λ_∞)⁻¹𝔼‖X‖.

Now, for any ε > 0, we can cover Θ with finitely many Euclidean balls of radius δ = ε/c, centered at θ₁, …, θ_M(ε). Let A_n(ε) be the event that F_n has Lipschitz constant less than c and

$$\underset{1\le j\le M(\epsilon )}{\text{sup}}|F_n({\theta }_j)|<\epsilon .$$ (44)

On A_n(ε), we have sup_θ∈Θ |F_n(θ)| < 2ε, and ℙ(A_n(ε)) → 1 as n → ∞.

Finally, we come to the main result of the section, in which we prove that the local case-control estimate is consistent when the pilot is. Because the functions are strictly convex, we can ignore everything but a neighborhood of θ*.

Theorem 5. Assume 𝔼‖X‖ < 0 and the classes are nonseparable. If ${\lambda }_n\stackrel{p}{\to }{\theta }^{*}$ then the local case-control estimate ${\mathrm{\theta ̂}}_n\stackrel{p}{\to }{\theta }^{*}$ as well.

Proof. Let Θ ⊆ ℝ^p be any compact set with θ* in its interior, and let

$$\epsilon =\underset{\theta \in \partial \mathrm{\Theta }}{\text{inf}}{Q}_{{\theta }^{*}}(\theta )-Q_{{\theta }^{*}}({\theta }^{*})>0,$$ (45)

where the strict inequality follows from strict convexity. Uniform convergence implies that with probability tending to 1,

$$\underset{\theta \in \mathrm{\Theta }}{\text{sup}}|{\mathrm{Q̂}}_{{\lambda }_n}(\theta )-Q_{{\theta }^{*}}(\theta )|<\epsilon /2$$ (46)

which implies in turn that

$$\underset{\theta \in \partial \mathrm{\Theta }}{\text{inf}}{\mathrm{Q̂}}_{{\lambda }_n}(\theta )>{\mathrm{Q̂}}_{{\lambda }_n}({\theta }^{*}).$$ (47)

Whenever this is the case, the strictly convex function Q̂_λn has a unique minimizer in the interior of Θ. Since Θ was arbitrary, we can take its diameter to be less than any δ > 0. Hence, ${\mathrm{\theta ̂}}_n\stackrel{p}{\to }{\theta }^{*}$.

4.3. Asymptotic distribution

In this section, we derive the asymptotic distribution of the local case-control logistic regression estimate, in the same asymptotic regime as the previous section. To prove our results here, we assume the pilot estimate λ_n is independent of our data set. This would not be the case if our pilot were based on a subsample of the data (the procedure we use for all our simulations), but it could hold if the pilot came from a model fitted to data from an earlier time period.

The main result of this section is that if the logistic regression model is correctly specified and the pilot is consistent, the asymptotic covariance matrix of the local case-control estimate for θ is exactly twice the asymptotic covariance matrix of a logistic regression performed on the entire data set. For the results in this section, we will need 𝔼‖X‖² < ∞.

It will be convenient to give names to some recurring quantities. First, we have seen that if 𝔼‖X‖ < ∞ we can differentiate Q_λ(θ) inside the integral to obtain the gradient of the population risk:

$$G(\theta ,\lambda )\triangleq -ā(\lambda ){\nabla }_{\theta }{Q}_{\lambda }(\theta )$$ (48)

$$=\int (\frac{e^{f(x)-\lambda \prime x}}{1+e^{f(x)-\lambda \prime x}}-\frac{e^{(\theta -\lambda )\prime x}}{1+e^{(\theta -\lambda )\prime x}}){â}_{\lambda }(x)xd\mathbb{P}(x).$$ (49)

Whereas G is the expectation of the logistic regression score with respect to ℙ_λ, we can also define its covariance matrix:

$$J(\theta ,\lambda )\triangleq {\text{Var}}_{\lambda }\left[\right(Y-\frac{e^{(\theta -\lambda )\prime X}}{1+e^{(\theta -\lambda )\prime X}}\left)X\right].$$ (50)

When 𝔼‖X‖² < ∞, J(θ, λ) < ∞, and is continuous in θ and λ by dominated convergence.

Since the derivatives of the integrand in (48) are uniformly bounded by 2‖x‖², dominated convergence implies we can again differentiate inside the integral. Differentiating with respect to θ we obtain

$$H(\theta ,\lambda )\triangleq -ā(\lambda ){\nabla }_{\theta }^2{Q}_{\lambda }(\theta )$$ (51)

$$=\int \frac{e^{(\theta -\lambda )\prime x}}{{(1+e^{(\theta -\lambda )\prime x})}^2}\left(\frac{e^{\lambda \prime x}+e^{f(x)}}{(1+e^{\lambda \prime x})(1+e^{f(x)})}\right)xx\prime d\mathbb{P}(x).$$ (52)

Here, the integrand is dominated by xx′, so dominated convergence again applies and thus we see that H is continuous in θ and λ. H(θ, λ) ≻ 0 for any θ, λ since we have assumed there is no nonzero υ for which 𝔼|υ′ X| = 0. Finally, define the matrix of crossed partials:

$$C(\theta ,\lambda )\triangleq {\nabla }_{\lambda }G(\theta ,\lambda ).$$ (53)

To be concrete, $C_{i,j}=\frac{{\partial }^2}{\partial {\theta }_i\partial {\lambda }_j}{Q}_{\lambda }(\theta )$. Continuity of C again follows from noting the derivative of the integrand in (48) with respect to λ is dominated by 8‖x‖².

To begin, we consider the behavior of θ̄(λ) for λ near θ*. By Proposition 2, we have G(θ*, θ*) = 0. Since H (θ, λ) ≻ 0, we can apply the implicit function theorem to the relation G(θ̄(λ), λ) = 0 to obtain

$$\mathrm{\theta ̄}(\lambda )={\theta }^{*}+H{({\theta }^{*},{\theta }^{*})}^{-1}C({\theta }^{*},{\theta }^{*})(\lambda -{\theta }^{*})+o(\Vert \lambda -{\theta }^{*}\Vert ).$$ (54)

By standard M-estimator theory, if we fix λ and send n → ∞ the coefficients of a logistic regression performed on a sample of size |S| from ℙ_λ would be asymptotically normal with covariance matrix

$$\frac{1}{|S|}H{(\mathrm{\theta ̄}(\lambda ),\lambda )}^{-1}J(\mathrm{\theta ̄}(\lambda ),\lambda )H{(\mathrm{\theta ̄}(\lambda ),\lambda )}^{-1}.$$ (55)

In light of this and the fact that |S| ≈ ā(λ)n, we might predict the following.

Theorem 6. Assume 𝔼‖X‖² < ∞. If ${\lambda }_n\stackrel{p}{\to }{\theta }^{*}$ independently of the data, then

$$\sqrt{n}({\mathrm{\theta ̂}}_n-\mathrm{\theta ̄}({\lambda }_n))\stackrel{𝒟}{\to }N(0,ā{({\theta }^{*})}^{-1}\mathrm{\Sigma })$$ (56)

with Σ = H(θ*, θ*)⁻¹ J(θ*, θ*)H(θ*, θ*)⁻¹.

Again, we defer the proof to the Appendix. We can combine (56) with (54) to immediately obtain the following reassuring facts.

Corollary 7. Assume 𝔼‖X‖² < ∞ and λ_n is a sequence of pilot estimators given independently of the data. Then:

1. If λ_n is $\sqrt{n}-\mathit{\text{consistent}}$, so is θ̂_n.

2. If λ_n is asymptotically unbiased, so is θ̂_n.

3. If $\sqrt{n}({\lambda }_n-{\theta }^{*})\stackrel{𝒟}{\to }N(0,V)$ then $\sqrt{n}({\mathrm{\theta ̂}}_n-{\theta }^{*})\stackrel{𝒟}{\to }N(0,\mathrm{\Sigma })$ with

$$\mathrm{\Sigma }=H^{-1}(CVC\prime +{ā}^{-1}J)H^{-1}.$$ (57)

In (57), we have suppressed the arguments of θ* in H, C, ā and J.

The first term in (57) characterizes the contribution of conditional bias (given λ_n) to the overall variance, and the second is the contribution of conditional variance.

In the special case where logistic regression model is correctly specified, we have the following.

Theorem 8. Assume the logistic regression model is correct and let $\frac{1}{n}{\sum }_{\text{full}}$ be the asymptotic variance of the MLE for the full sample. Then if 𝔼‖X‖² < ∞ and ${\lambda }_n\stackrel{p}{\to }{\theta }_0$ independently of the data, we have

$$\sqrt{n}({\mathrm{\theta ̂}}_n-{\theta }_0)\stackrel{𝒟}{\to }N(0,a{({\theta }_0)}^{-1}\mathrm{\Sigma })=N(0,2{\mathrm{\Sigma }}_{\text{full}}).$$ (58)

Hence, although the size of a local case-control subsample is roughly nā(λ), the variance of θ̂ is the same as if we took a simple random sample of size n/2 from the full data set. In other words, each point sampled is worth about $\frac{1}{2ā({\lambda }_n)}$ points sampled uniformly.

Proof of Theorem 8. If logistic regression is correctly specified for ℙ, it is also for ℙ_λ, regardless of λ, so θ̄(λ) ≡ θ₀. Furthermore, by standard maximum likelihood theory J(θ₀, λ) = H(θ₀, λ)⁻¹ for each λ. Therefore, (56) specializes to

$$\sqrt{n}({\mathrm{\theta ̂}}_n-{\theta }_0)\stackrel{𝒟}{\to }N(0,ā{({\theta }_0)}^{-1}H{({\theta }_0,{\theta }_0)}^{-1}).$$ (59)

But

$$H(\theta ,\lambda )=ā{(\lambda )}^{-1}\int \left[\frac{e^{(\theta -\lambda )\prime x}}{{(1+e^{(\theta -\lambda )\prime x})}^2}\right]\left[\frac{e^{\lambda \prime x}+e^{f(x)}}{(1+e^{\lambda \prime x})(1+e^{f(x)})}\right]xx\prime d\mathbb{P}(x).$$ (60)

If $f(x)={\theta }_0^{\prime }x$ and λ = θ₀, then (60) simplifies to

$$H({\theta }_0,{\theta }_0)=ā{({\theta }_0)}^{-1}\frac{1}{2}\int \frac{e^{{\theta }_0^{\prime }x}}{{(1+e^{{\theta }_0^{\prime }x})}^2}xx\prime d\mathbb{P}(x)$$ (61)

$$=ā{({\theta }_0)}^{-1}\frac{1}{2}H({\theta }_0,0)$$ (62)

$$={(2ā({\theta }_0){\mathrm{\Sigma }}_{\text{full}})}^{-1}.$$ (63)

This result is surprisingly simple. No characterization like Theorem 8 is available for the case-control and weighted case-control estimates, whose variances are not simple scalar multiples of Σ_full.

We can offer a simple heuristic argument for Theorem 8, similar to that of Proposition 2. In ℙ_θ0, the acceptance probability â_λ(x) for an observation at x is 2p(x) (1 −p(x)), and given that it is accepted it contributes $\frac{1}{4}xx\prime$ to the observed information. In the full sample, a point at x is always accepted but contributes less, p(x) (1 − p(x))xx′, to the observed information. Again, the sampling probability stands in for the reweighting we would have done in the full sample. If p(x) (1 − p(x)) is very small, we are discarding most of the data instead of keeping all of it and assigning it a tiny weight in the fit.

The practical meaning of Theorem 8 is that local case-control sampling is most advantageous when ā(θ₀) = 𝔼(|Y − p̃(X)|) is small, that is, when Y is easy to predict throughout much of the covariate space. This can happen as a result of marginal or conditional imbalance, or both. Standard case-control sampling can also improve our efficiency in the presence of marginal imbalance, but unlike local case-control sampling, it does not exploit conditional imbalance. Hence, we would expect local case-control to outperform standard case-control most dramatically when the marginal imbalance is very high, as in the simulation of Section 5.2.

For data-dependent pilots, the efficiency picture is somewhat more complicated. For example, θ̄(λ) is approximately a linear function of λ − θ*. Thus, if λ is unbiased but correlated with the noise in the data, we might get more or less variance relative to (58), depending on how this correlation interacts with C. If the model is correctly specified, it less clear whether an adversarially chosen pilot can affect the efficiency.

Either way, we do not anticipate serious problems from nonindependence. To stress-test our results against violations of independence, we expressly use a data-dependent pilot for all of our experiments: namely, a weighted case-control sample with sample points allowed to be recycled for the second-stage fit.

4.4. Variance for a larger sample

In Section 3.3, we proposed increasing the size of the local case-control subsample by multiplying all the acceptance probabilities a(x, y) by a constant c > 1 and assigning weight w = ca(x, y) when ca(x, y) > 1. We analyze the asymptotic variance here as a function of c. To simplify matters, suppose the model is correctly specified and λ is fixed at θ₀.

The weighted log-likelihood for the subsample and its derivatives are then

$${\ell }_w(\theta )=\sum _{i=1}^n{z}_i{w}_i(y_i\theta \prime x_i-\text{log}(1+e^{\theta \prime x_i})),$$ (64)

$${\nabla }_{\theta }{\ell }_w(\theta )=\sum _{i=1}^n{z}_i{w}_i(y_i-p_{\theta }(x_i))x_i,$$ (65)

$${\nabla }_{\theta }^2{\ell }_w(\theta )=\sum _{i=1}^n{z}_i{w}_i{p}_{\theta }(x_i)(1-p_{\theta }(x_i))x_i{x}_i^{\prime }.$$ (66)

Conditionally on x, there is a p(x)·(c(1 − p(x)) ∧ 1) chance y = z = 1 and w = c(1 − p(x))∨1, where p(x) = p_θ0(x). Similarly, there is a (1 − p(x))·(cp(x) ∧ 1) chance y = 0, z = 1, and w = cp(x) ∨ 1. We immediately obtain

$$𝔼(yzw|x)=cp(1-p),𝔼(zw|x)=2cp(1-p),𝔼(z{w}^2|x)\le c(c+1)p(1-p).$$ (67)

The expectation and variance of the score evaluated at 0 are

$$𝔼{\nabla }_{\theta }{\ell }_w(0)=n\int 𝔼(zw(y-1/2)|x)xd\mathbb{P}(x)=0,$$ (68)

$$J=\text{Var}({\nabla }_{\theta }{\ell }_w(0))=n\int 𝔼(z^2{w}^2{(y-1/2)}^2|x)xx\prime d\mathbb{P}(x)$$ (69)

$$=\frac{n}{4}\int 𝔼(z{w}^2|x)xx\prime d\mathbb{P}(x)\preccurlyeq \frac{c(c+1)}{4}{\mathrm{\Sigma }}_{\text{full}}$$ (70)

and the expected Hessian is

$$H=𝔼{\nabla }_{\theta }^2{\ell }_w(0)=\frac{n}{4}\int 𝔼(zw|x)xx\prime d\mathbb{P}(x)=\frac{c}{2}{\mathrm{\Sigma }}_{\text{full}}^{-1}.$$ (71)

We have derived

$$H^{-1}J{H}^{-1}\preccurlyeq (1+\frac{1}{c}){\mathrm{\Sigma }}_{\text{full}}.$$ (72)

For c = 1, we recover the factor of two from (58), but, for example, c = 5 we only pay 20% increased variance relative to the full sample.

5. Simulations

Here, we compare our method to standard weighted and unweighted case-control sampling for two-class Gaussian models like the one considered in Section 2.2. The standard case-control estimates use a 50–50 split between the two classes.

5.1. Simulation 1: Two-class Gaussian, different variances

We begin with a five-dimensional two-class Gaussian simulation where the classes have different covariance matrices. If X|Y = y ~ N(μ_y, Σ_y), then

$$\text{log}\frac{\mathbb{P}(x|Y=1)}{\mathbb{P}(x|Y=0)}=\frac{1}{2}(x-{\mu }_1)\prime {\Sigma }_1^{-1}(x-{\mu }_1)+\frac{1}{2}(x-{\mu }_0)\prime {\Sigma }_0^{-1}(x-{\mu }_0)+\text{const}.$$ (73)

Equation (73) is linear if Σ₁ = Σ₀, and quadratic otherwise, so if the two covariance matrices were the same the linear logistic model would be correctly specified. In this case the model is incorrectly specified, letting us compare the behavior of the different methods under model misspecification.

Take ℙ(Y = 1) = 1%, μ₀ = 0, and μ₁ = (1, 1, 1, 1, 4)′. The covariance matrices are Σ₀ = diag(1, 1, 1, 1, 9) and Σ₁ = I₅. Hence f(x) is additive, but with a nonzero quadratic term in x₅.

For our simulation, we first generate a large (n = 10⁶) sample from the population described above. Second, we obtain a pilot model using the weighted case-control method on n_s = 1000 data points. Next, we take a local case-control sample of size 1000 using that pilot model.

For comparison, we obtain standard case-control (CC) and weighted case-control (WCC) estimates. For the comparison estimators we do not use a sample of size 1000 again but rather use the total number of observations seen by the LCC model or the pilot model, roughly 2000, so the LCC estimate must pay for its pilot sample. We repeat this entire procedure 1000 times.

Table 2 shows the squared bias and variance of β̂ over the 1000 realizations for each of the three methods. As expected, we face a bias-variance tradeoff in choosing between the WCC and CC methods, whereas the LCC method improves substantially on the bias of CC and the variance of WCC. Standard errors for both bias and variance are computed via bootstrapping the 1000 realizations.

Table 2.

Estimated bias and variance of β̂ for each sampling method. For β̂ ∈ ℝ^p, we define Bias² = ‖𝔼β̂ − β‖² and $\text{Var}={\sum }_{j=1}^p\text{Var}({\mathrm{\beta ̂}}_j)$

Simulation 1 (Σ0 ≠ Σ1 ⇒ model misspecified)
	${\widehat{\text{Bias}}}^2$	(s.e.)	$\widehat{\text{Var}}$	(s.e.)
LCC	0.0049	(0.00031)	0.025	(0.00059)
WCC	0.023	(0.0022)	0.16	(0.0038)
CC	0.15	(0.0016)	0.043	(0.00096)
Simulation 2 (Σ0 = Σ1 ⇒ model correct)
	${\widehat{\text{Bias}}}^2$	(s.e.)	$\widehat{\text{Var}}$	(s.e.)
LCC	0.0037	(0.0083)	0.039	(0.00045)
WCC	0.59	(0.064)	1.7	(0.017)
CC	0.06	(0.042)	0.87	(0.0086)

More surprising is the fact that LCC enjoys smaller bias than WCC and smaller variance than CC, dominating the other two methods on both measures. The improvement in variance over the CC estimate is likely due to the conditional imbalance present in the sample, while the improvement in bias over the WCC estimate may come from the fact that the methods are only unbiased asymptotically and the LCC estimate is closer to its asymptotic limiting behavior.

5.2. Simulation 2: Two-class Gaussian, same variance

Next, we simulate a two-class Gaussian model with each class having the same variance, so that the true log-odds function f is linear. We also increase the dimension to 50 for this simulation.

Since the model is now correctly specified, all three methods are asymptotically unbiased. However, in this case we introduce more substantial conditional imbalance, to demonstrate the variance-reduction advantages of local case-control sampling in that setting.

For this example, ℙ(Y = 1) = 10%, ${\mu }_1=\left(\begin{array}{c}\hfill 1_{25}\hfill \\ \hfill 0_{25}\hfill \end{array}\right)$, μ₀ = 0₅₀, and Σ₀ = Σ₁ = I₅₀. We repeat the procedure from Section 5.1, now with n_s = 10⁴. Instead of generating a full sample, the full data set is implicit and we sample directly from ℙ_S.

In this example, the difference between the methods is more dramatic. Table 2 shows the squared bias and variance of the three methods. Here, local case-control enjoys substantially better bias than the other two methods, improving on CC more than twenty-fold. For the correct pilot model, ā(θ₀) is roughly 0.005, so the local case-control subsample size is around n/200. Since the model is correctly specified, the variance is roughly twice that of logistic regression on the full sample of size n. In other words, local case-control subsampling is roughly 100 times more efficient than uniform subsampling.

Asymptotically, all three methods are unbiased but it appears that LCC again enjoys a smaller bias in finite samples.

6. Web spam data set

Relative to standard case-control sampling, local case-control sampling is especially well-suited for data sets with significant conditional imbalance, that is, data sets in which y_i is easy to predict for most x_i.

One such application is spam filtering. To demonstrate the advantages of local case-control sampling and compare asymptotic predictions to actual performance, we test our method on the Web Spam data available on the LIBSVM website³ and originally from Webb, Caverlee and Pu (2006). The data set contains 350,000 web pages, of which about 60% are labeled as “web spam,” that is, web pages designed to manipulate search engines rather than display legitimate content. This data set is marginally balanced, though as we will see the conditional imbalance is considerable.

As features, we use frequency of the 99 unigrams that appeared in at least 200 documents, log-transformed with an offset so as to reduce skew in the features. In this data set, the downsampling ratio ā is around 10%, that is, when using a good pilot we will retain about 10% of the observations.

Since we only have a single data set, we use subsampling as a method to assess the sampling distribution of our estimators. In each of 100 replications, we begin by taking a uniform subsample of size n = 100,000 from the population of 350,000 documents. After obtaining 100 data sets of size n = 100,000, we use the same procedure as we used in our two simulations with n_S = 10,000.

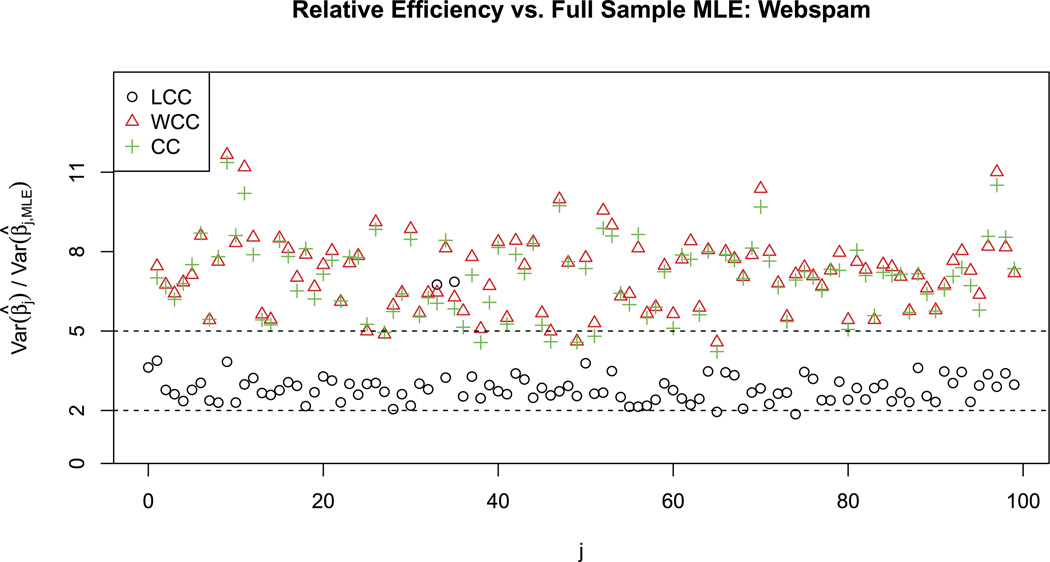
Our asymptotic theory predicts that the variance of the local case-control sampling estimate of θ should be a little more than twice the variance using the full sample (more because the model is misspecified and our pilot has some variance). Because the full sample is close to marginally balanced, the standard case-control sampling methods should do about as well as a uniform subsample of size 20,000—that is, they should have variance roughly 5 times that of the full sample.

Note that 20,000 is roughly twice the size of the local case-control sample, since we are counting the pilot sample against the local case-control method. If we had a readily available pilot model, as we would in many applications, it would be more relevant to give the CC and WCC methods access to only 10,000 data points, doubling their variance relative to the observed variance in this experiment.

The theoretical predictions come reasonably close in this experiment, as shown in Figure 3. The horizontal axis indexes each of the 100 coefficients to be fit (there are 99 covariates and an intercept), and the vertical axis gives the variance of each estimated coefficient, relative to the variance of the same coefficient in a model fitted to the full sample.

Fig. 3.

Relative variance of coefficients for different subsampling methods. The theoretical predictions (2× variance for local case-control, 5× variance for standard) are reasonably close to the mark, though a bit optimistic.

The magnitude of our improvement over standard case-control sampling is substantial here, but could be much larger in a data set with an even stronger signal. The key point is that standard case-control methods have no way to exploit conditional imbalance, so the more there is, the more local case-control dominates the other methods.

7. Discussion

We have shown that in imbalanced logistic regression, we can speed up computation by subsampling the data in a biased fashion and making a post-hoc correction to the coefficients estimated in the subsample. Standard case-control sampling is one such scheme, but it has two main flaws: it has no way to exploit conditional imbalance, and when the model is misspecified it is inconsistent for the population risk minimizer.

Local case-control sampling generalizes standard case-control sampling to address both flaws, subsampling with a bias that is allowed to depend on both x and y. When the pilot is consistent, our estimate is consistent even under misspecification, and if the model is correct then local case-control sampling has exactly twice the asymptotic variance of logistic regression on the full data set. Our simulations suggest that local case-control performs favorably in practice.

7.1. Translating computational gains to statistical gains

In the Introduction, we motivated our inquiry by identifying four ways that computational gains can translate to statistical ones. Specifically, we suggested that computational savings can:

1. enable us to experiment with and prototype a variety of models, instead of trying only one or two,

2. allow us to refit our models more often to adapt to changing conditions,

3. allow for cross-validation, bagging, boosting, bootstrapping, or other computationally intensive statistical procedures or

4. open the door to using more sophisticated statistical techniques on a compressed data set.

It is relatively clear how our proposed method can help with points (1) and (2). As for point (3), faster fitting procedures can directly speed up straightforward resampling techniques like bootstrapping or cross-validation, possibly making them feasible at scales where they previously were not. We discuss in Section 7.2 how it can also help with boosting.

The basic method as we have described it above does not deliver on point (4), because the pilot model and second-stage model are the same. However, an extension of our method can help, which we discuss below.

There is no reason in principle why the pilot model must be linear, or belong to the same model class as the model we fit to the local case-control sample. We can use any pilot predictions $\mathrm{p̃}(x)=\frac{e^{\mathrm{f̃}(x)}}{1+e^{\mathrm{f̃}(x)}}$ in the sampling algorithm, and then model the log-odds in the subsample quite flexibly—by a GAM, kernel logistic regression, random forests or any other method—so long as we can use offsets − f̃(x_i) in the second-stage procedure. For example, we could use as our pilot fit a simple model with a few important variables explaining most of the response, and in the second stage estimate more complex models refining the first.

Formally, our theoretical results may not cover this use. Suppose the second-stage model can be written as a logistic regression after some basis expansion. Then consistency of the second-stage estimate requires either that the pilot be consistent (the new variables contribute nothing to the population fit) or that the second-stage model be correctly specified. If neither of these assumptions holds approximately, then our estimate could be biased—though perhaps not as biased as case-control sampling, which is a special case of local case-control with an intercept-only pilot.

If we are prototyping, guarantees of consistency may not be a high priority. If they are, then as with case-control sampling, we can repair the inconsistency of the local case-control estimate by using a Horvitz–Thompson estimator with weights a_θ̃(x_i, y_i)⁻¹. This may come at a cost of some added variance. It would be interesting to examine the bias of local case-control and the variance of weighted local case-control in this more general problem setting.

7.2. Extensions

This work suggests extensions in several directions, described below.

Indifference point other than 50%

In some applications (e.g., diagnostic medical screening), a false negative may be more costly than a false positive, or vice-versa. One of the implications of the discussion in Section 2.2 is that the Bernoulli log-likelihood implicitly places most emphasis on approximating the log-odds well near the 0 (50% probability) level curve, which may not be appropriate if the decision boundary relevant to our application is at 10%. In general, we would expect to obtain a better model in the large-n limit if we target the decision boundary we care most about.

In a sense, the reason that standard case-control sampling performed so badly in Example 2 of Section 2.2 is that it targeted a level curve of ℙ(Y = 1|X = x) other than 50%. Specifically, it targeted the level curve corresponding to 50% in the subsampling population for equal-sampled case-control sampling, which corresponds to the marginal ℙ(Y = 1) level curve in the original population.

What happened by accident in Example 2 need not always be one, and it would be interesting to generalize our procedure so as to target any chosen decision threshold. More generally still, our indifference point could depend on our features x—in online advertising, for instance, some advertisers may be willing to pay more per click than others.

Boosting

In Section 7.1 we suggested using offsets to obtain a complex second-stage fit. Alternatively, we can obtain any fitted log-odds function f_s(x) for the sample and simply add it to the pilot f̃(x) to obtain an estimate for f(x).

This observation suggests the possibility of iteratively fitting a “base model” to the subsample, then adding it to f̃(x) to obtain a new pilot for the next iteration. Indeed, that iterative algorithm is closely related to the AdaBoost algorithm of Freund and Schapire (1997). Even more similarly to AdaBoost, we could weight each point by |y_i − p̃(x_i)| instead of sampling it with that probability.

Friedman, Hastie and Tibshirani (2000) show that the AdaBoost algorithm can be thought of as fitting a logistic regression model additive in base learners. In AdaBoost, the function $F_M(x)={\sum }_{m=1}^M{f}_m(x)$ simply records the number of classifiers f_m classifying x as belonging to class +1 minus the number classifying it as class −1, and Friedman et al. show that $\frac{1}{2}{F}_M(x)$ can be thought of as approximating the log-odds of Y = +1 given X = x.

The difference is that while AdaBoost weights the point (x_i, y_i) by e^{(2y_i−1)F_m(x_i)}, the local case-control version would use weights

$$|y_i-p_M(x_i)|=\frac{e^{y_i{F}_m(x_i)}}{1+e^{F_m(x_i)}}=\frac{e^{(2y_i-1)F_m(x_i)}}{1+e^{(2y_i-1)F_m(x_i)}}.$$ (74)

Operationally, this alternative weighting scheme limits the influence of “outliers,” that is, hard-to-classify points that can unduly drive the AdaBoost fit.

Logistic regression with regularization

In high-dimensional settings, lasso- or ridge-penalized logistic regressions are often preferable to standard logistic regression, the model considered here. One could use local case-control sampling with a regularized version of logistic regression, but our asymptotic results might need revisiting in such a case—especially in a high-dimensional asymptotic regime [p ≫ n or p/n → γ ∈ (0, ∞)]. Since the high-dimensional setting is important in modern statistics and machine learning, this bears further investigation.

Other generalized linear models

One way of viewing the method is as a way of “tilting” the conditional distribution of Y by a linear function of X in the natural parameter space so as to enrich our subsample for more informative observations. We could use similar tricks on other GLMs.

For instance, suppose we are given a Poisson variable with natural parameter η = log 𝔼Y. By sampling with acceptance probability proportional to e^ξY, we obtain (conditional on acceptance) a Poisson with natural parameter η + ξ. Since Poisson variables with larger means carry more information, this could yield a substantial improvement over uniform subsampling.

If our data arise from a Poisson GLM with η(x) ≈ α + β′x, we could generalize the local case-control scheme by sampling (x_i, y_i) with probability proportional to exp{(ξ₀ − α − β′x_i)y_i}, where the extra parameter ξ₀ guarantees that we always tilt the conditional mean of y_i upward. Similar generalizations may apply for multinomial logit and survival models.

APPENDIX A

PROOF OF LEMMA 1 (UNIQUENESS OF θ*)

Because R_λ(θ) is strictly convex, it is sufficient to show that R_λ(θ) → ∞ as θ → ∞ in any direction.

Assume w.l.o.g. there is some neighborhood N ⊆ ℝ^p for which

$$\underset{x\in N}{\text{inf}}\frac{\theta \prime x}{\Vert \theta \Vert }=\epsilon >0,\mathbb{P}(X\in N)>0\text{and}\mathbb{P}(Y=1|X\in N)={\pi }_N<1.$$ (75)

h(η; π_N) is linear in its second argument, and is increasing for sufficiently large η. Thus, for large enough ‖θ‖ε, the population risk for ℙ is

$$R(\theta )=\int h(\theta \prime x;p(x))d\mathbb{P}(x)$$ (76)

$$\ge {\int }_{N}h(\Vert \theta \Vert \epsilon ;p(x))d\mathbb{P}(x)$$ (77)

$$=h(\Vert \theta \Vert \epsilon ;{\pi }_N)\mathbb{P}(X\in N)\to \infty .$$ (78)

ℙ_λ ≫ ℙ for any λ, so (75) holds for ℙ_λ with the same N (but a different π_N < 1). Thus, we can repeat the same argument with ℙ replaced by ℙ_λ.

APPENDIX B

PROOF OF PROPOSITION 3 (POINTWISE CONVERGENCE)

Fix θ and begin by writing

$${\ell }_i^{\lambda }=y_i(\theta -\lambda )\prime x_i-\text{log}(1+e^{(\theta -\lambda )\prime x_i}).$$ (79)

Let $z_i^{\lambda }$ be the Bernoulli selection decisions, generated by comparing mutually independent u_i ~ U(0, 1) to the threshold a_λ(x_i, y_i). The $z_i^{\lambda }$ are independent conditional on λ and the data. Also, write $q_i^{\lambda }=z_i^{\lambda }{\ell }_i^{\lambda }$, so that ${\mathrm{Q̂}}_{\lambda }(\theta )=\frac{-1}{nā(\lambda )}{\sum }_{i=1}^n{q}_i^{\lambda }$.

By the Cauchy–Schwarz inequality, we have

$$|{\ell }_i^{\lambda }|\le 1+|\Vert \theta -\lambda \Vert \Vert x_i\Vert .$$ (80)

Now, for δ > 0 define Λ_δ = {λ: ‖λ − λ_∞‖ < δ}. For λ ∈ Λ₁, we have

$$|q_i^{\lambda }|\le m_i\triangleq 1+(\Vert \theta -{\lambda }_{\infty }\Vert +1)\Vert x_i\Vert$$ (81)

which is integrable by assumption. Finally let 𝔼_n denote an average taken over indices i = 1, …, n, that is, ${𝔼}_{n}f=\frac{1}{n}{\sum }_{i=1}^n{f}_i$. Then

$${\mathrm{Q̂}}_{{\lambda }_n}(\theta )-Q_{{\lambda }_{\infty }}(\theta )=ā{({\lambda }_n)}^{-1}{𝔼}_n{q}^{{\lambda }_n}-ā{({\lambda }_{\infty })}^{-1}𝔼q^{{\lambda }_{\infty }}.$$ (82)

By continuity, $ā({\lambda }_n)\stackrel{p}{\to }ā({\lambda }_{\infty })>0$. Therefore, it suffices to show ${𝔼}_n{q}^{{\lambda }_n}\stackrel{p}{\to }𝔼q^{{\lambda }_{\infty }}$. Because ${𝔼}_n{q}^{{\lambda }_{\infty }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }𝔼q^{{\lambda }_{\infty }}$ by the law of large numbers, it suffices equally well to show that ${𝔼}_n{q}^{{\lambda }_n}-{𝔼}_n{q}^{{\lambda }_{\infty }}\stackrel{p}{\to }0$.

Now fix ε > 0 and take K large enough that 𝔼(m1_m>K) < ε. For λ_n ∈ Λ₁ we have

$$|{𝔼}_n{q}^{{\lambda }_n}-{𝔼}_n{q}^{{\lambda }_{\infty }}|\le |{𝔼}_n(q^{{\lambda }_n}-q^{{\lambda }_{\infty }}){\mathbf{1}}_{m\le K}|+2{𝔼}_{n}m{\mathbf{1}}_{m>K.}$$ (83)

With probability one the second term is eventually less than 2ε. Further, for λ_n ∈ Λ_δ, we have

$$|q_i^{{\lambda }_n}-q_i^{{\lambda }_{\infty }}|=\frac{1}{2}|(z_i^{{\lambda }_n}-z_i^{{\lambda }_{\infty }})({\ell }_i^{{\lambda }_n}+{\ell }_i^{{\lambda }_{\infty }})+(z_i^{{\lambda }_n}+z_i^{{\lambda }_{\infty }})({\ell }_i^{{\lambda }_n}-{\ell }_i^{{\lambda }_{\infty }})|$$ (84)

$$\le |z_i^{{\lambda }_n}-z_i^{{\lambda }_{\infty }}|m_i+\delta \Vert x_i\Vert .$$ (85)

Now, write

$$d_i=|z_i^{{\lambda }_n}-z_i^{{\lambda }_{\infty }}|m_i{\mathbf{1}}_{m_i\le K}.$$ (86)

$z_i^{{\lambda }_n}\ne z_i^{{\lambda }_{\infty }}$ iff u_i lies between a_λn (x_i, y_i) and a_λ∞(x_i, y_i). Hence, conditionally on λ_n and the data, the d_i are mutually independent nonnegative random variables bounded by K with means

$${\mu }_i=|a_{{\lambda }_n}(x_i,y_i)-a_{{\lambda }_{\infty }}(x_i,y_i)|m_i{\mathbf{1}}_{m_i\le K}<\delta K^2$$ (87)

since ∇_λa_λ(x_i, y_i) ≤ ‖x_i‖ < m_i.

Continuing, we have

$$|{𝔼}_n(q^{{\lambda }_n}-q^{{\lambda }_{\infty }}){\mathbf{1}}_{m\le K}|\le {𝔼}_n(d-\mu )+{𝔼}_{n\mu }+\delta {𝔼}_n\Vert x\Vert {\mathbf{1}}_{m\le K}$$ (88)

$$\le {𝔼}_n(d-\mu )+\delta K^2+\delta K.$$ (89)

Conditioning on λ and {(x_i, y_i)}, the first term is a sum of independent zero-mean random variables that are bounded in absolute value by K. By Hoeffding’s inequality,

$$\mathbb{P}\left(\right|\frac{1}{n}\sum _{i=1}^n{d}_i-{\mu }_i|\ge \epsilon |{\lambda }_n,\{(x_i,y_i)\})\le 2\text{exp}[-n{\epsilon }^2/(2K^2)].$$ (90)

Since this bound is deterministic, the same applies to the unconditional probability that 𝔼_n(d − μ) is large. Take δ = ε/(K + K²). With probability tending to 1, λ_n ∈ Λ_δ and the event in (90) holds, in which case

$$|{𝔼}_n(q^{{\lambda }_n}-q^{{\lambda }_{\infty }})|\le 4\epsilon .$$ (91)

Since ε was arbitrary, the proof is complete.

APPENDIX C

PROOF OF THEOREM 6 [DISTRIBUTION OF θ̂ − θ̄(λ)]

By the mean value theorem, we have for each n

$${\nabla }_{\theta }{\mathrm{Q̂}}_{{\lambda }_n}({\mathrm{\theta ̂}}_n)={\nabla }_{\theta }{\mathrm{Q̂}}_{{\lambda }_n}(\mathrm{\theta ̄}({\lambda }_n))+{\nabla }_{\theta }^2{\mathrm{Q̂}}_{{\lambda }_n}({\varphi }_n)({\mathrm{\theta ̂}}_n-\mathrm{\theta ̄}({\lambda }_n)),$$ (92)

where ϕ_n is some convex combination of θ̂_n and θ̄(λ_n). Noting that the LHS is by definition 0 and rearranging, we obtain

$$\sqrt{n}({\mathrm{\theta ̂}}_n-\mathrm{\theta ̄}({\lambda }_n))={\nabla }_{\theta }^2{\mathrm{Q̂}}_{{\lambda }_n}{({\varphi }_n)}^{-1}·\sqrt{n}{\nabla }_{\theta }{\mathrm{Q̂}}_{{\lambda }_n}(\mathrm{\theta ̄}({\lambda }_n)).$$ (93)

If we can show the first factor tends in probability to ${\nabla }_{\theta }^2{Q}_{{\theta }^{*}}{({\theta }^{*})}^{-1}$ and the second tends in distribution to N(0, ā(θ*)⁻¹ J(θ*, θ*)), then by Slutsky’s theorem we have the desired result.

Using the Skorokhod construction define a joint probability space for λ_n such that ${\lambda }_n\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\theta }^{*}$. We will condition on the sequence λ_n and use a triangular array central limit theorem for the random variables

$$g_{ni}=\frac{z_{ni}}{ā({\lambda }_n)}(y_i-\frac{e^{(\mathrm{\theta ̄}({\lambda }_n)-{\lambda }_n)\prime x_i}}{1+e^{(\mathrm{\theta ̄}({\lambda }_n)-{\lambda }_n)\prime x_i}})x_i$$ (94)

$$=\frac{z_{ni}}{ā({\lambda }_n)}{\nabla }_{\theta }\ell (\theta -{\lambda }_n;x_i,y_i){|}_{\theta =\mathrm{\theta ̄}({\lambda }_n)}.$$ (95)

Because λ_n is independent of the data, 𝔼(f(g_ni)|λ_n, z_ni = 1) = 𝔼_λn(f(g_ni)) for any f. The triangular array CLT applies since

$$𝔼(g_{ni}|{\lambda }_n)=0,$$ (96)

$$\text{Var}(g_{ni}|{\lambda }_n)=𝔼[\text{Var}(g_{ni}|{\lambda }_n,z_{ni})|{\lambda }_n]$$ (97)

$$=\mathbb{P}(z_{ni}=1|{\lambda }_n)ā{({\lambda }_n)}^{-2}{\text{Var}}_{{\lambda }_n}({\nabla }_{\theta }\ell (\mathrm{\theta ̄}({\lambda }_n)-{\lambda }_n;x_{ni},y_{ni}))$$ (98)

$$=ā{({\lambda }_n)}^{-1}J(\mathrm{\theta ̄}({\lambda }_n),{\lambda }_n)$$ (99)

$$\stackrel{\mathrm{a}.\mathrm{s}.}{\to }ā{({\theta }^{*})}^{-1}J({\theta }^{*},{\theta }^{*}).$$ (100)

Therefore, defining $S_n=n^{-1/2}{\sum }_{i=1}^n{g}_{ni}$ and Z = N(0, a(θ*)⁻¹ J(θ*, θ*)), the CLT tells us ℙ(S_n ∈ A|λ_n) → ℙ(Z ∈ A) whenever λ_n → θ*, which we assumed occurs with probability 1. By dominated convergence, we also have ℙ(S_n ∈ A) → ℙ (Z ∈ A).

Next we turn to the Hessian. We have ${\mathrm{\theta ̂}}_n\stackrel{p}{\to }{\theta }^{*}$ by Theorem 5, so ${\varphi }_n\stackrel{p}{\to }{\theta }^{*}$ as well. Writing

$$h_i^{\theta ,\lambda }=\frac{e^{(\theta -\lambda )\prime x_i}}{{(1+e^{(\theta -\lambda )\prime x_i})}^2}{x}_i{x}_i^{\prime }{z}_i^{\lambda }$$ (101)

we need to show that

$$ā{({\lambda }_n)}^{-1}{({𝔼}_n{h}^{{\varphi }_n,{\lambda }_n})}^{-1}\stackrel{p}{\to }ā{({\theta }^{*})}^{-1}{(𝔼h^{{\theta }^{*},{\theta }^{*}})}^{-1}.$$ (102)

Note that ${\Vert h_i^{\theta ,\lambda }\Vert }_F\le {\Vert x_i\Vert }^2$, which is integrable; hence ${𝔼}_n{h}^{{\theta }^{*},{\theta }^{*}}\stackrel{p}{\to }𝔼h^{{\theta }^{*},{\theta }^{*}}=H({\theta }^{*},{\theta }^{*})\succ 0$. Since ā is continuous and strictly positive, and ${\lambda }_n\stackrel{p}{\to }{\theta }^{*}$, it suffices to show that

$${\Vert {𝔼}_n{h}^{{\varphi }_n,{\lambda }_n}-{𝔼}_n{h}^{{\theta }^{*},{\theta }^{*}}\Vert }_F\stackrel{p}{\to }0.$$ (103)

Note that $h_i^{{\theta }^{*},{\theta }^{*}}=\frac{1}{4}{x}_i{x}_i^{\prime }$, and define $w_{ni}=\frac{e^{({\varphi }_n-{\lambda }_n)\prime x_i}}{{(1+e^{({\varphi }_n-{\lambda }_n)\prime x_i})}^2}$.

Following the structure of the proof of Proposition 3, take K large enough that 𝔼‖x‖²1_‖x‖>K < ε and truncate the h_i:

$${\Vert {𝔼}_n{h}^{{\varphi }_n,{\lambda }_n}-{𝔼}_n{h}^{{\theta }^{*},{\theta }^{*}}\Vert }_F\le {\Vert {𝔼}_n(h^{{\varphi }_n,{\lambda }_n}-h^{{\theta }^{*},{\theta }^{*}}){\mathbf{1}}_{\Vert x\Vert \le K}\Vert }_F+{\Vert {𝔼}_n(h^{{\varphi }_n,{\lambda }_n}-h^{{\theta }^{*},{\theta }^{*}}){\mathbf{1}}_{\Vert x\Vert >K}\Vert }_F$$ (104)

$$\le K^2{𝔼}_n|w_n{z}_n^{{\lambda }_n}-\frac{1}{4}{z}_n^{{\theta }^{*}}|{\mathbf{1}}_{\Vert x\Vert \le K}+2{𝔼}_n{\Vert x\Vert }^2{\mathbf{1}}_{\Vert x\Vert >K}.$$ (105)

The second term is eventually less than 2ε. Now, $w_{ni}-\frac{1}{4}$ is small, because

$$\left|\frac{d}{d\eta }\right(\frac{e^{\eta }}{{(1+e^{\eta })}^2}\left)\right|=\left|\frac{e^{\eta }(e^{\eta }-1)}{{(1+e^{\eta })}^3}\right|\le \frac{e^{\eta }}{{(1+e^{\eta })}^2}\le \frac{1}{4}.$$ (106)

Hence, by Cauchy–Schwarz

$$|w_{ni}-\frac{1}{4}|\le \frac{1}{4}\Vert {\varphi }_n-{\lambda }_n\Vert \Vert x_i\Vert .$$ (107)

So on the event {max ‖λ_n − θ*‖, ‖ϕ_n − θ*‖ < δ}, we have

$${𝔼}_n|w_n{z}_n^{{\lambda }_n}-\frac{1}{4}{z}_n^{{\theta }^{*}}|{\mathbf{1}}_{\Vert x\Vert \le K}$$ (108)

$$=\frac{1}{2}{𝔼}_n|(z^{{\lambda }_n}-z^{{\theta }^{*}})(w_n+\frac{1}{4})+(z^{{\lambda }_n}+z^{{\theta }^{*}})(w_n-\frac{1}{4})|{\mathbf{1}}_{\Vert x\Vert \le K}$$ (109)

$$\le {𝔼}_n|z^{{\lambda }_n}-z^{{\theta }^{*}}|{\mathbf{1}}_{\Vert x\Vert \le K}+\delta K.$$ (110)

Finally, we can bound the first term exactly as we did in the proof of Proposition 3, defining $d_i=|z_i^{{\lambda }_n}-z_i^{{\theta }^{*}}|K^2{\mathbf{1}}_{\Vert x_i\Vert \le K}$ and μ_i = 𝔼(d_i|x_i, y_i, λ_n) ≤ δK³. The same argument implies ℙ(𝔼_n(d − μ) ≥ ε) ≤ 2 exp[−nε²/(2K⁴)], so as n → ∞ we have with probability approaching 1,

$${\Vert {𝔼}_n(h^{{\varphi }_n,{\lambda }_n}-h^{{\theta }^{*},{\theta }^{*}})\Vert }_F\le {𝔼}_n(d-\mu )+{𝔼}_n\mu +\delta K^3+2{𝔼}_n{\Vert x\Vert }^2{\mathbf{1}}_{\Vert x\Vert >K}$$ (111)

$$\le 3\epsilon +2\delta K^3$$ (112)

so taking δ < ε/K³, the right-hand side is less than 5ε.