Force distribution affects vibrational properties in hard-sphere glasses

Significance

How a liquid becomes rigid at the glass transition is a central problem in condensed matter physics. In many scenarios of the glass transition, liquids go through a critical temperature below which minima of free energy appear. However, even in the simplest glass, hard spheres, what confers mechanical stability at large density is highly debated. In this work we show that to quantitatively understand stability at a microscopic level, the presence of weakly interacting pairs of particles must be included. This approach allows us to predict various nontrivial scaling behavior of the elasticity and vibrational properties of colloidal glasses that can be tested experimentally. It also gives a spatial interpretation to recent, exact calculations in infinite dimensions.

Abstract

We theoretically and numerically study the elastic properties of hard-sphere glasses and provide a real-space description of their mechanical stability. In contrast to repulsive particles at zero temperature, we argue that the presence of certain pairs of particles interacting with a small force f soften elastic properties. This softening affects the exponents characterizing elasticity at high pressure, leading to experimentally testable predictions. Denoting $\mathbf{\mathbb{P}}\left(f\right)\sim f^{{\theta }_e}$, the force distribution of such pairs and ${\varphi }_c$ the packing fraction at which pressure diverges, we predict that (i) the density of states has a low-frequency peak at a scale $\omega *$, rising up to it as $D\left(\omega \right)\sim {\omega }^{2+a}$, and decaying above $\omega *$ as $D\left(\omega \right)\sim {\omega }^{-a}$ where $a=\left(1-{\theta }_e\right)/\left(3+{\theta }_e\right)$ and ω is the frequency, (ii) shear modulus and mean-squared displacement are inversely proportional with $\langle \delta R^2\rangle \sim 1/\mu \sim {\left({\varphi }_c-\varphi \right)}^{\kappa }$, where $\kappa =2-2/\left(3+{\theta }_e\right)$, and (iii) continuum elasticity breaks down on a scale ${\ell }_c\sim 1/\sqrt{\delta z}\sim {\left({\varphi }_c-\varphi \right)}^{-b}$, where $b=\left(1+{\theta }_e\right)/\left(6+2{\theta }_e\right)$ and $\delta z=z-2d$, where z is the coordination and d the spatial dimension. We numerically test (i) and provide data supporting that ${\theta }_e\approx 0.41$ in our bidisperse system, independently of system preparation in two and three dimensions, leading to $\kappa \approx 1.41$, $a\approx 0.17$, and $b\approx 0.21$. Our results for the mean-square displacement are consistent with a recent exact replica computation for $d=\infty$, whereas some observations differ, as rationalized by the present approach.

The emergence of rigidity near the glass transition is a fundamental and highly debated topic in condensed matter and is perhaps most surprising in hard-sphere glasses where rigidity is purely entropic in nature. The rapid growth of relaxation time around a packing fraction ${\varphi }_g\approx 0.58$ suggests that metastable states have appeared in the free-energy landscape, and that activation above barriers is required for the system to flow (1). This scenario is presumably what mode-coupling theory captures (2, 3) and can be rationalized via density functional theory (4) and via the replica method (5). Recently a real-space description of mechanical stability and elasticity in hard-sphere glasses has been proposed (6, 7), which is most easily tested at large pressure, deep in the glass phase. It is based on two results. First, in elastic networks and athermal packings of soft spheres (8–10), mechanical stability is controlled by the mean number of contacts per particle, or coordination z (as already discussed by Maxwell in ref. 11), and the applied compressive strain e (10). As one may intuitively expect, increasing coordination is stabilizing, whereas increasing pressure at fixed coordination is destabilizing. Second, within a long-lived metastable state the vibrational free energy of a hard-sphere system can be approximated as a sum of local interaction terms between pairs of colliding particles, which are said to be in contact. On a time scale that contains many collisions, at high packing fraction the interaction follows approximately $V\left(h\right)\approx -k_{B}T\log h$, where h is the time-averaged distance between two adjacent particles (6, 7). This directly leads to an effective force law $f\left(h\right)\approx k_{B}T/h$ and allows one to map a hard-sphere system near the random close packing ${\varphi }_c$ to a zero-temperature elastic network. These two sets of results yield a stability constraint on the microscopic structure of hard-sphere glasses, which in practice appears to lie very close to saturation (6, 7, 12). Such marginal stability implies the abundance of very soft elastic modes, as confirmed empirically (6, 7, 12–16), and fixes the scaling behavior of elasticity as jamming is approached (7). In particular the particles’ mean-squared displacement was predicted to follow $\langle \delta R^2\rangle \sim {\left({\varphi }_c-\varphi \right)}^{\kappa }$ with $\kappa =1.5$ (7) instead of the naive $\kappa =2$, which would hold in a crystal: Particles in the glass fluctuate much more than the size of their cage (defined as the typical distance between particles), due to the presence of collective soft modes.

Very recently a replica calculation (17, 18) predicted $\kappa =1.41574$ in infinite dimensions, close but different from the prediction of refs. 6 and 7. At ${\varphi }_c$ it also predicted for the force distribution $\mathrm{\mathbb{P}}\left(f\right)\sim f^{{\theta }_f}$ with ${\theta }_f=0.42311$ and for the gap distribution $g\left(h\right)\sim h^{-\gamma }$ with $\gamma =0.41269$. Some of these latter results are consistent, and some differ, from an earlier analysis based on the stability of jammed packings (at ${\varphi }_c$) toward changes of their network of contacts (19, 20). In these works γ was argued and numerically shown to be related to the force distribution exponents ${\theta }_e$ and ${\theta }_{\ell }$, characterizing respectively two kinds of contacts at low forces (20) (see Hard Spheres). Here we propose a resolution of these issues: Heterogeneity in contact strength was neglected in refs. 6 and 7, but the prevalence of weak forces in hard-sphere systems corrects scaling exponents and leads to the scaling relation $\kappa =2-2/\left(3+{\theta }_e\right)$, consistent with the result of ref. 17, if ${\theta }_f={\theta }_e$ in dimension $d=\infty$. We compute the associated modification in the scaling of elastic properties as $\varphi \to {\varphi }_c$. Furthermore, we argue that some key properties of packing differ in finite and infinite dimensions, so that ${\theta }_f={\theta }_{\ell }$ in $d=\mathrm{2,3}$ while ${\theta }_f={\theta }_e$ in $d=\infty$. In general, our approach leads to a description of the structure of packings in terms of four exponents related by three scaling relations.

This work is organized as follows. In Elastic Networks, we present a variational argument for the density of vibrational modes in weakly coordinated networks with stiffness heterogeneity. We also use scaling arguments to compute the shear modulus and the mean-squared displacement. In Effective Medium Theory, we confirm these predictions using a standard mean-field approximation, and furthermore predict the length scale below which continuum elasticity breaks down in such systems. In Hard Spheres, we show how these results apply to colloidal glasses and discuss the subtle issue associated with the existence of two kinds of contacts at low forces in sphere packings. We also present numerical results supporting our views. In Comparison with Replica Theory in d = ∞ and Conclusion, we compare our results with replica calculations and discuss prospects for experimental tests in colloidal systems.

Elastic Networks

We consider an elastic network of N points of mass m, connected by $N_c$ springs, of coordination $z=2N_c/N$, in spatial dimension d. The quadratic expansion of the elastic energy for an imposed displacement field $|\delta R\rangle$ follows (21, 22):

$$\delta E\equiv \frac{1}{2}\langle \delta R|\mathrm{ℳ}|\delta R\rangle =\frac{1}{2}{\displaystyle \sum _{\beta }{k}_{\beta }\delta R_{\beta }^{\parallel 2}-\frac{f_{\beta }}{r_{\beta }}\delta R_{\beta }^{\perp 2}},$$ [1]

where the sum is over springs β. Here $r_{\beta }$, $k_{\beta }$, and $f_{\beta }$ are the spring length, stiffness, and force (chosen positive for a repulsive interaction) and $\delta R_{\beta }^{\parallel }$ and $\delta R_{\beta }^{\perp }$ are, respectively, the magnitude of displacements parallel and perpendicular to the spring β, i.e., $\delta R_{\beta }^{\parallel }=\left(\delta {\overrightarrow{R}}_i-\delta {\overrightarrow{R}}_j\right)\cdot {\overrightarrow{n}}_{\beta }$ and $\delta R_{\beta }^{\perp }=\left|\delta {\overrightarrow{R}}_i-\delta {\overrightarrow{R}}_j-{\overrightarrow{n}}_{\beta }\delta R_{\beta }^{\parallel }\right|$, where ${\overrightarrow{n}}_{\beta }$ is a unit vector along the spring β.

We assume that $r_{\beta }$ are narrowly distributed about their mean $\langle r_{\beta }\rangle =\sigma$, which defines our unit length, and introduce $k_c\equiv \langle k_{\beta }\rangle$ and ${\omega }_c=\sqrt{k_c/m}$. Eq. 1 defines the stiffness matrix $\mathrm{ℳ}$, which is positive definite in a stable configuration. The eigenvalues of $\mathrm{ℳ}$ are $\lambda =m{\omega }^2$, where the ω are the frequencies of vibrational modes, of density $D\left(\omega \right)$.

Variational Argument.

First we consider the springs at rest length, so that all $f_{\beta }=0$ and only the parallel term in Eq. 1 is present. Let $\delta z\equiv z-z_c$ with $z_c=2d$. As pointed out by Maxwell, if $Nd>N_c$ (or equivalently $\delta z<0$), then it is clear from Eq. 1 that there are at least $Nd-N_c$ displacement fields with no restoring force ($\delta E=0$), the so-called floppy modes. They are solutions to the set of linear equation $\delta R_{\beta }^{\parallel }=0$ at each spring β. We assume that the shape of the stiffness distribution $\mathrm{\mathbb{P}}\left(k\right)$ is independent of z, and wish to compute the scaling properties of $D\left(\omega \right)$ as $\delta z\to 0^{+}$. Here we sketch our arguments and present our main results; details appear in Supporting Information.

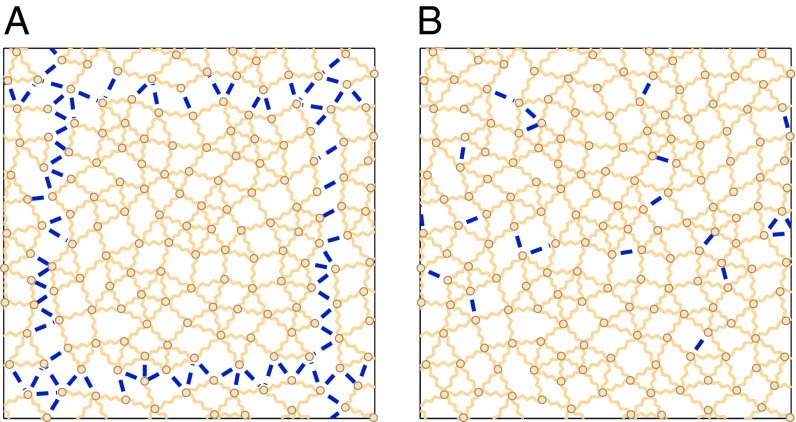
Our strategy to estimate $D\left(\omega \right)$ is to build trial modes which are orthonormal displacement fields with small energy. Using the fact that $\mathrm{ℳ}$ is positive definite then allows one to bound from below the number of eigenvalues below some threshold, leading to a lower bound on $D\left(\omega \right)$. This strategy was used in refs. 10 and 23, where trial modes were constructed using the following idea. A system at $\delta z=0$ has exactly the number of contacts $N_c$ necessary to maintain its mechanical rigidity. This implies that each contact cut creates one floppy mode. By cutting the system into compact regions of size L, as shown in Fig. 1A, one cuts a fraction $q\sim 1/L$ of bonds, thus inducing a density of floppy modes q. These modes can be distorted to lead to trial modes of frequency $\omega \left(q\right)\sim {\omega }_{c}q$ in the original, uncut system (23). A variational inequality (24) implies that the number of modes per particle with frequency smaller than ω, $\mathcal{N}\left(\omega \right)$, is then $\gtrsim q\left(\omega \right)$. Because $\mathcal{N}\left(\omega \right)\propto {\displaystyle {\int }_0^{\omega }d\omega D\left(\omega \right)\sim \omega D\left(\omega \right)}$, one gets $D\left(\omega \right)\gtrsim {\omega }^0/{\omega }_c$, implying that the vibrational spectrum does not vanish at zero frequency at the Maxwell bound.

Fig. 1.

Illustrative diagram of cutting argument, showing cut bonds in blue (thick lines). (A) Bonds are cut around blocks of size $L\times L$, a useful procedure when $\alpha >0$. (B) When $\alpha <0$, the variational argument is improved by cutting instead the fraction q of weakest bonds.

If $\delta z>0$, then the system is overconstrained, and when a fraction q of bonds are cut, the density of induced floppy modes is $q-\delta z/z_c$. This leads to a cutoff frequency ${\omega }^{\mathrm{\ast }}\sim {\omega }_c\delta z$, such that $D\left(\omega \right)\gtrsim 1/{\omega }_c$ above ${\omega }^{\mathrm{\ast }}$, as numerically observed (8–10, 25, 26).

We now show that if the distribution of stiffnesses is broad enough, then the above bound is not saturated. In this case, we can improve the variational argument by creating a different set of trial modes (illustrated in Fig. 1B); we cut a fraction q of the weakest links, and use the induced floppy modes. We then make the key assumption that these floppy modes do not decay appreciably with distance from the broken bonds, but extend in the entire system, displacing particles by some characteristic amplitude. We shall see below that for hard spheres, our assumption only holds for a fraction of the contacts at low force.

We assume that the distribution of stiffnesses follows $\mathrm{\mathbb{P}}\left(k\right)\sim k^{\alpha }/k_c^{\alpha +1}$ at low stiffnesses, where $\alpha >-1$. The fraction q of the weakest extended bonds then have a characteristic stiffness $k_0\sim k_c{q}^{1/\left(1+\alpha \right)}$. In the original system, the induced floppy modes stretch or compress the fraction q of weak springs of characteristic stiffness $k_0$, leading to an energy $E\sim q{k}_0$ as discussed in Supporting Information. This leads to a characteristic frequency

$$\omega \left(q\right)\sim {\omega }_c{q}^{\frac{2+\alpha }{2+2\alpha }}.$$ [2]

The variational inequality then implies

$$D\left(\omega \right)\gtrsim \frac{1}{{\omega }_c}{\left(\frac{\omega }{{\omega }_c}\right)}^{\frac{\alpha }{2+\alpha }}.$$ [3]

As above, when $\delta z>0$, the system is overconstrained and there is a frequency scale

$${\omega }^{\mathrm{\ast }}\sim {\omega }_c{\left(\frac{\delta z}{z_c}\right)}^{\frac{2+\alpha }{2+2\alpha }},$$ [4]

above which [3] applies. These are our central results: At the Maxwell threshold ($\delta z=0$), when weak interactions are abundant ($\alpha <0$), the density of states must diverge at zero frequency, with a nontrivial exponent. When the coordination is larger ($\delta z>0$), the scaling for $D\left(\omega \right)$, [3], holds above the characteristic frequency ${\omega }^{\mathrm{\ast }}$.

For $\alpha >0$ the new bound is not useful and the previous argument of ref. 23 applies. Note that in all cases we consider $q\ll 1$ so that $\omega \ll {\omega }_c$.

Assuming harmonic dynamics, we can obtain from [3] a bound on the particles’ mean-squared displacement $\langle \delta R^2\rangle$:

$$\frac{k_c\langle \delta R^2\rangle }{k_{B}T}={\omega }_c^2{\displaystyle \int \frac{D\left(\omega \right)}{{\omega }^2}d\omega }\gtrsim {\left(\frac{{\omega }^{\mathrm{\ast }}}{{\omega }_c}\right)}^{\frac{-2}{2+\alpha }}.$$ [5]

Using previous results on floppy mode displacements, the shear modulus can also be estimated. As discussed in Supporting Information, one finds

$$\mu \sim k_0\sim k_c\delta z^{\frac{1}{1+\alpha }}.$$ [6]

Role of Prestress.

So far we have considered stress-free elastic networks. The presence of a compressive force in the bonds reduces the modes’ frequency, as implied by Eq. 1, and can lead to an elastic instability. It was argued and checked numerically in ref. 10 that the strongly scattered modes that appear above ${\omega }^{\mathrm{\ast }}$ have large relative displacements, of order of the displacement itself: $\left|\delta R_{\beta }^{\perp }\right|\sim \left|\delta {\overrightarrow{R}}_i\right|$. Following Eq. 1, this implies that some soft modes will be shifted to a frequency ${\omega }_0$ satisfying $\delta E\equiv m{\omega }_0^2=m{\omega }^{\mathrm{\ast }2}-A{f}_c$, where $f_c$ is the characteristic compressive force and A is a numerical constant. Stability requires $\delta E>0$, implying

$${\omega }^{\mathrm{\ast }}\gtrsim {\omega }_c\sqrt{e},$$ [7]

where we have defined the contact strain $e\equiv f_c/k_c$. Using [4], this becomes $\delta z\gtrsim e^{\left(1+\alpha \right)/\left(2+\alpha \right)}$, extending the previous result $\delta z\gtrsim \sqrt{e}$ (10) to the case $\alpha <0$. In packings of particles, $e\propto \left|\varphi -{\varphi }_c\right|$, and the latter bound was argued to be saturated, based on dynamical considerations (6, 7, 10).

Effective Medium Theory

All of the above predictions can be derived and extended with effective medium theory (EMT), a mean-field approximation that treats disorder in a self-consistent way (27–32). EMT has been shown to give quantitatively correct values for scaling exponents related to the vibrational spectrum and heat transport properties of frictionless packings (29, 31). In EMT, a random elastic network, such as depicted in Fig. 1, is modeled by a regular lattice with effective frequency-dependent spring constants. Here we follow the EMT developed in ref. 31, which includes the effect of forces in Eq. 1. In ref. 31, the randomness in the interaction between two nodes was limited to the presence or absence of a spring; when a spring was present, its stiffness was always identical. Here we relax this assumption and allow a full distribution of stiffnesses, behaving as $\mathrm{\mathbb{P}}\left(k\right)\sim k^{\alpha }$ for small k, and allow a distribution of contact forces, $\mathrm{\mathbb{P}}\left(f\right)\sim f^{{\theta }_f}$ at small f. Details of the EMT are presented in Supporting Information.

The EMT confirms that when $\alpha >0$, previous results of refs. 10 and 31 are obtained. When $\alpha <0$, in addition to confirming the scaling results presented above, EMT gives the form of the complex shear modulus and density of states when $\delta z$ is small, and can be used to extract other vibrational and heat transport properties. In general, two frequency scales are predicted, as in the variational argument: ${\omega }^{\mathrm{\ast }}$ and ${\omega }_0={\omega }^{\mathrm{\ast }}\sqrt{1-e/e_c}$, where $e_c\sim \delta z^{\left(2+\alpha \right)/\left(1+\alpha \right)}$ is the contact strain at elastic instability (31). For a marginally stable material, $e\approx e_c$ and therefore ${\omega }_0/{\omega }^{\mathrm{\ast }}\ll 1$. Above its peak at ${\omega }^{\mathrm{\ast }}$, EMT predicts that $D\left(\omega \right)$ decays as $D\left(\omega /{\omega }_c\right)\sim {\left(\omega /{\omega }_c\right)}^{\alpha /\left(2+\alpha \right)}$, in agreement with [3], with a logarithmic correction in $d=2$. Between ${\omega }_0$ and ${\omega }^{\mathrm{\ast }}$, EMT predicts

$$D\left(\omega \right)\sim \frac{1}{{\omega }_c}{\left(\frac{\omega }{{\omega }_c}\right)}^{1+\frac{2}{\alpha +2}}{\left(\frac{{\omega }^{\mathrm{\ast }}}{{\omega }_c}\right)}^{\frac{-4}{\alpha +2}}.$$ [8]

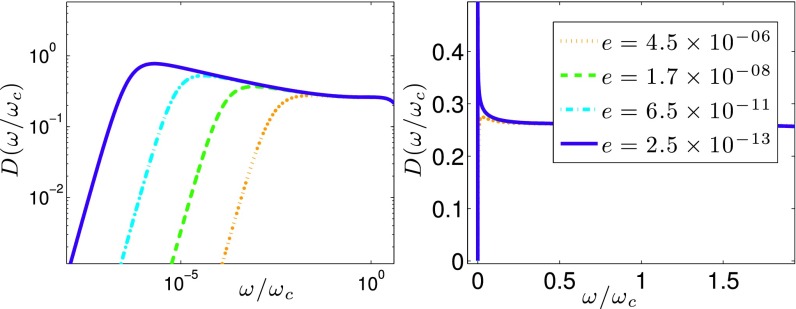
A numerical solution of the leading-order EMT equation for a marginally stable material in $d=2$ gives the result shown in Fig. 2, where we have taken $\alpha =-0.30$. The visible curvature is due to logarithmic corrections, which are only present in $d=2$.

Fig. 2.

EMT prediction for the density of states $D\left(\omega \right)$ for a marginally stable material in $d=2$ with $\alpha =-0.30$, at indicated values of $e={\varphi }_c-\varphi$, in (Left) log–log axes and (Right) linear axes. As discussed in the text, this corresponds to a hard disk glass with ${\theta }_e=0.41$. The peak appears at the frequency scale ${\omega }^{\mathrm{\ast }}\sim {\omega }_c\sqrt{e}$.

Regarding the shear modulus, EMT confirms the scaling 6, and in addition we find the dependence on $e/e_c$. At fixed $\delta z$, we find that μ drops by a finite factor at elastic instability, relative to its unstressed value. Finally, EMT predicts that modes at ${\omega }^{\mathrm{\ast }}$ have a scattering length ${\ell }_c\sim \delta z^{-1/2}$, also characterizing the response to a point force (33).

Hard Spheres

The above results on elastic networks can be applied to the free energy of hard spheres within a metastable state, and near maximum packing at ${\varphi }_c$. To do so, we consider a mesoscopic time scale τ, much larger than the typical interval between collisions, ${\tau }_C$, and define a contact network by those particles that collide on the time scale τ (6, 7, 10). Using the fact that the contact network at ${\varphi }_c$ is isostatic, one can show that the Helmholtz free energy of the metastable state is well approximated by a sum of two-body effective potentials, which follow

$$V\left(h\right)\approx -k_{B}T\log h,$$ [9]

where h is the time-averaged gap between contacting particles. Hence in link β the force $f_{\beta }\approx k_{B}T/h_{\beta }$ and the stiffness $k_{\beta }\approx k_{B}T/h_{\beta }^2$. It was previously checked in simulations that this effective potential is very closely followed near ${\varphi }_c$, and in particular deviations are less than 5% within the glass phase (6, 7). We therefore assume that the effective potential is fixed and independent of z.

Although missing from many theoretical approaches (5, 34), the distribution of contact forces at ${\varphi }_c$ is known empirically to follow $\mathrm{\mathbb{P}}\left(f\right)\sim f^{{\theta }_f}$ at small f, with ${\theta }_f\approx 0.2$ (20, 35). This directly yields a diverging distribution of stiffnesses: $\mathrm{\mathbb{P}}\left(k\right)=\mathrm{\mathbb{P}}\left(f\right)df/dk\sim k^{\alpha }$, with $\alpha =-\left(1-{\theta }_f\right)/2<0$. Hence there are indeed very many contacts with a weak stiffness. However, to apply our earlier results, we have also assumed in the variational argument that each opened weak link induces an extended mode that does not decay appreciably with distance. This condition leads to a subtlety in the exponent α.

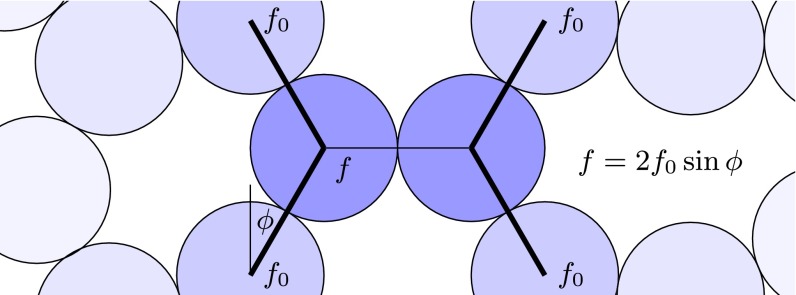
In ref. 20 it was observed that when contacts are opened from hard-sphere packings at ${\varphi }_c$, there are in addition to the extended modes discussed above, also localized modes, i.e., deformations that decay on the scale of a few grains. Such localized modes occur because of local correlations in the structure, as illustrated in Fig. 3. In Supporting Information, we show that the variational argument is not improved by including the localized contacts, and therefore we want to consider only the extended type. In $d=2$ and $d=3$, the distribution of localized contacts was observed to follow $f^{{\theta }_{\ell }}$ with ${\theta }_{\ell }\approx 0.17$, whereas that of the extended contacts follows $f^{{\theta }_e}$ with ${\theta }_e\approx 0.44$ (20). Because the localized contacts are more numerous, the distribution of forces follows $\mathrm{\mathbb{P}}\left(f\right)\sim f^{{\theta }_f}$ with ${\theta }_f={\theta }_{\ell }$. However, only the extended contacts can be included in our theory, therefore we have $\alpha =-\left(1-{\theta }_e\right)/2$.

Fig. 3.

Illustration of a local configuration of particles that gives rise to small displacements when opening the central horizontal contact. Line thickness represents, schematically, force magnitude in the central region. Even if the force $f_0$ in the surrounding contacts is on the order of the mean force, $f_0\sim \langle f\rangle$, the force in the horizontal contact can be small if the angle ϕ is small, and displacements resulting from opening that contact will be of order $\delta R\sim \sin \left(\varphi \right)$.

We can now present our results for hard spheres. Geometrically, the characteristic gap $h_c\sim {\varphi }_c-\varphi$ so that the characteristic force and stiffness are, respectively, $f_c\sim k_{B}T/h_c$ and $k_c\sim k_{B}T/h_c^2$. Stability requires that the Hessian is positive-definite, and therefore following [7] that ${\omega }^{\mathrm{\ast }}\gtrsim {\omega }_c{\left(f_c/k_c\right)}^{1/2}\sim {\left({\varphi }_c-\varphi \right)}^{-1/2}$, a result identical to the previous approach (6, 7) neglecting stiffness heterogeneity. In refs. 7 and 12 this bound was observed to be saturated, and here we assume such marginal stability, ${\omega }^{\mathrm{\ast }}/{\omega }_c\sim {\left({\varphi }_c-\varphi \right)}^{1/2}$. From [3–6] and [8] we then deduce

$$D\left(\omega \right)\sim \{\begin{array}{ll}{\omega }^{2+a}\hfill & \mathrm{for}\hspace{1em}\omega <{\omega }^{\mathrm{\ast }}\hfill \\ {\omega }^{-a}\hfill & \mathrm{for}\hspace{1em}{\omega }^{\mathrm{\ast }}<\omega \ll {\omega }_c\hfill \end{array}$$ [10]

$$\langle \delta R^2\rangle \sim \frac{1}{\mu }\sim {\left({\varphi }_c-\varphi \right)}^{\kappa }$$ [11]

$$\delta z\sim {\left({\varphi }_c-\varphi \right)}^{2b},$$ [12]

where

$$a=\frac{1-{\theta }_e}{3+{\theta }_e},\hspace{1em}b=\frac{1+{\theta }_e}{6+2{\theta }_e},\hspace{1em}\kappa =\frac{4+2{\theta }_e}{3+{\theta }_e}.$$ [13]

Using that the pressure $p\sim f_c$, our prediction for $\delta z\left(p\right)$ appears satisfied in recent simulations (35) if it is assumed that the contact network corresponds to those particles closer than a characteristic gap $h^{†}$ where $g\left(h\right)$ changes behavior. In Supporting Information, F. Effect of Change of Stiffness Distribution with ϕ, we argue that these results are not changed if the evolution of $\mathrm{\mathbb{P}}\left(k\right)$ with packing fraction is taken into account.The new scaling relation 11 relates two experimentally accessible quantities, $\langle \delta R^2\rangle$ and ${\varphi }_c-\varphi$, but through an exponent κ that depends on ${\theta }_e$, which is not easily measurable. In refs. 19 and 20, stability of jammed packings at ${\varphi }_c$ was shown to relate the exponent γ describing the distribution of gaps between particles, $g\left(h\right)\sim h^{-\gamma }$ (20, 35–37), and the exponents ${\theta }_e$ and ${\theta }_{\ell }$. In particular, triggering one of these contact-opening excitations can lead to the rewiring of the contact network. Stability of the system to extensive avalanches of rewiring was shown to imply (19, 20)

$$\gamma \ge \frac{1-{\theta }_{\ell }}{2}$$ [14]

$$\gamma \ge \frac{1}{2+{\theta }_e}.$$ [15]

In ref. 20 it was observed that contact-opening excitations in packings are marginally stable, so that the bounds 14 and 15 are satisfied with equality, with numerical values $\gamma \approx 0.4$, ${\theta }_{\ell }\approx 0.17$, and ${\theta }_e\approx 0.44$. Saturation of [15] was recently proven for certain dynamics (38). Assuming such marginal stability, it follows that ${\theta }_f={\theta }_{\ell }<{\theta }_e$ and the exponent ${\theta }_e$ can be determined from ${\theta }_e=2{\theta }_f/\left(1-{\theta }_f\right)\approx 0.41$, a value consistent with the direct measurement 0.44. [11], [14], and [15] lead to a description of jammed packings and glasses based on four exponents, with three scaling relations between them. We have in particular $\kappa =2/\left(1+\gamma \right)$, both sides of which can be measured independently.

Comparison with Numerics

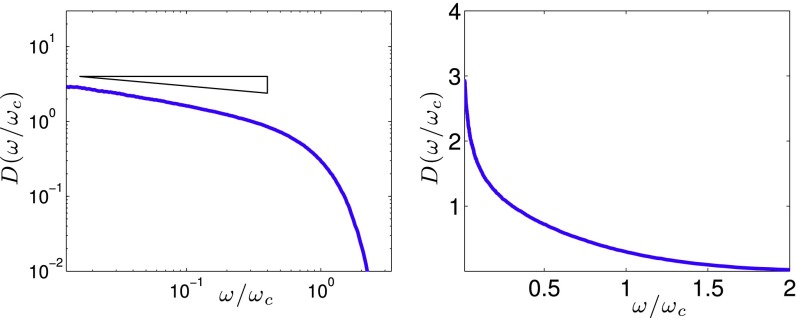
To confirm the prediction that $D\left(\omega \right)$ is not flat but scales with frequency as jamming is approached from the hard-sphere side, we perform numerical simulations of a hard-sphere glass in $d=2$, at pressure $p={10}^{12}{k}_{B}T$, and volume fraction $\varphi \approx 0.83$ (details are in Supporting Information). The density of states $D\left(\omega \right)$ can be computed by identifying a contact network via time averaging as done in refs. 6 and 7. Our result for the largest pressure is shown in Fig. 4, confirming the presence of a weak divergence of $D\left(\omega \right)$ with frequency. The exponent appears close to that predicted by [3], but larger simulations are needed, preferably in $d=3$, to avoid logarithmic corrections. We note that this prediction could be tested in colloidal systems using static pair correlation to extract $\mathrm{ℳ}$ and $D\left(\omega \right)$ (12–16).

Fig. 4.

Numerical density of states $D\left(\omega \right)$ for a hard-sphere glass in $d=2$, at pressure $p={10}^{12}$, in (Left) log–log axes and (Right) linear axes. The triangle has the predicted slope $-0.17$, assuming ${\theta }_e=0.41$, as discussed in the main text. The characteristic frequency ${\omega }^{\mathrm{\ast }}$ is expected to be $\sim {10}^{-6}{\omega }_c$, outside the accessible numerical range at this pressure.

Comparison with Replica Theory in $d=\infty$

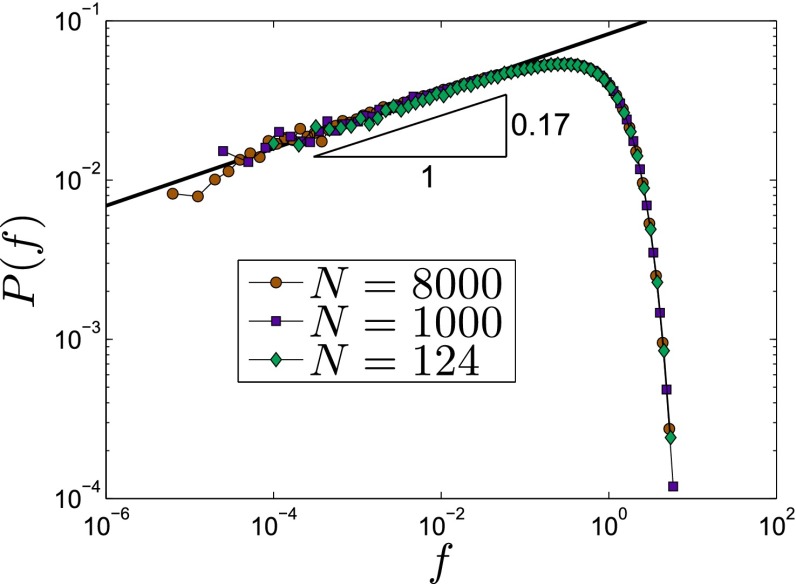
A very recent replica computation (17, 18, 39, 40) was used to compute exponents in $d=\infty$ to arbitrary precision, and results in $\gamma =0.41269$, $\kappa =1.41574$, and ${\theta }_f=0.42311$. These values are consistent with our prediction $\kappa =2/\left(1+\gamma \right)$, which appears to be exactly satisfied. However, the numerical value we found previously (20, 41) for ${\theta }_f\approx 0.17$ in two and three dimensions differs from the replica computation at $d=\infty$. It was argued based on numerics (35) that exponents weakly depend on spatial dimensions up to $d=10$, leading to the suggestion that dimension does not play a role. The same work also reported that ${\theta }_f$ depends somewhat on system preparation. However, the statistics in that work are very limited (one single configuration for each dimension probed). To check that our value of ${\theta }_f$ is not due to the specific methods we used (in ref. 41, results were obtained in two dimensions by shear-jamming hard disks, whereas in ref. 20 hard spheres were compressed in an overdamped medium), we repeat the measurement of force distribution by decompressing soft spheres as done in ref. 35, but with much higher statistics for the dimension considered. Fig. 5 shows $\mathrm{\mathbb{P}}\left(f\right)$ in three dimensions, and again we find ${\theta }_f=0.17\pm 0.02$ (details in Supporting Information). Our results therefore support that system preparation does not affect the exponent ${\theta }_f$, and that its value is indeed about 0.17 for the bidisperse system used. Note that for monodisperse packings in three dimensions our numerics suggest a slightly larger exponent ${\theta }_f\approx 0.23$ as shown in Supporting Information.

Fig. 5.

Probability distribution of forces $\mathrm{\mathbb{P}}\left(f\right)$ for isostatic packings of soft spheres at indicated system sizes, showing that $\mathrm{\mathbb{P}}\left(f\right)\sim f^{{\theta }_f}$ at small f, with an exponent ${\theta }_f=0.17$.

The value for ${\theta }_f$ in $d=\infty$ is therefore distinct from its value in $d=\mathrm{2,3}$, and our relation 14 is not satisfied in $d=\infty$. This is puzzling, because γ appears to be independent of dimension (20, 35). To resolve this dilemma, note that [15] is also exactly satisfied by the $d=\infty$ result if ${\theta }_f={\theta }_e$. This suggests a simple reconciliation: If it is assumed that localized excitations do not exist for $d=\infty$, then ${\theta }_f={\theta }_e$, and one is left with three exponents constrained by two scaling relations: [15] (where ${\theta }_f={\theta }_e$), and [11], both exactly satisfied in the replica calculation. The scaling description we propose based on the marginality of real-space excitations (both linear and nonlinear) is thus fully consistent with the replica calculation, as these two scaling relations are satisfied.

The fact that localized excitations appear to be absent in large dimension seems plausible, as their existence depends on the presence of local arrangements of particles that are very soft (illustrated in Fig. 3), which may become unlikely when each particle shares many contacts. This situation may be similar to the behavior of rattlers, i.e., particles which are trapped in a packing but do not contribute to mechanical stability. The fraction of rattlers is observed to decay exponentially with d (35), so that in large dimension, it is extremely rare to find a gap that is large enough to hold a particle. A similar decay may occur for localized excitations. This could be checked by explicit enumeration of localized contacts, as described in ref. 33.

Conclusion

We have shown that the stability of hard-sphere glasses is affected by heterogeneity in contact strengths. Our numerics on the force distribution exponent ${\theta }_f$, together with the marginal stability relations described above, support that the key exponent ${\theta }_e\approx 0.41$ in $d=2$ and $d=3$, independent of system preparation. This yields specific predictions for the exponents (13):

$$a=0.17,\hspace{1em}b=0.21,\hspace{1em}\kappa =\mathrm{1.41.}$$ [16]

If localized excitations are absent in large dimension, then our results are fully consistent with the replica theory valid for $d=\infty$; in this case the exponent ${\theta }_e=\mathrm{0.42311..}$ and the exponents 16 may change in their final digit.

Our scaling predictions on $D\left(\omega \right)$, $\langle \delta R^2\rangle$, and μ, Eqs. 10 and 11, may be tested experimentally in colloidal systems. From the covariance matrix of particle displacements, ${\mathcal{C}}_{ij}\equiv \langle \delta {\overrightarrow{R}}_i\delta {\overrightarrow{R}}_j\rangle$, one may define a stiffness matrix ${\mathrm{ℳ}}_{ij}\equiv {\left(m_i{k}_{B}T\right)}^{-1}{\mathcal{C}}_{ij}^{-1}$. Provided the system remains trapped in a metastable state for the duration of the experiment, and assuming that states are sampled according to equipartition, the stiffness matrix corresponds to that of a system interacting with an effective potential, which for hard spheres is [9]. Given sufficient temporal resolution, one can also extract the effective density of states from displacement autocorrelations (42). This procedure has been carried out in simulations (6, 7, 43) and experiments (13–15), confirming the presence of a peak in $D\left(\omega \right)$ at low frequency.

When $\varphi <{\varphi }_c$, the hard-sphere systems considered in this work are a limiting case of more realistic soft potentials in the regime when cage-breaking rearrangements are rare. This occurs when the temperature $k_{B}T$ is much smaller than the elastic energy ε needed to overlap particles by the characteristic gap in the system, thus facilitating rearrangement (12). For commonly studied harmonic soft spheres, $\mathit{ϵ}\sim k{\left({\varphi }_c-\varphi \right)}^2$, where k is a stiffness, this gives the hard-sphere regime as $T\mathrm{\lesssim }{\left({\varphi }_c-\varphi \right)}^2$, as observed (12, 42, 44). The peak in $D\left(\omega \right)$ that we predict should appear at small ${\varphi }_c-\varphi$ is indeed observed in this regime (12, 42, 44). It is also observed that $D\left(\omega \right)$ changes shape at larger T. This expected crossover from hard- to soft-sphere behavior corresponds to departures from [9], and will be discussed elsewhere.

Overall, our approach leads to a description of jamming in finite dimensions based on the marginal stability of three distinct types of excitations, both linear and nonlinear. It remains to be seen if plastic flow under shear and thermally activated process near the glass transition can be expressed in terms of the relaxation of these excitations.