Static network structure can stabilize human cooperation

Significance

Human populations are both extremely cooperative and highly structured. Mathematical models have shown that fixed network interaction structures can lead to cooperation under certain conditions, by allowing cooperators to cluster together. Here, we provide empirical evidence of this phenomenon. We explore how different fixed social network structures can promote cooperation using economic game experiments. We find that people cooperate at high stable levels, as long as the benefits created by cooperation are larger than the number of neighbors in the network. This empirical result is consistent with a rule predicted by mathematical models of evolution. Our findings show the important role social networks can play in human cooperation and provide guidance for promoting cooperative behavior.

Abstract

The evolution of cooperation in network-structured populations has been a major focus of theoretical work in recent years. When players are embedded in fixed networks, cooperators are more likely to interact with, and benefit from, other cooperators. In theory, this clustering can foster cooperation on fixed networks under certain circumstances. Laboratory experiments with humans, however, have thus far found no evidence that fixed network structure actually promotes cooperation. Here, we provide such evidence and help to explain why others failed to find it. First, we show that static networks can lead to a stable high level of cooperation, outperforming well-mixed populations. We then systematically vary the benefit that cooperating provides to one’s neighbors relative to the cost required to cooperate (b/c), as well as the average number of neighbors in the network (k). When b/c > k, we observe high and stable levels of cooperation. Conversely, when b/c ≤ k or players are randomly shuffled, cooperation decays. Our results are consistent with a quantitative evolutionary game theoretic prediction for when cooperation should succeed on networks and, for the first time to our knowledge, provide an experimental demonstration of the power of static network structure for stabilizing human cooperation.

Human societies, in both ancient and modernized circumstances, are characterized by complex networks of cooperative relationships (1–10). These cooperative interactions, where individuals incur costs to benefit others, increase the greater good but are undercut by self-interest. How, then, did the selfish process of natural selection give rise to cooperation, and how might social arrangements or institutions foster cooperative behavior? Evolutionary game theory has offered various explanations, in the form of mechanisms for the evolution of cooperation(10). For example, theory predicts (and experiments confirm) that repeated interactions between individuals and within groups can promote cooperation (11–22), as can competition between groups (23–26).

However, one important class of theoretical explanations remains without direct experimental support: the prediction that static (i.e., fixed) network structure should have an important effect on cooperation (27–40). When interactions are structured, such that people only interact with their network “neighbors” rather than the whole population, the emergence of clustering (or “assortment”) is facilitated. Clustering means that cooperators are more likely to interact with other cooperators, and therefore to preferentially receive the benefits of others’ cooperation. Thus, clustering increases the payoffs of cooperators relative to defectors and helps to stabilize cooperation. Across a wide array of model details and assumptions, theoretical work has shown that static networks can promote cooperation, making spatial structure one of the most studied mechanisms in the theory of the evolution of cooperation in recent years (27–40).

However, numerous laboratory experiments have found that static networks do not increase human cooperation relative to random mixing (41–50) [in contrast to dynamic networks, where players can make and break ties, which have been shown to promote cooperation experimentally (42, 46, 51)]. One explanation for these findings is that static networks cannot maintain assortment because humans often spontaneously switch strategies (41). This conclusion is a pessimistic one for the large body of theoretical work demonstrating the success of cooperation on such networks.

Here, we propose an alternative explanation. A central theoretical result is that networks do not promote cooperation in general. Rather, specific conditions must be met before cooperation is predicted to succeed. Thus, prior experiments may have failed to find a positive effect of static networks on cooperative behavior because they involved particular combinations of payoffs and network structures that were, in fact, not conducive to cooperation.

To assess this possibility, we conduct a set of laboratory experiments using artificial social networks. We arrange subjects on a ring connected to k/2 neighbors on each side (resulting in k total neighbors in the network; Fig. 1) and have them play a series of Prisoner’s Dilemma games. In each game, they can defect (D) by doing nothing or cooperate (C) by paying a cost of c = 10k units to give each of the k neighbors a benefit of b units (they must choose a single action, C or D, rather than choosing different actions toward each neighbor). Following each decision, subjects are informed of the decisions of each of their neighbors, as well as the total payoff they and each neighbor earned for the round.

Fig. 1.

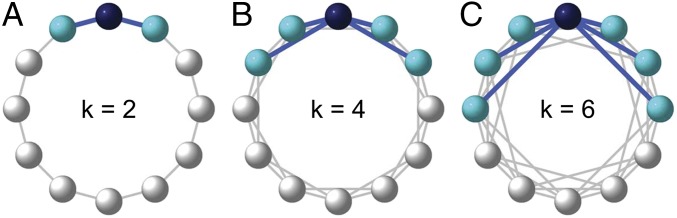
Examples of the network structure for the k = 2 (A), k = 4 (B), and k = 6 (C) cases. Consider the topmost player as the ego (in dark blue); her links are highlighted in blue, and her neighbors are colored light blue.

Our experiments take inspiration from recent work in evolutionary game theory predicting that in static networks, cooperation will be favored over time if and only if the condition b/c > k is satisfied (33, 37); discussion of the derivation of this condition, which arises from a model where players use fixed strategies (C or D) and then learn by imitating successful neighbors, is provided in SI Appendix. We therefore experimentally test (i) whether stable cooperation emerges in networks satisfying the b/c > k condition and (ii) whether, as a result, networked interactions promote cooperation relative to well-mixed populations when b/c > k.

Results

In experiment 1, we fix b/c = 6 and k = 2, and recruit n = 109 students from Yale University to play 50 rounds of our game (8.4 subjects per session on average). Subjects are assigned either to a “network” treatment, in which their position on the ring is held constant every round, or a “well-mixed” treatment, in which their position is randomly shuffled every round (subjects in the well-mixed treatment are informed of this shuffling). Further details are provided in Methods.

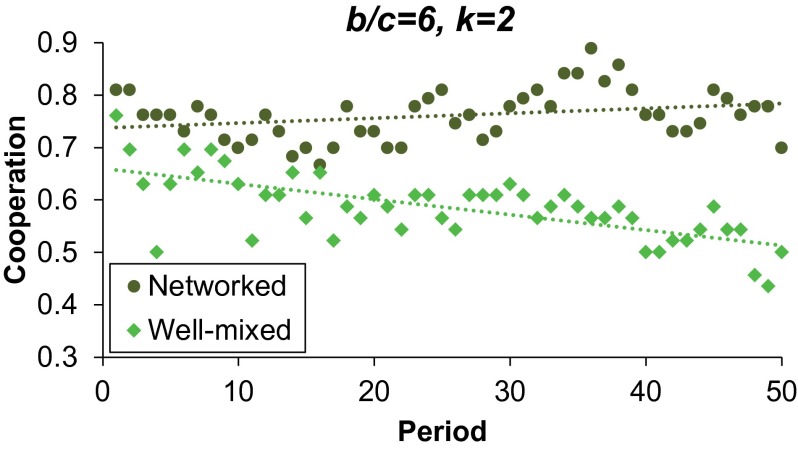
Because the b/c > k condition is satisfied, we expect cooperation to succeed in the network treatment. As shown in Fig. 2, our results are consistent with this theoretical prediction. We observe a high stable level of cooperation when subjects are embedded in the network (no significant relationship between cooperation and round number; P = 0.290). In the well-mixed treatment, by contrast, cooperation decreases over time (relationship between cooperation and round is significantly more negative in the well-mixed treatment compared with the network treatment; P = 0.030). As a result, cooperation rates in the second half of the session are significantly higher in the network treatment than in the well-mixed treatment [P = 0.039; similar results are obtained when considering the last third (P = 0.027) or quarter (P = 0.033) of the session; P values generated using logistic regression at the level of the individual decision with robust SEs clustered on subject and session, including a control for the total number of players in the session]. Statistical details are provided in SI Appendix.

Fig. 2.

Networked interactions promote cooperation when b/c = 6 and k = 2 in experiment 1, run in the physical laboratory. Shown is the fraction of subjects choosing cooperation in each round, for network (dark green circles) and well-mixed (light green diamonds) conditions.

Thus, experiment 1 demonstrates that interaction structure does matter for stabilizing human cooperation and that static networks can promote cooperation under the right conditions.

In experiment 2, we build on this finding by providing evidence that it is the theoretically motivated b/c > k condition in particular that determines when cooperation succeeds on networks. To do so, we take advantage of the online labor market Amazon Mechanical Turk (AMT) (52) to recruit a large number of subjects (1,163 in total) and systematically vary b/c and k across the values of 2, 4, and 6 in our network treatment. Thus, we have nine main treatments: [k = 2, k = 4, k = 6] × [b/c = 2, b/c = 4, b/c = 6]. We also include three additional well-mixed control conditions: one for each [b/c,k] combination that satisfies the b/c > k criterion. We run four experimental sessions of each treatment, with each consisting of 24.2 subjects on average (no subject participated in more than one session). Given the practical constraints of online experiments, games in experiment 2 last 15 rounds rather than 50 rounds as in experiment 1. Because of this shorter length, subjects are not told the total number of rounds to avoid substantive end-game effects.

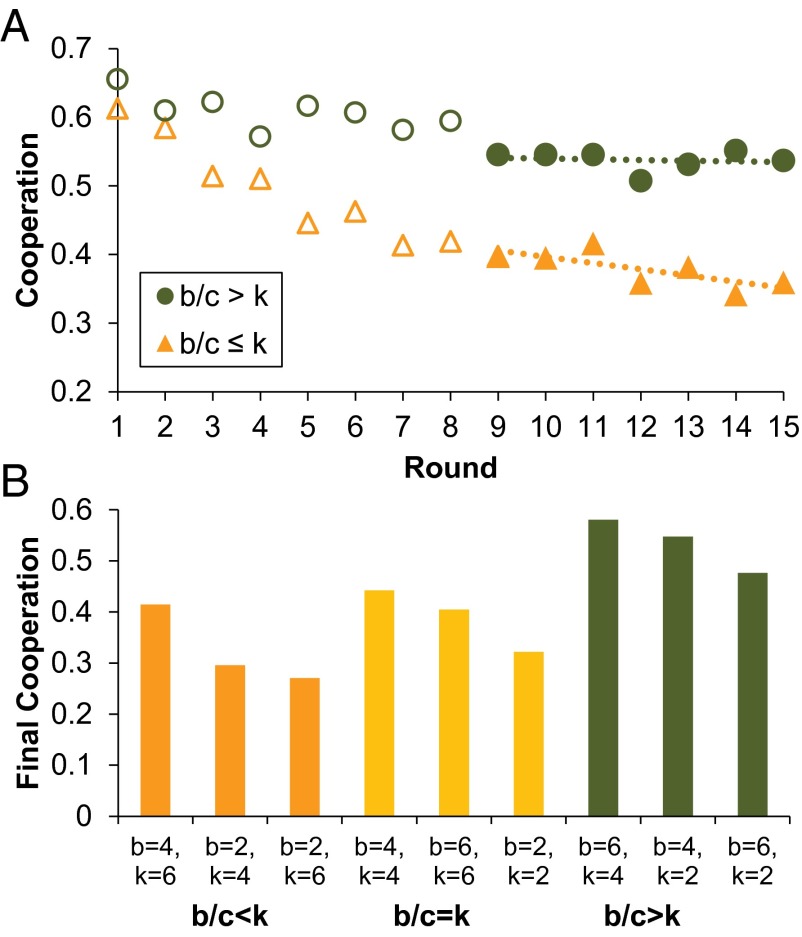
We begin by considering the network treatments and ask whether the b/c > k condition determines the success of cooperation. Consistent with the results for experiment 1 and theoretical predictions, we observe a stable high level of cooperation when b/c > k (Fig. 3A). After an initial transient adjustment, cooperation in the b/c > k treatments stabilizes in the second half of the game (no significant relationship between cooperation and round number; P = 0.838), whereas cooperation continues to decline in the b/c ≤ k treatments [P = 0.028; results are equivalent when considering the last third of the game instead of the second half or when defining the second half as starting at round 8 instead of round 9 (SI Appendix)]. This difference in how cooperation unfolds over time is further demonstrated by a significant interaction between round number and a b/c > k indicator (P = 0.001) in a regression with all of the data.

Fig. 3.

Stable cooperation emerges when b/c > k, but not b/c ≤ k, in experiment 2, run online. (A) Fraction of subjects choosing cooperation in each round, for b/c > k (green circles) and b/c ≤ k (orange triangles). Observations from the first half of the game are open, and observations from the second half are filled. (B) Fraction of subjects choosing cooperation in the final round, for each [b/c,k] combination. Bars are grouped by [b/c < k, b/c = k, b/c > k] and are sorted in decreasing order of final cooperation level within each grouping.

As a result, in the final round, cooperation is significantly higher when b/c > k compared with b/c ≤ k (Fig. 3B; P = 0.002). Importantly, there is no significant difference in final round cooperation comparing b/c < k with b/c = k (P = 0.355) and there is more final round cooperation in b/c > k compared with b/c = k (P = 0.034). Thus, we provide evidence that b/c > k, in particular, is needed for stable networked cooperation (P values generated using logistic regression at the level of the individual decision with robust SEs clustered on subject and session, including a control for the total number of players in the session; statistical details are provided in SI Appendix).

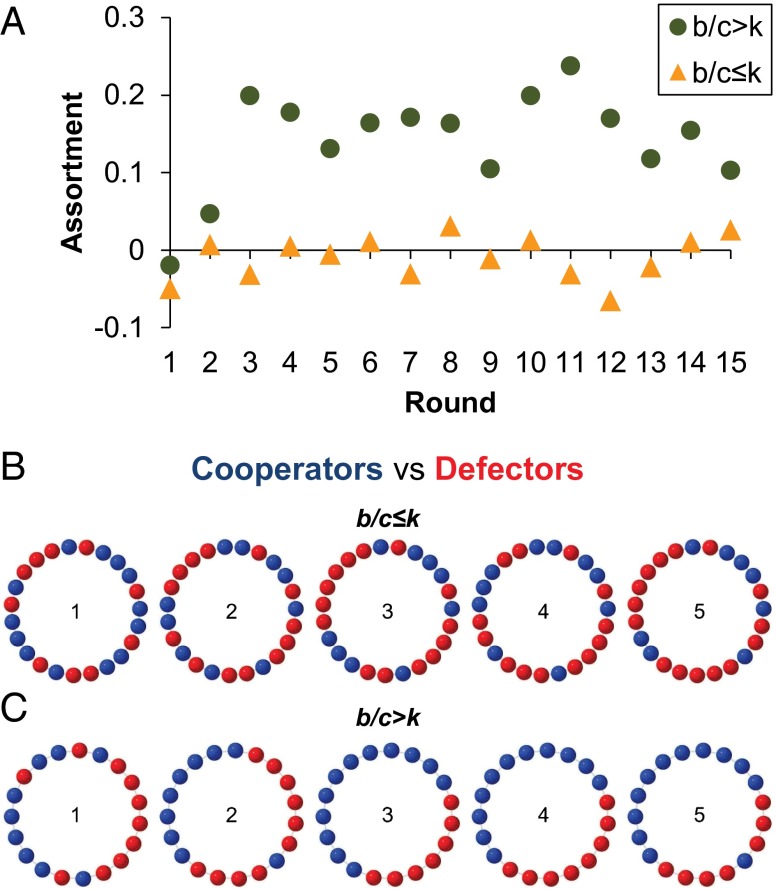
These differences in the level of cooperation reflect deeper differences in how players are distributed over the network. When b/c > k, clusters of cooperators emerge and are maintained, whereas no such clusters form when b/c ≤ k. We quantify clustering following the standard definition of assortment in evolutionary game theory (53), operationalized here as a cooperator’s average fraction of cooperative neighbors minus a defector’s average fraction of cooperative neighbors. As shown in Fig. 4A, assortment rapidly emerges when b/c > k, but not when b/c ≤ k. Thus, we observe a level of assortment that is significantly greater than zero for b/c > k (P < 0.001), but not for b/c ≤ k (P = 0.461), and we observe significantly more assortment at b/c > k than b/c ≤ k (P < 0.001). In other words, the b/c > k environment gives rise to substantial clustering of cooperators, stabilizing cooperation. To illustrate this point, sample b/c > k and b/c ≤ k networks for rounds 1 through 5 are shown in Fig. 4 B and C. Despite similar initial levels of cooperation across the two networks, the distribution of cooperators within the networks quickly becomes noticeably different [P values generated using linear regression taking one observation per session per round, with robust SEs clustered on session; results are robust to controlling for k (SI Appendix)].

Fig. 4.

Substantial assortment emerges when b/c > k, but not b/c ≤ k. (A) Shown is the average level of assortment (cooperators’ average number of cooperative neighbors minus defectors’ average number of cooperative neighbors) by round for b/c > k (green circles) and b/c ≤ k (yellow triangles). Also shown are two sample networks across the first five rounds (which are labeled), where cooperators are shown in blue and defectors in red; low clustering with b/c ≤ k (B; b/c = 2, k = 2) and high clustering with b/c > k (C; b/c = 6, k = 2). Despite similar initial levels of cooperation, clustering maintains cooperation when b/c > k, whereas cooperation decays when b/c ≤ k.

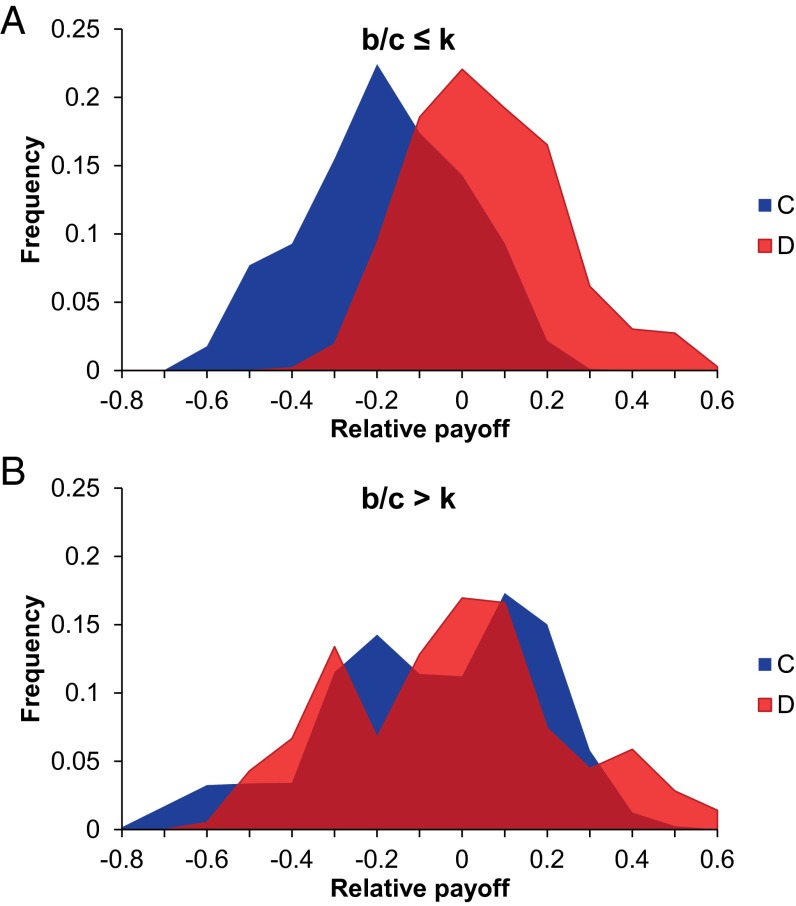
This assortment has important strategic implications. Defectors earn significantly higher payoffs than cooperators when b/c ≤ k (P < 0.001; Fig. 5A). The clustering that arises when b/c > k, however, allows cooperators to interact preferentially with other cooperators. Thus, the cost of cooperating may be balanced out by increased access to the benefits created by other cooperators, improving the payoffs of cooperators relative to defectors. Indeed, cooperators earn significantly higher payoffs relative to defectors when b/c > k compared with b/c ≤ k (P < 0.001), so much so that when b/c > k, defectors no longer earn significantly more than cooperators (P = 0.152; Fig. 5B; P values generated using linear regression on payoff relative to session average per subject per round, with robust SEs clustered on subject and session; statistical details are provided in SI Appendix).

Fig. 5.

Defectors (D) significantly out-earn cooperators (C) when b/c ≤ k (A), but not when b/c > k (B). Shown is the distribution of payoffs relative to average session payoff, with one observation per subject per round, for C (blue) and D (red). To make payoffs comparable across conditions, they are normalized by the maximum possible relative payoff [bk − ck(N − 1)]/N, where N is the number of players in the session.

Thus far in experiment 2, we have shown that stable cooperation emerges in static networks when b/c > k and that this cooperation is supported by assortment. We now provide evidence that it is indeed the network structure of interactions that is driving these results, by ruling out two potential alternatives.

First, we show that the key factor determining outcomes is the b/c > k criterion, rather than merely the b/c ratio itself (which is larger when b/c > k than when b/c ≤ k). When we include a control for the b/c ratio (statistical details are provided in SI Appendix), we continue to find a significant interaction between round number and a b/c > k indicator (P = 0.004). We also continue to find that when comparing b/c > k to b/c ≤ k, there is significantly more cooperation in the final round (P = 0.047), significantly more assortment (P < 0.001), and significantly higher payoffs of cooperators compared with defectors (P < 0.001). Thus, the network properties (i.e., the relationship between b/c and k) must be considered, and the results cannot be explained by b/c alone.

Second, we replicate the result from experiment 1 that shuffling the network results in a decay of cooperation even if the b/c > k condition is satisfied. In our well-mixed b/c > k control conditions, there is (by design) significantly less assortment than in the networked treatments (P = 0.001). As a result, we find that cooperation significantly declines in the second half of the game when the population is well mixed (P = 0.004), even though b/c > k. Furthermore, the well-mixed controls show less cooperation in the final round (P = 0.033) and lower payoffs to cooperators compared with defectors (P < 0.001). Together with experiment 1, these results show that it is not enough to interact with k players in each round. Interactions must be embedded in static networks to achieve stable cooperation in our experiments (statistical details and further analysis are provided in SI Appendix).

Discussion

Here, we have demonstrated the power of static interaction networks to promote human cooperation. With the right combination of payoffs and structure, networked interactions allow stable cooperation via the clustering of cooperators. This clustering offsets the costs of cooperating and makes it possible to maintain high levels of cooperation in sizable groups and to avoid the tragedy of the commons. Our experimental results support the substantial theoretical literature suggesting that cooperation can be favored in structured populations under the right conditions (27–40). Our findings provide insight into the profoundly important role that networks may play in the origins and maintenance of cooperation in human societies.

Our results also help to explain why previous studies concluded that static network structure does not promote cooperation in experiments with human subjects (41–48). We find that the b/c > k condition is required for cooperation to succeed and that this condition was not satisfied in most previous experiments where cooperation failed in networked populations. Traulsen et al. (41) used b/c = 3 and a lattice with k = 4; Rand et al. (42) used b/c = 2 and a random graph with average k = 3.25; Suri and Watts (43) used a Public Goods game with an effective b/c = 2.67 and various different network structures all having k = 5. Other experiments used Prisoner’s Dilemma games that are not decomposable into a benefit-to-cost ratio, but can be analyzed using a generalized form of the b/c > k condition [for a general Prisoner’s Dilemma game, where a player earns T from defecting while the partner is cooperating, R from mutual cooperation, P from mutual defection, and S from cooperating while the partner is defecting; the condition for cooperation to succeed is Q* > k with Q* = (P + S − R − T)/(R + S − P − T) (37)]. Cassar (44) used Q* = 4 and various network structures all having k = 4, Grujić et al. (45) used Q* = 5.67 and a lattice with k = 8, and Wang et al. (46) used Q* = 2.2 and cliques or random regular graphs with k = 5. Thus, the fact that networked interactions did not promote cooperation in any of these experiments is consistent with the theory and our results. It is also important to note that in some of these previous experiments (42–44, 46), participants were not given information about the payoffs of their neighbors, precluding the method of strategy updating which allows cooperation to succeed when the b/c > k condition is satisfied; thus, we would not predict stable cooperation in these settings even with b/c > k.

Importantly, the decline of cooperation in these previous network studies shows that the stability we observe when b/c > k is not driven purely by repeated game effects. Even though all of these experiments (as well as our b/c < k treatments) involved repeated interactions between the same fixed neighbors, stable cooperation was not observed [and in experiments that included shuffled control conditions, cooperation was not greater with fixed partners than with shuffled partners (41, 42, 45)]. This failure of cooperation in these repeated games suggests that interaction structure plays a key role in the stability we observe.

There are two previous experiments that did satisfy the theoretical condition and, nonetheless, did not find stable cooperation. However, these studies involved design features that make inference regarding the b/c > k condition difficult. Gracia-Lázaro et al. (47) used Q* = 5.67 and a lattice with k = 4 or a heterogeneous network with an average k = 3.13, but they ran only a single replicate of each network (yielding only two independent observations). Kirchkamp and Nagel (48) used b/c = 5 and networks with k = 4 (satisfying the condition) or k = 10 (not satisfying the condition), but subjects were given no information about the payoff structure of the game. Instead, they received information each round regarding choices and resulting payoffs for themselves and their neighbors, from which they could try to make inferences about the payoff structure. Thus, it seems likely that subjects in this experiment may have engaged in a high degree of experimentation in an effort to understand the game, and experimentation undermines the ability of networks to promote cooperation. (Similarly, subjects in the study by Gracia-Lázaro et al. (47) were high-school students, and thus may have also engaged in more experimentation and nonstrategic behavior than our older subjects).

Issues related to experimentation in network experiments were first emphasized by Traulsen et al. (41), who linked this behavior to the theoretical concept of “exploration dynamics” (54). Experimentation was defined as switching to a strategy not currently played by any of one’s neighbors (a process similar to mutation in evolutionary models). Exploration/mutation disrupts the clustering of cooperators, because a player surrounded by cooperators might spontaneously switch to defection. Thus, theory predicts that, as the mutation rate increases, the b/c required to maintain cooperation rises above k (40). It may be that by concealing the payoff structure from subjects, Kirchkamp and Nagel (48) induced a rate of exploration large enough to derail cooperation even with b/c = 5 and k = 4.

What, then, is the role of exploration in our data? We find that defectors with all defecting neighbors switch to cooperation 15.7% of the time when b/c ≤ k and 17.4% of the time when b/c > k, a nonsignificant difference (P = 0.464). Thus, “mutations” from defection to cooperation, which do not prevent the clustering of cooperators, are common in both cases. However, spontaneous changes from cooperation to defection are significantly less common when b/c > k compared with b/c ≤ k (P = 0.010). Cooperators with all cooperating neighbors switch to defection 14.1% of the time when b/c ≤ k, but only 5.1% of the time when b/c > k. Importantly, this 5.1% mutation rate is low enough that the success of cooperation in our b/c > k experimental conditions comports well with theoretical predictions, even taking into account exploration/mutation (with a 5.1% mutation rate, b/c > 3.35 is required for k = 2 and b/c > 4.99 is required for k = 4, both of which are satisfied by our relevant b/c > k conditions; SI Appendix). Moreover, these results suggest that the extremely high exploration rates observed by Traulsen et al. (41) may have been the result of subjects (correctly) judging those game settings as unfavorable to cooperation. Exploring the evolutionary dynamics of strategies that can modify their mutation rates across settings is an important direction for future work.

An important limitation of the extant theory generating the b/c > k condition is that it does not take into account expected game length (in the case of “indefinitely repeated” games with uncertain ending conditions) or end-game effects (in the case of “finitely repeated” games of known length). The reason is that the theory assumes very simplistic agents who merely copy their neighbors proportional to payoff, without engaging in any more complex strategic thinking. Thus, these agents’ decisions are unaffected by game length/ending. However, previous experimental work shows that expected game length has a notable effect on cooperation in pairwise (non-networked) repeated games (10, 17, 55), and end-game effects (where participants begin defecting as the end of a finitely repeated game approaches) have been found in a wide range of settings, including games on networks (46, 56–58). Thus, exploring how game length effects interact with payoffs and network structure is an important direction for future experimental work.

The success of the b/c > k condition in predicting experimental play in our repeated games, despite its derivation in the context of unconditional strategies (33), suggests that this theory may have wider implications than previously conceived. Perhaps when players are informed of the payoffs of others, they focus on this information when choosing C or D, rather than reciprocating neighbors’ behavior (as prescribed by typical strategies from repeated games theories). There may also be rationales for the b/c > k criterion that come from behavioral models or myopic learning models in addition to the evolutionary model in which it was first derived, or from update rules other than the rules assumed by the particular evolutionary theory that originally generated the b/c > k rule (33). For example, when b/c > k is satisfied, cooperators need only one cooperative neighbor to “break even” (i.e., to earn more than the zero payoff they would earn if they had not played the game or if they had played in a group where all players defected). Thus, the b/c > k condition may be relevant for agents who, rather than maximizing their payoff through imitation as in most evolutionary models, engage in a variant of conditional cooperation (59), where they cooperate as long as doing so does not make them worse off than the baseline reference point. For similar reasons, the b/c > k condition may also be relevant for learning models that seek a “satisficing” payoff, rather than a maximal payoff (60). Further exploration of these possibilities, as well as other behavioral and learning models (49, 50), is a promising direction of future study.

Experimentally manipulating the cooperative dynamics of the network, for example, by using artificial agents that evince particular strategies, and thus help stimulate the emergence and maintenance of cooperative clusters, will also be instructive. So too will looking at how our findings for cycles with different numbers of neighbors extend to other network structures.

Our results suggest that regularity in network structure can contribute to cooperation, and this effect may help to explain why such structures exist and have been maintained. They also emphasize the important role that even static networked interactions can play in our social world and suggest that it may be possible to construct social institutions that foster improvements in collaboration simply by organizing who is connected to whom.

Methods

Experimental Design.

Subjects are arranged on a ring and connected to one, two, or three neighbors on each side (k = 2, 4, or 6 total neighbors). They begin with 100 points in their account and then play a repeated cooperation game. In each round, they can choose D by doing nothing or C by paying a cost of c = 10 * k points to give all k neighbors a benefit of b points (b = 20, 40, or 60). Thus, subjects make a single cooperation decision and cannot selectively opt for cooperation with some neighbors but not others (making the game closer to a repeated Public Goods game than a repeated Prisoner’s Dilemma game). Following each decision, subjects are informed of the decisions of each of their neighbors, as well as the total payoff for the round earned by themselves and by each neighbor.

Subjects begin by reading the instructions and then play one practice round that does not count toward their final payoff. Positions in the network are then rerandomized, and subjects proceed to play the game for 50 rounds in experiment 1 and 15 rounds in experiment 2. In experiment 1, we were not concerned about end-game effects because, over 50 rounds, it is difficult to keep track of exactly which round one is in, and therefore to know which round is the final round. In experiment 2, however, the game was much shorter; therefore, subjects are not informed about the game length to simulate an infinitely repeated game (as in ref. 19). If a subject drops out of the game in experiment 2 at some point (an issue that is much more pronounced in online experiments compared with traditional laboratory experiments), her spot on the ring is eliminated and her neighbors are rewired accordingly (although they are not notified of this change to minimize the disruption caused by the dropout).

Recruitment: Experiment 1.

Subjects in experiment 1 were recruited from the Yale University School of Management’s subject pool. Subjects participated in the experiment at the Yale University School of Management’s behavioral laboratory, consisting of 12 visually partitioned computers. Subjects read instructions on the computer and then interacted via custom software designed to implement our game in the laboratory.

Subjects received a $10 fixed rate for completing the experiment, plus an additional $1 for every 300 points earned during the game (mean additional earnings of $11.92 from the game: minimum of $3 and maximum of $18). Instructions and screenshots of the game interface are provided in SI Appendix.

Experiment 1 has two treatments. In the network treatment, subjects play with the same partners for 50 rounds. In the well-mixed treatment, subjects’ positions on the ring are reshuffled before each of the 50 rounds, destroying the possibility for assortment to arise. We ran 13 sessions over the course of 2 d. To preserve random assignment to condition, we alternated sessions on each day between the network treatment (seven sessions in total) and the well-mixed treatment (six sessions in total); thus, there was no systematic variation between treatments in terms of date or time of day at which the experiments were carried out. In total, we recruited n = 109 subjects. The number of subjects per session did not vary significantly across treatments (χ² test, P = 0.413).

For completeness, we note that two additional well-mixed sessions were run on a separate day (an additional 17 subjects), but because no corresponding network treatments were run on that same day, these sessions violated our random assignment scheme. Therefore, we do not include them in our analyses. Including these extra well-mixed sessions, however, does not qualitatively change our results: We still find stable cooperation in the network treatment (because including the extra well-mixed sessions does not change these data), and we still find significantly more cooperation in the network treatment compared with the well-mixed treatment in the second half (P = 0.010), last third (P = 0.008), and last quarter (P = 0.010) of the game (note that these results actually become more statistically significant when including the randomization-violating treatments).

Recruitment: Experiment 2.

Subjects in experiment 2 were recruited online using AMT (43, 52, 61) and redirected to an external website where our experimental was implemented. AMT is an online labor market in which employers contract with workers to complete short tasks for relatively small amounts of money. Workers are paid a fixed baseline wage (show up free for experiments) plus an additional variable bonus (which can be conditioned on their performance in the game).

AMT and other online platforms are extremely powerful tools for conducting experiments, allowing researchers to recruit easily and cheaply a large number of subjects who are substantially more diverse than typical college undergraduates. Nonetheless, there are potential issues in online experiments that either do not exist in the physical laboratory or are more extreme [a detailed discussion is provided by Horton et al. (52)]. Most notably, experimenters have substantially less control in online experiments, because subjects cannot be directly monitored as in the traditional laboratory. Thus, multiple people might be working together as a single subject or one person might log on as multiple subjects simultaneously (although AMT goes to great lengths to prevent multiple accounts and, based on Internet Protocol address monitoring, it happens only rarely). One might also be concerned about the representativeness of subjects recruited through AMT, although they are substantially more demographically diverse than subjects in the typical college undergraduate samples.

To address these potential concerns, numerous recent studies have explored the validity of data gathered using AMT [an overview is provided by Rand (61)]. Most relevant here are two direct replications using economic games, demonstrating quantitative agreement between experiments conducted in the physical laboratory and experiments conducted using AMT with ∼10-fold lower stakes in a repeated Public Goods game (43) and a one-shot Prisoner’s Dilemma (52). It has also been shown that play in one-shot Public Goods games, Trust games, Dictator games, and Ultimatum games on AMT using $1 stakes is in accordance with behavior in the traditional laboratory (62).

Consistent with standard wages on AMT, subjects received a $3 fixed rate for completing the experiment, plus an additional $0.01 for every 10 points earned during the game [average additional earnings of $0.93 (SD = $0.83) from the game: minimum of $0 and maximum of $4.62]. Experimental instructions and screenshots of the game interface, as well as participant demographics, are provided in SI Appendix.

In total, we have nine main treatments: [k = 2, k = 4, k = 6] × [b/c = 2, b/c = 4, b/c = 6]. In these treatments, subjects play with the same partners for 15 rounds. We also include additional control conditions where subjects’ positions on the ring are reshuffled before each of the 15 rounds, destroying the possibility for assortment to arise. Our design has three such controls, one for each [b,k] combination satisfying b/c > k (i.e., k = 2, b = 4; k = 2, b = 6; k = 4, b = 6).

For each treatment, we ran four sessions, for a total of 48 sessions. Each session consisted of 24.2 subjects on average (minimum of 15 players and maximum of 34 players), for a total of 1,163 participants. The number of subjects per session did not vary significantly across treatments (χ² test, P = 0.321). An average of 1.38 subjects per session had dropped out by the final round (minimum of zero players and maximum of five players). The number of players dropping out did not vary significantly across treatments (χ² test, P = 0.771).