Stochastic simulation in systems biology

Abstract

Natural systems are, almost by definition, heterogeneous: this can be either a boon or an obstacle to be overcome, depending on the situation. Traditionally, when constructing mathematical models of these systems, heterogeneity has typically been ignored, despite its critical role. However, in recent years, stochastic computational methods have become commonplace in science. They are able to appropriately account for heterogeneity; indeed, they are based around the premise that systems inherently contain at least one source of heterogeneity (namely, intrinsic heterogeneity).

In this mini-review, we give a brief introduction to theoretical modelling and simulation in systems biology and discuss the three different sources of heterogeneity in natural systems. Our main topic is an overview of stochastic simulation methods in systems biology.

There are many different types of stochastic methods. We focus on one group that has become especially popular in systems biology, biochemistry, chemistry and physics. These discrete-state stochastic methods do not follow individuals over time; rather they track only total populations. They also assume that the volume of interest is spatially homogeneous. We give an overview of these methods, with a discussion of the advantages and disadvantages of each, and suggest when each is more appropriate to use. We also include references to software implementations of them, so that beginners can quickly start using stochastic methods for practical problems of interest.

1. Introduction

The recent paradigm of systems biology sets out to examine biological phenomena at the systems level. This is in contrast to the widespread approach of reductionism, whereby researchers attempt to understand entire systems by studying them one small component at a time. The reductionist approach has given us valuable insights and a detailed understanding of the molecular components of biological processes. However, it is becoming clear that we need a complementary approach that takes a holistic view of these processes by looking at their systems-level dynamics: this is systems biology [1,2]. Reductionism implicitly assumes that the entire system is just the sum of its parts, which is not necessarily true: complex patterns can arise from collections of simple components [3]. The challenge of systems biology is to understand extremely complex systems without breaking them into easy-to-digest parts, and for this, the right computational and mathematical tools are essential [4].

Mathematical modelling and computational simulation perform essential roles in biology. This popular mantra of the theoretical biologist is often heard stated, but one could easily ask why. Models are useful for many different purposes: perhaps the most important of these are crystallising our assumptions and testing them, guiding experiments and looking at experimentally unreachable scenarios [5], as well as the much-vaunted ability to make new predictions [6]. Ideally, there should be a virtuous cycle between experiment and theory to understand the natural system in which we are interested [7] (Fig. 1). This starts off from our system and question of interest (green box, Fig. 1), for which we generate an initial hypothesis. This can be very simple, as it is just a starting point: for instance, if our question was “what is the shape of the Earth?”, then an initial hypothesis could be “the Earth is flat”. Then, a mathematical model can be constructed, and solved or simulated computationally; in parallel, experiments can be run and their results compared to the model outputs (blue boxes, Fig. 1). If the model and experiments agree, then parameters for the model can be inferred from the data and the model refined, again leading to further experiments (large arrows, Fig. 1). If they do not agree, this implies that the hypothesis was inappropriate: the model needs revision, and theoretical tests using different models can provide a starting point for further experiments. For this we need to go back to our natural system and propose revisions (major or minor) to the model and new avenues for experiment, as well as verifying our findings (small arrows, Fig. 1). Of course, in our example the model, based on the assumption of a flat Earth, would disagree with our experimental observations. Therefore we would have to reconsider our initial hypothesis, and by iterations settle on the correct answer to our question.

Fig. 1.

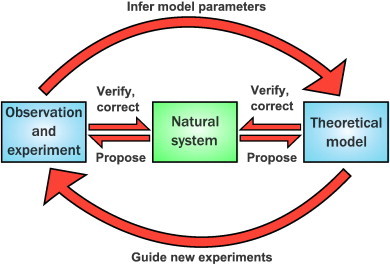
Illustration of the cycle of information flow between the natural world and our theoretical and experimental efforts to understand it.

Adapted from Ref. [7].

At this point, we pause to clarify some terminology: a model is an abstract representation of the system in which we are interested, usually formulated mathematically. This model can, in simple cases, be solved analytically for a particular question, giving us an exact analytical solution to the question posed to the model. In general, however, analytical solutions for all but the most simple models do not exist, and we have to resort to methods to solve the model numerically. These give rise to numerical solutions, which are approximations to the analytical solution that become more and more accurate as we use smaller and smaller numerical steps (the unit of discretisation of a numerical approach). Numerical solutions are (nowadays) evaluated computationally because they are very time-consuming to carry out by hand. In many cases, the numerical solution will try to mimic the behaviour of the real system over time — this is a simulation. A well-known example might be a flight training simulator for pilots that simulates flying an aeroplane. This is based on a complicated mathematical model that is composed of equations for flight dynamics and for how the aeroplane should react to the controls, as well as other factors such as weather. The numerical solutions to these equations describe how the aeroplane behaves over time — they constitute the simulation that the pilot sees displayed on the screen.

An important point to remember when we talk about mathematical models is that, in a sense, “all models are wrong” [8]. This does not mean their conclusions or predictions are false — as the famous quote continues, “but some are useful” [8]; rather, we should bear in mind that all models are abstractions of reality, simplified versions of the real systems that they represent. A model is a vehicle for gaining understanding [6], and we would not gain any new understanding from a model that was as complicated as the real system. Indeed, if we could construct a perfect model we would not need a model at all, since we would already have perfect knowledge of the system. Almost all models are phenomenological; that is, they are based on a set of simplified assumptions that we have distilled from the real system using intuition rather than rigorous proof from basic principles [9]. Incorporating only the important ones allows us to crystallise our understanding of the system (and if the model gives wrong results, we know that our assumptions were wrong or incomplete). Creating phenomenological models is not a trivial task: “sensing which assumptions might be critical and which irrelevant to the question at hand is the art of modeling” [10].

The choice of modelling/simulation method is determined by the aspects of the natural system in which we are interested, how realistic an estimation of it we want, and our mathematical and computational resources. There are many types of methods that could be used, each incorporating different levels of detail and requiring different computational effort (Fig. 2). At one end of the scale, the most accurate, and computationally expensive, methods are molecular dynamics simulations. These can be separated into two broad categories: quantum methods [11], which evaluate the wavefunctions at the level of individual electrons and are necessary when quantum effects become important (surprisingly, there are examples of this in macroscopic biological processes [12,13]), or classical methods, which go one step up and solve the classical equations of motion for molecules to simulate their motion deterministically [14]. Although these methods are as close as we can get to exactly and fully describing systems at the microscopic level, they nonetheless still make considerable simplifications (for instance, the approximations of the Schrödinger equations/deterministic force fields in quantum/classical molecular dynamics, respectively).

Fig. 2.

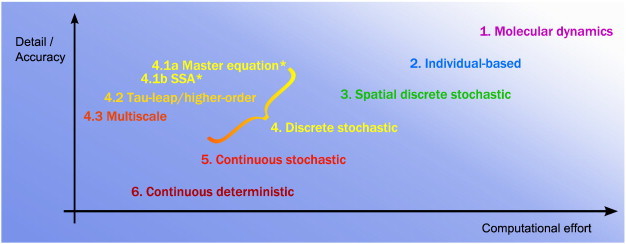
Modelling and simulation methods compared based on their level of detail/accuracy versus their computational difficulty. We focus on the fourth category of methods, which we have broken down into sub-categories that we describe in Section 5. The figure is not to scale. *The master equation and the SSA are both ‘exact’ as such (see Section 5), but there are some caveats. The master equation can be solved exactly, numerically or by approximations, whilst the SSA is strictly only exact in the limit of infinite simulations.

Going up in scale, there are several classes of stochastic methods (our main focus in this paper), and at the highest end of the scale are continuous deterministic methods such as ordinary and partial differential equations [15–17] (Fig. 2). There are several transitions between random (quantum molecular dynamics, stochastic simulations) and deterministic methods (classical molecular dynamics, ordinary differential equations), and the reason for this is the level at which we view the system and the information in which we are interested (we explore this further in Section 4). Each of these methods is best suited for solving problems of certain scale and complexity. For instance, classical molecular dynamics can simulate huge numbers of discrete particles for very short simulation times (usually nanoseconds, microseconds or sometimes up to the millisecond scale), whereas ordinary differential equations look only at concentrations of macromolecules but can simulate these for many hours (or longer). An important point to remember is that no method type can be said to be ‘better’ than the rest, only more suitable for a certain problem. Each has its own uses, arising from its inherent advantages and disadvantages.

In this mini-review, we give an overview of discrete-state stochastic simulations (henceforth, shortened to ‘discrete’; the time variable is continuous) that are commonly used in systems biology. Specifically, we will focus on the fourth group of methods in Fig. 2 (in yellow). These can be used to simulate molecular populations over relatively long time periods, whilst still regarding them as being composed of discrete units. However, as we do not keep track of each molecule's position or momentum, these methods lose their spatial aspect and must also assume that the system is stochastic (see Section 4). We have attempted to keep this overview as non-technical as possible. For this reason, we give only general descriptions of each method type and avoid delving into their mathematical definitions, derivations or background; for those readers who are interested, we provide references to the primary literature. For more mathematical overviews of stochastic methods, we refer the reader to several useful works [18–21]. In addition, Ref. [22] is a short non-technical overview of stochastic methods and parameter inference (Fig. 1, top arrow), and Ref. [23] gives an accessible introduction to the mathematical details.

This mini-review consists of five further sections. We start with the concepts of heterogeneity and noise, introduced in Section 2. In Section 3, we explicitly illustrate the difference between deterministic and stochastic methods using an example. Next, in Section 4 we introduce some non-technical background for discrete stochastic methods. Section 5 contains the descriptions of the main types of discrete stochastic methods and discussions of their respective advantages and disadvantages. Finally, in Section 6 we give a brief summary and discuss fruitful research directions for the future.

2. Heterogeneity

Heterogeneity is a key property of biological systems at all scales: from the molecular level all the way up to the population level [24–26]. In order to gain a better quantitative understanding of these systems, it is important to incorporate heterogeneity into systems biology models. Although during the past century and half the contributions of ‘nature versus nurture’ to heterogeneity evoked endless debate, nowadays it is common scientific consensus that ‘nature’ and ‘nurture’ are not two sides of a coin: rather they have a complex and interconnected relationship [27]. In recent years, it has been noted that we must consider another source of heterogeneity, arising from ‘chance’ [28–30]. Thus we can classify heterogeneity as arising from three main sources: genetic (nature), environmental (nurture) and stochastic (chance) (Fig. 3). We give a brief overview below; Ref. [25] provides an excellent and more in-depth discussion of this topic.

Fig. 3.

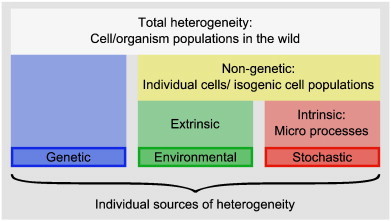
Sources of heterogeneity. The total observed heterogeneity in a natural system broken down into its three components: genetic, environmental, and stochastic. Different sources of heterogeneity are present at different scales, and the typical scales are given.

Adapted from Ref. [25].

Perhaps the most obvious of these is genetic heterogeneity. Since Darwin, it has become canonical knowledge that cells and animals with different genes should clearly be different. This is certainly the case in most populations of cells and animals in the wild. One counterexample is convergent evolution, where different species evolved similar phenotypic features independently [31]. This phenotypic similarity is thought to usually have a different genetic basis, showing that the relationship between genotype and phenotype is not a simple, linear one [32]. However, recent work has shown that there are a surprising number of cases of convergent (phenotypic) evolution with a corresponding convergence in genotype [33,34]. As genetics is a very well-established topic and covered in many textbooks [35], we do not go into further details about genetic heterogeneity here.

However, even isogenic (that is, genetically identical) organisms or populations of cells can be very different; the famous cloned animals from recent decades are excellent illustrations of this phenomenon, known as non-genetic or phenotypic heterogeneity [25,26,36,37]. In other words, heterogeneity is not only generated by genetic variation, and we can identify two other sources of heterogeneity.

The first can loosely be called environmental, or extrinsic [38,39]. This is a very broad term whose usage various by author and context, and can best be labelled as ‘heterogeneity from neither genetic nor intrinsic sources’ (this definition will become more apparent shortly). Depending on the context, any of the following can be contributing factors: the external environment of a metazoan; the external environment of constituent cells inside a metazoan; the external environment of a cell population (either unicellular organisms or a cell line in vitro); the internal environment of the cells themselves; and cell state [40]. Examples of each of these factors could be: the weather an animal experiences in a particular year; the amount of water or oxygen in the blood of an animal; the pH or nutrient level in which a cell population is propagated; numbers and positions within each cell of shared gene expression machinery such as ribosomes; and cell cycle stage or cell age, respectively. Clearly, not all of these sources will be considered for the same system, and they must be chosen phenomenologically. For instance, if we were interested in animal populations we would look only at the external environment of an animal, whereas if we were interested in levels of protein expression of a cell population, we might look at differences in individual cells such as ribosome number and cell cycle stage. Unfortunately, there is a strong possibility of confusion when the same term is applied at so many different scales. Despite this, we have deliberately given such a broad definition as we feel that it is helpful to bear in mind the generality of these ideas, and that they have been used at various scales and for many different problems. As always, the choice of what to include in the model lies with the modeller.

The final source of heterogeneity, present in all living (and non-living) systems but often masked by the macroscopic scale at which we observe them, was perhaps first observed in a cell biology context by Spudich and Koshland [41]. They noticed that individual bacteria from an isogenic population maintained different swimming patterns throughout their entire lives. This was a visible manifestation of the third source of heterogeneity [26]: chance, otherwise known as stochasticity or intrinsic heterogeneity (often interchangeably called intrinsic noise, without the same negative connotations as the colloquial usage of the word). This arises from random thermal fluctuations at the level of individual molecules [24,36,42]. It affects the DNA, RNA, protein and other chemical molecules inside cells in many ways, most notably by ensuring that their reactions occur randomly, as does their movement (via Brownian motion). It is inherent to the process of gene expression and cannot be predicted (except in a statistical sense) or fully eliminated. Thus two identical genes in an identical intracellular environment would still be expressed differently, even in the absence of the previous two sources of heterogeneity [36,43]. In contrast, extrinsic heterogeneity arises from other, outside, sources and affects all genes inside a cell equally. The reason for this terminology is that these phrases were popularised in the literature of intracellular gene expression, where only the random fluctuations are actually inherent to the expression of a single gene, and all other sources of heterogeneity can be accounted for.

It is possible to separate the contributions of intrinsic and extrinsic noise in a gene expression network inside a single cell: this is the classic experiment of Elowitz et al. [44]. In brief, they incorporated two fluorescent proteins (cyan and yellow, although they are usually represented as red and green for conceptual purposes) into the genome of an isogenic population of Escherichia coli bacterial cells at equidistant points from the origin of replication. The hypothesis, then, is that if intrinsic noise does not exist, the two proteins would be expressed equally, albeit varying (identically) over time due to extrinsic noise. However, in the presence of both intrinsic and extrinsic noise, the expression of the two proteins would be uncorrelated, as intrinsic noise affects the expression of each protein differently (Fig. 4A). At the level of the bacterial population, the presence of only extrinsic noise would result in cells that are all yellow (i.e., both red and green fluorescent proteins expressed equally) but have different brightness; adding intrinsic noise, the population would be a mix of red, green and yellow cells of different brightness (Fig. 4B). The respective noise contributions can also be visualised on a plot of the expression level of green versus red fluorescent proteins: extrinsic noise results in cells distributed along the diagonal (full line, Fig. 4C), and intrinsic noise shifts the cells away from this diagonal (dashed lines, Fig. 4C). Of course, Elowitz et al. found that both sources of heterogeneity were present [44]. The respective contributions can also be elegantly quantified using theoretical analysis [45]; however these calculations are not valid in all situations, for instance when regulatory molecules are shared between genes [46].

Fig. 4.

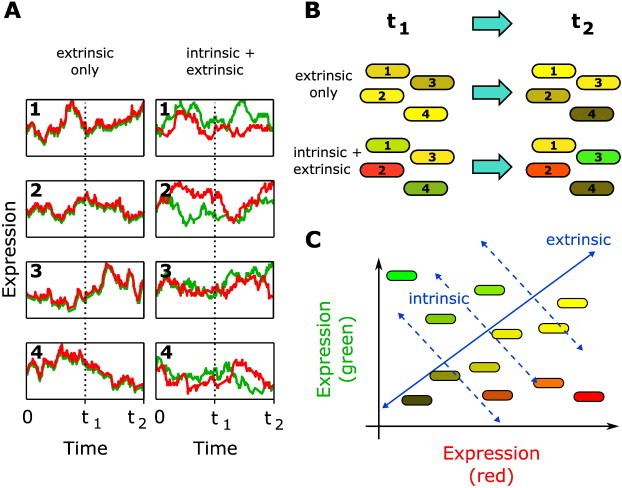
Separating intrinsic and extrinsic noise with a two-colour experiment. Here we illustrate the classic two-colour experiment of Elowitz et al. [44]. Two differently-coloured fluorescent proteins (here, red and green) are inserted into the genome of E. coli. (A) Hypothetical time series of fluorescent protein expression for either extrinsic noise only (correlated expression), or both intrinsic and extrinsic noise (uncorrelated expression). Numbers are labels for each bacterial cell. (B) The corresponding population-level view of the bacterial cells at each of the two time points t₁ and t₂. (C) Plotting the expression levels of the fluorescent proteins on the same figure, extrinsic noise results in variation along the diagonal (blue line). Intrinsic noise results in deviations from the diagonal (dashed blue lines).

Adapted from Ref. [44].

Intrinsic noise is an important biological phenomenon, and its effects have to be accounted for by cells and organisms. It has both a positive and negative influence. Some biological systems have evolved to make use of it: a good example is the case of persister-type bacteria, which form a subset of some bacterial populations and can withstand antibiotic treatments even though they do not have genetic mutations for resistance [47,48]. This is an example of cellular decision making, the ability of cells to randomly transition between different stable, heritable states [49]. These stable states arise from the architecture of the gene expression network, with positive feedback loops leading to bistability at the single-cell level [50]. The individual cells randomly change between states (called stochastic switching); the stability of the states at the population level is then achieved by regulating the switching rates of each state [51]. Some of the most well-known examples of cellular decision making are bacteria [52,53] and yeast [54], which are easier to investigate experimentally than large multicellular organisms. Yet, this phenomenon is common to cells at all levels of life (for example, human progenitor cells [55]), and is argued to be one of the key processes in cellular development [49]. The main difference is that in unicellular organisms, cellular decision making is useful for cheap, non-genetic adaptation in the face of fluctuating environments, whereas in multicellular organisms it is used to produce distinct cell types and functions within a constant environment [42]. Finally, of course, stochasticity plays a crucial role in causing genetic mutations [56,57]; these are essential for creating the heritable variation upon which natural selection can act, thus allowing evolution to occur [58].

However, mutations are a double-edged sword, as they can often have strong negative effects. Deleterious mutations that are phenotypically expressed frequently result in loss of important functions or even organismic death, and it has been shown that a substantial proportion of mutations are deleterious [59]. Mutations in stem and somatic cells are also thought to cause cancer, which has become a serious disease in modern times [60,61]. Another major negative effect of intrinsic noise is to interfere with precise regulation of molecular numbers by gene expression [62], and cells have to compensate for this by adopting mechanisms that enable robustness of certain key properties [63,64], such as feedback loops [36,43]. Indeed, it has been found that critical cellular systems have evolved to minimise their levels of noise [65,66].

It is important to remember that these three sources of heterogeneity are not independent, and they are all interconnected in their effects on cells and populations [26]. For instance, in order for cellular decision making to occur, the cell must be able to settle in two (or more) stable states, which are non-genetic in nature. Thus cellular decision making involves both environmental and intrinsic heterogeneity, the former in affecting which stable states are possible and the latter in switching between them. Another example is that of genetic mutations, where intrinsic noise causes the mutations that then contribute to genetic heterogeneity. Finally, a powerful example of the interplay of all three types of heterogeneity is evolution, one of the most fundamental processes in nature: evolution acts on phenotypes, which have a genetic basis but are also affected by both extrinsic and intrinsic noise [40].

3. Deterministic versus stochastic models

For the rest of this mini-review, we will use the language of cell biology, both to keep the text simple, as well as because many of these concepts have been extensively used in cell biology. Therefore, we will refer to reactions occurring inside a cell volume between different types of biochemical molecules (or, interchangeably, particles) with various reaction rates. These will generally be genes (for our purposes, sections of DNA that are copied into mRNA and initiate a gene expression network), RNA or proteins, as well as chemical compounds. The terminology we use transfers easily to other systems, and we emphasise that the methods we describe can be, and have been, also applied more generally.

As we have discussed in the previous section, there is considerable heterogeneity at every scale of biological systems. The first two sources are now well-known, but until recently the effects of intrinsic noise have generally been ignored in biology [28], both conceptually as well as in the mathematical and computational methods that have traditionally been used. These are typically systems of differential equations, which are both continuous and deterministic — that is, their state variables are real numbers representing the concentrations of molecules and they do not include noise [67]. Such models are indeed useful for many problems, but they can only be regarded as accurate when we are interested in the mean dynamics of a large number of molecules, large enough that we need not worry about individual molecules but can approximate them as concentrations. This becomes viable when molecular populations are of the order of many hundreds or above, for instance in enzymatic reactions in the cytoplasm or solutions in test tubes. Above this population size, the fluctuations from intrinsic noise are averaged out and the deterministic approximation becomes increasingly valid. This is because intrinsic noise, as a rule of thumb, behaves as $\frac{1}{\sqrt{X}}$, where X is the number of molecules in the system.

We define noise level here as the coefficient of variation of the abundance of a molecule, that is, the standard deviation of its distribution divided by its mean. Roughly, the above rule of thumb arises because molecular reactions are random Poissonian birth–death processes (see Section 4). More rigorous theoretical efforts to characterise the scaling also invoke a simple birth–death model of transcription (the copying of a section of DNA to mRNA) and translation (protein production from mRNA), the analysis of which yields a scaling law. This scaling does indeed behave roughly as stated above for both mRNA and proteins, with a Poisson term of $\frac{1}{\sqrt{X}}$ plus other, more complicated, term(s) [43,68–70]. For mRNA, these depend on the type of regulation, with constitutive expression producing a Poisson distribution as expected for a single birth–death process, and more complicated regulation strategies producing non-Poisson mRNA distributions [71]. Proteins also have non-Poisson distributions (albeit their scaling is also roughly Poissonian), as they are dependent on both mRNA birth and death as well as translation rates [43,69]. Experimental studies have confirmed these results, finding that total noise does scale roughly as the inverse square of abundance until high abundances. At this point, extrinsic noise is thought to take over as the dominant source of noise [72–74].

Thus intrinsic noise rapidly increases as molecular populations decrease, and it often becomes necessary to include the effects of stochasticity in biological models, especially for small systems with low populations of some molecular species, such as gene expression networks [75]. Here, discrete stochastic models must be used, whose variables represent actual molecular numbers. An intermediate model type between these two scales is that of continuous stochastic models (stochastic differential equations) [76]. These can be used to model biological systems that are relatively large (of the order of hundreds and up) and so can approximate molecular numbers as concentrations, but also include the effects of noise. They are similar in form to deterministic differential equations, but contain extra terms that represent noise [77,78].

An informative example for illustrating the key differences between the deterministic and stochastic approaches is the Schlögl reaction system [79]. This is a system of four chemical reactions, commonly used as a benchmark system in the literature, given by

$$\begin{array}{c}A+2X\underset{c_2}{\overset{c_1}{\rightleftharpoons }}3X,\\ B\underset{c_4}{\overset{c_3}{\rightleftharpoons }}X\text{.}\end{array}$$ (1)

There are three different molecule types, X, A and B, with X the molecule whose numbers we are interested in, and levels of A and B held constant. This system has a bistable distribution under certain parameter configurations, with an unstable equilibrium state at an intermediate value between the two stable ones. We simulate trajectories of this system over non-dimensional time T = 10 using both a discrete stochastic method (the SSA, see Section 5) as well as a deterministic (ordinary differential equation) method (Fig. 5). In the stochastic case, the trajectories are different in each simulation (Fig. 5, coloured lines), and when many of them are run a full probability density function can be found (Fig. 5, blue curves). When initial X (denoted X(0)) numbers are high, X at final time (X(T)) is generally also high (Fig. 5A), and similarly for low X(0) (Fig. 5C). However, X(T) can often end up in the other stable state, especially for intermediate values of X(0) (Fig. 5B). In contrast, using the deterministic model, each X(0) always produces the same X(T) (Fig. 5, black lines). The deterministic solution switches from one trajectory (corresponding to high or low X(T)) to the other at the intermediate, unstable equilibrium state (around X(0) = 250 for these parameters). Note that with the parameter regime used here, the system is always bistable: although it appears that there is only one stable state in Fig. 5A and C, if the stochastic simulations were run for a long simulation time T the resulting probability distributions would all look similar to that in Fig. 5B.

Fig. 5.

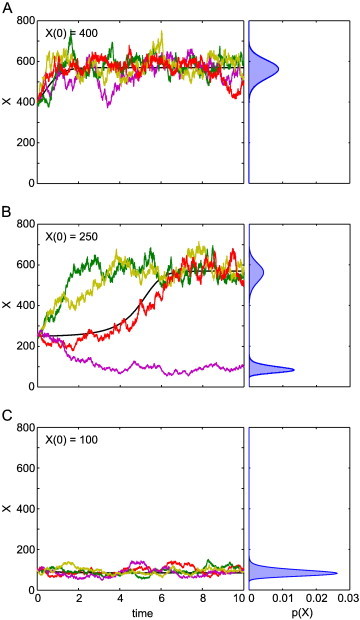
Simulations of the Schlögl system using deterministic and stochastic methods. Four typical trajectories of the SSA (coloured lines, left panels) and ordinary differential equations (black lines, left panels). The full distribution at simulation time T = 10, in the limit of a large number of simulations, is shown in the right panels for each initial configuration. Note that here we actually used the master equation (see Section 5), which can be solved numerically for this problem, to generate these as it allowed for faster computation. Parameters used are A = 10⁵, B = 2 × 10⁵ and c₁ = 3 × 10^− 7, c₂ = 10^− 4, c₃ = 10^− 3, and c₄ = 3.5.

Running many stochastic simulations reveals the full probability distribution, asymptotically approaching exactness as simulation number is increased; in contrast, a deterministic simulation can only ever find one point from the full distribution, an obvious simplification even of a unimodal distribution. Moreover, in the case of bimodal systems such as the Schlögl reactions, a deterministic simulation can find at best one point on one of the peaks and so cannot be considered representative of the true behaviour of the system. On the other hand, deterministic simulations are generally much faster to run than their stochastic counterparts, and in many cases their result does represent some useful statistic of the system (for instance, the mean of a symmetric, unimodal distribution) — but this can usually only be determined after comparison with stochastic results. For a more technical description of the precise relationship between stochastic and deterministic models, see Ref. [80]. Deterministic methods are an important class of modelling and simulation methods: they have been used extensively in many fields, they often obtain good results, are much faster to solve than stochastic methods, and have mature fields dedicated to their analysis and solution. They are complementary to the stochastic methods we focus on in this mini-review and both can be employed in concert with each other.

4. Accounting for stochasticity

In an ideal world with infinite computational power, we might think that we could run simulations involving every single atom and its electrons to solve every possible problem with perfect accuracy, by tracking their individual positions and momenta (a hypothetical perfectly accurate version of molecular dynamics). However this would not be possible for two reasons: 1) quantum effects would introduce randomness (the only way to fully incorporate this is to use a quantum framework that is inherently probabilistic, rather than deterministic); and 2) even forgetting about quantum effects, the simulations would be very sensitive to initial conditions because of the extreme complexity of the problem. But the accuracy of a model's initial conditions depends on the sensitivity of our instruments, which will never be fully perfect. Thus, at best, our simulations could give us excellent approximations to reality for finite time spans. Finally, we do not live in an ideal world and even our current, approximate, molecular dynamics simulations are extremely computationally intensive, so we are nowhere near to the ideal-world scenario above. For now, therefore, when we are interested in simulating relatively complicated systems for longer than milliseconds, it makes sense to simplify the model to remove extraneous information. If we are not explicitly interested in the positions and momenta of all molecules, then we can simply forget about them and focus only on how the total number of each molecular species changes through time. Doing this means we must now abandon our deterministic formulation, label all this extra information that we have abandoned as a ‘black box’ represented as randomness (see below), and treat the problem as a stochastic one.

Biochemical systems can involve many different types of molecules, which vary in size and number, moving around in a solution (for instance, the inside of a cell or a test tube); we are typically only interested in a subset of them. Inevitably, the molecules will experience a series of collisions with each other, sometimes with another molecule of interest and sometimes with other molecules. A fraction of these collisions will be between molecules of the correct type, energy and direction to be reactive, rather than elastic, collisions. We now make two key assumptions, that non-reactive collisions are much more frequent than reactive ones, and that the system is in thermal equilibrium. These ensure that the system is ‘well-mixed’ and our molecules of interest are distributed ‘macroscopically homogeneously’ throughout the volume (that is, randomly with a uniform distribution) [81]. Looking at the probability that a reaction occurs in an infinitesimal time interval, we can show that the time between reactions has an exponential distribution. We do not go into the mathematical details here; Gillespie's original text gives a coherent step-by-step account (Ref. [82], p. 2344). This implies that the number of reactions occurring in some time interval is given by a Poisson random number (Ref. [83], p. 1719), as was also suggested by Spudich and Koshland to explain their observations [41]. These results arise directly from considering the interactions of the molecules of the system in a probabilistic sense under the assumptions above. The derivation justifies the use of mass action kinetics, where the propensity, or instantaneous probability, of a reaction is given by a rate constant multiplied by the abundance of reactants (number for discrete methods, concentration for continuous ones; the rate constant changes accordingly [84]). The population numbers are random variables, since the reactions occur randomly. Combined with the above conditions, this means that we can use a Markov jump process to model the time evolution of this system [81,82,85,86]. These make discrete jumps in state, with the current state of the system only depending on the previous state. The mathematics behind this Markov formalism has been thoroughly researched and we do not focus on it here [68,86] — it is, however, important to know that our models are based on this framework.

For biochemical reaction systems that satisfy the assumptions above, the simplification we have made results in a huge decrease in computational effort whilst still allowing us to tell how the molecular populations behave over time in a statistically exact way (where ‘statistically exact’ means that the simulation results have statistics identical to that of the Markov process that we have assumed describes our system) [81]. Indeed, this exactness should also hold for other systems that obey the same assumptions, i.e. they are spatially homogeneous and well-mixed by frequent collisions (or an active mixing mechanism), and whose interactions can be assumed to be collision-driven. Of course, for systems that do not satisfy these assumptions, the simulations will not be exact; in this case, we may be able to assume similar principles but can no longer rely on a rigorous derivation, leaving us with a standard phenomenological model.

Now, how important is this property of exactness? Overall, it may not be a hugely important factor, for three reasons. Firstly, although the simulation results may exactly stick to our model, by its very nature the model will not be an exact representation of reality, and so will itself be ‘inexact’ to some degree, as discussed in the Introduction section. Secondly, even when a method is exact in this way, it is only in the limit of infinite simulations (or when solved analytically, for the master equation), and as we are restricted by computational time the simulation number will often not be as close as we would like to this limit. Finally, and most significantly, there is usually a large amount of uncertainty in the measurements that experiments can produce due to the numerous sources of error (e.g., [87]). Experimental error levels can often be much higher than the difference between exact and approximate simulations, thus negating the advantage of an exact method.

This approach was initially introduced to simulate the time evolution of dilute gases, as it relies on the assumption that the reactions are activation-controlled (called ‘ballistic’ by Gillespie), meaning that the molecules diffuse to within reacting distance of each other faster than the reaction can occur [18,88]. More recently, it has been extended to dilute solutions in a bath of solvents, which because of their slow rate of diffusion are diffusion-controlled, that is the molecules diffuse slowly compared to the reaction time [88,89]. This latter case is clearly the more relevant to cell biology, as both the interior and exterior environments of cells are much more like a dilute solution than a gas. In fact, although most applications of these methods in cell biology were for simulating liquid solutions, it had not been rigorously shown prior to Ref. [89] that the formulation would still hold for such cases.

There is now overwhelming evidence that the inside of the cell is far from being a homogeneous environment, and there are many factors that constrain the movement of molecules (known as macromolecular crowding) [90–92]. When these effects become too strong, our main assumptions no longer hold and the methods we describe in this mini-review may not be accurate anymore. This is currently an active area of research [88,93,94]. Despite this, there are many cases where macromolecular crowding is not an issue [92], or where we can approximately say that this is the case. Thus, like ODEs, non-spatial stochastic methods remain extremely useful theoretical tools, but even more so for systems with low numbers of molecules. As always with modelling, we have to be aware of our assumptions and make sure they hold in each particular problem.

5. Stochastic methods

Summarising the previous section, we have assumed that our system is well-mixed and in thermal equilibrium, and the molecules inside are moving around randomly. This implies that the molecules are distributed randomly, roughly homogeneously inside the volume (with equal probability of being found anywhere, that is). This tells us that the probability of a single reaction occurring within some short time period is a function only of X, the current state of the system (and a rate constant) [81,82,85,86]. Therefore, because the molecular populations are random variables and their values after the next reaction depend only on their current values, we can model the time evolution of such systems as Markov jump processes [81,86].

We saw earlier the three types of heterogeneity in biological systems. So far in our discussion of stochastic methods, we have only considered intrinsic heterogeneity. Thus the methods below inherently incorporate intrinsic, but not other sources of heterogeneity. However, this is not a problem: genetic and environmental heterogeneity can be included even in deterministic simulations, and it is the intrinsic contribution that they are missing. Genetic heterogeneity can roughly be assumed to stay constant over simulation time, whereas environmental heterogeneity can vary on a timescale that is comparable to the cell cycle time [62]. The way to incorporate these is by using different initial conditions, parameters and reaction propensities. In the case of genetic or slowly-changing environmental heterogeneity, these are set at the start and kept constant; for faster-changing environmental heterogeneity, the parameters or reaction propensities can be varied over the course of the simulation [95]. Their values can be chosen randomly from some distribution (known or assumed), or set manually if we have enough information about the system.

5.1. Master equation

One starting point in the Markov formalism is to write down a so-called master equation [85], which gives an exact and full description of the behaviour of the Markov process through time. It consists of a system of coupled differential equations, with one equation for each possible state of the system at each time point, that can be evaluated to give a full probability distribution.

In simple terms, this chemical master equation asks the question “what is the probability that the system is in some state X at time t + 1?” The answer is made up of two contributions:

• 1.the probability that the system was already in state X at time t and did not change +
• 2.the probability that the system was in another state at time t and changed into state X.

Repeating this to find the probabilities of all possible states (and then forming it into a set of differential equations by taking the rate of change of these probabilities over time) yields the master equation.

Solving the master equation would seem to be the ideal way of looking at stochastic systems, as it can tell us the full distribution of possible states the system can be in over time, but for one major disadvantage: its complexity. This becomes apparent when considering how many equations must be solved at each time point, and bearing in mind that the number of possible states can increase exponentially with time. Analytical solutions can only be found for very simple systems with linear (mass action) reaction propensities [96]. The equations can also be directly solved numerically, giving approximations of the probability distribution; although for more complicated problems this is still impractical due to the large number of possible states, recent work has shown that it is becoming a viable approach that can sometimes be faster than simulation for realistic systems [97–102].

It is also possible to derive the moment equations for the stochastic model from the master equation; these are deterministic differential equations that describe only the values of the moments (for instance, the mean) through time, rather than the entire distribution. In general, except for the case of linear reactions again, they also form an infinite set of equations that must be closed manually, thus introducing errors [103–105]. Another approach is to use the linear noise approximation of van Kampen on the master equation, which yields information on the behaviour of the mean plus small fluctuations about it (that is, the second central moment of the full distribution) in the limit of continuous molecular populations [68,106].

Nevertheless, it is often the case that the systems in which we are interested are too complicated to solve using the master equation approach, even numerically or via an approximate method. Thus we must use trajectory-based approaches, which differ from the master equation in that they do not find the distribution of all possible states over time. Rather, they simulate single realisations, meaning that at each step they choose one out of all the possible outcomes. The trajectory of each stochastic simulation is different (as in Fig. 5), since each is a single realisation sampled randomly from the full distribution given by the master equation. Given many of these random single trajectories, we can build up a picture of the full distribution.

5.2. Stochastic simulation algorithm

This brings us to the workhorse stochastic method for many researchers today: the stochastic simulation algorithm (SSA; also known as the Gillespie method or Gillespie SSA) [82]. This method is statistically exact — that is, a full probability distribution built up from an infinite number of simulations will be identical to the distribution of the Markov process, given by the master equation (Fig. 6). The direct method implementation of Gillespie [82] is arguably the simplest SSA variant, and it is conceptually very easy to understand: in order to simulate one stochastic realisation, we must step along in time, choosing 1) when the next reaction will happen, and 2) what that reaction will be. The SSA is very popular and its algorithmic simplicity ensures that it is easy to start using for practical simulations. For this reason, we recommend it as a starting point for readers interested in trying stochastic simulations in their own research. We do not give exact algorithmic instructions here, as there are detailed instructions in many other sources, such as Refs. [18,20,23,82,88]. There is also complete software available to start using the SSA straight away (see Table 1). The SSA can also be used to simulate delays in intracellular processes [107,108].

Fig. 6.

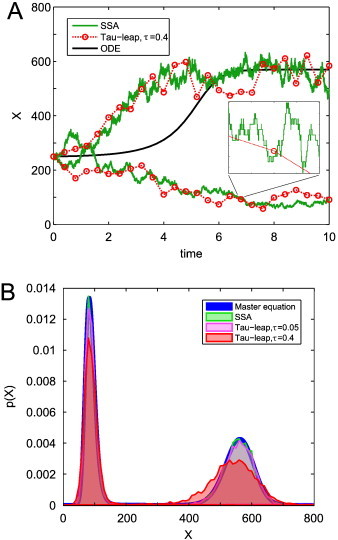
Comparison of simulation methods. (A) Two typical trajectories each from the SSA (green line) and tau-leap (red dotted line) and ordinary differential equation solutions (black line). The inset shows an enlargement between t = 6.7 and t = 6.9 to highlight the discrete steps of the SSA. (B) Full probability distributions at final time T = 10 generated from 10⁴ simulations of the SSA and tau-leap with step sizes 0.05 and 0.4, compared to the solution of the master equation (from which the SSA is almost indistinguishable). Here X(0) = 250.

Table 1.

Advantages and disadvantages of several modelling/simulation methods.

Simulation method	Cat.	Advantages	Disadvantages	References	Software
Master equation	4	Exact	Very computationally intensive	[85,143]
SSA	4	Statistically exact	Very computationally intensive	[82,109]	COPASI [144] StochKit [145] STOCKS [146] BioNetS [147]
Tau-leap	4	Relatively fast	Approximate; too slow for large systems or frequent/multiscale reactions	[83,113,118]	StochKit [145]
Higher-order	4	Relatively fast; accurate	Approximate; too slow for large systems or frequent/multiscale reactions	[83,121,122,124,125]
Multiscale/hybrid	4	Fast; good for systems with disparate reaction scales	Approximate; problems with coupling different scales	[131,132,137,139,148]	COPASI [144] BioNetS [147]
Brownian dynamics	2	Tracks individual molecules	Slow; molecule size must be artificially added	[149,150]	Smoldyn [149,151] MCell [152]
Compartment-based	3	Accounts for diffusion between homogeneous compartments	Slow; compartment size must be set manually; each compartment is homogeneous	[150,153,154]	MesoRD [153] URDME [155]
SDE	5	Fast	Continuous; Gaussian noise	[76]	BioNetS [147]
PDE (R-D)	6	Very fast; spatial	Continous; no noise	[156]
ODE	6	Very fast	Continuous; no noise	[157]

Cat. represents Category from Fig. 2. Abbreviations: SSA, stochastic simulation algorithm; SDE, stochastic differential equation; PDE (R-D), partial differential equation (classical reaction-diffusion equations); ODE, ordinary differential equation.

Unfortunately, the direct method SSA pays the price for its simplicity in computational time, as two random numbers must be generated at each step. The next reaction method is significantly more complicated but also faster for large systems and many reactions, with several algorithmic improvements to increase speed [109]; several other variants of the SSA have since been developed, also making improvements in computational speed [110,111] (further examples are helpfully summarised in two recent reviews [18,88]). However, despite these increases in computational speed, the SSA has an inherent limitation: it must simulate every single reaction. This is, of course, its great strength too, but in cases where there are many reactions or larger molecular populations, it often becomes too slow to generate useful numbers of simulations in a practical time period.

5.3. Tau-leap

In such cases, which occur quite often in real applications, we must turn to the tau-leap method [83]. This is similar to the SSA in that each simulation is a single stochastic realisation from the full distribution at each step. However, the steps are much larger (hence its name), their selection now being based on considerations of efficiency and accuracy. It counts the total number of occurrences of each type of reaction over that step. Thus if there are M reactions, we take M Poisson random number samples based on the molecular populations at the beginning of the step. This has the key advantage that we now do not need to spend time simulating individual reactions. Therefore, the tau-leap is much faster than the SSA: although this is very problem-dependent, it is not uncommon to observe speedups of two orders of magnitude. However, its main drawback is that we have lost accuracy compared to the SSA, in three ways: first, we do not know exactly how many reactions occurred (we can only estimate this), second, we do not know exactly when each reaction occurred within the time step, and third, we cannot account for the fact that each reaction may affect the probability of the other reactions occurring by altering the chemical populations. This is illustrated in Fig. 6, comparing the master equation and SSA to the tau-leap with two different error levels. With the larger error level, the tau-leap has quite noticeably lost some accuracy. Finally, taking M Poisson random number samples per step can also be computationally intensive, depending on the size of M. The accuracy issue can be mitigated (at the expense of computational time) as the error level, and so time step size, is decreased; indeed, as the time step tends to zero, the tau-leap effectively becomes the SSA, with each step experiencing either zero or one reaction. Some implementations combine the SSA with tau-leaping via a threshold on the number of molecules in the system at any given time.

The steps of the tau-leap are chosen to maximise both computational efficiency and accuracy. However, these are generally mutually exclusive, so inevitably there is a trade-off to find the most optimal step size: the larger the time step, the less processing time the simulation takes but the more it loses accuracy, and vice versa. Several schemes have been devised to optimise the time step [112,113].

There is another, complementary, issue with the tau-leap: as many reactions are simulated at once, molecular species that are depleted in any reaction can go negative if the time step is too large. This is obviously unphysical, and so undesirable, and schemes have been developed that allow the choice of larger time steps whilst avoiding negative populations [113–118].

5.4. Higher-order tau-leap

Recently, another aspect of tau-leap methods has received attention, namely the order of accuracy. This is a mathematical property of numerical methods, and gives the answer to the question “by how much does the error of this method decrease as the time step is decreased?” The (weak) order of accuracy of the tau-leap is one [119–121], meaning that its error decreases proportionally to the time step. Higher-order methods have order greater than one, meaning that as the time step is decreased we gain accuracy compared to order one methods. Therefore, they allow us to use larger time steps to achieve the same error level, thus decreasing computational time. Their disadvantage is that they are mathematically more complicated. In addition, in the stochastic case it is not clear that methods up to arbitrarily high order can be constructed. Although, in fact, Gillespie himself first proposed the simplest such method along with the original tau-leap [83], this line of inquiry has only recently been the focus of more effort [121–126].

5.5. Multiscale methods

Although it is not uncommon for systems of interest to be rather complicated, this can often be overcome by using fast leaping methods. However, the classic counterexample is a system with reactions that operate at very different timescales, for instance one very slow and one very fast (called a ‘stiff’ system). These are not tractable via a master equation approach, either analytically or numerically, because the fast reactions increase the possible state space very quickly. The SSA would simulate every single fast reaction, and in doing so require huge computational effort. Ironically, although they constitute the vast majority of reactions in stiff systems, often the fast reactions are transient (that is, they settle down quickly after a slow reaction occurs) and what we are really interested in is the overall slow-scale dynamics of the system. Thus we again rely on approximate methods. Although standard tau-leap and higher-order tau-leap methods are able to simulate these systems, their time steps must be reduced, which can dramatically slow down simulation time when the separation of the scales is large and the fast reactions very frequent.

In such cases, we have two options: implicit methods or multiscale methods. On the one hand, implicit methods are based on deterministic methods for stiff systems. Their approach is to allow the use of normal-sized time steps by expanding the range of time steps where the method is stable, thus opening the door for stiff systems to be simulated in similar time periods as non-stiff ones [127–129].

On the other hand, multiscale methods partition reactions into fast and slow types, then simulate the reactions separately. Many different multiscale methods have been developed, so here we discuss their general outlines. The fast reactions are usually simulated using an approximate method (often deterministic approaches like moment equations derived from the master equation, or stochastic or ordinary differential equations) and the slow reactions using a more accurate stochastic method (stochastic differential equation, tau-leap, or SSA) [130–136]. The fast reactions can assume that the slow reactions are constant over their timescale; the slow reactions can assume that the fast reactions have relaxed to asymptotic values between each slow reaction. Thus, the two sets of reactions are simulated semi-independently. This can also be generalised to three or more regimes [137]. This approach allows for significant reductions in computational time as the fast reactions, which would take up the most computational effort, can be simulated very quickly with continuous methods. However, it also introduces errors associated with coupling the two scales, as well as the possibility of errors from the simulation of the fast reactions. These can be substantial when some molecular populations are very low. An interesting exception runs short bursts of a single SSA for the fast reactions, which is used to infer parameters for a differential equation approximation of the slow reactions [138,139].

6. Summary and outlook

In this mini-review, our aim has been to give an introduction to the background and an overview of discrete-state stochastic modelling and simulation methods that are commonly used in systems biology today to take account of stochasticity. We have deliberately avoided the mathematics that is typically used in such reviews to make this work more accessible for beginners and those with non-mathematical backgrounds interested in these methods. For a more mathematical introduction, the reader is encouraged to consult Refs. [18,20,21,23]. We have covered the major groups of methods within the discrete stochastic umbrella, and discussed their advantages and disadvantages; this information is distilled into Table 1. Where possible, we have also included in Table 1 software available for making use of these methods quickly and easily.

These methods are not only used in cell biology; they have also been employed in many other settings. For instance, the SSA has been used for population biological models [140]. In addition, it is widely used in chemistry and physics [141]; in fact, an identical approach was developed simultaneously for use in physics, known as the kinetic Monte Carlo algorithm [142].

As our space is limited, we have focussed our attention only on discrete stochastic methods that do not take spatial considerations into account (category 4, Fig. 2). However, there are many related methods (categories 2–6, Fig. 2) and the problems they can be used to address have a large amount of overlap. Although we have included molecular dynamics simulations in Fig. 2, the figure is not to scale, and there is a much bigger gap between molecular dynamics (category 1) and individual-based methods (category 2) than between individual-based methods and the rest. We have included methods in categories 2 to 6 in Table 1 with some references as a starting point. Common examples, with their category from Fig. 2 given in brackets, include Brownian dynamics (2), compartment-based methods (3), stochastic differential equations (5), reaction-diffusion equations (6, spatial) and ordinary differential equations (6).

One related area that we have not covered in this work is parameter inference and model selection (top arrow, Fig. 1), which is very important for testing and improving mathematical models. This involves using statistical methods to find model parameters from the available experimental data, and to discriminate between which model best fits this data (e.g., [67,158–160]). This is typically not an easy task, as there is often not as much data as would be statistically desirable and what data is available can be noisy; Bayesian approaches offer a way of surmounting these problems [84]. Three useful references that give an introduction to this fast-developing field are Refs. [22,23,84].

Finally, we turn to our opinion of what lies ahead for the field. There is still a lot of work ongoing to refine both the SSA and approximate methods. This is obviously an important task. However, as more and more new and improved such methods are being developed, it may be time to focus on the step-change improvements we can make. In particular, there are three areas where we stand to make significant improvements. Firstly, we are in the age of parallel processing, and parallelised stochastic methods allow us to start harnessing this power. This can be done using a standard desktop computer [161] or high-performance clusters. Moreover, modern graphics cards now have substantially more raw processing power than CPUs, as they consist of thousands of parallel graphical processing units. Because of the architecture of graphics cards this does not translate into a like-for-like decrease in computational time, but with proper parallelised methods it can be greatly reduced. Work in this area is ongoing [162–164]. Secondly, many multiscale methods have already been developed, but as multiscale problems are so common in real applications, we still have plenty of potential for development in this area. In particular, linking the fast and slow reactions introduces errors. The future promises super-multiscale models, where processes on many different scales are integrated into one model. For instance, one long-term goal of systems biology is patient-specific medicine, where a customised model of the entire body is generated and then used to diagnose and pinpoint remedial action for the patient [165]. In such cases, we would need more than two or three different modelling regimes because of the sheer differences in scales involved. Thus it is necessary to think about how we can develop models with many different scales, and link them together accurately. Finally, we believe that there is excellent potential in the related area of spatial stochastic methods. The limitation of non-spatial methods is that they can only be accurately applied to spatially homogeneous systems, but this assumption does not hold in many (or even most) cases of interest. For instance, the membrane of the cell is an extremely heterogeneous environment, and even the cytoplasm contains many macromolecules that impede diffusion [90]. It is important to develop methods that can take proper account of such heterogeneous environments.

In summary, discrete-state stochastic methods have now come into their own, especially in the last two decades, and they are now widely used in the sciences. Although we have made good progress in improving the basic methods and developing new ones, we still have some way before we can accurately simulate the wide variety of systems presented by the natural world.