Mechanism of Spatial Ca²⁺ Selectivity of a Ca²⁺ Sensor in Complex with a Ca²⁺ Source

Abstract

Calmodulin (CaM) in complex with Ca²⁺ channels constitutes a prototype for Ca²⁺ sensors that are intimately co-localized with Ca²⁺ sources. The C-lobe of CaM senses local, large Ca²⁺ oscillations due to Ca²⁺ influx from the host channel, and the N-lobe senses global, albeit diminutive Ca²⁺ changes arising from distant sources. Though biologically essential, the mechanism of global Ca²⁺ sensing has defied explanation. Here, we advance a theory of how global selectivity arises, and validate this proposal with new experimental tools enabling millisecond control of Ca²⁺ oscillations within nanometers of channels. We find that global selectivity arises from rapid Ca²⁺ release from CaM combined with greater affinity of the channel for Ca²⁺-free versus Ca²⁺-bound CaM. The emergence of complex decoding properties from the juxtaposition of common elements, and the techniques developed herein, promise generalization to numerous molecules residing near Ca²⁺ sources.

Ca²⁺ constitutes a ubiquitous signal with wide-ranging biological impact (Berridge et al., 2000). Despite the pervasive nature of Ca²⁺, its detection can be highly selective in space and time, as required for specificity in signaling to appropriate targets (Bootman et al., 2001; Cullen, 2006; De Koninck and Schulman, 1998; Dolmetsch et al., 1998; Gu and Spitzer, 1995; Li et al., 1998; Oancea and Meyer, 1998; Winslow and Crabtree, 2005). Among the most critical of these detection modes are those relating to Ca²⁺ sensors positioned in close proximity, i.e. within nanometers, of Ca²⁺ sources. This placement of sensors in the ‘nanodomain’ of sources promotes rapid and privileged Ca²⁺ signaling (Augustine et al., 2003; Bootman et al., 2001; Catterall, 1999). However, such proximity to a Ca²⁺ source challenges a sensor's ability to integrate Ca²⁺ signals from distant sources, which is essential for coordinated signaling at the whole-cell level.

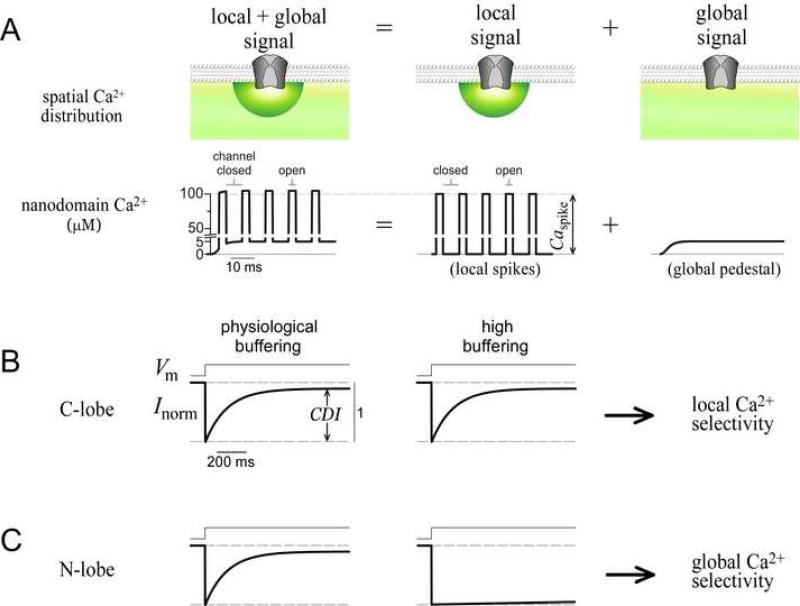
A prototype for coupled sensors and sources is the Ca²⁺ sensor calmodulin (CaM), in its regulation of the Ca_V1-2 family of Ca²⁺ channels (Dunlap, 2007). CaM is continuously complexed with channels as a resident Ca²⁺ sensor (Erickson et al., 2001; Pitt et al., 2001), and Ca²⁺ binding to the C- and N-terminal lobes of CaM can each induce a separate form of regulation on the same target channel (DeMaria et al., 2001; Yang et al., 2006). Given the approximate diameter of Ca²⁺ channels (Wang et al., 2002), the resident CaM would be positioned ~10 nm from the channel pore, in the nanodomain of these channels. As such, it is intriguing that each lobe responds selectively to distinct Ca²⁺ signals (cartooned in Figure 1A), which differ in both their spatial distribution (top row) and temporal characteristics (bottom row). Under physiological conditions, the composite Ca²⁺ signal (Figure 1A, left column) is the sum of two distinct components. First, Ca²⁺ inflow during channel openings produces a ‘local signal’ component (Figure 1A, middle column) comprising brief yet intense local spikes of amplitude Ca_spike ~100 μM (bottom row). These spikes are tightly synchronized with openings of the host channel, and localized to the nanodomain (top row, green hemisphere) (Neher, 1998; Sherman et al., 1990) (Supplementary Information 3). Second, accumulation of Ca²⁺ from distant sources (e.g., other Ca²⁺ channels) generates a ‘global signal’ component (Figure 1A, right column) consisting of a far smaller (~5 μM) global pedestal (bottom row), which is spatially widespread (top row, green shading). In the Ca_V1-2 family of Ca²⁺ channels, regulation triggered by the C-lobe of CaM exploits channel proximity and responds almost maximally to the local Ca²⁺ signal alone (Liang et al., 2003). This ‘local selectivity’ is schematized for a Ca²⁺-dependent inactivation process (CDI) triggered by the C-lobe (Figure 1B). CDI produces a strong decay of Ca²⁺ current during sustained voltage activation whether Ca²⁺ is buffered at physiological levels, or much more strongly (Figure 1B). Since high Ca²⁺ buffering eliminates the global pedestal while hardly affecting local spikes (Figure 1A, middle column; Supplementary Information 3) (Neher, 1998), the sparing of CDI under this condition indicates that the local signal alone is sufficient. By contrast, N-lobe mediated regulation of all Ca_V2 channels somehow prefers the diminutive global pedestal over the far larger local spikes. The hallmark of this ‘global selectivity’ is the presence of strong CDI in physiological buffering (Figure 1C, left), and its near absence in high buffering (Figure 1C, right) (DeMaria et al., 2001; Liang et al., 2003). Without this detection mode, Ca²⁺ feedback would be restricted to isolated complexes, and lack coordination over larger regions. Global selectivity is thus critical to the Ca²⁺ signaling repertoire of Ca²⁺ sensors positioned near Ca²⁺ sources.

Figure 1. Definition of spatial selectivity.

(A) Cartoon of Ca²⁺ signals near a channel. Spatial (top row) and temporal (bottom row) profiles are shown. Note axis break in nanodomain Ca²⁺. Composite signal (left column) is the sum of local (middle column) and global (right column) components.

(B) Schematic of C-lobe CDI, which exemplifies local selectivity. Intracellular buffering conditions cause the Ca²⁺ input signals to correspond to those shown directly above in (A).

(C) Schematic of N-lobe CDI, which exemplifies global selectivity, buffering as in (B).

What are the mechanisms for the contrast in spatial Ca²⁺ selectivity of the lobes of CaM? The local preference of the C-lobe might be expected, since this lobe responds to the component of greater intensity. However, the global selectivity of the N-lobe is difficult to imagine. The simplest explanation would presume that while the C-lobe resides within the nanodomain, the N-lobe lies outside this zone, where the local signal would be smaller than the global pedestal (Figure 1A, top row). However, each channel is known to constitutively associate with a single CaM (Mori et al., 2004; Yang et al., 2007), and the lobes of CaM are very close to one another (< 6 nm), indicating that both lobes are likely within the nanodomain (Dunlap, 2007; Stern, 1992). Hence, the N-lobe must be insensitive to Ca²⁺ intensity, and instead may respond to certain temporal features of nanodomain Ca²⁺ (Figure 1A, bottom row). Though some Ca²⁺-dependent mechanisms that favor specific temporal patterns of Ca²⁺ have been characterized (De Koninck and Schulman, 1998; Oancea and Meyer, 1998 ), none can respond to signals of low amplitude and frequency (global pedestal), while ignoring signals of high amplitude and frequency (local spikes). Thus, global selectivity must employ a novel Ca²⁺ sensing mechanism.

Here, theoretical and experimental advances explain how global selectivity could be produced by a mechanism that favors persistent, rather than intense Ca²⁺ signals. This unusual property emerges from the combination of two common elements: rapid Ca²⁺ release from CaM, together with greater channel affinity for Ca²⁺-free (apoCaM) versus Ca²⁺-bound CaM (Ca²⁺/CaM). Since our proposed mechanism requires CaM/channel interactions as present within intact channels, we develop the means to probe Ca²⁺ dynamics within this integrated setting, using channels engineered for enhanced opening, with a novel ‘voltage block’ electrophysiological technique to precisely control nanodomain Ca²⁺. These tools resolved Ca²⁺ response characteristics clearly distinctive of the proposed mechanism. Combining this approach with manipulation of a recently identified CaM regulatory site (Dick et al., 2008) enables quantitative confirmation of a key prediction—selectivity can be incrementally changed from global to local by adjusting the ratio of apoCaM versus Ca²⁺/CaM affinities for a given channel. Our findings generalize across Ca_V1–Ca_V2 channels, and likely extend to diverse Ca²⁺ sensors situated near Ca²⁺ sources.

RESULTS

Dominant conformations of the CaM/channel complex involved in Ca²⁺ sensing

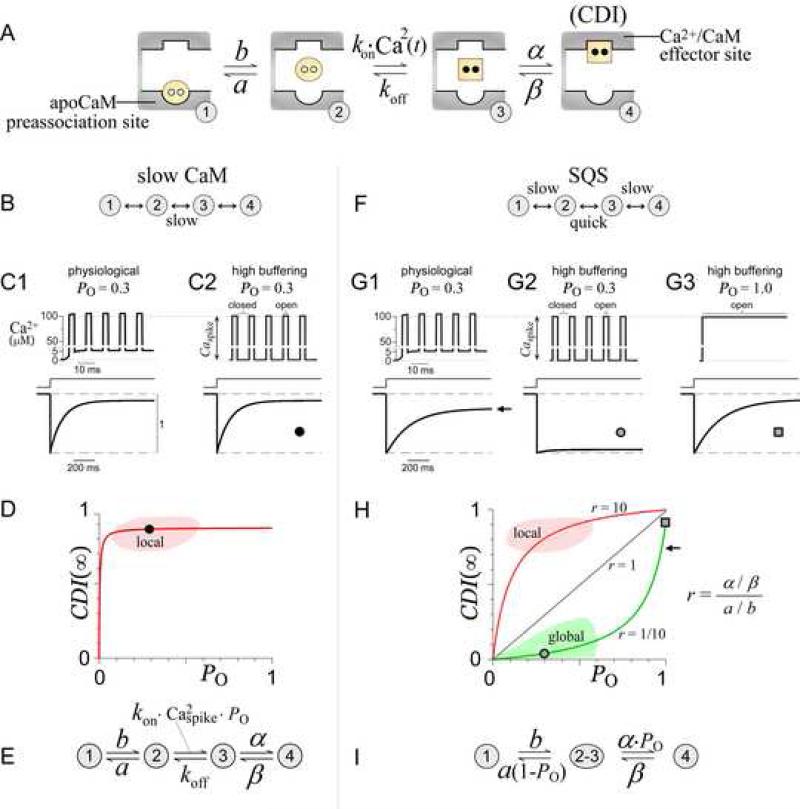
To explore how the CaM/channel complex could produce both local and global Ca²⁺ selectivity, we outlined a basic system comprised of the dominant conformations of this molecular assembly (Figure 2A). Several established features were considered. First, a 1:1 CaM/channel stoichiometry has been demonstrated (Mori et al., 2004; Yang et al., 2007). Second, two distinct types of CaM/channel interactions are known to exist: apoCaM binding, which anchors CaM to the channel as a resident sensor; and Ca²⁺/CaM binding, which here produces CDI. Finally, an appropriate first-order approximation was to separately consider the operation of the C- and N-terminal lobes of CaM, each with simultaneous (un)binding of two Ca²⁺ ions (Linse et al., 1991; Martin et al., 1985). This single-lobe approximation was reinforced in our experiments by the use of mutant CaM molecules that restrict Ca²⁺ binding to one lobe or the other (DeMaria et al., 2001; Peterson et al., 1999). Based upon these features, four main conformations result (Figure 2A, valid for either the N- or C-lobe). State 1 represents apoCaM (yellow circle) bound to the channel preassociation site (round pocket). Direct Ca²⁺ binding to CaM in state 1 is not considered, as such interaction is unlikely according to an analogous apoCaM/peptide structure (Houdusse et al., 2006). State 2 portrays apoCaM after it releases from the preassociation site, at which point it can bind Ca²⁺ to produce Ca²⁺/CaM (square) in state 3. We reason that a transiently dissociated lobe of CaM (state 2 or 3) does not diffuse away (retained within a channel alcove), because of the slow rate of exchange between perfused CaM and channel-associated CaM (Chaudhuri et al., 2005). Finally, in state 4, Ca²⁺/CaM binds the channel effector site (square pocket), which triggers CDI. The effector site is unlikely to bind apoCaM, because CDI is absent without Ca²⁺. Further arguments in support of this basic four-state configuration appear in the Discussion and Supplementary Information 1F.

Figure 2. Ca²⁺ decoding mechanisms for the CaM/channel complex.

(A) Basic states for a lobe of CaM in complex with a Ca²⁺ channel. In state 1, apoCaM (yellow circle) is bound to the apoCaM site (round pocket). In state 2, apoCaM is a transiently dissociated. In state 3, CaM binds two Ca²⁺ ions (black dots) to become Ca²⁺/CaM (yellow square), which can then bind the Ca²⁺/CaM effector site (square pocket), yielding CDI (state 4).

(B) Slow CaM mechanism, configurations of the basic system where switching between states 2 and 3 is slow relative to channel gating.

(C) Slow CaM numerical simulations exhibit local selectivity. Ca²⁺ signals (top) are given as input. Note Ca²⁺ axis break in panels C and G. Parameters (in ms^-1) α = 0.5, β = 0.05, a = 60, b = 0.04, k_off = 0.003, and k_on = 1.2×10¹⁰ M^-2 ms^-1.

(D) Slow CaM CDI(∞)–P_O relations exhibit local Ca²⁺ selectivity. Round symbol corresponds to simulation in (C2). Red curve corresponds to Equation 1, with parameters as in (C).

(E) Equivalent slow-CaM mechanism (see Supplementary Information 2).

(F) SQS mechanism has slow state 1-2 and state 3-4 switching, and quick state 2-3 switching, all relative to channel gating.

(G) SQS numerical simulations exhibiting global selectivity. Parameters (in ms^-1) α = 0.1, β = 0.01, a = 0.4, b = 0.004, k_off = 3, and k_on = 3.7×10¹² M^-2ms^-1.

(H) SQS CDI(∞)–P_O relations exhibit global or local selectivity. Symbols (circle, square, and arrow) correspond to simulations in (G). Green curve corresponds to Equation 2, with parameters as in (G). Gray and red curves demonstrate that increasing r, the ratio of channel affinity for Ca²⁺/CaM versus apoCaM, induces a shift from global to local selectivity.

(I) Equivalent SQS mechanism (see Supplementary Information 1).

Hypothesis for local Ca²⁺ sensing by the C-lobe of CaM

With this basic outline (Figure 2A), we first considered how the local Ca²⁺ selectivity of the C-lobe might arise. The C-lobe of CaM is known to release Ca²⁺ slowly compared to the millisecond duration of Ca²⁺ channel closings (Bayley et al., 1984; Black et al., 2005; Chaudhuri et al., 2007; Imredy and Yue, 1994; Martin et al., 1985), yielding a ‘slow CaM’ mechanism (Figure 2B). Given this scheme, numerical simulations readily exhibit local selectivity, with strong CDI produced by Ca²⁺ signals appropriate for both physiological Ca²⁺ buffering (Figure 2C1) and high buffering (Figure 2C2) (see legend and Methods for simulation details). This outcome is plausible because once CaM binds Ca²⁺ during a channel opening (Figure 2A, state 3), CaM will likely retain Ca²⁺ during millisecond closures, causing accumulation in state 3 that subsequently drives entry into state 4 (CDI) (Supplementary Information 2).

An analytical understanding of this mechanism is facilitated by considering a graphical ‘input-output’ relation for Ca²⁺ detection (Figure 2D). The ‘output’ is taken as the extent of CDI reached at steady-state (CDI(∞)), and the ‘input’ as the channel open probability P_O, both as observed under high Ca²⁺ buffering. In this regime, P_O specifies the fraction of time Ca²⁺ is present (the ‘fractional presence’ of Ca²⁺). This quantity is useful because nanodomain Ca²⁺ will achieve a steady concentration of Ca_spike within microseconds of channel opening, and rapidly decay to zero upon channel closing (Figure 2C2, top; Supplementary Information 3) (Sherman et al., 1990). Accordingly, P_O becomes directly proportional to Ca²⁺ entry, and thereby serves as shorthand for the Ca²⁺ input in this simplified context. A first beneficial outcome of this format is a visual definition of local Ca²⁺ selectivity. Specifically, an essential feature of local selectivity is the preservation of near maximal CDI under high buffering, with inputs spanning the range of naturally occurring P_O (~0.1 to 0.6). Therefore, the CDI(∞)–P_O relation for all processes with local selectivity must intersect the red zone in Figure 2D, as exemplified by the data point (round symbol) corresponding to our numerical simulation (Figure 2C2). The second advantage is that we can obtain a simple formula for the CDI(∞)–P_O response of the slow CaM mechanism. Under high buffering, slow Ca²⁺ release from the C-lobe allows the time-varying rate constant for transitions from state 2 to 3 (= k_on·Ca²(t)) to be replaced by a fixed value equal to k_on · Ca_spike² · P_O (Supplementary Information 2A). This yields the equivalent system in Figure 2E, from which algebraic manipulation gives the analytic CDI(∞)–P_O relation, with CDI(∞) proportional to steady-state occupancy of state 4. Specifically,

$$CDI\left(\infty \right)=G\cdot \frac{P_{\mathrm{o}}}{P_{\mathrm{o}}+K_{\mathrm{eff}}}$$ (1)

This relation resembles the Michaelis-Menton equation, with P_O analogous to substrate concentration. G incorporates the affinity of the channel effector site for the Ca²⁺-bound C-lobe, and K_eff reflects the balance between Ca_spike and CaM affinity for Ca²⁺ (Supplementary Information 2B). Though defined for high buffering, Equation 1 can be constrained by the strong CDI characteristic of Ca²⁺-detection processes under physiological Ca²⁺ buffering. In particular, it can be shown that strong CDI under physiological buffering requires G ~ 1 and K_eff << 1 (Supplementary Information 2C). Hence, any slow CaM mechanism will invariably produce local selectivity, with saturating CDI(∞)–P_O relations that intersect the red zone (Figure 2D, smooth curve).

Hypothesis for Ca²⁺ sensing by the N-lobe of CaM

Turning to the N-lobe, we ask whether an alternate operational mode of the scheme in Figure 2A can explain the unusual selectivity of the N-lobe for the diminutive global signal. In contrast to the slow Ca²⁺ kinetics of the C-lobe, N-lobe Ca²⁺ (un)binding should rapidly reach steady state within the millisecond durations of channel openings and closings (Bayley et al., 1984; Black et al., 2005; Chaudhuri et al., 2007; Imredy and Yue, 1994; Martin et al., 1985). Thus, the system would switch ‘quickly’ between states 3 and 2, in sync with channel openings and closings. A second difference from the C-lobe regime is that the kinetics of entry and exit from the outermost states become important. Switching between states 3 and 4 must be ‘slow’ because experimentally, both CDI onset and recovery take much longer than milliseconds (Schnee and Ricci, 2003). Remarkably, if switching between states 1 and 2 is similarly slow, the resulting SQS mechanism (‘slow quick slow’ in Figure 2F) can produce global selectivity—simulated CDI is strong under physiological buffering (Figure 2G1), but absent in high buffering (Figure 2G2) (see legend and Methods for simulation details). A more quantitative definition of the kinetic constraints for the SQS regime appears in Supplementary Information 1A.

Intuitively, this mechanism achieves global selectivity by combining two factors which collaborate to resist inactivation in response to transient and high-amplitude local Ca²⁺ spikes. Consider the case where only local spikes are present, such as in high buffering (Figure 2G2, top). First, since the preassociated form of apoCaM (Figure 2A, state 1) binds Ca²⁺ poorly, the long lifetimes in state 1 can ‘protect’ CaM from binding Ca²⁺ during brief Ca²⁺ spikes of high intensity. Second, should this first line of protection fail and state 3 be reached, rapid Ca²⁺ release ensures prompt return to state 2 during channel closures, thus preventing CDI (state 4) and favoring return to the apoCaM preassociated site (state 1). Under physiological buffering, however, global signals would bypass both protective measures. The persistence of a ~5 μM global Ca²⁺ pedestal (Figure 2G1, top), whose amplitude exceeds the micromolar Ca²⁺ affinity of the N-lobe, would outlast lifetimes in protected state 1 (Figure 2A) and subsequently allow state 2 to bind Ca²⁺ and accumulate in state 3, thus driving strong CDI (state 4). Likewise, even under high buffering, if a channel had a P_O of 1, the continuous local Ca²⁺ entry would produce a ~100 μM Ca²⁺ pedestal (Figure 2G3, top). This sustained Ca²⁺ signal would again overwhelm both measures of protection, resulting in strong CDI (bottom). This CDI is only slightly stronger than seen at the native channel P_O under physiological buffering (compare Figures 2G3 and 2G1), illustrating that the SQS mechanism is relatively insensitive to Ca²⁺ intensity. Instead, the contrast in CDI produced by different P_O values under high buffering (compare Figures 2G2 and 2G3) implicates a striking preference for the fractional presence of Ca²⁺.

Viewing these events in the graphical CDI(∞)–P_O format helps frame an analytical understanding of these events (Figure 2H). For orientation, the red zone associated with local selectivity is reproduced from Figure 2D. Additionally, a corresponding green zone for global Ca²⁺ selectivity can be specified, because all processes with global Ca²⁺ selectivity, regardless of mechanism, must exhibit near elimination of CDI by high Ca²⁺ buffering. Indeed, mapping the high-buffering SQS simulation (Figure 2G2) onto this graph (Figure 2H, round symbol) confirms the ability of the SQS mechanism to intersect this global zone (Figure 2H, green shading). Given this graph-based context, we can achieve an analytical understanding of the SQS mechanism, by obtaining the closed-form CDI(∞)–P_O solution (Supplementary Information 1A). Because multiple transitions will occur between states 2 and 3 before exiting to either state 1 or 4, a number of simplifications can be made according to the analysis of Neher and Steinbach (Neher and Steinbach, 1978). States 2 and 3 may be combined into a single state ‘2-3,’ with all rate constants replaced by time-independent equivalents (Figure 2I). Since transitions to state 4 can only occur from state 3, which is only occupied during channel openings, the rate constant from compound state ‘2-3’ to state 4 becomes α · P_O. Similarly, the rate constant from compound state ‘2-3’ to state 1 is a · (1 - P_O). From this equivalent system (Figure 2I), an analytic relation can be obtained:

$$CDI\left(\infty \right)=CD{I}_{\max }\cdot \frac{P_{\mathrm{o}}\cdot r}{P_{\mathrm{o}}\cdot (r-1)+1∕\epsilon +1}$$ (2)

with individual rate constants (a, b, α, β) defined in Figure 2A, γ = α / β, ε = a / b, and r = γ / ε. CDI_max accounts for the small P_O of inactivated channels (Imredy and Yue, 1994).

Equation 2 does more than codify a mechanism of global selectivity—this relation suggests that spatial Ca²⁺ selectivity is in fact a tunable property. In particular, the spatial selectivity of the N-lobe is predicted to be transformable between global and local extremes by adjusting the ratio of channel affinity for Ca²⁺/CaM versus apoCaM (parameter r). To appreciate these results, we note that CDI at P_O = 1 (square in Figures 2G3 and 2H) will always exceed the strong CDI present in physiological buffering (arrow in Figures 2G1 and 2H). This is true because the Ca²⁺ input from a channel with P_O = 1 under high buffering (Figure 2G3, top) is larger than the input from a channel with native P_O under physiological buffering (Figure 2G1, top). Hence, we need only consider parameters yielding CDI(∞)–P_O relations with strong CDI at P_O =1, as exemplified by our simulation. Given this constraint, we first evaluate the case where r = 1/10 in Equation 2, as is the case for the simulations in Figure 2G. Here, the equation produces a CDI(∞)–P_O relation that intersects the global zone, as well as the numerically simulated data points (Figure 2H, green curve). Because r < 1, the P_O coefficient in the denominator becomes negative, and Equation 2 now differs from a Michaelis-Menton relation. This yields an upward curvature indicating high sensitivity to the fractional presence of Ca²⁺, as represented by P_O. However, this is not the only mode of operation. Setting r = 10 yields a saturating relation that intersects the local selectivity region (Figure 2H, red curve). Finally, if r = 1, the relationship becomes a straight line, suggesting that spatial Ca²⁺ preference need not be categorized as strictly local or global (Figure 2H). In fact, the parameter r represents a bias which competes against the two measures of protection described above. If r < 1, with apoCaM binding stronger than Ca²⁺/CaM binding, the protective measures prevail, and a global selectivity results. By contrast, if r > 1, the protective measures are overpowered, and a local profile arises.

Stochastic view of Ca²⁺ sensing in the nanodomain of a Ca²⁺ channel

To obtain analytic solutions, we have thus far used ‘continuum’ equations, where the nanodomain Ca²⁺ concentration at every open channel (Figure 2G2, Ca_spike) is considered to be identical. This continuum view has often been used to model Ca²⁺ dynamics in the channel nanodomain (Naraghi and Neher, 1997; Neher, 1998; Sherman et al., 1990; Stern, 1992). However, given the small volume of a nanodomain (~20 nm hemisphere approximating the CaM/channel complex (Wang et al., 2002)), an average of only ~1 Ca²⁺ ion would be present during channel openings. While this corresponds to a large average Ca²⁺ concentration of ~100 μM, the actual integer number of nanodomain Ca²⁺ ions would differ considerably from one CaM/channel complex to the next. This scenario might raise concerns about the accuracy of continuum assumptions. To validate the slow CaM and SQS mechanisms as deduced by the continuum approach, we used MCell algorithms (Stiles and Bartol, 2001) to stochastically simulate individual Ca²⁺ ions as they diffuse and interact with the CaM/channel complex (Supplementary Information 3; Supplementary movie). These stochastic simulations fully confirm Equations 1 and 2. The main factor reconciling continuum and stochastic outcomes is the large flux of Ca²⁺ ions through an open channel (>2000 per millisecond). When viewed over the millisecond timescale of channel gating, every CaM/channel complex samples essentially the same large number of Ca²⁺ ions passing through the nanodomain. Thus, despite differences in the number of Ca²⁺ ions at a given instant of time, the continuum equations remain appropriate.

Experimental predictions for candidate mechanisms of Ca²⁺ decoding

We now state important and testable predictions of these Ca²⁺ sensing schemes.

(1) For C-lobe regulation, the slow CaM mechanism (Figure 2B) predicts that CDI(∞)–P_O relations should follow a saturating Michaelis-Menton profile (Equation 1, Figure 2D).

For N-lobe regulation, two predictions would confirm the SQS mechanism (Figure 2F).

(2) N-lobe processes need not always exhibit global Ca²⁺ selectivity, and adjusting the ratio of channel affinities for Ca²⁺/CaM to apoCaM (parameter r) should incrementally transform spatial selectivity between global and local extremes (Figure 2H). In particular, the value of r, as determined from fits of electrophysiological data with Equation 2, should be linearly related to the actual ratio of channel binding affinities for Ca²⁺/CaM relative to apoCaM.

(3) Experimentally resolved N-lobe CDI(∞)–P_O relationships should quantitatively match Equation 2, particularly in regard to nuances of shape (Figure 2H). The strongest support for the SQS mechanism would be the resolution of upward curvature in CDI(∞)–P_O relations with r < 1, because this outcome uniquely identifies the SQS mechanism from among a large class of alternatives (Supplementary Information 1).

Voltage-block technique for experimental determination of CDI(∞)–P_O relations

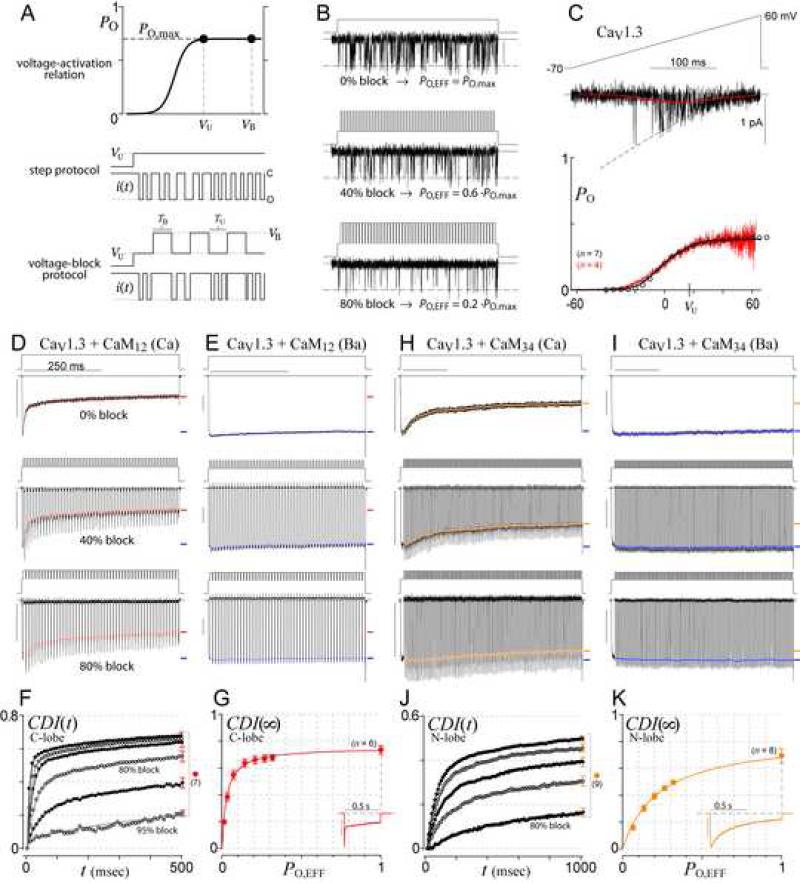
The main challenge in testing these predictions was the lack of an experimental method to determine CDI(∞)–P_O relations. This would require incremental adjustment of channel P_O, while holding unitary current size (and thereby Ca_spike) constant. Here we describe a novel ‘voltage block’ protocol that enables such P_O adjustability (Figure 3A). A key principle is that the P_O and thereby the pattern of channel gating will be identical during depolarizations to either the step potential (top graph, V_U, ‘unblocked’ voltage) or the reversal potential (V_B, ‘blocked’ voltage), so long as both potentials reside on the plateau of the voltage activation curve, drawn with maximal P_O = P_O,max. At V_U, channel openings would produce single-channel current i(t) as shown (middle row), characterized by P_O = P_O,max. At V_B, however, there is no driving force for Ca²⁺ entry even when the channel is open. Thus, by inserting repetitive blocking sojourns to V_B (bottom row), the same gating pattern (middle row) would appear to have a lower effective P_O (bottom row). By adjusting the time spent at V_B (=T_B) and the time spent at V_U (=T_U), we can freely dial-in this effective P_O according to P_O,EFF = P_O,max · T_U / (T_U + T_B). Ca_V1.3 single-channel records illustrate this paradigm (Figure 3B). The top row shows a Ba²⁺ current record without voltage block, with open probability P_O,max. The middle row illustrates a 40% block (P_O,EFF = 0.6·P_O,max), and the bottom an 80% block (P_O,EFF = 0.2·P_O,max).

Figure 3. Voltage block theory and experiment.

(A) Voltage block theory. Since both V_U and V_B are on the plateau of the voltage-activation relation (top row), the true channel open probability at either voltage is P_O,max, with channel gating as cartooned in the middle row. By choosing V_B at the reversal potential, sojourns to V_B effectively lower P_O (bottom row).

(B) Schematic of block effects on single Ca_V1.3 channel activity (Ba²⁺ currents).

(C) P_O,max calibration. Voltage ramps (top) evoked Ca_V1.3 single-channel Ba²⁺ records (middle, black trace), which were averaged (middle, red trace), and normalized by the open current level (middle, dashed curve) to yield the voltage-activation relation (bottom, red trace). The whole-cell tail-activation curve (bottom, circles) was scaled in amplitude to match that of the single-channel curve, whereas the whole-cell curve calibrated the single-channel relation along the voltage axis. Cell numbers (n) as shown. See Supplementary Information 4A-B for details.

(D-E) Voltage-block traces for Ca_V1.3 C-lobe inactivation (isolated with CaM₁₂₊) in Ca²⁺ (D) and Ba²⁺ (E). Voltage waveforms are above each current trace. Red symbols indicate time course of inactivation during each block cycle (Supplementary Information 4C). Final extent of inactivation indicated by red (Ca²⁺) or blue (Ba²⁺) dash. Scale bars 1 nA, 250 ms, throughout.

(F) Time course of pure CDI (Ca²⁺ inactivation normalized by Ba²⁺ inactivation). SEM is shown for the 500-ms time points, and is similar at other times. From top to bottom: 0%, 40%, 60%, 80%, 90%, 95% block.

(G) Experimentally determined CDI(∞)–P_O relationship, corresponding to 500-ms points in (F).

Inset: Low buffer data in 0.5 EGTA is a lower-limit proxy for P_O~1.

(H-K) Voltage block of N-lobe CDI (isolated with CaM₃₄); format as in (D-G), except all analysis is done after 1 sec. CDI time course (J) for 0%, 20%, 40%, 60%, 80% block (top to bottom).

Testing the slow CaM hypothesis by voltage-block of C-lobe CDI in Ca_V1.3 channels

We first applied voltage block analysis to Ca_V1.3 channels, as they exhibit strong C- and N-lobe mediated forms of CDI (Yang et al., 2006), facilitating tests of both slow CaM and SQS mechanisms in a uniform background. For P_O,max calibration, we determined the activation curve from single Ca_V1.3 records evoked by voltage ramps (Figure 3C, top). By averaging such records (middle, red trace), and normalizing by the open current level (dashed curve), we specified the activation curve (bottom, red trace). The single-channel result then calibrated whole-cell activation curves (circles, Supplementary Information 4A-B).

Thus armed, we explored the local Ca²⁺ selectivity properties of the C-lobe form of CDI. This type of CDI was isolated by coexpressing channels with CaM₁₂, a mutant CaM with selective retention of C-lobe Ca²⁺ binding (DeMaria et al., 2001; Yang et al., 2006). Figure 3D (top row) shows the sharp decay of Ca²⁺ current in the absence of voltage block, where the symbols indicate the precise inactivation time course (Supplementary Information 4C). Remarkably, with 40% block (middle row), inactivation is hardly changed. Not until ~80% block (bottom row) does inactivation weaken. Further, to account for any voltage-dependent effects, we repeated protocols using Ba²⁺ as the charge carrier (Figure 3E), given the poor binding of this ion to CaM. Though experiments showed little Ba²⁺ inactivation or sensitivity to voltage block, we still normalized inactivation time points in Ca²⁺ (Figure 3D) by those in Ba²⁺ (Figure 3E) to fully isolate the time evolution of pure CDI (Figure 3F). Plotting the terminal points (~CDI(∞)) as a function of P_O,EFF yielded the experimentally resolved CDI(∞)–P_O relation in Figure 3G. To obtain a lower-limit estimate of the P_O = 1 data point, we used the CDI measured under physiological buffering (Figure 3G, inset). As presented earlier, this is reasonable because the nanodomain Ca²⁺ signal for a channel with P_O = 1 under high buffering (Figure 2G3, top) would be larger than for a channel with native P_O ≈ 0.3 under physiological buffering (Figure 2G1, top). The data (Figure 3G) fit well with Equation 1 for the slow CaM mechanism (red curve), thus fulfilling prediction 1.

Testing the SQS hypothesis by voltage block of N-lobe CDI in Ca_V1.3 channels

For voltage-block of N-lobe mediated CDI in Ca_V1.3, we isolated this component of regulation by coexpressing a mutant CaM₃₄ , with selective retention of N-lobe Ca²⁺ binding (DeMaria et al., 2001; Yang et al., 2006). In this case, voltage-block yielded CDI(∞)–P_O data (Figures 3H-K) which formed a shallower, but still local Ca²⁺ profile (panel K), corresponding to an SQS profile with r = 5.44 (Equation 2). This outcome suggests that N-lobe mediated regulation of Ca_V1.3 may be a naturally occurring example where channel affinity for Ca²⁺/CaM exceeds its affinity for apoCaM (r > 1). Indeed, our recent data demonstrate that, unlike Ca_V2 channels, Ca_V1.3 channels contain an additional Ca²⁺/CaM binding site in their amino terminus, called NSCaTE (Dick et al., 2008). These findings may now be understood as fulfilling predictions of the SQS mechanism. Because NSCaTE only binds Ca²⁺/CaM but not apoCaM (Supplementary Information 5A), this additional site could tilt the balance of Ca²⁺/CaM versus apoCaM affinities towards an increased r, causing a shift to local selectivity.

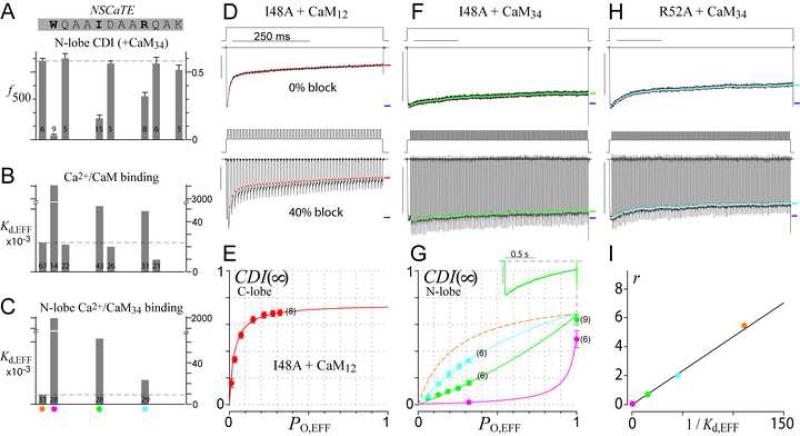
Stronger tests of prediction 2 would require experimental means to incrementally adjust r. Accordingly, we scanned the Ca_V1.3 NSCaTE (Figure 4A, top sequence) for alanine point mutations yielding graded effects on CDI and Ca²⁺/CaM affinity. The far left data bar reflects the baseline N-lobe CDI (f₅₀₀) for wild-type Ca_V1.3 channels under high buffering. Data bars to the right reveal a reduction in CDI for alanine substitutions at three residues (Figure 4A, top sequence, in bold) with the rank order of reduction: W44A > I48A > R52A. Consistent with expectations of the SQS mechanism, these mutations induced proportional effects on the live-cell FRET two-hybrid interaction between Ca²⁺/CaM and NSCaTE (Figure 4B). Here, EYFP fused to CaM was tested for FRET interaction with ECFP fused to a Ca_V1.3 amino terminal fragment bearing NSCaTE. Cell-to-cell variation in expression permitted resolution of binding curves which specified a relative dissociation constant, K_d,EFF (Erickson et al., 2003). The strong Ca²⁺/CaM interaction with intact NSCaTE (far left bar) was disrupted (heightened K_d,EFF) by alanine substitution at the same three residues. To more accurately estimate NSCaTE affinity for the Ca²⁺-bound N-lobe, as relevant for N-lobe CDI, we measured the FRET interaction between Ca²⁺/CaM₃₄ and NSCaTE (Figure 4C). Reassuringly, these changes in affinity mirrored more closely the functional alterations of N-lobe CDI (Figure 4A; Supplementary Information 5A).

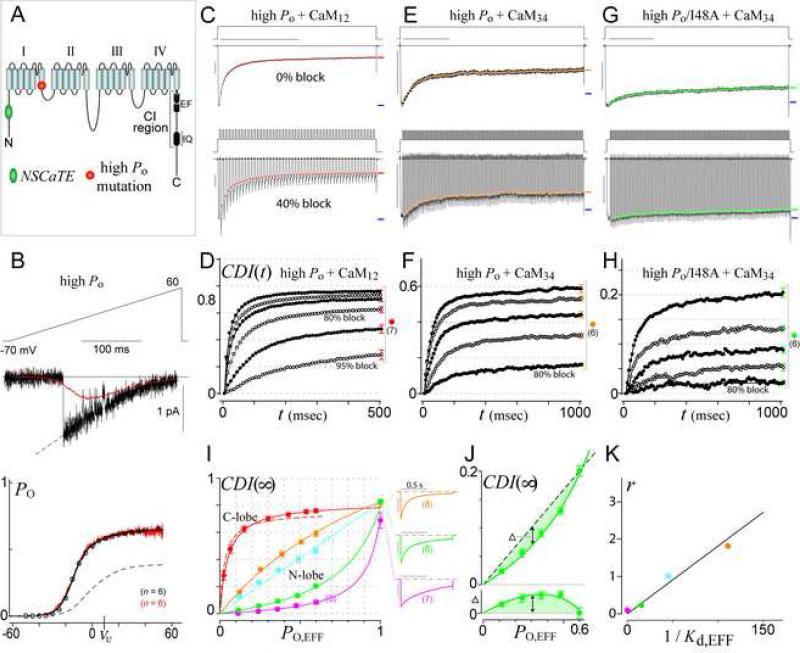
Figure 4. Mutations in NSCaTE transform N-lobe spatial selectivity of Ca_V1.3.

(A) Scanning alanine mutagenesis of Ca_V1.3 NSCaTE (top), with corresponding N-lobe CDI (isolated with CaM₃₄) in high buffering (bottom); f₅₀₀ is the difference in fractional Ba²⁺ vs. Ca²⁺ currents remaining after 500-ms depolarization. Leftmost bar, wildtype.

(B-C) Effects of alanine mutations on FRET interaction between α_1D NSCaTE and Ca²⁺/CaM (B) or Ca²⁺/CaM₃₄ (C). K_d,EFF is the effective dissociation constant (Supplementary Information 5A).

(D-E) Voltage-block of C-lobe CDI for I48A mutant of Ca_V1.3 (as in Figures 3D, G).

(F-H) Voltage-block of N-lobe CDI for I48A (F, G, green), and R52A (G, H, cyan). W44A mutant is coarsely plotted and fit (G, magenta). Dashed orange curve (G) replicates the native channel relation from Figure 3K.

(I) Correlation between 1/K_d,EFF from (C) and model parameter r from fits in (G). Color schemes as before (orange: wild-type NSCaTE; cyan: R52A; green: I48A; magenta: W44A).

Vested with these mutations, we examined their effects on CDI(∞)–P_O behavior. Our initial experiments investigated the I48A construct, because of its weak, but still readily measurable N-lobe CDI in 10 mM BAPTA. Single-channel activation was unchanged from wildtype (Supplementary Information 5B). As well, voltage block of its C-lobe mediated CDI (Figures 4D-E) produced data points (panel E, symbols) that were readily fit by the identical CDI(∞)–P_O relation as the wildtype channel (curve). These results emphasize that NSCaTE mutations can specifically modulate N-lobe regulation, and confirm that C- and N-lobes trigger genuinely distinct processes. Contrasting with the lack of collateral effects, the N-lobe CDI(∞)–P_O relation for I48A was converted into a global relation with apparent upward curvature (Figure 4F; Figure 4G, green), fitting nicely with a diminished r = 0.69. The wild-type NSCaTE relation (dashed orange) gauges the extent of this conversion. Additionally, the R52A construct yielded an intermediate relation (Figure 4H; Figure 4G, cyan, r = 1.98), and W44A produced the most extreme global relation (Figure 4G, magenta, r = 0.04). According to the SQS mechanism (Equation 2), r should be proportional to channel affinity for the Ca²⁺-bound N-lobe, assuming channel affinity for apoCaM is held constant. In this regard, NSCaTE only binds Ca²⁺/CaM and not apoCaM (Supplementary Information 5A), and its amino terminal location is distinct from carboxy-terminal apoCaM binding (Erickson et al., 2003; Pitt et al., 2001). Hence, the parameter r should be directly proportional to NSCaTE affinity for Ca²⁺/CaM₃₄ (∝ 1 / K_d,EFF in Figure 4C). The tight linear relation in Figure 4I between electrophysiological determinations of r (Figure 4G) and corresponding NSCaTE binding affinities for Ca²⁺/CaM₃₄ (Figure 4C) fulfills prediction 2, and furnishes substantive support for the SQS mechanism.

High P_O variant of Ca_V1.3 enables high-resolution voltage-block analysis

Though compelling, our high-buffering data have thus far been restricted by the low native P_O,max of Ca_V1.3 channels (=0.3), thus limiting important conclusions about CDI(∞)–P_O shape (prediction 3). Extensive mutagenesis revealed a novel L396P point mutation in Ca_V1.3 (Figure 5A) that considerably hyperpolarizes activation and doubles P_O,max (=0.6, Figure 5B). Fortunately, this P_O-enhancing mutation left both forms of CDI largely unchanged. The C-lobe profile for the L396P construct (Figures 5C-D; Figure 5I, solid red curve) was indistinguishable from the saturating wild-type relation (Figure 5I, dashed red curve), in support of prediction 1. As well, the N-lobe behavior was mostly unperturbed (Figures 5E-F; Figure 5I, orange, r = 1.8). Against this high-P_O background, the I48A mutation produced a highly-resolved global profile with r = 0.21 (Figures 5G-H; Figure 5I, green). The stronger W44A mutation showed a more pronounced global profile with smaller r = 0.075 (Figure 5I, magenta; Supplementary Information 5B), and the mildest R52A manipulation yielded the smallest conversion from local behavior (Figure 5I, cyan, r = 1.0). The linear relation between r and the channel affinity for Ca²⁺/CaM₃₄ (Figure 5K), here obtained from highly-resolved CDI(∞)–P_O data, further validates prediction 2. Importantly, both the high-P_O I48A and W44A mutants clearly exhibited upward curvature that was resolved even without the estimated P_O ~ 1 data. In particular, if the high-buffer I48A data from Figure 5I (green) is compared to a linear profile on an expanded scale (Figure 5J, top), the upward curvature becomes obvious. The undershoot of the data compared to the dashed linear profile is quantified by the difference plot below (Figure 5J, bottom), and the nonlinear fit of the SQS mechanism (green curve) statistically outperforms a linear fit (p = 0.003, F-test statistic). Analysis of W44A also indicates significant upward curvature (p = 0.05). These outcomes for high-P_O I48A and W44A constructs thus fully satisfy prediction 3 (Supplementary Information 4E). In sum, the fulfillment of all predictions by high-resolution data constitutes formidable evidence for both slow CaM (C-lobe) and SQS (N-lobe) mechanisms.

Figure 5. High P_O variant of Ca_V1.3 enables high-resolution voltage-block analysis.

(A) Cartoon of α_1D pore-forming subunit of Ca_V1.3, locating NSCaTE and high-P_O mutations.

(B) P_O,max calibration for high-P_O variant of Ca_V1.3 (as in Figure 3C). Dashed curve in bottom graph replicates the native channel relation from Figure 3C.

(C-D) Voltage-block of C-lobe CDI for high-P_O Ca_V1.3. Format as in Figures 3D, F.

(E-H) Voltage-block of N-lobe CDI for high-P_O Ca_V1.3 (E-F) and high-P_O I48A (G-H).

(I) High-P_O CDI(∞)–P_O relationships. Solid red curve corresponds to C-lobe CDI from (D). Dashed red curve replicates the native-P_O C-lobe profile from Figure 3G. Other curves correspond to high-P_O N-lobe CDI, with colors as before (orange: wild-type NSCaTE from (F); cyan: R52A; green: I48A from (H); magenta: W44A). Low buffer data in 0.5 EGTA (exemplars to right) are lower-limit proxies for P_O~1. Error bars show SEM, with cell numbers (n) as shown.

(J) Magnified view of high-P_O I48A profile from (I), showing only high-buffer voltage-block data obtained in 10 mM BAPTA. Comparison of data to a dashed linear relation (top), with difference between dashed line and data points (bottom), demonstrates clear upward curvature.

(K) Correlation between 1/K_d,EFF from Figure 4C and model parameter r from fits in (I).

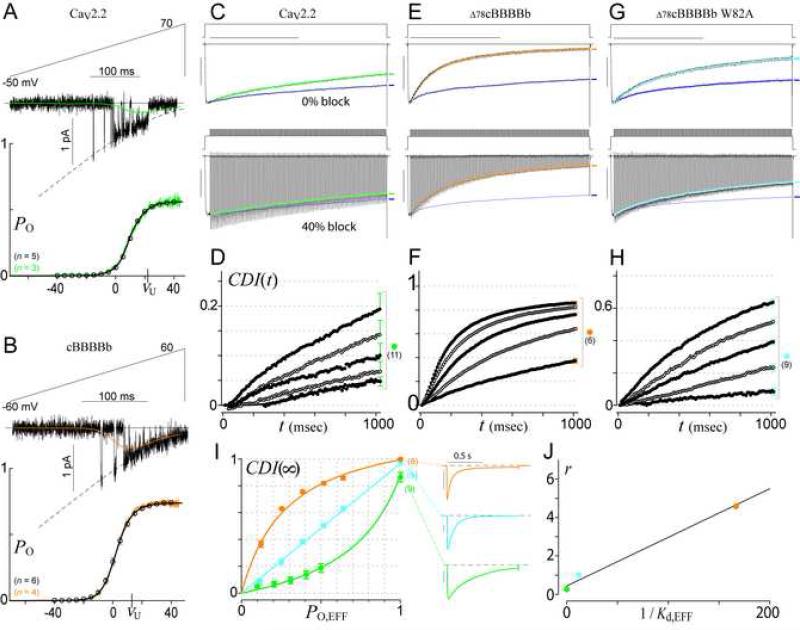
Generalization of the SQS Ca²⁺ -sensing mechanism to Ca_V2.2 channels

Given the success with Ca_V1.3 channels, we tested if the SQS mechanism could apply more generally and explain the well-known global Ca²⁺ selectivity of N-lobe mediated CDI in Ca_V2 channels (Evans and Zamponi, 2006; Liang et al., 2003). According to this mechanism, the global selectivity of Ca_V2 channels would arise from the absence of intrinsic NSCaTE domains, rendering these channels the natural equivalent of Ca_V1.3 NSCaTE mutants. Fitting with this view, our recent data indicate that the inclusion of NSCaTE within the amino terminus of Ca_V2.2 channels renders their N-lobe CDI insensitive to high Ca²⁺ buffering (Dick et al., 2008). To test the SQS mechanism in Ca_V2.2, we calibrated P_O,max (Figure 6A), and performed voltage-block experiments that confirmed a global CDI(∞)–P_O relation with r = 0.25 (Figures 6C-D; Figure 6I, green). Substitution of a Ca_V1.2 amino terminus containing NSCaTE (Δ78cBBBBb) imparted a striking conversion to a local saturating relation with r = 4.6 (Figures 6B, E-F; Figure 6I, orange). Moreover, attenuation of CaM/NSCaTE interaction through a W82A mutation (~W44A in Ca_V1.3) yielded an intermediate profile with r = 1.0 (Figures 6G-H; Figure 6I, cyan). Finally, Figure 6J demonstrates the predicted correlation between Ca_V1.2 NSCaTE affinities for Ca²⁺/CaM₃₄ (Dick et al., 2008) and CDI(∞)–P_O determinations of r (Figure 6I). This array of transformations generalize the SQS mechanism across Ca_V1 and Ca_V2 channels.

Figure 6. The SQS mechanism generalizes to Ca_V2 channels.

(A-B) P_O,max calibration for Ca_V2.2 (A) and cBBBBb (B). Format as in Figure 3C.

(C-I) Voltage-block analysis of Ca_V2.2 (C-D, I, green), Δ78cBBBBb (E-F, I, orange), and W82A mutant of Δ78cBBBBb (G-I, cyan). Blue waveforms in (C, E, G) follow the Ba²⁺ current trajectory (e.g., symbols in Figure 3E) corresponding to the same percentage block.

(J) Correlation between 1/K_d,EFF from FRET binding of α_1C NSCaTE with Ca²⁺/CaM₃₄ (Dick et al., 2008) and model parameter r from fits in (I).

Discussion

The tight coupling of Ca²⁺ sensors to Ca²⁺ sources affords rapid and privileged signaling, but requires special Ca²⁺-sensing capabilities. In the CaM/Ca²⁺-channel complex, these capabilities are exemplified by the contrasting spatial Ca²⁺ selectivities of the two lobes of CaM. Here, we establish that these selectivities are achieved not by sensing Ca²⁺ in different locations (Figure 1A, top row), but by decoding distinct temporal characteristics of nanodomain Ca²⁺ (bottom row). Local selectivity of the C-lobe arises from a slow CaM mechanism that exploits channel proximity and responds to intense yet intermittent Ca²⁺ signals. This local selectivity mechanism likely pertains to all forms of C-lobe regulation of Ca²⁺ channels, including the Ca²⁺-dependent facilitation (instead of CDI) of Ca_V2.1 channels (DeMaria et al., 2001). In contrast, global selectivity of the N-lobe disregards these local signals and responds to weaker Ca²⁺ signals from distant sources. This biologically crucial capability arises from an SQS mechanism highly attuned to the fractional presence, but not intensity of Ca²⁺ signals. This mechanism also explains the switching of N-lobe selectivity between global (Ca_V2) and local (Ca_V1) extremes (Dick et al., 2008). These results merit discussion of validity, methodology, and physiological modulation.

Validity and uniqueness of the SQS mechanism of Ca²⁺ sensing

The arguments for the SQS mechanism warrant special emphasis. For prediction 2, the parameter r is drawn from fits of Equation 2 to data that are highly constrained (Supplementary Information 4D). Thus, a key aspect of this prediction—the linear correlation between r and CaM/NSCaTE binding affinity (e.g., Figure 5K)—is well satisfied. For prediction 3, upward curvature of CDI(∞)–P_O relations not only supports validity, but also the uniqueness of the SQS mechanism. For the four-state configuration (Figure 2A), moderate kinetic deviations from the SQS regime (e.g., slowing Ca²⁺/CaM interactions, speeding channel/CaM interactions) always diminish the upward curvature of CDI(∞)–P_O relations, and larger deviations altogether preclude such curvature (Supplementary Information 1B-E). Thus, the SQS mechanism embodies the core principles by which any four-state mechanism can produce upward curvature. Moreover, if other states are included (Ca²⁺/CaM binding to the apoCaM site, apoCaM binding to the Ca²⁺/CaM site), upward curvature is only achieved insofar as these extra states are rarely occupied (Supplementary Information 1F). Hence, the upward curvature seen in four constructs (Figure 5J, Supplementary Information 4E) argues most strongly for the SQS mechanism.

Methodology for investigating Ca²⁺ sensing within intact signaling complexes

Ca²⁺ decoding often entails multiple CaM/protein interactions whose function may not be apparent when taken out of context. Hence, successful mechanistic dissection may require experimental tools tailored to the intact signaling complex. Here, this is achieved by voltage block of high-P_O channels, which affords millisecond control of the nanodomain Ca²⁺ signal of intact channels. Voltage block may be adapted to other Ca²⁺-permeable channels (Bradley et al., 2004; Myers and Julius, 2007; Saimi and Kung, 2002; Xiong et al., 2002; Zhang and Huganir, 1999), which may well employ SQS-like mechanisms, given the prevalence of key features like apoCaM interaction and rapid Ca²⁺ release from CaM. The technique could also be extended to sensors which do not regulate ionic current (Jurado et al., 1999), so long as the Ca²⁺-regulated molecule is engineered to give an optical readout (Takao et al., 2005). This approach could be applied to activity-dependent signaling cascades leading to nuclear transcriptional activation (Cullen, 2006; Oliveria et al., 2007; Winslow and Crabtree, 2005).

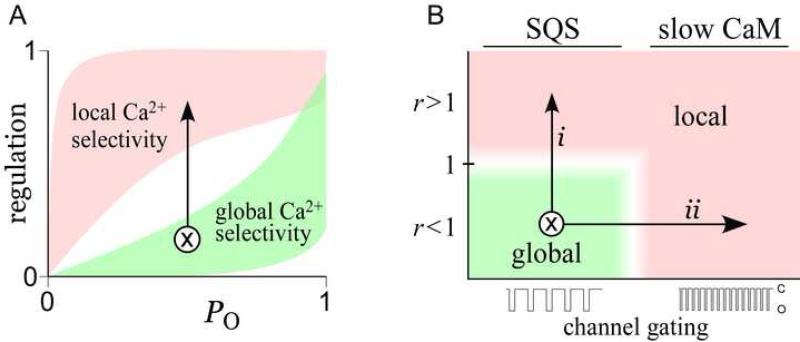
Potential physiological modulation of spatial Ca²⁺ selectivity

The SQS mechanism suggests how spatial Ca²⁺ selectivity could be physiologically modulated. Such regulation can best be understood with our graphical definition of spatial Ca²⁺ selectivity (Figure 7A), where the black arrow represents a transformation from global (green shaded area) to local (red area) selectivity. This transformation can be achieved in two main ways, as illustrated by a related graph (Figure 7B). Here, the vertical axis shows r, the ratio of channel affinity for Ca²⁺/CaM versus apoCaM; and the horizontal axis depicts the speed of channel gating, given fixed CaM kinetics. For orientation, global selectivity only occurs when CaM kinetics are quick relative to channel gating (as in the SQS mechanism) and when apoCaM affinity exceeds Ca²⁺/CaM affinity (r < 1). Thus, global selectivity corresponds to the green shaded area in Figure 7B. One means of modulating spatial selectivity involves increases in r, yielding a global-to-local shift in selectivity along trajectory i. Such changes in r could result from physiological modulation of either the Ca²⁺/CaM or apoCaM interaction sites; for example by phosphorylation (De Koninck and Schulman, 1998) or by competition with phospholipids and ATP (Myers and Julius, 2007). A second way to regulate spatial selectivity involves changes in channel gating itself. Since ‘slow’ and ‘quick’ binding interactions are defined relative to channel gating, accelerating gating, while CaM binding dynamics are held fixed (Figure 7B, trajectory ii), could induce deviations from global SQS behavior to a local, slow CaM profile. In heart failure, for example, ryanodine receptor closed times are dramatically shortened (Marx et al., 2000), potentially promoting local selectivity that would contribute to long-range signaling deficits. In all, this study elucidates the mechanism of a novel type of Ca²⁺ decoding, suggests how this sensing can be physiologically tuned, and expands our understanding of the Ca²⁺ signaling ‘toolkit’ (Bootman et al., 2001) prevalent throughout biology.

Figure 7. Physiological modulation of the SQS mechanism.

(A) Graphical depiction of transformation from global to local selectivity.

(B) Physiologically plausible mechanisms of spatial selectivity transformation. Vertical axis shows model parameter r. Horizontal axis shows channel gating speed. Transformation from global to local could arise from increasing r (trajectory i), or by speeding channel gating (trajectory ii).

Methods

Numerical Simulations

Numerical simulations (Figures 2C, G) were performed in MATLAB (MathWorks, Natick, MA), as detailed in Supplementary Information 4F. Additional numerical simulations, including those demonstrating the equivalence of continuum and stochastic views of nanodomain Ca²⁺ decoding, are elaborated in Supplementary Information 1-3, and should not be overlooked.

Molecular biology

Point mutations of Ca_V1.3 (α_1D) NSCaTE (Figure 4) were made in rat α_1D (Xu and Lipscombe, 2001). A 600-bp stretch containing NSCaTE (bounded by NheI and BsiWI) was cloned into Zero Blunt® TOPO® (Invitrogen), yielding NT_D-TOPO. QuikChange® (Stratagene) was used to mutate NSCaTE within NT_D-TOPO, and the relevant region was transferred into α_1D by NheI/BsiWI sites. The high-P_O Ca_V1.3 (Figure 5) was similarly constructed via a 2.3-kb stretch bounded by BsiWI and Eco47III. α_1cBBBBb, α_1c78BBBBb and α_1c78BBBBb W82A were as described (Dick et al., 2008). CFP-NT_D was made by PCR of α_1D NSCaTE residues 35-94, as present within NT_D-TOPO (± mutations), followed by substitution for CaM_WT in CFP-CaM_WT/pcDNA3 (Erickson et al., 2003) via NotI/XbaI. All segments subject to PCR were verified by sequencing.

Transfection of HEK293 cells

For electrophysiology, HEK293 cells were cultured on 10-cm plates, and transiently transfected by a calcium phosphate protocol (Peterson et al., 1999). We combined 8 μg each of cDNAs encoding channel α₁ subunit, rat brain β_2a (Perez-Reyes et al., 1992), rat brain α_2δ (Tomlinson et al., 1993), and rat brain CaM₁₂ or CaM₃₄ (Peterson et al., 1999), along with 1-2 μg of SV40 T antigen. All subunits were driven by a CMV promoter. Experiments were done 1–2 d later.

FRET two-hybrid assay

FRET two-hybrid was performed as described (Erickson et al., 2003) (Supplementary Information 5A). Experiments were carried out in a 10 mM Ca²⁺ Tyrode's buffer with 10 μM ionomycin (Sigma-Aldrich, MO) added for all Ca²⁺/CaM conditions.

Whole-cell electrophysiology

Whole-cell recordings were obtained at room temperature (Axopatch 200A, Axon Instruments). Electrodes were pulled borosilicate glass capillaries (World Precision Instruments, MTW 150-F4), with 1–3 MΩ resistances, before 80% series resistance compensation. Currents were filtered at 2 kHz for routine rectangular steps, and 5 kHz for voltage-block and tail-activation (4-pole Bessel). A P/8 leak-subtraction protocol was used. For all voltage-block, tail-activation, and high-buffer-CDI experiments, the internal solution contained (in mM): CsMeSO₃, 114; CsCl₂, 5; MgCl₂, 1; MgATP, 4; HEPES (pH 7.4), 10; and BAPTA, 10; at 295 mOsm adjusted with CsMeSO₃. For physiological buffering experiments, 135 mM CsMeSO₃ and 0.5 mM EGTA were used. For whole-cell experiments based on Ca_V1.3 (Figures 3-5), external solutions contained (in mM): TEA-MeSO₃, 102; HEPES (pH 7.4), 10; and CaCl₂ or BaCl₂, 40; at 300 mOsm, adjusted with TEA-MeSO₃. For Ca_V2.2 (Figure 6), 5 mM BaCl₂ or CaCl₂ and 140 mM TEA-MeSO₃ were used. Further details in Supplementary Information 4B-C.

Single-channel recordings

On-cell recordings were obtained at room temperature (integrating mode, Axopatch 200B; Axon Instruments). Patch pipettes (5–20 MΩ) were pulled from ultra-thick-walled borosilicate glass (BF200-116-10, Sutter Instruments), and coated with Sylgard. Currents were filtered at 2 kHz. To zero membrane potential, the bath contained (in mM): K glutamate, 132; KCl, 5; NaCl, 5; MgCl, 3; EGTA, 2, glucose, 10; and HEPES (pH 7.4), 20 at 300 mOsm adjusted with glucose. The pipette solution for Ca_V1.3 was the same as the Ba²⁺ bath solution in whole-cell experiments. The Ca_V2.2 pipette solution contained (in mM): TEA-MeSO₃, 20; HEPES (pH 7.4), 10; and BaCl₂, 90; at 300 mOsm, adjusted with TEA-MeSO₃. Further details in Supplementary Information 4A.