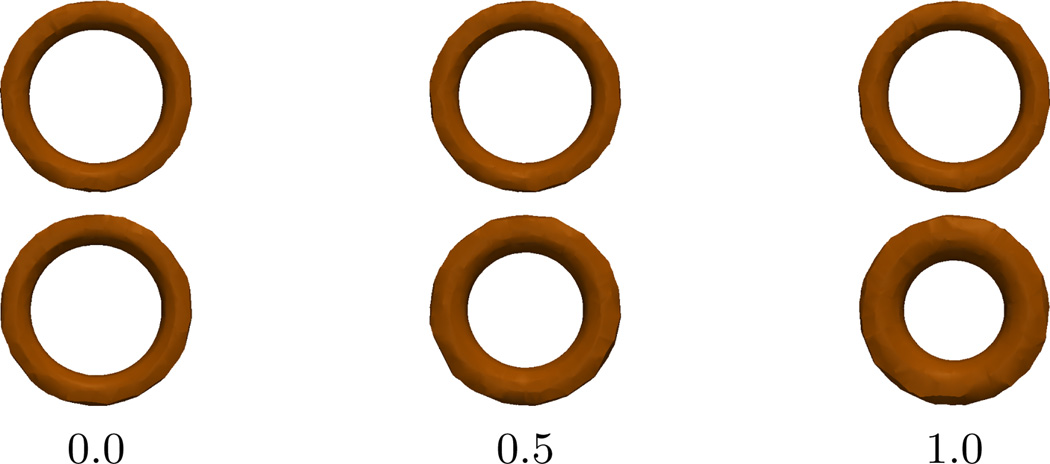Mixed-Effects Shape Models for Estimating Longitudinal Changes in Anatomy

Abstract

In this paper, we propose a new method for longitudinal shape analysis that fits a linear mixed-effects model, while simultaneously optimizing correspondences on a set of anatomical shapes. Shape changes are modeled in a hierarchical fashion, with the global population trend as a fixed effect and individual trends as random effects. The statistical significance of the estimated trends are evaluated using specifically designed permutation tests. We also develop a permutation test based on the Hotelling T² statistic to compare the average shapes trends between two populations. We demonstrate the benefits of our method on a synthetic example of longitudinal tori and data from a developmental neuroimaging study.

1 Introduction

Longitudinal imaging studies involve the collection of imaging data at multiple time points for each participant. Such studies have the potential to provide a rich picture of the anatomical changes occurring during development, disease progression or recovery. Tracking each individual in a longitudinal study gives a model of change with a clarity that cannot be achieved in a cross-sectional study. Further, a more accurate model is possible if each individual in a longitudinal study acts as their own control, that is, factors that vary between individuals remain constant within the same individual. This control over nuisance factors reduces the variance in measurements and results in higher statistical power to quantify change.

Previous work on characterizing anatomical shape changes has focused primarily on the analysis of cross-sectional data. Approaches to the shape regression problem have been formulated for several shape representations or metrics, including diffeomorphic shape changes [1], medial shape representations [2], atlas appearance models [3], deformation tensors [4], and shape regression using particle-based representation in [5]. Work on longitudinal shape modeling includes the use of diffeomorphic mappings and parallel transport by Qiu et al. [6] to track changes in an individual and mapping the individual trends to a population atlas. Durrleman et al. [7] construct spatiotemporal image atlases from longitudinal data. Lorenzi et al. [8] use a hierarchical model on stationary velocity fields, in a framework that does not include a Riemannian metric on the manifold of diffeomorphisms. Fishbaugh et al. [9] estimate smooth growth trajectories as deformations defined through ows with regularized acceleration fields. Barry and Bowman [10] built mixed-effects models on a small number of manually selected landmarks to model the development of facial shape. [11] develop a manifold version of a mixed-effects model to analyze longitudinal data taking values on a Riemannian manifold.

Linear mixed-effects models, pioneered by Laird and Ware [12] have become a natural choice when modeling univariate longitudinal data. These models are hierarchical, characterizing each individual trend as a linear model, which in turn can be modeled as a perturbation of the overall population trend. While these models are powerful for analyzing univariate or low-dimensional multivariate data, little has been done in the high-dimensional setting, such as longitudinal data extracted from medical images. A major bottleneck is the difficulty of estimating the large number of parameters involved in covariances between random effects.

In this paper, we present a new method for characterizing longitudinal shape change that combines point correspondences across shapes with the statistical modeling of individual and population trends via the linear mixed-effects model. Our shape models are based on the particle correspondence framework introduced by Cates et al [13], where particle positions on the object surfaces are optimized in a variational framework that seeks a balance between model simplicity and geometric accuracy of the surface representations.

2 Background

In the following section we provide a brief overview the particle-system correspondence optimization method as proposed in [13]. The general strategy of this method is to represent correspondences as point sets that are distributed across an ensemble of similar shapes by minimizing an objective function that quantifies the entropy of the system. We also review the linear mixed-effects model, described by Laird and Ware [12], and used as the underlying statistical descriptor of longitudinal changes in our system.

2.1 Correspondence Optimization

Let us define a surface as a smooth, closed manifold of codimension one, which is a subset of ℝ^d (e.g., d = 3 for volumes). We sample the surface 𝒮 ⊂ ℝ^d using a discrete set of N points that are considered as random variables S = (Y₁, Y₂, …, Y_N)^T, Y ∈ ℝ^d drawn from a probability density function (PDF), p(Y). We denote a realization of this PDF with lower case, and thus we have s = (y₁, y₂, …, y_N)^T, where s ∈ 𝒮^N. We refer to the positions y as particles, and a set of particles, a particle system.

The amount of information encoded in this random sampling is, in the limit, the differential entropy of the PDF, given by H[Y] = −E{logp(Y)}, where E{·} is the expectation. Approximating the expectation by the sample mean, we have $H[\mathbf{Y}]\approx -\frac{1}{Nd}{\sum }_i\text{log}p({\mathbf{y}}_i)$. To determine the probability of a particle’s position, p(y_i), [13] uses a nonparametric Parzen-window density estimation given by a mixture of multivariate, isotropic Gaussian kernels with standard deviation σ that determines the strength of particle interaction with N neighbouring particles within the defined window. An ensemble comprised of M surfaces, ℰ = s¹, … s^M can be described by a N_d × M matrix of particle positions $P=({\mathbf{y}}_j^k)$, where k = 1, …, M and j = 1, …, N. Let s^k ∈ ℝ^Nd be an instance of a random variable S, then, the combined ensemble and shape cost function is defined by

$$Q=H(\mathbf{S})-\sum _{k}H(P^k)$$ (1)

This cost function is composed of two interacting terms. The first term produces a compact distribution of samples in shape space, while the second term provides uniformly-distributed correspondence positions on the shape surfaces, to achieve a faithful shape representation. The optimization process of this cost function is defined via gradient descent as described in [13].

2.2 The Laird and Ware linear mixed-effects model

In a linear mixed-effects model, the response or observed variable y_i is assumed to have a set of parameters α, fixed across individuals. In addition, each individual i, is assigned a set of random parameters b_i that model the deviation from the fixed effect α. For i ∈ {1, 2, …, m}, the model reads as follows:

$$y_i=X_i\alpha +Z_i{b}_i+{\epsilon }_i,$$ (2)

where for the i^th individual, X_i and Z_i are known independent variables which influence y_i through fixed and random effects respectively. b_i are distributed as N(0, D), D being an arbitrary covariance matrix. ε_i models the error from the observed data, and is distributed as N(0, σ²I_i), I_i being an identity matrix.

A simple case of the mixed-effects model occurs when we have a single independent variable (such as time or age) that is used for both fixed and random effects. In this case we have Z_i = X_i and (2) simply reduces to

$$y_i=X_i(\alpha +b_i)+{\epsilon }_i,$$ (3)

where for the i^th individual, α and b_i are 2-vectors interpreted as slope-intercept pairs of the group and random effects of the individual, respectively.

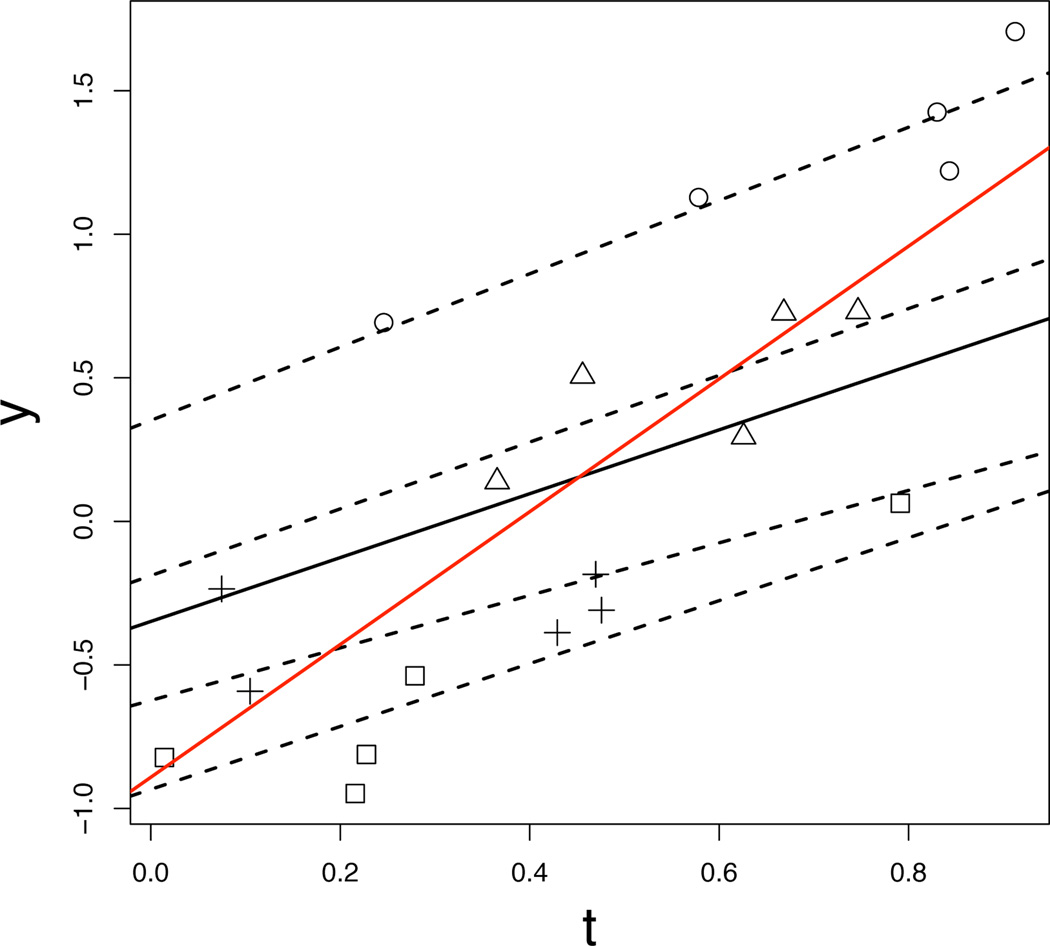
An example of synthetically generated data from the model (3) is shown in Fig. 1. This example illustrates the power of mixed-effects models and the importance of modeling correlations within each individual. Ignoring these correlations leaves us with a simple linear regression model. Fig. 1 shows the estimated linear regression model, which does not concur with the trends of the individuals. In contrast, the estimated α from mixed-effects modeling optimally summarizes the overall group trend.

Fig. 1.

Example of randomly-generated, synthetic longitudinal data. Data points for each “individual” are displayed with different symbols. The estimated mixed-effects model is shown with both the fixed effects, i.e., group trend (solid black line), and random effects, i.e., individual trends (dashed lines). The estimated linear regression model, which ignores correlations within individuals, is shown as a red line.

3 Methodology

The correspondence optimization framework described in Sec. 2.1 was extended to incorporate a linear regression based approach in [5]. However, this approach may not model longitudinal data correctly due to differences in relationships across individuals. To address this issue, we propose a method that incorporates the linear mixed-effects model described in Sec. 2.2 into the framework in Sec. 2.1. Parameters of the linear mixed-effects model are simultaneously estimated along with the correspondence optimization. The following section describes our approach and revisits the parameter estimation for the linear mixed-effects model given by [12].

3.1 Correspondence with Linear Mixed-effects Modeling of Shapes

With the assumption of a Gaussian distribution in shape space, we can introduce a generative statistical model

$$\mathbf{y}=\mu +\epsilon ,\epsilon ~𝒩(\mathbf{0},\Sigma )$$ (4)

for correspondences, where μ is the vector of mean correspondences, and ε is normally-distributed error. Replacing μ in this model with a function of an explanatory variable x gives the more general, regression model

$$\mathbf{y}=f(x)+\mathrm{\epsilon ̂},\mathrm{\epsilon ̂}~𝒩(\mathbf{0},\mathrm{\Sigma ̂}).$$ (5)

We propose to optimize correspondences under the linear mixed-effects model described in Sec. 2.2 to facilitate the estimation of individual and population trends in longitudinal data. Using the same explanatory variable (age of the individual, in case of real data) for both fixed and random effects as in (3), we assume that correspondences for shapes belonging to individual i are generated by the following analogous statistical model:

$$Y_i=X_i\alpha +X_i{b}_i+{\epsilon }_i,$$ (6)

where X_i represents the explanatory variable (age; in the case of real data), Y_i is the matrix containing correspondences for all shapes in the population, α represents the fixed-effects parameters (slope, intercept), while b_i represents the random-effects parameters (slope, intercept) for the individual i and ε_i represents the error in correspondences.

The algorithm proceeds as follows. (1) Correspondences are first optimized under the nonregression model (4) to minimize the entropy associated with the total error ε, and are used to compute an initial estimate of the linear mixed-effects model parameters. (2) We then follow the optimization procedure as described in Sec. 2.1, with the replacement of the model covariance Σ by the covariance Σ̂ of the underlying residual relative to the regression model. (3) We interleave the two estimation problems, re-estimating the mixed-effects model parameters after each iteration of the gradient descent on the correspondences.

3.2 Estimation of Parameters

We denote the parameters in the covariance matrix D and σ² by a vector θ. We compute maximum likelihood (ML) estimates for α and θ and empirical Bayes estimates for b_i. If we were to able to observe b_i and ε_i, we could compute closed-form ML estimates of α and θ, but this is not the case. Therefore, an expectation maximization (EM) algorithm is used to estimate α and θ, treating b_i and ε_i as hidden variables. The EM algorithm guarantees that the likelihood increases or stays constant at each iteration, but it can converge to a local maximum instead of the global one.

We model the response variable y_i in (2) as being marginally distributed as $N(\alpha ,{\sigma }^2{I}_i+Z_{i}D{Z}_i^T)$. Since we don’t observe b_i and ε_i, let us replace σ² and D by their current estimates σ^2(j) and D̂^(j) at iteration j of the EM algorithm. Let us also define $r_i^{(j)}≔y_i-X_i{\mathrm{\alpha ̂}}^{(j)}$, and $N:={\sum }_{i=1}^m{n}_i$. The ML estimate for α is given by

$${\mathrm{\alpha ̂}}^{(j)}={\left(\sum _{i=1}^m{X}_i^T{W}_i^{(j)}{X}_i\right)}^{-1}\sum _{i=1}^m{X}_i^T{W}_i^{(j)}{y}_i,\text{where}{W}_i^{(j)}={({\mathrm{\sigma ̂}}^{2(j)}{I}_i+Z_i{\mathrm{D̂}}^{(j)}{Z}_i^T)}^{-1}.$$

The random-effects, b_i, are estimated using empirical Bayes as

$${\mathrm{b̂}}_i^{(j)}=E[b_i|y_i,{\mathrm{\alpha ̂}}^{(j)},{\mathrm{\theta ̂}}^{(j)}]={\mathrm{D̂}}^{(j)}{Z}_i^T{W}_i^{(j)}{r}_i^{(j)}$$

The covariances σ² and D are estimated by taking the expectation over hidden variables ε_i and b_i, conditioned on y_i and the current estimates of α and θ. This step combines both the estimation and a maximization. The resulting estimate for the error variance is

$${\mathrm{\sigma ̂}}^{2(j+1)}=\frac{1}{N}E\{\sum _{i=1}^m{\epsilon }_i^T{\epsilon }_i|y_i,{\mathrm{\alpha ̂}}^{(j)},{\mathrm{\theta ̂}}^{(j)}\}=\frac{1}{N}\sum _{i=1}^m[{ê}_i^T{ê}_i+\mathrm{t}\mathrm{r}\text{Var}\{{\epsilon }_i|y_i,{\mathrm{\alpha ̂}}^{(j)},{\mathrm{\theta ̂}}^{(j)}\left\}\right]=\frac{1}{N}\sum _{i=1}^m[{ê}_i^T{ê}_i+{\mathrm{\sigma ̂}}^{2(j)}\mathrm{t}\mathrm{r}(I_i-{\mathrm{\sigma ̂}}^{2(j)}{W}_i^{(j)}\left)\right],$$

where ${ê}_i=E[{\epsilon }_i|y_i,{\mathrm{\alpha ̂}}^{(j)},{\mathrm{\theta ̂}}^{(j)}]=r_i^{(j)}-Z_i{\mathrm{b̂}}_i^{(j)}$. Similarly, the estimate for covariance matrix D is given by

$${\mathrm{D̂}}^{(j)}=\frac{1}{m}E[\sum _{i=1}^m{b}_i{b}_i^T|y_i,{\mathrm{\alpha ̂}}^{(j)},{\mathrm{\theta ̂}}^{(j)}]=\frac{1}{m}\sum _{i=1}^m{\mathrm{b̂}}_i^{(j)}{\mathrm{b̂}}_i^{(j)T}+{\mathrm{D̂}}^{(j)}(I-Z_i{W}_i^{(j)}{Z}_i{\mathrm{D̂}}^{(j)}).$$

We initialize the covariance matrix D̂⁽⁰⁾ to the identity matrix and σ̂²⁽⁰⁾ to 1 before starting the EM iterations.

3.3 Permutation test for significance of random-effects

In the case of longitudinal data, correlations may exist within shapes at different time-points for a given individual and break the independence assumption of the simple linear regression model. Another assumption that can be broken is homoscedasticity, i.e., the property that the variance of the residuals is constant across the independent parameter. When these assumptions are not met, simple linear regression models give less reliable (i.e., higher variance) estimates of the α parameters.

We use a nonparametric permutation test based on an estimate of the error variance V_ε to confirm the significance of the random-effects introduced in the mixed-effects model. This permutation test works by permuting the assignment of shapes to individuals. The explanatory variable for the shape is not permuted only “group memberships” are permuted. For every permutation, we can compute the squared norm of the residual vector for each shape, and use the average value as an estimate of V_ε in fitting the linear mixed-effects model to this permuted ensemble of shapes. This allows us to compute a distribution of V_ε of the model as a test statistic and test the null hypothesis that random-effects have no effect on the final parameter estimates of the model, and consequently lead to unaltered V_ε values across permutations. Then comparing our unpermuted V_ε to this distribution, we can compute a p-value to test the null hypothesis. We perform the correspondence optimization on each permutation separately, and thus the results of our permutation test are not biased by the correspondence optimization method.

3.4 Permutation test for group discrimination

One of the major motivations of longitudinal data analysis is to test if changes observed in one group differ from those found in another. For instance, one might ask if the brain anatomy of Alzheimer’s patients deteriorates faster than those of healthily aging subjects. In this section, we develop a permutation test on the Hotelling T² statistic to test the statistical significance of group-parameter differences between two groups of longitudinal data.

Recall the Hotelling T² statistic is a test statistic often used in a multivariate test of the difference between sample means, p̄, q̄, of two groups of data {p₁, …, p_m} and {q₁, … q_n}, with all p_i, q_i ∈ ℝ^d. The idea is to compare the difference between the two means, relative to the pooled sample covariance:

$$W=\frac{{\sum }_i(p_i-\mathrm{p̄}){(p_i-\mathrm{p̄})}^T+{\sum }_i(q_i-\mathrm{q̄}){(q_i-\mathrm{q̄})}^T}{m+n-2}.$$

The T² statistic can be thought of as a squared Mahalanobis distance between the means, using this pooled covariance, W. The sample T² statistic is given by

$$t^2=\frac{mn}{m+n}{(\mathrm{p̄}-\mathrm{q̄})}^T{W}^{-1}(\mathrm{p̄}-\mathrm{q̄})$$ (7)

The permutation test procedure is as follows: (1) compute the t² statistic, (2) randomly permute (swap) data points between the p and q groups, computing a $t_k^2$ statistic for the permuted groups, (3) repeat step 2 for k = 1, …, P, (4) compute the p-value: p = B/(P +1), where B is the number of $t_k^2<t^2$. The final p-value can be interpreted as the probability of finding a larger group difference by random chance under the null hypothesis (that there is no difference between the means).

Consider the specific problem of comparing the mean trends in two different groups G and H. Let $Y_{ij}^{(G)}$ and $Y_{ij}^{(H)}$ be two sets of longitudinal data and the resulting parameter estimates for the two groups to be $({\mathrm{\alpha ̂}}_1^G,{\mathrm{\alpha ̂}}_2^G)$ and $({\mathrm{\alpha ̂}}_1^H,{\mathrm{\alpha ̂}}_2^H)$. It is often most interesting to separate the tests of the slope parameter α₁ and the intercept parameter α₂. For example, in testing the differences in anatomical changes between a healthy and disease group, it is important to distinguish if the shape differences are present at baseline (intercept) or if they develop over time (slope). To make this distinction, we can separate the above Hotelling T² test into these two components. We will thus look at the two separated statistics, $t_{{\alpha }_1}^2$ and $t_{{\alpha }_2}^2$ given by (7).

4 Results and Discussion

We validate the proposed method through experiments on synthetic longitudinal tori, and test the significance of our estimated parameters via a nonparametric permutation test. We present applications of the method in longitudinal studies of early development of brain shapes from a neuroimaging study.

4.1 Synthetic Tori

Test of model significance

We generated longitudinal tori comprising of 11 “individuals”, at 3 different time points. The two radii of the tori within a group are generated according to the mixed-effects model in (6).

For each individual i, X_i ~ 𝒰(2, 10) drawn independently, random-effects b_i ~ 𝒩(0, 0.4), and errors ε_i ~ 𝒩 (0, 0.3). The slope-intercept pair for the fixed-effects are given as: (α_1R, α_2R) = (2, 30) and (α_1r, α_2r) = (−1, 15), where R, r are the outer and inner radii respectively. The particle correspondence positions and model parameters can then be estimated as prescribed in Section 3. Figure 2 shows the change in shape obtained using the fixed-effects of particle positions. The parameter R, increases whereas r decreases, which is consistent with the slope parameters used in the generative model.

Fig. 2.

Visualizing fixed effects on the synthetic data

We evaluate the significance of the b_i parameters using the nonparametric permutation test described in Sec. 3.3. Each of the 11 groups are assigned 3 random shapes from the total pool without repetition. We generate 500 such permutations and estimate V_ε(P), for each permutation P. Over these permutations, V_ε(P) ranges from 2500 to 6500. V_ε for unpermuted group memberships is 940. This implies a p-value ~ 0. If it was possible to explain the population by only using fixed-effects, the permutation of group memberships should not have affected V_ε values significantly. This test shows that using random-effects gives significant reduction in V_ε independent of the increase in the number of model parameters.

Test for group differences

Here, we generate two groups of 11 “individuals” each, with 3 time-points per individual, with X_i for each individual at 0, 0.5, 1, random effects b_i ~ 𝒩(0, 0.3), and errors ε_i ~ 𝒩(0, 0.1). For one of the groups, the fixed-effect slope is kept at zero, but for the other the r fixed-effect is given a slope 3. Figure 3 shows the tori generated using this configuration of parameters. When looking for group differences based on baseline intercepts, as expected, the permutation test prescribed in Section 3.4 did not a yeild a significant p-value. But when comparing groups based on the slope parameter, we obtained a p-value ~ 0, which confirms a stark difference in group trends.

Fig. 3.

Visualizing the trends in the two groups created to test group differences: constant trend (top), trend with increasing r (bottom)

4.2 Mixed-Effects Model for Brain Structures

Test for model significance and trend variation

In this experiment, we work with brain structures from a developmental neuroimaging study. We have 11 subjects scanned at approximately (6, 12, 24) months. The scans are preprocessed and segmented to obtain the brain structures (cerebellum, left and right hemispheres) which are input to the optimization process.

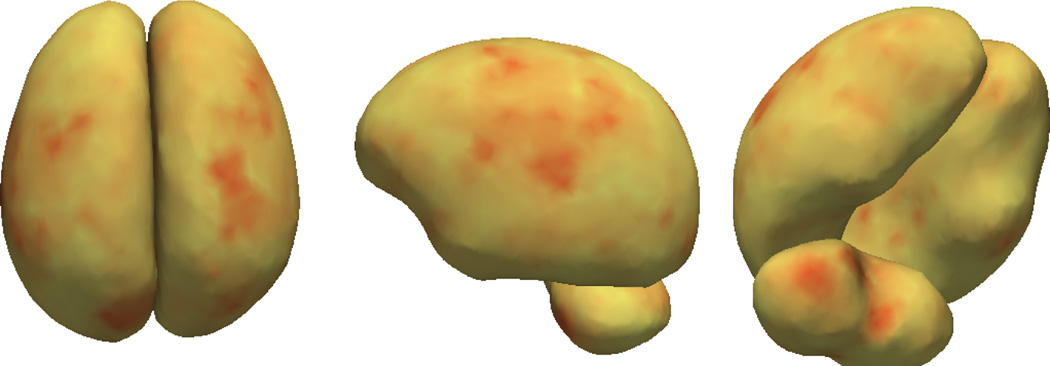
The fixed effects in Fig. 4 clearly show two changes happening in the infant brain. The first is an elongation of both hemispheres, which can be seen as a stretching of the frontal lobe and narrowing of the hemisphere shapes. The second effect is the growth near the top of the cerebellum. These trends are qualitatively consistent with the cross-sectional results found in [5].

Fig. 4.

Visualizing the fixed-effects of brain structures (blue denotes expansion, and yellow denotes contraction)

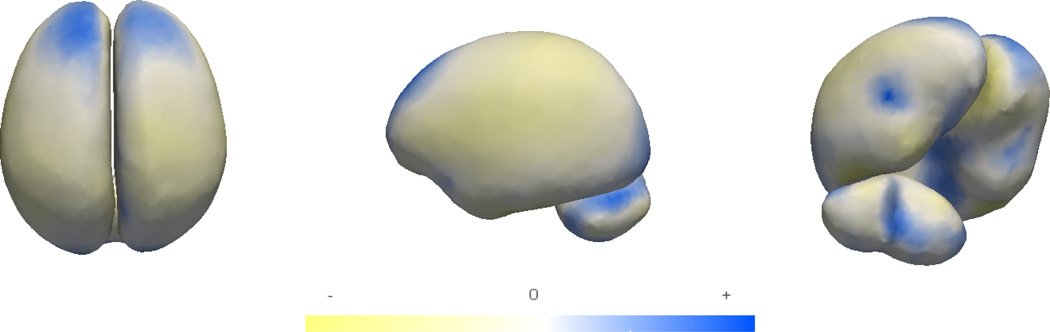
The longitudinal model can tell us more, however, than a regression model of cross-sectional data. First, we know that these fixed effects are representative of the growth trend that individuals undergo on average, rather than a trend seen between multiple subjects. Second, and more interestingly, we can say something about the variability of these trends in the population. Fig. 5 encodes the variance of the random slopes at each point and is indicative of regions where the variation in the growth trend across individuals is high (red regions in Fig. 5). An example inference is that the elongating frontal lobe and expanding cerebellum are relatively stable across the sample (i.e. the variance of these trends is low). We also evaluate the significance of the b_i using the nonparametric permutation test described in Sec. 3.3. Group memberships are permuted 500 times and V_ε(P) is estimated for each permutation P. While V_ε(P) ranges from 10000 to 17000 for the permuted sets, the value for the unpermuted set is 5400. This suggests a p-value ~ 0 and implies that the random effects play a significant role in describing the early development of the brain.

Fig. 5.

Visualizing the random-effects of brain structures (red denotes high variance regions)

Test for differences in group trends

We also evaluate our method using a longitudinal database from an Autism Center of Excellence, part of the Infant Brain Imaging Study (IBIS). The study consists of high-risk infants as well as controls, scanned at approximately (6, 12, 24) months. At 24 months, symptoms of autism spectrum disorder (ASD) were measured using the Autism Diagnostic Observation Schedule (ADOS). A positive ADOS score indicates the child has a high probability of later being diagnosed with autism. Finally, we have two groups: 15 high-risk subjects with positive ADOS (HR+) and 14 low-risk subjects with negative ADOS (LR−).

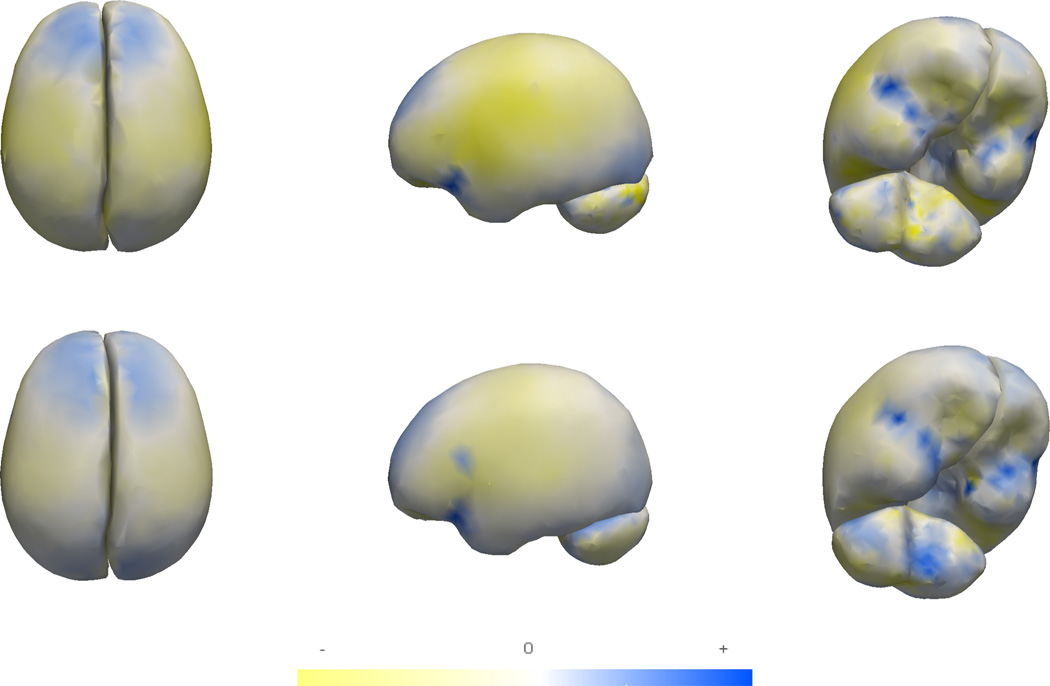
Fig. 6 visualizes the group trends for the HR+ and LR− groups and clarifies that the global trends are similar across both groups. There are localized differences near the frontal end of the hemispheres and also near the cerebellum, but these are not found to be significant by the permutation test for group differences. The t² statistic for differences in group trends in cerebellum, left hemisphere and right hemisphere independently were 6.1039, 5.155 and 4.5693 respectively. The p–values were 0.112, 0.454 and 0.515 for the same.

Fig. 6.

Variation in group trends for the HR+ (top) and LR− (bottom) groups (yellow denotes contraction, blue denotes expansion)

5 Conclusion and Future Work

We presented a new mixed-effects shape model for analyzing longitudinal shape changes, which is based on a particle system representation and entropy minimization framework for point correspondences. We demonstrated the ability of the model to characterize both group-level and individual-level shape trends on synthetic data and developmental brain data. As for future work, the current work does not handle spatial correlations between points on a shape. We plan to investigate this issue, possibly using a pseudolikelihood estimation of the covariance matrix of the shape parameters, similar to [10]. Such an estimation could possibly take advantage of the entropy minimization, as this tends to decrease the dimensionality of the covariance matrix.