Detecting Rhythms in Time Series with RAIN

Abstract

A fundamental problem in research on biological rhythms is that of detecting and assessing the significance of rhythms in large sets of data. Classic methods based on Fourier theory are often hampered by the complex and unpredictable characteristics of experimental and biological noise. Robust nonparametric methods are available but are limited to specific wave forms. We present RAIN, a robust nonparametric method for the detection of rhythms of prespecified periods in biological data that can detect arbitrary wave forms. When applied to measurements of the circadian transcriptome and proteome of mouse liver, the sets of transcripts and proteins with rhythmic abundances were significantly expanded due to the increased detection power, when we controlled for false discovery. Validation against independent data confirmed the quality of these results. The large expansion of the circadian mouse liver transcriptomes and proteomes reflected the prevalence of nonsymmetric wave forms and led to new conclusions about function. RAIN was implemented as a freely available software package for R/Bioconductor and is presently also available as a web interface.

At the core of research on biological rhythms lies the methodological problem of how to detect periodicities in measured data. This is reflected in the richness of the literature on this subject as well as in the wealth of methods and algorithms devoted to this task. Our group investigates circadian rhythms, and in this field the demand for rigorous and efficient methods for periodicity detection is only increasing as more genome- and proteome-wide data accumulate. The accuracy of the detection of rhythmic messages and proteins is crucial in modern circadian high-throughput cell biology, since it greatly affects the validity of subsequent conclusions about function.

Most available methods for periodicity detection can be traced back to Fourier methods in some form (Halberg et al., 1967; Straume, 2004; Wichert et al., 2004; Wijnen et al., 2005). These methods generally assume an underlying rhythm in the form of one or more sine waves. Further, they are often so-called parametric methods that make certain assumptions about the deviations from the biological signal: These deviations are the measurement noise and biological noise. One general assumption is that the noise variance is both Gaussian (normally) distributed and independent of measurement magnitude, which, however, sometimes is not even close to reality for biological data, regardless of, for example, log-transformation. In such cases, it is worthwhile to explore nonparametric statistical methods, which then can perform much better than parametric methods. It is therefore not surprising that a nonparametric method implemented as the program “JTK_CYCLE” (Hughes et al., 2010) has had a large impact and has been widely adopted in the field.

Another property of biological data that presents a problem for classic Fourier-based methods is the prevalence of spiky or sawtooth-shaped wave forms deviating significantly from sine waves. This also highlights a shortcoming of JTK_CYCLE: It assumes that any underlying rhythms have symmetric wave forms. This means, for example, that (as we demonstrate later here) sawtooth-shaped rhythms often go undetected by this algorithm. The HAYSTACK method (Michael et al., 2008) addresses this problem but relies on a small set of predefined wave form alternatives and is thus not really general.

JTK_CYCLE builds on the nonparametric Jonckheere-Terpstra test (Jonckheere, 1954; Terpstra, 1952), which detects monotonous trends in data consisting of a dependent variable (e.g., mRNA expression levels) and an independent variable (e.g., time). What about instead aiming to detect the case of an initial increase and a subsequent decrease in the dependent variable? This problem, which is a generalization of the Jonckheere-Terpstra test, was addressed and solved by Mack and Wolfe (1981), resulting in the so-called rank test for umbrella alternatives (the name due to the rising and falling shape of the pattern to be detected). The test also allows for asymmetry (a variable umbrella peak, in the authors’ terminology), for example, a steep rise and slow decay or vice versa.

We have leveraged and extended available umbrella methods to allow for nonparametric detection of both symmetric and nonsymmetric rhythms. We present here the resulting method, which we have dubbed RAIN (Rhythmicity Analysis Incorporating Nonparametric methods). This method can detect rhythms of any period and makes few assumptions about wave forms. We demonstrate the usefulness of RAIN for detecting circadian rhythms in gene expression data, which is our primary research interest. In particular, we demonstrate that RAIN detects strong but asymmetric circadian rhythms in many genes in mouse liver, often obvious to the human eye, that go unnoticed by JTK_CYCLE. Furthermore, RAIN significantly enlarged the circadian mouse liver proteome compared with the studies that first charted it (Mauvoisin et al., 2014; Robles et al., 2014), which led us to note a functional enrichment for circadian proteins involved in protein folding and unfolded protein binding. This functional enrichment had gone unnoticed in the original studies. RAIN is available as an R/Bioconductor package at www.bioconductor.org and through a web service (rain.biologie.hu-berlin.de/rain) that provides an easy-to-use interface to the algorithm.

Methods

RAIN

Nonparametric methods avoid many assumptions regarding the experimental noise and the underlying model for the generation of rhythms by concentrating on the ranks of the measured values, rather than the measured values themselves. The program JTK_CYCLE uses such a method for rhythm detection, and it works by comparing the ranks of measured values to those of an assumed underlying curve shape (a sine curve by default). However, this method is not suitable for detecting various nonsymmetric wave forms.

The purpose of RAIN was to build on the strengths of JTK_CYCLE but to significantly expand the territory of detectable rhythms to include nonsymmetric wave forms, such as sawtooth-like shapes. The aim was to accomplish this in a general way, specifically not requiring a library of guessed wave forms to match to (which is the case for previous methods such as JTK_CYCLE or HAYSTACK). Still, we sought to continue the robust nonparametric approach that is often necessary when analyzing RNA or protein abundances, since these kinds of measurements are subject to experimental uncertainties often resulting in outliers. The core idea behind RAIN was the realization that a rhythmic time series consists of alternating rising and falling patterns but that the rising pattern may be unrelated in shape to the falling pattern: These shapes should not be tested against each other. Given an oscillation period to test against, RAIN works by organizing the data into groups belonging to either the rising part or the falling part of an oscillation period (Fig. 1). The rising and falling parts are then tested separately using the test against umbrella alternatives (Mack and Wolfe, 1981). This is a main point of departure of RAIN compared with JTK_CYCLE: RAIN does not care about the rising part having a particular shape compared with the falling part (Fig. 1), whereas JTK_CYCLE by design tests measurements in both rising and falling parts against each other. In addition, JTK_CYCLE by default assumes a perfectly symmetric wave form, where the falling part has the mirror-image shape of the rising part. Although the user may define any one waveform from within the code base of JTK_CYCLE, the rising and falling parts of the curve shape are by JTK_CYCLE always locked into the particular relationship defined by the one chosen waveform (such as one of the triangular or “shark fin” shaped examples in the lower part of Fig. 1). This limitation is overcome by RAIN, which thus has the potential to discover a broader spectrum of rhythmic waveforms.

Figure 1.

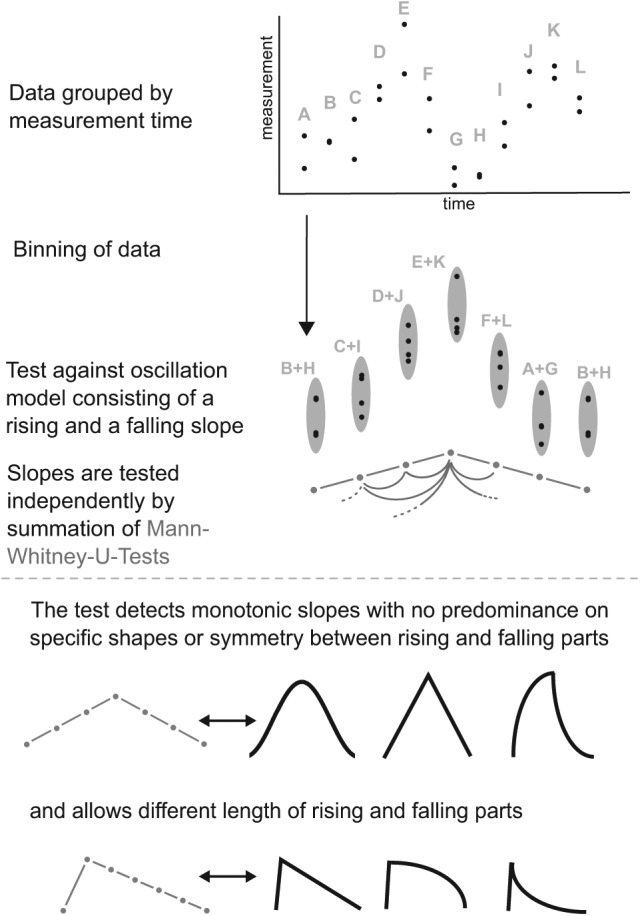
Description of RAIN. RAIN works by grouping measurements by time point (such as circadian or zeitgeber time). The ranks rather than the values are used, and groups are compared with each other against the alternative hypothesis of a rising pattern followed by a falling pattern. Only groups belonging to the same pattern (either rising or falling) are compared with each other. This releases many constraints on shape, allowing detection of, for example, “shark fin” wave forms. By cyclically reordering groups, and by further varying the umbrella peak location, further asymmetries and phases are tested against.

As in the original formulation of the test against umbrella alternatives, the umbrella peak is allowed to vary so that different steepnesses of the rising and falling parts are allowed for (Fig. 1). This allows RAIN to test against skewed (e.g., sawtooth-like) waveforms. Finally, as in JTK_CYCLE, a set of periods prespecified by the user, as well as all possible phases, are tested, and p-values are adjusted for these multiple tests of peak shape, period, and phase, to obtain a final p-value.

We have implemented RAIN as a freely available package for the (also free) statistical software R/Bioconductor. A web interface for RAIN is also currently available at rain.biologie.hu-berlin.de/rain. The run time of the software for typical data sets is relatively short, comparable to JTK_CYCLE. Missing values and non-even sampling intervals are accommodated for. The user chooses periods to test for, steepness of rising and falling parts of the time series (umbrella peak locations) to consider, and the method for correction for multiple testing due to varying umbrella peaks and phases; the default, also used for the result of the present report, is the adaptive Benjamini-Hochberg method (Benjamini and Hochberg, 2000). RAIN computes the null distribution against umbrella alternatives exactly (Harding, 1984; Streitberg and Röhmel, 1988), leveraging the R package “gmp” to achieve arbitrary precision integer arithmetic. The run time of RAIN is comparable to that of JTK_CYCLE (on the order of 1-2 min for 25,000 samples and 24 time points). The exact derivation of the particular null distribution assumed by RAIN and details regarding the implementation are given in the Supplementary online material.

Synthetic Data for Rigorous Benchmarking

One part of assessing the performance of RAIN was running the algorithm on synthetic computer-generated data that include realistic artificial experimental noise but where we know the underlying rhythmic wave form. We chose to study and simulate the experimental noise of microarray mRNA expression; specifically, the mouse liver microarray experiment by Hughes et al. (2012). These data encompass 25,817 genes and 24 time points spanning CT0 to CT46, where CT stands for circadian time. To the time series y_g(t) measured for each gene g in this data set, a first Fourier harmonic ${\widehat{y}}_g\left(t\right)=k\left(1+a\cos \left(\text{ω}t\right)+b\sin \left(\text{ω}t\right)\right)$ was fitted, and errors were calculated as ${\text{ε}}_g\left(t\right)=y_g\left(t\right)-{\widehat{y}}_g\left(t\right)$; noise variances were estimated from the sum of the errors squared. We found that the noise standard deviation (SD) scales almost linearly with the average magnitude of measured signal; the coefficient of variation (SD divided by mean) is constant and ~0.10 (Suppl. Fig. S1). This motivated us to formulate the following model for the synthetic data, with a normalized mean magnitude of 1:

$$y\left(t\right)=\left(1+f\left(\text{ω}t,\text{φ}\right)\right)\left(1+\text{η}\right),$$

where $f\left(\text{ω}t,\text{φ}\right)$ is either a cosine function with amplitude a, frequency $\text{ω}=2\pi /24$ h⁻¹, and phase ϕ: $f\left(\text{ω}t,\text{φ}\right)=a\cos \left(\text{ω}t-\text{φ}\right)$, or it is a sawtooth function of the same frequency (for which a is half the peak-to-trough distance and ϕ determines the position of the maximum), and where $\text{η}~N\left(0,\sigma \right)$ is a Gaussian noise term with SD $\sigma =0.1$ for all cases in the present study (which for all practical purposes rules out negative values of y(t)). The amplitudes of the normalized oscillatory functions necessarily lie between $a=0$ and $a=1$, and in one setting, we considered amplitudes of 0, 0.1, 0.2, and 0.3—the latter amplitude being 3 times the noise SD in the microarray experiment, as described above. In another setting, amplitude-to-noise ratios were sampled from an estimated distribution based on the mouse liver microarray data (Hughes et al., 2012), with amplitudes and noise levels estimated as described above. For synthetic data with outliers, an additional large positive deviation of 20 was added to one randomly chosen time point of each time series, as done by Hughes et al. (2010).

ROC Curves and False Discovery Rates

We assessed the quality and performance of the different algorithms using ROC (receiver operator characteristic) analysis, which assays the true positive rate (TPR) and false positive rate (FPR) of a classification method (our case concerns classification of time series as rhythmic or nonrhythmic). The TPR is the fraction of truly rhythmic time series also classified as such (true positive rate), while the FPR is the fraction of truly nonrhythmic time series misclassified as rhythmic by the algorithm. An increasing TPR comes at a cost of an increasing FPR, but a good algorithm reaches a high TPR already at low FPRs. ROC curves—plots of TPR on the y-axis versus FPR on the x-axis—visualize the quality of an algorithm: Random choices (“monkey pushing a button”) produce a straight-line ROC curve $(\text{TPR}=\text{FPR})$, while the curves are pushed toward the upper left corner $(\text{TPR}\gg \text{FPR})$ as algorithms improve. A perfect algorithm would yield a constant $\text{TPR}=1$ for all FPRs. In this way, the performance of algorithms can be ranked. ROC curves are independent of the prevalence, defined as the proportion of actual rhythmic time series, and thus give a picture valid for any real-world scenario. This comes at the cost of not being able to reflect the fraction of truly nonrhythmic time series among all those classified as rhythmic. This is the false discovery rate (FDR; Suppl. Fig. S2), and it is highly dependent on the prevalence—that is, the fraction of truly rhythmic time series in the data set (between 0 and 1): If a data set consists of only a small percentage of truly rhythmic time series, a high TPR and low FPR can still result in a high FDR (Suppl. Fig. S2). In biological data analysis, it is usually the FDR that is controlled for, often using Benjamini-Hochberg adjusted p-values as conservative estimates. Fortunately, some algebraic work result in the equation

$$\text{TPR}=\frac{\left(1-f_{\text{rhythmic}}\right)\times \left(1-\text{FDR}\right)}{f_{\text{rhythmic}}\times \text{FDR}}\times \text{FPR},$$

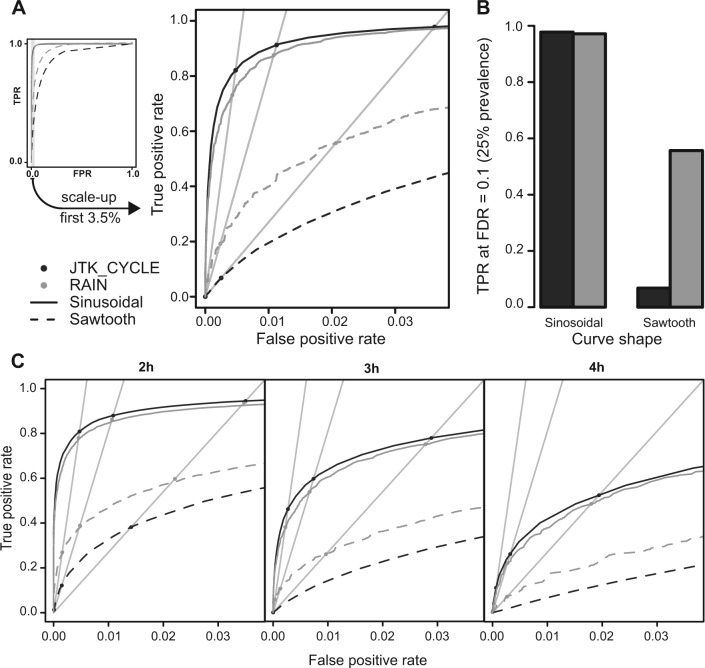
where $f_{\text{rhythmic}}$ is the prevalence. This means that a given FDR threshold and prevalence are manifested as a straight line in the ROC diagram, in which the TPR is plotted against the FPR. Where this straight line crosses the ROC curve of an algorithm, the TPR achieved by the algorithm can be read off the y-axis (Fig. 2). This combination of ROC curves and straight lines gives a complete bird’s-eye view of the quality of algorithms as well as their detection power at different FDR thresholds. To obtain the ROC curves in Figure 2, 100,000 synthetic time series were generated for each wave form and amplitude-to-noise ratio; any irregularities in the ROC curve shapes were due to the intrinsic granularities of the null distributions rather than the effects of small sample sizes.

Figure 2.

RAIN benchmarking. Synthetic data and ROC curves were used to assess the power and accuracy of RAIN compared with those of JTK_CYCLE. (A) ROC curve showing results for 100,000 sine curves and sawtooth-shaped curves, respectively, with an amplitude-to-noise ratio of 0.2 and sampled every 3 h for two full 24-h periods. The straight lines correspond to an FDR of 0.1 with (from steepest to least steep slope) prevalences of 5%, 10%, and 25%, or equivalently due to the symmetry of Equation 2, a prevalence of 10% and FDRs of 0.05, 0.1, and 0.25, respectively. True positive rates (TPRs) for these criteria can be read off the diagrams at the intersections between the straight lines and the ROC curves. (B) TPRs for $\text{FDR}=0.1$ and a prevalence of 25% (or vice versa). (C) Effect of different sampling rates. Here, amplitude-to-noise ratios were sampled from estimates coming from mouse liver microarray experiments (Methods and Suppl. Fig. S3). Thus, the result for a 3-h sampling interval is different from that depicted in panel A. Many more such panels are provided in Supplementary Figure S4.

Analysis of Microarray and Mass Spectrometry Data

Microarray data were obtained from the Gene Expression Omnibus, accession numbers GSE30411 (Hughes et al., 2012) and GSE11923 (Hughes et al., 2009), and were normalized using RMA and GCRMA, respectively, grouping transcripts using ENSEMBL gene annotations (Dai et al., 2005). Amplitudes and SDs of the noise (residuals) were estimated as described above using harmonic regression (Cornelissen, 2014); amplitudes of transcript groups with a Benjamini-Hochberg-adjusted p ≤ 0.05 were used to sample amplitudes for the synthetic data (described above). The amplitude-to-noise distribution of these estimations is shown in Supplementary Figure S3.

Present/absent calls were possible for the older microarray data due to the earlier platform used in that study (Hughes et al., 2009); transcript groups were considered present if more than half of the samples produced an MAS5 present call. Harmonic regression p-value correction was performed for present transcripts only.

Protein mass spectrometry data were obtained from the supplementary material of the original publications (Mauvoisin et al., 2014; Robles et al., 2014).

RAIN and JTK_CYCLE (version 2) were in all cases run to detect oscillations of a period of 24 h. RAIN was further set to allow an umbrella peak between 30% and 70% of a whole period when analyzing microarray and mass spectrometry data and between 10% and 90% when analyzing the synthetic data.

Results

RAIN Detects Both Sawtooth-shaped and Sinusoidal Wave Forms

We first aimed to rigorously study the power of RAIN for rhythm detection. For this, we applied the algorithm to synthetic data. The synthetic data were designed to have a random error component that is representative of the biological data that RAIN is supposed to analyze. To achieve this, we carefully studied the noise characteristics of 2 microarray studies of mouse liver and were able to extract a good noise model from those data (Methods). With this model, we generated synthetic time series of 3 types. The first one consisted of noise only; the second type was noise plus sine curves with amplitudes 1, 2, and 3 times as large as the noise SD, respectively, or with amplitude-to-noise ratios sampled from mouse liver microarray data (Methods); the third type consisted of noise plus sawtooth-shaped curves with amplitudes 1, 2, and 3 times as large as the noise SD, respectively, or with amplitudes sampled from microarray data. We then ran both RAIN and JTK_CYCLE with the synthetic data as inputs and used ROC curves (Methods) of the results to investigate the power of RAIN to detect rhythms. These curves allow an assessment of the power for rhythm detection of RAIN versus JTK_CYCLE while controlling for the FDR. The expectation was that RAIN, due to its design, should show a clear advantage when the rhythms are sawtooth-like, while both methods should readily be able to detect rhythms shaped as sine curves.

This expectation turned out to be valid in all cases. Figure 2 shows representative ROC curves for RAIN and JTK_CYCLE applied to computer-generated sine and sawtooth-shaped time series, respectively. The null background consisted of pure noise (Methods). Figure 2A gives results for synthetic data consisting of 16 samples taken every 3 h with an amplitude-to-noise ratio of 2. RAIN was able to detect a significant fraction of sawtooth-shaped wave forms that largely went undetected by JTK_CYCLE: For a prevalence for true positives of 25% and with an FDR of 0.1, RAIN recovered almost 60% of the sawtooth wave forms compared with less than 10% for JTK_CYCLE (Fig. 2B). For the sine curves, the difference between the methods was very small. This is the pattern of other sampling rates and amplitudes as well—examples are shown in Figure 2C also for cases where samples were taken every 2, 3, and 4 h, with a distribution of the oscillation amplitude-to-noise ratio sampled from estimates based on mouse liver microarray data (Methods). A complete survey of different sampling rates and amplitude-to-noise ratios is given as Supplementary Figure S4, including results for a set of synthetic time series with outliers.

In summary, RAIN was able to recover significant fractions of asymmetric sawtooth-shaped wave forms, in contrast to the previous comparable method, without losing power to detect symmetric sine waves.

The Circadian Transcriptome of Mouse Liver Exhibits a Wealth of Sawtooth-shaped Wave Forms

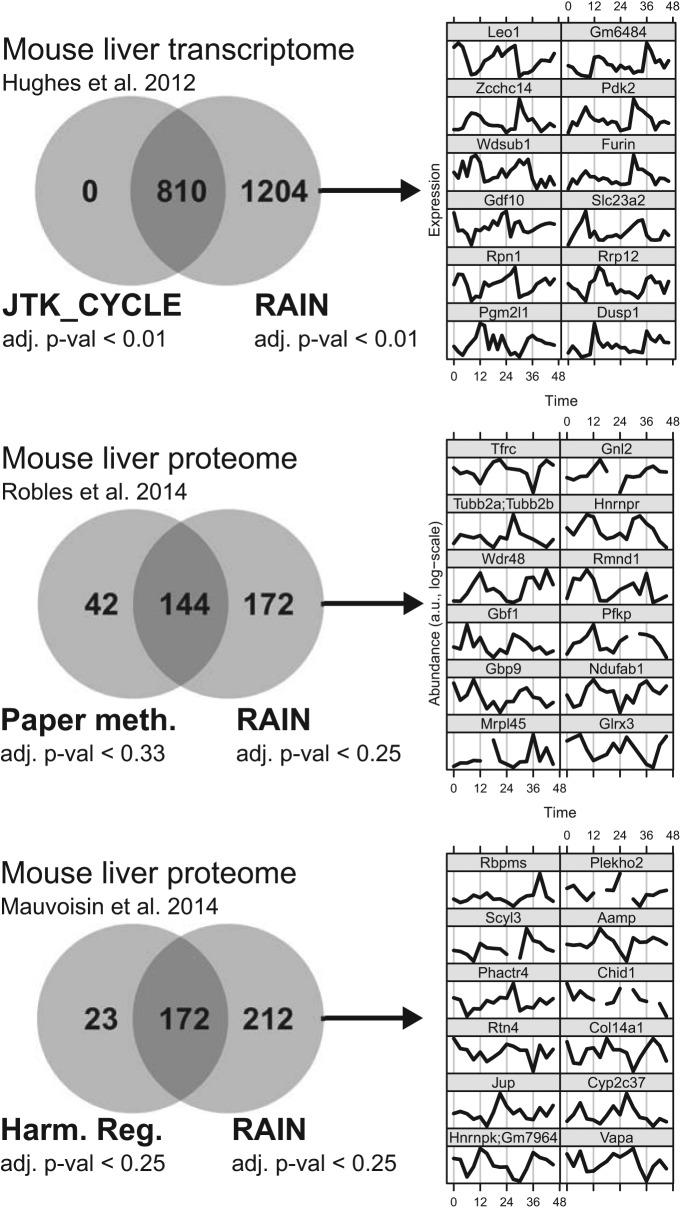
Considering the design and benchmarking of RAIN, we expected the method to discover hitherto undetected rhythms in biological data, in particular rhythms with nonsymmetric waveforms. The mouse liver microarray study by Hughes et al. (2012), consisting of 24 samples taken every 2 h, served to put this expectation to the test. Under a strict Benjamini-Hochberg corrected p-value cutoff of 0.01, RAIN detected 2014 rhythmically transcribed genes, compared with 810 genes detected by JTK_CYCLE. All genes detected by JTK_CYCLE were also detected by RAIN, whereas, in contrast, RAIN exclusively identified 1204 rhythmic transcripts (Fig. 3). Using a more liberal cutoff of 0.05 for JTK_CYCLE, while staying with the strict cutoff for RAIN, still resulted in 564 rhythmically transcribed genes that were exclusively detected by RAIN (with no genes exclusively detected by JTK_CYCLE under the same criteria). A visual inspection of the top hits (Fig. 3) confirms strong circadian rhythmicity and, indeed, markedly nonsymmetric and often sawtooth-like wave forms.

Figure 3.

Significantly expanded circadian transcriptomes and proteomes. With an FDR of 0.01, RAIN detects more than twice as many circadian transcripts in a mouse liver microarray data set (Hughes et al., 2012) as does JTK_CYCLE. Rhythms only detected by RAIN were validated using a control data set (Hughes et al., 2009) and an independent method (harmonic regression). The 12 transcripts with the lowest (adjusted) p-values that were only detected by RAIN under the FDR cutoff are shown and exhibit clear oscillations with asymmetric wave forms. Data from 2 studies using mass spectrometry to chart the mouse liver circadian proteome (Mauvoisin et al., 2014; Robles et al., 2014) were similarly analyzed, resulting in more than twice as many circadian proteins compared with the original studies.

We next sought to systematically assess the general quality of the time series exclusively detected by RAIN: Are these time series really rhythmic? To this end, we analyzed a control study: an earlier mouse liver microarray study consisting of 48 samples taken every hour (Hughes et al., 2009). We assessed rhythmicity in these control data using an unrelated method (harmonic regression with an adjusted p-value cutoff 0.01), which due to the much higher sampling rate used in this earlier study should be able to detect nonsinusoidal wave forms. We reasoned that if those transcripts of the primary study (Hughes et al., 2012) that were detected exclusively by RAIN are truly rhythmic, many of these should also be detected by harmonic regression in the control data. Our results confirmed this conjecture: of the 1204 rhythmic transcripts that only RAIN detected in the primary data set (Fig. 3), 946 were present in the control data set. It turned out that 65% of these 946 transcripts were flagged by the harmonic regression method as being rhythmic in the control data. For comparison, only 40% of expressed genes in that study were classified as rhythmic by the same method and criteria. This indicates that rhythms detected exclusively by RAIN are indeed reproducible biological phenomena rather than computational or measurement artifacts.

To further gauge the performance of RAIN with time series sampled every 4 h (a common experimental design), we down-sampled the primary microarray time series (Hughes et al., 2012) to comprise 12 measurements every 4 h. Also in this case, even when we used a stringent adjusted p-value cutoff for RAIN (0.1) and a less stringent cutoff for JTK_CYCLE (0.25), RAIN detected significantly more rhythmically transcribed genes than did JTK_CYCLE (1590 vs. 701 genes). Among those transcripts uniquely detected by RAIN that were also present in the control study, 66% were independently classified as rhythmic in the control study using harmonic regression, compared with the overall 40% rhythmic transcripts.

In summary, RAIN was able to detect much more rhythmically transcribed genes than was JTK_CYCLE. Detected rhythms exhibited nonsymmetric waveforms and were confirmed using a control data set and an independent method.

An Expanded Circadian Proteome

Mass spectrometry (MS) approaches have been used to quantify circadian rhythmicity in protein abundances on a proteome-wide scale (Mauvoisin et al., 2014; Robles et al., 2014). However, MS cannot presently quantify the entire mouse liver proteome but is biased in its detection capability to abundant, long-lived proteins. Since amplitudes of rhythms inevitably decrease with increasing protein lifetimes (Lück et al., Forthcoming), oscillations in protein abundances observed in these studies tend to have small amplitudes. In addition to this, significant non-Gaussian experimental noise is inherent to MS measurements. Rhythm detection is thus challenging for these data, and it is therefore not surprising that only 195 and 186 proteins were flagged for rhythmic abundances in the Mauvoisin et al. (2014) and Robles et al. (2014) studies, respectively (both with an experimental design of 16 tissue samples pooled from several mice and taken every 3 h). These calls were made using methods based on harmonic regression and with quite high Benjamini-Hochberg adjusted p-value cutoffs: 0.25 and 0.33, respectively (serving as FDR estimates).

We applied RAIN to these data and detected 316 and 384 proteins with circadian rhythms in their abundance, respectively, using an adjusted p-value cutoff of 0.25. This represents a significant expansion on previous results, with the caveat of having the same relatively high FDR as in the original studies. Instead using a lower adjusted p-value cutoff of 0.15, we detected 181 and 196 circadian proteins—almost the same numbers as in the original studies but with much improved FDRs. One should note, however, that these numbers must not be used as estimates for the total number of circadian proteins; rather, for this, methods such as the lowest slope estimator are appropriate (Benjamini and Hochberg, 2000).

Time series of the top 12 rhythmic proteins (lowest Benjamini-Hochberg adjusted p-values) that were not detected in the original studies are plotted in Figure 3, and circadian patterns are obvious by visual inspection. Noteworthy also are the peculiar experimental noise characteristics of these data, manifested as missing values and outliers, which particularly call for robust nonparametric methods such as RAIN and JTK_CYCLE. The latter method, however, was only able to detect 35 and 25 proteins from the Mauvoisin et al. (2014) and Robles et al. (2014) studies, respectively, with a high FDR of 0.25.

Further analysis of the functions of proteins whose abundances were classified as rhythmic illustrates that the method of rhythm detection matters for conclusions about biological function. The proteins classified as rhythmic in the original study (Mauvoisin et al., 2014) are highly enriched for secreted proteins, according to the functional annotation service DAVID. We recovered this result also with the proteins that RAIN classified as rhythmic, but additionally we found previously unnoticed functional characteristics of the circadian proteome. This includes enrichment for proteins associated with the mitochondrion, as well as chaperones and binding to unfolded proteins, lysosomal proteins, and proteins involved in iron and drug metabolism. If we expand the analysis to the proteins with abundances classified as rhythmic in both studies, a different picture emerges. Cofactor and vitamin binding are enriched functions in the smaller set of proteins resulting from the detection methods in the original studies (31 proteins). In contrast, RAIN detects a considerably larger overlap of rhythmic proteins between the studies (61 proteins, FDR 0.25), and here again, protein folding and unfolded protein binding are overrepresented functions. The DAVID results for these 61 circadian proteins are given in Supplementary Table S1. These protein numbers could be compared with the mere 5 common proteins detected by JTK_CYCLE, FDR 0.25.

Thus, with RAIN, the circadian proteome was significantly expanded. Studying this expanded group of proteins, we recovered previous results but also discovered previously unidentified functions of proteins with rhythmic abundances.

Discussion and Outlook

We have presented RAIN, a robust nonparametric method for detection of rhythms in time series, that makes few assumptions about wave form shape. We have shown rigorously that the method has a sensitivity that is superior to previous methods while controlling the false discovery rate. This largely stemmed from an ability to detect nonsymmetric wave forms, such as sawtooth-like shapes, while preserving a robust sensitivity for symmetric wave forms. Consequently, a result of RAIN when applied to mouse liver transcriptome- and proteome-wide data was significantly expanded sets of transcripts and proteins with circadian rhythms in abundance, compared with previous studies.

Although RAIN was designed for research on circadian rhythms, the method is applicable for rhythm detection in any time series. We do, however, recommend sampling over more than one period in order to readily discriminate between sawtooth-shaped waveforms and linear trends. A practical limitation could be time series length: The algorithm was developed and tested for time series with moderate numbers of time points (on the order of 10-100), for which rhythm detection is challenging when the experimental noise characteristics are complex. We point out that the run time of the algorithm can be significant for very long time series (the same is true for JTK_CYCLE). Fortunately, for these cases, classic parametric methods, such as harmonic regression or periodogram-based methods, often perform very well also when the noise is non-Gaussian. Another limitation to RAIN and JTK_CYCLE, but also to harmonic regression, is the assumption of uncorrelated or at least only weakly correlated noise. This assumption is certainly justified for data coming from experimental designs where different animals are sacrificed at each time points, such as those data analyzed here. However, for certain types of experiments, for example where all samples are taken from one cell culture that in addition exhibits strongly correlated fluctuations in the readout, simulations of more realistic null models may be required (Futschik and Herzel, 2008).

RAIN readily detects symmetric wave forms (Fig. 2), but there is still a small but measurable advantage of using JTK_CYCLE if the underlying wave form is perfectly symmetric. This is because RAIN does not make comparisons between measurements in the rising and falling parts of the time series. Thus, when the goal is to explicitly detect symmetric rhythms only, JTK_CYCLE will still be the method of choice. The same is true if the goal is to detect one known particular curve shape, since this can be implemented as a minor modification of the JTK_CYCLE code base.

RAIN does not measure periods, amplitudes, and phases, although naive estimates would be easy to obtain. The reason for this is that such so-called point estimation should preferably fulfill the criteria of consistency (estimates converging to the true values as the number of time points sampled goes to infinity) and unbiasedness (the expected estimate for a finite number of time points sampled should be equal to the true value). These criteria are not met when one is using the results of RAIN to estimate periods, amplitudes, and phases. The algorithm was designed for hypothesis testing rather than for point estimation. For this reason, we also recommend against using the period and phase estimates provided by JTK_CYCLE, which are not consistent or unbiased. However, JTK_CYCLE does implement an interesting and promising amplitude estimation method. We furthermore recommend complementing hypothesis testing with amplitude estimation when selecting genes or proteins of interest, since it is safe to assume that biological function of rhythms requires reasonable amplitudes. Classic harmonic regression is still well suited for this, although there is also a need in the field for new point estimation methods more robust to outliers.