Density dependent state space model for population abundance data with unequal time intervals

Abstract

The Gompertz state-space (GSS) model is a stochastic model for analyzing time series observations of population abundances. The GSS model combines density dependence, environmental process noise, and observation error toward estimating quantities of interest in biological monitoring and population viability analysis. However, existing methods for estimating the model parameters apply only to population data with equal time intervals between observations. In the present paper, we extend the GSS model to data with unequal time intervals, by embedding it within a state-space version of the Ornstein-Uhlenbeck process, a continuous-time model of an equilibrating stochastic system. Maximum likelihood and restricted maximum likelihood calculations for the Ornstein-Uhlenbeck state-space model involve only numerical maximization of an explicit multivariate normal likelihood, and so the extension allows for easy bootstrapping, yielding confidence intervals for model parameters, statistical hypothesis testing of density dependence, and selection among sub-models using information criteria. Ecologists and managers previously drawn to models lacking density dependence or observation error because such models accommodated unequal time intervals (for example, due to missing data) now have an alternative analysis framework incorporating density dependence, process noise and observation error.

INTRODUCTION

Gaps in time series observations of population abundances pose challenges for analysis. Various statistical models for ecological time series data, especially models incorporating realistic population dynamics, require observations spaced at equal time intervals. However, ecological sampling involves constraints of time, personnel, and budgets that do not always live up to the designs and requirements of statistical models. As well, various ecological systems such as aquatic or microbial systems (Kirchman 2012) have intrinsically continuous-time dynamics and are sometimes sampled at unequal time intervals. Ordinarily equal time intervals will be stretched and shrunk into unequal intervals in systems in which time is measured in degree days (Metcalf and Luckmann 1994). The data that do exist in studies with missing data or unequal time intervals are potentially informative, and precluding such data from analysis could affect conclusions regarding the biological resources in question. The monitoring and management of biological populations would benefit from having better models for analyzing time series data with unequal time intervals.

Dennis et al. (2006) described a “state-space” population model for use in ecological time series analysis. The model, termed the Gompertz state space (GSS) model, is one of the simplest possible formulations containing density dependence, stochastic process variability, and stochastic observation or measurement error. The simplicity of the model allows for an explicit likelihood function and for parameter estimation through ordinary numerical maximization. Although the GSS model can accommodate missing observations from otherwise equally spaced time series, the GSS model does not allow observations collected at unequal, non-integer time intervals and hence is not suitable for ecological situations in which time is considered to be real-valued.

Various state space population models of greater complexity can handle unequally spaced data (de Valpine and Hastings 2002, de Valpine 2002, 2004, Clark and Bjørnstad 2004, Ionides et al. 2006, Lele et al. 2007, Ponciano et al. 2009). Such models require custom programming of simulation-intensive computer algorithms for fitting (parameter estimation) and other statistical inferences. For example, Lele et al. (2007) and Ponciano et al. (2009) used data cloning (a Monte Carlo Markov Chain method) to calculate maximum likelihood estimates of parameters in state space models for analyzing the well-known laboratory Paramecium (sp.) data of Gause (1934) which have missing observations on day 1. Adapting such models to other data sets with other configurations of missing observations would require reprogramming the calculations for each new case.

A special case of the GSS model is a density independent state space model. The exponential growth state space (EGSS) model was introduced by Holmes (2001), and parameter estimation was studied by Lindley (2003) and Staples et al. (2004). By contrast to the GSS model, the EGSS model has been generalized to apply to unequal, real-valued time intervals (Staudenmayer and Buonaccorsi 2006, Humbert et al. 2009).

This paper extends the full, density dependent GSS model to unequal, real-valued time intervals. The method used employs a stochastic version of the continuous-time, deterministic Gompertz growth model as the underlying model of population growth (process model). The stochastic version is a continuous-time diffusion process representing Gompertz-type density dependent growth perturbed by environmental noise. Transforming the process model to the logarithmic scale produces the Ornstein-Uhlenbeck process, a well-studied diffusion process. Finally, adding an observation error component produces a state-space version of the Ornstein-Uhlenbeck model. The state space model has discrete-time statistical properties identical to those of a GSS model, but has a likelihood function that can be written for time series observations recorded at arbitrary real-valued time intervals. The likelihood makes accessible a variety of statistical inferences based on parametric bootstrapping. Four example data sets serve to illustrate statistical inferences with the model. Procedures for calculating confidence intervals for model parameters and for conducting bootstrap tests of density dependence are described in the online Appendix to this paper, and R programs for all statistical inferences are provided (Supplementary Material online).

POPULATION MODEL

Deterministic Gompertz model

The Gompertz curve (after Gompertz 1825) originally was an actuarial model of mortality, but since the 1920s biologists have been using the curve as a deterministic model of biological growth, variously to describe the growth of tumors, individuals, or populations (Winsor 1932). The model is frequently presented in the form of an ordinary differential equation:

$$\frac{\mathit{dn}\left(t\right)}{\mathit{dt}}=\theta n\left(t\right)[\log \kappa -\log n(t\left)\right].$$ (1)

Here n(t) is the abundance of the growing entity at time t, θ and κ are positive constants, with κ being the equilibrium abundance and θ being a measure of the speed of equilibration. The similar logistic growth model has the density dependence term proportional to n(t) instead of log n(t). The solution trajectory for Eq. 1 is given by

$$n\left(t\right)=\kappa \exp \left[e^{-\theta t}\log \right(n_0∕\kappa \left)\right],$$ (2)

with n₀ = n(0) denoting the initial population abundance. The Gompertz trajectory has an inflection point at κ/e if the initial population abundance is below that level (inflection for the logistic model is at k/2).

Stochastic Gompertz model

A stochastic version of the Gompertz model is represented by the following stochastic differential equation (SDE):

$$\mathit{dN}\left(t\right)=\theta N\left(t\right)[\log \kappa -\log N(t\left)\right]\mathit{dt}+\beta N\left(t\right)\mathit{dW}\left(t\right).$$ (3)

Here an infinitesimal increment of the Gompertz growth model (Eq. 1 written in differential form) is perturbed by a random noise term in which dW(t) has a normal distribution with a mean of 0 and a variance of dt (where the correlation between dW(t_i) and dW(t_j) is assumed equal to 0 if t_i ≠ t_j), and in which the intensity of the noise is scaled by the term βN(t), with β > 0. The scaling term proportional to population abundance is a common model of environmental stochasticity (Tier and Hanson 1981, Dennis and Patil 1984). Such stochasticity can produce substantial population variability at high as well as low abundances. The assumption of zero-correlated process noise describes the unpredictability of growth increment fluctuations in response to environmental buffeting has theoretical and empirical utility (Allen 2010, Dennis et al. 1991). Temporal correlation in process noise, if present, is difficult to estimate in the presence of sampling error (Staples et al. 2008).

The SDE as written in the form of Eq. 3 can be understood as an easy recipe for simulating a trajectory of population abundance for specified values of θ, κ, and β (for instance, Higham 2001, Allen 2010): (1) Over a tiny time interval dt, calculate an increment dN(t) of abundance from a normal distribution with a mean of θN(t)[log κ − log N(t)]dt and a variance of [βN(t)]²dt, with N(t) being the current population abundance and t being the current time in the simulation. (2) Update population abundance as N(t) + dN(t) and update time as t + dt. (3) Return to step (1) and repeat the process for a new time interval, generating a new normal random growth increment using the updated population abundance. The accuracy of the simulation (in terms of the statistical properties of N(t)) is degraded if the time interval dt is not small. While various alternative simulation algorithms can improve the numerical accuracy of SDEs in general (Allen 2010) and the OU process in particular (Gillespie 1996), the preceding “Euler-Maruyama” method for SDEs serves as an accessible pedagogical entry point to a highly mathematized subject.

Ornstein-Uhlenbeck model

Written as an SDE in the form of Eq. 3, population abundance is a type of stochastic process known as a diffusion process with infinitesimal mean function given by m(n) = θn(log κ − log n) and infinitesimal variance function ν(n) = β²n² Karlin and Taylor 1981). A useful property of diffusion processes is that a smooth invertible transformation of a diffusion process is also a diffusion process (Karlin and Taylor 1981). Let X(t) = g(N(t)) be such a transformation (perhaps log N(t) or $\sqrt{N\left(t\right)}$, etc.). The infinitesimal mean and variance of X(t) are given by the Itô transformation formulas: $m_x\left(x\right)=m\left(n\right)g^{\prime }\left(n\right)+\frac{1}{2}\nu \left(n\right)g^{″}\left(n\right)$, ν_x(x) = ν(n)[g′(n)]², with n = g⁻¹(x). The transformation property opens the possibility that a given diffusion process might be transformed to a scale for which results helpful for analysis and inference can be derived. Such a transformation exists for the stochastic Gompertz model.

The logarithmic transformation, X(t) = log N(t), converts population abundance N(t) under the stochastic Gompertz model into a well-studied diffusion process known as an Ornstein-Uhlenbeck (OU) process (after Uhlenbeck and Ornstein 1930; see Allen 2010). Under the Itô transformation formulas, the infinitesimal mean and variance functions for X(t) become

$$m_X\left(x\right)=\theta (\mu -x),$$ (4)

$$v_X\left(x\right)={\beta }^2,$$ (5)

where μ = log κ − β²/(2θ). The SDE for X(t) takes the form

$$\mathit{dX}\left(t\right)=\theta [\mu -X(t\left)\right]\mathit{dt}+\beta \mathit{dW}\left(t\right),$$ (6)

which is a growth increment θ[μ − X(t)]dt from a linear deterministic model perturbed by normally-distributed noise with constant variance β²dt. The SDE given by Eq. 6 defines an OU process X(t). Among the well-known results (see Allen 2010) are that X(t) has a normal transition probability distribution with a mean function given by

$$\mathrm{E}\left[X\right(t)\mid X(0)=x_0]=\mu -(\mu -x_0)e^{-\theta t},$$ (7)

where x₀ = log n₀, and a variance function given by

$$\mathrm{V}\left[X\right(t)\mid X(0)=x_0]=\frac{{\beta }^2}{2\theta }(1-e^{-2\theta t}).$$ (8)

The covariance of the process at two different times is given by

$$\mathrm{Cov}\left[X\right(t),X(t+s\left)\right]=\frac{{\beta }^2}{2\theta }(1-e^{-2\theta t})e^{-\theta s},t,s>0,$$ (9)

and values of the process at multiple different times have a joint multivariate normal distribution. As time t becomes large, the transition distribution converges to a normal stationary distribution with mean

$$\mathrm{E}\left[X\right(\infty \left)\right]=\mu ,$$ (10)

and variance

$$\mathrm{V}\left[X\right(\infty \left)\right]=\frac{{\beta }^2}{2\theta }.$$ (11)

The stationary distribution on the original abundance scale is a lognormal distribution and represents the stochastic counterpart to the point equilibrium or “carrying capacity” in the deterministic model (Dennis and Patil 1984).

Ornstein-Uhlenbeck state space model

We define an Ornstein-Uhlenbeck state space (OUSS) model by adding an observation error component. The observations can be taken at arbitrary times which need not be equally spaced. The observed population log-abundance at time t_i is modeled as

$$Y\left(t_i\right)=X\left(t_i\right)+F_i,$$ (12)

where F_i has a normal distribution with mean 0 and variance τ², with F_i, F_j uncorrelated (i ≠ j). Observation error on the original abundance scale thereby has a lognormal distribution, which can be regarded as a model of ecological sampling under heterogeneous sampling conditions (Dennis et al. 2006). Eqs. 6 and 12 together constitute the OUSS model. The underlying actual population log-abundance X(t_i) is unobserved.

The observations Y(0), Y(t₁), Y(t₂), …, Y(t_q) (estimates or indexes of log-population abundance) recorded at times t₀ = 0, t₁, …, t_q need not be equally spaced. The observations under the OUSS model have a joint multivariate normal distribution, but the distribution takes two different forms, non-stationary and stationary, depending on the situation being modeled. If the population abundances have commenced far from equilibrium, the observations have the non-stationary distribution in which the mean of each Y(t_i) is

$$\mathrm{E}\left[Y\right(t_i\left)\right]=\mu -(\mu -x_0)e^{-\theta t_i},$$ (13)

the variance is

$$\mathrm{V}\left[Y\right(t_i\left)\right]=\frac{{\beta }^2}{2\theta }(1-e^{-2\theta t_i})+{\tau }^2,$$ (14)

and the covariance of the process at two different times t_i and t_j is given by

$$\mathrm{Cov}\left[Y\right(t_i),\mathrm{Y}(t_j\left)\right]=\frac{{\beta }^2}{2\theta }\left(1-e^{-2\theta \min (t_i,t_j)}\right)e^{-\theta \mid t_i-t_j\mid }.$$ (15)

If however the population abundances have become stationary (fluctuating stochastically around an equilibrium) before sampling commenced, the observations have the stationary distribution in which the mean of each Y(t_i) is

$$\mathrm{E}\left[Y\right(t_i\left)\right]=\mu ,$$ (16)

the variance is

$$\mathrm{V}\left[Y\right(t_i\left)\right]=\frac{{\beta }^2}{2\theta }+{\tau }^2,$$ (17)

and the covariance of the process at two different times t_i and t_j is given by

$$\mathrm{Cov}\left[Y\right(t_i),\mathrm{Y}(t_j\left)\right]=\frac{{\beta }^2}{2\theta }{e}^{-\theta \mid t_i-t_j\mid }.$$ (18)

In either the stationary or non-stationary case the joint distribution of the observations is similar to that of the underlying OU process, except that the quantity τ² is added to the variance of each Y(t_i). Two different methods for fitting the model to data (Statistical Methods, below) arise from whether or not the population has become stationary.

The OUSS model can be regarded as a continuous time version of the GSS model. The GSS model is defined (in the notation of Dennis et al. 2006) by X_t = a + cX_t−1 + E_t, Y_t = X_t + F_t, where X_t and Y_t are respectively the underlying and observed population log-abundances at times t = 0, 1, 2, …, q, and E_t and F_t have independent normal distributions with means of 0 and respective variances of σ² and τ². The parameters a, σ², and τ² are positive, and −1 < c < +1. If 0 < c < 1, the transition probability distributions of the OUSS and GSS models evaluated at integer times coincide as identical normal distributions means and variances given by Eqs. 13 and 14, with the relationships between parameters given by the following transformations: a = μ(1 − e^−θ), c = e^−θ, σ² = (1 − e^−2θ)β²/(2θ); μ = a/(1 − c), θ = −ln(c), γ² = −[2σ²ln(c)]/(1 − c²), with τ² having the same value in both models. If −1 < c < 0 the, GSS model has a deterministic component with damped oscillatory behavior for which there is no straightforward continuous time version. However, oscillatory behavior in population data, damped or otherwise, suggests the presence of nonlinear dynamic forces (May 1994), and one should explore alternative model structures with additional state variables and/or nonlinear interactions.

STATISTICAL METHODS

Maximum likelihood estimation for the OUSS stationary case

Under stationarity, the initial log-population abundance, X(0), is assumed to arise from the stationary normal distribution of the population abundances. Such an assumption of might be plausible if the monitoring program commenced after the population had been existing for a time long enough for stochastic equilibration in the particular environment. The model then has four unknown parameters: θ, μ, β², and τ².

Fitting the model to data means estimating the unknown model parameters. Using the multivariate normal distribution, the model can be fitted to data with maximum likelihood (ML) estimation. For ML estimation with the OUSS model, the likelihood function is the joint multivariate normal probability density for the observations evaluated at their realized data values. The ML estimates then are the parameter values that jointly maximize the likelihood or log-likelihood function. The multivariate normal log-likelihood for the stationary OUSS model is given by

$$\log L(\mu ,\theta ,{\beta }^2,{\tau }^2)=-\frac{(q+1)}{2}\log \left(2\pi \right)-\frac{1}{2}\log (\mid \mathbf{V}\mid )-\frac{1}{2}{(\mathbf{y}-\mathbf{m})}^{\prime }{\mathbf{V}}^{-1}(\mathbf{y}-\mathbf{m}),$$ (19)

where the elements of the column vector y are the data values y₀, y₁, y₂, …, y_q (realized values of the random variables Y(0), Y(t₁), Y(t₂), …, Y(t_q)) recorded at times 0, t₁, t₂, …, t_q. Also, the column vector m has all q + 1 elements identically equal to μ (Eq. 16), the variances on the main diagonal of the variance-covariance matrix V are all equal to τ² + [β²/(2θ)] (Eq. 17), and the (i, j)th and (j, i)th covariance elements in V are both equal to [β²/(2θ)]e^−θ_Sij, where S_ij = |t_i − t_j| (Eq. 18).

The ML estimates must be calculated with numerical optimization (for instance, with the “optim” function in R; R Core Development Team 2006). An R program for such calculation is provided in the Supplementary Material online.

Restricted ML estimation for the stationary case

Restricted maximum likelihood (REML) estimation for the multivariate normal distribution uses a linear combination of the observations that eliminates the parameters in the mean vector, leaving only parameters in the variance-covariance matrix. The statistical properties of the resulting estimates for the GSS and EGSS models are frequently better than those of ML estimates (Dennis et al. 2006, Humbert et al. 2009). For the OUSS model under the stationary case, a linear combination that produces a zero-mean vector is the simple differencing of the observations. Let W_i = Y(t_i) − Y(T_i−1), i = 1, 2, …, q. The W_i’s have a joint multivariate normal distribution with a mean vector of all zeros and a variance-covariance matrix given by

$$\Phi ={\mathbf{DVD}}^{\prime },$$ (20)

where D is the q×(q+1) differencing matrix given by

$$\mathbf{D}=\left[\begin{array}{cccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\cdots \hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 1\hfill & \hfill 0\cdots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 1\cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right].$$ (21)

For REML estimation, the multivariate normal log-likelihood is a function of three of the parameters in the OUSS model:

$$\log L(\theta ,{\beta }^2,{\tau }^2)=-\frac{q}{2}\log \left(2\pi \right)-\frac{1}{2}\log (\mid \Phi \mid )-\frac{1}{2}{\mathbf{w}}^{\prime }{\Phi }^{-1}\mathbf{w}.$$ (22)

Here the column vector of differenced observations is w = Dy. After numerical maximization of the REML log-likelihood, the mean parameter μ is estimated by

$$\widehat{\mu }={\mathbf{j}}^{\prime }{\widehat{V}}^{-1}\mathbf{y}∕\left({\mathbf{j}}^{\prime }{\widehat{V}}^{-1}\mathbf{j}\right),$$ (23)

where $\widehat{\mathrm{V}}$ is the variance-covariance matrix V (for the undifferenced observations, Eq. 19) evaluated with the REML estimates of θ, β², and τ², and j is a (q + 1)×1 column vector of ones. The R program for parameter estimation accompanying this paper (Supplementary Material online) calculates the REML estimates in addition to the ML estimates.

ML estimation for the nonstationary case

The nonstationary OUSS model should be considered for use when an appreciable proportion of the observations are recorded during a transient growth phase, as for instance when a population displays a sigmoid trajectory instead of a trajectory solely fluctuating around a steady state. Examples of such situations might occur when monitoring the translocation of a species by release of a few individuals into the wild, the colonization of a new area by an invading species, the increase of an agricultural pest through a growing season starting from low density, the recovery of a species after a catastrophic decline, or the growth of microbial populations in experimental laboratory cultures (Ponciano et al. 2005). The initial population log-abundance χ₀ usually becomes an additional unknown parameter in the nonstationary model, unless its value is known without sampling error (such as might be the case for a species translocation or a laboratory inoculation).

ML estimation is available for the nonstationary case, but REML estimation is not available. ML estimation uses the multivariate normal log-likelihood (Eq. 19) for the data values y₀, y₁, y₂, …, y_q, but with a different mean vector and variance-covariance matrix. The element in the mean vector m corresponding to the data value y_i is given by Eq.13, the variances on the main diagonal of V are computed with Eq. 14, and the (i, j)th and (j, i)th covariance elements in V are obtained with Eq. 15. The log-likelihood must be numerically maximized jointly for the five unknown parameters χ₀, θ, μ, β², and τ².

If the initial log-abundance χ₀ is known, the log-likelihood has just the four unknown θ, μ, β², and τ², with χ₀ fixed at its known value. Also, when χ₀ is known the initial observation y₀ is equal to χ₀ and is omitted from the likelihood (that is, omitted from the data vector y). ML estimation uses the multivariate normal log-likelihood (Eq. 19) modified to apply to just the q observations y₁, y₂, …, y_q recorded at times t₁, t₂, …, t_q. The modifications consist of substituting a q×1 vector m containing means defined by Eq. 13, a q×q variance-covariance matrix V containing elements defined by Eqs. 14 and 15, and a leading term $-\frac{q}{2}\log \left(2\pi \right)$ instead of $-\frac{q+1}{2}\log \left(2\pi \right)$. The R program for parameter estimation accompanying this paper also optionally calculates estimates for the non-stationary case (Supplementary Material online).

Additional statistical inferences for the OUSS model include confidence intervals for parameters, hypothesis tests for density dependence, and model selection among submodels. The statistical justifications and calculations involved in the additional inferences are described in the Appendix.

EXAMPLES

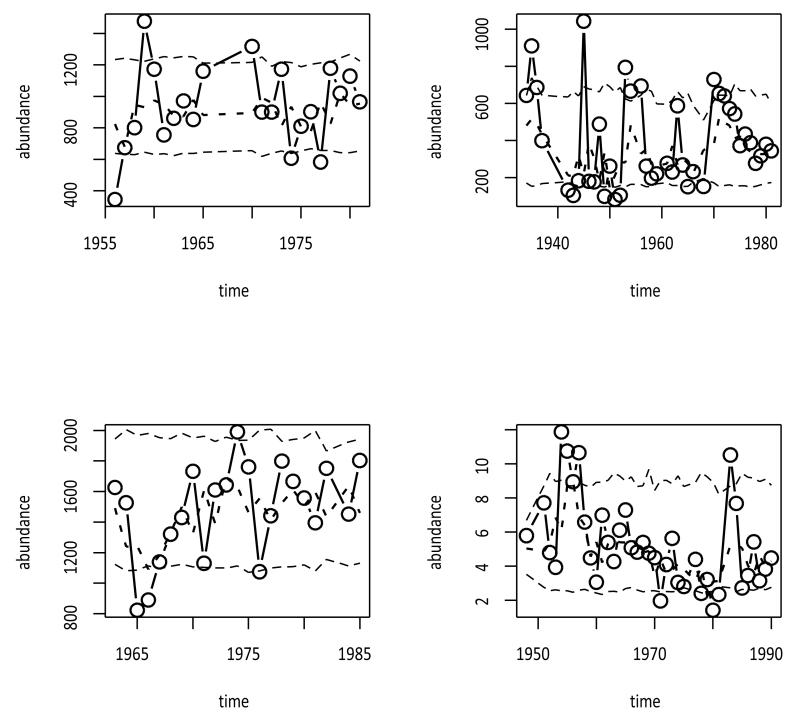
Bobcat (Lynx rufus) abundances in Idaho seemingly held steady, albeit with substantial fluctuations, over a 25 yr period beginning in 1956 (Figure 1, upper left). Bobcat abundances in Maine displayed fluctuations of even greater magnitude (Figure 1, upper right). The bobcat data are furbearer harvest records listed in the Global Population Dynamics Database (NERC Centre for Population Biology 2010), data sets 212 (Idaho) and 216 (Maine). As an index of population abundance, fur harvest records can be assumed to arise from a variable and heterogeneous sampling process, and any models of such time series should incorporate an appropriate sampling component. In Idaho, an unexplained hiatus in the data occurs during the years 1966-69, while in the Maine data the years 1938-41, 1967 and 1969 are missing. Mark-recapture estimates of the elk (Cervus elaphus) population in the central valley of Grand Teton National Park, Wyoming, are missing the year 1983 (Figure 1, lower left; data reported by Boyce 1989 as used by Dennis and Taper 1994). Yearly sampling of adult rangeland grasshopper (Orthoptera: Acrididae, mixed species) abundances in Montana began in 1948, with the years 1949-50, 1977, and 1982 missing (Figure 1, lower right; data reported by Kemp and Dennis 1993). The gaps are the main reason for the selection of the particular data sets here to illustrate the OUSS model. All the data sets in Figure 1 are among those included in the R programs accompanying this paper (Supplementary Material online).

Figure 1.

Four population abundance time series (circles), with expected values of true abundances given the other observations (short dashed lines), and bootstrapped 95% confidence intervals for true abundances (long dashed lines), estimated with restricted maximum likelihood under the Ornstein-Uhlenbeck state space model. Upper left: bobcat furbearer harvest records from Idaho, USA (parameter estimates with bootstrapped 95% confidence intervals: $\widehat{\mu }=6.79(6.61,6.97)$, $\widehat{\theta }=1.26(3.91\times {10}^{-7},20.2)$, ${\widehat{\beta }}^2=0.272(7.43\times {10}^{-3},3.94)$, ${\widehat{\tau }}^2=7.48\times {10}^{-4}(9.14\times {10}^{-10},0.0847)$). Upper right: bobcat furbearer harvest records from Maine, USA ($\widehat{\mu }=5.78(5.47,6.08)$, $\widehat{\theta }=0.877(0.0226,10.3)$, ${\widehat{\beta }}^2=0.735(0.0202,2.40)$, ${\widehat{\tau }}^2=0.00475(1.79\times {10}^{-8},0.334)$). Lower left: elk population estimates from Grand Teton National Park, Wyoming, USA ($\widehat{\mu }=7.29(7.14,7.44)$, $\widehat{\theta }=0.868(0.229,19.3)$, ${\widehat{\beta }}^2=0.0990(0.0296,1.45)$, ${\widehat{\tau }}^2=9.80\times {10}^{-9}(2.93\times {10}^{-11},1,22\times {10}^{-3})$). Lower right: grasshopper density estimates from the western mountainous region of Montana, USA ($\widehat{\mu }=1.56(1.31,1.82)$, $\widehat{\theta }=0.722(0.272,2.01)$, ${\widehat{\beta }}^2=0.347(0.160,0.752)$, ${\widehat{\tau }}^2=2.27\times {10}^{-7}(3.81\times {10}^{-8},2.27\times {10}^{-5})$).

The parameter μ tends to be estimated with precision, according to the REML bootstrap confidence intervals (Figure 1). The parameters θ, β² and τ² are estimated well for these data, as suggested by the wide confidence intervals (Figure 1). The GSS model, and by implication the OUSS model, sometimes has ridge-like likelihoods, or likelihoods with multiple local maxima corresponding to sub-models with all observation error or all process noise (Dennis et al. 2006, 2011, Knape 2008), especially for short time series. Replicating the sampling process one or more times at selected sampling times can substantially improve parameter estimation (Dennis et al. 2011), as can substantial amounts of transience in the data (nonstationarity) resulting from initiating the time series far from equilibrium (Dennis and Taper 1994).

DISCUSSION

If unequal sampling intervals are due simply to data missing from otherwise equally spaced observations (such as the data in Figure 1), then the ordinary GSS model can in fact be used with modification. The GSS model, like the OUSS model, has observations with a multivariate normal log-likelihood (Eq. 19). To calculate ML estimates for the GSS model, the missing observations in question are deleted from the vector y, the entries corresponding to the missing observations are deleted from m, and the rows and columns corresponding to the missing observations are deleted from V. The resulting expression is the proper log-likelihood function for the multivariate normal distribution of the remaining observations, under a standard property of the multivariate normal distribution (Seber 1984). While deleting observations from the GSS is easy in principal, programming software to automate the deletions in order to analyze many data sets would not be straightforward.

An additional problem with missing observations occurs for restricted maximum likelihood (REML) estimation. For the GSS model, REML estimates are calculated from the likelihood function for the first differences (Dennis et al. 2006). For the EGSS model, REML estimates are calculated from the likelihood function for the second differences (Staples et al. 2004). The problem is that each missing observation removes two observations from REML estimation in the GSS model and three observations from REML estimation in the EGSS model. REML estimation with missing data thus becomes costly, in terms of information about parameters, for the low sample sizes common in ecological time series.

Also, the GSS model cannot be used for systems sampled naturally at unequal time intervals. Plankton sampling schedules in aquatic systems, for instance, might not adhere to rigidly equal intervals. In insect ecology, degree days are routinely used as a time scale, and the application of a degree-day transformation to sampling times with equal intervals invariably produces unequal intervals on the new scale. In such cases, the unequal intervals cannot be handled merely by dropping observations from the multivariate normal log-likelihood function. A solution instead is to use the OUSS model.

Alternative ways for accommodating unequal intervals in state space models are computationally challenging. The basic approach treats the underlying population abundance as an unobserved “latent variable” in a hierarchical statistical model. Parameters are estimated with intensive MCMC simulation, coupled with either a Bayesian (Clark and Bjornstadt 2004) or frequentist (Lele et al. 2007) inferential method. While the approach allows the use of more complex ecological models of population growth and/or sampling, the problems of parameter estimability are not made any easier. Recent developments in estimation diagnostics (Lele et al. 2010, Ponciano et al. 2012) at least are helping investigators recognize when problems exist. As well, the MCMC calculations require considerable expertise in programming and statistical theory. By contrast, the OUSS model presented here brings density dependence, process noise, and observation error within reach of ordinary numerical maximization.