Critical slowing down as early warning for the onset of collapse in mutualistic communities

Significance

Little is known on whether structurally diverse ecological networks may respond abruptly to anthropogenic stress and even less on our ability to detect such responses in advance. By simulating mutualistic communities en route to a tipping point, we show how critical slowing-down indicators may be used as early warnings for the collapse of ecological networks. Our findings not only confirm the existence of the generic dynamical signatures of tipping points in ecological networks but also suggest a promising way for identifying most vulnerable components in a broad class of networks at the brink of collapse.

Abstract

Tipping points are crossed when small changes in external conditions cause abrupt unexpected responses in the current state of a system. In the case of ecological communities under stress, the risk of approaching a tipping point is unknown, but its stakes are high. Here, we test recently developed critical slowing-down indicators as early-warning signals for detecting the proximity to a potential tipping point in structurally complex ecological communities. We use the structure of 79 empirical mutualistic networks to simulate a scenario of gradual environmental change that leads to an abrupt first extinction event followed by a sequence of species losses until the point of complete community collapse. We find that critical slowing-down indicators derived from time series of biomasses measured at the species and community level signal the proximity to the onset of community collapse. In particular, we identify specialist species as likely the best-indicator species for monitoring the proximity of a community to collapse. In addition, trends in slowing-down indicators are strongly correlated to the timing of species extinctions. This correlation offers a promising way for mapping species resilience and ranking species risk to extinction in a given community. Our findings pave the road for combining theory on tipping points with patterns of network structure that might prove useful for the management of a broad class of ecological networks under global environmental change.

Systems as complex as the climate (1), financial markets (2), or ecosystems (3) have experienced tipping points in the past and may do so in the future. Tipping points are crossed when small changes in external conditions trigger the sudden collapse of a system to an undesirable state that is usually difficult to reverse. For example, the shutdown of the thermohaline circulation in the North Atlantic (4), or the occasional switches of shallow lakes from clear to turbid waters (5) are examples of sudden transitions that might have been caused by gradual changes in external conditions. It is this “small changes can have big effects” pattern that makes tipping points important to study but notoriously difficult to detect. Nonetheless, recent work has suggested that the possibility of detecting nearby tipping points may not be that distant (6).

According to theory, before tipping points, systems tend to recover slowly back to equilibrium upon a random disturbance (7). This phenomenon of “critical slowing down” appears to be generic for a wide class of local bifurcations (8), at which the current equilibrium state of a system loses stability before being replaced by another equilibrium state. Critical slowing down may be captured by two simple statistical signals in the dynamics of complex systems (6): increasing variance and rising correlation. These signals can be used to indicate the proximity of a system to a tipping point and are suggested to serve as indicators of loss of resilience, or, more broadly, as early-warning signals for the impending transition (6). Critical slowing-down indicators (CSD indicators hereafter) have been experimentally shown to detect abrupt transitions between alternative states in yeast cultures (9), plankton chemostats (10), zooplankton populations (11), or even whole lake communities (12). However, these indicators have been mostly studied in systems with single populations or few aggregated components that lack the complexity that characterizes structurally heterogeneous systems of interacting species, such as ecological networks.

Although ecological networks have been experiencing an increasing amount of anthropogenic pressures, it is still unclear how strongly they may respond to this stress. Responses might range from local extinctions and species distribution shifts (13) to whole community reorganization and massive biodiversity losses (14). In the best-case scenarios, these responses will be gradual, predictable, or even reversible. However, little is known on whether ecological networks could also respond in abrupt and unexpected ways (15). Theoretical work shows that gradual environmental change in mutualistic communities may have different effects on species tolerance to stress, but the path to extinction appears to be gradual (16). Only recently, it has been suggested that strongly nested mutualistic networks may run a high risk of experiencing a tipping point (17). For these latter cases, the challenge is to detect whether they are approaching a tipping point in advance.

Here, we explore whether we can detect tipping points in structurally diverse ecological networks with CSD indicators. We used the structure of 79 mutualistic communities reconstructed from empirical plant–pollinator and plant seed–disperser networks to simulate dynamical scenarios of gradual environmental change that lead to species loss and community-wide collapses. We demonstrate that CSD indicators derived from monitoring biomasses at the species and community level may signal the proximity to the onset of community collapse. We investigate how species structural traits influence the predictive performance of the indicators at the species level. Last, we suggest that species-level indicators may be used to rank species risk to extinction even before the onset of community collapse. Despite the challenge of identifying these patterns in empirical dynamics of observed populations, to our knowledge, our work offers a first theoretical framework for detecting tipping points and mapping species resilience in mutualistic communities that can help to detect potential abrupt transitions in a broad class of ecological networks.

Results and Discussion

The Abrupt Onset of Community Collapse.

We estimated changes in CSD indicators, variance and autocorrelation at lag 1, in simulated time series of 79 empirically described bipartite plant–pollinator and plant seed–disperser mutualistic communities before their collapse. We assumed that species compete weakly with each other but coexist due to their mutualistic benefits (i.e., obligate mutualism). We simulated community dynamics in the presence of environmental noise, and we exposed all communities to a scenario of gradual environmental stress. Although our simulations do not necessarily capture the complexity of observed dynamics, they serve as a good first approximation. We slowly decreased the strength of mutualistic interactions between plant and animal species. This led to species extinctions until the complete community collapsed. Our scenario follows the overall weakening or even disruption of mutualistic interactions (18) that has been observed in declining visitation rates (19), or phenological mismatching (20) due to habitat fragmentation or changes in seasonal temperature patterns.

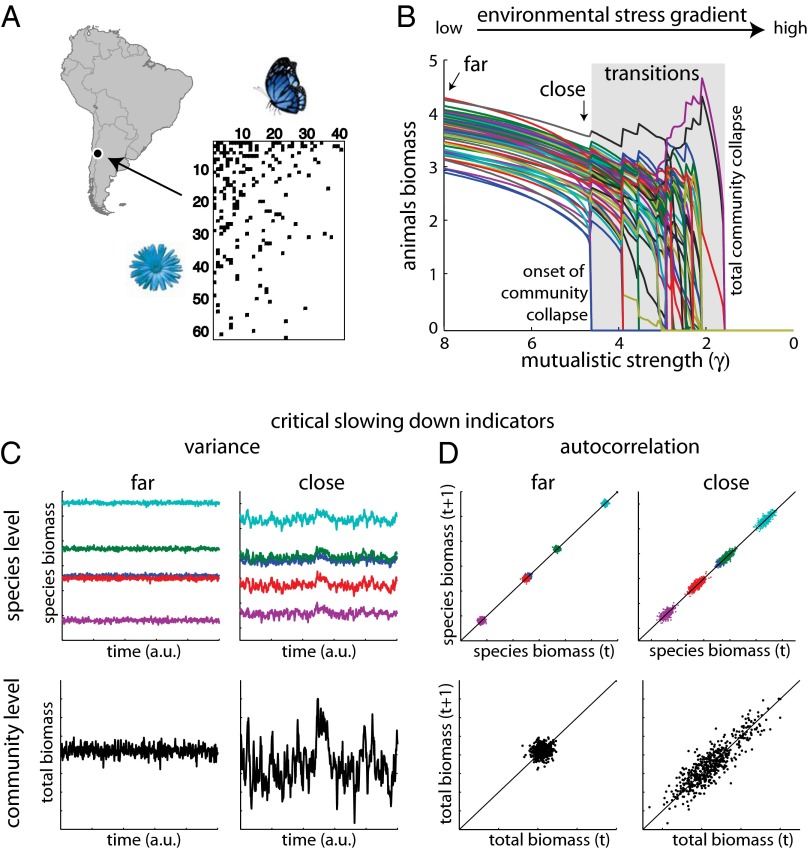
Fig. 1 demonstrates a simulated example of a collapsing plant–pollinator community from the Chilean Andes (Fig. 1A). As benefits from species mutualistic interactions gradually declined, species were progressively decreasing in biomass. In our communities, we assumed a trade-off between the strength of mutualistic interactions and the number of species interactions. This meant that specialists benefited strongly from their partners, whereas generalists did not (Materials and Methods). As a result, all species suffered proportional losses up to a point where the first extinction event suddenly occurred (Fig. 1B). We defined this first extinction event as the tipping point that marked the onset of the complete collapse of the community. We observed an abrupt onset of community collapse in all 79 communities.

Fig. 1.

Detection of the abrupt onset of collapse using critical slowing-down (CSD) indicators in mutualistic communities. (A) A plant–pollinator community from Cordon del Cepo, Chile. The black boxes represent mutualistic links between plants and animals. We used the structure of 79 empirical mutualistic networks to simulate their dynamics and potential collapse under gradual environmental change. (B) Decreasing mutualistic strength γ stresses species biomasses until unexpectedly an abrupt transition is induced. This first transition marks the onset of a sequence of extinctions until the collapse of the complete community. (C and D) Identifying critical slowing down at the species and community level. Close to the onset of community collapse, variance and correlation tend to increase. This increase is evident measured both from species biomasses and from the aggregated total community biomass.

What makes such tipping points important to detect is that they happen without any prior substantial loss in species biomass (SI Text, section S1). Obviously, a gradually declining trajectory toward extinction would by itself be evidence that the community is at risk. At the moment, we are largely unaware of how general an abrupt onset of community collapse is, although there is theoretical evidence that the nested pattern of mutualistic networks would favor the occurrence of abrupt transitions (17). In that case, CSD indicators can prove useful for anticipating abrupt transitions. Comparing time series of species far and close to the onset of community collapse, we found that both their variability and correlation increased (Fig. 1 C and D). A similar pattern was also found when looking at aggregate measures of total community biomass (Fig. 1 C and D), implying that CSD indicators can indeed be used to identify the onset of collapse in structurally complex mutualistic communities.

CSD Indicators at Species and Community Level.

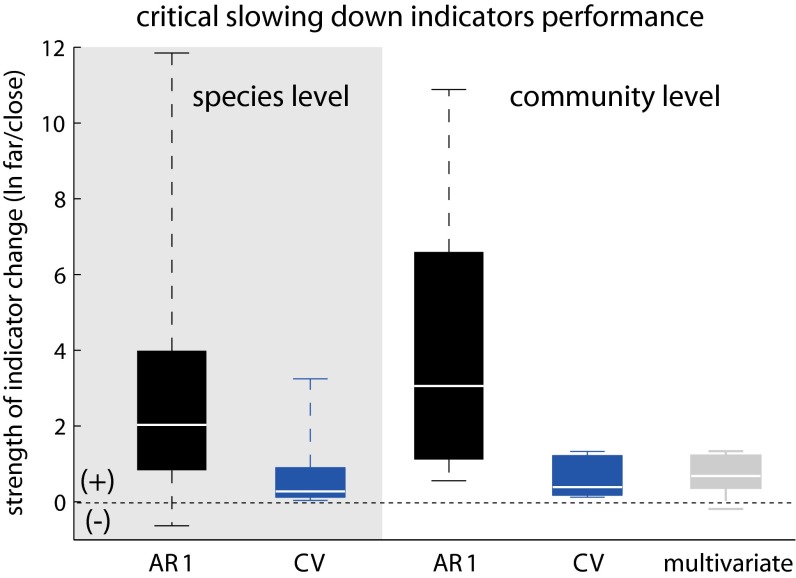
We confirmed increasing patterns in critical slowing indicators in all our 79 communities before the onset of community collapse. We measured variance as coefficient of variation ($\mathit{CV}=std\_dev/mean$), and autocorrelation at lag 1 (AR1) as the correlation of the time series to itself shifted by one time step. As CV and AR1 tend to smoothly change up to the onset of collapse (Fig. S1), we reported only their relative changes (natural log differences) at the start of the simulation and just before the onset of community collapse (Fig. S1 and Materials and Methods). Indicators increased both at species and community level (Fig. 2), regardless of being estimated for plant or animal species (Fig. S2). We also found similar patterns when we estimated the change in indicators 10 steps instead of just 1 step before collapse (Fig. S3). AR1 trends were stronger than CV trends (paired t test 206.45, $P<0.05$, df = 11,194). However, AR1 trends at the species level were occasionally negative, whereas CV always increased (Fig. 2). Instead, AR1 and CV trends estimated at the community rather than the species level were always positive as differences across species smoothed out at the aggregate level (Fig. 2).

Fig. 2.

Performance of critical slowing-down (CSD) indicators measured at the species (n = 11,195) and community (n = 79) level in 79 mutualistic communities. Performance was estimated as the natural logarithmic ratio of autocorrelation at lag 1 ($\mathrm{AR}1$) and coefficient of variation ($\mathrm{CV}$) close and far from the onset of community collapse. The multivariate index of variability was estimated on the community biomass variance–covariance matrix. Positive values indicate an increase in the indicators before the onset collapse. The boxplots include the median, box edges represent the 5th and 95th percentiles, and box whiskers indicate the minimum and maximum values.

Best-Indicator Species for Detecting Community Collapse.

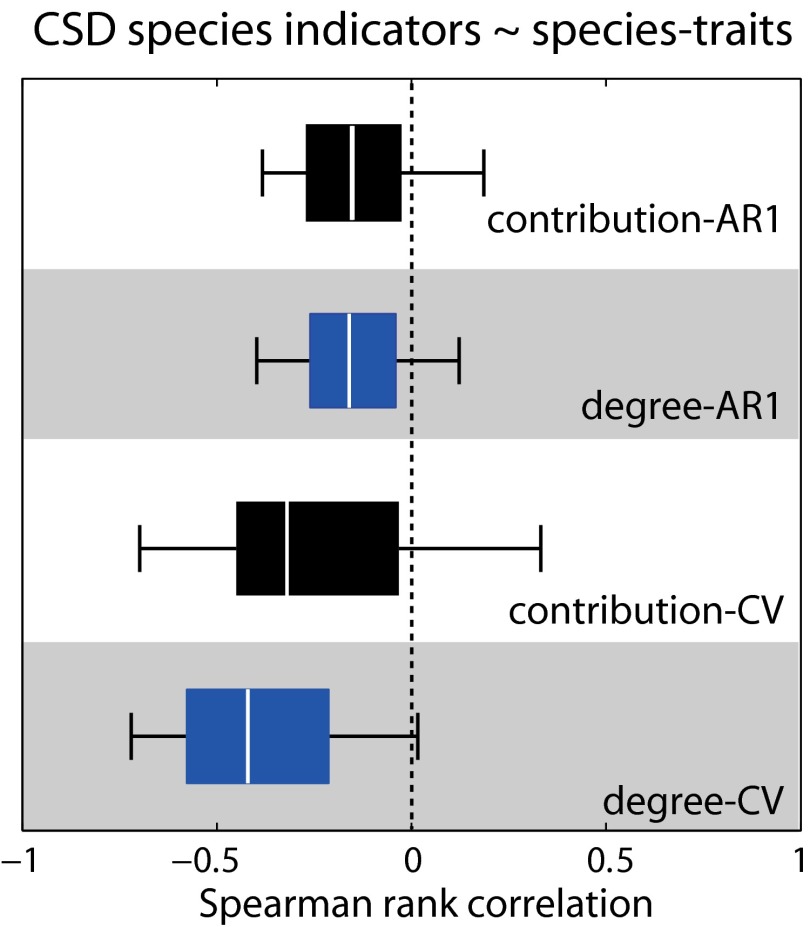
Although these results broadly support that CSD indicators could announce abrupt transitions in a community, they are constrained by the need of collecting high-resolution time series for all species. However, a closer look at indicator trends across species shows that some species have better reflected community proximity to the collapse than others (Fig. 2). Such species could qualify as best-indicator species of community collapse (i.e., the ones with the potential to demonstrate the strongest changes in CSD indicators). We searched for the profile of these best-indicator species by estimating correlations between indicator trends and species structural traits. We selected two commonly used structural traits: degree (i.e., number of the interactions of a species), and contribution to nestedness (i.e., the level of shared interacting partners in the community). We chose these traits based not only on the fact that they have been related to the persistence of mutualistic communities (21) but also because they can be easily derived from species interaction matrices.

We found negative correlations between CV trends and species degree, and negative but weak correlations between AR1 trends and species degree (Fig. 3). Similar but more variable patterns were observed for correlations between indicator trends and contribution to nestedness (Fig. 3). Despite the variation in the correlations, specialists (and to a less extent least contributors to nestedness) tended to be best-indicator species of community collapse. This can be best explained by the fact that specialists were generally the first to collapse (Fig. S4 A and B), and that specialists’ dynamics were less muffled by noise as opposed to generalists whose dynamics were affected by the multiple noisy dynamics of their partners. These observations imply that declining community resilience might be strongly reflected in CSD indicators when measured from peripheral species in a network. Although this qualifies specialists as target species for monitoring community resilience, CSD indicators from specialist dynamics might not always reflect community-wide risk of collapse. As specialists are usually most vulnerable to disturbances, changes in their dynamics might just imply individual rather then community-wide risk of extinction. Thus, monitoring a mix of specialists and generalists in a network may help avoid such potential false positives. Still, the challenge will be to strike the right balance between monitoring the minimum number of species in a network and the effort required for robustly estimating community resilience.

Fig. 3.

Structural traits and critical slowing-down (CSD) indicators. Spearman rank correlations between species traits (degree and contribution to nestedness) and species indicators performance. Boxplots include the median, box edges represent the 25th and 75th percentiles, and box whiskers indicate the 5th and 95th percentiles.

From Detecting Tipping Points to Mapping Species Resilience.

The fact that most species indicated the proximity to the onset of community collapse implies that differences in indicator trends across species might reflect how close a species is to its own point of extinction or more general how resilient a species is. In the example of the plant–pollinator community from Fig. 1, we ordered species according to their timing of extinction, and we colored them based on the magnitude of the change in their CVs (Fig. 4; white reflects weak, and black reflects strong changes). As expected, species that went first extinct showed the strongest changes in CV. This was generally true for specialists. We confirmed such correlations between the timing of species extinctions and trends in CSD indicators in all 79 communities. Correlations for CV were stronger than for AR1 (Fig. S4 C and D). This finding implies that we could rank species risk to extinction before any event of collapse by just comparing species’ relative changes in CV. Such across-species comparisons of CV have been proposed earlier for estimating species resilience (22) and have been used for exploring population vulnerability, for instance, to overexploitation in fish stocks (23, 24). Nonetheless, these comparisons are based on snapshot measurements that might be compromised by differences in species traits (like mortality or growth rates). Instead, comparing relative changes in CSD indicators might reduce such biases and allow direct across-species comparisons given that all species in a community are experiencing similar environmental stress.

Fig. 4.

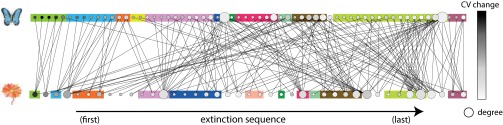
Mapping species resilience based on critical slowing-down (CSD) indicators. Each node represents a species in the plant–pollinator community from Fig. 1. Species are ranked according to their order of extinction (from Left to Right), their size corresponds to the number of their interactions (degree), and are colored according to their changes in $\mathrm{CV}$ before the onset of community collapse. Black colors indicate strong increases in $\mathrm{CV}$. We used color boxes to group species that went coextinct. We found a positive correlation between the magnitude of the $\mathrm{CV}$ change and the order of species extinctions. Similar patterns were confirmed in all 79 communities (Fig. S4). This information can be used to rank species risk to extinction.

Challenges to Detecting Tipping Points in Mutualistic Communities.

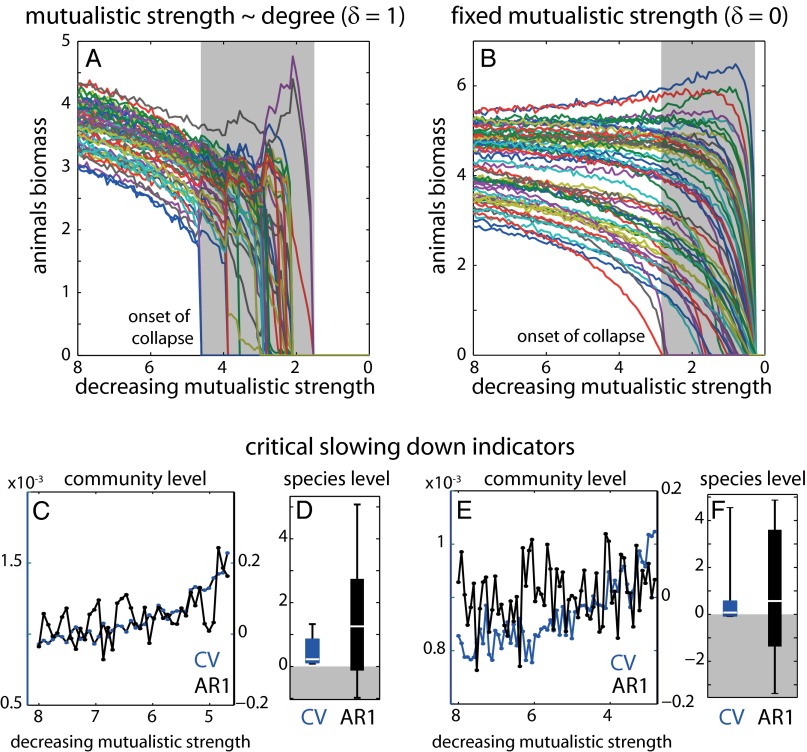
Although our results show that we could implement CSD indicators for mapping species resilience and detecting abrupt community transitions, we are still largely ignorant whether abrupt collapses are the rule or rather the exception in mutualistic communities. Theory suggests that the nested structure of mutualistic networks would increase the probability of abrupt transitions (17), but it is unresolved how the overall parameter space affects the probability of community collapse and the performance of the CSD indicators. For example, it has been demonstrated that species tend to reorganize their interactions in a community, especially under stress (25). Such adaptation would probably minimize the probability of an abrupt collapse. Additionally, it has been theoretically shown that species responses to environmental stress in mutualistic communities are largely dependent on how mutualistic strengths are assigned between species (16). For example, in our communities we assumed a trade-off between mutualistic strength and the number of species interactions (δ = 1) (26, 27). Under such trade-off, the gradual decrease in mutualistic strength caused the abrupt onset of community collapse as all species suffered proportional losses (Fig. 5A, plant–pollinator community from Fig. 1). Had we, however, assumed no trade-off for the same community (δ = 0), generalists would enjoy mutualistic benefits proportional to the number of their mutualistic partners and suffer less losses than specialists. Consequently, we would expect specialists to first go extinct probably in a gradual rather than abrupt way (Fig. 5B). Indeed, only in 21 out of the 79 communities, the onset of community collapse remained abrupt when we assumed no mutualistic trade-off while keeping the rest of the parameters the same. Nonetheless, even in the case of gradual transitions, we still found positive CSD trends mostly at the species (Fig. 5 D and F) rather than community level (Fig. 5 C and E).

Fig. 5.

The effect of trade-offs in mutualistic strengths on CSD indicators. (A) In the presence of a trade-off, mutualistic strengths are inversely proportional to the number of species interactions (δ = 1). All species suffer similar losses to the decreasing mutualistic strength and the onset of community collapse usually occurs abruptly. (B) In the absence of a mutualistic trade-off (δ = 0, all of the rest of the parameters are the same as in A), mutualistic strengths are the same across all species. As a result, mutualistic benefits are proportional to the number of their interactions and the onset of community collapse is gradual. (C and E) Community level $\mathrm{CV}$ and $\mathrm{AR}1$ indicators clearly increase up to the onset of collapse in the presence of the trade-off (δ = 1). (D and F) Indicators at species level have mostly positive trends but perform poorer in the absence of the mutualistic trade-off (δ = 0).

Regardless of the type of transition, our ability to detect CSD in a network is consequent with monitoring stochastic community dynamics around an underlying stable equilibrium (6). However, observed population dynamics usually follow erratic, highly variable patterns driven by a mix of nonlinear and stochastic effects (28, 29), at times interrupted by long transients far from equilibrium (30). This may question whether CSD indicators could be identified at all under such nonequilibrium conditions (31). Or it might be challenging to conclude whether CSD indicators are a consequence of the progressive approach to a tipping point or due to the natural patterns of variability in real populations (32). Despite the real topologies we used, our simulated communities reproduced dynamics that are far from the variability found in empirical data (Fig. S5). Such difference challenges the capacity of interpreting natural patterns of variability from a CSD perspective. Instead, at the moment, the theory behind CSD indicators only allows us to explore how CSD indicators may be identified in structurally complex communities under stable equilibrium dynamical regimes in the presence of weak stochasticity.

Clearly, our work is only a first step when it comes to assessing our ability to detect community collapses. Although we confirmed our conclusions also under an alternative stress scenario (Figs. S6 and S7), there are more cases to be explored. For instance, species will most likely be differentially affected by changing conditions (18). Similarly, variation in stochastic effects across species will affect indicators’ performance, as CSD indicators have been shown to be sensitive to the magnitude and color of environmental noise (33, 34). Further studies would need to test the possibility of detecting tipping points under such conditions and to expand the current findings to other types of networks like food webs, competition communities, or metapopulations.

Conclusions

In this study, we showed that CSD indicators can be used to infer proximity to tipping points and to map species risk to extinction in systems as structurally diverse as mutualistic networks. No doubt we remain largely ignorant of whether such networks will respond abruptly to increasing pressure at all. However, in the case they do, the generality of the dynamical signatures of tipping points implies that CSD indicators may be used for identifying vulnerable system components and for detecting abrupt transitions in networks ranging from ecological communities to globally linked financial markets.

Materials and Methods

Empirical Networks.

Our mutualistic plant–pollinator and plant seed–dispersal networks were accessed from the Web of Life database (www.web-of-life.es). We only selected networks that have more than 20 species. This resulted in 79 networks covering a wide geographic range across all continents and climatic zones and with a high variation in their architectural properties. Table S1 summarizes the ranges of the most important structural properties of these communities.

Model.

The empirical mutualistic networks provided the skeleton that we used to simulate the dynamics of our communities. The dynamics of plants P and animals A (i.e., pollinators, seed dispersers) were given by a model presented by ref. 35:

$$\begin{array}{c}\frac{d{P}_i}{dt}=P_i\left({\alpha }_{Pi}-{\displaystyle \sum _j{\beta }_{Pij}{P}_j}+\frac{{\displaystyle {\sum }_j{\gamma }_{Pij}{A}_j}}{1+h{\displaystyle {\sum }_j{\gamma }_{Pij}{A}_j}}\right)+u\\ \frac{d{A}_k}{dt}=A_k\left({\alpha }_{Ak}-{\displaystyle \sum _j{\beta }_{Akj}{A}_j}+\frac{{{\displaystyle {\sum }_j{\gamma }_{Akj}P}}_j}{1+h{\displaystyle {\sum }_j{\gamma }_{Akj}{P}_j}}\right)+u\\ \mathrm{for}\hspace{0.17em}i=\left[1,n\right],\hspace{1em}k=\left[1,m\right],\end{array}$$ [1]

where both plant and animal biomasses grow with rate α, compete within their respective guilds with interspecific rate β, and enjoy a mutualistic benefit following a saturating function with handling time $h\left(=0.1\right)$ and mutualistic strength γ between plants and animals. We slightly modified the model by assuming that there is a small immigration rate $u\left(={10}^{-5}\right)$ for all species. Parameter u does not affect the dynamics of the model, but helps to avoid the occurrence of underflow errors in the presence of environmental noise. To account for asymmetries in the strength of interactions between generalist and specialist species (36), we used a trade-off that defines the mutualistic dependence between species j and i and that depends on species degree (number of mutualistic links) (16):

$${\gamma }_{ij}=\frac{{\gamma }_o{y}_{ij}}{k_i^{\delta }}.$$ [2]

${\gamma }_o$ represents the average level of mutualistic strength, $k_i$ the degree of species i, and $y_{ij}=1$ if species i and j interact and zero otherwise. Parameter δ modulates the trade-off and determines the actual mutualistic interaction strength of plant (animal) species i and the j animal (plant) species in the community (16). Here, we adopt a scenario of equal total strengths for all species by assuming an inversely proportional mutualistic strength to species degree ($\delta =1$) that can be justified by classical empirical (26) and theoretical work (27). Last, to ensure that our communities are feasible (all species present) before we impose any stress, and to minimize the chance that transitions are driven by the direct competition within plants or animals (β), we did not allow interspecific competition to exceed intraspecific competition $\left[{\displaystyle {\sum }_j\left({\beta }_{ij}\le 1\left(i\ne j\right)\right)}\right]$ (37). We did this by sampling competition coefficients ${\beta }_{ij}$ for each plant and animal guild from a uniform distribution with minimum 0.001 and mean $\overline{\beta }=1/\left(n^{\left(A\right),\left(P\right)}\right)$, where $n^{\left(P\right),\left(A\right)}$ are the number of plant or animal species, respectively, until the assumption ${\displaystyle {\sum }_j{\beta }_{ij}\le {\beta }_{ii}\left(i\ne j\right)}$ was fulfilled. Intraspecific competition ${\beta }_{ii}$ was set to 1.

Collapsing Mutualistic Communities by Declining Mutualistic Strength.

In our numerical experiments, we slowly decreased mutualistic strength ${\gamma }_o$ for all plant–animal interactions (16). We started simulations assuming conditions of obligate mutualism (38), which implies that species can survive only in the presence of strong mutualistic benefits. We imposed obligate mutualism by drawing negative growth rates for plants and animals ${\alpha }_{\left(P\right),\left(A\right)}$ uniformly from [−0.5, −0.1]. To ensure that the level of mutualistic strength that we chose was relative to the actual size and structure of each community, we assigned mutualistic strengths ${\gamma }_o$ to be higher than the limit τ (${\gamma }_o=8\tau$) at which mutualistic benefits exceeded competitive costs for all communities (16). Under these conditions, we randomly initialized species biomasses from a uniform distribution ([0, 10]) and let communities reach equilibrium. We only selected parameterizations that allowed all species to be present in each community (feasible equilibrium). If that condition was not satisfied, we resampled competition and growth rate terms and repeated the initialization. Once we attained parameters that allowed for a feasible equilibrium, we gradually decreased ${\gamma }_o$ to zero in 200 equal steps. At each step, we discarded transients by simulating for 500 time steps before recording equilibrium species biomasses. We assumed that species went extinct when their biomass was lower than 10 times the immigration rate u (i.e., $<{10}^{-4}$). The gradual decrease of mutualistic strength led to the progressive loss of species until the collapse of the complete community. At each extinction event, we recorded the level of mutualistic strength ${\gamma }_o$ and the identity of species that went extinct. We categorized the first extinction event as abrupt or gradual depending on the slope of the decline in species biomasses [where the slope was given by $\left(N_{\left(t\right)}-N_{\left(t-1\right)}\right)/\left({\gamma }_{\left(t\right)}-{\gamma }_{\left(t-1\right)}\right)$ and t was the time index corresponding to the first extinction event]. If the slope was larger than 15, we characterized the onset of community collapse as abrupt (17). If that condition was not satisfied, we characterized the transition as gradual. We repeated the above procedure to attain an abrupt transition in all communities for 10 of the total 79 networks (on average 3.6 times for each).

CSD Indicators as Early Warnings for the Onset of Community Collapse.

We quantified CSD indicators in the mutualistic communities to test whether they can provide early warnings for the proximity to the onset of community collapse. We measured variance (expressed as $\mathit{CV}=std\_dev/mean$) (39) and autocorrelation at lag 1 [AR1, as the $corr\left(x_t,x_{t+1}\right)$, where $x_t$ denotes a point in the time series] (40). To estimate these indicators, we simulated a stochastic version of our differential Eqs. 1:

$$\begin{array}{c}d{P}_i=f\left(P_i,A_k\right)dt+\sigma P_{i}d{W}_i\\ d{A}_k=f\left(P_i,A_k\right)dt+\sigma A_{k}d{W}_k\end{array},$$ [3]

where $f\left(\right)$ is the deterministic part of Eq. 1, and $dW$ is a Wiener process uncorrelated across all species with mean 0 and variance scaled by $\sigma \left(=0.025\right)$ and species biomasses (multiplicative noise). We used Euler integration with time step 0.01 following Ito calculus to solve the equations and to generate the stochastic time series for all species in the community. We chose CV as an unbiased measure of variability rather than the commonly used SD (39) to account for the scaling effect of environmental stochasticity to species biomass (multiplicative noise). Multiplicative noise can alter patterns in variance when studying CSD indicators (34). We discuss this issue in the SI Text, section S3 and Fig. S8. Previous studies have shown that CSD indicators change smoothly before bifurcation points (8, 41). We confirmed smooth changes in CV and AR1 in our mutualistic communities under a gradual decline of mutualistic strength (Fig. S1). Based on these observations, we only estimated CV and AR1 far (i.e., ${\gamma }_o=8\tau$) and close (i.e., one step before the threshold ${\gamma }_o={\gamma }_{thr-1}$) to the onset of community collapse. We did this by simulating communities for 100 time steps far and close to the first tipping event starting from equilibrium conditions. To reduce random effects due to noise, we repeated this 20 times. For each repetition, we estimated CV and AR1 and used average values to estimate indicators for each species. We also measured CV and AR1 on total community biomass by aggregating plant and animal biomasses. We lastly computed a community level multivariate index of variability based on the maximum eigenvalue of the variance–covariance matrix of all species biomasses at equilibrium (42) that is commonly used in multivariate analysis of community changes (e.g., principal component analysis). We quantified the strength of the change in the indicators as the natural log difference of the indicator values close and far from the onset of collapse [$ln\left(indicato{r}_{thr-n}/indicato{r}_o\right)$] for each species in all communities.

Structural Traits.

We used Spearman rank correlation to explore correlations between changes in CSD indicators and structural traits for identifying potential best-indicator species. The two structural traits were degree (number of mutualistic links) and contribution to nestedness. Contribution to nestedness for each species quantifies the amount to which nestedness compares with the nestedness when randomizing the interactions of that particular species (21). In calculating nestedness contributions, the interactions of a species are randomized according to the null model specified in ref. 43; we used 1,000 random replicates.

We did all analyses in MATLAB (R2010b; The Mathworks) using Grind for MATLAB (available online at www.sparcs-center.org/grind).