Significance
Chemical gardens are plant-like mineral forms existing in nature at various scales. Even though they have been described for more than three centuries thanks to their beauty and analogies with biological forms, their growth mechanisms remain largely not understood. To gain insight into their formation processes, we develop an innovative strategy to study these systems in which chemical gardens grow in a quasi-2D confined geometry upon injecting one reagent solution into the other. The advantage of this procedure over previous works is to allow studying, in controlled and reproducible conditions, the effects of variable concentrations and injection rates on the selected morphology.
Keywords: chemical gardens, pattern formation, precipitation, reaction–advection, spirals
Abstract
Chemical gardens are mineral aggregates that grow in three dimensions with plant-like forms and share properties with self-assembled structures like nanoscale tubes, brinicles, or chimneys at hydrothermal vents. The analysis of their shapes remains a challenge, as their growth is influenced by osmosis, buoyancy, and reaction–diffusion processes. Here we show that chemical gardens grown by injection of one reactant into the other in confined conditions feature a wealth of new patterns including spirals, flowers, and filaments. The confinement decreases the influence of buoyancy, reduces the spatial degrees of freedom, and allows analysis of the patterns by tools classically used to analyze 2D patterns. Injection moreover allows the study in controlled conditions of the effects of variable concentrations on the selected morphology. We illustrate these innovative aspects by characterizing quantitatively, with a simple geometrical model, a new class of self-similar logarithmic spirals observed in a large zone of the parameter space.
Chemical gardens, discovered more than three centuries ago (1), are attracting nowadays increasing interest in disciplines as varied as chemistry, physics, nonlinear dynamics, and materials science. Indeed, they exhibit rich chemical, magnetic, and electrical properties due to the steep pH and electrochemical gradients established across their walls during their growth process (2). Moreover, they share common properties with structures ranging from nanoscale tubes in cement (3), corrosion filaments (4) to larger-scale brinicles (5), or chimneys at hydrothermal vents (6). This explains their success as prototypes to grow complex compartmentalized or layered self-organized materials, as chemical motors, as fuel cells, in microfluidics, as catalysts, and to study the origin of life (7–18). However, despite numerous experimental studies, understanding the properties of the wide variety of possible spatial structures and developing theoretical models of their growth remains a challenge.
In 3D systems, only a qualitative basic picture for the formation of these structures is known. Precipitates are typically produced when a solid metal salt seed dissolves in a solution containing anions such as silicate. Initially, a semipermeable membrane forms, across which water is pumped by osmosis from the outer solution into the metal salt solution, further dissolving the salt. Above some internal pressure, the membrane breaks, and a buoyant jet of the generally less dense inner solution then rises and further precipitates in the outer solution, producing a collection of mineral shapes that resembles a garden. The growth of chemical gardens is thus driven in 3D by a complex coupling between osmotic, buoyancy, and reaction–diffusion processes (19, 20).
Studies have attempted to generate reproducible micro- and nanotubes by reducing the erratic nature of the 3D growth of chemical gardens (10, 11, 13, 15, 21). They have for instance been studied in microgravity to suppress buoyancy (22, 23), or by injecting aqueous solutions of metallic salts directly into silicate solutions in 3D to dominate osmotic processes by controlled flows (10, 11). Analysis of their microstructure has also been done for different metallic salts, showing a difference of chemical composition on the inner and the outer tube surfaces (24, 25). The experimental characterization and modeling of the dynamics remains however dauntingly complex in 3D, which explains why progress in quantitative analysis remains so scarce.
We show here that growing chemical gardens in a confined quasi-2D geometry by injecting one reagent solution into the other provides an innovative path to discover numerous original patterns, characterize quantitatively their properties, and explain their growth mechanism. A large variety of structures including spirals, filaments, worms, and flowers is obtained in a horizontal confined geometry when varying the reagent concentrations at a fixed flow rate. The patterns differ from those in 3D as the growth methodology decouples the different effects involved in the formation of classical chemical gardens. The buoyancy force is reduced by the vertical confinement, whereas injection decreases the influence of osmotic effects.
Experimental Results
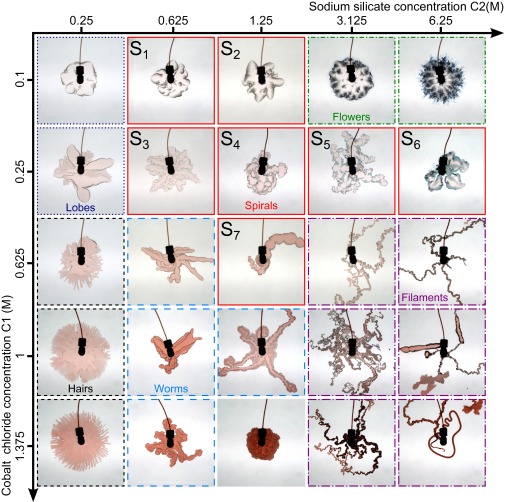
Experiments are conducted in a horizontal Hele–Shaw cell (26) consisting of two transparent acrylate plates separated by a small gap initially filled by a solution of sodium silicate. A solution of cobalt chloride (CoCl2) is injected radially from the center of the lower plate at a fixed flow rate. Upon contact and displacement of one reactant solution by the other one, precipitation occurs and various dynamics and patterns are observed when the concentrations of sodium silicate and CoCl2 are varied (Fig. 1).
Fig. 1.
Experimental patterns. Classification of confined chemical gardens in a parameter space spanned by the concentration of the injected aqueous solution of cobalt chloride and the concentration of the displaced aqueous solution of sodium silicate. The diagram is divided into different colored frames referring to the various classes of patterns observed: lobes (dotted dark blue), spirals (solid red), hairs (dashed black), flowers (dashed-dotted green), filaments (long dashed-dotted purple), and worms (long dashed blue). The separation between each domain is not sharp as, for example, worms are sometimes delimited by curly boundaries that are reminiscent of spirals. The spiral category is divided into subcategories analyzed in Fig. 3 and in SI Text. The injection rate is 0.11 mL/s and the field of view is 15 cm × 15 cm, shown 15 s after injection starts. SI Text shows some of the dynamics.
The global trend of the phase diagram is that, if one reagent is much more concentrated than the other one, a rather circular precipitation pattern is obtained. This precipitate is concentrated at the outer rim as dark petals of flowers, out of which viscous fingers grow if the sodium silicate is the more concentrated reagent. At the beginning of the injection, precipitation occurs inside the viscous fingers, whereas at longer times the precipitate lags behind them. If, on the contrary, the metal salt is much more concentrated than the sodium silicate, a compact circular pink precipitate grows radially. Above a critical radius, we observe a destabilization of the circle rim toward small-scale hairs growing radially with a characteristic wavelength.
When the concentration of both reactants is in the large range of Fig. 1, thin filaments growing with complex turnarounds are observed. Along the fifth column of the phase diagram, the transition from flowers to filaments occurs smoothly when the concentration of CoCl2 is increased at this fixed large concentration in sodium silicate.
Intermediate concentrations are characterized by worms, as seen in the lower middle zone of the diagram. These worm patterns are reminiscent of structures observed in micellar systems when a viscous gel product is formed in situ at the interface between reactive aqueous solutions (27). At later time, terrace-like precipitate layers grow along the first structure.
Along the lower line of the phase diagram, i.e., at a large concentration in CoCl2, the transition upon an increase of the sodium silicate concentration from hairs to worms and eventually filaments transits at intermediate values via the most compact precipitate structure from all those observed.
In the upper middle zone (squares to in Fig. 1), spirals growing upon successive break-ups of precipitate walls are observed. A zoom-in on some of these spirals (Fig. 2) shows that, after a longer time, other precipitates with a rich variety of colors start growing diffusively out of their semipermeable walls. A preliminary test with Raman microscopy has shown that some green precipitates (as in Fig. 2, for instance) are made of Co(OH)2 and Co3O4, compounds also found in the inner surface of 3D tubes (25). This highlights the fact that different types of solid phases can form in the reaction zone between the two solutions (28).
Fig. 2.
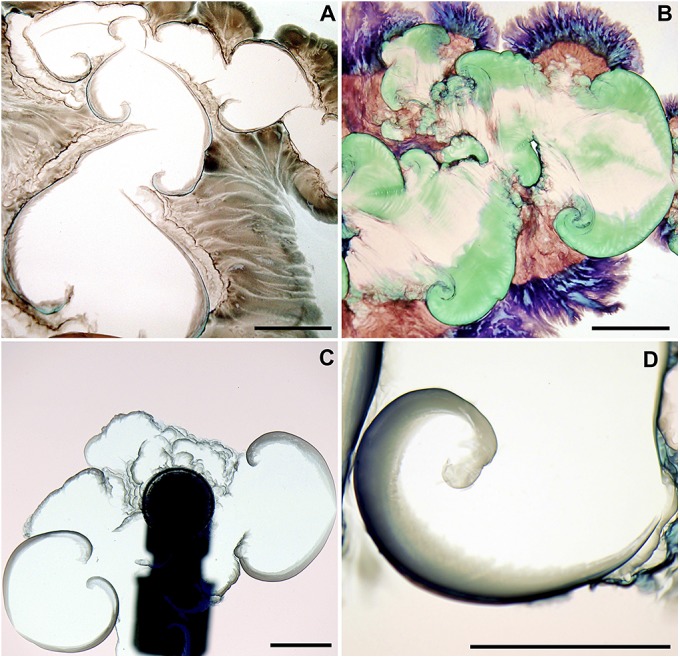
Spiraling precipitates. A and B feature spirals and the subsequent precipitates with various colors growing diffusively out of the semipermeable spiral walls when cobalt chloride is injected into sodium silicate [(A) case and (B) case of Fig. 1]. Pictures are taken a few minutes after the end of the injection. C and D show examples of spirals in a reverse chemical garden obtained when sodium silicate in concentration 0.625 M is injected into pink cobalt chloride 0.25 M [inverse of case S3; (C) s, mL/s and (D) few minutes after the end of injection, mL/s]. (Scale bars, 1 cm.)
We note that friction phenomena with the cell plates do not seem to be crucial to understand the properties of the patterns as no stick–slip phenomena are observed during the growth of the patterns. Preliminary data also show that the area A enclosed by the visible spiral, worm, and filament patterns scales linearly with time with an angular coefficient proportional to the flow rate Q divided by the gap b of the Hele–Shaw cell, i.e., . This suggests that the related patterns hence span the whole gap of the reactor. Additional experiments must be conducted to obtain statistical information on such growth properties for these patterns and for the other structures observed.
In the following, we focus on the spiral shape precipitate, because it is a robust pattern existing over a quite large range of concentrations and is also formed in reversed gardens, i.e., when sodium silicate is used as the injected fluid (Fig. 2 C and D).
Geometrical Model
The spiral formation mechanism can be understood with a minimal geometrical argument. Consider a reagent 1 injected radially from a source point S into reagent 2 in a 2D system (Fig. 3A). The contact zone between the reactive solutions, in which precipitation occurs, initially grows as a circle of arbitrarily small radius r. If, because of further injection, this layer of precipitate breaks at a critical value , the new precipitate, formed as the bubble of reagent 1 expands, pushes the already existing solid layer. As a result, the branch of solid precipitate starts being advected out of the growing bubble and rotates as a whole around the breaking point, which later on identifies as being the tip of the spiral (see also SI Text for growing spirals). An arc of spiral is hence observed to develop with its tip moving in the fixed frame of reference centered on S. It further grows by precipitation at its tail located on the circle of growing radius .
Fig. 3.
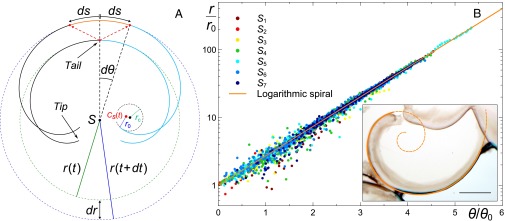
Spiral growth mechanism and scaling of logarithmic spiral-shaped precipitates. (A) Schematic of the growth mechanism of the curly shaped precipitates during an infinitesimal interval of time where is the radius of the expanding bubble of injected reagent and S is the point source. (B) Scaling law for the experimentally measured evolution of the radial distance as a function of the scaled angle for 173 spirals (9 experiments) corresponding to the 7 different categories in Fig. 1. (Inset) Superimposition of a logarithmic spiral on a spiraled precipitate. (Scale bar, 2 mm.) The procedures for the measurements of and the distributions of and are given in SI Text.
The equation of the resulting curly shaped precipitation layer is obtained by considering two infinitesimally close time steps as shown in Fig. 3A. At time , the precipitate layer formed at time t is pushed away by the newly added material and rotates by an angle . The precipitate layer produced between t and is created from the reaction occurring at the new section of the contact line between the two reagents (29). Because this new section of contact line is generated by the bubble expansion, its length is proportional to the increase of perimeter of the expanding bubble, namely
| [1] |
where is a constant growth rate controlling the length of the precipitate layer created as the bubble radius increases. A large value of implies that the length of the new segment of precipitate created at is large compared with the increase of length along the radial direction and leads to a more coiled spiral.
Upon integration of Eq. 1 we get , where s is the length of the curve from the tip to the tail. The constant of integration was fixed by considering that the tip of the curve () is generated from a circle of radius . In addition, the radius r of the expanding bubble coincides with the radius of curvature of the tail because the bubble is also the osculating circle (Fig. 3A). Therefore, we obtain , which is the Cesàro equation of a logarithmic spiral giving the evolution of the radius of curvature along the curve as a function of the arclength (ref. 30, p. 26) (see SI Text for more details).
Alternatively, we can also proceed as follows to obtain the expression of the spiral curve in polar coordinates. To derive this equation, the relation existing between and should be known everywhere along the curve in the fixed frame of reference centered around S. For nonmoving curves, this relation is usually found by analyzing how varies in a sector of constant central angle which rotates to span the entire curve. In our case, the growing arc of spiral is moving in a fixed system of coordinates centered on the source point S. Its equation is therefore alternatively obtained by considering a nonmoving sector of constant central angle as in Fig. 3A and analyzing how varies in it when the curve spans this angular sector thanks to its motion (SI Text).
As seen in Fig. 3A, the length of the precipitate layer added at in the fixed sector of angle is given by , which at first order in and , reduces to
| [2] |
| [3] |
which is readily integrated to yield
| [4] |
is a constant of integration that can be computed for each spiral if we note that fixes the starting point of the spiral, i.e., its tip. Reminding that the tip originated from the breaking by injection of the initial small circle of radius , the radius of curvature of the spiral at is nothing else than . Therefore, , which relates the constant of integration to . Note that Eq. 4 exactly describes the (blue) segments of spiral of Fig. 3A in the frame of reference centered on S provided this segment is translated and rotated such that the center of the spiral coincides with S (SI Text).
Eq. 4 constructs a logarithmic spiral in polar coordinates and quantitatively describes structures in many natural systems such as seashells, snails, or the horns of animals where the growth mechanism preserves the overall shape by the simple addition of new material in successive self-similar steps (31). It appears thus logical that a similar logarithmic shape is recovered here in the case of regular additional precipitation at the tail of a growing arc of solid precipitate upon further injection of reactants at a fixed flow rate. Eq. 4 quantitatively describes the spiral structures observed in a large part of our phase diagram as demonstrated in the next section.
Comparison Between Experiments and Model
To test our geometrical model, the radii of 173 spirals observed in 9 experiments for 7 pairs of concentrations (sectors of Fig. 1) have been measured as a function of the polar angle (Fig. 3B and SI Text). We have selected precipitate layers which were not deformed by other structures growing in their neighborhood or fractured. Among them, we have also selected sufficiently coiled segments such that their polar angle spans the interval with to obtain significant constraints on the model, i.e., large enough in Fig. 3B. Indeed, segments which are not sufficiently coiled cannot be used to determine the type of spiral emerging in the system. If the interval spanned by θ is too small, Eq. 4 is hardly distinguishable from the equation describing an Archimedean spiral. The distribution of among the analyzed spirals is shown in SI Text. As seen in Fig. 3B, where the radial distance and the polar angle are rescaled by and , respectively, all of the analyzed spiral profiles collapse onto an exponential master curve, illustrating that indeed they are all logarithmic to a good accuracy.
The dispersion occurring at low θ (near the spiral center) is related to the fact that the experimental spiral structures emerge from an arc of an initial tiny circular section of radius . Sixty-three other spirals corresponding to the inverted cases and (i.e., sodium silicate injected into cobalt chloride) have also been analyzed and prove to follow the same logarithmic scaling law (SI Text). We note that, in our confined chemical gardens, the spiral growth continues only as long as the precipitate can pivot within the system. When it becomes pinned by encountering a solid wall or another precipitate, the spiral growth ceases, the membrane breaks, and a new radial source is produced, leading regularly to a new fresh spiral. This behavior is reminiscent of the periodic pressure oscillations reported in the growth of some 3D chemical gardens (13, 32).
Thus, self-similar logarithmic spirals emerging in a significant part of the phase diagram can be quantitatively analyzed on the basis of a simple geometrical argument. The model, which describes an isolated source producing a circular precipitation zone that then ruptures, proves to be robust even when spirals are interacting, as in the current experiments.
Conclusions
This work shows that new insight into the complexity of self-assembled chemical garden structures can be obtained by growing them by injection of reactive solutions in confined geometries. The control of the concentrations of the reagents and of the flow rate will allow the study of phase diagrams in reproducible experimental conditions (15, 33), as well as the switch from dominant reaction–diffusion processes to flow-driven ones. Moreover, the quasi-2D nature of the precipitates will permit, as done here, an easier characterization of the patterns using tools of classical 2D pattern selection analysis (34). Modeling and numerical simulations of this injection-driven aggregation process will thus be simplified. This will facilitate the analysis of growth mechanisms and of the relative effects of reactions, hydrodynamics, and mechanics in the resulting structure, a prerequisite to the rational design of complex, hierarchical microarchitectures (10, 35).
Materials and Methods
The experimental setup is a horizontal Hele–Shaw cell consisting of two transparent acrylate plates of size 21.5 cm × 21.5 cm × 0.8 cm separated by a gap of 0.5 mm and initially filled with a sodium silicate solution. A cobalt chloride solution of concentration is injected into the sodium silicate solution of concentration . Acrylate was chosen instead of glass to avoid interactions between the sodium silicate and the glass. For visualization purposes, the cell is placed on top of a diffuse light table and the dynamics is recorded from above using either a complementary metal-oxide–semiconductor (CMOS) camera or a photography camera. Some earlier work on chemical gardens used a similar confined geometry but used seed crystals rather than injection, which leads to different dynamics than those studied here (20). The metallic salt solution is prepared from dissolution in water of crystals of cobalt (II) chloride hexahydrate (CoCl2⋅6H2O) (Sigma-Aldrich). The sodium silicate solution is prepared from a commercial aqueous solution (Sigma-Aldrich), with linear formula Na2(SiO2)x·xH2O and the composition SiO2 ∼ 26.5% and Na2O ∼ 10.6%, with a concentration of silica equal to 6.25 M at 25 °C. Cobalt chloride is one of the classical metallic salts used to grow chemical gardens in 3D: structures form with a smaller induction time and a higher linear growth than with calcium, nickel, and manganese salts, for instance (25). In Fig. 1, we used a constant injection rate of 0.11 mL/s, which is larger than those typically used for 3D injection experiments (11) and leads to a growth process mainly driven by the flow. We vary the concentration of sodium silicate within the same range as in 3D experiments (25), from 6.25 M (commercial solution) to 0.25 M by dilution. The cobalt chloride concentration is varied from 0.100 to 1.375 M.
Supplementary Material
Acknowledgments
We thank P. Borckmans and C. I. Sainz-Díaz for discussions. We are very grateful to K. Baert and I. Vandendael from Vrije Universiteit Brussel for the Raman analysis. A.D., F.B., and F.H. acknowledge PRODEX (Programme de Développement d'Expériences Scientifiques) and Fonds de la Recherche Scientifique (FORECAST project) for financial support. J.H.E.C. acknowledges the financial support of the Ministerio de Ciencia e Innovacíon Grant FIS2013-48444-C2-2-P. This work has been performed within the framework of the NASA Astrobiological Institute focus group on thermodynamics, disequilibrium, and evolution.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.A. is a guest editor invited by the Editorial Board.
See Commentary on page 17346.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1409552111/-/DCSupplemental.
References
- 1.Glauber JR. Furni Novi Philosophici. Fabel; Amsterdam: 1646. [Google Scholar]
- 2.Glaab F, Kellermeier M, Kunz W, Morallon E, García-Ruiz JM. Formation and evolution of chemical gradients and potential differences across self-assembling inorganic membranes. Angew Chem Int Ed Engl. 2012;51(18):4317–4321. doi: 10.1002/anie.201107754. [DOI] [PubMed] [Google Scholar]
- 3.Double DD, Hellawell A. The hydration of Portland cement. Nature. 1976;261(5560):486–488. [Google Scholar]
- 4.Butler G, Ison HCK. An unusual form of corrosion product. Nature. 1958;182(4644):1229–1230. [Google Scholar]
- 5.Cartwright JHE, Escribano B, González DL, Sainz-Díaz CI, Tuval I. Brinicles as a case of inverse chemical gardens. Langmuir. 2013;29(25):7655–7660. doi: 10.1021/la4009703. [DOI] [PubMed] [Google Scholar]
- 6.Corliss JB, et al. Submarine thermal springs on the Galapagos rift. Science. 1979;203(4385):1073–1083. doi: 10.1126/science.203.4385.1073. [DOI] [PubMed] [Google Scholar]
- 7.Russell MJ, Hall AJ. The emergence of life from iron monosulphide bubbles at a submarine hydrothermal redox and pH front. J Geol Soc London. 1997;154(3):377–402. doi: 10.1144/gsjgs.154.3.0377. [DOI] [PubMed] [Google Scholar]
- 8.Barge LM, et al. Characterization of iron-phosphate-silicate chemical garden structures. Langmuir. 2012;28(8):3714–3721. doi: 10.1021/la203727g. [DOI] [PubMed] [Google Scholar]
- 9.Barge LM, et al. Pyrophosphate synthesis in iron mineral films and membranes simulating prebiotic submarine hydrothermal precipitates. Geochim Cosmochim Acta. 2014;128:1–12. [Google Scholar]
- 10.Cooper GJT, et al. Osmotically driven crystal morphogenesis: A general approach to the fabrication of micrometer-scale tubular architectures based on polyoxometalates. J Am Chem Soc. 2011;133(15):5947–5954. doi: 10.1021/ja111011j. [DOI] [PubMed] [Google Scholar]
- 11.Thouvenel-Romans S, Steinbock O. Oscillatory growth of silica tubes in chemical gardens. J Am Chem Soc. 2003;125(14):4338–4341. doi: 10.1021/ja0298343. [DOI] [PubMed] [Google Scholar]
- 12.Maselko J, et al. Spontaneous formation of chemical motors in simple inorganic systems. J Mater Sci Lett. 2005;40(17):4671–4673. [Google Scholar]
- 13.Pagano JJ, Bánsági T, Jr, Steinbock O. Bubble-templated and flow-controlled synthesis of macroscopic silica tubes supporting zinc oxide nanostructures. Angew Chem Int Ed Engl. 2008;47(51):9900–9903. doi: 10.1002/anie.200803203. [DOI] [PubMed] [Google Scholar]
- 14.Makki R, Al-Humiari M, Dutta S, Steinbock O. Hollow microtubes and shells from reactant-loaded polymer beads. Angew Chem Int Ed Engl. 2009;48(46):8752–8756. doi: 10.1002/anie.200903292. [DOI] [PubMed] [Google Scholar]
- 15.Makki R, Roszol L, Pagano JJ, Steinbock O. Tubular precipitation structures: Materials synthesis under non-equilibrium conditions. Philos Trans A Math Phys Eng Sci. 2012;370(1969):2848–2865. doi: 10.1098/rsta.2011.0378. [DOI] [PubMed] [Google Scholar]
- 16.Makki R, Steinbock O. Nonequilibrium synthesis of silica-supported magnetite tubes and mechanical control of their magnetic properties. J Am Chem Soc. 2012;134(37):15519–15527. doi: 10.1021/ja3064843. [DOI] [PubMed] [Google Scholar]
- 17.Roszol L, Makki R, Steinbock O. Postsynthetic processing of copper hydroxide-silica tubes. Chem Commun (Camb) 2013;49(51):5736–5738. doi: 10.1039/c3cc41516c. [DOI] [PubMed] [Google Scholar]
- 18.Makki R, Ji X, Mattoussi H, Steinbock O. Self-organized tubular structures as platforms for quantum dots. J Am Chem Soc. 2014;136(17):6463–6469. doi: 10.1021/ja501941d. [DOI] [PubMed] [Google Scholar]
- 19.Coatman RD, Thomas NL, Double DD. Studies of the growth of “silicate gardens” and related phenomena. J Mater Sci. 1980;15(8):2017–2026. [Google Scholar]
- 20.Cartwright JHE, Garcia-Ruiz JM, Novella ML, Otalora F. Formation of chemical gardens. J Colloid Interface Sci. 2002;256(2):351–359. [Google Scholar]
- 21.Cooper GJT, et al. Directed assembly of inorganic polyoxometalate-based micrometer-scale tubular architectures by using optical control. Angew Chem Int Ed Engl. 2012;51(51):12754–12758. doi: 10.1002/anie.201204405. [DOI] [PubMed] [Google Scholar]
- 22.Jones DEH, Walter U. The silicate garden reaction in microgravity: A fluid interfacial instability. J Colloid Interface Sci. 1998;203(2):286–293. doi: 10.1006/jcis.1998.5447. [DOI] [PubMed] [Google Scholar]
- 23.Cartwright JHE, Escribano B, Sainz-Díaz CI, Stodieck LS. Chemical-garden formation, morphology, and composition. II. Chemical gardens in microgravity. Langmuir. 2011;27(7):3294–3300. doi: 10.1021/la104193q. [DOI] [PubMed] [Google Scholar]
- 24.Pagano JJ, Thouvenel-Romans S, Steinbock O. Compositional analysis of copper-silica precipitation tubes. Phys Chem Chem Phys. 2007;9(1):110–116. doi: 10.1039/b612982j. [DOI] [PubMed] [Google Scholar]
- 25.Cartwright JHE, Escribano B, Sainz-Díaz CI. Chemical-garden formation, morphology, and composition. I. Effect of the nature of the cations. Langmuir. 2011;27(7):3286–3293. doi: 10.1021/la104192y. [DOI] [PubMed] [Google Scholar]
- 26.Nagatsu Y, Ishii Y, Tada Y, De Wit A. Hydrodynamic fingering instability induced by a precipitation reaction. Phys Rev Lett. 2014;113(2):024502. doi: 10.1103/PhysRevLett.113.024502. [DOI] [PubMed] [Google Scholar]
- 27.Podgorski T, Sostarecz MC, Zorman S, Belmonte A. Fingering instabilities of a reactive micellar interface. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(1):016202. doi: 10.1103/PhysRevE.76.016202. [DOI] [PubMed] [Google Scholar]
- 28.Bohner B, Schuszter G, Berkesi O, Horváth D, Tóth Á. Self-organization of calcium oxalate by flow-driven precipitation. Chem Commun (Camb) 2014;50(33):4289–4291. doi: 10.1039/c4cc00205a. [DOI] [PubMed] [Google Scholar]
- 29.Clément R, Douady S. Ocean-ridge-like growth in silica tubes. Europhys Lett. 2010;89(4):44004. [Google Scholar]
- 30.Struik DJ. Lectures on Classical Differential Geometry. 2nd Ed Dover Publications; New York: 1988. [Google Scholar]
- 31.Thompson DW. On Growth and Form. Macmillan; New York: 1942. [Google Scholar]
- 32.Pantaleone J, et al. Pressure oscillations in a chemical garden. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79(5):056221. doi: 10.1103/PhysRevE.79.056221. [DOI] [PubMed] [Google Scholar]
- 33.Tóth A, Horváth D, Smith R, McMahan JR, Maselko J. Phase diagram of precipitation morphologies in the - system. J Phys Chem C. 2007;111(40):14762–14767. [Google Scholar]
- 34.Cross M, Greenside H. Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge Univ Press; Cambridge, United Kingdom: 2009. [Google Scholar]
- 35.Noorduin WL, Grinthal A, Mahadevan L, Aizenberg J. Rationally designed complex, hierarchical microarchitectures. Science. 2013;340(6134):832–837. doi: 10.1126/science.1234621. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.