Collapse of cooperation in evolving games

Significance

This study offers a new perspective on an age-old question: When does cooperation emerge in populations? Two-player games used to study this question produce an array of counterintuitive results. And yet a consensus has emerged that, in an evolving population, cooperation tends to triumph over cheating––through reciprocity and generosity. But, what happens when players can influence not only their tendencies to cooperate, but also the rewards they reap for cooperation? We analyze coevolution of strategies and payoffs and find that, as individuals maximize the benefits of cooperation, they often pave the way for its collapse. Our analysis provides a framework for studying the coevolution of games and strategies, and suggests that maintaining cooperation may be more difficult than previously thought.

Abstract

Game theory provides a quantitative framework for analyzing the behavior of rational agents. The Iterated Prisoner’s Dilemma in particular has become a standard model for studying cooperation and cheating, with cooperation often emerging as a robust outcome in evolving populations. Here we extend evolutionary game theory by allowing players’ payoffs as well as their strategies to evolve in response to selection on heritable mutations. In nature, many organisms engage in mutually beneficial interactions and individuals may seek to change the ratio of risk to reward for cooperation by altering the resources they commit to cooperative interactions. To study this, we construct a general framework for the coevolution of strategies and payoffs in arbitrary iterated games. We show that, when there is a tradeoff between the benefits and costs of cooperation, coevolution often leads to a dramatic loss of cooperation in the Iterated Prisoner’s Dilemma. The collapse of cooperation is so extreme that the average payoff in a population can decline even as the potential reward for mutual cooperation increases. Depending upon the form of tradeoffs, evolution may even move away from the Iterated Prisoner’s Dilemma game altogether. Our work offers a new perspective on the Prisoner’s Dilemma and its predictions for cooperation in natural populations; and it provides a general framework to understand the coevolution of strategies and payoffs in iterated interactions.

Iterated games provide a framework for studying social interactions (1–6) that allows researchers to address pervasive biological problems such as the evolution of cooperation and cheating (2, 7–12). Simple examples such as the Iterated Prisoner’s Dilemma, Snowdrift, and Stag Hunt games (13–18) showcase a startling array of counterintuitive social behaviors, especially when studied in a population replicating under natural selection (16, 19–25). Despite the subject’s long history, a systematic treatment of all evolutionary robust cooperative outcomes for even the simple Iterated Prisoner’s Dilemma has only recently emerged (21, 26–29).

Understanding the evolution of strategies in a population under fixed payoffs already poses a steep challenge. To complicate matters further, in many biological settings the payoffs themselves may also depend on the genotypes of the players. Changes to the payoff matrix have been studied in a number of contexts, including one-shot two-player games (13), payoff evolution without strategy evolution (30, 31), under environmental “shocks” to the payoff matrix (32–34), and using continuous games (22, 23, 35). Here we adopt a different approach, and we explicitly study the coevolutionary dynamics between strategies and payoffs in iterated two-player games. We decouple strategy mutations from payoff mutations, and we leverage results on the evolutionary robustness of memory-1 strategies with arbitrary payoff matrices to explore the relationship between payoff evolution and the prevalence of cooperation in a population. We identify a feedback between the costs and benefits of cooperation and the evolutionary robustness of cooperative strategies. Depending on the functional form (35) of the relationship between costs and benefits, this feedback may either reinforce the evolutionary success of cooperation or else precipitate its collapse. In particular, we show that cooperation will always collapse when there are diminishing returns for mutual cooperation.

Methods and Results

Iterated Two-Player Games.

In an iterated two-player game, players X and Y face each other in an infinite number of successive “rounds.” In each round the players simultaneously choose their plays and receive associated payoffs. We study games with a $2\times 2$ payoff matrix, so that the players have two choices in each round. We label these choices “cooperate” (c) and “defect” (d), using the traditional language for the Prisoner’s Dilemma. The four corresponding payoffs for player X facing player Y are ${\mathbf{R}}_{\mathbf{xy}}=\left(R_{xy}\left(cc\right),R_{xy}\left(cd\right),R_{xy}\left(dc\right),R_{xy}\left(dd\right)\right)$, where X’s play is denoted first. In general, X may choose her play in each round depending on the outcomes of all previous rounds.

We will focus on memory-1 players (21, 26–29, 36–39), whose choice each round depends only on the previous round. Such a strategy is described by the probabilities of cooperation given the four possible outcomes of the previous round: $\mathbf{p}=\left(p_{cc},p_{cd},p_{dc},p_{dd}\right)$. The long-term average payoff to player X facing opponent Y, denoted $s_{xy}$, can be calculated directly from her strategy ${\mathbf{p}}_{\mathbf{x}}$, her opponent’s strategy ${\mathbf{p}}_{\mathbf{y}}$, and her payoffs ${\mathbf{R}}_{\mathbf{xy}}$. When the population is monomorphic in the player’s payoffs, as typically occurs under weak mutation (Fig. 1), all players have the same payoff matrix and ${\mathbf{R}}_{\mathbf{xy}}={\mathbf{R}}_{\mathbf{yx}}=\mathbf{R}$ (SI Appendix).

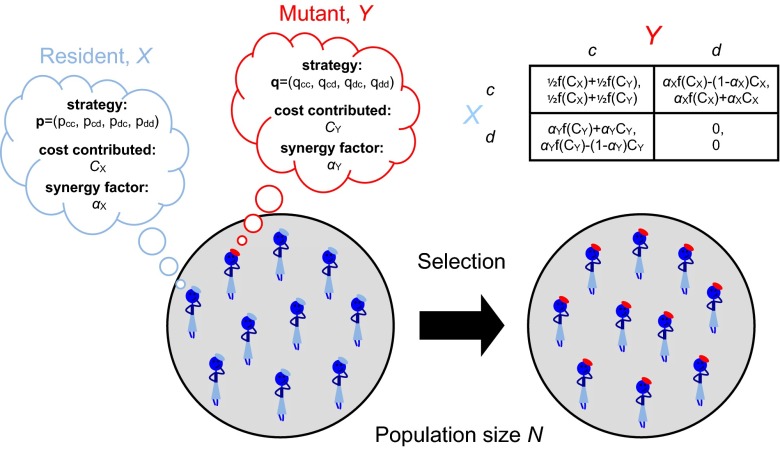
Fig. 1.

Evolving the rules of the game. We study the coevolution of strategies and payoffs in a replicating population of N individuals playing an iterated, two-player public-goods game. Each individual has a “genotype” consisting of a memory-1 strategy vector, p, a cost C contributed to the public good, and a synergy factor α. A player X who contributes a cost $C_X$ generates a benefit $B_X$ when her opponent also cooperates, and generates a benefit $2{\alpha }_X{B}_X$ when she alone cooperates. The benefit B is determined by the cost C according to the equation $B-C=f\left(C\right)$, where B−C is the payoff for mutual cooperation and $f\left(C\right)$ is typically assumed to be a monotonically increasing function of C. The payoff matrix when player X faces player Y is determined by their associated trait values C and α, as shown in the figure. The payoffs actually received in the iterated game depend on both players’ strategies as well as the payoff matrix. Mutations are introduced that change either a player’s strategy p, her cost of contribution, C, or her synergy factor α. Mutant strategies are drawn uniformly from the four-dimensional space of memory-1 strategies. Mutations to payoffs are generated through local mutations to the traits C and α. Natural selection and genetic drift occur according to a “copying” process (52), in which two players, X and Y, are selected at random from the population, and Y adopts the genotype of X with probability $f_{y\to x}=1/\left(1+\exp \left[\sigma \left(s_y-s_x\right)\right]\right)$, where $s_x$ and $s_y$ denotes the total payoffs the players receive in pairwise match-ups against the entire population, and σ is the strength of selection. We model evolution under weak mutation, so that a new mutant Y is introduced into a monomorphic population with resident genotype X, and then either Y fixes in the population, with probability (52) $\rho ={\left(1+{\displaystyle {\sum }_{i=1}^{N-1}{\displaystyle {\prod }_{j=1}^i{e}^{-\sigma \left[\left(j-1\right)s_{yy}+\left(N-j\right)s_{yx}-j{s}_{xy}-\left(N-j-1\right)s_{xx}\right]}}}\right)}^{-1}$, or else Y is lost (SI Appendix).

Evolution of Strategies.

We consider a well-mixed population of N individuals evolving under weak mutation who are each characterized by a memory-1 strategy. An individual’s reproductive success depends on her total payoff when pitted in pairwise iterated games against all other individuals in the population, so that the composition of strategies in the population evolves over time. The strategies that tend to succeed in evolving populations can be understood in terms of evolutionary robustness (21, 26). A strategy is evolutionary robust if, when resident in a population, no new mutant strategy is favored to spread by natural selection. Evolutionary robustness is a weaker condition than that of an evolutionary stable strategy (ESS) (16, 40) (SI Appendix). Robustness is a useful notion because there is rarely if ever an ESS, as many strategies ${\mathbf{p}}_{\mathbf{x}}\ne {\mathbf{p}}_{\mathbf{y}}$ are neutrally equivalent and can invade each other by genetic drift (41). And so we focus on the evolutionary robust strategies, which are neutral to one another but resist invasion by any strategy outside of the set. Indeed, it is already known that the evolutionary robust strategies that cooperate among themselves can dominate in evolving populations playing the Iterated Prisoner’s Dilemma (21, 26).

It may seem restrictive to focus on memory-1 strategies (36, 37). However, Press and Dyson (27) have shown that a memory-1 player can treat all opponents as although they also have memory-1. As a result of this lemma, a memory-1 player that resists invasion by all memory-1 opponents also resists invasion by all longer-memory opponents. So, even though we restrict our analysis to memory-1 strategies, we nonetheless identify the memory-1 strategies that are robust against all opponents, regardless of the opponent’s memory capacity within a given iterated game (SI Appendix). However, our analysis does not allow a player to retain memory of prior interactions with different opponents, in which case such a superlong-memory player could discern the composition of strategies in the population and gain an evolutionary advantage (42–44).

Coevolution of Strategies and Payoffs.

Here we expand the traditional purview of evolutionary game theory by allowing heritable mutations that affect a player’s payoffs, as well as mutations that affect her strategy, so that the composition of payoffs and strategies in a population coevolve over time (Fig. 1). We study evolution in the iterated two-player public-goods game, with payoffs initially chosen to produce a Prisoner’s Dilemma.

In the public-goods game, a player cooperates by contributing an amount C to a public pool, producing a group benefit whose size depends in some way on the total amount contributed by both players. The benefit is then shared between the two players. We consider a generalized form of the public-goods game in which a player X contributes a cost $C_X$ when she cooperates, which produces a benefit $B_X$ if her opponent also cooperates or, alternatively, produces a benefit $2{\alpha }_X{B}_X$ if her opponent refuses to cooperate. The term $2{\alpha }_X$ represents a “synergy factor” that determines how the total benefit scales when both players cooperate compared with when only one cooperates. In the standard public-goods game $\alpha =1/2$ for all players, and so the benefit added to the public pool by a cooperating player does not depend on whether her opponent cooperates. In the volunteer’s dilemma (45), by contrast, $\alpha =1$ for all players and no additional benefit is added to the public pool when two players cooperate as opposed to one.

We allow heritable mutations that affect the payoff matrix, by allowing small changes to a player’s cost C or synergy factor α. It is natural to assume that the benefit of mutual cooperation increases with the cost of contribution, and so we enforce the relationship $B-C=f\left(C\right)$ for some function $f\left(C\right)$ which we usually choose to be monotonically increasing. Given the choice of function $f\left(C\right)$, the genotype of player X is comprised of her strategy vector p, her contributed cost $C_X$, and her synergy factor ${\alpha }_X$. The payoff matrix that results when player X faces player Y has entries $R_{xy}\left(cc\right)=f\left(C_X\right)/2+f\left(C_Y\right)/2$, $R_{xy}\left(cd\right)={\alpha }_{X}f\left(C_X\right)-\left(1-{\alpha }_X\right)C_X$, $R_{xy}\left(dc\right)={\alpha }_{Y}f\left(C_Y\right)+{\alpha }_Y{C}_Y$, and $R_{xy}\left(dd\right)=0$, where we have assumed that when both players cooperate they receive equal payoffs, and so they both benefit from any increase in the amount of the public good. The resulting long-term payoffs to players X and Y in the iterated game, however, depend on the players’ strategies as well as this payoff matrix.

We consider populations evolving under weak mutation, so that any new mutant genotype either fixes or is lost before another genotype is introduced (Fig. 1). As a result, a mutation that changes a player’s strategy is introduced into a population of individuals who all share the same payoff matrix. Strategy mutations are drawn uniformly from the space of all memory-1 strategies, whereas mutations that alter an individual’s cost C or synergy factor α are drawn locally.

Collapse of Cooperation in the Iterated Prisoner’s Dilemma.

How does cooperation fare when both strategies and payoffs evolve in a population? To study this we first analyze coevolution of strategies and payoffs in games restricted to the Iterated Prisoner’s Dilemma. We assume a linear relationship between B and C, by stipulating $f\left(C\right)=\gamma C+k$, where we choose $\gamma >0$ to ensure that the benefits of mutual cooperation increase with costs. (Later, we will explore other functional relationships between B and C.) We choose γ and k such that $B<2C$, to ensure that the game is always a Prisoner’s Dilemma: each player has an incentive to defect even though the players would receive a greater total payoff for mutual cooperation. Also, we assume for now that $\alpha =1/2$ is fixed for all players.

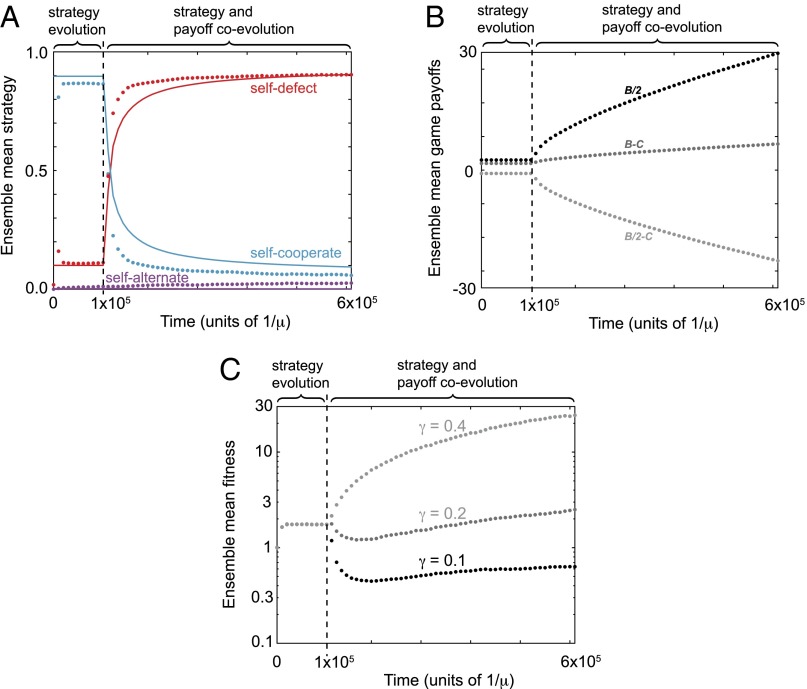
Starting from a game with fixed payoffs $B=6$ and $C=4$, cooperation quickly rises to high frequency in populations undergoing strategy evolution alone (Fig. 2A), in agreement with previous results (14, 21). However, when both strategies and payoffs coevolve there is a striking reversal of fortunes. Evolution favors increasing the benefits of mutual cooperation as well as the benefits of unilateral defection (Fig. 2B). The evolution of the payoff matrix is accompanied by a dramatic collapse of cooperation, so that the population is eventually dominated by defection (Fig. 2A). Paradoxically, defection comes to dominate even as the payoffs available for mutual cooperation continually increase (Fig. 2B). Moreover, this collapse of cooperation is often accompanied by an erosion of mean population fitness (Fig. 2C).

Fig. 2.

Collapse of cooperation in the Prisoner’s Dilemma. We simulated populations playing the iterated public-goods game, proposing mutant strategies until reaching equilibrium, and then also proposing mutations to the cost C, each at rate $\mu /2$. In these simulations $\alpha =1/2$ was fixed for all players. Mutations to strategies were drawn uniformly from the full space of memory-1 strategies. Mutations perturbing the cost C by Δ were drawn uniformly from the range $\mathrm{\Delta }\in \left[-0.1,0.1\right]$, with the corresponding change to the benefit B chosen to enforce the relationship $B-C=\gamma C+k$. Evolution was modeled according to an imitation process under weak mutation (21, 28, 52). (A) Cooperative strategies are initially robust and dominate the population, but they are quickly replaced by defectors as payoffs evolve. Dots indicate the proportion of 10⁵ replicate simulated populations, at each time point, within distance $\delta =0.01$ of the three strategy types self-cooperate, self-defect, and self-alternate. Lines indicate analytic predictions for the frequencies of these strategy types, which depend upon the corresponding volumes of robust strategies (SI Appendix, Fig. S2). (B) As payoffs evolve, the Prisoner’s Dilemma becomes more acute, with both greater costs C and benefits B of cooperation. Cooperation collapses even though the payoff for mutual cooperation, $B-C$, increases over time. (C) The mean population fitness can decline over time, depending on the choice of parameter γ. Populations of size $N=100$ were initiated with $B=6$ and $C=4$ (which determine k), and they were evolved under selection strength $\sigma =1$ (corresponding to strong selection on strategies), with $\gamma =0.1$ in A and B. The collapse of cooperation also occurs under weak selection (i.e., $N\sigma \sim 1$; SI Appendix, Fig. S9), under local mutations to strategies (SI Appendix, Fig. S11), and also when mutations to payoffs are more rare than mutations to strategies (SI Appendix, Fig. S10).

There is a simple intuition for this disheartening evolutionary outcome: Initially, the population is typically composed of self-cooperating strategies and so mutations to C that increase the reward for mutual cooperation, $B-C$, are favored. However, such mutations also decrease the ratio $B/C$, which increases the temptation to defect, making the dilemma progressively more acute so that eventually defection outcompetes cooperation (10).

The Volume of Robust Strategies.

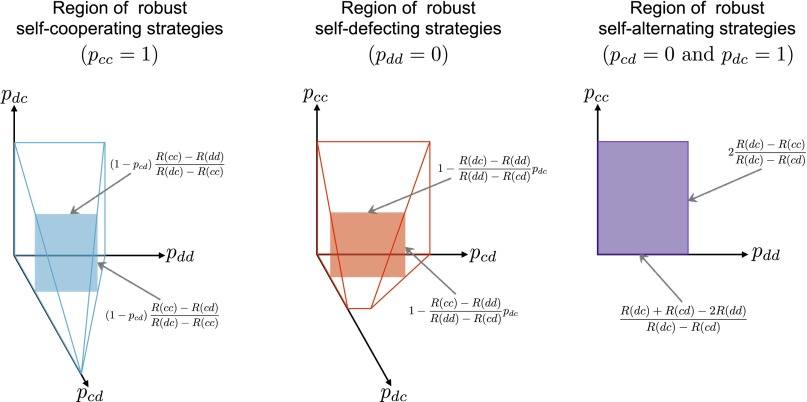
We can understand the collapse of cooperation, and the coevolution of strategies and payoffs more generally, by determining which strategies are evolutionary robust and how robustness varies as payoffs evolve. To do so, we have analytically characterized all evolutionary robust memory-1 strategies for arbitrary $2\times 2$ two-player iterated games (Fig. 3 and SI Appendix). In particular, we have proven the following necessary condition: a robust memory-1 strategy must be one of three types––self-cooperate, self-defect, or self-alternate. Self-cooperative strategies $\mathcal{C}$ cooperate at equilibrium against an opponent using the same strategy, meaning $p_{cc}=1$. Conversely, self-defecting strategies $\mathcal{D}$ satisfy $p_{dd}=0$. Self-alternating strategies $\mathcal{A}$ alternate between cooperation and defection in subsequent rounds, meaning $p_{cd}=0$ and $p_{dc}=1$. Monte Carlo simulations on the full space of memory-1 strategies confirm that populations adopt one of these three types $>97\text{\%}$ of the time, reflecting the fact that all robust strategies fall within these three types. However, the robust strategies are strict subsets of these types and, crucially, the volume of robust strategies within each type depends on the payoffs of the game (Fig. 3). The robust volumes can be computed analytically (SI Appendix) and they determine whether a population tends to adopt self-cooperation, self-defection, or self-alternation (Fig. 2 A and B).

Fig. 3.

Evolutionary robust strategies in iterated two-player games. For an arbitrary $2\times 2$ payoff matrix, an evolutionary robust memory-1 strategy must be one of three possible types: those that cooperate against an opponent who cooperates (Left, $p_{cc}=1$), those that defect against an opponent who defects (Center, $p_{dd}=0$), and those that alternate between cooperate and defect against an alternating opponent (Right, $p_{cd}=0$ and $p_{dc}=1$). Within each of these strategy types, the strict subsets that are evolutionary robust can be determined analytically from the payoff matrix, as indicated on the figure (see SI Appendix for full derivations). The regions of robust self-cooperating and robust self-defecting strategies are 3D, whereas the robust self-alternating strategies are 2D. Monte Carlo simulations exploring the full space of memory-1 strategies confirm that these are the only evolutionary robust solutions (SI Appendix, Fig. S1). As payoffs evolve in a population, the volumes of robust strategies change according to the equations in the figure, and they determine the evolutionary dynamics of cooperation and defection (Fig. 2).

For the generalized public-goods game illustrated in Fig. 1, for example, the evolutionary robust strategies of each type satisfy

$${\mathcal{C}}_r=\left\{\left(p_{cc},p_{cd},p_{dc},p_{dd}\right)|p_{cc}=1,p_{dc}\le \frac{\left(f\left(C\right)+C\right)\left(1-\alpha \right)}{\alpha C-\left(1-\alpha \right)f\left(C\right)}\left(1-p_{cd}\right),p_{dd}\le \frac{f\left(C\right)}{\alpha C-\left(1-\alpha \right)f\left(C\right)}\left(1-p_{cd}\right)\right\},$$

$${\mathcal{D}}_r=\left\{\left(p_{cc},p_{cd},p_{dc},p_{dd}\right)|p_{dd}=0,p_{cc}\le 1-\frac{f\left(C\right)}{\left(1-\alpha \right)C-\alpha f\left(C\right)}{p}_{dc},p_{cd}\le 1-\frac{\alpha \left(f\left(C\right)+C\right)}{\left(1-\alpha \right)C-\alpha f\left(C\right)}{p}_{dc}\right\},$$

$${\mathcal{A}}_r=\left\{\left(p_{cc},p_{cd},p_{dc},p_{dd}\right)|p_{cd}=0,p_{dc}=1,p_{cc}\le 2\frac{\alpha C-\left(1-\alpha \right)f\left(C\right)}{C},p_{dd}\le \frac{2f\left(C\right)+\left(1-2\alpha \right)C}{C}\right\}.$$

As these equations show, in the case of the Prisoner’s Dilemma with $\alpha \in \left(0,1\right)$ increasing the temptation to defect [i.e., decreasing $f\left(C\right)/C$] will enlarge the volume of robust self-defecting strategies and reduce the volume of the robust self-cooperating strategies. Thus, it is the ratio of benefits to costs (10) that matters for the prospects of cooperation in the Iterated Prisoner’s Dilemma, as payoffs and strategies coevolve.

The robust self-cooperators, self-defectors, and self-alternators contain many of the “classic” strategies known to be successful in the Iterated Prisoner’s Dilemma (1, 20, 21, 28). For example, “win–stay–lose–shift” (21) belongs to the robust self-cooperators [provided $f\left(C\right)/C>\alpha /\left(2-\alpha \right)$], and “always defect” belongs to the robust self-defectors. Tit-for-tat is a special, limiting case that satisfies the conditions to be a self-cooperator, a self-defector, and a self-alternator. Tit-for-tat belongs to the robust self-cooperators only if it plays cooperate on the first move, and if the game contains no noise (SI Appendix).

Functional Relationships Between Costs and Benefits.

So far we have assumed that benefits of cooperation increase linearly with costs. However, our analysis in terms of volumes of robust strategies allows us to study any functional relationship between benefits and costs. We can therefore extend our results to explore more generally under what circumstances the collapse of cooperation will occur.

We first consider cases in which $f\left(C\right)$ is monotonically increasing with C––that is, when the benefit of mutual cooperation always increases with the cost of cooperation [see SI Appendix for analogous results with $f\left(C\right)$ monotonically decreasing]. If $f\left(C\right)$ increases superlinearly with C then any social dilemma will quickly disappear, as benefits for cooperation quickly become much greater than costs, and cooperative strategies reach high frequency (SI Appendix, Figs. S4 and S6). If $f\left(C\right)$ increases linearly with C but with intercept $k<0$, then again cooperation persists at high levels (SI Appendix, Fig. S5). In the more realistic and interesting cases, for which the benefits of mutual cooperation either saturate or increase sublinearly with C, then the collapse of cooperation will always occur as C increases, just as in the linear case with $k>0$. The collapse of cooperation occurs in all these cases because the volume of robust self-cooperating strategies decreases with the ratio $f\left(C\right)/C$, which in turn decreases as C gets large. Examples of these functional forms, which feature diminishing returns for increasing costs of cooperation, are shown in SI Appendix, Fig. S6A for $f\left(C\right)=\sqrt{C}$ and SI Appendix, Fig. S6B for $f\left(C\right)$ saturating.

Alternatively, $f\left(C\right)$ may be a nonmonotonic function of C such that there is an optimal value of C. In this scenario the long-term prevalence of cooperation in a population will depend on the ratio $f\left(C\right)/C$ at the optimal value; and its prevalence can again be calculated using our analytical framework (SI Appendix, Fig. S8).

Evolution Away from the Prisoner’s Dilemma.

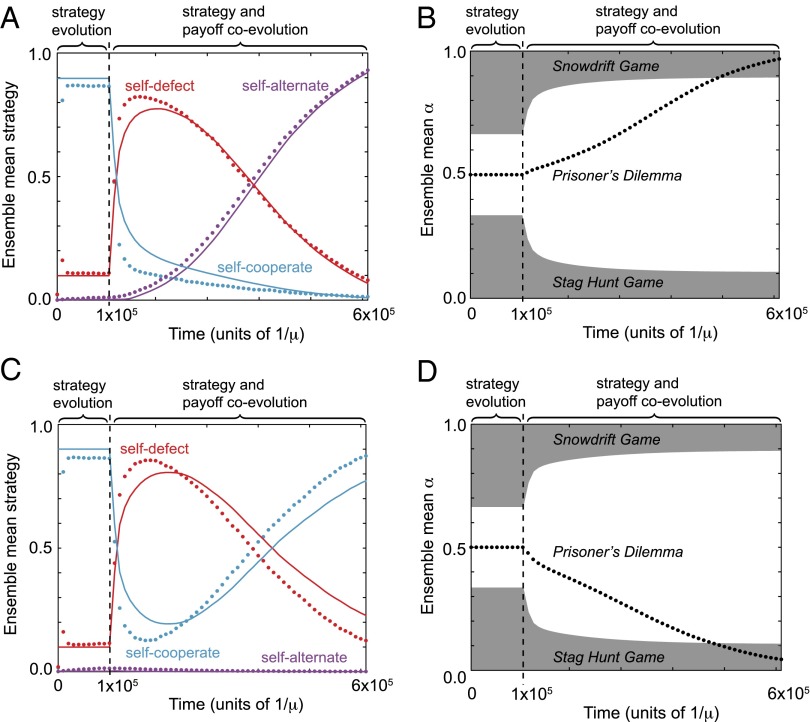
So far we have explored public-goods games whose payoffs form a Prisoner’s Dilemma. However, our analysis in terms of the volume of robust strategies applies to arbitrary $2\times 2$ games and mutation schemes, and so it can be used to study evolution between qualitatively different types of games. To explore this possibility, instead of fixing the synergy parameter $\alpha =1/2$ for all players, as in Fig. 2, we now allow mutations that change both α and C. The parameter α has a simple biological interpretation in terms of synergism ($\alpha <1/2$) or antagonism ($\alpha >1/2$) between mutual cooperators: the total amount of public good produced per cost C may be augmented or depreciated when both players cooperate, as opposed to when only one cooperates. As before, we assume $f\left(C\right)$ is a linear function of C. If α and C evolve independently and can adopt any values then this mutation scheme produces all possible qualitative $2\times 2$ games, i.e., all 12 different orderings of the 4 payoffs $R\left(cc\right)$, $R\left(cd\right)$, $R\left(dc\right)$, and $R\left(dd\right)$ up to symmetry (SI Appendix, Fig. S3). In particular, when $f\left(C\right)/\left(f\left(C\right)+C\right)<\alpha <C/\left(f\left(C\right)+C\right)$ the payoffs correspond to a Prisoner’s Dilemma; when $C/\left(f\left(C\right)+C\right)<\alpha <1$ the payoffs encode a Snowdrift game; and when $0<\alpha <f\left(C\right)/\left(f\left(C\right)+C\right)$ the payoffs encode a Stag Hunt game (13–18).

Fig. 4 illustrates the emergence of qualitatively new games in a population initialized at the Iterated Prisoner’s Dilemma. In this figure we assume that mutations that increase the cost C will either increase antagonism (Fig. 4, Top) or increase synergy (Fig. 4, Bottom). As payoffs and strategies coevolve in this more general framework, the benefits and costs of cooperation initially increase, resulting again in the collapse of cooperation (Fig. 4A). However, the subsequent increase (or decrease) in α leads to qualitatively different outcomes for the payoff matrix. Under the mutation scheme in which α increases with C, the Prisoner’s Dilemma eventually gives way to a Snowdrift game and populations are dominated by self-alternating strategies (Fig. 4, Top). Under the mutation scheme in which α decreases with C, the Prisoner’s Dilemma gives way to a Stag Hunt game and self-cooperating strategies recover high prevalence in populations (Fig. 4, Bottom).

Fig. 4.

Evolution away from the Prisoner’s Dilemma. We simulated populations under weak mutation, proposing mutant strategies drawn uniformly from the full space of memory-1 strategies. Alongside mutations to the contributed cost C, as in Fig. 2, we also allowed mutations to an additional payoff parameter α, which determines whether mutual cooperation is synergistic ($\alpha <1/2$) or antagonistic ($\alpha >1/2$) for the amount of public benefit produced. (A) When mutations that increase C are constrained to increase α (i.e., increase antagonism), then evolution initially produces a rapid loss of cooperative strategies and an increase in the frequency of defecting strategies, as in Fig. 2. Subsequently, as α continues to increase, alternating strategies increase to high frequency. Points indicate the proportion of simulated populations within a distance $\delta =0.01$ of the three strategy types; lines indicate analytic predictions (SI Appendix). (B) Following the collapse of cooperation, the Prisoner’s Dilemma (unshaded region) is replaced by the Snowdrift game (shaded region), for which $\alpha >C/\left(f\left(C\right)+C\right)$. (C) When mutations that increase C are constrained to decrease α (i.e., decrease antagonism), evolution initially produces a rapid loss of cooperative strategies and an increase in defecting strategies, as in Fig. 2. Subsequently, as α continues to decrease, cooperative strategies recover to high frequencies. Points indicate the proportion of simulated populations within a distance $\delta =0.01$ of the three strategy types; lines indicate analytic predictions (SI Appendix). (D) Following the collapse of cooperation, the Prisoner’s Dilemma (unshaded region) is replaced by the Stag Hunt game (shaded region), for which $\alpha <f\left(C\right)/\left(f\left(C\right)+C\right)$. Parameter values as in Fig. 2 A and B. Populations of size $N=100$ were initiated with $C=4$ and $\alpha =1/2$, and evolved under selection strength $\sigma =1$ (corresponding to strong selection on strategies) with $\gamma =1/9$. The value of α was constrained to a sigmoidal function of C in the range $\left[\mathrm{0,1}\right]$, namely $\alpha =1/\left(1+\exp \left[h\left(C_0-C\right)\right]\right)$ (A and B) and $\alpha =1/\left(1+\exp \left[-h\left(C_0-C\right)\right]\right)$ (C and D), with $h=0.1$ and $C_0=4$.

When α and C are allowed to evolve independently, the resulting coevolutionary dynamics are similar to the case of increasing antagonism: both α and C increase and the population is eventually dominated by self-alternating strategies (SI Appendix, Fig. S7). If α is constrained to the range $\left[0,1\right]$ then a Snowdrift game emerges and is stable (SI Appendix, Fig. S7 A and B), whereas if α is unconstrained it evolves to values exceeding unity and the game $R\left(dc\right)>R\left(cd\right)>R\left(cc\right)>R\left(dd\right)$ emerges (SI Appendix, Fig. S7 C and D). The instability of the Iterated Prisoner’s Dilemma in favor of the Iterated Snowdrift or Iterated Stag Hunt games is striking, although the potential for increasing antagonism or synergy in evolving games may be subject to physical constraints in natural populations.

Discussion

We have studied coevolution of strategies and payoffs in populations of individuals reproducing according to their payoffs in pairwise interactions. We have focused primarily on payoff mutations that enforce a tradeoff, by simultaneously increasing the benefits and costs of cooperation. However, our framework for analyzing payoff-strategy coevolution, based on computing the evolutionary robustness of strategy sets, can be applied to any mutation scheme and can produce a potentially vast array of evolutionary outcomes. For example, the way in which benefits are shared between players who mutually cooperate but contribute differentially to the public good may alter how payoffs and hence strategies evolve (23). In general, for two-player public-goods games, if there are diminishing returns for increasing costs of cooperation, then the ratio $f\left(C\right)/C$ will decrease over time and the frequency of cooperators will collapse. Alternatively, if the ratio $f\left(C\right)/C$ increases over time, then cooperation will become increasingly prevalent. However, this latter scenario may be implausible, because it implies that the benefits for mutual cooperation can accelerate without bound.

What types of payoff mutations can arise in a natural population will depend upon the biological context. Examples of the tradeoff between costs and benefits that we have studied (Figs. 2 and 4) are found in nature at many scales (8, 9, 46), from human societies, where individuals modulate both how frequently and how much they punish free-riders (8, 47), to microorganisms such as the marine bacteria Vibrionaceae (9). Our framework decouples strategy and payoff evolution, allowing us to explore the relationship between the “behavior” prevalent in populations (that is, the frequency of cooperation) and the amount contributed to the public good when cooperation occurs (that is, the cost C). In Vibrionaceae populations, for example, individuals cooperate in a public-goods game by sharing siderophores required for iron acquisition. Mutations that alter whether the siderophore biosynthetic pathway is activated or not alter an individual’s strategy, whereas mutations that improve or degrade the siderophore transport pathway alter an individual’s payoffs, by imposing a greater or lesser metabolic cost along with an increased benefit from the public good.

Decoupling strategy evolution from payoff evolution may not be appropriate in all biological contexts. Alternative modeling frameworks such as continuous games, which allow players to modulate their levels of investment in a social interaction (22, 23, 35), can provide a contrasting or complementary perspective on the evolution of cooperation. What is clear from Vibrionaceae populations, as well as many other biological systems with opportunities for cooperative interactions (9, 46, 48–51), is that both cooperators and defectors are often found at appreciable frequencies in nature. As we have shown, the predicted prevalence of these behaviors depends critically on the payoffs resulting from social interactions. Understanding the feedback between strategy evolution and payoff evolution is therefore critical for understanding social interactions in natural populations.