Optimal Allocation of Resources in a Biomarker Setting

SUMMARY

Nutrient intake is often measured with substantial error both in commonly used surrogate instruments such as a food frequency questionnaire (FFQ) as well as in gold standard type instruments such as a diet record (DR). If there is correlated error between the FFQ and DR, then standard measurement error correction methods based on regression calibration can produce biased estimates of the regression coefficient (λ) of true intake on surrogate intake. However, if a biomarker exists and the error in the biomarker is independent of the error in the FFQ and DR, then the method of triads can be used to obtain unbiased estimates of λ, provided that there is replicate biomarker data on at least a subsample of validation study subjects. Since biomarker measurements are expensive, for a fixed budget one can either use a design where a large number of subjects have 1 biomarker measure and only a small subsample is replicated, or have a smaller number of subjects and have most or all subjects validated. The purpose of this paper is to optimize the proportion of subjects with replicated biomarker measures, where optimization is with respect to minimizing the variance of ln(λ̂). The methodology is illustrated using vitamin C intake data from the EPIC study where plasma vitamin C is the biomarker. In this example, the optimal validation study design is to have 21% of subjects with replicated biomarker measures.

1. INTRODUCTION

In nutritional epidemiology, the weighed diet record (DR) is considered the gold standard for assessing nutrient intake. However, it is expensive to obtain diet records and the food frequency questionnaire (FFQ) is usually used as an instrument to obtain dietary intake data from large numbers of people. It is well known that the FFQ and other dietary assessment methods have appreciable measurement error. To correct for measurement error, a validation study is often performed where both the FFQ (Z) and DR (X) are administered to the same subjects. The regression calibration factor estimated by the regression coefficient of DR on FFQ can then be used as an unbiased estimate of the regression coefficient (λ) of true dietary intake (T) on Z, which can then be used for measurement error correction. However, this is only valid if measurement error in the DR and FFQ are uncorrelated, an assumption which may be violated. To address this issue this design is often enhanced with additional biomarker measurements (W). If the error in W is uncorrelated with the error in Z and X, then correlated error methods [1] can be used to estimate the regression calibration factor λ. The only requirement is that there be available replicate biomarker measurements on at least a subset of participants.

However, since biomarker measurements are expensive, it would be desirable to estimate the optimal proportion of subjects (θ) with replicate values of W, given a fixed total number of biomarker measures (B). The goal of this paper is to obtain a closed-form expression for var(λ̂) and to use it to estimate the optimal value of θ.

2. METHODS

2.1 Balanced Design

We let Z_ij = surrogate measure for the j^th replicate from the i^th subject, j=1, …, m_z, i=1, …, N; X_ik = gold standard measure for the k^th replicate from the i^th subject, k=1, …, m_x, i=1, …, N; W_il = biomarker for the l^th replicate from the i^th subject, l=1, …, m_w ≥2, i=1, …, N.

Thus, each subject provides m_z replicates for the surrogate, m_x replicates for the gold standard and m_w replicates for the biomarker.

From Spiegelman, Zhao and Kim [1] we consider the model

$$\begin{array}{l}{Z}_{ij}=a+{bx}_i+r_i+e_{z_{ij}},j=1,\dots ,m_z;i=1,\dots ,N\\ X_{ik}=x_i+s_i+e_{x_{ik}},k=1,\dots ,m_x;i=1,\dots ,N\\ W_{il}=c+{dx}_i+e_{w_{il}},l=1,\dots ,m_w\ge 2;i=1,\dots ,N\end{array}$$ (1)

where x_i = true intake for the i^th subject

• r_i= person-specific bias in the surrogate measure $~N(0,{\sigma }_r^2)$

• s_i= person-specific bias in the gold standard measure $~N(0,{\sigma }_s^2)$

e_zij, e_xik, e_wil are distributed $N(0,{\sigma }_{ez}^2),N(0,{\sigma }_{ex}^2),N(0,{\sigma }_{ew}^2)$ and are mutually independent of each other. $r_i~N(0,{\sigma }_r^2),s_i~N(0,{\sigma }_s^2)cov(r_i,s_i)={\mathrm{\rho }}_{rs}{\sigma }_r{\sigma }_s$, and r_i, s_i are mutually independent of e_zij, e_xik, e_wil. Our goal is to estimate the regression calibration factor (λ_x|Z) = regression coefficient of x on Z. It can be shown from (1) that the MLE of λ_x|Z is given by

$${\widehat{\lambda }}_{x\mid Z}=\frac{\mathit{cov}(Z_{ij},W_{ik})\mathit{cov}(X_{ij},W_{ik})}{\mathit{cov}(W_{{il}_1},W_{{il}_2})\mathit{var}(Z_{ij})}$$ (2)

We have found that, in simulation studies, that the distribution of λ̂_x|Z is generally skewed, while the distribution of ln(λ̂_x|Z) is approximately normal. Hence, two-sided 100% × (1-α) confidence limits for λ_x|Z are obtained from [exp(c₁), exp(c₂)], where $(c_1,c_2)=ln({\widehat{\lambda }}_{x\mid Z})\pm z_{1-\alpha /2}\sqrt{\mathit{var}[ln({\widehat{\lambda }}_{x\mid Z})]}$ and z_p = p^th percentile of a N(0,1) distribution. It remains to derive an analytic expression for var[ln(λ̂_x|Z)]. For this purpose, we take the natural log of each side of equation 2 and obtain:

$$\begin{array}{c}ln({\widehat{\lambda }}_{x\mid Z})=ln[\mathit{cov}(Z_{ij},W_{ik})]+ln[\mathit{cov}(X_{ij},W_{ik})]\\ -ln[\mathit{cov}(W_{{il}_1},W_{{il}_2})]-ln[\mathit{var}(Z_{ij})]\\ \equiv A+B-C-D\end{array}$$ (3)

Thus,

$$\begin{array}{l}\mathit{var}[ln({\widehat{\lambda }}_{x\mid Z})]=\mathit{var}(A)+\mathit{var}(B)+\mathit{var}(C)+\mathit{var}(D)+2\mathit{cov}(A,B)\\ -2\mathit{cov}(A,C)-2\mathit{cov}(A,D)-2\mathit{cov}(B,C)-2\mathit{cov}(B,D)+2\mathit{cov}(C,D)\end{array}$$ (4)

We derive var(A). The other components can be derived in a similar manner. For notational purposes, it will be useful to introduce the notation:

μ_abc =E[(Z_ij − Z̄)^a(X_ik − X̄)^b(W_il − W̄)^c] which we estimate by

$${\widehat{\mu }}_{\mathit{abc}}={\mathrm{\sum }}_{i=1}^N{\mathrm{\sum }}_{j=1}^{m_z}{\mathrm{\sum }}_{k=1}^{m_x}{\mathrm{\sum }}_{l=1}^{m_w}{(Z_{ij}-\overline{Z})}^a{(X_{ik}-\overline{X})}^b{(W_{il}-\overline{W})}^c/(N{m}_z^{a^{\ast }}{m}_x^{b^{\ast }}{m}_w^{c^{\ast }})$$ (5)

where a^* = 1 if a ≥ 1,=0 else, b^* =1 if b ≥ 1,=0 else and c^* =1 if c ≥ 1,=0 else. Using the delta method, we have that

$$\mathit{var}(A)=\mathit{var}({\widehat{\mu }}_{101})/{({\widehat{\mu }}_{101})}^2$$ (6)

Furthermore,

$$\begin{array}{c}\mathit{var}({\widehat{\mu }}_{101})=\mathit{var}[{\mathrm{\sum }}_{i=1}^N{\mathrm{\sum }}_{j=1}^{m_z}{\mathrm{\sum }}_{k=1}^{m_w}(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})/(N{m}_z{m}_w)]\\ =\mathit{var}\left[\sum _{j=1}^{m_z}\sum _{k=1}^{m_w}(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})/(N{m}_z^2{m}_w^2)\right]\\ =\left\{\begin{array}{c}\mathit{var}[(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})]+(m_w-1)\mathit{cov}[(Z_{ij}-\overline{Z})(W_{{ik}_1}-\overline{W}),(Z_{ij}-\overline{Z})(W_{{ik}_2}-\overline{W})]\\ +(m_z-1)\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{ik}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{ik}-\overline{W})]\\ +(m_z-1)(m_w-1)\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{{ik}_1}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{{ik}_2}-\overline{W})]/(N{m}_z{m}_w)\end{array}\right\}\end{array}$$ (7)

where k₁ ≠ k₂ and j₁ ≠ j₂. We can write

$$\begin{array}{c}\mathit{var}[(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})]=\mathrm{E}\left[{(Z_{ij}-\overline{Z})}^2{(W_{ik}-\overline{W})}^2\right]-{\mathrm{E}}^2[(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})]\\ ={\widehat{\mu }}_{202}-{\widehat{\mu }}_{101}^2\end{array}$$ (8)

Similarly, we can write

$$\begin{array}{c}\mathit{cov}[(Z_{ij}-\overline{Z})(W_{{ik}_1}-\overline{W}),(Z_{ij}-\overline{Z})(W_{{ik}_2}-\overline{W})]\\ =\mathrm{E}\left[{(Z_{ij}-\overline{Z})}^2(W_{{ik}_1}-\overline{W})(W_{{ik}_2}-\overline{W})\right]-{\mathrm{E}}^2[(Z_{ij}-\overline{Z})(W_{ik}-\overline{W})]\end{array}$$

In general, we introduce the notation

$${\widehat{\mu }}_{a_1{a}_2\dots a_r,b_1{b}_2\dots b_s,c_1{c}_2\dots c_t}=\mathrm{E}\left[\prod _{f=1}^r{\left(Z_{{ij}_f}-\overline{Z}\right)}^{{\alpha }_f}\prod _{g=1}^s{\left(X_{{ik}_g}-\overline{X}\right)}^{b_g}\prod _{h=1}^t{(W_{{il}_h}-\overline{W})}^{c_h}\right]$$

where j₁ ≠ j₂ ≠ ··· ≠ j_r, k₁ ≠ k₂ ≠ ··· ≠ k_s, and l₁ ≠ l₂ ≠ ··· ≠ l_t.

Thus, we have:

$$\mathit{cov}[(Z_{ij}-\overline{Z})(W_{{ik}_1}-\overline{W}),(Z_{ij}-\overline{Z})(W_{{ik}_2}-\overline{W})]={\widehat{\mu }}_{2,0,11}-{\widehat{\mu }}_{101}^2$$ (9)

Similarly,

$$\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{ik}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{ik}-\overline{W})]={\widehat{\mu }}_{11,0,2}-{\widehat{\mu }}_{101}^2$$

and

$$\begin{array}{c}\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{{ik}_1}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{{ik}_2}-\overline{W})]\\ =\mathrm{E}[(Z_{{ij}_1}-\overline{Z})(Z_{{ij}_2}-\overline{Z})(W_{{ik}_1}-\overline{W})(W_{{ik}_2}-\overline{W})]-{\widehat{\mu }}_{101}^2={\widehat{\mu }}_{11,0,11}-{\widehat{\mu }}_{101}^2\end{array}$$ (10)

Upon combining equations 6–10, we obtain

$$\mathit{var}(A)=\frac{1}{{\widehat{\mu }}_{101}^{2}N{m}_z{m}_w}\left[\begin{array}{c}{\widehat{\mu }}_{202}+(m_w-1){\widehat{\mu }}_{2,0,11}+(m_z-1){\widehat{\mu }}_{11,0,2}+(m_w-1)(m_z-1){\widehat{\mu }}_{11,0,11}\\ -m_w{m}_z{\widehat{\mu }}_{101}^2\end{array}\right]$$ (11)

The other components in equation 4 are obtained similarly and are provided in Web Appendix A.

Upon combining equations A1–A10, we obtain var[ln(λ̂_x|Z)] in equation 4.

To obtain confidence limits for λ_x|Z we assume asymptotic normality of ln(λ̂_x|Z) whereby a two-sided 100% × (1-α) CI for λ_x|Z is given by [exp(c₁), exp (c₂)], where

$$(c_1,c_2)=ln({\widehat{\lambda }}_{x\mid Z})\pm z_{1-\alpha /2}\sqrt{\mathit{var}[ln({\widehat{\lambda }}_{x\mid Z})]}$$ (12)

and z_1−α/2= upper α/2 percentile of a N(0,1) distribution.

2.2 Unbalanced Design

We now consider the unbalanced design situation. In this case, we assume all subjects have the same number of replicates for the surrogate dietary instrument (e.g., FFQ) and the gold standard dietary instrument (e.g., DR) denoted by m_z and m_x, respectively. However, since biomarker measurements are the most expensive, we assume that n_g of the subjects have g biomarker measurements, where g = 1,2 and n₁ + n₂ = N. Also, let b_i = the number of replicate biomarker measurements for the i^th subject and let $M={\mathrm{\sum }}_{i=1}^N{b}_i=2n_2+n_1$. Finally, let θ = proportion of biomarker measurements that are replicated =2n₂/M where 0 ≤ θ ≤ 1. We assume that M is fixed due to budgetary constraints and we wish to determine the value of θ that minimizes var[ln(λ̂_x|Z)] in equation 4.

We will derive var(A) in the unbalanced case and present the results for the other components of equation 4 in Appendix B. In the unbalanced case, we estimate μ_abc by

$${\widehat{\mu }}_{\mathit{abc}}=\sum _{i=1}^N\sum _{j=1}^{m_z}\sum _{k=1}^{m_x}\sum _{l=1}^{b_i}{(Z_{ij}-\overline{Z})}^a{(X_{ik}-\overline{X})}^b{(W_{il}-\overline{W})}^c/m_z^{a^{\ast }}{m}_x^{b^{\ast }}M$$ (13)

where a^* and b^* are defined in equation 5.

We have

$$\mathit{var}(A)=\mathit{var}({\widehat{\mu }}_{101})/{\widehat{\mu }}_{101}^2$$ (14)

where μ₁₀₁ is estimated using equation 13.

We have:

$$\mathit{var}({\widehat{\mu }}_{101})=\frac{1}{m_z^2{M}^2}{\mathrm{\sum }}_{i=1}^N\mathit{var}[{\mathrm{\sum }}_{j=1}^{m_z}{\mathrm{\sum }}_{l=1}^{b_i}(Z_{ij}-\overline{Z})(W_{il}-\overline{W})]$$ (15)

Furthermore,

$$\begin{array}{c}\mathit{var}[{\mathrm{\sum }}_{j=1}^{m_z}{\mathrm{\sum }}_{l=1}^{b_i}(Z_{ij}-\overline{Z})(W_{il}-\overline{W})]=m_z{b}_i\mathit{var}[(Z_{ij}-\overline{Z})(W_{il}-\overline{W})]\\ +m_z{b}_i(b_i-1)\mathit{cov}[(Z_{ij}-\overline{Z})(W_{{il}_1}-\overline{W}),(Z_{ij}-\overline{Z})(W_{{il}_2}-\overline{W})]\\ +m_z(m_z-1)b_i\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{il}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{il}-\overline{W})]\\ +m_z(m_z-1)b_i(b_i-1)\mathit{cov}[(Z_{{ij}_1}-\overline{Z})(W_{{il}_1}-\overline{W}),(Z_{{ij}_2}-\overline{Z})(W_{{il}_2}-\overline{W})]\\ =m_z{b}_i({\widehat{\mu }}_{202}-{\widehat{\mu }}_{101}^2)+m_z{b}_i(b_i-1)({\widehat{\mu }}_{2,0,11}-{\widehat{\mu }}_{101}^2)+m_z(m_z-1)b_i({\widehat{\mu }}_{11,0,2}-{\widehat{\mu }}_{101}^2)\\ +m_z(m_z-1)b_i(b_i-1)({\widehat{\mu }}_{11,0,11}-{\widehat{\mu }}_{101}^2)\end{array}$$ (16)

If we denote ${\mathrm{\sum }}_{i=1}^N{b}_i^2$ by M⁽²⁾ and combine equations 14, 15 and 16, we obtain

$$\begin{array}{c}\mathit{var}(A)=\frac{1}{m_z{M}^2{\widehat{\mu }}_{101}^2}\{M({\widehat{\mu }}_{202}-{\widehat{\mu }}_{101}^2)+[M^{(2)}-M]({\widehat{\mu }}_{2,0,11}-{\widehat{\mu }}_{101}^2)+(m_z-1)M({\widehat{\mu }}_{11,0,2}-{\widehat{\mu }}_{101}^2)+\\ (m_z-1)[M^{(2)}-M]({\widehat{\mu }}_{11,0,11}-{\widehat{\mu }}_{101}^2)\}\end{array}$$ (17)

Note, if there are a total of N subjects of whom n₁ have one replicate and n₂ have two replicates, then M = 2n₂ + n₁, M⁽²⁾ = 4n₂ + n₁, and M⁽²⁾ − M =2n₂. In this case, equation 17 reduces to:

$$\begin{array}{c}\mathit{var}{(A)}_{\mathit{unbalanced}}=\frac{1}{m_z{(2n_2+n_1)}^2{\widehat{\mu }}_{101}^2}\{(2n_2+n_1)({\widehat{\mu }}_{202}-{\widehat{\mu }}_{101}^2)+2n_2({\widehat{\mu }}_{2,0,11}-{\widehat{\mu }}_{101}^2)\\ +(m_z-1)(2n_2+n_1)({\widehat{\mu }}_{11,0,2}-{\widehat{\mu }}_{101}^2)+(m_z-1)2n_2({\widehat{\mu }}_{11,0,11}-{\widehat{\mu }}_{101}^2)\}\end{array}$$ (18)

Derivation of the other components of equation 4 under an unbalanced design are obtained similarly and are provided in Web Appendix B.

Finally, a large sample 100% × (1-α) CI for λ_x|Z is given by [exp(c₁), exp(c₂)] where

$$(c_1,c_2)=ln({\widehat{\lambda }}_{x\mid Z})\pm z_{1-\alpha /2}\sqrt{\mathit{var}[ln({\widehat{\lambda }}_{x\mid Z})]}$$

2.3 Optimization

We wish to minimize var[ln(λ̂_x|Z)] in equation 4 in the setting where b_i= 1 or 2. We can re-express equation B.1 in Web Appendix B as a function of θ as follows:

$$\mathit{var}(A)=f_{1A}+f_{2A}\theta$$ (19)

where

$$\begin{array}{c}\theta =2n_2/(n_1+2n_2)\\ f_{1,A}=\frac{{\widehat{\mu }}_{202}-{\widehat{\mu }}_{101}^2+(m_z-1)({\widehat{\mu }}_{11,0,2}-{\widehat{\mu }}_{101}^2)}{m_z{\widehat{\mu }}_{101}^{2}M}\\ f_{2,A}=\frac{{\widehat{\mu }}_{2,0,11}-{\widehat{\mu }}_{101}^2+(m_z-1)({\widehat{\mu }}_{11,0,11}-{\widehat{\mu }}_{101}^2)}{m_z{\widehat{\mu }}_{101}^{2}M}\end{array}$$

Similarly,

$$\mathit{var}(B)=f_{1B}+\theta f_{2B}$$ (20)

$$\mathit{var}(C)=f_C/\theta$$ (21)

$$\mathit{var}(D)=f_D/(2-\theta )$$ (22)

$$\mathit{cov}(A,B)=f_{1,AB}+\theta f_{2,AB}$$ (23)

$$\mathit{cov}(A,C)=f_{AC}$$ (24)

$$\mathit{cov}(A,D)=f_{AD}/(2-\theta )$$ (25)

$$\mathit{cov}(B,C)=f_{BC}$$ (26)

$$\mathit{cov}(B,D)=f_{BD}/(2-\theta )$$ (27)

$$\mathit{cov}(C,D)=f_{CD}/(2-\theta )$$ (28)

The expressions for f_1A, …, f_CD are given in Appendix C.

Note that in general if there is positive correlation among replicate Z, X and W values, then it can be shown that f_2A > 0, f_2B > 0, f_C > 0, f_D > 0, f_2,AB > 0, f_AD > 0, f_BD > 0, and f_CD > 0. Hence, var (A), var (B), var (D), cov(A, B), cov(A, D), cov(B, D) and cov(C, D) are minimized if θ = 0, i.e., all subjects have only one biomarker measurement, since this will maximize the number of subjects. Conversely, var(C) is minimized if θ = 1; where all subjects have two biomarker measurements.

Assume all subjects have either one or two biomarker measurements. If we combine equations 4 and 19–28, we obtain:

$$\mathit{var}[ln({\widehat{\lambda }}_{x\mid Z})]=C_0+C_1\theta +C_2/\theta +C_3/(2-\theta )\equiv V(\theta )$$ (29)

where

$$\begin{array}{c}{C}_0=f_{1A}+f_{1B}+2f_{1,AB}-2f_{AC}-2f_{BC}\\ C_1=f_{2A}+f_{2B}+2f_{2,AB}\\ C_2=f_C\\ C_3=f_D-2f_{AD}-2f_{BD}+2f_{CD}\end{array}$$

If we differentiate V(θ) with respect to θ in equation 29 and collect terms, we obtain the 4^th degree polynomial equation as follows:

$${\theta }^4-4{\theta }^3+d_1{\theta }^2+d_2\theta -d_2=0$$ (30)

where

$$d_1=4-\frac{(C_2-C_3)}{C_1},d_2=\frac{4C_2}{C_1}$$

Although it is possible to obtain an exact solution to this equation, it is simpler to use a polynomial equation solver (e.g., the POLYROOT function of SAS) to determine the solution that satisfies 0 < θ < 1.

3. SIMULATION STUDY

We simulated data from a hypothetical dataset with a similar correlation structure as in our example with (Z₁, Z₂, X₁, X₂, W₁, W₂)~N(μ, Σ) where μ = (100, 100, 100, 100, 50, 50) and

$$\mathrm{\sum }=\left(\begin{array}{cccccc}400& 232& 208& 172& 48& 48\\ 232& 400& 172& 208& 48& 48\\ 208& 172& 400& 240& 64& 64\\ 172& 208& 240& 400& 64& 64\\ 48& 48& 64& 64& 100& 40\\ 48& 48& 64& 64& 40& 100\end{array}\right)$$

We then estimated ln(λ_x|Z) in equation 3, its variance in equation 4 and a 95% CI for λ_x|Z in equation 12 from 4,000 simulated samples. The results are given in Table 1. We see that there is good agreement between the mean theoretical variances and covariances considered in equation 4 and derived in Appendix B and the corresponding empirical variances and covariances obtained from the 4,000 simulated samples. Also, the overall estimate of λ_x|Z has little bias and the estimated 95% confidence intervals have approximately (94.1%) coverage.

4. EXAMPLE

We analyzed data from the EPIC-Norfolk study [2]. Individuals were seen at a baseline visit and at a 4-year follow-up visit as part of the study. At both baseline and follow-up, a food frequency questionnaire (FFQ) and a 1-week diet record (DR) were obtained. In addition, a blood sample was obtained at both the baseline and 4-year follow-up visit. In this example, we focus on dietary vitamin C and assess the regression coefficient of true dietary vitamin C intake (x_i in equation 1) on FFQ vitamin C intake (Z_ij in equation 1) which is given by λ̂_x|Z in equation 2 using plasma vitamin C as a biomarker. We refer to λ̂_x|Z as the estimated regression calibration factor. For this example, we assume that true dietary intake has not changed over four years, but allow for the possibility of correlated error between FFQ and DR intake (ρ_rs in equation 1). We also assume that there is no systematic error in the biomarker and that the random error in FFQ intake, DR intake and plasma vitamin C are uncorrelated. The marginal and joint distribution of FFQ intake (Z_ij), DR intake (X_ij) and plasma vitamin C (W_ij) are given in Table II. There is moderate correlation between dietary vitamin C (Z, X) and plasma vitamin C (W) which are similar for the FFQ and DR when the intake assessments at year 4 are compared with the biomarker values at baseline (which provides the most appropriate assessment of their relative measurement of long-term intake). For the purpose of better approximating a normal distribution, the log transform was used for each of dietary vitamin C from FFQ (Z_ij) and DR (X_ik) in subsequent analyses.

Table II.

Marginal and Joint Distribution of FFQ vitamin C, DR vitamin C and plasma vitamin C in the EPIC-Norfolk study

variable	mean	sd	correlation matrix
			Zi1	Zi2	Xi1	Xi2	Wi1	Wi2
$Z_{i1}^{\ast }$	134.4	54.5	1.0	0.60	0.47	0.42	0.25	0.18
$Z_{i2}^{\ast }$	135.6	58.7		1.0	0.45	0.57	0.25	0.27
$X_{i1}^{†}$	90.5	50.1			1.0	0.59	0.40	0.23
$X_{i2}^{†}$	94.6	52.0				1.0	0.28	0.34
$W_{i1}^{‡}$	57.7	21.2					1.0	0.43
$W_{i2}^{‡}$	64.8	23.2						1.0

^*Z_i1, Z_i2 = baseline and 4-year calorie-adjusted FFQ vitamin C intake (mg/day)

^†X_i1, X_i2 = baseline and 4-year calorie-adjusted DR vitamin C intake (mg/day)

^‡W_i1, W_i2 = baseline and 4-year plasma vitamin C intake (μmol/L)

Computer program: :/proj/stross/stros0a/example_usevitc.sas 09/19/13

In Table III we provide the point estimate and 95% CI for λ_x|Z as well as the individual components used in equation 12. We see that the estimated regression calibration factor (λ_x|Z) is 0.308 with 95% confidence limits from 0.201 to 0.471. The point estimate implies that there is substantial measurement error in the assessment of dietary vitamin C. For example if the estimated hazard ratio based on observed vitamin C is 1.2 then the deattenuated estimate would be 1.2^1/0.308 = 1.8, indicating substantial deattenuation. The degree of measurement error in the FFQ will vary depending on the nutrients/foods being considered. In general, beverage intake has less measurement error, while food intake can have considerable measurement error. Dietary vitamin C is derived mainly from fruits and vegetables which have moderate measurement error.

Table III.

Estimation of Regression Calibration factor in EPIC data example, n=323

A*	2.998
B*	5.003
C*	263.319
D*	0.1852
var(A)	0.034
var(B)	0.019
var(C)	0.019
var(D)	0.007
cov(A,B)	0.018
cov(A,C)	0.013
cov(A,D)	0.009
cov(B,C)	0.011
cov(B,D)	0.004
cov(C,D)	0.003
λ̂x|Z	0.308
log(λ̂x|Z)	−1.179
var[log(λ̂x|Z)]	0.0473
95% CI for λx|Z	(0.201,0.471)

^*A = cov(Z_ij, W_ik); B = cov(X_ij, W_ik); C = cov(W_il1, W_il2); D = var(Z_ij)

Computer run: :/proj/stross/stros0c/measurmentErrBio/example1/example_usevitc.sas 6/4/12

5. OPTIMIZATION

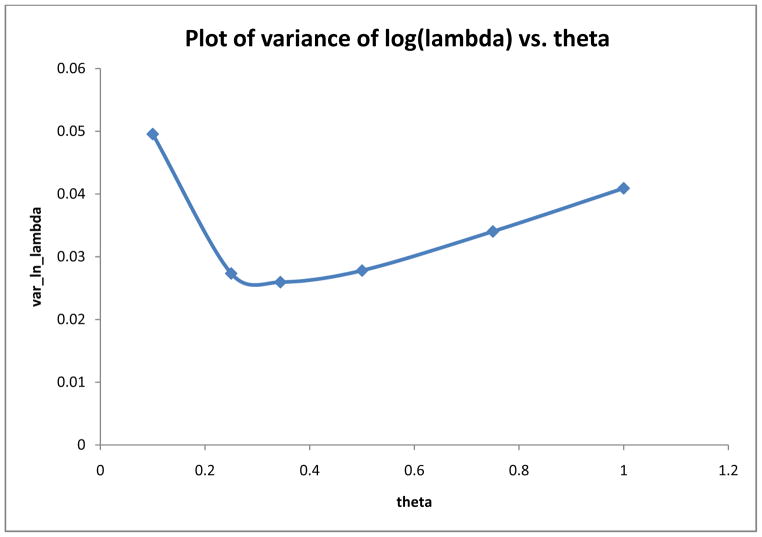
We also used the EPIC data to estimate the optimal proportion of replicated biomarker measurements based on equations 29 and 30. The results are presented in Table IV. The estimated parameters (C₁, C₂, C₃), (d₁, d₂) in equations 29 and 30 are given in the left side of the table. The solution using the POLYROOT function of SAS was θ̂ = 0.349 = the optimal proportion of replicated biomarker measurements (i.e., 2n₂/(n₁ + 2n₂)). It follows directly that the optimal estimate of n₂/n₁ = 0.349/[2(0.651)] = 0.268 or equivalently n₂/(n₁ + n₂) = 0.268/1.268 = 0.211. Thus, the optimal design (i.e., min var[ln(λ̂_x|Z)]) is for approximately 21% of the sample to have replicated biomarker measurements given a fixed total of M biomarker measurements. To assess the sensitivity of var[ln(λ̂_x|Z)] to variation in θ we computed var[ln(λ̂_x|Z)] for different values of θ. The results are given in the right hand side of Table IV and are plotted in Figure 1. We see that the variance function is fairly flat between θ̂ = 0.2 – 0.5 corresponding to a proportion of subjects with replicated biomarkers of 0.14 to 0.33. However, the variance increases moderately outside these limits.

Table IV.

Results of Optimization Procedure based on EPIC dataset

Parameter	Value	θ	var[ln(λ̂x|Z)]	n2/(n1 + n2)
C1	0.04120	0.10	0.0496	0.053
C2	0.00472	0.25	0.0273	0.143
C3	−0.00664	0.349	0.0259	0.208
d1	3.72420	0.500	0.0278	0.333
d2	0.45839	0.75	0.0340	0.600
θ̂	0.349	0.90	0.0382	0.818

Computer program:

:/proj/stross/stros0c/measurmentErrBio/example1/example2_usevitc.sas 9/30/13

:/proj/stross/stros0c/measurmentErrBio/example1/test_getLambda.sas 9/30/13

Figure 1.

6. DISCUSSION

Correlated error between gold standard dietary measures such as a diet record and surrogate measures such as a food frequency questionnaire can bias standard techniques for correcting for measurement error such as regression calibration. The method of triads using a biomarker in addition to the above dietary instruments is an effective method for eliminating this bias. However, it requires replicate measurements on the biomarker for at least a subset of study participants [1]. In the current paper, we derive a closed form expression for the variance estimate of the Spiegelman, Zhao and Kim estimator of the regression calibration factor (λ_x|Z) and associated 95% confidence limits for both balanced (same number of biomarker replicates per subject) and unbalanced (different number of biomarker replicates per subject) designs.

Ideally, all subjects in a validation study would have replicated biomarker measurements; however, these measures are usually expensive. Thus, in this paper, we derive an expression for the optimal proportion of validation study subjects with replicated biomarker measures given a fixed total number of biomarker measures (M), where optimality is defined as minimizing var[ln(λ̂_x|Z)]. In the EPIC example, this was about 21%, but would be expected to vary for other biomarkers or in other studies.

The algorithms used to derive var[ln(λ̂_x|Z)] and associated confidence limits and the optimal design formulas in equations 29 and 30 are available in the form of SAS macros from the authors upon request.

Table I.

Simulation Study Results, 4000 replications

Component	Theoretical value*	Empirical estimate	Coverage probability
var(A)	0.0351	0.0389
var(B)	0.0204	0.0233
var(C)	0.0234	0.0234
var(D)	0.0041	0.0041
cov(A,B)	0.0169	0.0181
cov(A,C)	0.0109	0.0116
cov(A,D)	0.0048	0.0049
cov(B,C)	0.0108	0.0116
cov(B,D)	0.0022	0.0023
cov(C,D)	0.0009	0.0010
cov(Zij, Wik)	48.0	48.0
cov(Xij, Wik)	64.0	63.9
cov(Wil1, Wil2)	40.0	39.8
var(Zij)	400.0	399.6
var[ln(λ̂x|Z)]	0.0609	0.0672
λ̂x|Z	0.192	0.194**	0.941

^*Based on Web Appendix B

^**median

Computer program :/proj/stross/stros0c/measurmentErrBio/Undesignx4000a.sas 09/27/13

:/proj/stross/stros0c/measurmentErrBio/all_new2.txt 09/27/13