Intrinsic Coupling Modes in Source-Reconstructed Electroencephalography

Abstract

Intrinsic coupling of neuronal assemblies constitutes a key feature of ongoing brain activity, yielding the rich spatiotemporal patterns observed in neuroimaging data and putatively supporting cognitive processes. Intrinsic coupling has been investigated in electrophysiological recordings using two types of functional connectivity measures: amplitude and phase coupling. These two coupling modes differ in their likely causes and functions, and have been proposed to provide complementary insights into intrinsic neuronal interactions. Here, we investigate the relationship between amplitude and phase coupling in source-reconstructed electroencephalography (EEG). Volume conduction is a key obstacle for connectivity analysis in EEG—we therefore also test the envelope correlation of orthogonalized signals and the phase lag index. Functional connectivity between six seed source regions (bilateral visual, sensorimotor, and auditory cortices) and all other cortical voxels was computed. For all four measures, coupling between homologous sensory areas in both hemispheres was significantly higher than with other voxels at the same physical distance. The frequency of significant coupling differed between sensory areas: 10 Hz for visual, 30 Hz for auditory, and 40 Hz for sensorimotor cortices. By contrasting envelope correlations and phase locking values, we observed two distinct clusters of voxels showing a different relationship between amplitude and phase coupling. Large clusters contiguous to the seed regions showed an identity (1:1) relationship between amplitude and phase coupling, whereas a cluster located around the contralateral homologous regions showed higher phase than amplitude coupling. These results show a relationship between intrinsic coupling modes that is distinct from the effect of volume conduction.

Introduction

Spontaneous brain activity is spatially and temporally structured in networks of cortical and subcortical regions (so called resting-state networks [RSN]). These networks have been originally observed with functional magnetic resonance imaging (fMRI) (Damoiseaux et al., 2006; Fox et al., 2005; Greicius et al., 2003). The time courses of functional connectivity are not constant – signifying the formation and dissolution of these resting-state networks—and typically show fractal scaling or 1/f properties (Bullmore et al., 2001; He, 2011; Maxim et al., 2005). Computational models show that resting-state dynamics reflect the slow modulations of long-range synchronization of fast local neuronal activity (Breakspear et al., 2004; Deco et al., 2009; Freyer et al., 2011; Ghosh et al., 2008; Honey et al., 2007). Recent studies on resting-state dynamics have hence focused on resting-state electrophysiology—with its high temporal resolution—to capture the synchronization dynamics of these faster time scales (Britz et al., 2010; Brookes et al., 2011; He et al., 2008; Hipp et al., 2012; Mantini et al., 2007; Mehrkanoon et al., 2014; Siegel et al., 2012).

In general, quantifying functional connectivity in oscillatory activity can be achieved by studying either phase or amplitude coupling (Bruns, 2004). The former arises from phase locking of band-limited oscillatory signals, whereas the latter results from coupled aperiodic fluctuations of signal envelopes (Engel et al., 2013). Both types of functional connectivity have been widely investigated in resting-state electrophysiology. Most studies initially focused on phase coupling (Engel et al., 2001; Lutz et al., 2004; Uhlhaas and Singer, 2006; Varela et al., 2001), whereas recent studies also investigated amplitude coupling (Brookes et al., 2011; De Pasquale et al., 2010; Hipp et al., 2012). Importantly, phase and amplitude coupling operate at different time scales: Phase coupling reflects the phase locking of fast band-limited oscillations, whereas amplitude coupling reflects the correlation between the slow envelopes of carrier frequencies (Siegel et al., 2012). Hence, a central question is if and how these two distinct types of functional coupling in resting-state electrophysiology are interrelated. It has been suggested that these two “intrinsic coupling modes” (ICMs) differ in their dynamics, the underlying coupling mechanisms and their putative functions (Engel et al., 2013).

A substantial limitation of resting-state electrophysiology is the low spatial resolution of magneto- and electroencephalography (M/EEG). Due to field spread, electrical potentials and magnetic fields generated by neuronal activity are not only measured in the direct vicinity of neuronal sources, but can also be measured at distant sites (Hamalainen et al., 1993; Sarvas, 1987). This is particularly problematic when connectivity analysis is performed at the channel level and multiple recording sites pick up signals from a single source resulting in spurious connectivity estimates (Nunez et al., 1997). Because volume conduction is always instantaneous, an effective strategy for addressing this confounding factor is to confine the analysis to noninstantaneous correlations. Hence, several methods have been proposed that only quantify phase locking at a nonzero phase lag, for example, imaginary coherence (Nolte et al., 2004) and the phase lag index (PLI) (Stam et al., 2007) or envelope correlations after orthogonalizing the band-limited signals (Hipp et al., 2012). Another approach to avoid artifacts from volume conduction is first to apply an inverse method to the data and then to perform connectivity analysis between the estimated source signals (Gross et al., 2001; Hillebrand et al., 2012; Schoffelen and Gross, 2009). However, even in source space, the spatial resolution of electrophysiological data remains limited and results in trivial spatial correlations that drop off with distance (Schoffelen and Gross, 2009). Hence, source connectivity analysis also requires connectivity measures that are robust against field spread (Hillebrand et al., 2012; Hipp et al., 2012).

To investigate the relationship between amplitude and phase coupling we investigate different functional connectivity measures in source-reconstructed resting-state EEG. Source signals of distributed solution points located in the cortical gray matter were estimated using low resolution electrical tomography (Pascual-Marqui et al., 1994). Following Hipp and colleagues (2012), we investigate functional connectivity at multiple frequencies between six seed locations (bilateral auditory, visual, and somatosensory cortices) and all other cortical voxels. In particular, we investigate four different connectivity measures: correlation between power envelopes, the phase locking value (PLV) (Lachaux et al., 1999), envelope correlation between orthogonalized signals (Hipp et al., 2012), and the PLI (Stam et al., 2007). We focus on functional connectivity with the homologous areas in the contralateral hemisphere and normalize our measures to a random distribution of voxels at the same physical distance to the seed location. Prior analyses of fMRI data show that higher than expected correlations between bilateral homologous regions are a robust property of functional connectivity (Lord et al., 2012; Salvador et al., 2005), and therefore a helpful benchmark for testing and comparing methods. Finally, we contrast amplitude and phase coupling across all voxels to investigate the interrelations between both types of ICMs. These findings demonstrate the feasibility of connectivity analysis in source reconstructed EEG and further elucidate the relationship between ICMs.

Methods

We first performed artifact rejection on channel-space resting-state EEG and then reconstructed source-level signals using LORETA. The power spectra of the source signals and four methods of functional connectivity were assessed between bilateral homologous brain regions. Bilateral connectivity was then compared to a null distribution obtained by computing connectivity between the seed region and a random distribution of voxels at the same physical distance. This approach allows assessment of the statistical significance of observed functional connectivity between homologous areas and comparison to previous studies showing enhanced connectivity between homologous areas (Biswal et al., 1995; Hipp et al., 2012; Salvador et al., 2005). Finally, the spatial patterns of amplitude and phase coupling were contrasted to investigate the interrelationship between ICMs and to differentiate genuine brain interactions from spurious connectivity resulting from source spread.

Data acquisition

Ten healthy participants (mean age 25 years; range 20–31 years; 4 females) participated after giving informed consent approved by the local ethics committee of the University of New South Wales. Participants were instructed to relax with eyes closed and refrain from falling asleep. Surface EEG was acquired from 64 channels during a single 12-min session using BrainAmp MR Plus amplifiers (Brain Products, Munich, Germany) and custom electrode caps (Easy Cap; Falk Minnow Services, Herrsching-Breitbrunn, Germany) arranged according to the international 10–20 system. Two channels were used for the electrocardiogram and one for the electro-oculogram, leaving 61 EEG channels. The 12-min EEG was continuously digitized with a sampling rate of 5 kHz and band-pass filtered between 0.5 and 70 online against an electrode at position FCz; all impedances at all electrodes were kept below 5 kΩ. Prior to source reconstruction, the EEG was band-pass filtered (5–45 Hz) using a third-order Butterworth filter, and Independent Component Analysis (ICA), InfoMax (Cardoso, 1997), was used to identify and remove cardiac, ocular, and muscular artifacts. On average, eight independent components containing artifacts were removed before back projecting the remaining components to channel space.

Source reconstruction

The EEG topography represents the electrical field sampled from a number of electrodes spaced across the surface of the scalp, and hence local measures of EEG amplitude are not independent samples of ongoing neuronal activity. Moreover, local measures are reference-dependent and hence functional connectivity measures should be performed on reference-free measurements of neuronal activity (Nunez et al., 1999). Source reconstruction has been proven to be a reliable approach to accurately detect functional connectivity (Gross et al., 2001; Hillebrand et al., 2012; Schoffelen and Gross, 2009). Source reconstruction is achieved by solving an inverse problem that is inherently ill-posed (Brunet et al., 2011; Lehmann and Michel, 1989; Pascual-Marqui et al., 1994). That is, given a set of sensor level data, there is no single, unique source-level solution. The inverse solution is derived from the forward model

where Y_(M×N) denotes the measurements (i.e., EEG recordings, N data points and M channels), H_(M×M) the lead field matrix, S_(M×N) the sources of interest (i.e., a 3-dimensional vector in XYZ coordinates), and e the measurement noise. The estimation of source vectors S is then given by

where 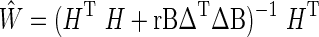denotes the inverse lead field matrix, B a diagonal matrix for the column normalization of H, and Δ the Laplacian operator. The Tikhonov regularization parameter r controls the spatial smoothness of the source estimates respectively. We used Low Resolution Electrical Tomography (LORETA) to estimate the source signals (Pascual-Marqui et al., 1994; Pascual-Marqui, 1999). LORETA was computed using a locally spherical model [LSMAC (Brunet et al., 2011)] using the MNI152 template brain (Collins et al., 1995; Mazziotta et al., 2001) as the standard brain for all subjects. The LSMAC model does not require the estimation of a best-fitting sphere, but instead uses the realistic head shape and local estimates for the thickness of scalp, skull, and brain underneath each local electrode.

A total of 4351 solution points (henceforth referred to as “voxels”) were regularly distributed within the gray matter of the cortex and limbic structures (solution points located in the cerebellum were excluded). The forward model was solved with an analytical solution using a 3-layer conductor model. Despite being somewhat simplified, this head model allows an accurate and rapid analytical solution comparable to boundary element head models (Guggisberg et al., 2011). To determine the seed regions, the source space was subdivided into 90 anatomically defined regions of interest according to the macroscopic anatomical parcellation of the MNI template using the Automated Anatomic Labeling map (Tzourio-Mazoyer et al., 2002), available from the MRIcro software (Rorden and Brett, 2000). We used the voxels in the Euclidian centers of left and right visual, auditory, and somatosensory cortices as seed regions and we correlated the time course of current density in those centroid voxels with the time courses of current density in all other voxels in the brain. The analysis was performed using the Cartool software developed by Denis Brunet [brainmapping.unige.ch/cartool; (Brunet et al., 2011)].

Each source vector or dipole estimated by LORETA is a vector with three components, projected onto the X-, Y-, and Z-axes. To obtain a single (scalar) time series for each solution point, taking the Euclidean norm of the source vector projected onto the X-, Y-, and Z-axes may lead to frequency doubling. That is, the discrete Fourier transform (DFT) of a source vector, x(t), is not equal to the DFT of 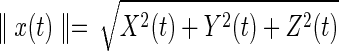, where is the Euclidean norm. In particular, when the source signal is a sine function, the norm will invert the negative phases and hence result in frequency doubling (see Supplementary Data; Supplementary Data are available online at www.liebertpub.com/brain). Principal component analysis (PCA) was applied to the covariance matrix of wide-band voxel data (i.e., time series) to find out a dominant orientation of the voxel under analysis.

Spectral decomposition

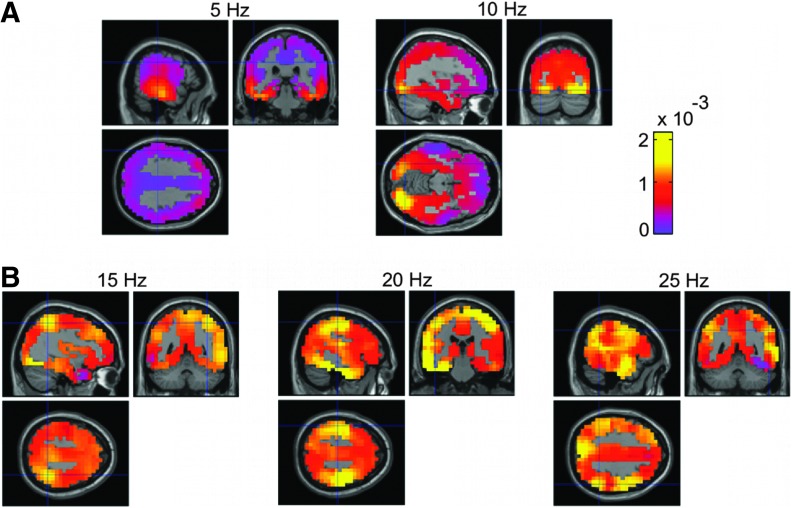
To obtain time–frequency spectra for each reconstructed source signal, we used complex Morlet wavelets with a center frequency of 1 Hz and a bandwidth of 6 cycles (Boonstra et al., 2007). The magnitude squared time–frequency spectra were averaged over time to estimate wavelet-based power spectra and then averaged across participants to yield the spatial distribution of power spectral density at the group level. The grand-average power spectra derived from broad-band activity is smoothly distributed across brain regions (Fig. 1). Alpha power (∼10 Hz) was most strongly observed in the right visual cortex, whereas the left visual cortex showed weaker power at 10 Hz (Fig. 1A), indicating an asymmetric power distribution for the homologous visual cortices in these resting-state data. Compared to alpha activity, beta band power (15–25 Hz) was weaker in the visual cortices and more strongly expressed in bilateral temporal lobes (Fig. 1B).

FIG. 1.

Spatial distribution of spectral power across brain regions. (A) Power spectra at 5 and 10 Hz, and (B) at 15, 20, and 25 Hz. The crosshairs are positioned close to the global maximum power. These positions correspond to the visual and sensorimotor regions of interest whose activities are investigated in this study. Color images available online at www.liebertpub.com/brain

Functional connectivity analysis

Two approaches were used to measure functional connectivity, based on the power envelope and an index of phase synchrony, respectively. The power envelope captures the energy of a signal a specific frequency. The power envelope of a band-limited oscillatory signal is obtained by the squared magnitude of the time-frequency signal of interest following wavelet decomposition. Pair wise correlations between two such envelopes give insight into the time-dependent functional connectivity between those signals at each specific frequency (Bruns, 2004; Hipp et al., 2012). This measure of functional connectivity derives from the slow fluctuations of the envelope of the underlying (fast) carrier frequency. To estimate the power envelope correlation, the Pearson correlation coefficient of the power envelopes of the time-frequency signals, X_f(t) and Y_f(t), at frequency f is given by

where 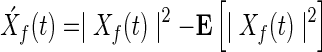, and 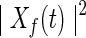denotes the power spectrum of signal x(t) at frequency f.

Since the time-frequency signals are complex-valued, the instantaneous phases can also be used to estimate the phase synchronization at each specific frequency. Phase synchronization is an alternative measure of functional connectivity at the fast frequency itself, rather than its slow fluctuating envelope. The measure of phase synchrony was assessed using the PLV between two complex-valued signals, given by

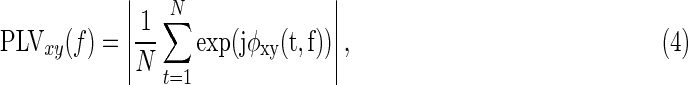where φxy(t,f):=φx(t,f)−φy(t,f) denotes the phase difference between instantaneous phases of φx(t,f) and φy(t,f) at given frequency f (Mormann et al., 2000; Rosenblum et al., 1996).

We considered bilateral functional connectivity measurement between the homologous auditory, visual, and somatosensory cortices using a seed-based approach (Hipp et al., 2012). For each area, the voxel at the geometric center of that area was taken and bilateral connectivity was hence assessed between two single voxels. This follows prior research that has established that functional connectivity is higher between homologous areas than between other randomly chosen pairs of regions separated by the same distance (Biswal et al., 1995; Hipp et al., 2012; Salvador et al., 2005). These six voxels include the centroids of the left and right auditory, visual, and somatosensory cortices. Centroid voxels refer to those voxels that have minimum Euclidean distance with all other voxels within the region of interest. While this may be an imperfect benchmark, it allows us to calibrate our approach against prior work in the field in the absence of a definitive ground truth.

Although source reconstruction largely negates the effect of volume conduction, spurious correlations still arise as source level due to volume spread (Schoffelen and Gross, 2009). The spatial resolution of EEG is limited, and thus the spatial correlation pattern (i.e., functional connectivity) is dominated by an unstructured decay from the reference site. Hence, in addition to envelope correlation and PLVs, we also assessed measures of amplitude and phase coupling that use orthogonalization procedures to confine the analysis to correlations at noninstantaneous phases.

Correcting for source spread in the estimation of envelope coupling

Let us briefly review the orthogonalization of two complex-valued time-frequency signals. Let x(t) and y(t) be the first PCA-projection signals at two distinct voxels, and X(t,f) and Y(t,f) the complex-valued time-frequency spectra of the source signals x(t) and y(t) respectively. As in the work by Hipp and others (2012), the orthogonalization of X(t,f) to Y(t,f) at frequency f is then given by

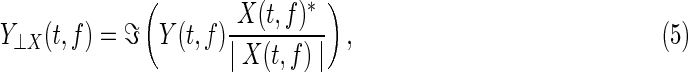where⊥denotes the orthogonality symbol, asterisk * the complex-conjugate, |.| the magnitude, and 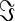the imaginary-part operator. The two-way orthogonalization is simply performed as X⊥Y and Y⊥X. Note that, the orthogonalization of two complex-valued signals X(t,f) and Y(t,f) should be separately performed at each specific frequency. Although the resulting signals X’:=X⊥Y and Y’:=Y⊥X are orthogonal and hence show no correlations, their envelopes are not necessarily linearly independent. Thus, nontrivial envelope correlations may arise between orthogonalized signals at distinct frequencies. As signals are pair wise orthogonalized, the procedure has to be repeated for each combination of a seed voxel and all other voxels. We computed the correlation for both directions of orthogonalized signals and averaged the values for subsequent analyses.

Correcting for source spread in the estimation of phase coupling

Similar to orthogonalization, the PLI was used to correct for source spread in the estimation of phase coupling (Stam et al., 2007). The PLV estimates phase synchrony at an arbitrary phase difference, whereas the PLI is only sensitive to nonzero phase differences. The PLI is defined by

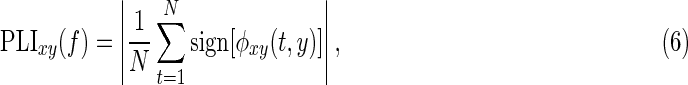where the phase difference, 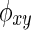, was centered around 0 mod π at each specific frequency (Stam et al., 2007).

Statistical analysis

Hence, functional connectivity between 6 seed voxels and the rest of the brain were assessed using the four approaches described above (i.e., envelope correlation, envelope correlation of orthogonalized signals, PLV, and phase-lag index). A two-stage statistical approach (mixed-effects analysis) was used to test the statistical significance of connectivity patterns. First, estimates of functional connectivity were converted to a z-score individually for each participant. Then, the T-statistic was used to determine the significance of the bilateral functional connectivity measures at the group level.

Z-statistic for single participant data

To determine the significance of functional connectivity in single participant data, the connectivity estimate between homologous voxels was compared against a null distribution. For each of the six voxels of interest (and each frequency), the null distribution was calculated by computing functional connectivity between the seed voxel and 100 randomly chosen voxels constrained to be approximately the same distance away as the homologous region in the opposite hemisphere. This null hence represents the likely distribution of functional connectivity values given the distance between the two sources: rejection of this null implies that the strength of functional connectivity between left-right homologous areas is higher than this background effect and is a pragmatic way to test and compare the sensitivity of these four methods. The mean and standard deviation of the null distribution was then used to define the z-score for each participant, which can be defined for the ith participant at frequency f as

where |Ai(f)| denotes the denotes the envelope correlation and/or phase synchronization measures, |μ_i(f)| the surrogate or null estimate, and σ_i(f) the standard deviation of the constructed surrogate data.

T-statistic across participants

To determine the statistical significance at the group level, the t-statistic was calculated based on the z-scores of each of the 10 participants. The effect in each participant is now considered as a random variable in a second-level analysis in the following way. Let Z(f)=[Z1(f),…,Z10(f)] such that Z(f)∈R^(fx10) be a data array whose entries are the z-scores given in Eq.(7) for each participant. The hypothesis H0: E[Zi(f)]=0 assumes the entries of the z-scores Z(f) are normally distributed [i.e., Zi(f)∼N(0,σzi)]. To examine whether the hypothesis H0 is rejected or not, a one-sample one-sided t-test was performed to compare the z-scores across the 10 participants against zero:

where E[Z(f)] and σz(f) denote the average and standard deviation of the z-scores array Z(f) across participants. The group-level significance values at p<0.05 were then calculated to distinguish between significant and nonsignificant functional connectivity between left and right homologous cortical regions.

Results

We first report bilateral functional connectivity between homologous brain areas using the four measures of functional connectivity. The effect of source spread on amplitude and phase coupling are investigated by comparing them to equivalent measures after orthogonalization of the source data. We then investigate the interrelationship between amplitude and phase coupling by contrasting the spatial connectivity patterns of both measures across all voxels.

Functional connectivity without orthogonalization

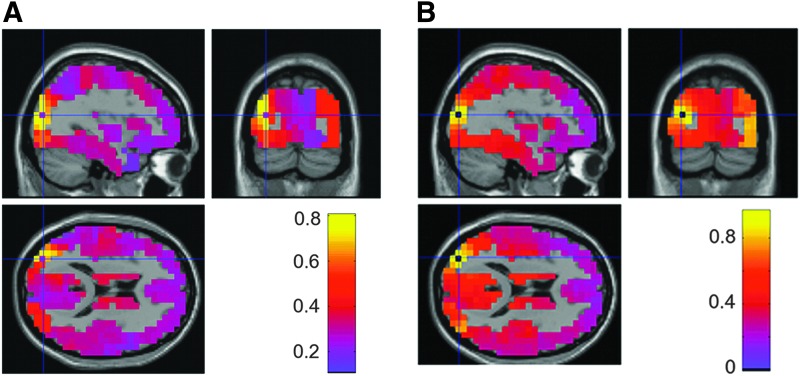
We first study an exemplar effect, focusing on functional connectivity at 10 Hz in a seed-voxel in the left visual cortex. Both the envelope correlation and the PLV showed bilateral connectivity between homologous visual cortices (Fig. 2): both measures showed interdependence between the seed voxel and a number of voxels in the contralateral hemisphere that exceeded a value of 0.55 for the envelope correlation (left panels) and 0.7 for the PLV (right panels). In addition, both measures show a gradual distance-based, isotropic decline in the strength of functional connectivity, spreading outward from the seed voxel. The range of functional connectivity was slightly higher for the PLV (0.2–0.7 for the PLV compared with 0.1–0.6 for envelope correlation), suggesting a higher null distribution for the PLV.

FIG. 2.

Grand-average connectivity patterns between a seed voxel in the left visual cortex and the rest of the brain at 10 Hz. (A) Sagittal, coronal, and horizontal sections of the envelope correlation; (B) Equivalent for the phase locking value (PLV). Color images available online at www.liebertpub.com/brain

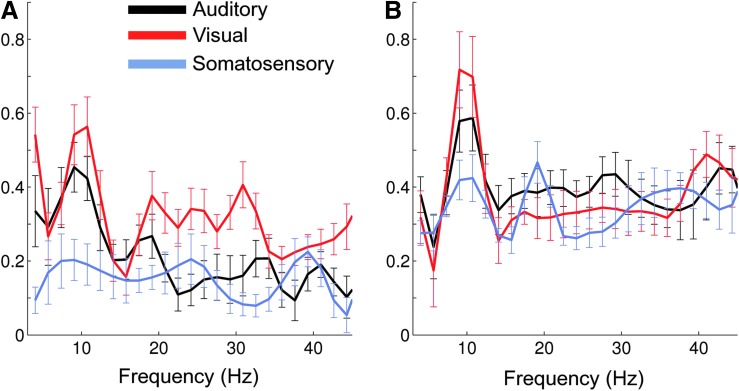
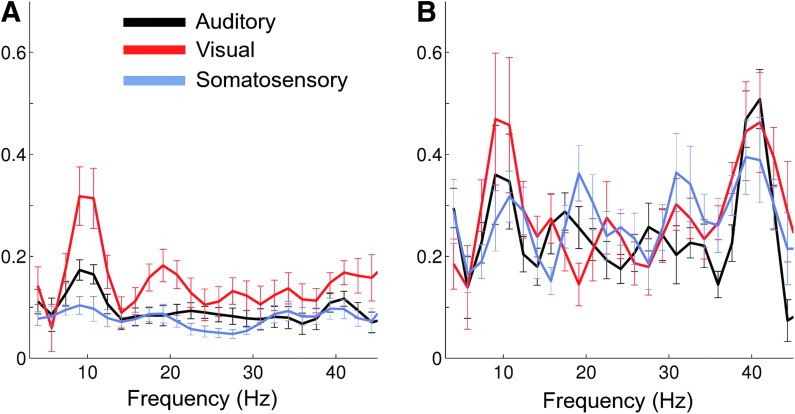
Measuring functional connectivity at one particular frequency provides only a narrow window onto the rich dynamics of neuronal communication. Functional connectivity was therefore assessed across a wide frequency range from the theta to the gamma bands (5–45 Hz). A nontrivial connectivity spectrum was observed for envelope correlations (Fig. 3A) and the PLV (Fig. 3B). Bilateral envelope correlation between visual cortices was pronounced in the alpha (8–12 Hz) and beta (18–30 Hz) bands. Envelope correlations were strongest in the alpha band for homologous auditory cortices and in the gamma range (∼40 Hz) for somatosensory areas. In contrast, strong bilateral PLV for all three homologous regions was primarily confined to the alpha rhythm, apart from a smaller secondary beta peak between the left and right somatosensory cortex. In general, variability was slightly higher for the envelope correlations than for the PLV.

FIG. 3.

Bilateral connectivity between homologous auditory, visual, and somatosensory cortices as a function of frequency at group level. (A) Envelope correlation, (B) PLV. Error bars depict the standard error across subjects. Color images available online at www.liebertpub.com/brain

Functional connectivity following orthogonalization

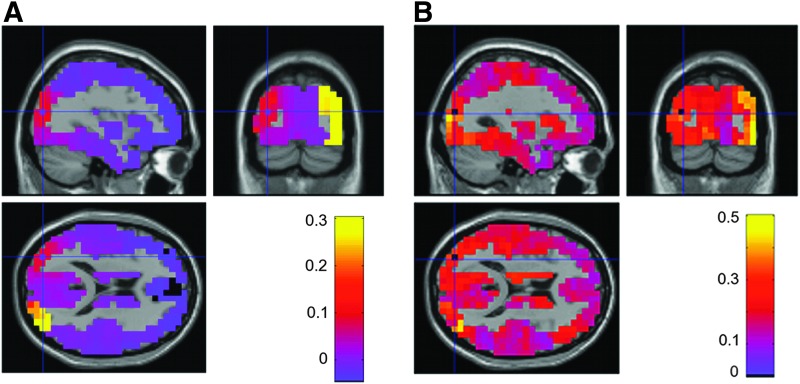
To reduce spurious correlations arising from source spread, amplitude and phase coupling were also examined after correcting for simple linear superposition of the signals. For amplitude coupling orthogonalization of the raw signals was performed before subsequent computation of bilateral envelope correlations; for phase coupling the PLI was employed. As expected, the resulting connectivity patterns show a reduction in spurious correlation. Figure 4 illustrates these orthogonalized connectivity measures between the left visual seed voxel and the rest of the brain at 10 Hz using the envelope correlation of the orthogonalized sources signals (left panels) and PLI (right panels). A tradeoff is observed between the reduction of spurious correlation and a reduction of actual correlation between homologous regions. For example, envelope correlations between bilateral visual areas decreased to a value of 0.30 (Fig. 4A), whereas it was closer to 0.55 (Fig. 2A) for the original envelope correlation (i.e., before orthogonalization). In addition, although the unstructured decay from the seed voxel is strongly reduced from 0.8 (Fig. 2A) to 0.15 (Fig. 4A), local connectivity was still slightly high. However, it is quite possible that this reflects a true underlying correlation between neighboring voxels. Similarly, the PLI also reduced spurious correlation and the left visual seed voxel shows less phase synchrony with its nearby voxels (∼0.35) (Fig. 4B) compared to the PLV (i.e., 0.9) (Fig. 2B). Of note, a small region with enhanced PLI persisted in the homologous right visual cortex.

FIG. 4.

Grand-average connectivity patterns between a seed voxel in the left visual cortex and the rest of the brain at 10 Hz after orthogonalization. (A) Sagittal, coronal, and horizontal sections of the envelope correlation between the orthogonalized signals; (B) Equivalent for the phase lag index (PLI). Color images available online at www.liebertpub.com/brain

Functional connectivity patterns were also investigated across frequencies using the correlation coefficient of the orthogonalized signals and PLI. Similar results to those shown in Figure 3 were observed, namely that bilateral envelope correlations peaked at 10 Hz for the auditory and visual cortices and at 40 Hz for somatosensory cortices and showed a secondary peak in the beta band (18–25 Hz) for homologous visual areas (Fig. 5A). Compared with the envelope correlations of the raw signals (Fig. 3A), correlations for the orthogonalized signals are generally strongly reduced outside the alpha peak. The PLI also showed enhanced bilateral correlation for the auditory, visual, and somatosensory cortices within the alpha (8–13 Hz) and gamma (40 Hz) bands. The peak in the gamma band is relatively heightened in comparison to the PLV (comparing the Figs. 3B and 5B).

FIG. 5.

Bilateral correlations between the homologous auditory, visual, and somatosensory cortices after orthogonalization across frequencies at group level. (A) The envelope correlation between the orthogonalized signals; (B) PLI between the raw signals. Error bars depict the standard error across subjects. Color images available online at www.liebertpub.com/brain

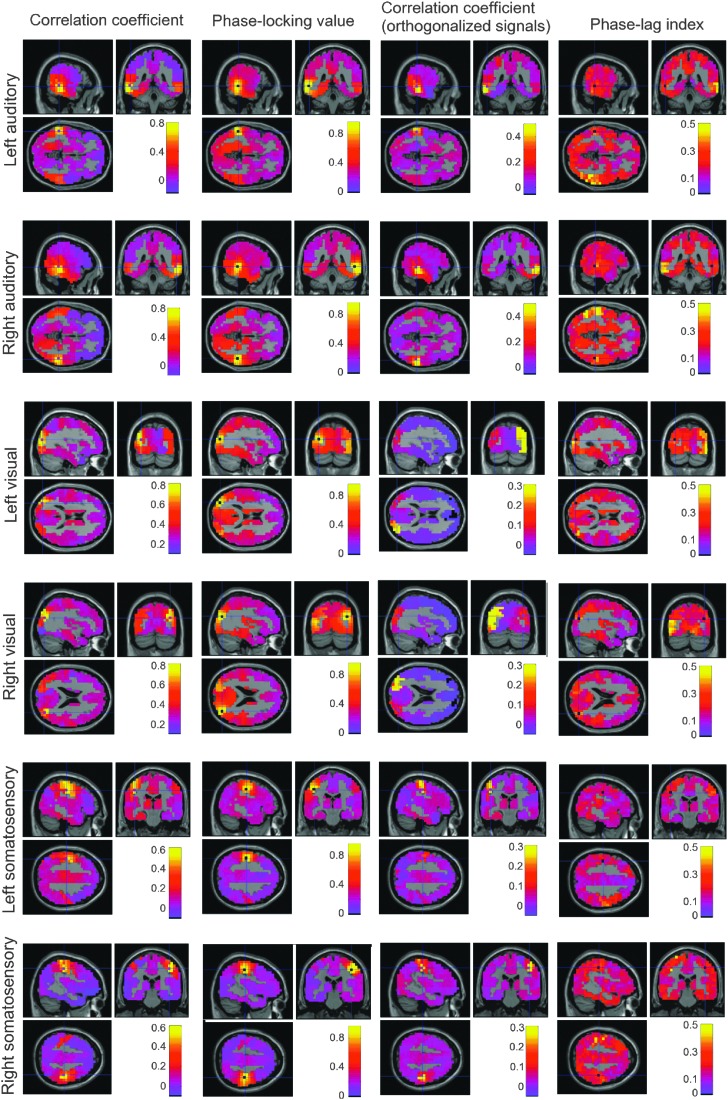
The spatial patterns of functional connectivity identified by the four approaches (envelope correlation, PLV, envelope correlation of orthogonalized signals, and PLI) are shown in Figure 6. As expected, and consistent with Hipp and colleagues (2012), the envelope of the raw signal (first column) is generally stronger than following orthogonalization (third column–see color bars). Both show apparent correlation with voxels immediately surrounding the seed voxel, which decays with increasing distance. Both also show some degree of correlation in the homologous region in the opposite hemisphere. In analogy to the envelope correlation, the PLV is generally stronger than the PLI. However, in contrast to the envelope correlations, the PLI revealed more pronounced connectivity between homologous areas than the PLV for all six seed voxels at 10 Hz. Note, however, that the background “noise floor” for this measure is also higher. While the overall functional connectivity is strongest at 10 Hz, similar patterns were observed at other frequencies.

FIG. 6.

Functional connectivity between each of the 6 seed voxels of interest and the rest of the brain at 10 Hz the four connectivity measures. Left column: sagittal, coronal, and horizontal sections of the envelope correlation; second column: PLV; third column: envelope correlation of orthogonalized signals; right column: PLI. Seed voxels include bilateral superior auditory (rows 1–2), bilateral inferior visual (rows 3–4), and bilateral inferior somatosensory (rows 5–6). Color images available online at www.liebertpub.com/brain

Statistical significance of functional connectivity between homologous regions

The functional connectivity patterns between bilateral voxels in homologous sensory cortices were then compared against a null distribution obtained from randomly selected voxels at the same distance from the seed region. The mean and standard deviation of the null distribution were used to convert the connectivity measures to z-scores (see Methods section). The z-scores facilitate comparison across different connectivity measures and establish statistically significant connectivity in single subjects. Table 1 summarizes the number of participants that showed significant bilateral functional connectivity (z-score >1.65, p<0.05) using the envelope correlations in both the raw and the orthogonalized signals, PLV, and PLI across a frequency range of 5–45 Hz. For the visual cortices, 8–9 out of 10 participants showed significant bilateral correlation in the alpha band (8.5–11 Hz), depending on which connectivity measure was employed (Table 1). In comparison, four to five participants showed significant connectivity for the auditory cortex in the high beta band (27–32 Hz), and three to four participants for the somatosensory bilateral correlation in gamma band (38.5–41 Hz).

Table 1.

z-Scores and Number of Participants Showing Significant Bilateral Functional Connectivity

	Frequency band (Hz)			No. of significant participants, (p<0.05)
	Visual	Auditory	Somatosensory	Visual	Auditory	Somatosensory
Envelope correlation (raw signals)	8.5–11	27–31	38.5–41	8	5	4
Envelope correlation (orthogonalized signals	8.5–11	27–32	39–40	8	4	3
Phase-locking value	9–11	28–30	38–39	9	5	4
Phase-lag index	10–11	28–30	38–39	8	4	4

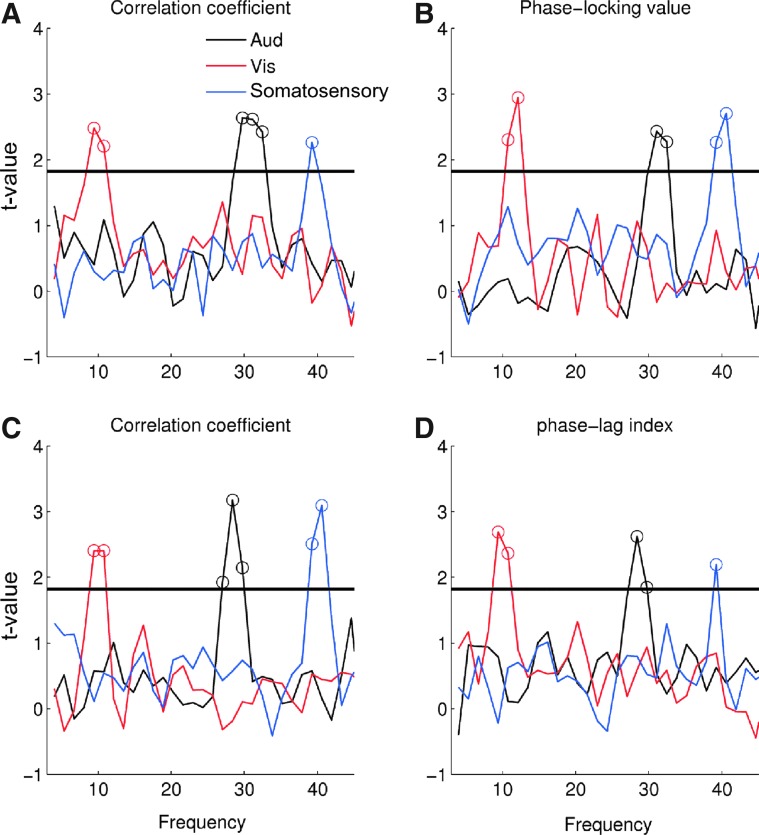
To investigate significant connectivity at the group level, we performed a one-sample t-tests comparing the z-scores against zero. This analysis confirms significant bilateral connectivity in three different frequency ranges at the group level: significant bilateral connectivity between visual areas at 8–10 Hz, significant connectivity between auditory cortices at 28–32 Hz, and significant connectivity at 39–40 Hz between somatosensory cortices (Fig. 7). These patterns of significant connectivity are surprisingly robust across the four different measures of functional connectivity, showing significant connectivity in the same frequency ranges for all four measures.

FIG. 7.

Statistically significant connectivity at group level for the four measures of functional connectivity. Each panels shows the t-values of one of the connectivity measures between homologous auditory (black line), visual (red line), and somatosensory cortices (blue line) across frequencies (A: Envelope correlation between the raw signals; C: Envelope correlation between orthogonalized signals; B: PLV, D: PLI). The dotted line represents the 95% confidence interval [t(10)=1.85 p<0.05]. Color images available online at www.liebertpub.com/brain

Relationship between intrinsic coupling modes

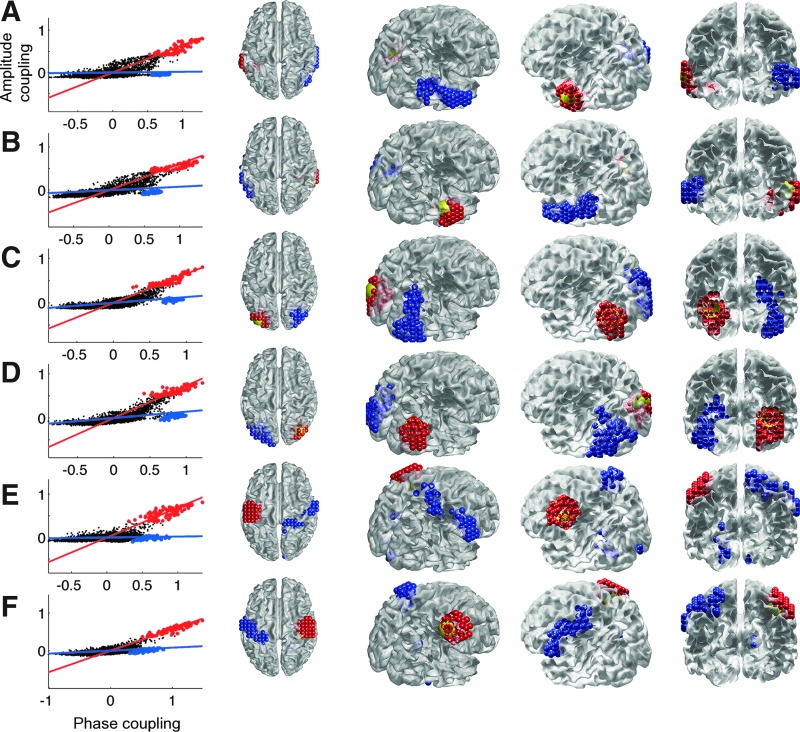
Finally, we directly contrast amplitude and phase coupling between all voxels to investigate the interrelationship of ICMs at 10 Hz. When plotting envelope correlations against the PLV (Fig. 8, left column), we observe two clusters of voxels: the first cluster shows both high amplitude and phase coupling, whereas the second cluster shows disproportionally higher phase coupling. FastICA was used to separate these two clusters. Visualization of the highest 2% weights of each IC shows that they exhibit very distinct spatial patterns: whereas the first IC includes voxels surrounding the seed voxel in the ipsilateral hemisphere (Fig. 8, red dots), the second IC captures voxels in the homologous region of the contralateral hemisphere (blue dots). Note that the blue voxels in Figure 8 are not all located in brain regions exactly contralateral to the seed voxel is, but also in nearby areas. For instance, blue voxels contralateral to the left auditory seed voxel (panel A) are located in the left parahippocampal and fusiform area and the left superior, mid, and inferior temporal gyri. Differences between the connectivity values depicted in Figure 8 and the t-values in Figure 7 may therefore be due to either the properties of the null distribution used to obtain the z-scores or the variability between subjects involved in the calculation of the t-values.

FIG. 8.

Contrast between intrinsic coupling modes showing distinct relationships between amplitude and phase coupling. Left column shows the scatter plots of all 4,351 voxels and the first (red line) and second (blue line) IC. Before ICA decomposition, the envelope correlations were mean centered. PLV values were first log-transformed before mean centering to obtain better convergence of the ICA. FastICA algorithm was used to jointly decompose the amplitude and phase coupling measures into two ICs. The voxels showing the top 2% weighting on the first and second IC are plotted as red and blue dots respectively. The spatial locations of these voxels are shown in the right panels using the same color-coding. The yellow ball shows the seed voxels. The decomposition is performed for all six seed regions: (A) left auditory, (B) right auditory, (C) left visual, (D) right visual, (E) left somatosensory, and (F) right somatosensory cortices. Color images available online at www.liebertpub.com/brain

A similar separation into ipsilateral and contralateral voxels was observed for all six seed regions showing distinct relationships between ICMs, robust across seed regions. Some show a very intriguing spatial spread: for example, the second cluster of the motor seed follows a distinct course along the entire bilateral primary motor cortex. For all seed voxels, the first IC shows an identity (1:1) relationship between amplitude and phase coupling with large clusters of voxels contiguous to the seed regions. This pattern of high amplitude and phase coupling is consistent with the effect of source spread. The second IC reveals a contralateral cluster located around the homologous regions with higher phase than amplitude coupling. This pattern of functional connectivity may reflect genuine neuronal interactions.

Discussion

We investigated the relationship between ICMs and their relative vulnerability to volume conduction. Source signals were estimated from resting-state EEG using LORETA, and functional connectivity between six seed locations and all other cortical voxels were estimated using four different connectivity measures. We observed high envelope correlation and PLV with large clusters of voxels contiguous to the seed regions. Local connectivity was strongly reduced for envelope correlations after orthogonalizing and for phase relations after looking at phase lags aside from zero lag (i.e., the PLI)—two methods known to reduce the effect of volume conduction by excluding near instantaneous effects. In addition, we observed elevated bilateral connectivity between homologous auditory, visual, and somatosensory cortices across frequencies. When statistically comparing functional connectivity between homologous sensory areas to other voxels at the same physical distance, we found that the frequency of significant coupling differed between sensory areas: 10 Hz for visual, 30 Hz for auditory, and 40 Hz for sensorimotor cortices. Finally, by contrasting envelope correlations and PLVs, we observe two distinct clusters of voxels showing a different relationship between amplitude and phase coupling. Voxels surrounding the seed location showed an identity (1:1) relationship between amplitude and phase coupling, which is likely caused by field spread. In contrast, a cluster of voxels in the contralateral homologous regions showed higher phase than amplitude coupling, which we interpret as reflecting true neuronal interactions.

This study shows significant functional coupling between homologous sensory areas in both hemispheres in source-reconstructed resting-state EEG. This is consistent with previous findings obtained using other data modalities and hence confirms the validity of functional connectivity analysis in source-reconstructed EEG. A previous study on source-reconstructed MEG also showed significant bilateral functional connectivity between homologous areas using the envelope correlation (Brookes et al., 2011; Hipp et al., 2012). Likewise, functional connectivity analysis of resting-state fMRI has consistently shown robust bilateral coupling between homologous motor areas (Biswal et al., 1995), or homologous regions in general (Lord et al., 2012; Salvador et al., 2005). Indeed, the finding of bilateral motor correlations (Biswal et al., 1995) in fMRI is perhaps the key finding that opened the study of functional connectivity in fMRI. Increased bilateral functional connectivity most likely reflects strong anatomical connections between homologous areas via the corpus callosum (De Lacoste et al., 1985; Klostermann et al., 2007). Empirical and computational studies have revealed a close link between structural and functional connectivity in general (Bullmore and Sporns, 2009; Honey et al., 2007, 2009; Sporns et al., 2002). Previous studies have mostly investigated connectivity analysis in source reconstructed MEG activity (Brookes et al., 2011; Gross et al., 2001; Hillebrand et al., 2012; Hipp et al., 2012; Mantini et al., 2007; Schoffelen and Gross, 2009), whereas this study shows the feasibility of EEG for the assessment of resting-state functional connectivity.

We observed increased bilateral amplitude and phase coupling for a broad frequency range, which was most pronounced around 10 Hz, although this varied between seed regions. Similarly, envelope correlation of resting-state MEG revealed a broad range of carrier frequencies (8–30 Hz), with slight variations between cortical regions (Brookes et al., 2011; Hipp et al., 2012). These findings suggest that brain networks do not generally display pure rhythms within distinct frequency bands—mostly generated in restricted neuronal circuits—but a coalescence of rhythms (Mantini et al., 2007; Mehrkanoon et al., 2014). When comparing to connectivity with other voxels at the same physical distance, we found that bilateral coupling was significantly higher at specific frequencies, which was dependent on the cortical region. Hillebrand and colleagues (2012) also found frequency band-dependent patterns of functional connectivity across the brain although the specific relationship between brain regions and frequency differed: they also found alpha-band coupling in the visual cortex, but found beta-band coupling in the sensorimotor cortex, whereas we found significant coupling at ∼40 Hz. Further studies are therefore needed to delineate the spatial differentiation in coupling frequency of ICMs.

We quantified amplitude and phase coupling in the same dataset and used the same spectral decomposition allowing direct comparison between both ICMs. By and large we find the same connectivity patterns for amplitude and phase coupling: both reveal a monotonic drop off to more distant sites and enhanced connectivity between homologous sensory areas. While also comprising true correlations, such patterns are likely to reflect spurious correlations arising from volume conduction that persists even following source reconstruction (Gross et al., 2001; Hillebrand et al., 2012; Hipp et al., 2012; Nolte et al., 2004; Schoffelen and Gross, 2009). Indeed, when using measures that confine the analysis to noninstantaneous correlations, that is, envelope correlations after orthogonalizing the band-limited signals (Hipp et al., 2012) and the PLI (Stam et al., 2007), connectivity with nearby voxels is strongly reduced while long-range connectivity is relatively preserved. However, the absolute connectivity levels did vary between the four connectivity measures. Interestingly, when normalizing bilateral connectivity to connectivity with other voxels at the same physical distance, all four measures revealed almost identical spectral profiles (Fig. 7). However, it should also be recalled that some local correlations may indeed be close to zero lagged—these orthogonalization approaches may thus reduce true effects (i.e., cause type II error).

When contrasting envelope correlations directly to the PLVs, two distinct clusters of voxels were observed (Fig. 8). The first cluster surrounds the seed region, showing a near identity relationship between envelope correlation and PLV. These findings suggest that field spread results in a proportional increase in amplitude and phase coupling. The second cluster was located in the contralateral hemisphere and showed higher phase than amplitude coupling. It is not clear how a simple physical effect (such as field spread) could preserve phase relationships over long distance while destroying amplitude effects. In contrast, a wealth of computational models exhibit strong phase locking among neuronal oscillations (Breakspear et al., 2004). We therefore assume this connectivity pattern reflects true neuronal interactions.

These findings add to an increasing body of literature suggesting that neuronal interactions result in both in phase and amplitude coupling (Bayraktaroglu et al., 2013; Chawla et al., 1999, 2000; Daffertshofer and van Wijk, 2011; Mehrkanoon et al., 2014). On the other hand, amplitude and phase coupling are considered to have different causes and putative functions (Engel et al., 2013), and to operate at different time scales (Siegel et al., 2012). As such, we may have found similar patterns of amplitude and phase coupling because we collapse fluctuations in both ICMs across a 12-min time interval. When looking at shorter time intervals we may hence observe deviations between both ICMs. Similar pattern has been observed between structural and functional connectivity, where functional connectivity from fMRI deviates from structural connectivity on short time scales but mirrors the anatomical connectivity pattern when assessed over longer time intervals (Honey et al., 2007).

Several clinical and ERP source imaging studies have shown that LAURA and LORETA yield very similar and comparably satisfactory results. It is hence almost arbitrary which one should be picked, however, a comprehensive and systematic comparison is still lacking and highly desired. A recent systematic study (Birot et al., 2014), however, compared the effect of different headmodels (boundary-element models, finite-element models, and a locally spherical model with anatomical constraints) for LORETA as implemented in the Cartool software and found no difference in the accuracy with which the sources of interictal epileptic discharges could be identified. We can hence conclude that the head-model of LORETA used in this study can be trusted to identify the source activity. On the other hand, theoretical studies have analytically shown that LORETA solution gives satisfactory results compared with other nonparametric inverse solution methods (Greenblatt et al., 2005; Grech et al., 2008). Direct comparisons of LORETA source estimation with intracranial recordings and electrocortical stimulation (Fuchs et al., 1999; Lantz et al., 1996; Michel et al., 1999; Zumsteg et al., 2006), fMRI (Groening et al., 2009; Schulz et al., 2008; Vulliemoz et al., 2009), and with postsurgical outcome (Michel et al., 2004; Sperli et al., 2006; Michel et al., 2012) show that LORETA can reliably identify intracranial sources. Therefore, functional connectivity patterns can be estimated by different source reconstruction approaches by which similar results will be approached.

Likewise, 61 EEG channels is on the lower end of what is recommended for source reconstruction and undersampling the scalp surface may lead to increased source spread. Several studies have investigated the effect of number of EEG electrodes on the accuracy of source reconstruction. These studies showed that close to optimal source localization was achieved using 68 EEG electrodes (Michel et al., 2004), and that increasing the number of EEG electrodes from 63 to 128 electrodes only slightly improved the accuracy of epileptic source localization (Lantz et al., 2003). Britz and colleagues used similar approaches of single-trial based source imaging and identified the same intracranial generators for the perceptual reversals of ambiguous figures using 204 electrodes (Britz et al., 2009) and during binocular rivalry using 61 electrodes (Britz et al., 2011). Both studies reliably identified right inferior parietal cortex as involved in the generation of perceptual reversals with different numbers of electrodes. Therefore, in this study, additional channels may have reduced source spread and improved the signal-to-noise ratio, but the findings would likely be qualitatively the same.

We assessed methods that attempt to minimize the effect of volume conduction by confining the analysis to noninstantaneous connectivity, that is, envelope correlations of orthogonalized signals (Hipp et al., 2012) and the PLI (Stam et al., 2007). These methods indeed strongly reduced spurious connectivity due to source spread; however, genuine connectivity between homologous sensory areas was also reduced. The reduction in bilateral connectivity is likely due to in-phase synchronization, which is a common mode of neuronal interaction (Gollo et al., 2014; Singer, 1999; Varela et al., 2001) that is suppressed by these methods. The joint decomposition of amplitude and phase coupling presented in this study may provide an alternative approach to distinguish genuine neuronal interactions from spurious connectivity patterns resulting from source spread, which does not exclude genuine in-phase synchronization. An alternative approach to bivariate orthogonalization, as used in this study and proposed by Hipp and colleagues (2012), is the use of a robust multivariate approach with a property of independency to additive signals. In the current approach the orthogonalization approach has to be applied to every signal pair and is hence computationally intensive. PCA is a multivariate approach that decomposes the correlation matrix into orthogonal modes. In a previous study we used PCA to decompose time resolved connectivity matrix into the orthogonal subspace of resting-state connectivity (Mehrkanoon et al., 2014). PCA may also be applied to power envelopes to obtain a multivariate extension of the method proposed by (Hipp et al., 2012). Hence, previous studies have mostly investigated connectivity analysis in source-reconstructed MEG activity (Brookes et al., 2011; Gross et al., 2001; Hillebrand et al., 2012; Hipp et al., 2012; Mantini et al., 2007; Schoffelen and Gross, 2009), whereas this study shows the feasibility of EEG for the assessment of resting-state functional connectivity.

Conclusion

The current findings demonstrate the feasibility of connectivity analysis in source-reconstructed resting-state EEG: we observed significant bilateral connectivity between homologous sensory areas consistent with previous MEG and fMRI connectivity and structural network architecture. We investigated the relationship between two ICMs, amplitude, and phase coupling, which reveal disparate relationships for connectivity caused by field spread or for true neuronal interactions. These results may motivate new ways of correcting for volume conduction in EEG connectivity analysis and speak to the inherent relationship between amplitude and phase coupling in coordinating large-scale brain dynamics.

Acknowledgments

This research was supported by the ARC Thinking Systems grant (TS0669860); the National Health and Medical Research Council; BrainNRG collaborative award (JSMF22002082), and the Netherlands Organization for Scientific Research (NWO 45110-030). The Cartool software (brainmapping.unige.ch/cartool) has been programmed by Denis Brunet, from the Functional Brain Mapping Laboratory, Geneva, Switzerland, and is supported by the Center for Biomedical Imaging (CIBM) of Geneva and Lausanne.

Author Disclosure Statement

No competing financial interests exist.