Host-to-host variation of ecological interactions in polymicrobial infections

Abstract

Host-to-host variability with respect to interactions between microorganisms and multicellular hosts are commonly observed in infection and in homeostasis. However, the majority of mechanistic models used to analyze host-microorganism relationships, as well as most of the ecological theories proposed to explain coevolution of hosts and microbes, are based on averages across a host population. By assuming that observed variations are random and independent, these models overlook the role of differences between hosts. Here, we analyze mechanisms underlying host-to-host variations of bacterial infection kinetics, using the well characterized experimental infection model of polymicrobial otitis media (OM) in chinchillas, in combination with population dynamic models and a Maximum Entropy (MaxEnt) based inference scheme. We find that the nature of the interactions between bacterial species critically regulates host-to-host variations in these interactions. Surprisingly, seemingly unrelated phenomena, such as the efficiency of individual bacterial species in utilizing nutrients for growth, and the microbe-specific host immune response, can become interdependent in a host population. The latter finding suggests a potential mechanism that could lead to selection of specific strains of bacterial species during the coevolution of the host immune response and the bacterial species.

Introduction

Outcomes of a pathogen exposure often vary from individual to individual in a population. Even in well controlled experiments, it is common to see wide variation in pathogen titers and in biomarkers of host immune response, between animals subject to identical pathogen loads(1–3). Variations in the relative abundances of members of the microbial community residing in homeostasis with the host immune system are also observed between individuals (4).

However, despite the ubiquity of such host-to-host variations of the host-microorganism relationship, our mechanistic understanding of such relationships or ecology of host-microorganisms(5, 6) are based primarily on average values obtained from experiments done on host populations. The variations around the averages are typically assumed to arise from independent inter-host variations of phenomena that affect the host-microorganism relationship, such as the host immune response or availability of nutrients for the microorganisms. Variations between hosts are often represented merely as error bars in data summaries(7, 8). This view overlooks the fact that the differences between hosts themselves may provide valuable clues regarding perturbations of the underlying mechanistic framework in a natural setting, and may relate directly to evolutionary selection of a particular host-pathogen or host-microbiota relationship based on sustaining the observed diversity in a population(9).

Here, we seek mechanistic insights into host-to-host variations of the host-microorganism relationship by analyzing the population kinetics of multiple bacterial species in the well characterized model of polymicrobial otitis media (OM) in adult chinchillas (Chinchilla lanigera). OM is a common childhood polymicrobial infection of the middle ear involving one or more of three predominant bacterial species that are normally carried within the microbiota in the upper respiratory tract (URT)(10, 11): Nontypeable Haemophilus influenzae (NTHI), Streptococcus pneumoniae (Sp), and Moraxella catarrhalis (Mcat). OM provides an excellent model system to dissect host-microbiota relationships because of the relatively small number of species in the relevant microbial community, and also because it offers practical advantages such as culturability of the three main bacterial species(11). While chinchillas are not a natural host for the bacteria or viruses that cause human OM, they can be infected with and colonized by all three of the predominant bacterial OM pathogens(11).

Using an in silico approach based on Maximum Entropy (MaxEnt) and population dynamics combined with samples recovered from the chinchilla middle ear, we quantified ecological interactions that regulate the kinetics of bacterial infection and the host immune response in individual hosts. We show that the nature of interspecies interactions (e.g., competition, cooperation or neutral) between the bacterial species NTHI and Sp, which is not directly related to the immune response, critically regulates the host-to-host variations of the ecological interactions. More importantly, seemingly independent ecological interactions, such as the ability of the bacterial species to utilize resources and the rate at which the host immune response eliminates specific bacterial species, become interdependent in hosts. This suggests the utility of this method to characterize evolutionary selection of interspecies interactions in microbial communities through host-bacteria interactions.

Variations of kinetics of polymicrobial infection

Animal-to-animal variations of kinetics of bacterial species are clearly observed in experiments studying OM in rodents such as rats(1) or chinchillas(2). For instance, in the experiments reported by Weimer et al.(2), the population of Sp showed an almost bimodal behavior three days after inoculation with mixed NTHI and Sp strains; the Sp population fell below the detectable limit in a few animals, but varied between 10⁴ to 10⁶ CFUs in other animals (Fig. 1). The population kinetics of NTHI, although less dramatic, showed animal-to-animal differences up to three orders of magnitude in animals challenged with single and mixed species inoculations (Fig.1). Small (<10%) differences in the initial dose of bacterial due to variations in preparations could be a minor contributing source to these variations, however, the majority of these variations are expected to arise from the animal-to-animal variations as these chinchilas were outbred animals. The bacterial species, NTHI and Sp, have been observed to interact with each other and with the host and these interactions affect the growth of the bacterial species. For example, in in vitro cultures, certain strains of Sp eliminate NTHI by secreting toxic hydrogen peroxide generated during aerobic metabolism(12). Alternatively, NTHI can trigger mobilization of neutrophils in the epithelial layer that eliminate Sp but not NTHI via complement-mediated opsonization(13, 14). In addition, the secretion of quorum sensing molecules by these bacterial species has been found to affect the growth of multiple bacterial species participating in the infection(15). The bacterial species also depend on the host for extracting essential nutrients such as metals for their growth. For example, the Gram-negative NTHI and Gram-positive Sp require iron extracted from the serum generated by the host during inflammation(16, 17). Therefore, it is plausible that variations of these factors across hosts would lead to differences in infection kinetics between hosts. Here, we quantify ecological interactions in the system and model the mechanisms that lead to the infection kinetics observed in the experiments reported by Weimer et al. (2). We have referred the infection experiments done in the chinchilla middle ears as in vivo experiments in the text, and in vitro experiments refer to the culture experiments.

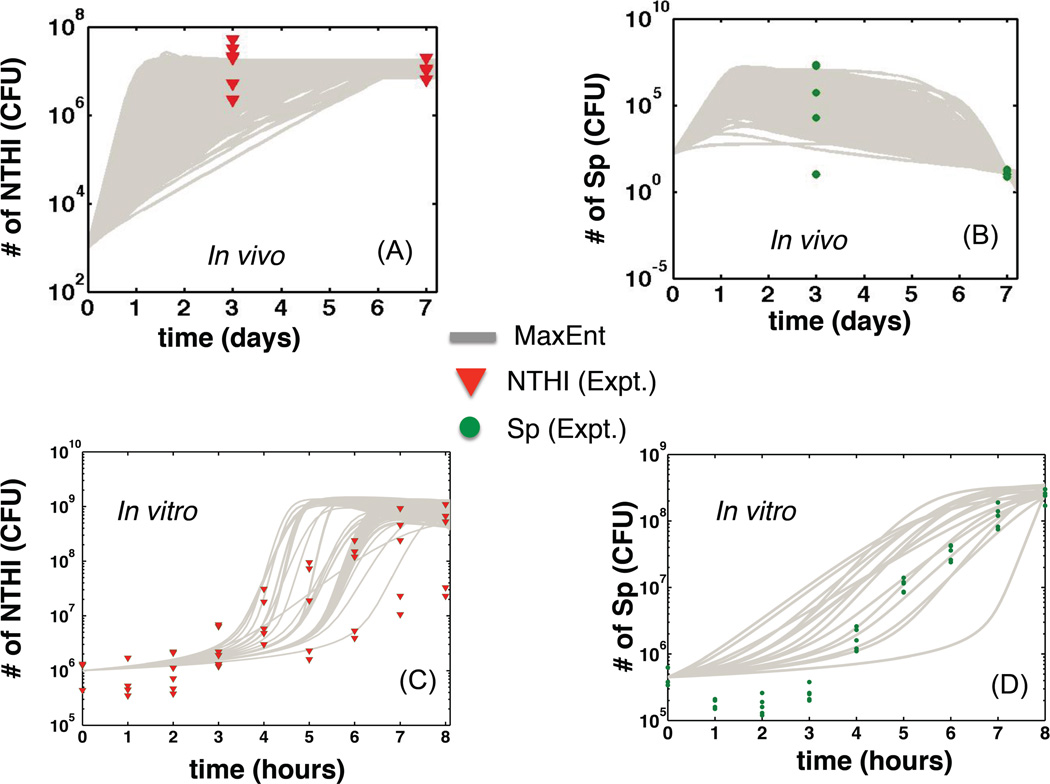
Fig. 1. Variations of bacterial kinetics between hosts and culture medium trials.

(A) The bacterial kinetics of “in silico” animals are shown with grey lines. An “in silico” animal is represented by a particular set of parameters in Table II that was drawn from the inferred MaxEnt distribution for the M₊₋ model. The “in silico” animal was co-inoculated or was assigned with initial numbers of NTHI and Sp, and then Eqn(2) was solved with that initial condition to obtain the population kinetics of NTHI in the middle ear of the “in silico” animal. The in vivo experimental data (each red triangle corresponds to an individual chinchilla middle ear) were taken from Ref.(2) where the animals received inocula of ~10³ CFU and ~150 CFU of NTHI and Sp, respectively. (B) Kinetics of Sp for the same set up as in (A) is shown using the same visualization scheme. The experimental data (in vivo) are shown using solid green circles. (C) Kinetics of NTHI (grey lines) generated by solving Eqn (S1) in individual trials in “in silico” culture experiments. Each “in silico” culture experiment is represented by a set of parameters in Table II, that was drawn from the inferred MaxEnt distribution for the M₊₀ model. The in vitro experimental data for each trial for the co-culture experiments with NTHI and Sp are shown in red triangles. (D) Kinetics of Sp for the same set up as in (C). The in vitro experimental data are shown in solid green circles.

MaxEnt based method to quantify variations of ecological niches

A. Population dynamic model

We constructed kinetic models based on ordinary differential equation (ODE) to describe the time evolution of populations of NTHI and Sp bacterial cells (Fig. S1). The equations are based on Lotka-Volterra (LV) type models(7), which describe the growth of two or more bacterial species interacting with each other to access available resources. These models have been successfully applied to characterize kinetics of bacterial populations in chemostat experiments(7, 18).

We modified the LV models to include the host immune responses during the acute infection phase, which is primarily regulated by innate immunity(11). In our models, the bacterial species consume nutrients from the local environment and replicate. NTHI and Sp can compete for a common nutrient (e.g., iron) for their growth. Additionally, each species can indirectly help in the growth of the other species by generating more inflammation because the serum generated during inflammation contains iron-containing chemical compound heme which provides the essential metal iron for growth of the bacterial species(16, 17). In addition, NTHI and Sp can affect each other’s growth by secreting small molecules, e.g., toxins or quorum sensing molecules. Therefore, NTHI and Sp can potentially oppose, help, or remain uninvolved in each other’s growth depending on the nature of inflammation or the concentration of secreted molecules in the microenvironment. We considered all 9 possibilities (see Table I) for interspecies interactions affecting the growth rates of NTHI and Sp.

Table I.

List of the models considered.

Effect on growth	M++	M+−	M+0	M−+	M−−	M−0	M0+	M0−	M00
NTHI on Sp	+	+	+	−	−	−	0	0	0
Sp on NTHI	+	−	0	+	−	0	+	−	0

+ = counteracts, − = helps, 0 = stays neutral

In addition, both species induce innate immune responses (release of antimicrobial proteins(19) or influx of neutrophils in epithelial layer(14)) in the middle ear. In our coarse-grained phenomenological models, we do not distinguish between antimicrobial proteins and neutrophils, and immune response is represented by a single variable, I, that eliminates NTHI and Sp with different rates. The dynamics of the abundances of NTHI and Sp in the presence of the host immune response in the middle ear of a particular animal (indexed by a) can be described by a pair of coupled ODEs:

$$\mathrm{d}{{\mathrm{N}}_{1,2}}^{(\mathrm{a})}/\mathrm{d}\mathrm{t}={{\mathrm{f}}_{1,2}}^{(\mathrm{a})}({{\mathrm{N}}_1}^{(\mathrm{a})},{{\mathrm{N}}_2}^{(\mathrm{a})})-{{\mathrm{g}}_{1,2}}^{(\mathrm{a})}({{\mathrm{N}}_1}^{(\mathrm{a})},{{\mathrm{N}}_2}^{(\mathrm{a})})$$ (1)

where, N₁^(a) and N₂^(a) denote the population sizes of NTHI and Sp, respectively. f₁^(a)(N₁^(a),N₂^(a)) and f₂^(a)(N₁^(a),N₂^(a)) describe the growth rate of NTHI and Sp, respectively, regulated by available resources and inter/intra species interactions. Both NTHI and Sp interact with the immune response elicited by the host that eliminates the bacteria, and g₁^(a)(N₁^(a),N₂^(a)) and g₂^(a)(N₁^(a),N₂^(a)) describe the rate of elimination of NTHI and Sp, respectively, by the immune response. To keep the notation simple, we will drop the superscript in the rest of the equations where all the variables and the parameters describe the kinetics in an individual animal or a trial in culture experiments. Following the LV model for interspecies interaction we use(7), f₁(N₁, N₂)=r₁ N₁(K₁–α₁₁N₁–α₁₂N₂) and f₂(N₁, N₂)=r₂N₂ (K₂–α₂₂N₂ – α₂₁N₁). The carrying capacities, {K₁, K₂}, determine the maximum values of the population that can be sustained by the available resources(7). {α₁₁, α₂₂} denotes the competition for resources between bacteria of the same species and {α₁₂, α₂₁} parametrizes interspecies interaction between NTHI and Sp. We have used {α₁₁, α₂₂> 0}, implying that the bacteria in the same species always compete with each other for resources. We considered positive, negative, and zero values for {α₁₂, α₂₁} to describe competing, cooperating, and neutral nature of interspecies interactions respectively. The interspecies interactions are generally not reciprocal, i.e., α_ij ≠ α_ji.

We considered nine different models, each denoting a specific type of interspecies interaction (see Table I for the list). For example, M₊₋ describes the model where the interspecies interactions are given by α₁₂ > 0 and α₂₁ < 0. The immune responses (I) are described by monotonically increasing functions of N₁ and N₂ representing concentrations of antimicrobial proteins or neutrophils attracted to the infection site, i.e., g₁(N₁,N₂)=k_d1N₁I, and, g₂(N₁,N₂)=k_d2N₂I. The immune response, I, is generated due to the immune response I₁ and I₂ induced by N₁ and N₂ respectively, and is assumed to be additive, i.e., I=I₁+I₂. We assume the immune response to depend on N₁ and N₂ as, I₁=k₁N₁/(K_M1+N₁) and I₂=k₂N₂/(K_M2+N₂). We have also studied the effect of immune responses as different functions of N₁ and N₂ which produced qualitatively similar results as the forms we have used here (Fig. S4–S5). We write g₁ (N₁,N₂) and g₂(N₁,N₂) as, g₁ (N₁,N₂)=k_d11(N₁)²/(K_M1+N₁) + k_d12N₁N₂/(K_M2+N₂), and, g₂(N₁,N₂)=k_d21N₁N₂/(K_M1+N₁) + k_d22 (N₂)²/(K_M2+N₂), where, k_dij=k_di k_j (i,j ∈ {1,2}). Thus the kinetics is described by the following ODEs,

$$\frac{d{N}_1}{dt}=r_1{N}_1(K_1-{\alpha }_{11}{N}_1-{\alpha }_{12}{N}_2)-\frac{k_{d11}{N}_1^2}{K_{M1}+N_1}-\frac{k_{d12}{N}_1{N}_2}{K_{M2}+N_2}\frac{d{N}_2}{dt}=r_2{N}_2(K_2-{\alpha }_{22}{N}_2-{\alpha }_{21}{N}_1)-\frac{k_{d22}{N}_2^2}{K_{M2}+N_2}-\frac{k_{d21}{N}_1{N}_2}{K_{M1}+N_1}$$ (2)

Depending on the values of the parameters, the kinetics described by the ODEs in Eq. (2) produce multiple fixed points. For example, N₁ is present but N₂ is absent, N₁ is absent but N₂ is present, or both N₁ and N₂ are present. With appropriate choices of parameter values, these fixed points can become stable fixed points that the system will eventually reach if the initial values are appropriately chosen to be within the domain of attraction (details in the supplementary material). The values of N₁ and N₂ at the stable fixed points as well as the kinetics of N₁ and N₂ leading to those fixed points vary as the parameters in the ODEs are changed. Since the parameters in the ODEs (representing the nature of resource utilization, inter- and intra-species interaction, host immune responses and their effect on the bacterial population) describe the role of the environment and interspecies interactions on the size of the bacteria population, we call these parameters ({e_i}) ‘ecological interactions’ (see Tables II and S1 for further details). We hypothesize that these ecological interactions vary from animal to animal, resulting in different populations of bacterial species infecting/colonizing middle ears in individual animals. Here, we address the following questions: (1) What can we deduce about any relationship between ecological interactions in individual animals from the experimentally observed host-to-host variations in bacterial populations? (2) Does the extent of variation of the other ecological interactions depend on the interspecies interactions between the bacterial species? (3) Is it possible that seemingly unrelated ecological interactions are interdependent, and does this occur in response to selective pressures on specific bacterial strains in a host population?

Table II.

Summary of the physical relevance and the range of variation of the parameters used in in silico models.

Single Species Parameters {e(S)i}	Range of variation	Physical significance
γ1, γ2	From 2–10 day−1 for in vivo experiments and from 1–10 hr−1 for in vitro culture experiments.	Growth rates of N1 and N2 respectively (Eqs. S1 and S2).
α11, α22	From 10−10 –10−7 CFU−1day−1 for in vivo experiments and from 10−9 -10−11 CFU−1hr−1 for in vitro culture experiments.	Strength of intraspecies interactions describing competition for resources.
kd11	From 0–200 day−1 for in vivo experiments.	The rate at which the immune response elicited by N1 eliminates N1.
kd22	From 0–200 day−1 for in vivo experiments.	The rate at which the immune response elicited by N2 eliminates N2.
KM1	From 106 –1011 CFU for in vivo experiments.	Michaelis constant (Eq. 2) for the immune response elicited by N1. When N1 >> KM1 the response saturates.
KM2	From 106 –1011 CFU for in vivo experiments.	Michaelis constant (Eq. 2) for the immune response elicited by N2. When N2 >> KM2 the response saturates.
Mixed Species parameters {e(M)i}
α12	From 10−9 –10−6 CFU−1day−1 for in vivo experiments and from 10−7 -10−11 CFU−1hr−1 for in vitro culture experiments.	Strength of the interspecies interaction induced by N2 on the N1 growth rate.
α21	From 10−9 –10−6 CFU−1day−1 for in vivo experiments and from 10−7 -10−11 CFU−1hr−1 for in vitro culture experiments.	Strength of the interspecies interaction induced by N1 on the N2 growth rate.
kd12	From 0–200 day−1 for in vivo experiments	The rate at which the immune response elicited by N2 eliminates N1.
kd21	Varied from 0–200 day−1 for in vivo experiments	The rate at which the immune response elicited by N1 eliminates N2.
Parameters used only for the culture models
Klag1, Klag2	Klag1 is varied from 1010 –1016 CFU2 and Klag2 from 109 –1014 CFU2 for in vitro experiments.	Effective parameters to incorporate the stunted growth phase of N1 and N2. When N1 and N2 become much larger than K1/2lag1 and K1/2lag2, the bacteria start to grow exponentially.

where γ₁ = r₁K₁, γ₂ = r₂K₂, α₁₁ = r₁α₁₁, α₁₂ = r₁α₁₂, α₂₁ = r₂α₂₁, and, α₂₂ = r₂α₂₂. A new parameter set (see Table S1) generated from a combination of these parameters was varied in a uniform distribution.

B. MaxEnt formalism to quantify host-host variations

MaxEnt is widely used in statistical physics(20–22), information theory(23), and statistics(24) to infer distributions of variables based on available measurements. The MaxEnt based approach enables us to estimate the distributions based solely on the available data and is free of any additional assumptions. Thus, the estimated distribution quantifies the minimal structure required in the distribution to describe the available data and could point to general principles in the system(25). In addition, the approach enables systematic incorporation of new data, and therefore continual improvement of the estimation as new data becomes available. Recently we used MaxEnt to quantify functional implications of cell-to-cell variations of chemotactic protein abundances(26, 27). Here, we use MaxEnt to infer the distribution of the ecological interactions in individual animals, using the observed populations of NTHI and Sp in OM as constraints. We introduce a parameter vector, {e_i}, that represents the parameters in the ODE models and use our MaxEnt based method to estimate the distribution, P̂({e_i}). We outline our method for a simple example below and provide further details regarding the full calculation in the supplementary material. The experimentally measured values of NTHI (or N₁) and Sp (or N₂) populations at different time points in single infections (where the middle ear is infected with a single bacterial species) or coinfections (where the middle ear is infected with both NTHI and Sp) provide us with average values and variances of NTHI and Sp populations over an animal population. For example, the average values of the NTHI and Sp populations can be described as,

$$(1/\#\text{of animals})\sum _{a=1}^m{N}_{1,2}^{(a)}(t)={\mathrm{N̅}}_{1,2}^{\text{expt}}(t)=\sum _{\{e_i\}}P(\{e_i\})N_{1,2}(\{e_i\},t)$$ (3)

where, N₁^(a)(t) and N₂^(a)(t) refer to the populations N₁ and N₂ in the middle ear of an animal indexed by a at time t (e.g., 7 days after inoculation). Thus, the first equality on the LHS defines the average value of N₁ measured at a time t over multiple animals. The second equality on the RHS equates the model values to the experimental measurements. If the ecological niches {e_i} are distributed according to a distribution P({e_i}) in the animals, and the infection kinetics of N₁ and N₂ follow the ODEs in Eq. (1), then the average of N₁({e_i},t) and N₂({e_i},t) over P({e_i}) should reproduce the observed average value at time t. There are many ways to choose a P({e_i}) that will satisfy Eq. (3). We use a MaxEnt based approach that enables us to infer P({e_i}) solely based on available data without any additional assumptions. This method selects a P({e_i}) that maximizes the Shannon Entropy, $S=-\sum _{\{e_i\}}P(\{e_i\})\text{ln}P(\{e_i\})$, in the presence of constraints imposed by the available data, such as the second equality in Eq. (3). Instead of directly maximizing S, we estimate P({e_i}) by minimizing a relative entropy (Eq. 4). Further details regarding the method are provided in the Methods section and the supplementary material.

Interspecies interactions regulate animal-to-animal variations of microbial kinetics

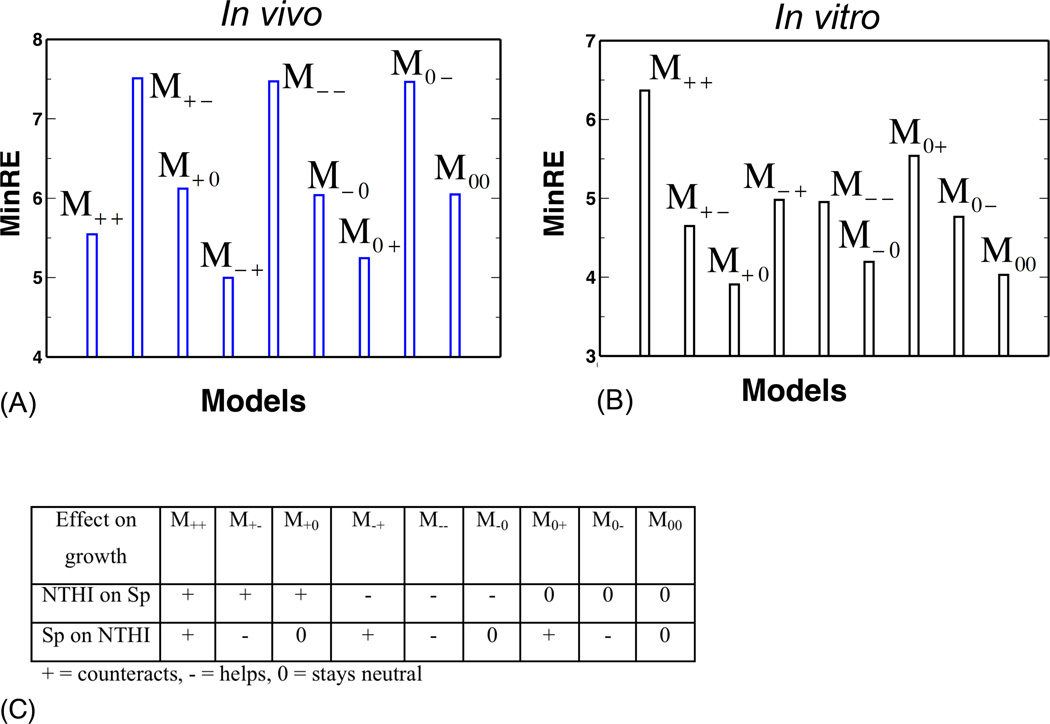
We quantified the extent of variation of the ecological interactions between animals by calculating the minimum value of the relative entropy, MinRE defined in Eq. 4 in Materials and Methods, for all nine models (Fig. 2A). All the models were constrained to reproduce the average values and variances of NTHI and Sp populations measured at 7 days post inoculation, for animals infected with NTHI and Sp simultaneously.

Fig. 2. Interspecies ecological interactions regulate variations of bacterial kinetics.

MinRE values, quantifying the extent of variations of ecological interactions, show differences in the abilities to accommodate individual-to-individual variances in models containing qualitatively different types of interspecies ecological interactions in an animal population (A) or a set of trials in culture experiments (B). (C) Table explaing the nomenclature used for different models.

The model in which Sp helps NTHI to access nutrients but NTHI competes with Sp (model M₋₊) produces the smallest MinRE, i.e., this model is consistent with the broadest parameter variations. The next best (MinRE) model was M₀₊, in which Sp stays neutral to NTHI growth and NTHI competes with Sp for resources. In contrast, the models M₊₋ and M₀₋, in which NTHI helps Sp to access resources, are consistent with only a very small amount of variation in the parameters. The results can be understood in the following way. The experiments show that at 7 days after coinoculation (NTHI~1000 CFU, Sp~150 CFU), the average population of NTHI (~10⁷ CFU) is substantially higher than that of Sp (~10 CFU). In contrast, when the animals are infected with either NTHI or Sp alone, both species reach high population (~10⁷ CFU). Therefore, the models that produce high growth for NTHI and low growth for Sp at later times (~7 days) across a wider range of parameter variations will be the models with smaller MinRE. In the model M₋₊, the interspecies interaction supports a higher NTHI and a lower Sp growth since Sp cooperates with NTHI in its growth, but the presence of NTHI counteracts Sp growth. The immune response, regardless of the type of interspecies interaction, can also support a larger NTHI population than Sp population by killing Sp at a higher rate compared to NTHI. In the model M₋₊ even when the elicited immune response kills NTHI at a higher rate than it eliminates Sp, which could lead to kinetics opposite to those observed in experiments, higher values of the interspecies interactions (e.g., α₁₂ and α₁₂) can counteract the effects induced by the immune response and produce a pattern similar to that observed in experiments. In contrast, in the model M₊₋, the interspecies interaction supports a higher population number for Sp compared to that of NTHI, so that the MaxEnt probability distribution is heavily concentrated on the subset of vectors of the ecological interaction parameters for which the immune response is able to counteract this effect and produce higher growth in NTHI compared to Sp. These patterns also indicate how seemingly unrelated ecological interactions, such as the interspecies interactions and the immune response, can become correlated. This is discussed in greater detail in the next section.

Next we compared the nature of variations of the ecological interactions explaining the infection data against the in vitro culture experiments (Fig. 2B). In vitro, populations of both NTHI and Sp grew in the medium, whether they were inoculated separately or simultaneously (Fig. S2). The population size of NTHI is similar to that of Sp when the bacterial species are cultured individually, and the NTHI population is slightly larger than that of Sp when cultured together. The models where Sp competes (model M₊₀) or stays neutral (model M₀₀) with NTHI for utilizing resources produce the smallest MinREs, whereas the model with only competitive interspecies interactions (model M₊₊) produces the highest MinRE. When both species are competing with each other for the common resources, the species can coexist only within a small range of parameter values, as a small difference between α₁₂ and α₂₁ can lead to elimination of one species (see the analysis of the ODEs in Eq. S1 in the supplementary material). In contrast, when a species is not interacting with another species it always reaches a population size determined by the carrying capacity. Therefore, the models that contain neutral interactions between the species allow for more variation in underlying parameters compared to the other models.

Testing Predictions

We used the estimated MaxEnt distributions to generate predictions for measurements that were not used as constraints in fitting the MaxEnt models. Specifically, we predicted the average values of populations of NTHI and Sp at day 3 when the animals were co-inoculated with these species. In addition, we also predicted the correlation between NTHI and Sp at day 7. The predictions from model (M₋₊), which was the best (MinRE) model under the original set of constraints, were in reasonable agreement with the data (Table S2). The models with larger MinRE values produced less agreement with the additional measurements compared to model M₊₋ (Table S2). In general, predictions were better for NTHI than Sp. The disagreement between the model predictions and the data for Sp could point to the importance of spatial structures such as biofilms in regulating the bacterial kinetics. This point is further deliberated in the discussion section.

Specific ecological interactions become interdependent

Because, N₁ and N₂ in the ODEs (Eq. 2) are complicated non-linear functions of the parameters {e_i}, it is not obvious that the inferred distribution P̂ ({e_i}) would follow a normal distribution. We evaluated whether the inferred distribution P̂ ({e_i}) of the model parameters could be well approximated by a multivariate normal distribution (Eq. 5). Since the distribution appeared to be well approximated by a multivariate normal distribution (Fig. S3), the average values and pair-correlations between the parameters capture the majority of the variations in the system and we quantified the interdependencies between the model parameters by using the inverse matrix, [Ω]_ij = [C⁻¹]_ij, where, C_ij denotes the correlation between the model parameters e_i and e_j. The correlation matrix, C, is defined as, $C_{ij}=\overline{(e_i-{\mu }_i)(e_j-{\mu }_j)}$ and µ_i = e̅_i, where, the over bar indicates the average over P̂({e_i}). We further quantified the strength of the interdependence or relationship between the model parameters by calculating a metric ({[Int]_ij}) for every pair of parameters e_i and e_j using the Ω matrix (see the Methods section for details). A larger magnitude of [Int]_ij implies a greater contribution of the pair of parameters to determining animal-to-animal (or trial-to-trial) variations (Fig. 3), and a negative or a positive value indicates whether the members of the pair vary in the same or opposite direction while keeping the response unchanged.

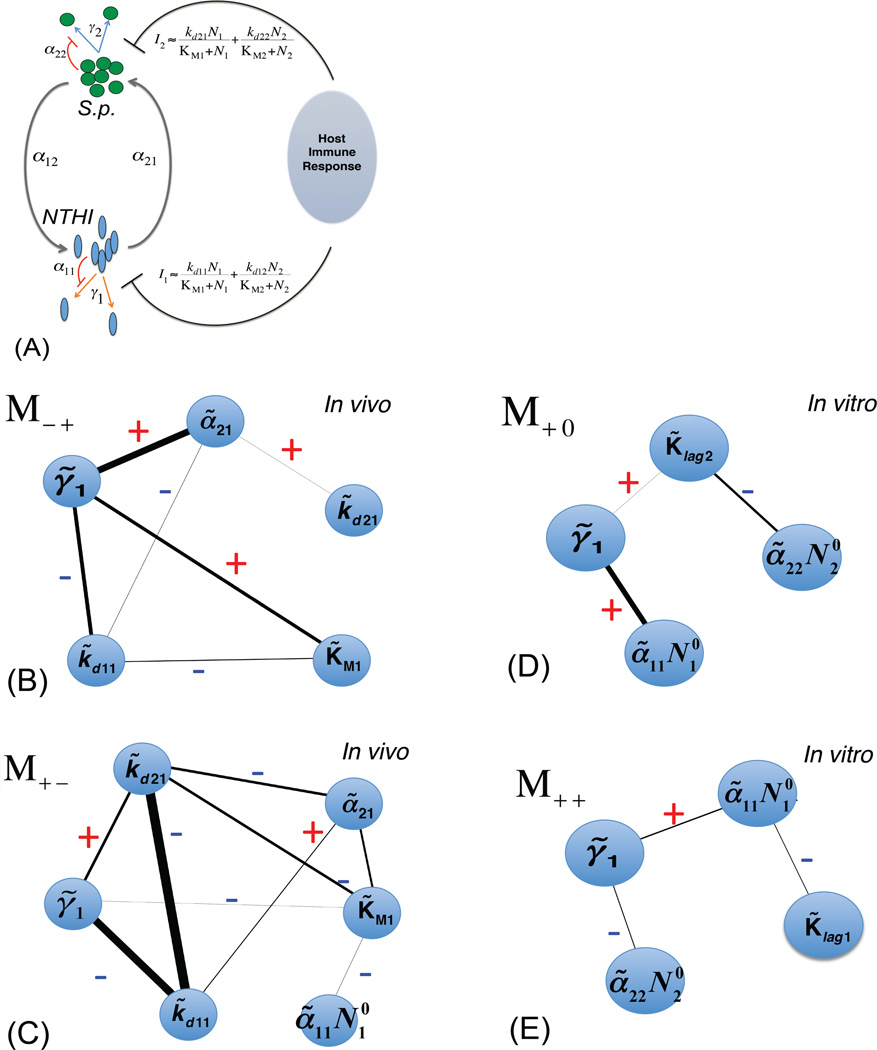
Fig. 3. Characteristics of the inferred distribution of the ecological interactions.

(A) Parameters used in (B–E) are explained using a schematic diagram depicting the in silico models describing infection by NTHI (species 1) and Sp (species 2). The bacterial kinetics are regulated by inter/intra species interactions for resources and the host immune response. NTHI and Sp replicate with rates γ₁ and γ₂, respectively. The bacterial species interact with their own species (described by α₁₁ and α₂₂) and the other species (α₁₂ and α₂₁) for utilizing the resources. NTHI and Sp also elicit host immune response shown by I₁ and I₂, respectively, which eliminate the bacterial species. Further details for the parameters are shown in Table II. (B) Interdependencies between ecological interactions (shown in terms of the parameters shown in Table S1) described by the metric [Int]_ij for the model M₋₊ (smallest MinRE) for the infection data. Higher [Int]_ij values are shown with thicker lines and [Int]_ij values less than the threshold (abs[[Int]_ij]> 0.1) are now shown. The +ve and the −ve signs are also indicted. (C) Same as in (B) for the model M₊₋ for the infection data which produce the largest MinRE value. (D) [Int]_ij shown for the model M₊₀ (smallest MinRE) explaining the culture data. (E) Same as in (D) for the model M₊₊ (largest MinRE).

Analysis of the interdependencies using {[Int]_ij} for M⁻⁺ showed (Fig. 3B) that parameters that are not directly related to the immune response, such as the carrying capacity or the strength of interspecies interactions, can become dependent on parameters directly related to the immune response, such as the rate of killing of Sp by the immune system. The number of such dependencies with higher magnitudes of {[Int]_ij}increases for the higher MinRE models (consistent with less variation in the parameters) in the niches considered here(Fig. 3C, E). This result can be intuitively understood as follows: requiring increased interdependence between the parameters imposes greater restrictions on the sets of parameter vectors that are able to reproduce the measured average values. The majority of the dependencies can be understood qualitatively by analyzing the ODEs, for example, the increase in the NTHI bacterial load required to induce the maximum immune response that favors an increase in the NTHI population is compensated for by a corresponding decrease in the available resources or the carrying capacity (Fig. 3B). This implies that a particular strain in NTHI that is less efficient in stimulating the immune response will also undergo changes that reduce its capability to utilize the nutrients for growth. Further explanations regarding the other interdependencies are provided in the supplementary material (Table S3).

These in vitro analyses show (Fig. 3D,E) that parameters describing interspecies interactions, in contrast to intra-species interactions, become more dependent during infections, e.g., a decrease in the carrying capacity for Sp, which would support a higher population of NTHI due to lower competitive interspecies interaction, is compensated by a decrease in the strength in interspecies competition between NTHI and Sp.

Discussion

We developed a method based on MaxEnt to quantify host-to-host variations of ecological interactions for two bacterial species, NTHI and Sp, which are responsible for polymicrobial OM infection. A key finding of this analysis is the dependency of the extent of host-to-host variations of the ecological interactions on the nature of the underlying bacterial interspecies interactions. Cooperative-competitive or neutralcompetitive interaction models between bacterial species allow for the largest variations (smaller values of MinRE) of the ecological interactions or model parameters, and are likely to be associated with host populations with greater heterogeneity and environmental perturbations. Interspecies interactions between NTHI and Sp arise via a range of processes, such as secretion of toxins, metabolic byproducts, inflammation and quorum sensing. Since the nature and magnitude of these processes can vary from strain to strain in a bacterial species, it is possible that specific strains of NTHI and Sp with interspecies interactions that are robust to the largest variations in ecological niches in the host population, are selected as the host immune system and the microorganisms coevolve in an evolutionary arms race(5).

The structure of the inferred variations of ecological interactions reveal that seemingly unrelated ecological variables, such as the carrying capacities and the host immune response, become interdependent. For example, in a model with large ecological variation (M₋₊), a mutually cooperative relationship between the carrying capacity and the rate of bacterial elimination suggests that an NTHI strain will be selected if it can use equivalent resources more efficiently despite its growth being suppressed by the host immune response (Fig. 3). These results suggest that if the microbial communities residing in the host have the flexibility to accommodate changes in the ecological interactions, such as, by altering gene expressions(28), these changes are likely to occur in a coordinated manner(29).

The in vitro culture experiments show that both the NTHI and Sp bacterial strains are able to coexist in the culture medium, while in the chinchilla host, the Sp strains are eliminated in the presence of NTHI. This clearly suggests a qualitative difference in ecological niches for growth in the host microenvironment and the in vitro culture. Our MaxEnt based analysis quantitatively characterizes the difference. Our analysis showed that the neutral model (M₊₀) produced a wider spread in ecological interactions in vitro over the purely competitive model (M₊₊). This result is consistent with Gause’s law in population dynamics(7), which states that two species competing for the same resources cannot coexist. In contrast, in the presence of the host immune response, the purely competitive model (M₊₊) showed a much wider variation compared to the neutral model (M₀₀). Therefore the models with the smallest MinRE values in vitro have very different interspecies interaction than the models with small MinRE values in vivo. In vivo, the model M₋₊ accommodating largest variation in “ecological interactions”, contains cooperative and competitive interactions whereas its counterpart (M₊₀ or M₀₀) in vitro contains non-interacting bacterial species. These differences emphasize the importance of the immune response in manipulating ecological niches and evolutionary selection of bacterial strains residing in the host.

We primarily studied models that approximated and simplified interspecies interactions in terms of a relatively small number of parameters. Therefore, these models need to be modified in order to investigate interspecies interactions such as quorum sensing, which increases fitness of the same strain, or the formation of spatial structures such as biofilms, which help bacterial species to evade the host immune response. The importance of these effects, in particular biofilm formation, becomes apparent from the disagreements between the model predictions and the experimental data (Table S2). The two-species model could be extended to include additional strains associated with biofilms found in the chinchilla middle ear(2). Investigation of the role of these additional strains in host-to-host variations of infection kinetics would be an interesting future direction. Stochastic fluctuations in bacterial growth(30, 31), especially when bacterial population sizes are small, for example, at early phases of infection or when a species is nearing clearance (e.g., Sp population in Fig. 1B) could potentially play a role in animal-to-animal variation of bacterial kinetics. We plan to study these effects in the future.

Our analysis showed that host-to-host variations of polymicrobial infection kinetics can provide valuable clues regarding evolutionary selection of bacterial strains and the role of the host immune response in shaping the fitness landscape of the polymicrobial community. A possible test of the results presented here could be analysis of gene expression from bacterial isolates obtained from the middle ear pre- and post-co-inoculation. If genes responsible for metabolism of essential metals are upregulated during coinfection in NTHI but not in Sp, this would lend additional support to our conclusion that specific attributes promoting NTHI growth are selected due to the combined effect of the presence of Sp and the host immune response. However, the modeling approach proposed here represents a general method, not limited to OM, which can be utilized to understand mechanisms of host-microorganism relationships and their evolutionary origin using measurements delineating host-to-host variations of microbial and host response kinetics.

Methods and Materials

Solution of the ODEs

The ODEs in Eq. (2) were solved using the software package BIONETGEN(32). The codes used in the simulations can be found at http://planetx.nationwidechildrens.org/~jayajit/.

Estimation of P̂({e_i})

We used measurements from infection and culture experiments studying kinetics of single or two bacterial species for estimating P({e_i}). We separate the parameter vector {e_i} into two sub-sets {e_i^(S)} and {e_i^(M)} (see Table II and Table S1) that represent respectively the parameters solely regulating bacterial kinetics for experiments with single species and the additional parameters required to describe the kinetics for the mixed coinfection/culture experiments. We described the kinetics in terms of a new set of parameters {ẽ_i} constructed from a particular combination of {e_i} (Table S1 and supplementary material) and carried out all the MaxEnt analysis on new set {ẽ_i}. Thus, {e_i} in the rest of the section refer to {ẽ_i}. We retained the same symbols for simplicity. P̂({e_i}) can be decomposed into $\mathrm{P̂}(\{e_i\})={\mathrm{P̂}}^{(M)}(\{e_i\}){\mathrm{P̂}}^{(S)}(\{e_i^s\},\{0\})$ (see the supplementary material for the derivation), where, P̂ ^(M)({e_i }) and ${\mathrm{P̂}}^{(S)}(\{e_i^s\},\{0\})$ describe the distributions of the parameters consistent with experiments done with single or two bacterial species, respectively. We briefly describe the numerical scheme used in estimating ${\mathrm{P̂}}^{(S)}(\{e_i^s\},\{0\})$ and P̂^(M)({e_i}).

(A) Infection (in vivo) experiments

${\mathrm{P̂}}^{(S)}(\{e_i^s\},\{0\})$ is estimated from the infection experiments where the chinchilla middle ears are infected with either Sp or NTHI. The a priori distribution of the parameters before the maximization of S was assumed to be a uniform distribution in {e_i^(S)}, since the uniform distribution represents the maximally uncertain state of a system. The parameters related to mixed two species experiments set to zero, i.e., $q_U(\{e_i\})=q_U(\{e_i^{(S)}\})\times \prod _i{\delta }_{e_i^{(M)},0}$, where, δ_ab =1 (or =0)when a=b (or a≠b).

We constrained the average values of populations of NTHI and Sp in the models, according to their experimentally measured values at two different times (3 and 7 days). P({e_i^(S)},{0}) is estimated by minimizing the relative entropy

$$MinR{E}^{(S)}=\sum _{\{e_i^{(S)}\}}P(\{e_i^{(S)}\},\{0\})\text{ln}[P(\{e_i^{(S)}\},\{0\})/q_U(\{e_i^{(S)}\},\{0\})]$$ (4a)

subject to the contraints imposed by the average values.

In the next step, we generate the a priori distribution q({e_i}) by choosing parameters {e_i^(S)} based on ${\mathrm{P̂}}^{(S)}(\{e_i^s\},\{0\})$ and the parameters {e_i^(M)} were chosen from a uniform distribution, i.e., $q^{(M)}(\{e_i\})={\mathrm{P̂}}^{(S)}(\{e_i^{(S)}\},\{0\})\times q_U(\{e_i^{(M)}\})$. Then we estimate the distribution, P^(M)({e_i }) when {e_i^(M)} are not vanishing using the measured values from the coinfection experiments as constraints and minimizing the relative entropy,

$$MinRE=\sum _{\{e_i\}}{P}^{(M)}(\{e_i\})\text{ln}[P^{(M)}(\{e_i\})/q_U(\{e_i\})],$$ (4b)

where, q_U({e_i}) denotes a uniform distribution for parameters in both the subsets {e_i^(S)} and {e_i^(M)}. The details regarding sample size and the sampling method are given in the supplementary material.

(B) In vitro culture

Since the immune response is absent in the culture experiments, we set g₁=g₂=0 in the models. The growth of NTHI and Sp are described by the rates, f₁(N₁,N₂) =r₁[N₁²/(K_lag1+N₁²)](K₁-α₁₁N₁-α₁₂N₂) and f₂(N₁,N₂) =r₂[N₂²/(K_lag2+N₂²)](K₂-α₂₂N₂-α₂₁N₁). The terms [N₁²/(K_lag1+N₁²)] and [N₂²/(K_lag2+N₂²)] describe the initial lag in the growth of NTHI and Sp. The ODEs are shown in Eq. (S1). The rest of the parameters are described in the same manner as in the infection models. The ODEs are unable to capture the initial drop in the bacterial populations in the first 3 hours (Fig. 1C and 1D), as well as, produce higher concentrations of bacterial populations at later times with a particular set of values for the parameters. This is because the ODEs use constant rates for bacterial replication and death. A possible solution would be to use time dependent replication and death rates, for example, higher death rate compared to the replication rate at early times and the opposite scenario at later times. Such modifications will complicate the models and we avoid using them here. Therefore, we used the experimental data and the model kinetics at later times in the MaxEnt method which would remain largely unchanged if the models are modified to match the early time kinetics in the experiments. The distribution of the parameters is estimated using the same scheme as described above from the in vitro measurements studying growth of NTHI and Sp growing individually or simultaneously in the medium.

Experimental techniques

Streptococcus pneumoniae TIGR4 and H. influenzae 86-028NP were cultured, alone or together in equivalent ratios, in brain-heart infusion (Difco) supplemented with hemin and NAD, and containing 10% horse serum (HemoStat Laboratories), as previously described in (33). Bacterial counts were derived by plate-count. Bacterial populations were assessed separately by plating the same serial dilutions on media selective for each species. Pneumococci were propagated on blood agar containing 2 micrograms/ml gentamicin, whereas H. influenzae was propagated on brain-heart infusion agar (Difco) supplemented with hemin and NAD and containing 3 micrograms/ml vancomycin. All counts are expressed as colony forming units per ml.

Quantification of the relationship between the model parameters

We approximate the distribution P̂^(M)({e_i}) by a multivariate normal distribution (Fig. S3), i.e.,

$${\mathrm{P̂}}^{(M)}(\{e_i\})\propto e^{-\sum _{i,j}(e_i-{\mu }_i){\mathrm{\Omega }}_{ij}(e_j-{\mu }_j)},$$ (5)

where, {μ_i} denote the average values of the parameters {e_i}, and, [Ω⁻¹]_ij = C_ij ; C_ij denoting the correlation between the niches e_i and e_j or $C_{ij}=\overline{(e_i-{\mu }_i)(e_j-{\mu }_j)}$ where the over bar indicates the average over P̂^(M)({e_i}). The elements of the matrix Ω demonstrate the “interaction” between the parameters or the nature of the relationship between the parameters in producing the observed correlations. E.g., a positive (or negative) value Ω_ij would imply the parameters e_i and e_j counter-act (or help) each other in producing the observed population kinetics. A vanishing value of Ω_ij would imply very little relationship between e_i and e_j. We evaluated which of the interactions in ({Ω_ij}) contribute the most in determining the observed covariance C_ij. This was done by not constraining a specific C_ij, and then comparing the inferred P̂ ^*(ij)({e_i}) with the original inferred distribution, P̂({e_i}) using the Kullback-Leibler distance, ${[D_{KL}]}_{ij}=\sum _{\{e_i\}}\mathrm{P̂}(\{e_i\})\text{ln}[\mathrm{P̂}(\{e_i\})/{\mathrm{P̂}}^{*(ij)}(\{e_i\})]$. A larger [D_KL]_ij implies a greater contribution of a particular Ω_ij in determining the animal-to-animal variations of the ecological niches (Fig. 3). Therefore, we use a metric, Int_ij=sgn(Ω_ij) [D_KL]_ij, to quantify inferred interaction strength between the pair of niches, i and j.