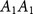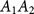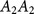Abstract
The traditional quantitative genetics model was used as the unifying approach to derive six existing and new definitions of genomic additive and dominance relationships. The theoretical differences of these definitions were in the assumptions of equal SNP effects (equivalent to across-SNP standardization), equal SNP variances (equivalent to within-SNP standardization), and expected or sample SNP additive and dominance variances. The six definitions of genomic additive and dominance relationships on average were consistent with the pedigree relationships, but had individual genomic specificity and large variations not observed from pedigree relationships. These large variations may allow finding least related genomes even within the same family for minimizing genomic relatedness among breeding individuals. The six definitions of genomic relationships generally had similar numerical results in genomic best linear unbiased predictions of additive effects (GBLUP) and similar genomic REML (GREML) estimates of additive heritability. Predicted SNP dominance effects and GREML estimates of dominance heritability were similar within definitions assuming equal SNP effects or within definitions assuming equal SNP variance, but had differences between these two groups of definitions. We proposed a new measure of genomic inbreeding coefficient based on parental genomic co-ancestry coefficient and genomic additive correlation as a genomic approach for predicting offspring inbreeding level. This genomic inbreeding coefficient had the highest correlation with pedigree inbreeding coefficient among the four methods evaluated for calculating genomic inbreeding coefficient in a Holstein sample and a swine sample.
Introduction
Genomic relationship among individuals is a measure of genomic relatedness or similarity among individuals and allows genomic prediction and variance component estimation to use theoretical results and computational strategies of best linear unbiased prediction (BLUP). Genomic relationship is calculated using genome-wide single nucleotide polymorphism (SNP) markers without referencing to pedigree information. Therefore, genomic relationship is particularly appealing for wildlife and animal populations where pedigree information is unavailable or incomplete.
The first attempt to use marker information to construct the G matrix for using BLUP to predict total marker effects was the approach of Nejati-Javaremi et al.
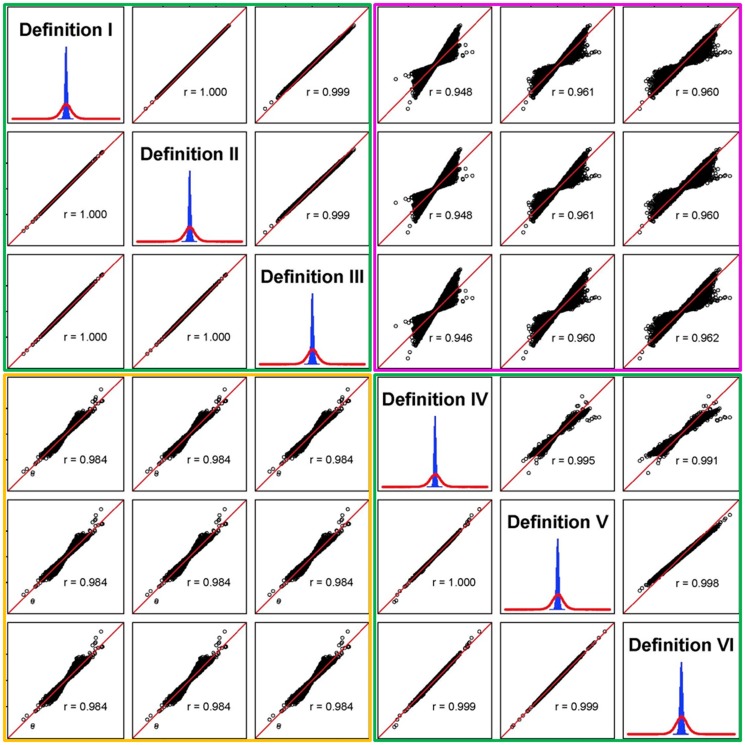
[1] that defines the G matrix as twice the average marker IBS probability (IBS = identity by state). VanRaden derived the first genomic additive relationship formula based on the standardization of the 2-1-0 (or 0-1-2) coding of SNP genotypes [2]. This formula divides the  matrix by the total expected heterozygosity of all SNP markers, where
matrix by the total expected heterozygosity of all SNP markers, where 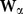 is the model matrix for SNP additive effects with each SNP coding being the deviation of the 2-1-0 coding from its mean. This approach leads to the prediction of genomic breeding values [2], [3]. Another method by Hayes and Goddard uses the average of the diagonal elements of the
is the model matrix for SNP additive effects with each SNP coding being the deviation of the 2-1-0 coding from its mean. This approach leads to the prediction of genomic breeding values [2], [3]. Another method by Hayes and Goddard uses the average of the diagonal elements of the 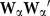 matrix in the denominator of the genomic relationships [3]. Rather than using a common denominator for all relationships, a third method divides each SNP's additive coding by the SNP's heterozygosity based on VanRaden's method for additive effects [4]. Da et al. proposed the quantitative genetics model that partitions a genotypic value into breeding value and dominance deviation for genomic prediction and variance component estimation of additive and dominance effects [5], [6]. The genomic additive relationships using the quantitative genetics model were identical to those based on standardization of SNP 2-1-0 coding. VanRaden derived the genomic dominance relationship formula based on the quantitative genetic model (Personal communication from P. VanRaden to Y. Da, March 3, 2013, described in [6]), and Da et al.
[6] extended the method of Hayes and Goddard for genomic additive relationships [3] to genomic dominance relationships. Su et al. proposed genomic dominance relationships using the approach of standardization of the 0-1-0 dominance coding [7]. Vitezica et al.
[8] derived the dominance relationships using the quantitative genetics model and showed that the genomic dominance relationship of Su et al. [7] was a reparameterization of the quantitative genetics model. Genomic relationships on average were consistent with the theoretical expectation of the corresponding pedigree relationships [6]. This consistency provides a justification for the interpretation of genomic relationships in parallel to pedigree relationships. In contrast to pedigree relationships, genomic relationships are realized relationships calculated from genome-wide SNP markers resulting from generations of drift, recombination, mutation and selection that are not considered by pedigree relationships, and estimates of genomic relationships for different individuals generally had their own genomic specificity unobservable from the pedigree estimates although on average genomic and pedigree relationships were consistent [6].
matrix in the denominator of the genomic relationships [3]. Rather than using a common denominator for all relationships, a third method divides each SNP's additive coding by the SNP's heterozygosity based on VanRaden's method for additive effects [4]. Da et al. proposed the quantitative genetics model that partitions a genotypic value into breeding value and dominance deviation for genomic prediction and variance component estimation of additive and dominance effects [5], [6]. The genomic additive relationships using the quantitative genetics model were identical to those based on standardization of SNP 2-1-0 coding. VanRaden derived the genomic dominance relationship formula based on the quantitative genetic model (Personal communication from P. VanRaden to Y. Da, March 3, 2013, described in [6]), and Da et al.
[6] extended the method of Hayes and Goddard for genomic additive relationships [3] to genomic dominance relationships. Su et al. proposed genomic dominance relationships using the approach of standardization of the 0-1-0 dominance coding [7]. Vitezica et al.
[8] derived the dominance relationships using the quantitative genetics model and showed that the genomic dominance relationship of Su et al. [7] was a reparameterization of the quantitative genetics model. Genomic relationships on average were consistent with the theoretical expectation of the corresponding pedigree relationships [6]. This consistency provides a justification for the interpretation of genomic relationships in parallel to pedigree relationships. In contrast to pedigree relationships, genomic relationships are realized relationships calculated from genome-wide SNP markers resulting from generations of drift, recombination, mutation and selection that are not considered by pedigree relationships, and estimates of genomic relationships for different individuals generally had their own genomic specificity unobservable from the pedigree estimates although on average genomic and pedigree relationships were consistent [6].
Inbreeding is a major issue in animal breeding and wildlife conservation because inbreeding may result in inbreeding depression associated with reduced survival and fertility [9], [10]. Inbreeding coefficients calculated from SNP markers do not require pedigree information and hence have wider applicability than pedigree inbreeding coefficients that cannot be calculated without pedigree information. Assuming the parallelism between genomic and pedigree relationships, inbreeding coefficients could be calculated using diagonal elements of the genomic additive relationship matrix as a function of the SNP model matrix for genomic prediction [11]. To improve the correlation between genomic and pedigree inbreeding coefficients, Yang et al. [4] proposed different diagonal elements of the genomic additive relationship matrix that are not from the SNP model matrix for genomic prediction, and Keller et al. [12] showed that genomic inbreeding coefficients using runs of homozygosity (ROH) achieved higher correlation with pedigree inbreeding coefficients than the method of Yang et al. [4]. All these methods for calculating genomic inbreeding coefficients use the individual's own SNP data. However, predicting offspring inbreeding levels before the offspring were born is an important issue in breeding plans. For this purpose, a method of calculating offspring inbreeding coefficient from parental genomic relationships can be developed.
In this study, we show that quantitative genetics theory can be the unifying theory for deriving existing and new genomic additive and dominance relationships and for studying the theoretical differences among various definitions of genomic relationships. We propose a method for calculating genomic inbreeding coefficient using a combination of genomic correlation from the quantitative genetics model, classical definition of inbreeding coefficient, and the theoretical expectation of genomic additive relationships. We also explore numerical differences among various genomic relationships and inbreeding coefficients using a Holstein sample and a swine sample.
Methods
Quantitative genetics model for SNP markers assuming HWE
Under the assumption of Hardy-Weinberg equilibrium (HWE), the traditional quantitative genetics model partitions a genotypic value into the summation of a common mean, breeding value and dominance deviation [6], [13], i.e.,
| (1) |
where 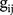 = genotypic value of SNP genotype
= genotypic value of SNP genotype 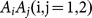 ,
, 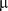 = common mean,
= common mean,  = average effect of gene substitution,
= average effect of gene substitution, 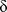 = dominance effect,
= dominance effect, 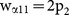 ,
, 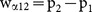 ,
, 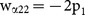 ,
, 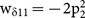 ,
, 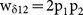 ,
, 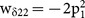 ,
, 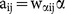 = breeding value,
= breeding value, 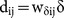 = dominance deviation, and where
= dominance deviation, and where 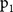 = frequency of
= frequency of 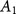 allele and
allele and 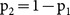 = frequency of
= frequency of 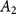 . Since each individual has one genotype for each SNP, the breeding value and dominance deviation of each SNP can be re-indexed as those of individual j with SNP i. The total genomic breeding value and total genomic dominance deviation of m SNP markers of individual j are
. Since each individual has one genotype for each SNP, the breeding value and dominance deviation of each SNP can be re-indexed as those of individual j with SNP i. The total genomic breeding value and total genomic dominance deviation of m SNP markers of individual j are 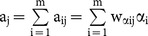 and
and 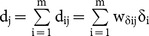 . The mathematical expectations of breeding values and dominance deviations are null under HWE, i.e.,
. The mathematical expectations of breeding values and dominance deviations are null under HWE, i.e., 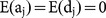 . The expected additive and dominance variances of the
. The expected additive and dominance variances of the 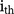 SNP based on the classical formulae from quantitative genetics [13] are:
SNP based on the classical formulae from quantitative genetics [13] are:
| (2) |
| (3) |
where 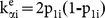 and
and 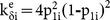 . The average of expected additive and dominance variances of the m SNPs are:
. The average of expected additive and dominance variances of the m SNPs are:
| (4) |
| (5) |
| (6) |
| (7) |
where 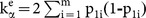 and
and 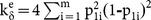 .
.
Genomic and pedigree covariances between two individuals
Based on the genomic breeding value and dominance deviation defined in Equation 1 and the results that the mean values of breeding values and dominance deviations are null assuming HWE [13], the covariances between genomic breeding values and between genomic dominance deviations of two individuals are:
| (8) |
| (9) |
Using pedigree relationships, the covariances between breeding values and between dominance deviations of two individuals [13], [14] are:
| (10) |
| (11) |
where 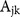 = additive relationship between individuals j and k = 2× (coancestry coefficient between individuals j and k), and
= additive relationship between individuals j and k = 2× (coancestry coefficient between individuals j and k), and 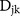 = dominance relationship between individuals j and k.
= dominance relationship between individuals j and k.
Mixed model for genomic prediction and variance component estimation
The mixed model to implement the quantitative genetics model of Equation 1 can be expressed as:
| (12) |
where Z = N × q incidence matrix allocating phenotypic observations to each individual = identity matrix for one observation per individual (N = q), α = m ×1 column vector of gene substitution (additive) effects of SNP markers, 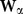 = q × m model matrix of α, δ = m ×1 column vector of dominance effects of SNP markers,
= q × m model matrix of α, δ = m ×1 column vector of dominance effects of SNP markers, 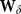 = q × m model matrix of δ, b = c ×1 vector of fixed effects, and X = N × c model matrix of b. Assumptions for the first and second moments are:
= q × m model matrix of δ, b = c ×1 vector of fixed effects, and X = N × c model matrix of b. Assumptions for the first and second moments are: 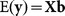 ,
, 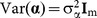 ,
, 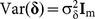 ,
, 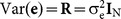 , where
, where 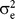 = residual variance, I
m = m × m identity matrix, and I
N = N × N identity matrix. The W matrices of Equation 12 are the primary information for calculating genomic relationships and inbreeding coefficients.
= residual variance, I
m = m × m identity matrix, and I
N = N × N identity matrix. The W matrices of Equation 12 are the primary information for calculating genomic relationships and inbreeding coefficients.
The average of the additive or dominance SNP coding in Equation 12 can be shown to be null, i.e., 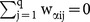 and
and 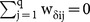 under the assumption of Hardy-Weinberg equilibrium (HWE) (S1 Text, Part A), so that the means of breeding values and dominance deviations for each SNP are null. Using this result, the sample additive and dominance variances of the
under the assumption of Hardy-Weinberg equilibrium (HWE) (S1 Text, Part A), so that the means of breeding values and dominance deviations for each SNP are null. Using this result, the sample additive and dominance variances of the 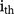 SNP are:
SNP are:
| (13) |
| (14) |
where 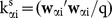 ,
, 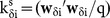 ,
, 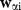 =
= 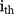 column of W
α in Equation 12 and
column of W
α in Equation 12 and 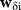 =
= 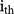 column of W
δ in Equation 12 corresponding to the
column of W
δ in Equation 12 corresponding to the 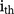 SNP. The average of sample additive and dominance variances of the m SNPs are:
SNP. The average of sample additive and dominance variances of the m SNPs are:
| (15) |
| (16) |
| (17) |
| (18) |
where 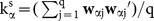 ,
, 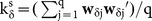 ,
, 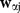 =
= 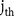 row of W
α in Equation 12, and
row of W
α in Equation 12, and 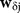 =
= 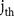 row of W
δ in Equation 12.
row of W
δ in Equation 12.
Results and Discussion
Genomic relationships derived from the quantitative genetics model
General formulations of genomic additive and dominance relationships
The general formulations of genomic additive and dominance relationships are obtained by equating the genomic covariances of Equations 8–9 to the pedigree covariances of Equations 10–11. Solving 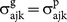 for
for 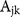 and solving
and solving 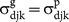 for
for 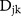 yield:
yield:
| (19) |
| (20) |
where 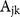 = genomic additive relationship,
= genomic additive relationship, 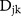 = genomic dominance relationship,
= genomic dominance relationship, 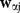 or
or 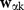 =
= 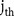 or
or 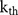 row of
row of 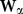 in Equation 12,
in Equation 12, 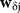 or
or 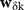 =
= 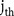 or
or 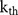 row of
row of 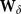 in Equation 12,
in Equation 12, 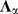 = diag{
= diag{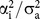 } and
} and 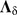 = diag{
= diag{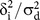 }, i = 1,..,m. In matrix notations, Equations 19–20 can be expressed as:
}, i = 1,..,m. In matrix notations, Equations 19–20 can be expressed as:
| (21) |
| (22) |
where A g = genomic additive relationship matrix and D g = genomic dominance relationship matrix.
Various existing and new definitions can be derived from Equations 19–20 or 21–22. In this study, four existing definitions of genomic relationships and two new definitions are derived based on these equations (Table 1). From the point of view of the quantitative genetics model, Definitions I-III assume equal SNP effects, Definitions IV-VI assume equal SNP variances across SNP markers, Definitions I and IV use expected SNP variance, and Definitions II and V use sample SNP variance. The standardization of SNP coding for defining genomic relationships is an across-SNP standardization using a common denominator for all SNPs for Definitions I-III, and is a within-SNP standardization of each SNP using its own SNP variance for Definitions IV-VI.
Table 1. Six definitions of genomic additive and dominance relationships.
| Equal SNP effects | Equal SNP variances | |
| (Across-SNP standardization) | (Within-SNP standardization) | |
| Expected variances | Definition I ( Equations 23 – 24 ) | Definition IV ( Equations 27 – 28 ) |
| •Additive relationships [2] | •Additive relationships, off-diagonals are the same as in [4] | |
| •Dominance relationships [6] | •Dominance relationships [This article] | |
| Sample variances | Definition II ( Equations 25 – 26 ) | Definition V ( Equations 29 – 30 ) [This article] |
| •Additive relationships: [3] | •Additive relationships | |
| •Dominance relationships [6] | •Dominance relationships | |
| Genomic correlations | Definition III ( Equations 31 – 32 , and Aij from Definition I or II) [6] | Definition VI ( Equations 31 – 32 and Aij from Definition IV or V) [This article] |
| •Additive correlations | •Additive correlations | |
| •Dominance correlations | •Dominance correlations |
Definition I – equal SNP effects (across-SNP standardization), expected variances
Assuming equal SNP additive and dominance effects, 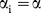 and
and 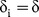 , and using the expected additive and dominance variances of Equations 2–3, the genomic relationships of Equations 19–20 reduce to:
, and using the expected additive and dominance variances of Equations 2–3, the genomic relationships of Equations 19–20 reduce to:
| (23) |
| (24) |
where 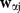 or
or 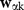 =
= 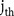 or
or 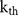 row of
row of 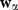 in Equation 12,
in Equation 12, 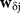 or
or 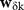 =
= 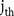 or
or  row of
row of 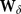 in Equation 12,
in Equation 12, 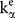 is defined in Equation 4, and
is defined in Equation 4, and 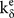 is defined in Equation 6. Equations 23–24 are the same as VanRaden's formulae [2], [6].
is defined in Equation 6. Equations 23–24 are the same as VanRaden's formulae [2], [6].
Definition II – equal SNP effects (across-SNP standardization), sample variances
Assuming equal SNP effects for all SNP markers and using the sample variances of Equations 15 and 17, the genomic relationships of Equations 19–20 reduce to:
| (25) |
| (26) |
where 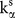 and
and 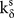 are defined in Equations 15 and 17. Equation 25 is the same as in [3], and Equation 26 is the same as in [6].
are defined in Equations 15 and 17. Equation 25 is the same as in [3], and Equation 26 is the same as in [6].
Definition IV – equal expected SNP variances (within-SNP standardization)
Assuming equal additive and dominance variances rather than equal additive and dominance effects across SNP markers and using the expected variances of Equations 2–3, the genomic relationships of Equations 19–20 reduce to:
| (27) |
| (28) |
where 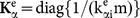 and
and 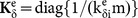 , i = 1,..,m, with
, i = 1,..,m, with 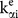 defined in Equation 2 and
defined in Equation 2 and 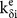 defined in Equation 3. Off-diagonal elements of Equation 27 are the same as the off-diagonal elements in [4].
defined in Equation 3. Off-diagonal elements of Equation 27 are the same as the off-diagonal elements in [4].
Definition V – equal sample SNP variances (within-SNP standardization)
Using sample variances of Equations 13–14 rather than the expected variances of Equations 2–3, the genomic relationships of Equations 19–20 reduce to:
| (29) |
| (30) |
where 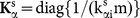 and
and 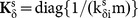 , i = 1,..,m, with
, i = 1,..,m, with 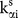 defined in Equation 13 and
defined in Equation 13 and 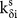 defined in Equation 14.
defined in Equation 14.
Definitions I-II and IV-V of genomic relationships can be represented by two sets of formulations in matrix notations. For Definitions I and II assuming equal SNP effects, 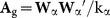 and
and 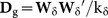 , where
, where 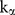 =
= 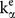 defined in Equation 4 and
defined in Equation 4 and 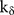 =
= 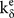 defined in Equation 6 for Definition I, or
defined in Equation 6 for Definition I, or 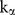 =
= 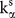 defined in Equation 15 and
defined in Equation 15 and 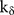 =
= 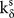 defined in Equation 17 for Definition II. For Definitions IV and V assuming equal SNP variances,
defined in Equation 17 for Definition II. For Definitions IV and V assuming equal SNP variances, 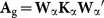 and
and 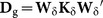 , with
, with 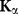 =
= 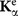 defined in Equation 27 and
defined in Equation 27 and 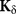 =
= 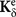 defined in Equation 28 for Definition IV, or
defined in Equation 28 for Definition IV, or 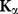 =
= 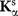 defined in Equation 29 and
defined in Equation 29 and 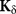 =
= 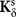 defined in Equation 30 for Definition V.
defined in Equation 30 for Definition V.
Genomic correlations
Genomic relationships between two individuals of Definitions I-II and IV-V as off-diagonal elements of the relationship matrices are not mathematically comparable for genomic relatedness because those off-diagonal elements are not exactly correlations. Genomic correlations (Definitions III and VI) among different individuals are mathematically comparable and provide a reference to evaluate other genomic relationship definitions.
Definitions III and VI – genomic correlations
The general formulations of genomic additive and dominance correlations are:
| (31) |
| (32) |
where 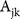 and
and 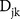 can be from any of Definitions I, II, IV and V. Equation 31 is the genomic version of Wright's coefficient of relationship or theoretical correlation between relatives [13], [15]. Based on Equations 31–32, the genomic additive correlation matrix (
can be from any of Definitions I, II, IV and V. Equation 31 is the genomic version of Wright's coefficient of relationship or theoretical correlation between relatives [13], [15]. Based on Equations 31–32, the genomic additive correlation matrix (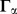 ) and the genomic dominance correlation matrix (
) and the genomic dominance correlation matrix (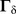 ) can be expressed as:
) can be expressed as:
| (33) |
| (34) |
where 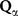 = diag{
= diag{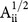 } = m × m diagonal matrix, and
} = m × m diagonal matrix, and 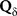 = diag{
= diag{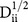 } = m × m matrix. The diagonal elements of these two correlation matrices are ‘1’. The off-diagonal elements of
} = m × m matrix. The diagonal elements of these two correlation matrices are ‘1’. The off-diagonal elements of 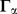 are
are 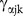 and the off-diagonal elements of
and the off-diagonal elements of 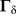 are
are 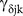 between individuals (j ≠ k). We will refer to Equations 31–34 as ‘Definition III’ if
between individuals (j ≠ k). We will refer to Equations 31–34 as ‘Definition III’ if 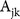 and
and 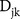 are from Definition I or II (Equations 23–24 or 25–26), or as ‘Definition VI’ if
are from Definition I or II (Equations 23–24 or 25–26), or as ‘Definition VI’ if 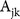 and
and 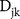 are from Definition IV or V (Equations 27–28 or 29–30). It can be readily shown that
are from Definition IV or V (Equations 27–28 or 29–30). It can be readily shown that 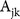 and
and 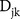 values from Definitions I and II yield identical
values from Definitions I and II yield identical 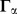 and
and 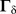 of Definition III. Numerical results showed that
of Definition III. Numerical results showed that 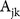 and
and 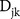 values from Definition IV and V were nearly completely correlated (correlation = 0.999, S1 Table). Therefore, we will use
values from Definition IV and V were nearly completely correlated (correlation = 0.999, S1 Table). Therefore, we will use 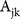 and
and 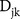 values from Definition V only in Definition VI. The six definitions of genomic additive and dominance relationships are implemented in GVCBLUP 3.9 [16], which is freely available at http://animalgene.umn.edu.
values from Definition V only in Definition VI. The six definitions of genomic additive and dominance relationships are implemented in GVCBLUP 3.9 [16], which is freely available at http://animalgene.umn.edu.
Genomic inbreeding coefficient based on parental genomic additive relationship
We formulate genomic inbreeding coefficients using parental genomic relationships based on the following results: 1) The inbreeding coefficient of an individual is the coancestry coefficient between the parents, 2) 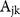 = additive relationship between individuals j and k = 2×(coancestry coefficient between individuals j and k) [13], and 3) Genomic additive relationships on average are consistent with pedigree ‘2×(coancestry coefficient)’ according to results in this article and in our previous report [6]. With these results, we define the genomic inbreeding coefficient of an individual as:
= additive relationship between individuals j and k = 2×(coancestry coefficient between individuals j and k) [13], and 3) Genomic additive relationships on average are consistent with pedigree ‘2×(coancestry coefficient)’ according to results in this article and in our previous report [6]. With these results, we define the genomic inbreeding coefficient of an individual as:
| (35) |
or
| (36) |
where individuals j and k are the parents of the individual; 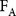 = genomic inbreeding coefficient using parental additive genomic relationship of Definition I, II, IV or V;
= genomic inbreeding coefficient using parental additive genomic relationship of Definition I, II, IV or V; 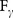 = genomic inbreeding coefficient using parental additive genomic correlation of Definition III or VI;
= genomic inbreeding coefficient using parental additive genomic correlation of Definition III or VI; 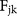 = genomic coancestry coefficient between parents j and k;
= genomic coancestry coefficient between parents j and k; 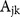 = genomic additive relationship between the parents calculated from any of Definitions I, II, IV or V; and
= genomic additive relationship between the parents calculated from any of Definitions I, II, IV or V; and 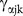 = genomic correlation between the parents from Definition III or VI. In this study,
= genomic correlation between the parents from Definition III or VI. In this study, 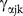 of Definition III uses
of Definition III uses 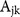 ,
, 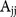 and
and 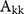 from Definition II, and
from Definition II, and 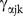 of Definition VI uses
of Definition VI uses 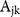 ,
, 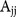 and
and 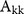 from Definition V.
from Definition V.
Comparison of different definitions of genomic relationships and correlations
Genomic additive and dominance relationships between individuals
The average values of genomic additive and dominance relationships were consistent with theoretical expectations of pedigree relationships in the Holstein sample (Fig. 1) and the swine sample (Fig. 2).
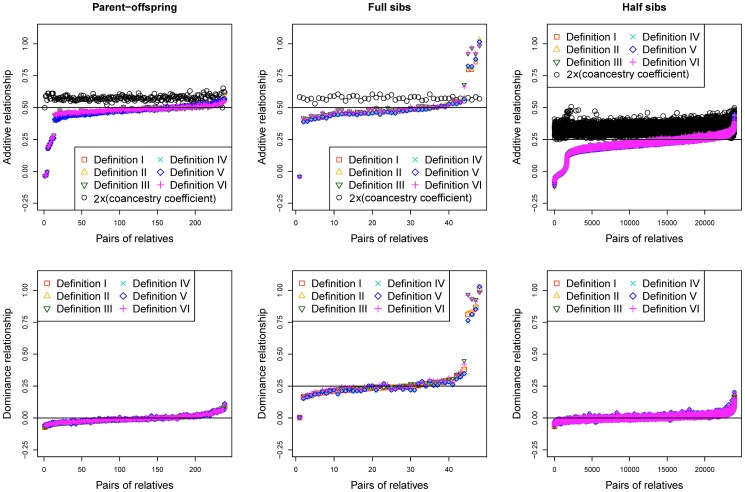
Figure 1. Genomic additive and dominance relationships by Definitions I-VI for parent-offspring (239 pairs), full-sibs (48 pairs) and half-sibs (23,941) of the Holstein sample.
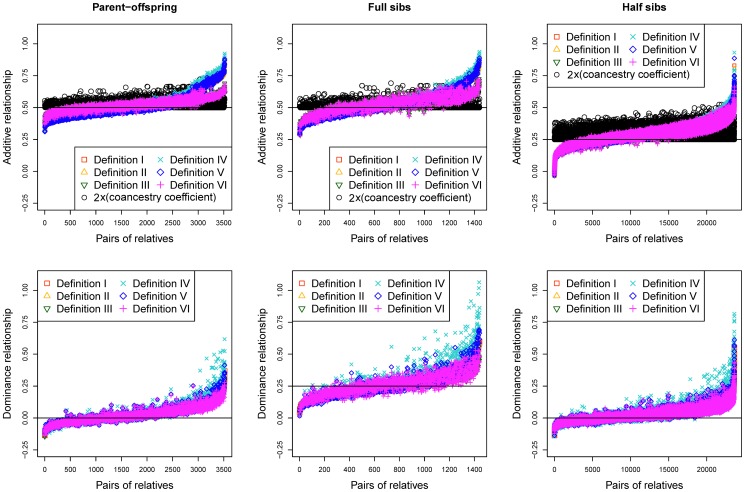
Figure 2. Genomic additive and dominance relationships by Definitions I-VI for parent-offspring (3518 pairs), full-sibs (1441 pairs) and half-sibs (23,628 pairs) of the swine sample.
For the Holstein sample, the average genomic additive relationships were below but close to those of ‘2×(coancestry coefficient)’ calculated from the pedigree data. The genomic additive relationships of Definitions I-VI were 0.459–0.469 for parent-offspring, 0.489–0.515 for full-sibs, and 0.205–0.212 for half-sibs, compared to ‘2×(coancestry coefficient)’ average value of 0.574 for parent offspring, 0.575 for full-sibs, and 0.341 for half-sibs (Table 2).
Table 2. Genomic and pedigree relationships of the Holstein sample.
| Definition | Additive | Dominance | ||
| Mean±SD | Range | Mean±SD | Range | |
| Parent-offspring (239 pairs) | ||||
| I | 0.459±0.087 | −0.038, 0.574 | −0.006±0.029 | −0.071, 0.092 |
| II | 0.468±0.089 | −0.039, 0.584 | −0.006±0.029 | −0.072, 0.094 |
| III | 0.469±0.084 | −0.037, 0.556 | −0.006±0.029 | −0.073, 0.089 |
| IV | 0.461±0.088 | −0.034, 0.567 | −0.005±0.028 | −0.057, 0.109 |
| V | 0.465±0.088 | −0.035, 0.571 | −0.005±0.027 | −0.062, 0.113 |
| VI | 0.469±0.084 | −0.035, 0.556 | −0.005±0.027 | −0.058, 0.107 |
| 2×(coancestry coefficient) | 0.574±0.022 | 0.500, 0.652 | - | - |
| Full-sibs (48 pairs) | ||||
| I | 0.489±0.143 | −0.042, 1.017 | 0.290±0.188 | 0.004, 1.011 |
| II | 0.498±0.146 | −0.042, 1.036 | 0.294±0.191 | 0.004, 1.027 |
| III | 0.515±0.159 | −0.041, 0.985 | 0.306±0.206 | 0.004, 0.986 |
| IV | 0.488±0.146 | −0.042, 1.008 | 0.283±0.186 | 0.005, 1.032 |
| V | 0.491±0.147 | −0.042, 1.015 | 0.284±0.186 | 0.005, 1.029 |
| VI | 0.514±0.159 | −0.041, 0.984 | 0.307±0.204 | 0.005, 0.984 |
| 2×(coancestry coefficient) | 0.575±0.016 | 0.531, 0.605 | - | - |
| Half-sibs (23,941 pairs) | ||||
| I | 0.205±0.073 | −0.118, 0.436 | 0.003±0.020 | −0.066, 0.168 |
| II | 0.208±0.074 | −0.120, 0.444 | 0.003±0.019 | −0.067, 0.171 |
| III | 0.212±0.074 | −0.119, 0.438 | 0.003±0.021 | −0.067, 0.168 |
| IV | 0.201±0.072 | −0.109, 0.439 | 0.003±0.019 | −0.058, 0.202 |
| V | 0.203±0.072 | −0.110, 0.442 | 0.003±0.021 | −0.059, 0.202 |
| VI | 0.210±0.073 | −0.110, 0.439 | 0.004±0.020 | −0.061, 0.201 |
| 2×(coancestry coefficient) | 0.341±0.023 | 0.250, 0.508 | - | - |
For the swine sample, the average genomic additive relationships were almost the same as those of ‘2×(coancestry coefficient)’ calculated from the pedigree data. The genomic additive relationships of Definitions I-VI were 0.513–0.534 for parent offspring, 0.526–0.543 for full-sibs and 0.289–0.299 for half-sibs, compared to ‘2×(coancestry coefficient)’ average value of 0.528 for parent offspring, 0.530 for full-sibs, and 0.294 for half-sibs (Table 3).
Table 3. Genomic and pedigree relationships of the swine sample.
| Definition | Additive | Dominance | ||
| Mean±SD | Range | Mean±SD | Range | |
| Parent-offspring (3518 pairs) | ||||
| I | 0.534±0.090 | 0.334, 0.856 | 0.033±0.066 | −0.137, 0.368 |
| II | 0.517±0.087 | 0.324, 0.829 | 0.032±0.064 | −0.132, 0.356 |
| III | 0.523±0.043 | 0.376, 0.691 | 0.029±0.060 | −0.148, 0.300 |
| IV | 0.533±0.108 | 0.321, 0.924 | 0.038±0.084 | −0.130, 0.618 |
| V | 0.513±0.099 | 0.310, 0.880 | 0.030±0.065 | −0.116, 0.414 |
| VI | 0.522±0.044 | 0.369, 0.685 | 0.026±0.059 | −0.139, 0.278 |
| 2×(coancestry coefficient) | 0.528±0.031 | 0.500, 0.723 | - | - |
| Full-sibs (1441 pairs) | ||||
| I | 0.543±0.100 | 0.300, 0.891 | 0.272±0.087 | 0.044, 0.598 |
| II | 0.526±0.097 | 0.290, 0.862 | 0.263±0.084 | 0.042, 0.579 |
| III | 0.529±0.067 | 0.284, 0.726 | 0.265±0.074 | 0.044, 0.499 |
| IV | 0.542±0.112 | 0.290, 0.938 | 0.287±0.138 | 0.017, 1.063 |
| V | 0.522±0.105 | 0.287, 0.889 | 0.257±0.103 | 0.015, 0.691 |
| VI | 0.527±0.067 | 0.278, 0.719 | 0.262±0.081 | 0.016, 0.528 |
| 2×(coancestry coefficient) | 0.530±0.037 | 0.500, 0.692 | - | - |
| Half-sibs (23,628 pairs) | ||||
| I | 0.299±0.091 | −0.037, 0.830 | 0.028±0.049 | −0.136, 0.551 |
| II | 0.289±0.088 | −0.036, 0.804 | 0.027±0.048 | −0.131, 0.533 |
| III | 0.295±0.073 | −0.034, 0.660 | 0.026±0.047 | −0.124, 0.413 |
| IV | 0.298±0.097 | −0.030, 0.932 | 0.031±0.060 | −0.147, 0.816 |
| V | 0.286±0.091 | −0.034, 0.886 | 0.026±0.049 | −0.138, 0.611 |
| VI | 0.293±0.071 | −0.032, 0.662 | 0.025±0.048 | −0.122, 0.438 |
| 2×(coancestry coefficient) | 0.294±0.039 | 0.250, 0.525 | - | - |
Genomic additive relationships from the swine sample were clearly more consistent with the pedigree relationships than those from the Holstein sample. This difference likely was due to two factors. First, most Holstein cattle with SNP genotypes were distributed in the last 3–5 generations of the pedigree that approximately comprised of ten generations [17], whereas pigs with SNP data were distributed across the entire swine pedigree (S1 Figure). Consequently, the Holstein cattle with SNP genotypes on average were subjected to more generations of genetic sampling than the pigs with SNP genotypes, resulting in less genomic relationships among the Holstein cattle. Second, sources of samples could have contributed to different degrees of genomic relatedness: the Holstein sample was from a diverse source of three companies and five universities [18], whereas the swine sample was from one company only [19]. In both Holstein and swine samples, genomic correlations of Definitions III and VI had mean additive correlations that were slightly closer to the mean of pedigree additive relationships (Tables 2 and 3). This slight advantage could be the reason why Definitions III and VI had better genomic inbreeding coefficients, as to be shown. Overall, the average genomic additive relationships were remarkably consistent with the theoretical expectation of ‘2×(coancestry coefficient)’.
For genomic dominance relationships, only full-sibs are expected to have dominance relationship value of 0.25 assuming no inbreeding. Parent-offspring and half-sibs are expected to have no dominance relationship. The observed genomic dominance relationships were consistent with these theoretical expectations. The average genomic dominance relationships of Definitions I-VI were 0.283–0.306 in the Holstein sample and were 0.257–0.272 in the swine sample for full-sibs, and were nearly zero for parent-offspring and half-sibs in both samples. The higher mean values of genomic dominance relationships of full-sibs in the Holstein sample were due to the three outliers that were nearly ‘1’ among the 48 data points (Fig. 1). With the removal of those three outliers that likely were identical twins, the mean of additive relationships drops to 0.228 for Definition I to 0.237 for Definition VI, and the mean of dominance relationships drops to 0.231 for Definition V or 0.249 for Definition VI. Overall, the average genomic dominance relationships were also remarkably consistent with the theoretical expectations.
Realized versus expected relatedness
Genomic and pedigree relationships had a major difference: genomic relationships had individual genomic specificity and large variations not observed in pedigree relationships. For the Holstein sample, the range of genomic additive relationships was −0.039 to 0.584 for parent-offspring, compared to pedigree relationships of 0.500–0.653; −0.042 to 1.036 for full-sibs (the 1.036 value likely was due to identical twins), compared to pedigree relationships of 0.531–0.605; and −0.120 to 0.444 for half-sibs, compared to pedigree relationships of 0.250–0.508 (Table 2). For the swine sample, the range of genomic additive relationships was 0.310–0.924 for parent-offspring, compared to pedigree relationships of 0.500–0.692; 0.278–0.938 for full-sibs, compared to pedigree relationships of 0.531–0.605; and −0.030 to 0.932 for half-sibs, compared to pedigree relationships of 0.250–0.525 (Table 3). Genomic dominance relationships also had large variations (Tables 2 and 3). These large variations indicate that genomic relationships can be used to find least related genomes within the same family or among closely related individuals on the pedigree. This is important for minimizing genomic similarity in breeding plans and wildlife conservation, particularly in populations with small effective population sizes such as in endangered species. In contrast, pedigree relationships generally do not reflect real variations of genomic relatedness because genomic and pedigree relationships were mostly uncorrelated except for the case of half-sibs where the correlation between genomic and pedigree additive relationships was 0.212–0.216 for the Holstein sample and was 0.141–0.247 for the swine sample (S1 Table). These results indicate that using pedigree relationships to select individuals with least related genomes would have only limited success. Genomic relationships can be viewed as the realized genetic relationships among individuals, because each individual's genome is the realization of various factors affecting an individual's genetic composition, including genetic sampling from parents to offspring, recombination, selection and mating systems over generations, whereas pedigree relationships do not consider all these factors. Therefore, genomic relationships should be preferred to pedigree relationships for measuring genomic relatedness of different individuals.
Genomic inbreeding coefficients
We compared four methods for calculating genomic inbreeding coefficients: i) Using the individual's diagonal element of genomic additive relationship based on the SNP model matrix for genomic prediction: 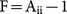 , where
, where 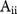 = the
= the 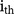 diagonal element of
diagonal element of 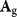 by Definition I, II, IV or V from the SNP model matrix for genomic prediction; ii) Using the individual's diagonal element of genomic additive relationship designed for calculating inbreeding coefficient (not from SNP model matrix for genomic prediction) [4], [12]:
by Definition I, II, IV or V from the SNP model matrix for genomic prediction; ii) Using the individual's diagonal element of genomic additive relationship designed for calculating inbreeding coefficient (not from SNP model matrix for genomic prediction) [4], [12]: 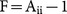 , where
, where 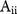 = the
= the 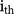 diagonal element of Definition IVb; iii) Using parental genomic additive relationship:
diagonal element of Definition IVb; iii) Using parental genomic additive relationship: 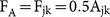 (Equation 35 using
(Equation 35 using 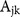 from Definition I, II, IV or V); and iv) Using parental genomic additive correction:
from Definition I, II, IV or V); and iv) Using parental genomic additive correction: 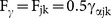 (Equation 36 using
(Equation 36 using 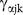 from Definition III or VI). The swine sample was used to compare these four methods (Table 4). The averages of genomic inbreeding coefficients of Methods ii)-iv) were close to the average of pedigree inbreeding coefficients, whereas the averages of genomic inbreeding coefficients Methods i) had the largest departure from the average of pedigree inbreeding coefficients. Method iv) using
from Definition III or VI). The swine sample was used to compare these four methods (Table 4). The averages of genomic inbreeding coefficients of Methods ii)-iv) were close to the average of pedigree inbreeding coefficients, whereas the averages of genomic inbreeding coefficients Methods i) had the largest departure from the average of pedigree inbreeding coefficients. Method iv) using 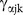 had exactly the same or almost the same largest inbreeding coefficient as that from the pedigree, whereas Methods i) and ii) all had much larger variations of inbreeding coefficients measured by SD and the range of the inbreeding coefficient estimates. Method iv) using
had exactly the same or almost the same largest inbreeding coefficient as that from the pedigree, whereas Methods i) and ii) all had much larger variations of inbreeding coefficients measured by SD and the range of the inbreeding coefficient estimates. Method iv) using 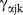 of Definition VI had the highest correlation (r) with pedigree inbreeding coefficients (r = 0.434), followed by Method iv) using
of Definition VI had the highest correlation (r) with pedigree inbreeding coefficients (r = 0.434), followed by Method iv) using 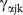 of Definition III (r = 0.419), Method iii) using
of Definition III (r = 0.419), Method iii) using 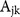 from Definitions I, II, IV and V (r = 0.367–0.380), Method ii) of Yang et al.
[4] (r = 0.305), and Method i) using
from Definitions I, II, IV and V (r = 0.367–0.380), Method ii) of Yang et al.
[4] (r = 0.305), and Method i) using 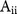 from Definitions I, II, IV and V (r = 0.071–0.131) (Table 5). While having the highest correlation with pedigree inbreeding coefficients, Method iv) as a method using parental SNP data also maintained most of the genomic specificity of the methods using the individual's own SNP data as discussed below.
from Definitions I, II, IV and V (r = 0.071–0.131) (Table 5). While having the highest correlation with pedigree inbreeding coefficients, Method iv) as a method using parental SNP data also maintained most of the genomic specificity of the methods using the individual's own SNP data as discussed below.
Table 4. Statistical summary of genomic inbreeding coefficients of 1022 individuals with genotyped parents in the swine sample.
| Method | Short name, source of Aii, Ajk or γαjk | Mean±SD | Range | |
| i) | F = Aii–1 | F-I, Aii of Equation 23 | 0.013±0.098 | −0.156, 0.436 |
| F = Aii–1 | F-II, Aii of Equation 25 | −0.019±0.095 | −0.183, 0.390 | |
| F = Aii–1 | F-IV, Aii of Equation 27 | 0.009±0.132 | −0.197, 0.541 | |
| F = Aii–1 | F-V, Aii of Equation 29 | −0.026±0.120 | −0.220, 0.478 | |
| ii) | F = Aii–1 | F-IVb, [4], [12] | 0.024±0.056 | −0.098, 0.309 |
| iii) | FA = 0.5Ajk | FA-I, Ajk of Equation 23 | 0.026±0.048 | −0.060, 0.190 |
| FA = 0.5Ajk | FA –II, Ajk of Equation 25 | 0.025±0.046 | −0.058, 0.184 | |
| FA = 0.5Ajk | FA –IV, Ajk of Equation 27 | 0.028±0.048 | −0.062, 0.199 | |
| FA = 0.5Ajk | FA –V, Ajk of Equation 29 | 0.025±0.045 | −0.058, 0.188 | |
| iv) | Fγ = 0.5γαjk | Fγ-III, γαjk from Equations 33 and 25 | 0.024±0.043 | −0.061, 0.159 |
| Fγ = 0.5γαjk | Fγ-VI, γαjk from Equations 33 and 29 | 0.023±0.042 | −0.059, 0.154 | |
| Pedigree | Fp | - | 0.021±0.024 | 0.000, 0.159 |
Table 5. Correlation (r) between genomic and pedigree inbreeding coefficients.
| F-II | F-IV | F-V | F-IVb | FA-I | FA-II | FA-IV | FA-V | Fγ-III | Fγ-VI | Fp | |
| F-I | 1.000 | 0.986 | 0.988 | 0.867 | 0.806 | 0.806 | 0.811 | 0.804 | 0.768 | 0.753 | 0.131 |
| F-II | 0.986 | 0.988 | 0.867 | 0.806 | 0.806 | 0.811 | 0.804 | 0.768 | 0.753 | 0.131 | |
| F-IV | 0.999 | 0.790 | 0.763 | 0.763 | 0.772 | 0.763 | 0.717 | 0.700 | 0.071 | ||
| F-V | 0.794 | 0.761 | 0.761 | 0.769 | 0.761 | 0.716 | 0.700 | 0.080 | |||
| F-IVb | 0.834 | 0.834 | 0.837 | 0.835 | 0.823 | 0.820 | 0.305 | ||||
| FA-I | 1.000 | 0.997 | 0.998 | 0.993 | 0.988 | 0.377 | |||||
| FA-II | 0.997 | 0.998 | 0.993 | 0.988 | 0.377 | ||||||
| FA-IV | 0.999 | 0.987 | 0.997 | 0.367 | |||||||
| FA-V | 0.990 | 0.985 | 0.380 | ||||||||
| Fγ-III | 0.989 | 0.419 | |||||||||
| Fγ-VI | 0.434 |
F-I, F-II, F-IV, F-V, F-IVb, FA-I, FA-II, FA-IV, FA-V, Fγ-III and Fγ-VI are defined in Table 4. Fp is the pedigree inbreeding coefficient.
The individual-by-individual comparison of Methods i), ii) and iv) with the pedigree method showed that Method iv) had similar patterns of the deviations as Method i) and ii) from the pedigree estimates of inbreeding coefficients and maintained most of the individual genomic specificity of a realized inbreeding coefficient. Fig. 3 shows that the three representative genomic methods for estimating inbreeding coefficient mostly had similar patterns of deviations from the pedigree estimates, but F-I (Method i) had the largest variations and Fγ-VI (Method iv) had the smallest variations. For the group of individuals marked by ‘A’, all three genomic methods had high inbreeding coefficients whereas the pedigree method had ‘0’ inbreeding coefficients. These large differences between the genomic and pedigree estimates could have been due to pedigree errors or missing pedigree information. If either problem were true, this would be an example showing the usefulness of genomic inbreeding in the absence of pedigree information or in the presence of pedigree errors. For the group of individuals marked ‘B’, all three genomic methods had lower inbreeding coefficients than the pedigree estimates that were among the highest inbreeding coefficients in this sample. The correlation of inbreeding coefficients was 0.70–0.75 between Method iv) and Method i), and was 0.82 between Method iv) and Method ii), indicating that Method iv) maintained most of the genomic specificity of Methods i) and ii) while having the highest correlation with pedigree inbreeding coefficients (Table 5). Method iv) and the other methods (including the ROH method to be discussed) could be complementary methods for calculating genomic inbreeding coefficients: Method iv) for predicting offspring inbreeding level using parental SNP genotypes even before the offspring were born, and the other methods for calculating genomic inbreeding coefficient using the individual's own SNP genotypes. Method iv) could be a useful genomic tool for managing inbreeding levels in breeding plans and wildlife conservation by calculating the predicted inbreeding coefficients for all hypothetical offspring of all possible mates and by selecting the mates with the lowest predicted offspring inbreeding coefficients, similar to the approach of a software for minimizing inbreeding in breeding plans using pedigree information [20].
Figure 3. Comparison of three methods for calculating genomic inbreeding coefficients with pedigree inbreeding coefficients using a swine sample of 1022 individuals with genotyped parents.
The three representative genomic methods for estimating inbreeding coefficient mostly had similar patterns of deviations from the pedigree estimates, but F-I (Method i) had the largest variations and Fγ-VI (Method iv) had the smallest variations. For the group of individuals marked by ‘A’, all three genomic methods had high inbreeding coefficients whereas the pedigree method had ‘0’ inbreeding coefficients. For the group of individuals marked ‘B’, all three genomic methods had lower inbreeding coefficients than the pedigree estimates that were among the highest inbreeding coefficients in this sample.
The high correlation between genomic inbreeding coefficients from Method iv) and pedigree inbreeding coefficients likely was due to two reasons. First, genomic correlations had smaller variations than genomic relationships, SD = 0.043–0.044 for Definitions III and VI of genomic additive correlations, and SD = 0.087–0.108 for Definitions I, II IV and V of genomic additive relationships (Table 3). Second, Method iv) used the same theoretical formula as pedigree inbreeding coefficient, i.e., inbreeding coefficient of the individual = coancestry coefficient of the parents, except that Method iv) uses parental SNP genotypes and pedigree inbreeding coefficient uses parental pedigree information. Within Method iv), the substantially higher correlation of Equation 36 than Equation 35 with the pedigree approach could be due to the fact that the genomic 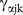 average values of Definition VI were closer to the pedigree average
average values of Definition VI were closer to the pedigree average 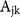 than genomic
than genomic 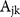 values of Definitions I, II, IV and V, as shown in Tables 2 and 3. The exact reason why genomic inbreeding coefficients using the individual's diagonal genomic additive relationship of Definitions I, II, IV and V had the lowest correlation with pedigree estimates was unclear, but two potential reasons could be identified. First, the diagonal elements of Definitions I, II, IV and V fluctuated above and below ‘1’ (S2 Figure) so that about half of the individuals had diagonal values below ‘1’. Second, diagonal elements of genomic relationships had large variations (Table 6, S2 Figure). It is worth noting that Definition IV had the largest variations in genomic relationships (additive and dominance), and its genomic inbreeding coefficient had the least correlation with pedigree inbreeding coefficient (r = 0.071, Table 5). Method ii) was a substantial improvement over Method i) in correlation with pedigree estimates, r = 0.305 for Method ii), compared to r = 0.071–0.131 for Method i). However, diagonal elements used by Method ii) also had a large number of individuals with diagonal elements less than ‘1’ (S2 Figure). The averages of diagonal elements of Definitions I, II, VI and V used by Method i) and Definition IVb used by Method ii) were about ‘1’ for the Holstein sample compared to the average of 1.05 of the pedigree diagonal values, and were 1.033–1.036 for the swine sample compared to the average of 1.017 of the pedigree diagonal values (Table 6).
values of Definitions I, II, IV and V, as shown in Tables 2 and 3. The exact reason why genomic inbreeding coefficients using the individual's diagonal genomic additive relationship of Definitions I, II, IV and V had the lowest correlation with pedigree estimates was unclear, but two potential reasons could be identified. First, the diagonal elements of Definitions I, II, IV and V fluctuated above and below ‘1’ (S2 Figure) so that about half of the individuals had diagonal values below ‘1’. Second, diagonal elements of genomic relationships had large variations (Table 6, S2 Figure). It is worth noting that Definition IV had the largest variations in genomic relationships (additive and dominance), and its genomic inbreeding coefficient had the least correlation with pedigree inbreeding coefficient (r = 0.071, Table 5). Method ii) was a substantial improvement over Method i) in correlation with pedigree estimates, r = 0.305 for Method ii), compared to r = 0.071–0.131 for Method i). However, diagonal elements used by Method ii) also had a large number of individuals with diagonal elements less than ‘1’ (S2 Figure). The averages of diagonal elements of Definitions I, II, VI and V used by Method i) and Definition IVb used by Method ii) were about ‘1’ for the Holstein sample compared to the average of 1.05 of the pedigree diagonal values, and were 1.033–1.036 for the swine sample compared to the average of 1.017 of the pedigree diagonal values (Table 6).
Table 6. Statistical summary of diagonal values of additive and dominance relationships.
| Definition | Additive | Dominance | ||
| Mean±SD | Range | Mean±SD | Range | |
| Holstein cattle (n = 1654) | ||||
| I | 0.982±0.056 | 0.751, 1.545 | 0.984±0.058 | 0.791, 1.631 |
| II | 1.000±0.057 | 0.764, 1.573 | 1.000±0.059 | 0.804, 1.658 |
| IV | 0.983±0.066 | 0.776, 1.699 | 0.980±0.163 | 0.701, 3.104 |
| V | 0.991±0.066 | 0.783, 1.707 | 0.991±0.157 | 0.708, 3.031 |
| IVb | 0.993±0.042 | 0.874, 1.441 | - | - |
| 2×(coancestry coefficient) | 1.050±0.021 | 1.000, 1.300 | - | - |
| Swine (n = 3534) | ||||
| I | 1.033±0.105 | 0.844, 1.649 | 1.034±0.123 | 0.825, 1.852 |
| II | 1.000±0.102 | 0.817, 1.600 | 1.000±0.119 | 0.798, 1.791 |
| IV | 1.035±0.142 | 0.803, 1.924 | 1.106±0.327 | 0.676, 3.922 |
| V | 0.999±0.131 | 0.780, 1.850 | 0.999±0.219 | 0.661, 3.137 |
| IVb | 1.036±0.060 | 0.883, 1.427 | - | - |
| 2×(coancestry coefficient) | 1.017±0.027 | 1.000, 1.259 | - | - |
We were unable to make direct comparison between Method iv) and the approach of runs of homozygosity (ROH) for calculating genomic inbreeding coefficients [12], because the Holstein sample has a small number of parents with SNP genotypes and the swine sample has anonymous SNP markers with unknown chromosome position. However, based on results in this study and in Keller et al. [12], Method iv) would be competitive for calculating genomic inbreeding coefficients in terms of correlation with pedigree inbreeding coefficients. In Fig. 6 of Keller et al., the correlation between the genomic inbreeding coefficients using ROH and the pedigree inbreeding coefficients were higher than that of Yang et al. [4] (or Method ii) in this article) by less than 0.10, whereas such correlation from Method iv) was 0.114–0.129 higher than Method ii) of Yang et al. [4].
GBLUP and GREML from different definitions of genomic relationships
Definitions I-VI essentially had the same GBLUP of breeding values and dominance deviations that mostly had correlations of 0.99 among GBLUP from different definitions (S2 Table). For GREML estimates of additive and dominance heritabilities, the six definitions also had similar results except the dominance heritability of Trait 3 for which Definitions IV and V had higher estimates, 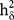 = 0.103 for Definition IV and 0.094 for Definition V, compared to
= 0.103 for Definition IV and 0.094 for Definition V, compared to 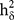 = 0.031–0.064 for the other four definitions (Table 7). The different GREML estimates of dominance heritabilities by Definitions IV and V could be due to differences between SNP dominance effects from these two definitions and those from the other definitions, see below.
= 0.031–0.064 for the other four definitions (Table 7). The different GREML estimates of dominance heritabilities by Definitions IV and V could be due to differences between SNP dominance effects from these two definitions and those from the other definitions, see below.
Table 7. Estimated genomic heritabilities from the swine sample.
| Trait | Heritability | Definition of genomic relationship or correlation | |||||
| I | II | III | IV | V | VI | ||
| 1 |
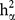
|
0.032 | 0.033 | 0.035 | 0.034 | 0.035 | 0.036 |
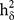
|
7.66×10−7 | 7.62×10−7 | 9.92×10−7 | 6.06×10−7 | 1.20×10−6 | 1.03×10−6 | |
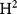
|
0.032 | 0.033 | 0.035 | 0.034 | 0.035 | 0.036 | |
| 2 |
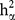
|
0.263 | 0.269 | 0.269 | 0.266 | 0.273 | 0.274 |
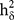
|
0.016 | 0.016 | 0.022 | 0.004 | 0.008 | 0.018 | |
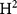
|
0.279 | 0.285 | 0.291 | 0.270 | 0.280 | 0.292 | |
| 3 |
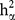
|
0.211 | 0.216 | 0.209 | 0.216 | 0.222 | 0.217 |
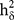
|
0.064 | 0.065 | 0.031 | 0.103 | 0.094 | 0.033 | |
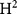
|
0.275 | 0.281 | 0.241 | 0.318 | 0.317 | 0.251 | |
| 4 |
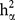
|
0.346 | 0.353 | 0.353 | 0.348 | 0.355 | 0.354 |
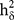
|
0.007 | 0.007 | 0.009 | 2.09×10−7 | 0.003 | 0.010 | |
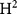
|
0.353 | 0.360 | 0.363 | 0.348 | 0.357 | 0.364 | |
| 5 |
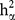
|
0.375 | 0.382 | 0.388 | 0.377 | 0.384 | 0.392 |
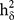
|
0.054 | 0.055 | 0.059 | 0.043 | 0.054 | 0.062 | |
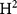
|
0.429 | 0.437 | 0.446 | 0.420 | 0.438 | 0.454 | |
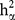 = additive heritability,
= additive heritability, 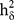 = dominance heritability, and
= dominance heritability, and 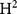 = total heritability (or heritability in the broad sense).
= total heritability (or heritability in the broad sense).
SNP additive and dominance effects
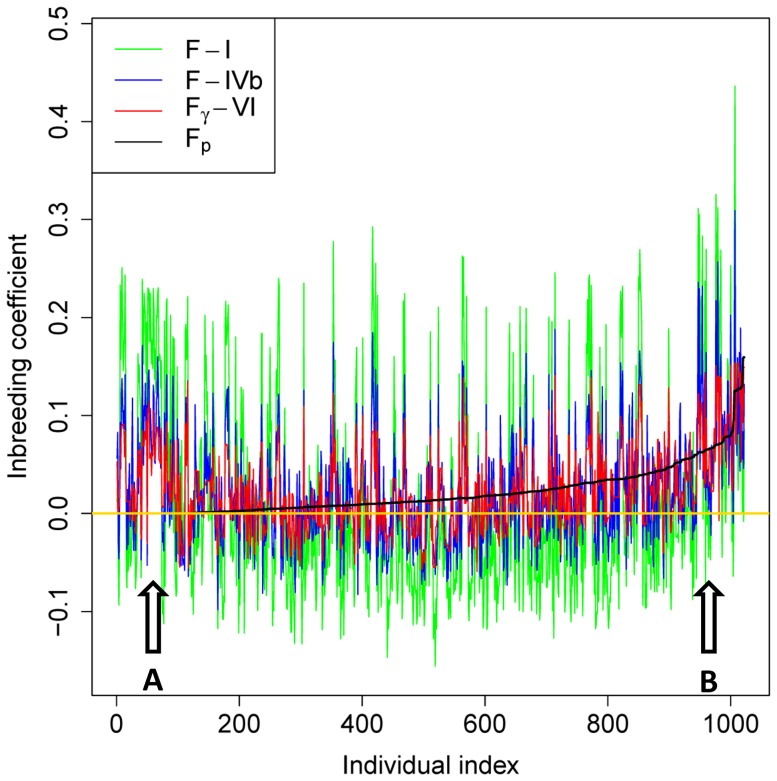
Fig. 4 shows the distribution of SNP additive and dominance effects from Definitions I-VI and correlations of SNP effects between different definitions of genomic relationships. Both additive and dominance SNP effects had bell-shape distributions, but dominance effects (blue histograms in diagonal graphs) had a much narrower distribution than additive effects (red curves in diagonal graphs), consistent with the low dominance heritability and high additive heritability of the trait. By the sizes and distributions of SNP additive and dominance effects, the six definitions could be divided into two groups: Definitions I-III under the assumption of ‘equal SNP effects’ or ‘across-SNP standardization’ as one group, and Definitions IV-VI under the assumption of ‘equal SNP variance’ or ‘within-SNP standardization’ as the other group. Graphs in the upper green box showed virtually identical additive and dominance effects from Definitions I-III. The lower green box showed virtually identical additive effects from Definitions IV-VI, and somewhat different dominance effects between Definition IV and Definitions V-VI. Graphs in the gold box showed similar additive effects between Definitions I-III and IV-VI although Definition VI led to substantially better estimates of genomic inbreeding coefficients (Tables 4 and 5, Fig. 3), and graphs in the pink box showed that the differences between Definitions I-III and IV-VI were mainly in the highest and lowest dominance effects. The use of ‘expected SNP variance’ (Definitions I and IV) or ‘sample SNP variance’ (Definitions II and V) had similar SNP additive and dominance effects (gold and pink boxes).
Figure 4. Distribution of SNP additive and dominance effects from Definitions I-VI and QQ plots of SNP effects relative to Definition I.
All graphs of this figure are based on Trait 5 with 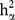 = 0.375–0.392 and
= 0.375–0.392 and 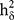 = 0.043–0.062 (Table 5). Definitions I-III in the upper green box assume equal SNP effects or across-SNP standardization, and Definitions IV-VI in the lower green box assume equal SNP variance or within-SNP standardization. Diagonal graphs are distributions of SNP additive effects (red curves) and SNP dominance effects (blue histograms). Off-diagonal graphs are QQ plots relative to Definition I, with r = correlation coefficient in each graph. The lower off-diagonal graphs of QQ plots of SNP additive effects, and the upper off-diagonal graphs are the QQ plots of SNP dominance effects.
= 0.043–0.062 (Table 5). Definitions I-III in the upper green box assume equal SNP effects or across-SNP standardization, and Definitions IV-VI in the lower green box assume equal SNP variance or within-SNP standardization. Diagonal graphs are distributions of SNP additive effects (red curves) and SNP dominance effects (blue histograms). Off-diagonal graphs are QQ plots relative to Definition I, with r = correlation coefficient in each graph. The lower off-diagonal graphs of QQ plots of SNP additive effects, and the upper off-diagonal graphs are the QQ plots of SNP dominance effects.
Conclusions
The traditional quantitative genetics model was shown to be a unifying model to derive genomic additive and dominance relationships and genomic inbreeding coefficients. Genomic additive and dominance relationships between individuals on average agreed well with the pedigree relationship, but genomic relationships were realized genetic relationships with individual genomic specificity and had large variations not observed from pedigree relationships. Genomic relationships assuming equal SNP variances had larger variations than assuming equal SNP effects. Genomic inbreeding coefficients calculated from parental genomic correlations had high correlations with pedigree inbreeding coefficients and could be an effective genomic tool for predicting offspring inbreeding levels in breeding plans.
Supporting Information
Pedigree of the swine sample with 3534 individuals.
(PDF)
Diagonal elements of genomic additive and dominance relationships and pedigree additive relationships of the swine sample with 3534 individuals. Definition IVb of diagonal elements of additive relationships was that of Yang et al. [4]. Pedigree inbreeding coefficient was calculated by Pedigraph 2.4 [21].
(PNG)
Correlations between genomic additive and dominance relationships under Definitions I-IV and pedigree additive relationship measured by ‘2×(coancestry coefficient)’.
(PDF)
Correlations of breeding values, dominance deviations and total genetic values under different genomic relationship definitions.
(PDF)
Proofs and animal data.
(PDF)
Data Availability
The authors confirm that, for approved reasons, some access restrictions apply to the data underlying the findings. The swine sample can be found from: Cleveland MA, Hickey JM, Forni S (2012) A common dataset for genomic analysis of livestock populations. G3: Genes| Genomes| Genetics 2: 429–435. The Holstein data samples can be obtained by contacting Dr. Tad Sorenson, Animal Genomics and Improvement Laboratory Research Geneticist (Animals) (tad.sonstegard@ars.usda.gov).
Funding Statement
This research was supported by United States Department of Agriculture (USDA) National Institute of Food and Agriculture Grant no. 2011-67015-30333 and by project MN-16-043 of the Agricultural Experiment Station at the University of Minnesota. The Holstein SNP data were supported by National Research Initiative Competitive Grant no. 2008-35205-18846 from the USDA National Institute of Food and Agriculture and by a financial contribution from Holstein Association USA. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Nejati-Javaremi A, Smith C, Gibson J (1997) Effect of total allelic relationship on accuracy of evaluation and response to selection. Journal of Animal Science 75:1738–1745. [DOI] [PubMed] [Google Scholar]
- 2. VanRaden P (2008) Efficient methods to compute genomic predictions. Journal of Dairy Science 91:4414–4423. [DOI] [PubMed] [Google Scholar]
- 3. Hayes B, Goddard M (2010) Genome-wide association and genomic selection in animal breeding. Genome 53:876–883. [DOI] [PubMed] [Google Scholar]
- 4. Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, et al. (2010) Common SNPs explain a large proportion of the heritability for human height. Nature Genetics 42:565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Da Y, Wang S (2013) Joint genomic prediction and estimation of variance components of additive and dominance effects using SNP markers. Abstract P1004. Plant and Animal Genome XXI, January 12–16, 2013. San Diego. Available: https://pag.confex.com/pag/xxi/webprogram/Paper7396.html. Accessed 2014 Nov 30.
- 6. Da Y, Wang C, Wang S, Hu G (2014) Mixed model methods for genomic prediction and variance component estimation of additive and dominance effects using SNP markers. PLOS ONE 9:e87666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Su G, Christensen OF, Ostersen T, Henryon M, Lund MS (2012) Estimating additive and non-additive genetic variances and predicting genetic merits using genome-wide dense single nucleotide polymorphism markers. PLOS ONE 7:e45293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Vitezica ZG, Varona L, Legarra A (2013) On the additive and dominant variance and covariance of individuals within the genomic selection scope. Genetics 195:1223–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bjelland D, Weigel K, Vukasinovic N, Nkrumah J (2013) Evaluation of inbreeding depression in Holstein cattle using whole-genome SNP markers and alternative measures of genomic inbreeding. Journal of Dairy Science 96:4697–4706. [DOI] [PubMed] [Google Scholar]
- 10. Charlesworth D, Willis JH (2009) The genetics of inbreeding depression. Nature Reviews Genetics 10:783–796. [DOI] [PubMed] [Google Scholar]
- 11. VanRaden P, Olson K, Wiggans G, Cole J, Tooker M (2011) Genomic inbreeding and relationships among Holsteins, Jerseys, and Brown Swiss. Journal of Dairy Science 94:5673–5682. [DOI] [PubMed] [Google Scholar]
- 12. Keller MC, Visscher PM, Goddard ME (2011) Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics 189:237–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Falconer DS, Mackay TFC (1996) Introduction to Quantitative Genetics. Harlow, Essex, UK: Longmans Green.
- 14.Lynch M, Walsh B (1997) Genetics and Analysis of Quantitative Traits. 23 Plumtree Road, Sunderland, MA: Sinauer Associates, Inc. 980 p.
- 15. Wright S (1922) Coefficients of inbreeding and relationship. The American Naturalist 56:330–338. [Google Scholar]
- 16. Wang C, Prakapenka D, Wang S, Pulugurta S, Runesha HB, et al. (2014) GVCBLUP: a computer package for genomic prediction and variance component estimation of additive and dominance effects. BMC Bioinformatics 15:270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ma L, Wiggans G, Wang S, Sonstegard T, Yang J, et al. (2012) Effect of sample stratification on dairy GWAS results. BMC Genomics 13:536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Cole JB, Wiggans GR, Ma L, Sonstegard TS, Lawlor TJ, et al. (2011) Genome-wide association analysis of thirty one production, health, reproduction and body conformation traits in contemporary US Holstein cows. BMC Genomics 12:408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Cleveland MA, Hickey JM, Forni S (2012) A common dataset for genomic analysis of livestock populations. G3: Genes| Genomes| Genetics 2:429–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Garbe JR, Da Y (2008) MiniInbred: a computer program for minimizing inbreeding coefficients in breeding plans. User Manual Version 2.0. Department of Animal Science, University of Minnesota. Available: http://animalgene.umn.edu/miniinbred/miniinbred_manual_2.0.pdf. Accessed 2014 Nov 30.
- 21.Garbe JR, Da Y (2008) Pedigraph: a software tool for the graphing and analysis of large complex pedigree. User manual Version 2.4. Department of Animal Science, University of Minnesota. Available: http://animalgene.umn.edu/pedigraph/. Accessed 2014 Nov 30.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Pedigree of the swine sample with 3534 individuals.
(PDF)
Diagonal elements of genomic additive and dominance relationships and pedigree additive relationships of the swine sample with 3534 individuals. Definition IVb of diagonal elements of additive relationships was that of Yang et al. [4]. Pedigree inbreeding coefficient was calculated by Pedigraph 2.4 [21].
(PNG)
Correlations between genomic additive and dominance relationships under Definitions I-IV and pedigree additive relationship measured by ‘2×(coancestry coefficient)’.
(PDF)
Correlations of breeding values, dominance deviations and total genetic values under different genomic relationship definitions.
(PDF)
Proofs and animal data.
(PDF)
Data Availability Statement
The authors confirm that, for approved reasons, some access restrictions apply to the data underlying the findings. The swine sample can be found from: Cleveland MA, Hickey JM, Forni S (2012) A common dataset for genomic analysis of livestock populations. G3: Genes| Genomes| Genetics 2: 429–435. The Holstein data samples can be obtained by contacting Dr. Tad Sorenson, Animal Genomics and Improvement Laboratory Research Geneticist (Animals) (tad.sonstegard@ars.usda.gov).