Hypothesis: Bones Toughness Arises from the Suppression of Elastic Waves

Abstract

Bone and other natural material exhibit a combination of strength and toughness that far exceeds that of synthetic structural materials. Bone's toughness is a result of numerous extrinsic and intrinsic toughening mechanisms that operate synergistically at multiple length scales to produce a tough material. At the system level however no theory or organizational principle exists to explain how so many individual toughening mechanisms can work together. In this paper, we utilize the concept of phonon localization to explain, at the system level, the role of hierarchy, material heterogeneity, and the nanoscale dimensions of biological materials in producing tough composites. We show that phonon localization and attenuation, using a simple energy balance, dynamically arrests crack growth, prevents the cooperative growth of cracks, and allows for multiple toughening mechanisms to work simultaneously in heterogeneous materials. In turn, the heterogeneous, hierarchal, and multiscale structure of bone (which is generic to biological materials such as bone and nacre) can be rationalized because of the unique ability of such a structure to localize phonons of all wavelengths.

Natural structural materials such as bone and nacre can have a resistance to fracture (toughness) that profoundly exceeds their major components. These materials appear to subvert the conflict between strength and toughness that limits the mechanical performance of synthetic materials¹,²,³,⁴,⁵,⁶. Flaw tolerance and toughness arise in natural materials due to local regions of high strain that undergo controlled deformation (plasticity) without initiating catastrophic fracture, as is the case with brittle but strong synthetic ceramics²,⁵,⁷,⁸,⁹,¹⁰,¹¹,¹². Numerous individual extrinsic and intrinsic toughening mechanisms have already been identified experimentally in bone; in fact one of the major differences between bone and synthetic materials is the presence of many different toughening mechanisms². What is lacking is a framework or principle that explains how each length scale and toughening mechanism act synergistically at the system level. We propose that the hierarchical nano- to macroscale structure of natural materials has specifically evolved to attenuate phonons, which are the elastic waves that propagate strain and thermal energy. As a direct result, bone and other natural material demonstrate surprising toughness because phonon attenuation allows multiple mechanisms to operate separately by limiting the transfer of elastic energy between areas of locally high stress. Preventing such interactions allows for greater energy dissipation and toughness by delaying the formation of a catastrophic crack⁴,⁵,¹⁰,¹³.

Bone is a nanoscale composite and the nanoscale is accepted as vitally important to bone's toughness⁷. It is also known that below a critical length scale, hydroxyapatite becomes flaw tolerant and that bone's structure can “transfer” this flaw tolerance to larger length scales⁷. The existence of nanoscale flaw tolerance has been validated by the appearance of flaw tolerant behavior in atomistic modeling⁷, experimentally¹⁴, and through scaling arguments⁷,¹⁵. Current explanations use the concept of hierarchy to explain how a flaw tolerant nanoscale can be “transferred” to the macroscale⁴,⁷,¹³. However, they cannot explain the physical origin of this flaw tolerant length scale and therefore cannot provide a mechanistic explanation as to how and under what conditions hierarchy transfers flaw tolerance to the macroscale⁴,⁷.

Ordinarily in linear fracture mechanics, the interface between collagen and hydroxyapatite acts as a weak point for the initiation of a catastrophic crack leading to brittle fracture. Bone, however, is much tougher than a homogenous sample of hydroxyapatite, its major component²,⁵,⁷,⁸,⁹,¹⁰,¹¹,¹². The difficulty in understanding arises because linear fracture mechanics cannot be applied at the atomic and nanoscales. This is due to the effective medium assumption where propagating elastic waves are not affected by the medium they travel through (λ ≫ MFP, Wavelength and Mean Free Path Respectively) being violated at small length scales by the existence of atoms, nanostructure, and surface reflections. Conversely, atomistic modeling is currently too computationally intensive to be applied to simulations of macroscale materials. In this article, we propose a novel explanation as to why heterogeneous materials can in fact lead to a tough material– by invoking the non-linear wave concept of phonon (elastic waves) localization⁴,¹⁶,¹⁷. We assert that multiscale hierarchy, material heterogeneity, and the nanoscale nature of bone are the root causes of the plasticity seen in natural materials and explain how bio-inspired tough mechanical materials can subvert the conflict between strength and toughness².

This paper is structured to first introduce the concepts of phonons and describe how wave localization and attenuation can explain how strain energy is localized in an inhomogenous medium. Developing this idea further, we explain how changes to the strain energy balance that underlies catastrophic crack propagation, changes when λ ≈ MFP (meaning a heterogenous medium such as bone) in comparison to λ ≫ MFP (a standard homogenous medium) to increase toughness. We then argues that bone's heterogeneous and multiscale structure is built on the principle of phonon localization.

Theory

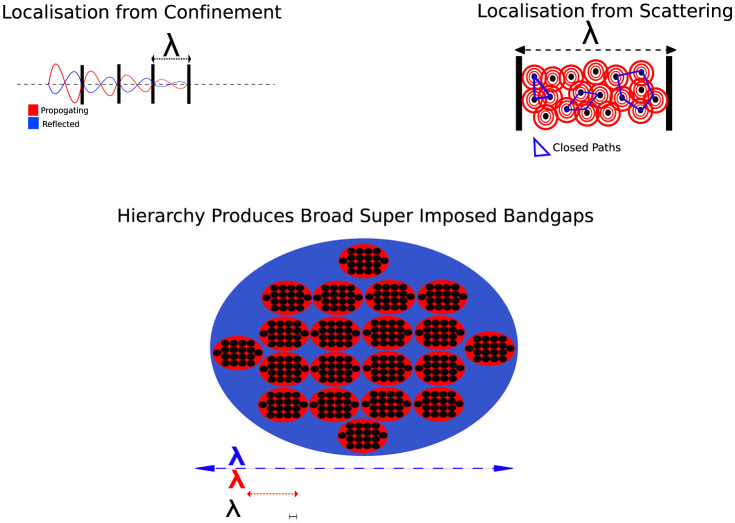
Phonons are quanta of elastic waves that are responsible for strain and thermal energy propagation. Because phonons are waves, they can be scattered, attenuated, and impeded by the medium they travel through (when λ ≈ MFP). Sufficient confinement and scattering of phonons can suppress strain propagation because the phonon amplitude decays with distance and becomes insignificant when the amplitude is smaller than the thermal and mechanical noise (Figure 1)¹⁷.

Figure 1. This figure demonstrates how a inhomogenous material can scatter waves through spatial variations in material properties and how a hierarchal structure scatters multiple wavelengths simultaneously¹⁸.

Note that with sufficient distance, on the order of a few wavelengths, the scattering of the elastic wave reduces to amplitude to the point it is smaller than thermal and mechanical noise.

Size effects and phonons are intimately related because the wavelength of phonons possible within a material is a function of the materials dimensions. In a material, the minimal resonant frequency is given by the atomic spacing, 2a, therefore any phonon in the material must be larger than 2a whilst also less than the dimension of the sample (2l).

Multiscale structures are therefore required for phonon localization in macroscale materials because a phonon can only be scattered by a structural feature that is similar in size to its wavelength and a broad spectrum of possible wavelengths are inherent in any macro scale material. In fact, bone's hierarchical structure consists of superimposed periodic variations of differing lengths (see Figure 1), resulting in superimposed bandgaps that suppress a range of phonon frequencies orders of magnitude wider than a single scale microstructure¹⁸. A way to express the degree of phonon localization in a material is to use Ψ, defined below, as the proportion of phonon energy that propagate freely throughout a material.

D(λ) = Density of States, λ = Wavelength, h = Planks Constant

Phonon localization links directly to crack propagation because it dramatically affects the energy balance that underlies fracture mechanics; the ubiquitous Griffith Criterion. The Griffith Criterion states that when redistributed strain energy released by an advancing crack is greater than energy required to open the crack, crack growth becomes self-sustaining and catastrophic fracture ensues (G_Critical > 2γ, see Figure 2). Due to the fact that crack growth is self-sustaining, no further external input of mechanical energy is required for fracture and toughness is comparatively low. As the strain energy released from the crack tip are phonons, then as Ψ →1 some and potentially all of the strain energy released during crack propagation is stopped from reaching the crack tip and sustaining further crack propagation. Strain energy that ordinarily drives catastrophic crack growth is dissipated as heat and deformation, effectively increasing the critical strain energy release rate and therefore material toughness. Previous studies have found that energy losses between the process zone and crack surface can be significant and have been observed to limit the maximum speed of crack propagation¹⁹,²⁰. As a result, Atrash et al argued that in the case of a moving crack, the Griffith Criteria should be modified to account for phonon transfer losses¹⁹,²⁰

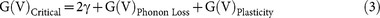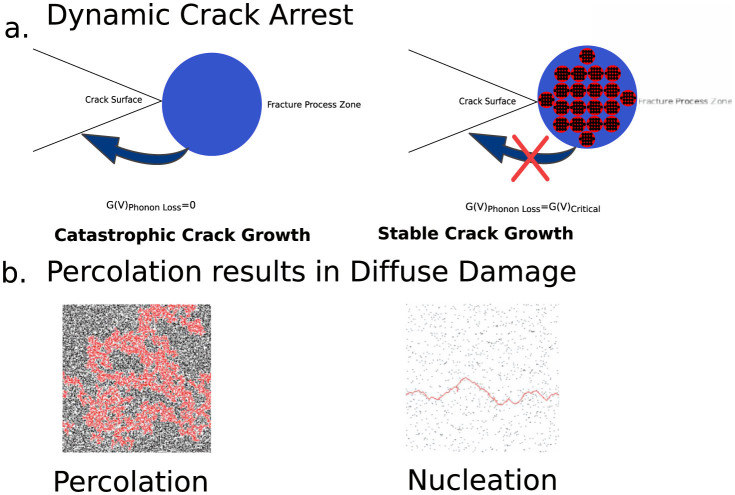
Figure 2. Phonon suppression leads to both stable crack grow of individual cracks (part A) but also eliminates the interaction of multiple cracks (part b) leading to extensive diffuse damage (black) before the final fracture (red)¹⁵.

Therefore if Ψ = 1, once a crack begins to propagate, it is dynamically arrested as G(V)_{Phonon Loss} is increased due to the disruption of energy flow between the process zone and crack tip. In practice, this is the same as utilizing materials with a large G(V)_Plasticity. In fact, we have demonstrated in this paper, through nothing more than a simple energy balance, that a material of sufficient heterogeneity can become tough precisely because it is sufficiently heterogeneous.

This is a counter-intuitive and novel result. Consider an otherwise homogenous material where the existence of a single crack and associated regions of locally high stress will quite obviously weaken the material. Yet in the case of a highly heterogeneous material with many regions of locally high stresses, such as bone, we demonstrated above that if Ψ → 1, then a material with many “defects” can be tougher than a homogenous material with a single defect. We stress that energy is not lost, but rather dissipated as heat, elastic deformation and plastic deformation. The key difference is that released strain energy is no longer able to drive self-sustaining crack growth that leads to brittle fracture instead strain energy is dissipated locally.

Beyond a single crack energy balance, phonon suppression also eliminates the long-range elastic field and hence the self-organizing avalanche-like dynamics of multiple cracks¹⁵,²¹,²². Fracture can be treated as a dynamic phase transition characterized by a continuum of two universality classes: at small scales (and large disorder) by the percolation universality class and at larger scales (and small disorder) by the pinned elastic line universality class¹⁵,²¹,²². The difference between both universality classes is the absence and presence of long-range interactions respectively¹⁵,²¹,²². Physically, the origin of the long-range elastic interactions is the phonon. Thus a flaw-tolerant, Ψ = 1 material eliminates long-range interactions between many cracks because the propagating elastic waves are suppressed¹⁵. This corresponds to the percolation universality class: a continuous phase transition characterized by extensive and diffuse localized damage and increased toughness (Figure 2b)¹⁵.

The concept of phonon localization is also elucidating because it explains why the disconnect between linear fracture mechanics and atomic modeling exists⁴. The disconnect arises because materials are made of atoms but continuum mechanics assumes that λ ≫ MFP. This assumption is made quite rationally to ensure that the resulting equations are analytically tractable. Naturally, at the atomic length scale when l → a, this assumption is not valid and Ψ →1. The physical mechanism is that defects in the atomic structure of the material and reflections at the surface of the material surface are sufficient to localize all permissible phonons.

Intriguingly, Ψ → 1 and flaw tolerance is possible at the macroscale for hierarchical materials if multiple length scales attenuate the extra phonon wavelengths that are permissible when l → macroscale¹⁶,¹⁸. The suppression of larger wavelengths is critical because as the size of the material increases, the number of possible phonons wavelengths increase, and without a larger scale structure these phonons can propagate strain energy freely.

We note that hierarchal structures approximate the case of infinite disorder in the random fuse model used by Shekhawat et al on their analysis of the effect of material disorder and size on fracture. Thus theoretically we show that through phonon attenuation a hierarchal and heterogeneous structure can increase toughness by dynamically arresting cracks and prevent existing cracks from acting co-operatively to cause catastrophic fracture.

Results

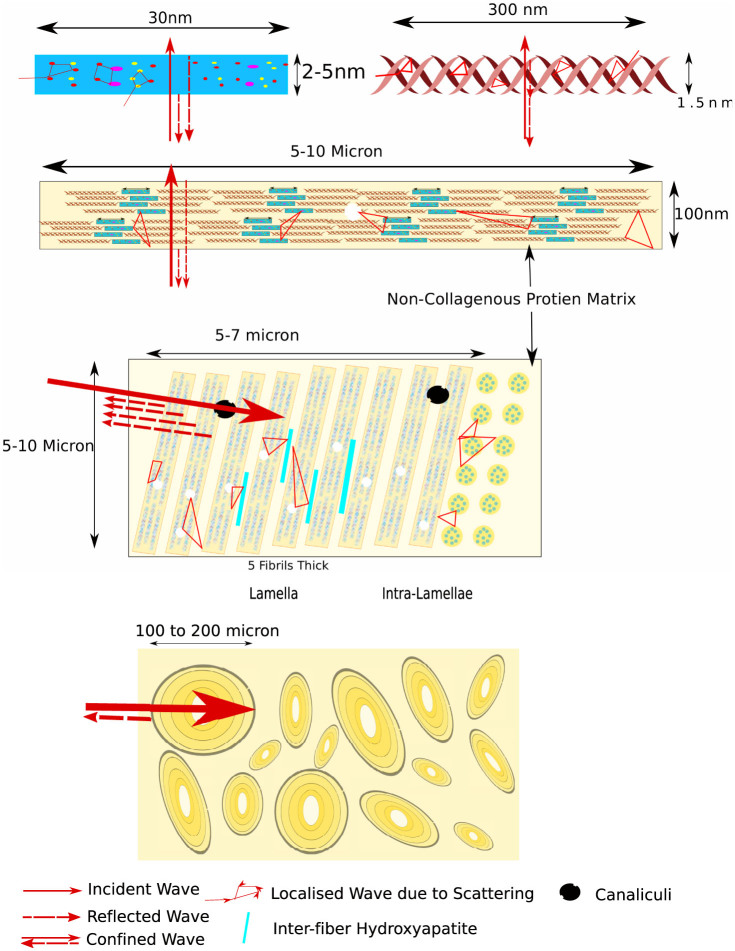
What evidence is there that bone actually suppresses phonon propagation? Bone exhibits the generic microstructure required to localize a broad wavelength of phonons: a large reflectance between collagen and hydroxyapatite (Reflectance = .83, S3) and a hierarchical structure capable of localizing multiple phonon wavelengths simultaneously⁵,¹⁷,¹⁸ (See Figure 3). We have estimated the propagating elastic energy by calculating the transmission of a wave through 3 and 5 consecutive interfaces with the same reflectance as collagen and hydroxyapatite (Reflectance = .83, S3) being .5% and .014% respectively. This corresponds to Ψ = .995 and .99986; for a single wavelength over a distance of 3 and 5 wavelengths respectively. We note that a collagen matrix when hydrated is visco-elastic, leading to the adsorption of elastic waves. Though not included in the above analysis for simplicity, this property would only serve to increase phonon attenuation because elastic energy is dissipated by the viscous component of the collagen matrix.

Figure 3. Multiscale Phonon Confinement and Localization in Bone.

The attenuation of phonons over distances only 5× the phonon wavelength is very relevant to fracture mechanics. The process zone is the region in front of the crack in which released strain energy (from crack growth) is used to grow the crack in a self-sustaining and catastrophic manner. Phonon attenuation or suppression places a limit on the size of the process zone that can contribute to self-sustaining crack growth and therefore the energy available for catastrophic crack growth. This is because released strain energy is not available to appreciably propagate energy to the crack tip and therefore do work to drive crack propagation if it is more than 5× the phonon wavelength from the crack tip. Instead the strain energy is dissipated locally as increased temperature, elastic deformation, and stable plastic deformation.

Achieving flaw tolerance is possible with homogenous structures at small length scales due to edge reflections alone, but it can be achieved at the macroscale if structural features are present similar in size to the longer wavelengths that become permissible in larger materials. Although data for bone or hydroxyapatite doesn't exist, an estimate based on crystalline semi-conductors shows that 50% of phonon energy is propagated by wavelengths greater than 2500 (+/−800) nanometers at 300 K²³. This indicates that for materials larger than a few microns in dimension, over half the phonon energy can propagate freely. Consequently, structural features to suppress the propagation of phonons with wavelengths greater than 1 micron (which also have large mean free paths) are required for flaw tolerant macroscale composites such as bone.

This mirrors the findings of a multiscale computer model by Sen et al who found that increasing structural hierarchies increase the flaw tolerant size of a material¹⁶. Bone possesses the required features: a large reflectance between collagen and hydroxyapatite (R = .83, S3) and a multiscale structure to localize multiple phonon wavelengths⁵,¹⁷,¹⁸. If only an atomic-scale microstructure is present, larger wavelength phonons are not suppressed and thus elastic interactions (and hence self-organizing crack growth) are restored in bulk materials. In bone however, hydroxyapatite and collagen form fibrils that form fibres, that in turn form lamellae, which are then arranged to produce osteons⁸,¹⁰,¹⁸,²⁴,²⁵,²⁶. This provides reflective interfaces and scattering at multiple length scales. Thus the heterogeneous nature of bone and other natural materials is rationalized by the need for large impedance mismatches to produce phonon scattering. Hierarchical structures in turn contain multiple length scales of variation in mechanical properties super-imposed upon one another to allow for much broader bandgaps than a single-scale periodic structure⁴,¹⁸. If this band gap encompasses a large proportion of the permissible phonon wavelengths then flaw tolerance, even in macroscale materials, is achieved⁴,¹⁸.

In terms of toughness, extrinsic mechanisms that operate only when a crack has formed are believed to be responsible for the majority of bone toughness; our analysis does not dispute this. Instead, we argue diffuse and stable crack growth enabled by hierarchy amplifies the effect of extrinsic toughening mechanisms–because more diffuse micro-cracks means more crack bridging, deflection, twisting, and ligament bridging–and therefore increased energy dissipation before failure²,¹⁶.

Discussion

We point out that the idea of a periodically varying stiffness inhibiting crack propagation is not novel but accepted; as demonstrated by Kolednik in the case of an individual crack using linear fracture mechanics²⁷,²⁸. These assumptions do not hold at the nanoscale because the assumption of a homogenous and isotropic medium breaks down. Consequently, this work can be viewed as extending the work of Kolednik. Our approach, unlike Kolednik's, is valid at the nanoscale and therefore allows us to explain directly how nanoscale flaw tolerance is fed to the macroscale. Furthermore our analysis can explain multiple interacting cracks, which Kolednik's work cannot; by utilizing the scaling arguments of Shekhawat et al, we can show that cracks are unable to grow co-operatively in a highly heterogeneous material¹⁵.

From a phononics perspective, we have described bone's structure as a periodic system with bandgaps combined with added scattering; this is an effective strategy to achieve at least partial suppression of 3D classical waves¹⁷. A wave scattering strategy is advantageous compared to a flaw minimization strategy because unavoidable defects–be they from accumulated damage, introduced by manufacturing, or purposely introduced for other functions (e.g Haversian canals for nutrient transport)–are integral to phonon suppression¹⁷. The flexibility and robustness of this strategy may explain the widespread use of multifunctional hierarchical materials in mammals, mollusks, and plants⁵.

The seemingly separate field of thermo-electrics provides direct experimental evidence that nano-structured materials do suppress phonon propagation and that multiscale structures can affect large and small wavelength phonons simultaneously²⁹. In fact, a multiscale structure with interfaces present at the atomic, nano, and mesoscale (reminiscent of natural materials) reduced the thermal conductivity by 50% without affecting electrical properties²⁹. Given that thermal or acoustic phonons are mechanical energy, it would be surprising in the extreme if such dramatic changes in thermal conductivity at the nanoscale are not somewhat related to similarly dramatic changes in strength and toughness seen at the nanoscale and at larger scales by hierarchical materials¹⁶.

Although this is strictly a hypothesis paper it is important to discuss the experimental evidence for and how this hypothesis can be tested. Gomopoulos et al used Brillouin light scattering to measure phonon dispersion in spider-silk, which like bone is a hierarchal material renowned for its toughness, and found that a wide phononic band gap existed³⁰. They concluded that multilevel structural organization has a major effect on the flow of the elastic energy and, to the best of their knowledge, similar band gaps are not present in synthetic semi-crystalline polymers³⁰. We stress that Gomopoulos et did not correlate band gap size to toughness but simply found a broad bandgap in silk, a material known for its toughness and multiscale structure. We note that bone theoretically has been demonstrated to possess similar bandgaps¹⁸. Testing of our hypothesis is difficult; it would require fabricating controlled hierarchal structures³,³¹, measuring their phonon dispersion³⁰,³², and mechanically testing toughness. We point out each individual experimental step has been demonstrated in principle and that it is only the combination of techniques that is novel.

Conclusion

The ultimate aim of biomimetics is to discern the design principles behind natural structures and apply them to produce superior synthetic materials. In this work, we have outlined how phonon suppression is a plausible principle to explain, at the system level, how bone's multiscale structure and multiscale extrinsic and intrinsic toughening mechanisms can operate synergistically.

Perhaps the most important aspect of this work is that techniques developed in thermal and acoustic phononics can, in theory, be directly applied to the rational design of tough bone-like mechanical metamaterials³³,³⁴,³⁵. Conversely, the hierarchal structure of natural materials could also serve as inspiration for thermoelectric materials³⁶. We hope work presented in this paper may spur the rational design of strong and tough materials with the diversity of form and function equal to that found in nature⁵.

Author Contributions

B.D. conceived and wrote the manuscript. A.K. and P.N. developed the concept and wrote the manuscript. A.M., C.D. and H.Z. were involved in discussions of the concept, reviewed the manuscript and funded the research.

Supplementary Material

Supplementary Information

Supplementary Info