An Active Patch Model for Real World Texture and Appearance Classification

Abstract

This paper addresses the task of natural texture and appearance classification. Our goal is to develop a simple and intuitive method that performs at state of the art on datasets ranging from homogeneous texture (e.g., material texture), to less homogeneous texture (e.g., the fur of animals), and to inhomogeneous texture (the appearance patterns of vehicles). Our method uses a bag-of-words model where the features are based on a dictionary of active patches. Active patches are raw intensity patches which can undergo spatial transformations (e.g., rotation and scaling) and adjust themselves to best match the image regions. The dictionary of active patches is required to be compact and representative, in the sense that we can use it to approximately reconstruct the images that we want to classify. We propose a probabilistic model to quantify the quality of image reconstruction and design a greedy learning algorithm to obtain the dictionary. We classify images using the occurrence frequency of the active patches. Feature extraction is fast (about 100 ms per image) using the GPU. The experimental results show that our method improves the state of the art on a challenging material texture benchmark dataset (KTH-TIPS2). To test our method on less homogeneous or inhomogeneous images, we construct two new datasets consisting of appearance image patches of animals and vehicles cropped from the PASCAL VOC dataset. Our method outperforms competing methods on these datasets.

1 Introduction

Visual appearance is one of the most essential cues for human vision cognition. In particular, analysis and recognition of the appearance on real-world textured surfaces/materials has been an increasingly important research topic in computer vision. It also has great significance in many applications such as remote sensing, biomedical image processing, object recognition and image segmentation. Previous texture analysis works have mainly concentrated on the recognition of material categories from a wide range of pose, viewpoint, scale and illumination variations. Accordingly, much effort has been devoted to building benchmark material datasets for texture classification, such as CuRET [8], Outex [22], Brodatz [32], KTH-TIPS [14] and KTH-TIPS2 [3]. In the left panel of Fig. 1, some example images are shown from the KTH-TIPS2 dataset [3]. As we can see, the material texture images tend to be roughly homogeneous and have frequently repeated local patterns. Although recent methods [13, 27, 28] show satisfactory results on those material datasets, these methods have not been systemically explored for the related tasks of recognizing the less homogeneous or inhomogeneous visual appearance of general object categories (e.g., animals and vehicles).

Fig. 1.

Sample images from the three types of appearance datasets studied in this paper. Left panel: material texture dataset (KTH-TIPS2); Middle panel: animal texture dataset (AniTex); Right panel: vehicle appearance dataset (VehApp). The images range from roughly homogeneous (KTH-TIPS2) to partially homogeneous (AniTex), and to inhomogeneous (VehApp). (Best viewed in color)

In order to explore less homogeneous texture and appearance, in this paper, we construct two new real-world appearance datasets (called “AniTex” and “VehApp”)¹. They include more complex and less homogeneous visual patterns than previous material datasets as shown in Fig. 1. More precisely, our AniTex and VehApp datasets include a variety of animal texture patches and vehicle appearance regions respectively, all of which are taken from the PASCAL VOC dataset [11]. From the middle panel of Fig. 1, we can see that the image patches from AniTex possess less homogeneous texture patterns compared to traditional material images. This results in larger intra-class variations and inter-class ambiguities, hindering discrimination of appearance between different categories. As shown in the right panel of Fig. 1, the inhomogeneity of appearance increases further for man-made vehicle objects, which exhibit larger visual variations spatially.

In the literature, there are different approaches for addressing the appearance classification problem. For material textures, the filter-bank-based methods [8, 16, 39] are the most widely used methods in the early stage. They typically exploit a variety of filter response features at multiple scales and orientations, to capture summary statistics for representing the texture images. Winn et. al [35] learned a universal dictionary based on these features to categorize objects. Recently, Varma et. al [33] demonstrated that local image patches can obtain better results than filter banks. They also provided theoretical arguments which justify the use of raw intensity image patches. Their approach, however, has several limitations such as some sensitivity to image rotations. For more complex and less homogeneous appearance of structural objects (e.g., animals and vehicles), some other descriptors such as SIFT [18] and HOG [7] are commonly adopted in literature, and traditional texture descriptors tend to be less investigated in these cases.

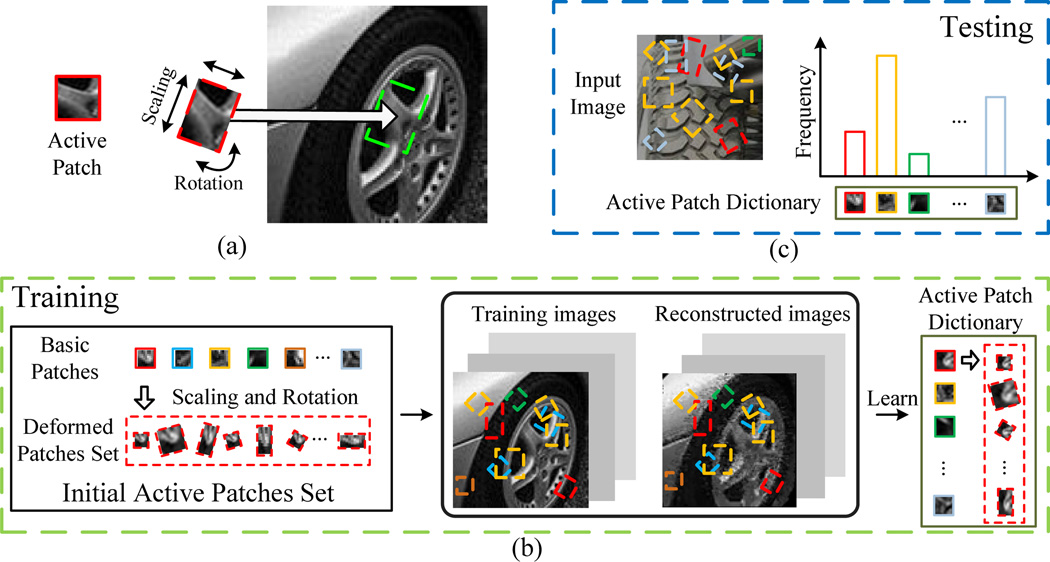
In this paper, we present a unified appearance classification method and apply it to all of the three types of datasets with different granularities of visual complexity and homogeneity. We develop a new image representation for appearance modeling and classification based on Active Patches. They are raw intensity patches which can undergo spatial transformations (e.g., rotation and scaling) and adjust themselves to fit the target image region (see Fig. 2). We use normalized cross-correlation to calculate the matching score. If the matching score is larger than a threshold, we treat it as a firing active patch for that region. Images can be reconstructed by a set of firing active patches in this way and we allow patches to overlap with each other. Compared with traditional filter-bank-based texture analysis approaches, our method, which utilizes raw intensity patches, has the advantages of being simple and intuitive. We introduce a probabilistic model based on our active patches to quantify the reconstruction quality. On the basis of this model, we propose a novel greedy learning algorithm to establish a compact yet representative active patch dictionary. Starting from a large candidate pool of active patches, our learning algorithm greedily selects the ones with high firing frequency, taking into account the criteria such as small reconstruction error and small overlapping area with other patches in the reconstructed image. For appearance classification task, we simply use the histogram of the firing frequency of the active patches in the dictionary as the image feature descriptor. In our experiments, we evaluate the proposed method on three challenging appearance/texture datasets (i.e., KTH-TIPS2 [3], AniTex and VehTex), which are illustrated in Fig. 1. The experimental results validate the effectiveness of our approach in real-world appearance classification, and show consistent performance improvement w.r.t. the previous texture classification approaches on all of the three datasets.

Fig. 2.

Illustration of our approach. (a). An active patch will take actions to best fit the image region near a target position (the green rectangle region in the image) in the best way. The actions consist of the combination of scaling and rotation. (b). To implement these actions efficiently, each active patch consists of a basic patch (e.g. the patch in the solid red rectangle in the left panel of (b)) and a deformed patches set (e.g. the patches in the dashed red rectangle). Given an image position, the active patch will find one of its deformed patches that has the maximum matching score with the image region near this position. If the score is larger than a threshold, the active patch is “fired” at the image region. In this way, the images can be reconstructed and represented by a set of firing active patches. We learn the active patch dictionary in a greedy manner using criteria based on the reconstruction of the training images. (c). The histogram of firing frequencies of the active patches in the dictionary will be treated as the feature for appearance classification. (Best viewed in color)

The main contributions of this paper are summarized as follows: (1) We present an active patch model and a probabilistic formulation to quantify the quality of images reconstructed using a set of active patches. (2) We propose a novel greedy forward feature selection algorithm to learn a compact and representative active patch dictionary based on the representation-by-reconstruction principle. (3) We build two new datasets (AniTex and VehApp) for real-world appearance recognition, which provide a comprehensive evaluation scenario for less homogeneous or inhomogeneous visual patterns than traditional material textures. Using image features based on the learned dictionary, our method consistently outperforms the previous approaches on these two datasets as well as a challenging material texture benchmark dataset (KTH-TIPS2).

2 Related work

Traditional filter-bank-based approaches [8,16, 39] have been dominant in texture analysis literature in early years. The filter banks extract salient statistical characteristics from a large support of image patch around the central pixel, and their responses can be used to represent the repeated visual patterns in texture images. Recently, the necessity of the use of filter bank was argued by many methods based on the local pixel neighborhood statistics [27, 4, 23, 30], which can capture the repeated micro-structure from relatively smaller texture patches (e.g., 3 × 3). This sort of approaches includes local binary patterns (LBP) [13,12, 23], local ternary patterns (LTP) [30], Weber local descriptor (WLD) [4], local higher statistics (LHS) [27], etc. In particular, the LHS method extends the original LBP by considering the second order statistics in local pixel intensities of a small patch using gaussian mixture model and fisher vector encoding [26]. It achieves the state-of-the-art results on several texture benchmark datasets such as KTH-TIPS2. Besides, there are some very recent works which utilize deep convolutional network [28] and semantic attributes [21] for texture analysis. However, the descriptors generated from above methods cannot be used to reconstruct the images and not very interpretable. On the other hand, Varma et. al [33] proposed a method based on intensity patches for material texture classification and demonstrated the power of using intensity patches both experimentally and theoretically.

Intensity patches have been increasingly used in the field of computer vision in recent years. In particular, patch-based methods have dominated the field of texture synthesis [9, 17]. Wolf et. al [36] used patches as an alternative to traditional filter-bank-based methods for edge detection and segmentation, but they did not use a large patch dictionary. In addition, Ullman and his collaborators used patches for object classification [10, 31] and image segmentation [2]. Coates et. al [6] exploited a single-layer network with optimal parameter settings using patches as features. Singh et. al [29] presented a mid-level patch work based on HOG descriptors to sparsely detect discriminative image regions. However, the patches used in the works mentioned above are not active and thus may not deal well with the scaling and rotation transformations of real-world appearance/ texture. In [15], an epitome framework was proposed for image representation, and was recently developed by [24, 5]. For an epitome, the basis patches spatially overlap in a single image (the epitome), which is not a constraint in this paper. Another related work is from Ye et. al [38]. It presented a deformable patch method for handwritten digit recognition. In addition, Wu et. al [37] propose a generative model for object detection based on active basis. Their active basis model consists of a small number of handcrafted Gabor wavelet filters at selected locations and orientations, which is different from our learned dictionary of raw pixel intensity active patches. Besides, their model concentrates on recognizing shape of objects and not modeling their appearance.

3 The Active Patch Model For Appearance Modeling

In Section 3.1, we introduce our active patch model and describe how to use a set of active patches to reconstruct and represent images. Then we present a probabilistic model to quantify the quality of the reconstruction in Section 3.2. A simple but effective greedy learning algorithm based on this probabilistic model will be introduced in Section 3.3 to build the active patch dictionary. Image features for classification can be generated using the dictionary. We show the implementation details in Section 3.4. Some important notations are summarized in Table 1.

Table 1.

Summary of important notations in section 3

Notation	Description	Notation	Description
𝔸	Active patch	IR(I)	Reconstructed image of I
SB	Basic patch	Ω	Training image set
𝕊D	Deformed patches set	λe, λov	Non-zero weights for energy terms
Sdt	Deformed patch in 𝕊D	M(𝔸, I, pos)	Matching score between 𝔸 & image I at pos
𝒟	Active patch dictionary	Mbest(I, pos)	Best matching score for image I at pos
𝒟o	Over-completed dictionary	$S_{d_t}^{\mathit{\text{best}}}$	Best fitted deformed patch in 𝕊D
𝒟f	Final dictionary	F (𝔸, I)	Firing frequency of 𝔸 for image I

3.1 The Active Patch Model

An active patch (denoted as 𝔸) consists of two parts: a basic patch S_B and a deformed patches set 𝕊_D (see Fig. 2(b)). The deformed patches (denoted as S_dt, t = 1, 2, …, n_T) in 𝕊_D are generated by applying various spatial transformations on the basic patch S_B. n_T is the number of the allowed transformations. The transformation, represented by T = (s^x, s^y, θ), involves combination of rotation and scaling. (s^x, s^y) denotes the width and height of the patch in its upright form after scaling. θ represents the rotation angle. Our active patches use the raw intensity pixels as basic features for its basic patch and deformed patches.

Given an input image I and a position pos, an active patch will automatically select one of its deformed patches which best fits the input image region near the position. To make the fitting robust and get rid of the redundancy for duplicate matches in the nearby positions, we apply a spatial max-pooling operation to the neighborhood positions 𝒩(pos) of pos. 𝒩(pos) is set as a 3 × 3 region centering at pos. Normalized Cross-Correlation (NCC) is adopted to calculate the matching score M(𝔸, I, pos):

$$M(𝔸,I,\mathit{\text{pos}})=\underset{\mathit{\text{pos}}\prime \in 𝒩(\mathit{\text{pos}})}{\text{max}}\underset{S_{d_t}\in {𝕊}_D}{\text{max}}\{NCC(S_{d_t},I(\text{pos}\prime ))\}$$ (1)

I(pos′) denotes the image region near pos′, which has the same dimension as S_dt. If the matching score is larger than a threshold (we use 0.8 to ensure perceptual similarity and high performance in this paper, please see supplementary material for detailed justification.), the active patch will be treated as a firing one for image I at pos. Otherwise, we will treat the position as “not fired” by this active patch.

We can learn a dictionary of active patches {𝔸⁽¹⁾, 𝔸⁽²⁾, …, 𝔸⁽ⁿ⁾} from the training set of a dataset (e.g. KTH-TIPS2, AniTex or VehApp). The dictionary size n equals to the number of different active patches. We will introduce the learning process later. Given the dictionary 𝒟, we can reconstruct the images using 𝒟. The reconstructed image I_R(I) is generated by copying the pixel value of the best fitted deformed patch of a fired active patch to the corresponding image position. Some of the image regions might not be covered by any active patches in the dictionary. We will treat the pixels in these regions as unreconstructed pixels and set the corresponding pixels in I_R(I) as void. If several fired active patches overlap over one pixel, that pixel will be set as the corresponding pixel value of the active patch with the largest matching score. We will use the quality of the reconstructed image and the compactness of the dictionary as the measurements for choosing the optimal active patch dictionary.

3.2 The Probabilistic Model as Criterion for Image Reconstruction

We model the probability of reconstructing and representing an image I by the active patch dictionary 𝒟 as an exponential distribution with energy term E(I|𝒟):

$$P(I|𝒟)=\frac{1}{|Z|}{e}^{-E(I|𝒟)}.$$ (2)

$${𝒟}^{*}=\text{arg}\underset{𝒟}{\text{min}}\sum _{I\in \Omega }E(I|𝒟).$$ (3)

We incorporate the reconstruction quality and the compactness of 𝒟 into the energy function (Equ. 4). It consists of three terms, where λ_e and λ_oυ are non-zero weights for the energy terms, #(I) denotes the number of pixels in I, p denotes the pixel value in the original image I, which is normalized to [0 1], and p_r denotes the corresponding reconstructed pixel in I_R(I).

$$E(I|𝒟)=\frac{1}{\#(I)}[\sum _{p_r\in I_R(I)}{E}_c(p_r)+{\lambda }_e·\sum _{p\in I}{E}_e(p|p_r)+{\lambda }_{o\upsilon }·\sum _{p\in I}{E}_{o\upsilon }(p|𝒟)]$$ (4)

The first term is ∑_pr∈IR(I) E_c(p_r), where E_c(p_r) = 1 if p_r = void (i.e. p_r is unreconstructed), otherwise E_c(p_r) = 0. This term encourages more reconstructed pixels.

The second term is ∑_p∈I E_e(p|p_r), where E_e(p|p_r) = |p − p_r| if p_r ≠ void, otherwise E_e(p|p_r) = 0. This term encourages a small difference of intensity value between the original image pixel and the corresponding reconstructed pixel.

The third term is ∑_p∈I E_oυ(p|𝒟), where E_oυ(p|𝒟) is set as the number of firing active patches overlapped on pixel p. This term encourages a small overlapping area for different active patches. If most of the reconstructed regions of an active patch 𝔸 overlap with those of other patches in 𝒟, it is highly possible that 𝔸 can be replaced. This term will reduce the redundancy in the dictionary and restrict the dictionary size.

The energy function of the whole training images can be calculated by Equ. 5, where #(Ω) represents the number of images in Ω.

$$E(\Omega |𝒟)=\frac{1}{\#(\Omega )}\sum _{I\in \Omega }E(I|𝒟)$$ (5)

We set λ_e and λ_oυ to get a relatively small dictionary that can reconstruct more than 90% pixels with the root-mean-square error of pixel intensity less than 0.1. In this paper, we set λ_e = 1, λ_oυ = 0.5 by cross validation on KTH-TIPS2. With these settings, we can acquire appropriate dictionaries for all the three datasets (i.e. KTH-TIPS2, AniTex and VehApp) in our experiments. Please refer to Section 4.5 to understand how performance varies with the dictionary size.

3.3 Greedy Learning of the Active Patch Dictionary

It is hard to learn the model directly because the parameter space of 𝒟 is very large. Instead, we first acquire an over-complete active patch dictionary 𝒟_o by unsupervised clustering (e.g. Kmeans) randomly sampled patches in dataset images to get the basic patches. Then we select active patches from 𝒟_o as the final dictionary 𝒟_f.

If we want to exhaustively search for the optimal 𝒟_f, we have to run the reconstruction process 2^m times, where m is the size of the 𝒟_o. This is impractical. To efficiently get the results, we adopt a fast greedy forward feature selection strategy to learn 𝒟_f and reconstruct training images at the same time (some reconstructed samples are shown in Fig. 3). This greedy algorithm sequentially selects the active patches that provide the highest reconstruction quality with the minimal redundancy. More specifically, we first

Algorithm 1.

Our learning method for active patch dictionary

Initialization:
1:	Get 𝒟o from clustering algorithm;
2:	𝒟f ← ∅; ∀Mbest(I, pos) ← 0; ∀pr ← void, pr ∈ ∀IR(I);
Process:
3:	Sort 𝔸(k) ∈ 𝒟o w.r.t. F(𝔸(k)) in descending order;
4:	for each 𝔸(k) ∈ 𝒟o do
5:	∀I ∈ Ω, record current IR(I) and Mbest(I, pos); ΔE ← 0;
6:	for each position pos of each image I ∈ Ω where 𝔸(k) is firing do
7:	for each pixel $p_d\in S_{d_t}^{\mathit{\text{best}}},S_{d_t}^{\mathit{\text{best}}}\in {𝕊}_D^{(k)}$ do
8:	Calculate ΔE according to Equ. 4;
9:	if the corresponding pr = void or M(𝔸(k), I, pos) > Mbest(I, pos) then
10:	pr ← pd; Mbest(I, pos) ← M(𝔸(k), I, pos);
11:	end if
12:	end for
13:	end for
14:	if ΔE < 0 then
15:	Add 𝔸(k) to 𝒟f
16:	else
17:	∀I ∈ Ω, restore IR(I) and Mbest(I, pos) to previous value;
18:	end if
19:	end for

sort the active patches 𝔸^(k) in 𝒟_o in the descending order of their firing frequency F(𝔸^(k)) for all the training images. F(𝔸^(k)) = ∑_I∈Ω F(𝔸^(k), I) where F(𝔸^(k), I) denotes the firing frequency of an active patch 𝔸^(k) for image I. We then check the active patches one by one. If the energy function decreases when adding 𝔸^(k) to 𝒟_f (i.e. ∆E< 0), 𝔸^(k) will be selected and its firing image regions will be reconstructed.

Fig. 3.

Sample reconstructed and the original images from VehApp and AniTex using the learned dictionaries from the two datasets respectively.

The detailed algorithm is shown in Algorithm 1. M^best(I, pos) records the current best matching score for image I at position pos for all the previously selected active patches in ${𝒟}_f·S_{d_t}^{\mathit{\text{best}}}\in {𝕊}_D^{(k)}$ is the deformed patch of an active patch 𝔸^(k) that best matches the target image region. Before each iteration of the greedy algorithm, we record the previous reconstruction state (line 5) in order to restore if the candidate active patch is not selected (line 17).

The learning algorithm is unsupervised and does not need the labels of the training images. This is an advantage because we can readily apply the algorithm to a large dataset without too much human labor.

Assuming that the learned dictionary is ${𝒟}_f=\{{𝔸}_f^{(1)},{𝔸}_f^{(2)},\dots ,{𝔸}_f^{(n)}\}$, the corresponding feature descriptor of an image I is set as the histogram of the firing frequencies of the active patches in 𝒟_f for I:

$$[F({𝔸}_f^{(1)},I),F({𝔸}_f^{(2)},I),\dots ,F({𝔸}_f^{(n)},I)]$$ (6)

We apply L1 normalization and power normalization (square root) [25] to this feature descriptor for classification taks.

3.4 Implementation Details

The possible transformations {T} applied on the basic patch S_B are described as follows. For rotation, the direction of the patches ranges from −45° to 45° with a step size of 15°. For scaling, the maximum and minimum heights of the deformed patches are 1.2× and 0.8× the height of the basic patch respectively. We adopt the same scaling setting for the width of the deformed patches. The step size for scaling is 2 pixels.

We use the Kmeans algorithm to initialize the greedy forward feature selection algorithm. The seed patches are randomly sampled from the training images. Their sizes are 10 × 10, 7 × 7, and 5 × 5. We also experimented with seed patches of larger sizes. However, it does not improve the performance. On the other hand, using larger patches requires much larger dictionaries if we want to achieve the same reconstruction ability as the small patch dictionary. We conduct zero-mean whitening [1] on seed patches before clustering them. The number of seed patches is about 500,000.

The normalized cross-correlation operation can be treated as a matrix multiplication operation if we normalize the patches and target image regions beforehand. We utilize highly optimized matrix operation packages (i.e. Matlab Distributed Computing Tool Box and CUDA with cudablas library) to efficiently calculate the matching statistics of a set of active patches. The speed of our algorithm is very fast. It takes 100 ms on average to extract the proposed feature descriptors for a KTH-TIPS2 image with a computer using one Tesla C1060 GPU.

4 Experiments

To validate the effectiveness of the active patch model, we test it on a range of real world appearance images from a roughly homogeneous dataset (KTH-TIPS2), to a partially homogeneous dataset (AniTex), and to a inhomogeneous dataset (VehApp). Some sample images of these datasets are shown in Fig. 1. The AniTex and VehApp datasets contain color images cropped from the PASCAL VOC dataset [11]. We will first introduce the details of these two datasets then compare the classification performance on all the three datasets with previous methods. Finally, the effect of the transformations and the dictionary size will be analyzed.

For a fair comparison, we use a SVM classifier with histogram intersection kernel [19] for all the methods. It is a very efficient kernel and has no hyperparameters. As most of the existing state-of-the-art texture analysis methods ([23,12,13, 27]), we focus on the analysis of gray scale texture information in the dataset images. We discuss the role of color in the supplementary material, and show that color will provide additional information and further improve the results.

4.1 The Two New Texture Datasets

The animal texture dataset (AniTex)

This dataset contains a main image set and a supplementary image set. The main image set contains 3120 texture patch images extracted randomly (i.e. cropped) from the torso region inside the silhouette of different animals in the PASCAL VOC 2012 database. Only one image will be cropped from the same object in an image. We do not re-scale or rotate the original PASCAL images before extraction. No object contour information is included. There are no background pixels and no easily identifiable features, such as the face of animals in these patch images. There are five classes of animals: cat, dog, sheep, cow and horse. Each class consists of 624 images. The size of the images in the dataset ranges from 64 × 64 to 100 × 100 pixels. The images in this database are under a range of harsh image conditions, such as scaling, rotation, viewing angle variations and lighting condition change. Some images suffer from low resolution. Occlusion sometimes occurs, such as the dog collars in some dog images and the sheepfold in some sheep images. We denote this dataset as the 3120 animal texture dataset (3120AniTex).

The supplementary image set contains 250 images of animals from the same five classes, with 50 images for each class. This dataset is built to meet the requirement of some psychophysics experiments for testing human’s performance on the classification of animals’ fur texture. We briefly discuss these experiments in section 5. The size of the images is 100 × 100 pixels. They are sampled using the same strategy as the 3120AniTex. But care was taken to select cropped regions which contained consistent textural information and no tell-tale signs of category membership (e.g., dog collars or sheepfold). There are no overlapping images between this set and the 3120AniTex set. Although the images in general are clearer than those in the 3120AniTex set, this dataset is also very challenging. The experiment shows that humans also do not perform very well in this task (see Section 5). We denote this image set as the 250 animal texture dataset (250AniTex).

For the 3120AniTex dataset, we separate it into training set and testing set randomly. There are 2496 training images and 624 testing images. We treat the 250AniTex dataset only as a testing dataset. Neither dictionary nor classifier is trained, or retrained, on this image set for any of the methods we compared in the experiments. Only the training set of 3120AniTex is available for learning the dictionary and the classifier. So the 250AniTex set can also be used to evaluate the effectiveness of algorithms on the learning transfer test. This is similar to the intuition behind the development of the KTH-TIPS2 dataset from the original KTH-TIPS dataset [3].

The vehicle appearance dataset (VehApp)

This dataset also contains a main image set and a supplementary image set. The main image set contains 13723 images cropped from the PASCAL VOC dataset. They consist of 6 kinds of vehicles: aeroplane, bicycle, car, bus, motorbike, and train. The image size is 100 × 100. The sampling strategy is similar to 3120AniTex and 250Anitex except that we allow the images to contain a small portion of background pixels (≤ 20%). The reason is that the contour of the vehicles (bicycle and motorbike in particular) is much more irregular than animals. Sometimes it is impossible to crop a 100 × 100 image patch that is totally inside the silhouette region. The large variance of the background pixels also makes this dataset challenging. We separate this image set into a training set (80%) and a testing set (20%) randomly. We denote this dataset as VehApp_crop.

To further evaluate the performance of existing method on long-range appearance patterns, we also build a supplementary image set consisting of the silhouette regions of the same kinds of vehicles. There are 2408 images in the dataset. All the images are rescaled to ensure that their height and width are both no larger than 100 pixels. We generate a foreground mask for each image and the background pixels are set to 0. All the methods are only allowed to extract features within the mask in order to insure that they only utilize the appearance information. We also separate this image set into a training set (80%) and a testing set (20%) randomly. Training and testing on this image set are independent of VehApp_crop. We denote this image set as VehApp_sih.

4.2 Performance Evaluation on AniTex and VehApp

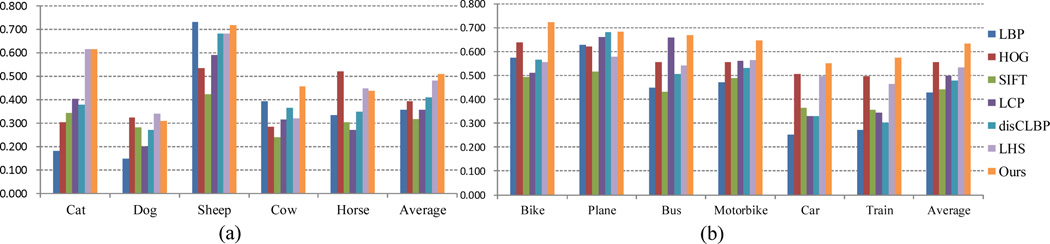
To validate the effectiveness of our algorithm on the AniTex and VehApp datasets, we compare it with four state-of-the-art texture descriptors and report their performance. They are the Local High-order Statistics (LHS) [27], the general Local Binary Patterns (LBP) [23] and two of its most recent extensions, the Discriminative Features of LBP Variants (disCLBP [13]) and the Local Configuration Pattern (LCP [12]). For LBP and disCLBP, we use the code released by the authors. For LHS, we implement the algorithm exactly according to the paper and the suggestions from the authors. We achieve similar classification accuracy of 71.1 ± 4.9 (rectangular sampling) on KTH-TIPS2 compared to 71.7 ± 5.7 reported by the original paper. The small difference might be due to the different settings of whitening or other implementation details. The feature dimension of LHS is 2048. In [27], it shows that LHS feature with larger dimension (e.g. 4096) does not improve the performance. HOG and SIFT features are extracted as the baselines in these two datasets. These two features have been successfully applied in the field of object detection and classification [7,18, 20]. We use VLFeat [34] implementation of HOG and SIFT. For HOG, the cell size is set to 10 pixels. For dense SIFT, the scale and step is set to 10 pixels and 5 pixels respectively. The bag-of-visual-word algorithm is applied to improve their performances. The number of visual words is set to 3000 for both HOG and SIFT.

The results are summarized in Table 2 and the detailed comparisons for different categories are given in Fig. 4. For our method, we learned the dictionaries of size 2799, 2981 and 2958 for AniTex, VehApp_crop and VehApp_sih respectively. Our method outperforms all the competing methods. For AniTex datasets, the performance gains are 2.7% and 6.8% on 3120AniTex and 250AniTex respectively compared to LHS (the second best performed method on 3120AniTex). The performance gains are 11.6% and 3.6% on 3120AniTex and 250AniTex respectively compared to HOG (the second best performed method on 250AniTex). In addition, for most of the categories, our algorithm is the best or the second best method. Some comparing methods might be more effective on some specific categories, such as LBP for sheep and HOG for horse. But their overall performances are much lower than our method. Since the AniTex dataset contains images under harsh real image conditions, the results show that our algorithm can handle the classification task of real world partially homogeneous texture. It is a little surprising that SIFT does not perform well in these datasets. It is perhaps because the small image size is not suitable for SIFT as discussed in [4].

Table 2.

Performance comparison on AniTex and VehApp

	LBP [23]	HOG [7]	SIFT [18]	LCP [12]	disCLBP [13]	LHS [27]	Ours
3120AniTex	35.6	39.2	31.7	35.5	40.8	48.1	50.8
250AniTex	30.4	53.2	33.6	29.6	36.8	50.0	56.8
VehAppcrop	42.9	55.6	44.0	49.8	47.8	53.3	63.4
VehAppsih	53.4	65.9	45.8	62.1	62.1	69.1	76.6

Fig. 4.

Performance comparisons on (a) 3120Anitex for the five animal categories, and (b) VehApp_crop for the six vehicle categories. (Best viewed in color)

It is also interesting to compare the results between 3120AniTex and 250AniTex. As stated in Section 4.1, the images in 250AniTex are clearer visually than those in 3120AniTex, which makes 250AniTex easier than 3120AniTex. We should expect the performance increase on 250AniTex even using the dictionary and the classifier trained by the training set of 3120AniTex. Our algorithm indeed performs better on 250AniTex than 3120AniTex with a margin of 6.0% in this training transfer experiment.

For VehApp_crop and VehApp_sih datasets, the performance gains of our method are 7.8% and 7.5% respectively compared to the second best methods. In addition, our algorithm is the best method for all the categories on VehApp_crop and four categories out of six on VehApp_sih. All the methods generally perform better on VehApp_sih than VehApp_crop because the former one provides more spatial structure information. These two datasets contain inhomogeneous appearance with more variance spatially. The high accuracy on these datasets demonstrates the capability of our algorithm to capture long-range appearance patterns.

4.3 Performance Evaluation on KTH-TIPS2

We also test our algorithm on a benchmark material texture dataset (i.e., KTH-TIPS2). It is developed based on the CUReT and KTH-TIPS, and contains more variations of scale, pose and illumination. There are 11 material categories in this dataset and each category is separated into 4 groups of samples. The samples are photographed under 9 scales, 3 poses and 4 different illumination conditions. The motivation of building this dataset is to evaluate the capability of the algorithm on previous unseen instances of materials [3]. All these settings make it an extremely challenging texture dataset. The best published result so far is 73% [27] to our best of knowledge while the highest accuracies of other traditional texture datasets are over 90%. We adopt the standard testing protocol [3, 4, 27] for this dataset: We run the classification four times and report the average accuracy. One group of samples will be treated as the testing set while the other three groups are treated as the training set at each time.

Because it is a publicly available dataset, we use the results reported by the authors of their methods for comparison. The methods are LBP [23], WLD & MWLD [4], LCP [12], Caputo et. al [3], LTP [30], and LHS [27]. We also try SIFT and HOG for this dataset. The results are shown in Table 3. Our algorithm achieves a better result than the previous best published result of LHS. Since KTH-TIPS2 is a very challenging benchmark dataset taken under the settings of the traditional material texture task, this demonstrates the effectiveness of our active patch model on homogeneous and densely repeated texture patterns with large variations of scale, pose and illumination.

Table 3.

Performance comparison on KTH-TIPS2

LBP [23]	HOG	SIFT	WLD [4]	MWLD [4]	LCP [12]	Caputo [3]	LTP [30]	LHS [27]	Ours
53.6	63.5	52.7	56.4	64.7	60.8	71.0	71.3	73.0	75.7

4.4 Active vs. Non-Active

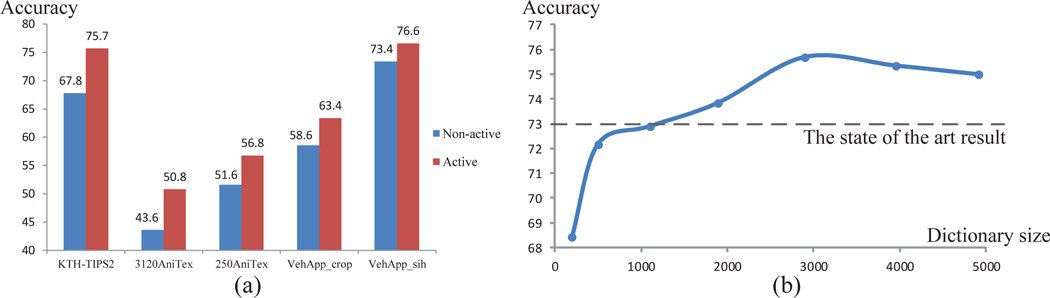
To evaluate the importance of our active patch model, we conduct experiments on a non-active dictionary that allows no transformations on basic patches. The results are shown in Fig. 5(a). We can see that the active patch dictionary performs better than the non-active counterpart on all the datasets. The performance gains are 7.9%, 7.2%, 5.2%, 4.8% and 3.2% respectively on KTH-TIPS2, 3120AniTex, 250AniTex, VehApp_crop and VehApp_sih, demonstrating the advantage and importance of applying rich transformations on the active patch dictionary. It has superior discriminability on handling scale, rotation and pose variations of real world appearance than the non-active one.

Fig. 5.

(a). Performance comparison between the non-active dictionary and the active patch dictionary. (b) Performance comparison with different sizes of dictionaries on KTH-TIPS2 (Best viewed in color)

4.5 The Effect of Dictionary Size

To investigate the effect of the dictionary size, we train several dictionaries with different sizes on KTH-TIPS2 by changing the value of λ_oυ in Equ. 4. λ_oυ is the weight for the energy term E_oυ(p|𝒟). A Larger value of λ_oυ means that there is a larger penalty when patches in the dictionary overlap with others in the reconstruction process, and will lead to a smaller dictionary size. The results are shown in Fig. 5(b).

From Fig. 5(b), we can see that the performance improves with the increase of dictionary size initially and reaches the maximum at a dictionary size of 2951. When the dictionary size increases further, the performance even deteriorates. The reason might be that a dictionary with 2951 active patches is large enough to model appearance patterns for KTH-TIPS2 images. Adding redundant patches is not useful and may lead to over-learning. We also show that an active dictionary of size 1100 can produce the same result as the state-of-the-art algorithm (LHS) which uses a feature of dimension 2096.

5 Discussion

We propose a probabilistic Active Patch Model for real world texture/appearance classification. A simple but effective greedy learning method is presented to obtain the active patch dictionary. Image features are generated using this dictionary, which are interpretable enough to reconstruct the images and have strong discriminability for the classification task. We validate our method on one published benchmark texture dataset (KTH-TIPS2) and two newly constructed datasets (AniTex and VehApp). Our algorithm performs better than previous methods in all of the three datasets. In the future work, we will explore the potential of this method on other tasks such as image labeling and object segmentation.

To study the difficulty of these classification tasks, in related work with C. Wall-raven, we also performed psychophysics experiments on the 250AniTex dataset. The experimental results show that humans do not perform very well in this task. The accuracy is 46.8% on average. Our method shows similar error patterns with humans (e.g., the tendency of confusing dog textures with cats or horses, see Fig. 6). We put the details of psychophysics experiments in the supplementary material.

Fig. 6.

The confusion matrice for (a) our algorithm and (b) humans on the 250AniTex dataset.