The Science of Sex Differences in Science and Mathematics

Summary

Amid ongoing public speculation about the reasons for sex differences in careers in science and mathematics, we present a consensus statement that is based on the best available scientific evidence. Sex differences in science and math achievement and ability are smaller for the mid-range of the abilities distribution than they are for those with the highest levels of achievement and ability. Males are more variable on most measures of quantitative and visuospatial ability, which necessarily results in more males at both high- and low-ability extremes; the reasons why males are often more variable remain elusive. Successful careers in math and science require many types of cognitive abilities. Females tend to excel in verbal abilities, with large differences between females and males found when assessments include writing samples. High-level achievement in science and math requires the ability to communicate effectively and comprehend abstract ideas, so the female advantage in writing should be helpful in all academic domains. Males outperform females on most measures of visuospatial abilities, which have been implicated as contributing to sex differences on standardized exams in mathematics and science. An evolutionary account of sex differences in mathematics and science supports the conclusion that, although sex differences in math and science performance have not directly evolved, they could be indirectly related to differences in interests and specific brain and cognitive systems. We review the brain basis for sex differences in science and mathematics, describe consistent effects, and identify numerous possible correlates. Experience alters brain structures and functioning, so causal statements about brain differences and success in math and science are circular. A wide range of sociocultural forces contribute to sex differences in mathematics and science achievement and ability—including the effects of family, neighborhood, peer, and school influences; training and experience; and cultural practices. We conclude that early experience, biological factors, educational policy, and cultural context affect the number of women and men who pursue advanced study in science and math and that these effects add and interact in complex ways. There are no single or simple answers to the complex questions about sex differences in science and mathematics.

Introduction

The National Science Board (2003) sounded an alarm about critical workforce shortages in jobs that require high-level mathematical and science skills. Their fears about a dwindling pool of mathematicians and scientists has fueled concern that the United States will not be able to maintain its leadership in science and technology, which translates directly to an inability to fill positions that are essential to homeland security. A similar call to arms had been made by leading economists, who warned that the shortage of workers with science and math skills is dampening our economic growth and posing a major threat to our economic well-being. In the 2000 Biennial Report to the United States Congress (Committee on Equal Opportunities in Science and Engineering, 2000, section 5), experts predicted that the overall rise in employment opportunities in the coming decade would be around 14%, with employment opportunities in science, technology, engineering, and mathematics (commonly abbreviated STEM) expected to increase by over 50%. Despite the serious need for a workforce with high-level skills in science and mathematics, data from the National Science Foundation show that “Women made up almost one-fourth (24 percent) of the [science and engineering] workforce but close to one-half (46 percent) of the U.S. workforce, in 1999” (National Science Foundation, 2002b). Making fuller use of the female talent pool could go a long way toward addressing workforce shortages. Women are also underrepresented in academic positions at research universities, especially in science and mathematics. A recent review found that women in science, engineering, and technology are less likely to obtain tenure (29% of women compared to 58% of men in full-time, ranked academic positions at 4-year colleges) and are less likely to achieve the rank of full professor (23% of women compared to 50% of men; Ginther & Kahn, 2006). Why are women underrepresented in high-level careers in math and science?

Questions about sex differences in the cognitive abilities needed for success in science and mathematics have a long history in scientific psychology. Helen Bradford Thompson's (later Woolley) 1903 doctoral dissertation, The Mental Traits of the Sexes, began with this sentence: “The object of the present monograph is to furnish some accurate information on the muchdiscussed question of the psychology of the sexes” (p. 1). Thompson's carefully controlled comparisons of males and females on various “intellectual faculties” is a perfect introduction to many of the underlying assumptions in explanations that were offered over the ensuing century for the unequal outcomes for men and women in academic careers in mathematics and science. It shows both how much and how little the science of sex differences has advanced in the last 100 years. Thompson had almost no empirical work to build upon, whereas contemporary psychologists have an extensive base of empirical studies to inform our conclusions; yet, in many ways, we are still asking the same basic questions. In this report, we present a summary of what is known about sex differences in mathematics and science achievement and abilities based on a review and evaluation of the best available scientific evidence.

The topic of unequal outcomes for men and women in science and math areas in academia was brought to the consciousness of the general public a few years ago, when Lawrence Summers (2005), then president of Harvard University, remarked publicly on these discrepancies. He offered three possible explanations for the low percentage of women in academic positions in science in mathematics. He raised the possibility that women are unwilling to reduce their time with family to work the long hours required to achieve the status of high-level academic scientists, which requires a near total commitment to one's work. He rhetorically asked, “Who wants to do high-powered intense work?” Summers also discussed the possibility that sex-related differences in socialization or discrimination during hiring or promotion could be barriers to female success in science, mathematics, and engineering, but he said he did not believe that these mechanisms contributed much to keeping women as minorities in these fields. His main hypothesis focused on the finding that there are many fewer females than males at the upper end of advanced mathematical achievement and ability tests, which led him to infer that fewer females than males have the “innate ability” to succeed in academic disciplines that require advanced mathematical abilities. Summers reasoned that it was the scarcity of females with exceptional mathematical talent that explains the disparate ratios of females and males in mathematics, engineering, and the natural sciences.

This issue of Psychological Science in the Public Interest was organized in direct response to the heated controversies generated by Summers’ remarks. There is a large research literature on the topic of whether and when (in the life span) there are differences between females and males in cognitive abilities needed for successful careers in STEM. The research literature directly addresses questions about the extent to which sex differences can be attributed to “innate” explanations, socialization, or the way these two types of influences reciprocally affect each other. Questions about the ways in which males and females differ are controversial because conclusions may have implications for public policies and for the way people think about education, career choices, and “natural” roles for males and females in society. We recognize that all social-science research is conducted in a cultural context that influences the nature of the questions that may be asked and the evidence that is accepted as valid. Science can never be free of all biases, but it is the best method available for finding answers to politically charged questions. In addressing questions about sex differences in mathematics and science, we rely on findings that have been replicated and on the relative transparency of the scientific method. We also recognize that science is a cumulative process, so that the conclusions that are drawn today may change as additional data are collected over time, as society and people change, and as our understanding of the phenomena being studied evolves.

Defining Terms

The terms we use in this report to describe constructs and the way we discuss and explain results are important in conveying our understanding of controversial phenomena. We do not want to become enmeshed in cultural struggles over “correct” terminology. Thus, we first clarify our usage of terms.

Sex and Gender

One area of contention concerns the use of the terms sex and gender. Some authors prefer sex to refer to biological distinctions between people, such as genitals and chromosomes, and gender to refer to those male and female differences that are thought to arise from social or environmental influences. On one side of this issue, there are psychologists who believe that using the term “gender differences” in research that compares females and males is preferable because it does not imply the origin of the differences or it conveys a more pro-nurture origin (Caplan & Caplan, 2005); other authors, writing in outlets such as the National Women's Studies Association Journal, have suggested that the distinction between sex and gender may have outlived its usefulness, because biology cannot be separated from its cultural influences and the continued use of two separate terms perpetuates the westernized view of mind–body dualism (Severin & Wyer, 2000). Those who oppose the restrictive use of sex for biological distinctions and gender for social or environmental ones further note that the dichotomy is often artificial.

When studying cognitive abilities, it is extremely difficult to separate biological influences from environmental ones because the two influences are reciprocal. Halpern (2000, 2004) and others have advocated a biopsychosocial model (sometimes called a psychobiosocial model) that emphasizes the complex influences of biological and social/environmental variables on cognitive abilities. Consider, for example, brain development. As we describe in a later section, there are differences between female and male brains that are influenced initially by prenatal hormones and later by other hormones over the course of life, but human brain development is also altered by life experiences, including the prenatal environment. Similarly, high-performing students report that the subjects they like the most in school correspond to the academic disciplines in which they achieve high scores on standardized tests of knowledge and ability. Not surprisingly, they engage in more activities that relate to areas that they like (e.g., reading, math clubs, science competitions), thus further increasing their knowledge and abilities in these areas (reviewed in Lubinski & Benbow, 2007). It is difficult to know whether high ability leads to increased interest and additional activities in an academic domain or whether high interest in an academic domain and engaging in activities that develop expertise in that domain lead to high ability. The distinction between sex and gender is entangled in the debate about what is biologically determined and what is environmentally determined. For these reasons, we have chosen— perhaps arbitrarily but for the sake of clarity—to use the term sex throughout our report.

Biological and Innate

Terms like biological and innate are often misunderstood. Humans are both biological and social beings shaped by the complex interaction of biology and environment. When psychologists use the term innate, they are referring to a potential that is “ready” for development in a supportive environment. Innate does not mean immutable or unchangeable. Hormones, for example, are chemicals, secreted by endocrine glands, that affect a wide variety of behaviors and brain development, yet hormonal secretions change in response to environmental events such as social victories or defeats (Schultheiss et al., 2005). Learning is both a biological and an environmental process, and the brain remains plastic into very old age, changing in response to learning and environmental events.

Abilities and Achievement

Abilities and achievement are terms used in assessment, and although they are theoretically different, in practice they are often difficult to separate. An achievement test is a test of what an individual knows at a particular time. A high score on an achievement test in calculus, for example, is interpreted to mean that the test taker learned calculus and was willing and able to demonstrate that learning by solving the problems on the test. Achievement tests are usually written to reflect a curriculum. Two people could have the same low score on a mathematics achievement test and differ widely in their mathematical ability. One of these individuals could have had several years of mathematics instruction and learned very little and the other could have had no mathematics instruction.

Ability is a more abstract construct; ability tests assess an individual's likelihood to benefit from instruction or, alternatively, how much instruction might be needed to reach a level of competence. Although the term ability connotes a “raw” or undeveloped talent, ability assessments usually test content information that was taught in school (except for projects that identify precocious talent). Unfortunately, one cannot measure ability without also measuring achievement to some extent, so the distinction between these two constructs is somewhat blurred. We use the term ability as it was defined by Fleishman (1972): a general trait of an individual that is the product of learning and development. (Some psychologists have suggested that the term abilities be replaced with more neutral terms like skills or performance; Sherman, 1977.)

Humans are born with innate abilities, such as the ability to learn a language, but the language they learn, if any, depends largely on their experience. Similarly, they are born with the innate ability to count and discern quantities, but how they develop those abilities depends on their environment and learning experiences. Abilities are developed in supportive environments. In this report, we shall refer to abilities in this broad and environmentally dependent way.

Intelligence and IQ

Intelligence is another abstract construct in assessment. It is usually summarized with a single score known as IQ, which stands for “intelligence quotient.” It was originally derived from a quotient that included an individual's test score divided by the score that would be obtained by an average person of the same age (then multiplied by 100 so average scores at any age are 100). The most commonly used intelligence tests have been designed so that there are no overall sex differences in IQ scores (Brody, 1992). When items are selected for inclusion in standardized intelligence tests, items that show an advantage for either males or females are either discarded during test construction or balanced with items that show an equal advantage for the other sex. Hence, overall, there are no sex differences in IQ scores for the most commonly used tests. Thus, we cannot turn to standardized intelligence tests to determine if there is a “smarter sex.”

The Grade–Test Disparity

In general, females receive higher grades in school in every subject, including mathematics and science, so the question is not whether females can learn advanced concepts in mathematics and science; class grades show that they can and do (Dwyer & Johnson, 1997; Kimball, 1989). Women constitute a substantial majority of college enrollments in the United States and many other countries. American women have received more college degrees than men every year since 1982, with the female advantage widening every year. Among women between 25 and 34 years old, 33% have completed college, compared to 29% of men (Bae, Choy, Geddes, Sable, & Snyder, 2000). Despite these successes, females score significantly lower on many (though not all) “high stakes” standardized tests used for admissions to college and graduate school, including both the Verbal and Mathematics sections of the SAT (previously called the Scholastic Aptitude Test) and the Graduate Record Examination (GRE). Females also score lower than males, on average, in science and mathematics when the tests are not closely related to material that has been taught in school (despite getting higher grades in school-based exams), and males and females participate in different subfields of mathematics and science at different rates (Willingham & Cole, 1997).

Thus, there is a grade–test disparity in successful achievement in mathematics and science for males and females, with females achieving better grades in school and males achieving higher scores on tests designed for admissions to colleges, universities, and graduate programs. A corollary of this discrepancy is the finding that standardized tests slightly underpredict college and graduate school performance for women and overpredict performance for men (Willingham & Cole, 1997).

There are many laws of cognitive psychology that are as certain as the law of gravity. Here is one: All cognitive abilities will improve with learning and practice. This is the reason we have schools: to provide instruction in math, science, and the other STEM areas and abilities covered in this review. Even when we conclude that there are meaningful differences between males and females, this conclusion leaves open the possibility that the performance gap could be narrowed or closed with appropriate instruction, just as it could be widened. Ceci and Papierno (2005) make the point that interventions often widen achievement gaps between groups because higher-ability groups can usually achieve greater gains than lower-ability groups can.

The questions addressed in this report are about two groups of females and males, those with average abilities and those at the highest ability levels, and the possible origins of the differences within and between these two groups. We are not addressing the question of whether males and females are similar or different in their mathematics and science abilities and achievement levels, because the answer is that males and females are both similar and different. The similarities between males and females are so numerous and obvious that we tend to overlook them and take them for granted. We need to heed the caveats that the overemphasis on studies of differences can distort the countless findings of “no significant differences” that routinely are ignored or unreported. Hyde (2005) has reviewed numerous areas of research on sex differences among females and males of average ability and concluded that “males and females are similar on most, but not all, psychological variables” (p. 581). There are many critical research-design issues to consider when evaluating research on sex differences in math and science abilities, but most critical is the inability to ever “prove” the null hypothesis that there is no difference between any groups using standard research methods. So when differences are not found, we are careful to avoid conclusions that would affirm the null hypothesis, although we can rely on aggregate analyses across multiple studies to decide if an effect size or average group difference is large enough to be meaningful in real-world contexts.

The Size of an Effect

When researchers say “males are better at X” or “females are better at Y,” it is important to know the magnitude of the difference claimed. If a nationally normed vocabulary test showed that females scored statistically significantly higher than males, this result might sound impressive, but what if it turned out to mean that, on average, females know 1.5 more vocabulary words than males? Such a small difference might be statistically but not practically meaningful. How many words, on average, would the difference need to be before it became meaningful? There are statistical formulas for computing effect sizes, but deciding when a difference is large enough to be important in everyday life is a matter of judgment, and reasonable people often disagree.

There are several statistical ways to present the size of the difference between two (or more) groups. Because we are often comparing results among several studies in which the dependent variables (what is measured) could be test scores like the SATs, reaction time to respond to a target, or accuracy in responding, a common metric is needed. The most widely used measure is d (Cohen, 1977):

$$d=\frac{{\overline{X}}_m-{\overline{X}}_f}{\sqrt{\frac{S{D}_m^2+S{D}_f^2}{2}}}$$

where X̄f is the mean for the female group and X̄_m is the mean for the male group, and SDf and SD_m are the respective standard deviations for females and males. Either group mean could be subtracted from the other, but when females are subtracted from males, positive values indicate a “male advantage,” and negative values indicate a “female advantage.” Thus, d provides a measure of how far apart the means of the two distributions are in standard deviation units. The value of d can range from 0—meaning no difference was found between the means for the groups being compared—to values as large as 2 or 3 (or –2 to –3, which signify the same distance between the means as the positive values). Large values mean that there is very little overlap in scores between the two groups. There is no theoretical limit to the size of d, but practically .8 is generally considered a large difference. Any value of d can be mathematically converted into a correlation or another indicator of percentage of “explained variance” (Rosenthal, Rosnow, & Rubin, 2000). It is important to understand effect sizes, because they are often used to label a difference between males and females as large or small. Rosenthal et al. (2000) weighed in on this critical matter: “Mechanically labeling… ds automatically as small, medium, and large can lead to later difficulties. The reason is that even small effects can turn out to be practically important” (pp. 15–16).

According to Rosenthal and Rubin (1982), an effect that accounts for only 4% of the variance (variability among scores) is associated with a difference of 60% versus 40% of a group's performance above average; for example, on a test designed such that an individual must attain at least an average score to qualify for admission to a graduate program, then, with this effect size, 60% of one group and 40% of the other group would qualify. Thus, although effect sizes may sometimes seem “small,” they can have substantial real-world consequences. In Valian's (1998) analysis of females’ slow advancement in academia and other professions, she showed how smaller disparities were compounded over time to create larger ones, so the seemingly small 4% of variance accounted for can be meaningful, depending on the context and variable being assessed.

Meta-analyses are used to assess effect sizes across multiple studies. As the term suggests, a meta-analysis is an analysis of previous analyses, or an analysis of many individual research results. The need for meta-analysis is obvious in a research area in which the size of the literature can be measured in linear yards or pounds of paper generated. Meaningful integrations of research findings are the best way to interpret the voluminous literature. Meta-analysis allows us to take a broad overview in summarizing research results (Hyde & Linn, 1988).

The What, When, And Where Of Sex Differences In Math And Science Achievement

The question of sex differences in mathematical and science achievements is really a set of embedded questions, because the answer depends on (a) which mathematical and science achievements are studied, (b) how those achievements are assessed, (c) when in the life span they are assessed, (d) which portion of the achievement/ability distribution is investigated, and (e) the context in which achievement is assessed. The majority of the literature on sex differences in mathematics and science has investigated differences in three different, broadly defined, but core cognitive abilities: verbal, visuospatial, and quantitative abilities (e.g., Carroll, 1992; Snow & Lohman, 1989). These types of abilities are linked in various ways, because they are used together and, sometimes, compensate for each other. All are necessary in learning and doing science and mathematics.

Terms like verbal, visuospatial, and quantitative are category headings used to organize and study cognition. They are not unitary constructs. Verbal abilities for example, apply to all the components of language usage, including skills like word fluency, grammar, spelling, reading, vocabulary, verbal analogies, and language comprehension. Verbal abilities also apply to tasks used by cognitive psychologists in laboratory settings, such as tasks measuring speed of lexical access, a reaction-time measure usually reported in fractions of a second, or those measuring working-memory span, such as the number of items an individual can maintain in memory while also engaged in a verbal processing task (e.g., a task of verbal reasoning). Examples of items used to assess verbal abilities include tasks such as (a) choosing which in a group of words are most nearly the same in meaning, (b) solving verbal analogies, (c) answering questions about complex passages just read (reading comprehension), (d) answering simple grammar questions, and (e) writing in response to prompts or other instructions. These tasks do not tap the same skills even though they all involve language, and males and females do not differ in the same way on all of these measures. Thus, different combinations of these measures give different answers to the question about sex differences in verbal abilities.

Visuospatial abilities are also not unitary. In a recent review of the literature, Halpern and Collaer (2005) described the multiple components of visuospatial information processing, including the many different combinations of retrieval from long-term memory; the generation, maintenance, transformation, and scanning of images; and the interplay among verbal, spatial, and pictorial mental representations. Visuospatial abilities are central to the work of architects, chemists, dentists, designers, artists, engineers, decorators, mechanics, taxi drivers, and many other professions. All of these fields rely heavily on the ability to maintain a visual image while simultaneously deciding what it would look like if it were viewed from another perspective, moved to another location, moved through space at various speeds, or physically altered in some way. Quantitative abilities are also heterogeneous. Consider the differences among tasks like simple rote multiplication, word problems, and other more advanced mathematical tasks (some of which are visuospatial in nature) like calculus, topology, and geometry.

Although the initial impetus for this review was the comment by Lawrence Summers, former president of Harvard, about the innate abilities of females to be scientists or professors of science, there are no “science abilities” per se. The cognitiveabilities literature lists different hierarchically organized abilities, which usually include verbal abilities; quantitative abilities; visuospatial abilities; and some combination of perceptual speed, mechanical reasoning (which often shares variance with visuospatial abilities), general reasoning, working memory, and other abilities (e.g., Carroll, 1993). The abilities needed for success in advanced and academic science are diverse and include verbal and social abilities such as communicating clearly, comprehending complex texts, working with people, writing journal articles and books, persuading granting agencies to fund one's work, attracting graduate students, and functioning in a bureaucratic structure (usually a university or other large institution); visuospatial abilities in imaging data and models and translating words to visuospatial formats; and mathematical abilities in solving equations and modeling scientific phenomena with mathematical properties. “Science” is a rubric for domains that use a common method of inquiry— similar in this regard to “history” or “literature,” which are not thought of as cognitive abilities.

Average Sex Differences In Cognitive Abilities

There are many different types of scientists and mathematicians— not just the ones seen in the media accepting the highest prizes in their disciplines. Society needs people with a broad range of skills to advance and support the fields of science and math. On average, do males and females differ in the skills and abilities needed to pursue careers in these complex disciplines? We begin to answer that question by first looking at average differences early in development, then examining mean differences during later stages of development and in the development of excellence in math and science.

Cognitive Sex Differences In Infancy

Psychologists often look for sex differences very early in life as clues to the relative contribution of biological and environmental factors. The reasoning is that newborns have had fewer social interactions, so the earlier that sex differences are reliably found, the more likely they may be assumed to be biological in origin. It does not necessarily follow, however, that differences found later in life are caused by social or environmental factors, because there are developmental timelines for biological processes, including the timing of puberty, the development of the forebrain, and the aging processes, all of which are also influenced by the environment. And the assumption about early sex differences reflecting biological differences may be questionable itself. Across species it is common for there to be few sex differences early in life, even when substantial differences emerge with reproductive maturation (Darwin, 1871). It may seem impossible to assess cognitive abilities in newborns, but psychologists who study cognitive development in infants have developed a variety of techniques to infer when, in early life, babies comprehend language, maintain a persisting mental representation of objects (memory), show interest in people and objects, make inferences about the paths of motion and rates of speed of moving objects, have basic “number sense,” and understand that an adult who looks at an object is likely to reach for it (Kotovsky & Baillargeon, 1998; Phillips, Wellman, & Spelke, 2002; Xu, Spelke, & Goodard, 2005). The usual finding, from many studies conducted by many researchers in different laboratories and across a range of tasks, is that boys and girls develop early cognitive skills relating to quantitative thinking and knowledge of objects in the environment equally well (Spelke, 2005). It usually requires very large samples to detect differences in infancy or the toddler years. For example, a study with over 3,000 2-year-old twins found that girls scored significantly higher than boys ( p < .0001) on measures of both verbal and nonverbal cognitive ability, but sex accounted for only 3% of the variance in verbal ability and 1% of the variance in nonverbal ability (Galsworthy, Dionne, Dale, & Plomin, 2000).

Verbal Abilities

Mean Verbal Abilities

Verbal abilities are essential for success in mathematics and science, given the densely written technical articles to comprehend, the need for clear communication skills, and the general language demands found in any advanced field of learning, even if they differ somewhat in qualitative ways from those that might be required in the humanities. Verbal abilities comprise different components, and the size of the sex differences between males and females is not the same across all of them. Based on a review of 24 large data sets (including several large representative samples of U.S. students, working adults, and military personnel), Willingham and Cole (1997) concluded that differences are small in the elementary school grades, with only writing, language use, and reading having d > .2, favoring females at fourth grade. In the United States, by the end of high school, the largest differences, again favoring females, are found for writing (d between .5 and .6) and language usage (d between .4 and .5).

In a report published by the U.S. Department of Education (Bae et al., 2000), titled “Trends in Educational Equity of Girls and Women,” the data on reading and writing achievement are described this way: “Females have consistently outperformed males in writing achievement at the 4th, 8th, and 11th grade levels between 1988 and 1996. Differences in male and female writing achievement were relatively large. The writing scores of female 8th graders were comparable with those of 11th grade males” (p. 18). In a meta-analytic review of the research literature, Hedges and Nowell (1995) reported that “the large sex differences in writing… are alarming. The data imply that males are, on average, at a rather profound disadvantage in the performance of this basic skill” (p. 45). Thus, the advantage for females on tests of writing is large and robust by the middle to end of secondary school.

If an assessment of verbal abilities is heavily weighted with writing, and language-usage items cover topics that females are familiar with, sex differences favoring females will be much larger than they will be in an assessment of verbal abilities lacking these components. This is the case in the review of sex differences in a recently published review conducted in the United Kingdom (Strand, Deary, & Smith, 2006). The SAT-Verbal (SAT-V) test has (up through 2004) contained many verbal-analogy questions—a question type that is conceptually closer to mapping relationships than it is to other types of verbal usage, and one that often shows an advantage to males. Therefore, it is not surprising that the SAT-V test, despite being labeled a “verbal” test, does not tap the same verbal abilities as do tests of writing or other language areas in which females excel; nor is it surprising that males score higher than females on the SAT-V test.

The female advantage in several specific verbal abilities, such as reading, is international. The data in Figure 1 were taken from the Progress in International Reading Literacy Study of 2001 (Mullis, Martin, Gonzalez, & Kennedy, 2003; Ogle et al., 2003). Fourth-grade females scored higher than fourth-grade males in every participating country. The advantage for females in reading literacy is replicated and is comparable in size for 15-year-olds in each of the 25 countries that participated in the Program for International Student Assessment (National Center for Education Statistics, 2002; data not shown).

Fig. 1.

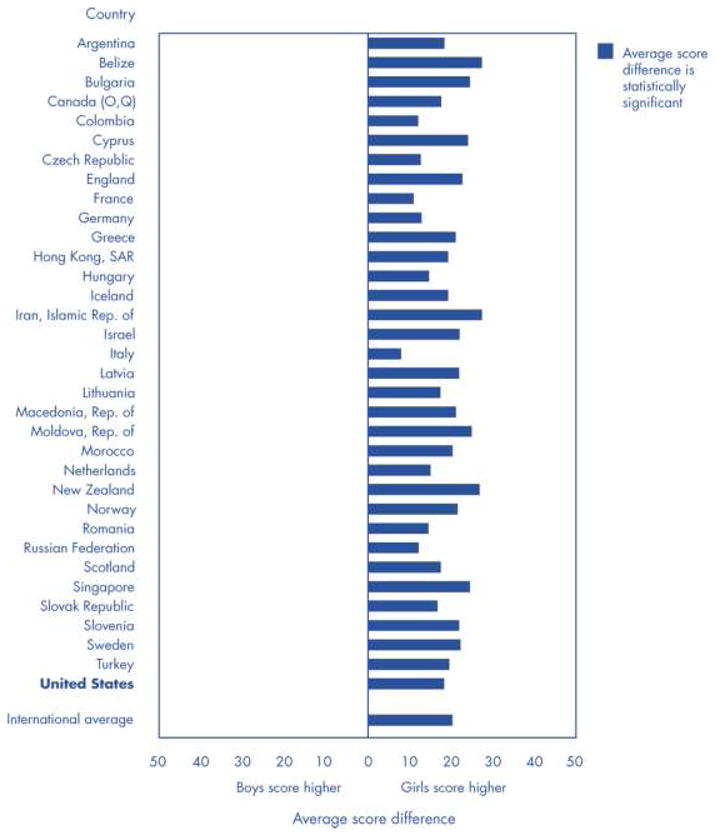
Difference in average scores between boys and girls for the combined reading literacy scale of fourth graders, by country. (Note that girls scored significantly higher than boys in all 33 countries in which the assessment was conducted.) Findings from the Progress in International Reading Literacy Study of 2001 (Mullis, Martin, Gonzalez, & Kennedy, 2003; Ogle et al., 2003).

Similar to sex differences in verbal abilities, sex differences in memory depend on the type of memory system examined. Most psychologists divide memory into qualitatively different subsystems, with two broad major classifications: working (or short-term) memory and long-term memory. Long-term memory is further divided into multiple types, one of which is episodic memory, or memory for events that are personally experienced and recalled with information about time and place. Given the female advantage on some verbal abilities, it might be expected that they also are better able than males to describe personal memories. In a recent review of the literature, Herlitz and Rehnman (2007) summarized multiple studies showing that females are better at episodic-memory tasks than males are. For example, they describe a large population-based study of adults (35–80 years old) in which sex differences were found on episodic-memory tasks that required participants to remember previously presented words, objects, or activities (Herlitz, Nilsson, & Bäckman, 1997). Across multiple studies, differences between men and women on such tasks are typically small to medium sized (e.g., Herlitz, Airaksinen, & Nordström, 1999). There is also an advantage for females in the ability to recognize faces, and this difference is found across the age span with both children and adults (e.g., Lewin & Herlitz, 2002; Lewin, Wolgers,& Herlitz, 2001). Perhaps the most surprising finding is that girls and women are most accurate when recognizing female faces—their own sex bias. This ability of girls and women to recognize female faces better than male faces andtoperform better than maleson all measures of face recognition has been replicated cross-culturally. Herlitz and Rehman attribute these results to differential attention paid by females to female faces. These findings provide ancillary support for the hypothesis that females are more “people oriented” than males are and thus choose careers and courses of study, such as teaching and social work, that involve greater social interaction, instead of careers that are more “thing oriented,” such as physics and engineering (Lippa, 1998).

Variability in Verbal Abilities

In Strand et al.'s (2006) sample of over 320,000 students aged 11 to 12 years, there was a greater percentage of females in the 5th, 6th, 7th, 8th, and 9th stanines than males on the verbal-abilities test that they used. (Stanines are standard scores indicating which 1/9 of a sample from a normal or bell-shaped population contains certain scores. A score in the 1st stanine is among the lowest 4% of all scores and a score in the 9th stanine is among the highest 4% of all scores; the 5th stanine corresponds to the middle portion of scores and comprises 20% of all scores.) The female mean was higher than the male mean, which explains the finding that there were more females in the upper tail. Thus, differences in mean scores between females and males and/or differences in variability will result in disproportionately more females or males in the upper tail of a distribution, with the advantage going to the group with the higher mean, greater variability, or both. The 2006 SAT data for college-bound seniors on the writing test show a similar pattern. The female mean was higher than the male mean (502 vs. 491) for the writing test, with 58.7% of the top 1% of all test takers being female. The 2006 SAT data for college-bound seniors in the (new) test of Critical Reading show a different pattern. The male mean is slightly higher than the female mean (505 vs. 502), but 53.04% of test takers in the top 1% are female, which runs counter to the usual conclusion that males are more variable in all cognitiveability domains. The males in Strand et al.'s sample were more variable on the quantitative and nonverbal reasoning ability tests, and the SAT data for college-bound seniors for the math test showed that males are more variable in math, suggesting that the male-variability hypothesis—or a higher proportion of males in the upper tail—extends across multiple measures of quantitative abilities but not to all cognitive-ability tests.

Visuospatial Abilities

A large body of research conducted over the last 25 years has revealed substantial sex differences for some, but not all, of the measures that reflect visuospatial information processing. These differences begin to emerge around the time children enter kindergarten or begin first grade, which may be as early as children can reliably perform tasks that assess visuospatial abilities. The preschool literature on sex differences in spatial skills was reviewed by Levine, Huttenlocher, Taylor, and Langrock (1999). They found that, on average, preschool boys are more accurate than girls at spatial tasks that measure accuracy of spatial transformations (d 5 = .31) and score higher on the Mazes subtest of the Wechsler Preschool and Primary Scale of Intelligence (d 5 = .30). They concluded that sex differences in favor of boys are present on spatial tasks by age $4\frac{1}{2}$.

There is a large research literature on visuospatial tasks with young adults (i.e., college students). Effect sizes vary considerably with the type of task, ranging from small and fragile (i.e., not worth talking about, although still favoring males when an effect size is found; e.g., Voyer, Voyer, & Bryden, 1995) for a commonly used task that involves imagining what a folded paper would look like if it had a hole punched in it and then was unfolded—a fairly simple task—to larger and more robust effects. Results using tasks that require generating an image and maintaining it in memory while “working” on it (i.e., mentally folding and unfolding it) vary depending on the complexity of the image to be generated and the specific nature of the task, with observed differences that range between d 5 .63 and d 5 .77 (Loring-Meier & Halpern, 1999). Mental rotation tasks that require maintaining a three-dimensional figure in working memory while simultaneously transforming it show very large sex differences, somewhere between .9 to 1.0 standard deviations (Masters & Sanders, 1993; Nordvik & Amponsah, 1998), although some researchers have reported smaller effect sizes (Voyer et al., 1995).

The largest differences are probably found with spatiotemporal tasks (judgments about moving objects), but there are not enough studies with spatiotemporal tasks to allow a reliable estimate of the effect size (Law, Pelligrino, & Hunt, 1993). For example, studies that used “time to collision” estimates that also involve spatiotemporal abilities found that males made more accurate estimates (McLeod, & Ross, 1983). Similar results were found with a Chinese sample that made time-tocollision estimates under varying conditions. The authors concluded that males were better than females in judgment accuracy with this task (Liu, & Huang, 1999). Thus, although the number of studies that examined spatiotemporal abilities is small, results consistently point to a male advantage. An example of a mental rotation task is shown in Figure 2. The task for the participant is to determine if the two figures labeled A and the two figures labeled B could be made identical by rotating them in space.

Fig. 2.

An example of a mental rotation task. The task is to determine if the two figures labeled A and the two figures labeled B could be made identical by rotating them in space. These are called mental rotation tasks because the rotation must be done in working memory.

Visuospatial Skills and Computer Games

With the meteoric rise of online games, there has been a great deal of interest in navigating through virtual space. The popularity of online learning has led to the creation of a large number of online simulations of real-world events in which learners can “practice” a wide variety of tasks, such as surgery or navigating through unknown territory in preparation for military excursions (Macedonia, 2002; Wrobel, 2005). The 3-D virtual environment literature consistently shows that males outperform females (e.g., Cutmore, Hine, Maberly, Langford, & Grant, 2000), although some accommodations, such as very large displays, can reduce or The 3-D virtual environment literature consistently shows that males outperform females (e.g., Cutmore, Hine, Maberly, Langford, & Grant, 2000), although some accommodations, such as very large displays, can reduce or eliminate this effect (Tan, Czerwinsk, & Robertson, 2006).

The results with virtual environments parallel those that are often found in real-world way-finding tasks. An important variable in such tasks involves the use of maps. In one study, participants were given a map that they were to use to give directions to a stranger (L.N. Brown, Lahar, & Mosley, 1998). Males were generally more accurate than females in the directions that they gave, and males were also more likely to use compass headings (North, South, East, West) when giving directions; females used landmarks more often when giving directions. This study, like many others, suggests that when women learn a route, either from a map or from direct experience, they tend to rely on landmarks to find their way, whereas men are more likely to attend to and keep track of the compass direction in which they are traveling (Lawton, 1994). Similarly, when adults learned a route from a map, the men made fewer errors in getting to a destination, but the women had better recall for landmarks along the way (Galea & Kimura, 1993).

Visuospatial Abilities and Mathematics

It has been suggested that certain visuospatial sex differences contribute to observed sex differences in some aspects of mathematical performance. For example, Casey, Nuttall, Pezaris, and Benbow (1995) found that the sex difference on the Mathematics portion of the SAT (SAT-M) was eliminated in several samples when the effects of mental rotation ability were statistically removed. This suggests that rotational skill may mediate the sex differences in certain high-level mathematical abilities or, at the least, that these two abilities tend to covary. Linkage of mathematical and visuospatial skill has important consequences, because high levels of both of these skills are required for careers in fields such as physics and engineering in which women are typically underrepresented. However, the precise relation between these variables is complex, varying with the specific visuospatial and mathematical measures considered (Tartre, 1990). In addition, these two variables appear to be more strongly linked in females than males, suggesting that females may be particularly hampered in mathematical domains if they have reduced visuospatial skill.

Quantitative Abilities

Of all of the sex differences in cognitive abilities, differences in quantitative abilities have received the most media attention because of the large sex differences at the highest end of the distribution among those who take the SAT-M test and other high-stakes mathematics tests. Differences depend on the portion of the distribution that is examined, and because males are more variable in quantitative and visuospatial abilities there are more males at both high- and low-ability ends (a phenomenon we explore more fully in a later section). The reasons why males show more variability are not known, but given the higher variability, even small mean differences between females and males will result in a disproportionately large number of males in both the high- and low-ability ends of the distribution. There is no large-scale examination that assesses writing in a comparable way to the SAT-M. If there were, we expect it would show the female advantage in verbal abilities in secondary school and throughout adulthood because females have higher mean scores on tests of writing.

Researchers have identified mathematically precocious preschoolers (scoring one to two standard deviations above the norm) and have concluded that males are overrepresented in this precocious group even at this young age (Robinson, Abbott, Berninger, & Busse, 1996). Sex differences in quantitative abilities do not follow a predictable developmental schedule, in that they vary by the type of quantitative task examined. In fact, on average, females get higher grades in school in math classes at all grade levels (Kimball, 1989; Willingham & Cole, 1997) and do slightly better on international assessments in algebra (National Center for Education Statistics, 2005), possibly because of algebra's language-like structure, but tend to score lower on quantitative tests when the content is not directly related to what is taught in their own curriculum (reviewed in Geary, 1996; Halpern, 2000). The differences between boys and girls in mathematical abilities in elementary school tend to be small and to favor girls. Abilities are assessed in elementary school mostly with school grades, which reflect other factors, including behavior and turning in assignments on time. Girls are slightly better at computational tasks in 4th grade and remain at the same advantage relative to males through 12th grade (d between .1 and .2; Willingham & Cole, 1997; but see Royer, Tronsky, Can, Jackson, & Marchant, 1999). Thus, we see advantages for females in the early primary-school years, when mathematics consists of computational knowledge and speed; little or no sex difference through the rest of the primary-school years; and then a male advantage when the mathematical concepts require more reasoning and are more spatial in nature, in the context of solving problems in geometry and calculus, subjects typically taught in the higher secondary-school grades (Geary, 1996; Hyde, Fennema, & Lamon, 1990).

The National Assessment of Educational Progress (NAEP) is regularly given to a representative sample of U.S. students and differs from the international assessments and the SAT-M test in that it is more closely aligned with curriculum. There is essentially no difference between males and females on the mathematics test of the NAEP (Coley, 2001). In fact, when the international assessments from the Trends in International Mathematics and Science Study (TIMSS; standardized across 33 countries) are compared for the final year of secondary school for math, science, and reading literacy, the female advantage in reading and the male advantage in science are considerably larger and more reliable than the male advantage found in mathematics. In order to achieve in science, learners need good mathematical abilities, but they also need verbal and visuospatial abilities, so science achievement cannot be explained by math scores alone. This conclusion is in accord with Hedges and Nowell's (1995) meta-analytic review, in which they concluded that “average sex differences in most measured abilities are small, with the possible exception of science, writing, and stereotypical vocational aptitudes” (p. 45). It seems that for the large-scale quantitative assessments they reviewed, sex differences were smaller in mathematical abilities than they were in these other areas, although the authors did not compare specific types of mathematical skills in their review.

Trends Over Time in Average Abilities

The question of whether sex differences have been decreasing over time depends on which data are examined. In a meta-analysis, Hyde, Fennema, and Lamon (1990) concluded that sex differences in some mathematical skills were decreasing. But different sorts of data give different answers, probably because mathematics is not a unitary domain and neither are the competencies assessed across studies. Hedges and Nowell (1995), in their meta-analysis, conclude that “differences do not appear to be decreasing … across the 32 year period” (p. 45).

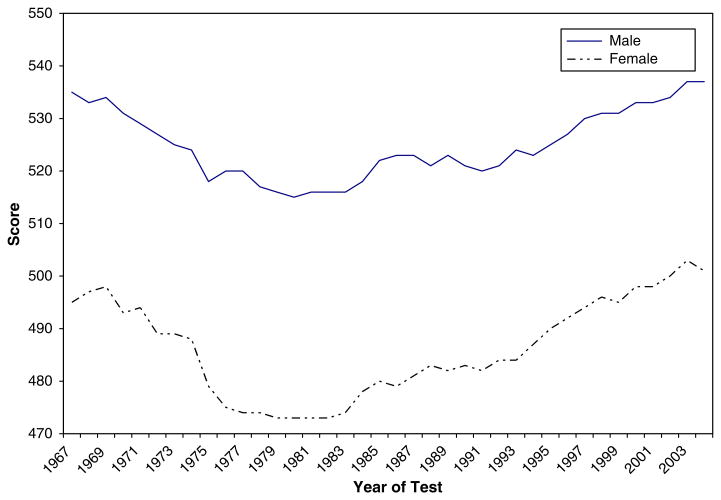
Despite all of the interest focused on the superior-ability tail of the SAT-M test as it relates to scientists, it is instructive to consider average male–female performance on this test over time, as shown in Figure 3. The average difference between males and females on the SAT-M test has remained unchanged for over 35 years, despite the large increase in the number of females entering fields that require mathematics. Logically, as more girls take advanced coursework in mathematics, their mean score on the SAT-M would be expected to increase, but this has not happened. Another possibility is that the large increase in the number of females taking the SAT-M test has been lowering the average scores (i.e., because an overall less select group of females is taking the test).

Fig. 3.

Average SAT-Mathematics scores of entering college classes, 1967–2004, by sex. Data from The College Entrance Examination Board (2004).

Racial and Ethnic Differences in Average Abilities

In thinking about sex differences in math and science abilities, one important question is the extent to which various races, ethnic groups, and peoples around the world show the same patterns of results. To answer this question, racial and ethnic groups were compared in terms of education and work in the United States (Coley, 2001). Large racial and ethnic group differences appear overall, and the size of the differences between females and males within each racial and ethnic group differs somewhat. Sex-typed cognitive patterns do not vary much among racial and ethnic groups, with a few exceptions. For example, Blacks are the only group in which females score higher than males on the verbal section of the Scholastic Aptitude Test (SAT-V), but the few-point difference on this test is too small to be meaningful (Coley, 2001). Prior to 2005, the SAT-V contained a large proportion of verbal analogies, and it did not have a writing component; therefore, despite being labeled a “verbal” test, it did not contain the components of verbal language in which females excel. Results from the NAEP showed that females scored higher, on average, in all racial or ethnic groups and across all ages, in reading, writing, and civics. The graduate admissions tests (the GRE and the Graduate Management Admission Test, GMAT, which is used for admissions to business schools) show that males score higher across all racial/ethnic groups, with the largest differences in quantitative areas. But White, Black, and Hispanic females are more likely than their male counterparts to graduate from college, an advantage that does not translate into higher earnings. The relationship between education and career success (when assessed with earnings) is moderated by sex and race in many job categories. The moderating variables may explain a portion of the sex differences in career success in math and science fields as well.

Sex differences in cognitive abilities and career achievement are complicated, but the fact that there are some tests and some areas of mathematics and science in which females, across all racial and ethnic groups, tend to excel, and some in which males, across all racial and ethnic groups, tend to excel, makes it difficult for any single theory such as motivation, learning, biology, or test-related anxiety to explain the difference. The consistency of the sex-related cognitive pattern of results is consistent with predictions based on an evolutionary perspective (Geary, 1998), but as we note later, there are many researchers who raise objections to evolutionary explanations for science and math data.

A Cognitive-Process Taxonomy of Average Abilities

Halpern (2000, 2004) offered a solution to the mismatch in outcomes for males and females of school grades—outcomes that are based, at least in part, on tests that reflect school curricula, as well as on scores on standardized tests that are comprised of questions that are novel or unrelated to the school curriculum. By considering the underlying cognitive processes used in solving different sorts of math problems, Halpern proposed a taxonomy in which math problems that were spatial in nature would be advantageous to males and those that did not require visuospatial abilities would show either no sex differences or an advantage to females. In a series of studies, Gallagher and her colleagues (Gallagher & DeLisi, 1994; Gallagher, Levin, & Cahalan, 2002) examined cognitive patterns of sex differences on GRE math problems. They found the usual sex differences favoring males when there was an advantage to solving problems with a spatially based solution strategy, but not when solution strategies were more verbal in nature or were similar to the ones presented in popular mathematics textbooks. They also found that there were no sex differences for GRE math problems when solutions required multiple algorithmic steps (i.e., differences were not due to the ability to hold information in working memory), but the usual male advantage was found with math problems that had multiple possible solution paths. Thus, some portion of the performance differences between males and females on GRE math problems lies in the recognition and/or selection of a solution strategy that may be novel. Gallagher et al. found that the usual male advantage on standardized mathematics tests can be minimized, equated for women and men, or maximized by altering the way problems are presented and emphasizing the particular types of cognitive processes that lead to the optimal solution. What is unknown is how these manipulations of test items affect the validity of the GRE in predicting grades in graduate school or success after graduation.

Gallagher's research on verbal and visuospatial representation of quantitative problems on the GRE is an exciting advance because it allows researchers to identify the locus of the sex difference and also shows that identical mathematical content can be presented in ways that are advantageous to males or females. In reviewing each problem on the quantitative portion of the GRE, she found that some problems had an optimal solution strategy; for other problems, different strategies were equally fast in yielding the correct answer. Research has shown that visuospatial training leads to improvement in a variety of tasks (Newcombe, 2002), so we can expect that training with multiple problem representations may have the same effects (Johnson, 1984). Recent meta-analyses have shown that children and adults can improve their visuospatial skills with training (Maruli, Liu, Warren, Uttal, & Newcombe, 2007). The overall mean effect size (mean of 13 effect sizes) is d 5 .52. The researchers explained that the effect size for visuospatial-skills training was moderated because control groups that did not receive the training also showed improvement. Recall that research by Casey et al. (1995) found that sex differences on the SAT-M could be eliminated when the effect of mental-rotation ability was removed. One possible educational intervention for females and males would be to teach them multiple ways to solve problems using both verbal and visuospatial solution strategies, thereby allowing for more flexibility in overall problem solving. In the most comprehensive test of the hypothesis that women can learn to enhance their visuospatial skills and thereby enjoy greater success in STEM fields, Sorby and Baartmans (2000) created a special course designed to enhance three-dimensional spatial skills. The skills that were targeted for instruction were those that are needed by students in engineering, architecture, and other fields in which success frequently depends on the use of visuospatial abilities. All students with low scores on a test of visuospatial ability were encouraged to enroll in a course to improve these skills. This course has been offered for many years for both women and men at Michigan Technological University. As Sorby and Baartmans explain, there are many theories to explicate the finding that men tend to have more highly developed spatial skills than women. One promising theory suggests that sketching three-dimensional objects is a significant factor (but not the only factor) in the development of these skills. Sorby and Baartmans designed and implemented a course to improve the spatial visualization skills of first-year engineering students. They measured improvement in spatial skills with standardized testing instruments in each of the 7 years of the project so far. The gains made by students on these spatial-skills tests as a result of participation in their course were statistically and materially significant. Both men and women who initially scored low on visuospatial tests benefitted from the instruction. This improvement in spatial skills resulted in improved performance in subsequent graphics courses, as measured by final grades in the courses, and better retention in engineering programs, which suggests that the effects lasted over time and were of practical significance.

Sex Differences In Math And Science Abilities In The Tails Of The Distribution

Studying sex differences in mathematical and scientific abilities by examining differences at the population mean is useful but can lead to misleading conclusions if the distribution of test scores is not similar for males and females (Feingold, 1995). This is particularly the case when the focus is on populations characterized by high abilities and the potential to become future mathematics or science professionals (Wise, Steel, & MacDonald, 1979). Differences in population variance, as well as potential skew in these distributions, could lead to overrepresentation of one sex over the other at the extremes.

Sex Differences in Distributions and Variances

Feingold (1992) and Hedges and Friedman (1993) examined the results from available test-norming studies to assess the possible effects of sex differences in both mean test scores and variances. There were differences in variances (males were more variable), and, when combined with mean differences, these two effects produced more males at the high end of the distribution. Drawing from data on abilities that were measured in six national surveys over a 32-year interval, Hedges and Nowell (1995) found that, in addition to the (small) mean differences in mathematical and science abilities favoring males (science: d 5 .32; math: d 5 .16), the test scores of males were more variable than were those of females, with variance ratios differing between 3% and 20% (Hedges & Nowell, 1995), with little change over the 32-year interval sampled. Similarly, Strand et al. (2006) found many more males than females in the top stanines in mathematics and nonverbal reasoning (also see Deary, Thorpe, Wilson, Starr, & Whalley, 2003, fig. 1, p. 537). In the 9th stanine (top 4% of all scores) of the quantitative test, 60% were males; in the 9th stanine of the nonverbal reasoning test, 54% were males. Similar results were reported by Stanley, Benbow, Brody, Dauber, and Lupkowski (1992) in their study of 86 nationally standardized achievement and aptitude tests (obtained from 1982 to 1987) and by Feingold (1995) with the Differential Aptitude Test. Thus, differences in mathematical and science abilities that are large enough to be of practical importance are found at the high end of the ability distribution (Humphreys, 1988; Hyde et al., 1990).

Data from the Study of Mathematically Precocious Youth (SMPY) exemplifies this phenomenon. In their first article on the topic, Benbow and Stanley (1980) observed sex differences in mathematical reasoning ability among 9,927 intellectually talented 12- to 14-year-olds who had taken the SATseveral years before the typical age. The sex difference on the SAT-M, which is a test of mathematical reasoning ability especially when administered to the precocious in the seventh and eighth grades, favored the males and averaged d 5 .40. There were essentially no differences on the SAT-V. Table 1, which is from another SMPY sample of precocious youth, illustrates these sex differences with four different samples.

Table 1. Ability and Values Profiles of Mathematically Gifted Students Attending a Summer Academic Program, 1988–1991.

Year and gender	SAT												Bennett Mechanical Compre- hension		Study of Values
		SAT-M		SAT-V		Advanced Raven's			Mental Rotation							Theoretical		Social		Economic		Aesthetic		Political		Religious
	N	X̄	SD	X̄	SD	N	X̄	SD	N	X̄	SD	N	X̄	SD	N	X̄	SD	X̄	SD	X̄	SD	X̄	SD	X̄	SD	X̄	SD
1991
• Males	68	532	101	426	78	68	25.1	3.9	68	29.9	8.1				68	47.7	7.0	37.1	7.3	41.6	7.2	36.4	8.2	42.9	6.6	34.2	10.4
• Females	51	480	87	418	87	51	25.8	4.3	51	25.1	10.2				51	42.9	6.8	43.2	8.1	37.8	6.9	42.6	7.1	39.0	7.2	35.4	10.2
▪ Males	107	579	101	413	81	92	25.2	4.2	95	30.0	8.3				77	47.6	6.9	37.1	7.0	41.8	6.9	36.5	8.3	43.1	6.8	33.8	10.1
▪ Females	67	472	85	418	80	58	25.9	4.2	63	24.1	10.0				57	41.7	7.0	43.8	8.3	37.5	7.0	42.8	7.5	38.7	7.0	35.6	10.3
1990
• Males	69	537	100	415	79	69	24.5	6.3	69	29.2	9.1				69	46.6	8.8	38.4	7.8	40.4	8.2	38.4	8.4	42.5	6.9	33.4	11.4
• Females	48	487	74	422	76	48	25.3	4.4	48	22.5	9.7				48	40.3	8.0	44.0	8.0	35.8	7.1	42.1	6.4	40.1	6.7	37.5	8.1
▪ Males	87	545	96	415	79	82	24.6	6.8	80	29.8	8.8				73	46.6	8.7	38.3	7.6	40.4	8.1	37.8	8.7	42.7	6.8	33.9	11.3
▪ Females	61	487	71	419	80	57	25.1	4.1	56	21.6	9.4				51	40.7	8.0	43.6	8.1	35.3	7.2	42.8	7.1	40.1	6.6	37.1	8.4
1989
• Males	20	585	86	441	98	20	27.3	4.4	20	24.9	9.9	20	40.2	9.4	20	49.3	7.4	35.4	5.9	40.3	9.4	37.3	8.0	45.0	7.8	30.8	11.1
• Females	11	505	80	449	96	11	24.7	5.1	11	17.8	4.1	11	35.6	8.0	11	39.0	9.1	42.3	9.1	41.1	9.6	40.6	5.2	40.4	9.3	36.6	12.5
▪ Males	43	593	95	446	78	21	27.0	4.4	40	23.8	9.7	42	42.2	10.0	43	50.0	6.8	34.8	7.5	42.2	8.2	37.0	7.7	44.1	8.2	30.9	10.7
▪ Females	34	514	82	455	79	11	24.7	5.1	34	21.8	7.9	32	35.2	9.4	34	41.8	7.4	41.2	8.3	39.6	7.7	43.9	8.2	39.2	7.2	34.3	10.9
1988
• Males	57	562	81	435	59	57	26.6	3.8							57	48.0	8.5	34.4	7.8	44.9	7.6	35.3	8.1	45.2	8.2	32.4	12.8
• Females	32	491	65	424	80	32	25.1	5.3							32	42.3	7.5	40.7	8.0	38.2	7.5	43.6	8.4	40.1	6.2	34.9	10.3
▪ Males	72	571	85	440	62	66	26.8	3.7				8	39.3	6.5	61	48.3	8.5	34.5	7.6	44.7	7.4	35.0	8.0	44.8	8.3	32.9	12.7
▪ Females	39	500	64	425	76	36	25.3	5.3				9	29.0	7.2	33	42.5	7.4	40.9	8.0	38.0	7.5	43.4	8.4	40.0	6.2	35.2	10.2

Note.

^•Students who took all the tests;

^▪Students who took at least one test.

X̄=mean; SD ‒ standard deviation.

Tests: College Board Scholastic Aptitude Test (mathematics = SAT-M, verbal = SAT-V); Raven's Progressive Matrices (Advanced); Vandenberg Test of Mental Rotations; Bennett Mechanical Comprehension Test (Form AA); Allport, Vernon, and Lindzey Study of Values. A blank means that a test was not given to the indicated group.

In a follow-up to the first study, Benbow and Stanley (1983) reported SAT data on another 40,000 young, intellectually talented adolescents, and the findings in the first studies were reaffirmed. No differences of any significance were found on the SAT-V, but the SAT-M revealed sex differences favoring males.

When these data were examined graphically (Benbow, 1988), the male and female SAT-V distributions were found to be isomorphic. However, the male SAT-M distribution, in contrast to the female SAT-M distribution, manifested a higher mean and larger variance, along with a skew, resulting in an exponential intensification of the ratio of males to females in the upper tail of the distribution. The male:female ratio was 2:1 for young adolescents with SAT-M scores of 500 or more, 4:1 for those with scores of at least 600, and 13:1 for those with scores of at least 700 (Benbow & Stanley, 1983). Because the Hedges and Nowell (1995) data showed that high sex ratios (5:1 among the top 3% and 7:1 among the top 1%) are found in the upper tails of the ability distributions of nationally representative samples, those authors concluded that the high sex ratios found in some highly talented samples like that of the SMPY need not be attributed to differential selection by sex.

Since the initial Benbow and Stanley studies were published in the 1980s, several million seventh and eighth graders have taken the SAT (or the American College Test, ACT) through annual talent searches (Benbow & Stanley, 1996; Van Tassel-Baska, 1996). Sex differences in the distributions of SAT-M scores among intellectually talented 12- to 14-year-olds have persisted and are also observed on the ACT-Math (Benbow & Stanley, 1996; Stanley, 1994). For reasons that are not well understood, current ratios of males to females at the high end are not as extreme as in the earlier studies, with male:female ratios among those scoring 700 or more on the SAT-M before age 13 now being less than 4:1 (Blackburn, personal communication, August 4, 2005). Stanley, who studied mathematically precocious youth for decades, explained that 25 years ago there were 13 boys for every girl who scored above 700 on the SAT-M at age 13. Now the ratio is only 2.8:1, which is a precipitous drop that has not been widely reported in the news media. According to Stanley, “It's gone way down as women have had the opportunity to take their math earlier” (quoted in Monastersky, 2005, ¶ 45). There are no studies exploring the reasons for the decline, although possible reasons include that fact that high-school mathematics coursework for boys and girls has become more similar and more girls are getting more encouragement in the form of special programs and mentoring to encourage their participation in higher-level math courses. Regardless, these results suggest that the male advantage for mathematical skills may be limited to the upper end of the ability distribution.

Sex Differences in Mathematical Reasoning in Gifted Students

Mills, Ablard, and Strumpf (1993) documented sex differences among intellectually gifted students in mathematical reasoning as early as second grade (average d = 5 .43). Robinson et al.(1996) reported sex differences in mathematical precocity before kindergarten (average d = .37). More significantly, these latter sex differences were maintained following exposure to mathematical enrichment opportunities aimed atboth males and females. Males gained more than females did on quantitative and visuospatial measures after an average of 28 biweekly intervention sessions (Robinson, Abbott, Berninger, Busse, & Mukhopadhyah, 1997).

The implications of these differences, and especially of the disparate ratios at the top for the math-science education pipeline, are clear: Given an early advantage in these fundamental quantitative skills, a greater number of males than females will qualify for advanced training in disciplines that place a premium on mathematical reasoning. As Hedges and Nowell (1995) stated, “Sex differences in variance and mean lead to substantially fewer females than males who score in the upper tails of the mathematics and science distributions and hence are poised to succeed in the sciences. The achievement of fair representation of women in science will be much more difficult if there are only one-half to one-seventh as many women as men who excel in the relevant abilities” (p. 45).

Other cognitive and noncognitive sex differences expand our understanding of the factors that influence the way precocious youth develop in math. Table 1 contains data on abilities and values of gifted students in the Midwest who were identified by SMPY from 1988 to 1991 and who attended a special summer program (Lubinski & Benbow, 1992). Again, sex differences in mathematical reasoning ability were consistently observed (average d 5 .84), but sex differences in the SAT-V were not observed. Table 1 includes other cognitive measures of general intelligence and specific abilities. No meaningful differences were observed among scores on the Advanced Raven Progressive Matrices (Lubinski & Benbow, 1992), which is a nonverbal measure of general intelligence. There were, however, substantial differences in spatial and mechanical reasoning abilities (average d 5 .92). In addition to these differences in specific abilities, there were also sex differences in vocational interests and values. Table 1 presents the differences in values. As can be seen, males are higher on theoretical values, and females are higher on social values, among other trends. Strongly held theoretical values are characteristic of physical scientists, while social values are negatively correlated with interests in the physical sciences (Achter, Lubinski, Benbow, & Eftekhari-Sanjani, 1999). Similar preference distinctions between males and females have been found using the Strong Interest Inventory (Lubinski & Benbow, 2006), with the SMPY males having stronger investigative and realistic interests and the SMPY females having stronger social interests (Achter, Lubinski, & Benbow, 1996, Appendix B, p. 76). Thus, it appears that early differences in mathematical skills may occur along with other factors relevant to the development of scientific expertise.

Sex Differences in Higher Education

Male–female differences are increasingly apparent as one moves up the educational-vocational continuum (Lane, 1999; Lawler, 1999, 2002; Mervis, 1999a, 1999b, 2000; Sax, 2001; Seymour & Hewitt, 1997; Wickware, 1997), with the disparity actually increasing dramatically at the highest levels (National Research Council, 2001). For example, in the late 1990s there was a 1.5:1.0 male:female ratio among undergraduates in science at MIT, but a more than 11.4:1.0 male:female ratio among faculty (Committee on Women Faculty, 1999). More current data, displayed in Table 2, yield the same pattern of increasing discrepancy at higher levels of achievement (Gottfredson, 1997).

Table 2. Representation of Women Among Tenure-Track Faculty in Elite Universities in Physical Science, Mathematics, and Engineering.

Academic field	Percentage
Mathematics	8.3
Chemistry	12.1
Chemical engineering	10.5
Physics	6.6
Mechanical engineering	6.7
Electrical engineering	6.5
Civil engineering	9.8
Computer science	10.6
Astronomy	12.6

As previously discussed, women now surpass men in the rate at which bachelor's and master's degrees in all areas are earned. The advances of women in terms of degrees earned, however, have not been even across disciplines. We still find fewer women than men in the physical sciences. Yet it is difficult to conclude that this is due to an aversion toward science among women. In 1996, women earned one third or more of the bachelor's degrees in astronomy, earth sciences, and oceanography, over 40% of the bachelor's degrees in chemistry, mathematics, and statistics, over 50% of those in biology, and 73% of those in psychology (Browne, 2002). By 2004, women earned over 42% of the mathematics undergraduate degrees, up from 37% in 1994 (American Mathematical Society, 2004; National Science Foundation, 2006, p. 1), and over 40% of the degrees in the physical sciences (up from 14% in 1966) and in the earth, atmospheric, and oceanic sciences (up from 9% in 1966; National Science Foundation, 2002a). Nonetheless, as Table 3 illustrates, women are earning more college degrees and master's degrees than men are, and they are earning close to half of all doctorate and professional degrees. However, as shown in Table 4, percentages vary by discipline, with more doctorates in education and the social sciences going to women; women are about par with men in the life sciences, but they are underrepresented in the physical sciences and engineering (National Science Foundation, 2002a; Nelson & Rogers, 2004; Valian, 1998, 2005).

Table 3. Trends in Degrees Awarded to Women (Percentages).

Year	Bachelors	Masters	Doctorate	Professional
1970	43	40	13	2
2002	57	59	46	47

Table 4. Doctorates Awarded to Women by Discipline (Percentages).

Year	Education	Social sci.	Life sci.	Physical sci.	Engineering
1980	45	35	25	12	4
2001	65	54	47	26	17

Data from 1995 (reported in Browne, 2002), however, give a more nuanced look at this trend and reveal that there are substantial differences among subdisciplines in addition to the differences among disciplines. In engineering, for example, women are scarce in mining/mineral and mechanical engineering (0% and 6%, respectively) but not in environmental health and bioengineering (25%). Among physics doctorates, 17% of acoustics but only 4% of particle physics degrees are earned by women. In biology, 22% of the entomology degrees went to women, in comparison to 68% of those in the nutritional sciences. And, in psychology, where 64% of the doctoral degrees went to women in 1995, physiological psychology attracted 38% women, in contrast to developmental psychology, which attracted 80% women. Finally, in the social sciences as a whole, fewer women chose statistics and economics (23% and 24%, respectively) than chose anthropology and sociology (58% and 53%; Browne, 2002).

It is tempting to ask whether these differences in higher education emanate from sex differences in abilities, but the combination of native ability, socioeconomic context, personal interests, and cultural influence is remarkably complex. For example, while women do not complete their doctorates in natural sciences and engineering at the same rates as men, the difference disappears when mathematical ability is adjusted for (J.C. Baker, 1998). Moreover, while sex differences in mathematical ability are associated with sex differences inoccupational status and income (Paglin & Rufolo, 1990), sex differences in interests—such as a preference for working with people—are also important in explaining educational and career choice.

Sex Differences in Career Development Choices

Xie and Shauman (2003) noted that the best understanding of the engagement of males and females in science is likely to emerge from studies that take a life-course perspective. The SMPY has collected longitudinal information on a large number of high-ability males and females to investigate their career development (Lubinski & Benbow, 2006). (The very oldest individuals in the study were born in 1959 and the youngest in the early 1980s.) Over 4,000 intellectually talented individuals, identified according to their performance on the SAT during seventh or eighth grade, have been tracked for over three decades in four separate cohorts (along with a comparison group of 714 nonprecocious individuals). There is no comparable study of its kind. Students were invited to take the SAT in the seventh or eighth grade if they had scored in the top percentiles on a standardized achievement test administered by their school. The first cohort comprised seventh and eighth graders from the Greater Baltimore Area who were identified in the early 1970s as representing the top 1% in mathematical ability. The second cohort included seventh graders from the Mid-Atlantic region who scored in the top .5% in mathematical ability, verbal ability, or both. The third cohort included seventh and eighth graders from across the nation who were identified in the early 1980s as being in the top .01% in mathematical ability, verbal ability, or both. The fourth cohort, drawn from the Midwest in the late 1980s and early to mid 1990s, comprised two groups: One represented the top .5% in mathematic ability, verbal ability, or both, and the other represented individuals who scored at least at the 97th percentile on any subtest of an achievement test administered by their schools.

Participants completed comprehensive surveys and inventories providing a detailed view of their development and educational/ career trajectories. The last survey of this group occurred when participants were in their mid 30s, with earlier data collection points occurring at ages 13, 18, and 23. Because it is likely that not all future talent for mathematics and science can be identified using the SAT at age 13, the SMPY decided to form a fifth cohort to determine the generalizability of its findings. Cohort five comprised 714 individuals, educated in the United States, who were enrolled in the top 15 U.S. graduate programs in mathematics and science. Because an equal sample of men and women was needed in departments where the male:female ratios often exceeded 3:1, the women were oversampled (i.e., more women were included in the sample than their proportional enrollment in graduate programs). This cohort was studied retrospectively, concurrently, and prospectively (age 33 and beyond; Lubinski, Benbow, Shea, Eftekhari-Sanjani, & Halvorson 2001; Lubinski, Benbow, Webb, & Bleske-Rechek, 2006).

As in other studies, no statistically significant sex differences in overall general intelligence were found for the SMPY samples, but differences were found in certain specific abilities. Individuals who were assessed by age 13 as being in the top 1% in mathematical reasoning ability (cohorts 1 and 2) became highly educated: Over 90% earned a bachelor's degree, and over 25% earned a doctorate, with essentially no sex differences in degrees earned (Benbow, Lubinski, Shea, & Eftekhari-Sanjani, 2000). About 50% earned at least one postsecondary degree in math and science areas, with 64% of the top .5% in mathematical ability securing at least one postsecondary math or science degree (Benbow et al., 2000). The men were at least twice as likely to earn degrees in the inorganic sciences and engineering as the women, with the men earning almost five times as many doctorates in these areas as the women. As shown in Figure 4, more women than men earned doctoral degrees in the life sciences and medicine (Benbow et al., 2000). Not surprisingly, the subsequent career choices of these mathematically talented individuals mirror the pattern seen for degree specialization.

Fig. 4.

Sex differences in eventual career choices for two cohorts of mathematically talented youth. Data are from Benbow, Lubinski, Shea,& Eftekhari-Sanjani (2000).

In a subsequent study to Benbow et al. (2000), mathematically talented individuals in cohorts 1 and 2 who had planned on majoring in mathematical or scientific areas when they entered college were studied in more depth at approximately age 33, to better understand the factors that differentiated those who remained in mathematics or science and earned such degrees from those who opted to pursue undergraduate degrees in other areas (Webb et al., 2002). More males had declared an intention to pursue a mathematics or science degree than females, as shown in Tables 5 and 6, and there was greater attrition from the mathematical or scientific disciplines by females than there was by males (26% vs. 17%). High-school educational experiences, abilities, and interests predicted whether an undergraduate degree was attained in mathematics or science or the individual left to pursue other areas of study. The ones persisting with mathematics or science degrees had higher SAT-M scores and more high-school course work in mathematics and science, and they more often reported a mathematics or science course as their favorite course. They also had congruent occupational interests as measured by the Study of Values and Holland Occupational codes. Once these variables had been entered into the discriminant function analysis (a statistical procedure for determining which variables are important in differentiating two or more groups), sex added essentially no explanatory power. (By itself, sex yielded a squared multiple correlation—a measure of the amount of variance that can be explained by or attributed to a variable—of only.01, independent of the other variables.) These results underscore the complex set of explanatory variables needed to predict career success in mathematics and science. In other words, among highly gifted individuals, those who pursued careers in science and mathematics also took more related coursework in high school, rated math and science courses as their favorites, and were interested in math and science. More of the highly gifted males than the females had these patterns of experiences and attitudes that were predictive of career choices in science and mathematics.

Table 5. Among Mathematically Talented Students Expecting to Major in Math/Sciences, the Specific Fields of the Expected Undergraduate College Major (Percentages by Sex).

Field	Men	Women		Effect size
Engineering	43.4	22.9		0.43
Mathematics	15.9	21.1		‒0.13
Biological science	13.4	23.4		‒0.26
Computer science	8.3	6.0		0.08
Medical science	3.6	12.9		‒0.34
Physical science	8.8	1.4		0.41
Chemistry	5.0	8.0		‒0.12
Earth science	1.2	2.3		‒0.08
Agricultural science	0.4	2.0		‒0.10

Note. From Webb, Lubinski, and Benbow (2005).

Table 6. Among Mathematically Talented Students Entering College Expecting to Major in Math/Sciences, the Completed College Majors (Percentages by Sex).

Field	Men	Women	Effect size
Math/science
Engineering	40.9	17.4	0.54
Biological science	9.5	18.9	‒0.26
Mathematics	9.3	10.9	‒0.07
Computer science	8.0	6.6	0.04
Chemistry	5.0	5.1	‒0.01
Physical science	7.0	0.9	0.34
Medical science	1.8	11.4	‒0.39
Agricultural science	0.5	1.7	‒0.17
Earth science	1.2	1.1	0.01
Total	83.3%	74.0%	0.22
Non-math/non-science
Business/economics	8.6	11.7	‒0.10
Social science	3.8	4.9	‒0.05
English	1.2	2.3	‒0.08
Arts	0.3	1.7	‒0.22
Philosophy/religion	0.8	0.6	0.04
Languages	0.1	1.7	‒0.26
History	0.4	0.6	‒0.04
Communications	0.3	0.3	0.00
Education	0.1	0.9	‒0.16
Environmental design	0.1	0.3	‒0.04
General studies	0.3	0.0	0.06
Other	0.8	1.1	‒0.05
Total	16.7%	26.0%	‒0.22

Note. From Webb, Lubinski, & Benbow (2005).

To pursue further the role of mathematical reasoning ability in math and science achievement, individuals in cohort 1 who by age 13 had scored in the top quartile of the top 1% were compared with those in the bottom quartile of the top 1% (Benbow, 1992; Wai, Lubinski, & Benbow, 2005). On 37 math/science achievement variables assessed at age 23 (these variables went well beyond grades), statistically and substan-tively significant effect sizes were observed favoring the top versus the bottom quartile on 34 of the variables (Benbow, 1992). (Effect sizes averaged d 5 .97 for continuous variables and d 5 .57 for categorical variables from the high-school years, d 5 .47 for the continuous variables and d 5 .39 for the categorical variables from the college years, and d 5 .41 from the early stages of graduate school.) Although sex differences were found in these analyses, they were smaller than the differences between the top and bottom quartiles, and they were not observed in the relation between mathematical ability and academic achievement.

At age 33, the same pattern emerged for the highly gifted individuals in Cohort 1 when the following variables were studied: secured doctorates, math/science PhDs, income, patents, and tenure-track positions at top U.S. universities (Wai et al., 2005). These results provide evidence against the “threshold” hypothesis, which maintains that there is some (high) level of ability needed for career success in cognitively demanding occupations and that scoring beyond that level will not increase the probability of success in those fields. What is missing from predictions based on the threshold hypothesis is an understanding that there is a great deal of variability in the extreme tails of ability distributions, such that the top quarter of the top 1% could be very far from the bottom quarter of the top 1% (with actual distances depending on the specific distribution). This idea can be visualized by imagining a bell-shaped curve with the tails never quite touching the horizontal axis. The results of this study contrast with a conclusion drawn by the authors of a letter published in Science (Muller et al., 2005), who claimed: “ [T]here is little evidence that those scoring at the top of the range in standardized tests are likely to have more successful careers in the sciences. Too many other factors are involved” (p. 1043). Yet ability is not everything. A congruent preference pattern is also a good predictor of the discipline in which one is likely to earn a four-year degree (Achter et al., 1999) and one's occupational setting at age 33 (Wai et al., 2005). Preference patterns add incremental (additional) validity beyond abilities, and the effect holds for both males and females.

Visuospatial Ability and Mathematics and Science Careers

All of the above studies speak to the power of mathematical reasoning ability in predicting subsequent math/science achievement. Yet prediction can be improved if one considers visuospatial ability and the relative strength of mathematical ability compared to verbal ability within a given individual, both of which display sex differences. Individual differences in the relative strength of verbal, mathematical, and quantitative abilities that are identified at an early age can predict differences in developmental trajectories and occupational pursuits (Achter et al., 1999; Lubinski, Webb, Morelock, & Benbow, 2001). We discuss both sets of findings next.

Proficiency in visuospatial ability has long been associated with success in cognitively demanding educational tracks and occupations such as engineering, architecture, physics, chemistry, and surgery (Smith, 1964; Snow & Yalow, 1982; Sorby, & Baartmans, 2000) and is a salient characteristic of physical scientists (Gohm, Humphreys, & Yao, 1998; Humphreys, Lubinski, & Yao, 1993). Yet, visuospatial ability is not routinely taught or assessed by schools and thus is not often developed and assessed in ways that influence students’ educational and career plans.

Using a sample of 393 precocious males and 170 precocious females, Shea, Lubinski, and Benbow (2001) employed multi-variate statistical methods (i.e., methods that use multiple dependent measures), using age-13 SAT-M, SAT-V, and visuospatial-ability scores for top-.5%-ability individuals, to predict a series of developmentally sequenced educational/ vocational outcomes: (a) favorite and least favorite high-school course, (b) field of undergraduate degree, (c) field of graduate degree, and (d) occupation at age 33. Visuospatial ability added incremental validity to SAT-M and SAT-V assessments in predicting educational/vocational outcomes over 20 years, an effect shown in Figure 5. Perusal of Figure 5 will show, for example, that students who reported that their favorite high-school subjects were in the humanities or social sciences tended to be above the mean on the SAT-V (above the horizontal axis), below the mean on the SAT-M (to the left of the vertical axis), and below the mean on spatial ability (indicated with an arrow facing left). The other three graphs in Figure 5, which show the profile for their least-favorite high-school courses, college majors, and occupations, can be read in the same way. It is not surprising, given these findings, that Humphreys et al.'s (1993) 13-year longitudinal study of 400,000 high-school students, assessed on mathematical, visuospatial, and verbal abilities, concluded that mathematics and science disciplines appear to be losing many talented individuals because selection for these educational tracks is limited to mathematical and verbal abilities.

Fig. 5.

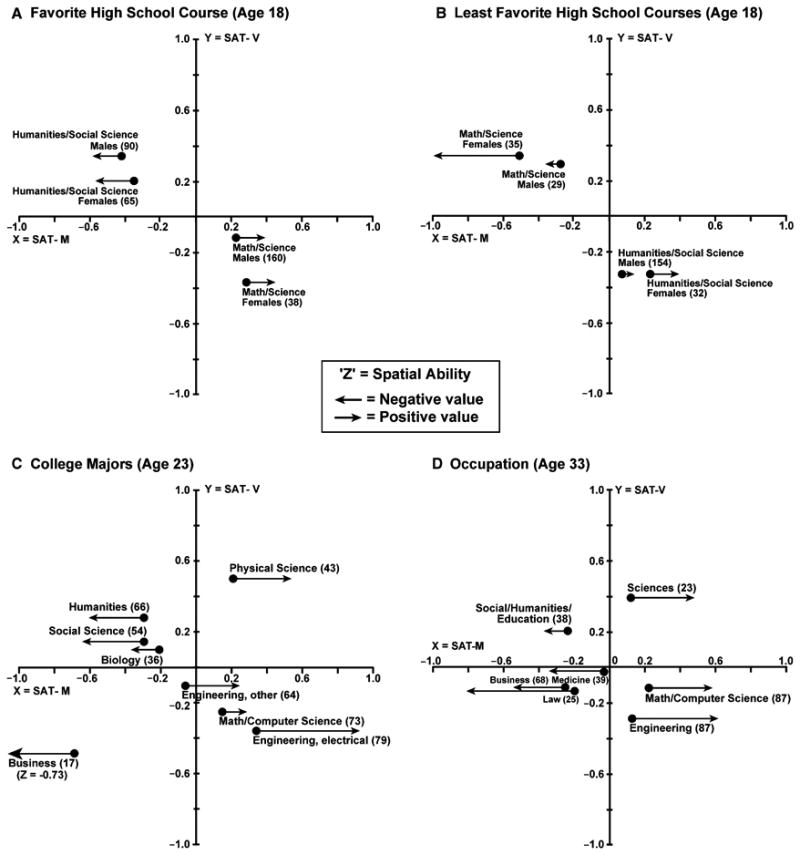
Favorite and least-favorite high-school courses at age 18 (panels A and B), college majors at age 23 (panel C), and occupations at age 3 (panel D) as predicted by SAT-Mathematics (SAT-M; x-axis), SAT-Verbal (SAT-V; y-axis), and visuospatial ability (left vs. right arrows) for sample of precocious males and females. These 4 figures depict the simultaneous effects of math, verbal, and spatial scores, using 3-dimensiona space. Panel A, for example, shows that students who reported that their favorite high-school subjects were in the humanities or social science tended to be above the mean on the SAT-V (above the horizontal axis), below the mean on the SAT-M (to the left of the vertical axis), and below th mean on spatial ability (indicated with an arrow facing left). The other three panels can be read in the same way. Reprinted from “Importanc of Assessing Spatial Ability in Intellectually Talented Young Adolescents: A 20-Year Longitudinal Study,” by D.L. Shea, D. Lubinski, & C.P. Benbow, 2001, Journal of Educational Psychology, 93, pp. 604–614. Copyright 2001, the American Psychological Association. Reprinte with permission.

Intellectually talented adolescents with stronger visuospatial ability relative to verbal ability (determined intraindividually) were more likely to be found in engineering, computer science, and mathematical fields, whereas those with the inverse ability pattern tended to gravitate toward humanities, social science, organic science, medical arts such as nursing, and legal fields (Shea et al., 2001). A similar pattern also emerged for relative intraindividual strengths in quantitative versus verbal abilities, with visuospatial ability exhibiting somewhat greater overall discriminative power. That is, students who are relatively more verbally than quantitatively or spatially talented gravitate toward the humanities and social sciences, whereas those with the opposite ability pattern lean more toward engineering and the physical sciences. Webb, Lubinski, and Benbow (in press) obtained similar results with an independent sample of 1,060 high-ability adolescents tracked for 5 years. These findings held for both males and females.

In a more definitive study, Lubinski, Webb, et al. (2001) found that among profoundly gifted individuals (top 1 in 10,000 in ability and who are disproportionately male), those whose ability strength was mathematical compared to verbal but nonetheless had very high verbal ability reported mathematics and science courses as their favorites in high school and college, and disproportionately pursued educational credentials in mathematics and science, reporting three times as many awards and special accomplishments in science and technology as compared to the humanities and arts. Those with the inverse ability pattern (i.e., V > M) reported the humanities to be their favorite courses in high school and in college, disproportionately pursued educational credentials in the humanities and law, and reported twice as many awards and special accomplishments in the humanities and arts compared to sciences and technology. Those with relatively flat profiles fell somewhere in between.

It must be acknowledged that the attribute of having a “tilt” favoring mathematical and visuospatial abilities compared to verbal (i.e., M > V), regardless of level of ability, is more frequently exhibited by males than by females across the four cohorts in the SMPY study. Females tend to be more balanced in their ability profile (i.e., M ≃ V) and this leads them to choose mathematics, engineering, or physical-science careers less frequently than their male counterparts do. In other words, these data show that having better math abilities relative to one's own verbal abilities is associated with selecting careers in mathematics and science and that this tilt is more frequently found in high-ability males than it is in high-ability females. When making career choices, highly gifted individuals consider their own pattern of abilities and not whether they have the absolute level of ability needed to pursue a career in a demanding field of study. They seem to be implicitly asking, “What am I better at?” and not asking “Am I smart enough to succeed in a particular career?”

The above studies illustrate how sex differences in mathematical and visuospatial abilities detected by age 13 have consequences that can be seen 20 years later. These sex differences in abilities and preferences predict differences in participation and achievement in mathematics and science for individuals in their mid 30s. Sharper predictive power is obtained if abilities are combined with preferences, which also display sex differences by age 13 (Achter et al., 1996, p. 76; Lubinski & Benbow, 2006). Males more frequently than females display preference patterns that are conducive to pursuing science and mathematics careers and that, when coupled with abilities, form aptitude complexes (Corno et al., 2002; Cronbach & Snow, 1977), vocational taxons (Dawis & Lofquist, 1984), or trait clusters (Ackerman, 1996; Ackerman & Heggestad, 1997) that contribute to the development of scientific skills. The finding that highly gifted individuals prefer academic areas in which they are most able further exacerbates discrepancies at the high levels of achievement, as do any differences in self-competency beliefs, with their effect on task values and, thus, engagement in science (Jacobs, Lanza, Osgood, Eccles, & Wigfield, 2002). High-ability males were found in one study to have unrealistically high self-competency beliefs; no such effect was found for females, whose beliefs also were high but were more accurate predictors of future performance (e.g., r 5 .38 for males vs. r 5 .61 for females; Gibbons, Benbow, & Gerrard, 1994).

Additional Factors Influencing Sex Differences in Career Choices of High-Ability Individuals

Occupational choices are not made in isolation orindependently of other life decisions such as marrying, having children, or living close to relatives (Benbow et al., 2000; Eccles, 1994). There are trade-offs, and for many successful women there exists considerable conflict between the traditionally feminine values and goals in life (e.g., child-care responsibilities) and the expectations from traditionally male highly competitive achievement activities (Browne, 2002; Eccles, 1994). Indeed, intellectually talented men in their mid 30s are on average more career focused (ds of .21 – .76), work longer hours, and are willing to work longer hours than women of the same age whose reports indicate that they tend to prefer a more balanced life approach with regard to career, family, and friends (Benbow et al., 2000; Lubinski, 2004, Webb et al., 2002). If these sex differences continue over a sustained time frame, women's additional family responsibilities may help explain some of the underrepresentation of women in science careers (Eccles, 1994) and at the highest levels of various professional careers. That is, if men remain more career focused and spend more hours working, for whatever the reasons, then, in all likelihood, men will accomplish more than their female counterparts and will likely be seen as more successful in the world of work. Already, men in the SMPY sample reported higher incomes, a difference that disappeared when hours worked was controlled (Benbow et al., 2000). This does not mean, however, that men are more successful in life or more personally satisfied: On all indicators examined, these talented men and women in their mid 30s reported feeling equally good about themselves and about their achieved success.

Xie and Shauman (2003), when studying women in science, found that most of the observed sex differences in research productivity could be attributed to personal characteristics and the structural features of the employment setting. Having children was one factor associated with less engagement in mathematical and science careers for women but not for men. Sex differences in mathematical and science careers are indeed extremely complex and are surely influenced by the social structures in which individuals are situated, the neighborhood resources, and the networks of interaction in which they participate (Eccles, 1994; Entwistle, Alexander, & Olsson, 1994; Farmer, Wardrop, Anderson, & Risinger, 1995; Xie & Shuman, 2003). The fact that social and environmental variables are important determinants of career success, however, does not mean that we cannot draw conclusions about the role of abilities, preferences, and other factors that may be responsible for producing sex disparities in participation, engagement, and achievement in the quantitative disciplines at the very highest levels. The SMPY studies clearly demonstrate that sex differences in mathematical and visuospatial abilities, the male tilt compared to female balance in ability profiles, and differing preferences and educational experiences all contribute to the sex differences in outcomes among the highly gifted.

An Evolutionary Account Of Sex Differences In Mathematics And Science

There are multiple perspectives for examining the origins and meaning of sex differences in science and mathematical achievement. In psychology, evolutionary theory emphasizes the adaptive value of behaviors and mental processes that have developed throughout the entire history of a species. Answering questions about sex differences in academic and cognitive domains from an evolutionary perspective is complicated because the knowledge bases, technical skills, and insights that are needed to achieve in math and science are rooted in the poorly understood interaction of cognitive and motivational factors and culture-specific educational goals and opportunities to master these academic domains. Most of the competencies that compose modern math and science are not the direct result of evolution (Geary, 1996). Studying advanced topics in mathematics and science, for example, are recent activities for humans, so they may be better thought of as being built upon earlier adaptive solutions for functioning in a specific cultural context rather than as direct reflections of the history of our species (Gazzaniga & Heatherton, 2006; Geary, 2007). Nonetheless, an evolutionary perspective can contribute to our understanding of sex differences in math and science by providing a way to understand proximate biological correlates (e.g., sex hormones) of these differences, and a perspective for simultaneously considering developmental and social correlates. A detailed consideration of potential indirect evolutionary influences on sex differences in math and science is beyond the scope of this monograph and, in fact, may not be possible given our current state of knowledge in these areas. Our goals are to provide examples of how an evolutionary perspective can be used to frame our understanding of current empirical findings and to generate hypotheses for future study.

Sexual Selection

Darwin (1871) proposed that many sex differences have evolved by means of sexual selection. The mechanisms involve competition with members of the same sex over mates and discriminative choice of mating partners. The most frequently studied dynamics are male–male competition over access to mates and female choice of mating partners. It is clear that female competition and male choice occur in many species. Whatever the pattern, the most common result is the evolutionary elaboration of physical, behavioral, or cognitive traits that facilitate competition and choice. In recent decades, the study of sexually selected sex differences has emerged as a vibrant area in the biological sciences and has yielded insights into the evolution and proximate expression of these differences across hundreds of species (Andersson, 1994; Andersson & Simmons, 2006). Although the results of these studies strongly confirm the importance of sexual selection, some sex differences may have evolved that are unrelated to sexual selection (Isaac, 2005). Even for traits related to sexual selection, many issues remain to be resolved regarding the nuances of competition and choice and the interaction of these dynamics (Andersson & Simmons, 2006).

Sex Hormones

The proximate expression of many of the traits that have evolved by means of sexual selection are influenced by prenatal and postnatal exposure to sex hormones, particularly androgens in mammals (e.g., Adkins-Regan, 2005; Morris, Jordan, & Breedlove, 2004). Androgens and other hormones can influence sex differences in cognition and behavior through early prenatal organization of associated brain areas, activation of these areas by postnatal exposure to androgens, or some combination. The influences of sex hormones are, however, complex and sometimes very subtle, and often interact reciprocally with genetic sex, physical health, and social and ecological context (Arnold et al., 2004; McEwen et al., 1997). As an example, these reciprocal relations are important for understanding how androgens interact with male health and social context in the expression (or not) of evolved sex differences.

Within-Sex Variation

The processes that are at work in sexual selection can also exaggerate within-sex variation (Houle, 1992; Pomiankowski & M0ller, 1995). Pomiankowski's and M0ller's cross-species review and analysis suggest that within-sex variation can occur when competition or choice favors traits toward the phenotypic extreme (observable traits such as the peacock's tail). Although much remains to be learned, it appears that selection that favors extreme traits can result in the evolution of genetic mechanisms that result in exaggerated within-sex variation as well as the evolution of condition-dependent traits.

As a way of understanding condition-dependent traits, consider for example, how the combination of the physical demands of maintaining a larger body size—a common result of male–male competition, with the advantage going to larger members of a species (Andersson, 1994)—and potential interactions between sex hormones and immune functioning may make males more vulnerable to infestation with parasites, fluctuations in food supply, or other ecological conditions (Moore & Wilson, 2002; Muehlenbein & Bribiescas, 2005). Infestation with parasites can leadtoanincreaseinimmune system activity, which can suppress the secretion of testosterone. The decline in testosterone will result in poorly developed secondary sexual characteristics, placing the male at a disadvantage in terms of female choice or male–male competition (Folstad & Karter, 1992). The result is that the least healthy males suffer the most under difficult ecological conditions and this exaggerates within-sex variation among males. A similar process may occur in species in which females are larger than males and compete more and parent less; age-specific mortality is higher infemales of these species (Moore & Wilson, 2002), and lifespan is shorter (Allman, Rosin, Kumar, & Hasenstaub, 1998).

Development

From an evolutionary perspective, nature and nurture are integrally and reciprocally linked and cannot be separated. The developmental process (e.g., length of infancy) and the responsiveness of the developing trait to experiences are evolved phenotypes (West-Eberhard, 2003). It is particularly important to consider the developmental patterns for slowly developing and highly social species; these species tend to have large brains and may be the most “plastic” in terms of learning and social behavior (e.g., Dunbar & Bever, 1998; Joffe, 1997).

Sex differences in life-history patterns (e.g., age of maturation, life span) are common and, depending on the species, are influenced by a combination of organizational and activational effects of sex hormones, as well as by nutritional status and social context (Adkins-Regan, 2005; Stearns & Koella, 1986). In many species, male–male competition and female choice result not only in larger males but also sex differences in life-history development. In these species, males often physically mature at a later age, reproduce later (if at all), engage in more risky and aggressive behaviors, and have a shorter life span (Allman et al., 1998; Leigh, 1996). Social and behavioral differences that may provide practice for adult reproductive activities also may emerge during development. Rough-and-tumble play among males is common in primates in which there is male–male competition in adulthood (Fagen, 1981), and females of many primate species often play parent with a sibling or other young member of the group (Nicholson, 1987). Even in these species, there is typically overlap in the play behaviors of the two sexes. However they are manifested, sex differences are often small early in development and become larger as individuals approach reproductive maturation, a finding that was originally noted by Darwin (1871).

An Evolutionary Understanding of Human Sex Differences

Evolutionary theory applies as well to human sex differences as it does to those of other species. However, the twin foundations of sexual selection—male competition and female choice—are nuanced, in humans, by the existence of female competition and male choice; the two latter components follow from male investment in children. The combination is predicted to result in more subtle and perhaps smaller sex differences in humans than for many other species.

Sexual Selection

Human sex differences in physical size, upper-body musculature, rate and pattern of physical development, and other traits are consistent with the view that sexual selection has contributed to some currently observed sex differences (Tanner, 1990). However, the relative importance of evolutionary (including sexual-selection) and cultural influences on cognitive, behavioral, and social sex differences is the subject of vigorous debate (Geary, 1998; Newcombe, 2002; Wood & Eagly, 2002).

It has been proposed by some evolutionary psychologists and anthropologists that male–male competition has been an important part of human evolutionary history and has contributed to some currently observed sex differences. In traditional societies, this competition includes coordinated group-level conflict for control of ecologically rich territories and for social and political influence (e.g., Chagnon, 1988), which is often manifested by low-level but frequent raiding, warfare, and political manipulation (Keeley, 1996). Within-group competition is seen in the formation of dominance hierarchies and control of in-group politics. Maintaining groups’ territorial borders, tribal warfare, and large-game hunting—all of which are almost exclusively male activities (Murdock, 1981)—in-volve movement across large ranges. Because warring males needed to move across large-scale space, it is only a short leap for evolutionary psychologists to hypothesize that this resulted in an evolutionary process that supports brain development for large-scale navigation in males. Contemporary manifestations can be seen today when males obtain much higher scores on some visuospatial tasks, particularly mental rotation and three-dimensional simulations. The male activities of hunting and warfare involve the construction and use of projectile weapons that require the ability to track movement in 3-D space.

Even though there are many nuances to the proposal that the contemporary male advantage in spatial abilities is a result of their roles as hunters and fighters—and the proposal itself has been questioned by many social scientists whose critiques are presented at the end of this section (e.g., Wood & Eagly, 2002)—these patterns are nonetheless consistent with predictions derived from sexual selection, and thus they merit some consideration. In the following sections, we provide just a few illustrations of how this perspective might broaden and enrich our understanding of currently found sex differences related to math and science achievement in the 21st century.

Sex Hormones and Cognitive Sex Differences

The male advantage in visuospatial abilities appears to contribute to the male advantage in some areas of mathematics and engineering, as discussed earlier (Sorby & Baartmans, 2000). It has been hypothesized that sex differences in visuospatial cognition have been influenced by male–male competition and other sex differences during human evolutionary history (Ecuyer-Dab & Robert, 2004; Geary, 1998; Sherry & Hampson, 1997). If the male advantage in visuospatial abilities and in some other areas of spatial cognition are related to sexual selection, then the proximate expression of these sex differences is predicted to be related to prenatal or postnatal exposure to sex hormones, particularly androgens.

One method to test such hypotheses is to study individuals with disorders that were caused by prenatal exposure to sex hormones that are not typical for their sex (Berenbaum, 1999). With one such disorder, congenital adrenal hyperplasia (CAH), individuals are prenatally exposed to excess androgens. Women born with CAH show masculine play behaviors, but findings about later-life behaviors and abilities are difficult to confirm because these children are treated with drugs for this condition as soon after birth as it is detected and as soon as treatment can be administered. It is also possible, even likely, that parents and other important adults in their lives treat them in ways that might exaggerate pressures for feminine behaviors because the adults know that the CAH girls were exposed to masculinizing hormonal influences in utero. The evidence is mixed with respect to the visuospatial and related abilities of these women; some studies show an advantage of women with CAH and others do not, or the advantage is found on some but not other spatial tasks (Hampson, Rovet, Altmann, 1998; Hines et al., 2003; Resnick, Berenbaum, Gottesman, & Bouchard, 1986). Thus, the data on the cognitive patterns of girls who were exposed prenatally to masculinizing hormones do not provide the conclusive evidence we need to link prenatal sex hormones directly to cognitive abilities.

The potential activational effects of sex hormones can also be studied in humans by assessing any cognitive changes that might follow hormonal therapy for female-to-male and male-to-female transsexuals. Female-to-male transsexuals are treated with testosterone, and male-to-female transsexuals are treated with a combination of androgen-suppressing drugs and estrogens to prepare them for their new life as either a male or female. Van Goozen and her colleagues found that performance on a spatial-ability measure improved after androgen administration for the female-to-male transsexuals, although they did not administer a measure of visuospatial ability (Van Goozen, Cohen-Kettenis, Gooren, Frijda, & Van de Poll, 1994, 1995). Performance on a test of the ability to rotate images in 2-D space—which typically show smaller sex differences than tests of 3-D spatial cognition (Voyer et al., 1995)—improved significantly (d 5 0.56) for a group of individuals after undergoing only 3 months of androgen treatment as part of their preparation for female-to-male sex-change surgery. In a follow-up study, Slabbekoorn and colleagues confirmed this effect, but only for a measure of 3-D spatial cognition (Slabbekoorn, Van Goozen, Megens, Gooren, & Cohen-Kettenis, 1999); the change on the 2-D measure was not significant. The improvement in performance on the 3-D spatial-ability test for these individuals following only 3 months of androgen treatment was very large (d 5 1.2). The magnitude of this effect did not increase with further treatment over the next 7 months, and the improved spatial abilities of these (new) men did not decline 5 weeks after stopping the hormonal treatment. Androgen suppression did not result in a decline in 3-D spatial performance for male-to-female transsexuals, suggesting some prenatal organizational effects on these abilities. The overall results across the different types of studies are consistent with postnatal activational influences on the expression of some aspects of spatial abilities.

Within-Sex Variation

In nonhuman species, sex differences in patterns of competition and choice are often associated with increased within-sex variation for the traits related to competition and choice, and in many species this is accompanied with an increase in disease risk and early mortality for the sex experiencing the most intense competition. Although much remains to be learned about these patterns, they do seem to hold for humans. As would be predicted, human males are more vulnerable to many diseases and suffer higher mortality at all ages, especially in unstable social contexts (Möller-Leimkuühler, 2003), and the increased mortality for males is in part due to the tendency to engage in more risky and aggressive behaviors associated with male–male aggression and status displays (Minino, Anderson, Fingerhut, Boudreault, & Warner, 2006; Wilson & Daly, 1985).

With respect to the sex differences in math and science, there are two predictions that highlight the potential utility of an evolutionary perspective. The first is that there will be greater within-sex variation in the 3-D spatial abilities of males, and the second is that males growing up in difficult circumstances will be more strongly affected behaviorally and cognitively than females growing up in the same circumstances. With respect to the latter, one corollary prediction is that the 3-D spatial abilities of these males will be lower than those of males growing up in better environments and that there will be no sex difference or a reversal of the sex difference for individuals growing up in the more difficult environments. This is the pattern found for height: The sex differences are largest in the healthiest populations and smallest for populations under nutritional stress (Gaulin & Boster, 1992). In other words, poverty and its correlates prevent children from reaching their full physical potential. The same appears to be true for cognitive potential.

The results from multiple large-scale studies have confirmed greater variability among males than among females in many cognitive domains, including on measures of mathematics, science, and spatial abilities, as noted earlier (Feingold, 1992; Hedges & Nowell, 1995; Strand et al., 2006; Stumpf & Stanley, 1998). As we described earlier, across two studies that included about 100,000 high school students inthe United States, Hedges and Nowell found 27% more variation in the spatial-ability scores of males than in those of females. Feingold's examination of national norms for several ability measures and across a variety of ages and cohorts found that males were always more variable on measures of spatial cognition, with a mean effect of about 20% more variance in male samples. Unfortunately, these studies did not distinguish among the different facets of spatial ability, and the meta-analyses that have separated these facets do not report within-sex variances (Voyer et al., 1995). In the just-described study of female-to-male transsexuals, the post-androgen increase in 3-D spatial ability was accompanied by a 54% increase in within-group variation on this test (Slabbe-koorn et al., 1999).

Levine and colleagues assessed a sample of 547 children from high-, middle-, and low-income backgrounds across the second and third grades on two spatial tasks (2-D rotation and an aerial map) and a syntax comprehension test (Levine, Vasilyeva, Lourenco, Newcombe, & Huttenlocher, 2005). There were no sex differences on the syntax test, as expected, but males outperformed females on both spatial tasks (ds 5 .35, .23) but only for children from high- and middle-income families. There were no sex differences for the low-income children. In other words, the low income level of the family was associated with lower scores for both males and females on all three tests, but, in comparison to same-sex peers, the scores of males seemed to be more strongly affected by poverty, especially for the spatial tasks. The results are consistent with evolutionary predictions regarding the influence of environmental circumstance on within-sex variation in traits that are potentially related to sexual selection. Further studies are needed to confirm this pattern and to more explicitly test the prediction that males growing up in difficult circumstances will be more strongly affected for traits predicted to be related to sexual selection (e.g., 3-D spatial cognition, which is needed to travel long distances for warfare and for hunting—both primarily male activities) than for other traits (e.g., grammatical structure of utterances).

Development

When they are found, sex differences in developmental activities are predicted to mirror sex differences in patterns of competition and choice that have evolved by means of sexual selection, and the proximate expression is predicted to be influenced by prenatal and postnatal exposure to sex hormones, as well as by social context (Geary, 1998; Pellegrini, 2004). Testing these predictions is complicated by the influence of early and current experiences on within-sex variation, and thus there is the potential for the magnitude of any sex differences to vary with context. Moreover, it is not always clear when in development an evolved sex difference might be expressed. As mentioned earlier, in many species, sex differences are small or nonexistent early in life and increase in magnitude as individuals approach reproductive maturation. But the developmental sex differences in behavior or cognition can emerge early if they provide practice for adult activities. With humans, early sex differences have been foundin many domains, ranging from play and toy preferences (Golombok & Rust, 1993) to peer relationships (Rose & Rudolph, 2006), but the relation of these behaviors to sexual selection remains to be explored.

In keeping with the focus on spatial abilities, and as described earlier, a male advantage on some spatial tasks emerges in childhood (e.g., Johnson & Meade, 1987) and perhaps during the preschool years (Levine et al., 1999). Levine et al. found an advantage of $4\frac{1}{2}$ - to 7-year-old males on a test that involved the rotation or transformation of 2-D shapes; unlike results for adults, the females were slightly more variable as a group. Voyer et al.'s (1995) meta-analysis revealed a male advantage in childhood for a measure of 3-D spatial cognition (d 5 .33) that was about the same magnitude as that found by Levine et al. By adulthood, the magnitude of the male advantage doubled (d 5 .66).

Voyer et al.'s (1995) analysis is informative, but it is based largely on cross-sectional data. Longitudinal studies of this emerging sex difference and potential contributing mechanisms are needed. If these sex differences are a reflection of human evolutionary history, then the mechanisms should include a combination of prenatal and postnatal exposure to sex hormones and a sex difference in spatial-related activity preferences. At the same time, it must be emphasized that any such influences do not preclude cultural and socialization effects; and in fact, cultural and social effects are expected to have greatereffects on a slow-developing and highly social species such as humans than they would on faster-developing species.

In any case, data about the relation between prenatal exposure to androgens and sex differences in spatial abilities are mixed and difficult to interpret, especially in light of the complexity of assessing spatial abilities in very young children and in determining levels of prenatal hormone exposure (Cohen-Bendahan, van de Beek, Berenbaum, 2005; Hines et al., 2003). Moreover, there is a postnatal surge in androgens in males, but we do not know if or how it is related to the development of spatial cognition.

It is also possible that the relation between prenatal hormone exposure and spatial cognition is indirect and mediated by hormone-influenced sex differences in activity preferences, which in turn would result in a gradually emerging sex difference in spatial abilities. Following the preschool years in both industrial and traditional societies, males’ play ranges (size of area in which they are permitted to roam during play) are 1.5 to 3.0 times the size of females’ play ranges; in general, parents are more restrictive of the play ranges of females. But sex differences emerge in the absence of these restrictions (Matthews, 1992; Whiting & Edwards, 1988). Although the relation between these activities and the widening male advantage on spatial measures remains to be convincingly demonstrated, it is an intriguing possibility that merits further study.

Critiques of Evolutionary Explanations of Sex Differences in Science and Math

Although the explanations offered by psychologists with an evolutionary perspective are congruent with many research findings, numerous thoughtful critiques that provide alternative explanations have been offered. For example, Newcombe (2007) and others (Halpern, 2000) have countered the underlying argument that males in their role as hunters in early societies needed navigational skills to traverse large distances with the fact that women also needed to travel large distances intheir role as gatherers. Although vegetation remains stationary, women needed to travel long distances to gather edible plants that ripened in different seasons of the year, escape from predators, and move their living sites with the seasons. Many of the tasks that females in traditional societies engaged in also required spatial skills, such as weaving (baskets were essential for gathering food) and making pots and other vessels for the household. These critiques are important to consider, as is the proposal that the male advantage in spatial abilities may be more strongly related to tribal warfare than to hunting, and that activities such as weaving emerged more recently than tool construction (e.g., weapons), which is almost exclusively a male activity (Murdock, 1981).

Newcombe also raises the fact that the relationship between testosterone levels and spatial ability is not linear. Males with lower levels of testosterone and women with higher levels of testosterone have the best visuospatial abilities, a finding that some have argued is inconsistent with evolutionary theory (Moffat & Hampson, 1996). A response to this concern is that it does not necessarily follow that male behaviors and cognitions associated with sexual selection will be linearly related to testosterone or any other hormone. There are potential costs to prolonged exposure to high levels of testosterone (e.g., premature death). In addition, circulating hormone levels do not provide information about the effects of prenatal hormone exposure.

Several investigators have found that spatial abilities vary over the menstrual cycle, with high scores on mental-rotation tests during the menstrual phase and low scores during the midluteal phase (d 5 .85; Halpern, & Tan, 2001; Hausmann, Slabbekoorn, Van Goozen, Cohen-Kettenis, & Guüntuürkuün, 2000). Evolutionary theories also would have difficulty explaining monthly variations inspatial abilities for women (but see Sherry & Hampson, 1997). Different approaches to explaining data that pertain to cognitive sex differences in humans have led to heated debates among proponents of different positions. We leave it to readers to weigh the reasoning and evidence on all sides of these debates. The authors of this report differ in the extent to which they attribute contemporary cognitive sex differences to evolutionary history, with evolutionary psychologists maintaining that the male brain is naturally better prepared to perform some spatial tasks and others who feel that the weight of the evidence is clearly on the environmental side.

Some psychologists have taken a more middle-of-the-road position by accepting the importance of evolution in shaping reproductive-related behaviors but emphasizing the principle that human behavior adapts to the context in which it develops. So while modern humans owe an evolutionary debt to our hunter-and-gatherer ancestors, the requirements of modern living may play a greater role in understanding how females and males develop their cognitive abilities. In thinking about the evolutionary heritage, it is important to keep in mind the fact that our ancestors did not engage in the prolonged study of advanced topics in science and math (Geary, 2007). Other perspectives stress the importance of sex differences in life experiences.

Sex Differences In Brain Structure And Function

The effects of evolution are ultimately expressed in tissue structure and function, and efforts to understand the biological substrates of sex differences in cognition require an examination of brain anatomy and physiology. Because our focus is on math and science abilities, our most direct data necessarily involve humans; however, ethical and technical considerations prevent rigorous experimental work of the kind possible in nonhuman species. Furthermore, when examining the neurobiology of behavior within a species, it is important to consider the additional complexity of age effects.

Beginning in the early 1980s, several safe methods for obtaining reliable measures of brain structure and function became available, and there have since been several large-scale efforts to examine sex differences in brain anatomy and physiology. The basic aim in these studies is to understand how the brain's activity relates to its structures and functions. A thorough review of this literature is beyond our scope. Instead, we briefly describe the main findings from neuroimaging in which sex differences in the brain and behavior have been established. Notably, because of their expense, most studies using neuro-imaging have been conducted for purposes other than examining sex differences in the healthy brain. Nonetheless, several large-scale prospective samples have produced consistent findings. These findings support some hypotheses relating to the neural substrates for sex differences in science and mathematical abilities and suggest future directions for research.

Sex Differences In Brain Structure

When it became possible for researchers to peer into healthy living brains while individuals were engaged in cognitive tasks, one of the first questions they asked was whether there are reliable differences between women and men in areas of the brain that are involved in the cognitive tasks in which sex differences are usually found. This question led investigators to focus specifically on the overall size of the brain; the frontal and temporal regions that regulate language and memory; and the corpus callosum, a key structure for integrating brain activity across the cerebral hemispheres.

Sex Differences in Cerebral Volume

The first studies toreveal new sex differences in the human brain used a noninvasive procedure to measure the proportion of tissue with fast blood flow—presumably, gray matter. Gray matter refers to areas of the brain where cell bodies and their immediate dendrites are closely packed. These studies showed substantial sex differences in the proportion of gray matter, as well as higher rates of blood flow, which suggests a greater proportion of gray matter, in women (R.C. Gur et al., 1982; R.E. Gur & Gur, 1990). The current method for studying brain anatomy in humans is magnetic resonance imaging (MRI). Structural MRI studies can be used to segment tissue into gray matter, both cortical and deep; white matter (areas of long axons covered with a fatty—hence “white”—myelin sheath that aids in the rapid conductance of nerve impulses); and cerebrospinal fluid (that both nourishes and cushions the brain), as illustrated in Figure 6, which shows these basic brain structures. Replicating the earlier findings, neuroimaging studies found a higher percentage of gray matter in females, but with MRI it was possible to establish also that males had higher volumes of white matter and cerebrospinal fluid (Blatter et al., 1995; Coffey et al., 1998; Filipek, Richelme, Kennedy, & Caviness, 1994; R.C. Gur et al., 1999; Passe et al., 1997; Pfefferbaum et al., 1994). Thus, on average, White females (who were used for these studies) have a smaller cranial volume (head size) than White males do. The higher proportion of gray matter in females and greater amount of white matter and cerebrospinal fluid in males results in similar absolute volumes of gray matter in men and women. It is noteworthy that life-span developmental sex differences have been found in the brain, with consistent reports that, with normal aging, brain volume, especially gray matter, declines faster in men than in women in middle to late adulthood (Coffey et al., 1998; Good et al., 2001; R.C. Gur et al., 1991).

Fig. 6.

Illustration of the brain using three different magnetic resonance imaging methods: acquired T2-weighted image (left), proton density image (middle), and the segmented image (right), in which gray matter is shown in white, white matter in light gray, and cerebrospinal fluid inblack. Reprinted from “Sex Differences in Brain Gray and White Matter in Healthy Young Adults: Correlations With Cognitive Performance,” by R.C. Gur, B.I. Turetsky, M. Matsui, M. Yan, W. Bilker, P. Hughett, & R.E. Gur, 1999, Journal of Neu-roscience, 19, p. 4066. Copyright 1999 by the Society for Neuroscience. Reprinted with permission.

Sex differences in hemispheric asymmetries also have been documented, with greater asymmetries in the percentage of gray matter and cerebrospinal fluid in males compared to females (Coffey et al., 1998; R.C. Gur et al., 1999). As shown in Figure 7, for males, the percentage of gray matter was higher in the left hemisphere, the percentage of white matter was symmetric, and the percentage of cerebrospinal fluid was higher on the right. No asymmetries were significant in females, and the differences in laterality between males and females were significant. These hemispheric differences were, however, quite small in absolute terms, and did not overshadow the main sex differences in cerebral volume. Thus, although males had a higher percentage of gray matter in the left relative to the right hemisphere and females had more symmetric gray matter, females still had a higher percentage of gray matter than males in both hemispheres.

Fig. 7.

Mean percentages of gray matter (GM) and white matter (WM) tissue and cerebrospinal fluid (CSF)inthe brainsof men versus women (top) and differencesinlaterality between the sexes (bottom). The laterality index shows left-hemisphere minus right hemisphere ofGM, WM, and CSFinmen (dark bars) and women (light bars). Reprinted from “Sex Differences in Brain Gray and White Matter in Healthy Young Adults: Correlations With Cognitive Performance,” by R.C. Gur, B.I. Turetsky, M. Matsui, M. Yan, W. Bilker, P. Hughett, & R.E. Gur, 1999, Journal of Neuroscience, 19, p. 4068. Copyright 1999 by the Society for Neuroscience. Reprinted with permission.

Anatomic differences between the brains of males and those of females can provide information about the neural substrates for sex differences in cognition only if the differences in brain anatomies correlate with performance on cognitive tasks. R.C. Gur et al. (1999) first examined whether a sample of males and females showed the reported sex difference of better verbal relative to spatial performance in females compared to males. As expected, the males and females did not differ in the Global (mean of Verbal and Spatial) performance score, but the Verbal Superiority index (Verbal minus Spatial) was positive in females and negative in males. Furthermore, performance correlated with intracranial volumes, for the whole sample as well as for males and females considered separately. While these correlations were moderate, scatter-plots suggested that relationships were quite uniform across the range of brain volumes and performance values for both gray and white matter, whereas the correlations with cerebrospinal-fluid volumes were nil (within this age range of adults less than 50 years of age). Consistent with these findings, Haier and colleagues (Colom, Jung, & Haier 2006; Haier, Jung, Yeo, Head, & Alkire, 2005) reported that higher g-loadings (g 5 general intelligence) of individual tests were associated with increased gray-matter volume throughout the brain.

It should be noted that despite the significant sex difference in spatial performance, most women in R.C. Gur et al.'s (1999) study performed comparably to the men on the spatial tests. As suggested in several sections of this monograph, it is possible that (some) females may achieve high levels of spatial performance using different strategies than males and possibly by using different regions ofthe brain. Haier et al. (2005) also found that males and females may solve some complex problems, such as items on IQ tests, differently, with females showing a greater use of language-related brain regions and males showing greater use of spatial-related brain regions. Specifically, the researchers used an advanced method (voxel-based morphometry) for comparing the gray matter in two groups of participants; they reported that, on average, compared to men, “women show more white matter and fewer gray matter areas related to intelligence. In men IQ/gray matter correlations are strongest in frontal and parietal lobes (regions BA [Brodmann area] 8, 9, 39, 40), whereas, the strongest correlations in women are in the frontal lobe (region BA10) along with Broca's area” (p. 320). Broca's area of the brain has long been known to underlie language production. Thus, based on these analyses of the brain, the evidence suggests that, on average, women's performance on measures of intelligence may be more related to language centers than is men's performance on these same measures.

Sex Differences in Corpus Callosum Structure

In contrast to overall lower white-matter volume in females, there is some controversial evidence that the largest white-matter structure in the brain, the corpus callosum, is more bulbous in females. The corpus callosum is the primary means of communication between the two cerebral hemispheres, prompting investigators to hypothesize that differences in callosal size exist between males and females and that female brains may be more bilaterally organized for language.

Because the corpus callosum has an irregular shape, there have been many controversies over how best to measure its size or volume. Most investigators have examined the shape and size of the mid-sagittal section of the callosum as a surrogate for the structure's overall shape. To date, however, no consensus has been reached on the presence of sex-based differences in the callosum. De Lacoste-Utamsing and Holloway (1982) reported that the female splenium (a portion of the corpus callosum) was more bulbous than the tubual male splenium. Follow-up studies by De Lacoste-Utamsing, Holloway, and Woodward (1986; Yoshi et al., 1986; Allen, Richey, Chai, & Gorski, 1991) all found increased size in the female splenium. In contrast, Going and Dixson (1990) and Witelson (1985) reported no such differences between the callosa of males and females.

A possible reason for this continuing controversy is a general lack of standards for callosal analysis. While cross-sectional area and callosal length are the more traditional indices reported in sex-difference investigations, there is little agreement over how to normalize these indices. Furthermore, gross dimensional measures will miss regional shape variations in callosa. Some investigators have divided the callosum into partitions and compared the areas of corresponding partitions between study groups (Witelson, 1985). This approach does not solve the problem of normalization, and the exact partitions used are arbitrary. Furthermore, partitioning schemes may still miss regional morphologic differences.

Template deformation morphometry (TDM) avoids many of the pitfalls associated with more traditional methods for measuring the callosum. By comparing each subject to a template callosum, TDM avoids the issue of normalizing callosal measurements to some arbitrary index of overall brain size. Davatzikos and Resnick (1998) used TDM and demonstrated that the splenium was larger in females than it was in males. Dubb, Gur, Avants, and Gee's (2003) TDM analysis likewise demonstrated sexual dimorphism in the splenium of the corpus callosum, with larger volumes in females. They also found relatively larger genu (the anterior part of the callosum) in males.

The reason for the intense debate over the corpus callosum is that a larger callosum in women supports the idea of greater connectivity between the two hemispheres, and a host of predictions, such as faster access to nonverbal information, might result from such a difference. It may also explain females’ better retention of language skills following unilateral brain damage, because language functions would be more likely to occur in both hemispheres.

The Need for Developmental and Longitudinal Studies

Studies of young infants and children (Matsuzawa et al., 2001), and especially longitudinal studies (Giedd et al., 1999), may help explain the causal direction and the development of sex differences in the relation between brain neuroanatomy and cognitive performance. Giedd et al. demonstrated sex differences in the pattern of gray- and white-matter development. The curves that represented gray- and white-matter development were similar for girls and boys but tended to peak at different ages. The peaks tended to be earlier (e.g., in terms of peak gray-matter volume for the frontal cortex) for females than they were for males, except for the temporal cortex, where females peaked at a slightly older age. A notable pattern was that occipital gray matter had not yet peaked for males by age 22 but peaked around age 13 for females. White matter increased for both sexes from 4 to 22 years, but at a higher rate for males than for females. The increased brain-development period for males, especially with respect to white matter and occipital gray matter, is intriguing given that these correlate with spatial performance in adults. The extended developmental period also makes male brain development more vulnerable to environmental conditions: Good health and nutrition are needed by males for a longer period of time to achieve their full potential, because brain development takes place over a longer period of time for males than it does for females. More recent studies have noted that correlations between regional brain structure and measures of cognitive performance evolve with development, and the sex differences seen in adult samples could be absent in childhood (Shaw et al., 2006).

To summarize the anatomic studies: Some sex differences are evident across the age range. In general, females have a higher percentage of tissue devoted to neuronal cell bodies and their immediate dendritic connections (gray matter), while males have a higher volume of connecting white-matter tissue. An exception is the splenium of the corpus callosum, a white-matter region that may be more bulbous in females than males. Furthermore, male brains seem to show greater volumetric asymmetries than female brains do. The higher white-matter volume may be associated with better spatial performance in males.

A hypothesis suggested by these neuroanatomic data is that male brains are optimized for enhanced connectivity within hemispheres, as afforded by overall higher white-matter volumes, while female brains are optimized for communication between the hemispheres—especially in language-processing and posterior brain regions, as indicated by the larger callosal splenia (R.E. Gur & Gur, 2004). In the near future, this hypothesis will be able to be tested directly using a more advanced MRI method for imaging white-matter integrity, called diffusion tensor imaging (e.g., Huang et al., 2005; Nucifora, Verma, Melhem, 2005; Salat et al., 2005).

Sex Differences in Brain Function

An alternative approach to investiga/ting sex differences in the anatomy of brain structures is to examine possible differences in how male and female brains respond to different cognitive tasks. This approach focuses on functions rather than on structural differences.

Sex Differences in Cerebral Blood Flow

Sex differences have not been examined as extensively with functional as with structural imaging. Using early noninvasive methods, R.C. Gur et al. (1982) reported that females had higher rates of resting cerebral blood flow than males did, across all ages (R.C. Gur, Gur, Obrist, Skolnick, & Reivich, 1987). The basic idea in measuring the rate of blood flow is that blood is expected to flow fastest in areas of the brain where neurons are most active. These findings were replicated with positron emission tomography (PET) studies (Esposito, VanHorn, Weinberger, & Berman, 1996; Kastrup, Li, Glover, Kruger, & Moseley, 1999; Ragland, Coleman, Gur, Glahn, & Gur, 2000).

The areas of the brain that are active during the performance of cognitive tasks are sometimes similar across different types of tasks, and sometimes they are task-related (for discussions see Kastrup et al., 1999). Greater bilateral activation for language tasks was reported in females. One hypothesis about sex differences in brain structure and function is that female brains are more bilaterally organized for language, which means that they rely on brain structures in both hemispheres for language tasks (e.g., speaking, comprehending), while males are more reliant on brain structures in one hemisphere (usually the left hemisphere) for the same language tasks (Shaywitz et al., 1995). For spatial tasks, the better performance of males on difficult items was associated with more focal activation of right visual-association areas, again supporting the hypothesis of more lateralization of cognitive abilities (reliance on one hemisphere) for males (R.C. Gur et al., 2000). In contrast, females recruited additional regions bilaterally for the more difficult spatial task.This finding was replicated and extended to mental rotation and numeric calculation by Kucian, Loenneker, Dietrich, Martin, and von Aster (2005), who also reported more distributed and bilateral recruitment of brain regions in females than in males as the complexity of the task increased. Similarly, Grön, Wunderlich, Spitzer, Tomczak, and Riepe (2000) suggested that males and females used different brain regions when performing tasks in a 3-D virtual maze. Females demonstrated more parietal and prefrontal activation (the latter suggesting it was an effortful task), whereas the males relied more on the hippocampus, suggesting a more automatic retrieval of geometric-navigation cues.

The importance of incorporating a neurodevelopmental perspective is underscored by several recent studies. Investigators report substantial developmental changes in the distribution, extent, and laterality of task-related activation, as well as sex-by-age interactions in areas of brain activation. It appears that, as with the neuroanatomic measures, adult patterns of sex differencesinbrain function are absentormore subtle in children (Plante, Schmithorst, Holland, & Byars, 2006; Schmithorst & Holland, 2006; Szaflarski et al., 2006). Here too, longitudinal studies would help us understand the factors that affect the development of sex differences.

Sex Differences in Cerebral Glucose Metabolism

Areas of the brain that are high in metabolic activity “take up” (metabolize) more glucose. So one way of studying areas of the brain that underlie different cognitive domains is to track which regions are metabolizing more glucose and determine whether these regions differ between women and men. Resting cerebral metabolic rates for glucose are equal in males and females (Andreason, Zametkin, Guo, Baldwin, & Cohen, 1994; R.C. Gur et al., 1995; Murphy et al., 1996). Sex differences are evident in the regional distribution of metabolic activity, with males showing higher metabolic glucose rates in all motor basal ganglia regions and the cerebellum, as well as all subcallosal limbic regions, and females showing higher metabolic glucose rates in the cingulate gyrus, a limbic region closer to language areas. Females showed more symmetric glucose utilization than males did, which provides additional evidence to the MRI data for the hypothesis that females are more bilateralized in the brain structures that underlie cognition than males are (R.C. Gur et al., 1995; Murphy et al., 1996).

Sex Differences in Neurotransmitter Function

Another set of physiological parameters that can be measured with functional neuroimaging is neurotransmitter function. Depending on the specific neurotransmitter, the abundance or scarcity of receptors available to respond to any particular neurotransmitter will facilitate or inhibit different brain functions. Few studies have included sufficiently large samples to examine sex differences in neurotransmitter function. Of these, Adams et al. (2004) reported no sex differences in serotonin binding. However, sex differences were found in dopamine function. Recent investigations of the relationship between cognition and dopamine transporter availability in males and females found that females and younger participants had higher dopamine availability in the caudate nucleus and that these groups also performed better on verbal learning tasks (Mozley, Gur, Mozley, & Gur, 2001). Furthermore, dopamine transporter availability was correlated with learning performance within groups. Relationships between dopamine availability and executive and motor functioning were observed in females but not in males. These results provide further evidence for age effects and sex differences in the influences of dopamine on human behavior.

Brain Imaging, Mathematics, and Science

To date, there are only a few brain imaging studies of science-related abilities (e.g., Fugelsang & Dunbar, 2005), and research on the brain systems involved in even a basic understanding of mathematics is still in the early stages. Most of the latter research has focused on representations of number and quantity or the process of solving simple arithmetic problems (Chochon, Cohen, van de Moortele, & Dehaene, 1999; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Gruber, Indefrey, Steinmetz, & Kleinschmidt, 2001; Halgren, Boujon, Clarke, Wang, & Chauvel, 2002; Pinel, Piazza, Le Bihan, & Dehaene, 2004; Rickard et al., 2000; Rivera, Reiss, Eckert, & Menon, 2005; Temple & Posner, 1998; Zorzi, Priftis, & Umilta′, 2002). Except for a tendency of females to use more language-based counting strategies to solve arithmetic problems and for males to have a small advantage on estimation tasks, sex differences are not typically found for these basic numerical domains (M. Carr & Jessup, 1997; Jordan, Hanich, & Kaplan, 2003). Thus, the current studies are not sufficient for making judgments about sex differences in brain activity during the processing of mathematical information.

It has been consistently found that magnitude comparison (Dehaene et al., 1999; Temple & Posner, 1998), mental number line (Zorzi et al., 2002), and many arithmetic tasks (Chochon et al., 1999; Rivera et al., 2005) bilaterally engage a structure in the inferior parietal lobe, the intraparietal sulcus, although other regions are also engaged (e.g., frontal regions associated with working memory; Rivera et al., 2005). The intraparietal sulcus is also active in nonhuman animals when they engage in numerical activities (Sawamura, Shima, & Tanji, 2002; R.F. Thompson, Mayers, Robertson, & Patterson, 1970), and it is anatomically very near to the visual-spatial and posterior spatial-attentional systems that are engaged when navigating and when mentally simulating how objects can be used as tools (Hodges, Spatt, & Patterson, 1999; Vanduffel et al., 2002). In fact, Pinel et al. (2004) found that the brain regions that represent numerical magnitude also represent spatial magnitude, and Zorzi et al. (2002) found that individuals with injury to the right parietal cortex showed deficits in spatial orientation and number-line estimation. Dehaene et al. (1999) showed adults’ computational estimation also may be dependent on a similar parietal-spatial system that supports generation of a mental number line. On the basis of a structural MRI study, Goldstein et al. (2001) found the inferior parietal lobe was 25% larger in males than in females in absolute terms, and 20% larger when an adjustment was made for the sex difference in overall brain volume; this region also has a high density of sex-hormone receptors during prenatal development, at least in some species.

Whether these areas are part of a system of biologically primary quantitative abilities or evolved for other functions is currently debated (e.g., Dehaene, 2003; Geary, in press; Pinel et al., 2004). Either way, children's intuitive understanding of quantity, magnitude, and simple addition and subtraction appear to provide the core for their learning of mathematics in school (Geary, 1995; Gelman, 1990; Spelke, 2000), and the supporting brain systems may bias how children represent and understand biologically secondary (school-taught) forms of mathematics. Geary, for instance, argued that the brain and cognitive systems that evolved to support navigation have implicit geometric knowledge built into their organization, because the function of these systems is to respond to and manipulate geometric features of physical space (Dehaene, Izard, Pica, & Spelke, 2006; Shepard, 1994). In an fMRI study of humans and monkeys, Vanduffel et al. (2002) found that the intraparietal sulcus was engaged when humans, but not monkeys, understood that geometric forms were three-dimensional based on movement cues. They concluded that “under evolutionary pressure, parietal but not earlier regions adapted to implement human-specific abilities such as excellent motion-dependent 3D vision for manipulating fine tools” (p. 415).

The studies conducted to date are not conclusive, but they provide converging evidence that the same brain regions that support early and possibly biologically primary quantitative abilities—or, at the very least, regions anatomically adjacent to them—are also involved in aspects of spatial cognition, complex object representation, and tool use. If these regions provide a core for early learning of biologically secondary mathematical knowledge, such as place value (i.e., three digits signifies hundreds, two digits signifies tens, and so on), then children might be biased such that this knowledge would be more readily learned when represented spatially (e.g., a mental number line). To the extent that these areas are larger in males than in females, a male advantage is predicted in (a) the tendency to rely on spatial representations for solving mathematical problems, (b) intuitive knowledge of certain features of geometry, and (c) ease of learning mathematics when it is presented in a spatial format. Alternatively, given the advantage of females in language domains, a female bias in the tendency to represent mathematical problems in a verbal format is predicted and, as discussed earlier, is found for solving the types of problems on standardized mathematical-abilities tests such as the GRE (Gallagher et al., 2002). Moreover, a male advantage in engineering and science tasks that involve object manipulation or generating complex 3-D images is predicted, as is a male advantage for integrating mathematical knowledge into spatially based science and engineering tasks, to the extent the intraparietal and adjacent regions are engaged with these tasks.

Speculative Hypotheses On The Relation Of Neural Structures To Science And Mathematics

The state of knowledge on the neurobiology of sex differences does not permit strong statements, predictions, or recommendations. Especially lacking are large-scale studies in which science and mathematics abilities are rigorously measured and related to brain anatomy and physiology. Nonetheless, several tentative hypotheses can be proposed.

Anatomically, male brains appear to be optimized for connectivity within the hemispheres, while female brains appear to have better interhemispheric connectivity. For females, better interhemispheric communication confers an advantage in language and the ability to better integrate verbal-analytical (left-hemispheric) with spatial-holistic (right-hemispheric) modes of information processing. Biologically, females have higher cerebral blood flow, and the metabolic glucose rates show differences for women and men that vary with brain region. Activation studies support the notion that females perform better on tasks such as language processing that require bilateral activation, while males excel in tasks requiring focal activation of the visual association cortex. Studies by O’Boyle, Gill, Benbow, and Alexander (1994) found that the right hemisphere may play a role in linguistic processing for mathematically precocious youth, a population that, as we discussed earlier, displays sex differences in mathematical and visuospatial abilities.

Single-Sex Schools

None of the data regarding brain structure or function suggest that girls and boys learn differently or that either sex would benefit from single-sex schools, yet that is exactly the claim that is driving a rapid increase in such schools. According to Sax (cited in MSNBC, 2006), who is the director of the National Association for Single-Sex Schools, at least 223 public schools across the country already offer some single-sex classrooms— up from 4 in 1998. Those who support single-sex schools have argued that new information about brain differences for girls and boys should change how we think about single-sex education and that each sex should be taught in a way that is compatible with its brain. Others who favor single-sex education provide social reasons for their support. Their argument is based on the idea that girls and boys spend too much time impressing each other when they are in the same classes and that, by separating them, each sex will be more focused on school work.

As already noted, girls get better grades in school in every subject and are now attending college at substantially higher rates than boys are. These data, which represent increased academic and career success over the decades when the number of single-sex schools declined, do not support the reasoning behind such schooling. The relative success of girls in academic settings has been labeled a “boy crisis” in the popular media (e.g., Tyre, 2006). Thus, one reason for proposing single-sex schools is to stem the loss of boys from higher education. But boys score higher than girls on standardized tests in math and science from the end of secondary school through graduate school, so it is not true that boys are failing to learn in coeducational schools—each sex is showing superior performance on different types of measures of learning. The question of whether grades in school or scores on standardized tests are better or more valid measures is a matter of considerable dispute. Some critics have argued that the grade–test disparity shows that schools are biased against boys; while others have argued that standardized tests are biased against girls. The data show different patterns of achievement on different types of assessments, so it could also be argued that, given an appropriate assessment, both sexes show evidence of learning in math and science.

Several different meta-analyses have examined the data in support of the claim that single-sex education is advantageous for either girls or boys. In a conceptual overview of single-sex education, Salomone (2006) asks: “Is there any evidence that separating students on the basis of sex might make a positive difference in academic performance and achievement or social adjustment, at least for some students?” (p. 791). She considers a range of possible advantages, including those that are motivational, social, and educational. Salomone concludes that “the evidence is undeniably inadequate” (p. 791). The Campbell Collaboration (2001) is a nonprofit organization that aims to help people make well-informed decisions about the effects of interventions in the social, behavioral, and educational arenas. They commission reviews that “synthesize evidence on social and behavioural interventions and public policy, including education, criminal justice, and social welfare, among other areas. The primary concern is with evidence on overall intervention or policy effectiveness and how effectiveness is influenced by variations in process and implementation, intervention components and recipients, as well as other factors” (The Campbell Collaboration, 2001). In two separate reviews of single-sex education, the conclusions were the same. In the words of one of the reviews: “The paradox of single-sex and co-education is that the beliefs are so strong and the evidence is so weak” (Smithers & Robinson, 2006, p 31).

The Biopsychosocial Model: An Integration Of Nature And Nurture

In thinking about the brain and applying the findings about brain structures and function to cognitive sex differences, it is important to keep in mind the fact that the environment also shapes the brain. Consider these two examples: A study of London cab drivers found that they had enlarged portions of their right posterior hippocampus relative to a control group of adults whose employment required less use of spatial skills. The cab drivers showed a positive correlation between the size of the region of the hippocampus that is activated during recall of complex routes and the number of years they worked in this occupation (Maguire, Frackowiak, & Frith, 1997; Maguire et al., 2000). The finding that the size of the hippocampus varied as a function of years spent driving taxis makes it likely that it was a lifetime of complex way-finding that caused the brain structure used in certain visuospatial tasks to increase in size, although other explanations also are possible. In a second recent study, a 3-month period of juggling practice led to an increase in grey-matter density in the putative motion-processing region of the temporal cortex (MT/V5; Draganski et al., 2004), showing a direct relationship between behavior and brain morphology (the brain area also changed back when the juggling practice stopped). These findings are consistent with many studies of non-human species and demonstrate that experience can alter the biological underpinnings of behavior and cognition—including the size of brain structures—making the nature–nurture distinction difficult to resolve. These data are important because they suggest that sex differences in structures or functions of the brain might not be “hard wired,” but could also result from differences in the experiences that men and women have in life. When most people think about the reasons why there are fewer females than males in math and science careers (or fewer males than females teaching kindergarten), they assume one of two alternatives: nature or nurture. However, a strict nature–nurture dichotomy is too simplistic; nature cannot exist without nurture. Instead of thinking about influences lining up along a continuum with nature and nurture at either end, the biopsychosocial model—which is more like a continuous loop in which variables exert reciprocal influences on each other—is a better metaphor. A biopsychosocial model is shown in Figure 8.

Fig. 8.

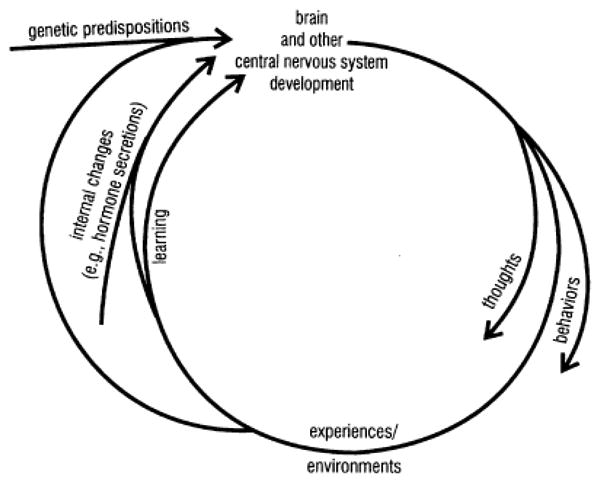
Biopsychosocial model showing how genes, hormones, and experiences alter brain development and how individuals select experiences from the environment based on their predilections and past experiences, thus also altering the size and connectivity of their brains. In this model, nature and nurture exert reciprocal effects on each other. From Halpern (2000).

Sociocultural Forces, Sex, And Mathematics And Science

The evidence for social and cultural influences on sex differences in math and science performance is plentiful and varied. First, we consider five categories of evidence: (a) research on family, neighborhood, peer, and school influences; (b) research on stereotype threat; (c) training studies; (d) cross-cultural analyses; and (e) trends over time. Then, we shift to the question of occupational choice and examine sociocultural influences on that process. Finally, we review the evidence on the impact of sex discrimination and women's roles.

Family, Neighborhood, Peer, and School Influences

There are multiple influences of parents, peers, and the schools on children's development (e.g., Bronfenbrenner & Morris, 1998; Vandell, 2000). Here we focus on these influences specifically in the domains of abilities, academic performance, and self-efficacy beliefs. A limitation to some of these studies is that they simply report a correlation, for example, between parents’ estimates of their children's mathematics ability and the children's scores on a standardized test. From this correlation, we cannot infer the direction of causality. We cannot tell whether the parents’ beliefs in their children influence the children's performance or whether the opposite process occurs—that children's test scores influence their parents’ estimates of their abilities. Moreover, it may be that both processes occur in reciprocal fashion. Some researchers have used more advanced designs, such as longitudinal research or controlling for ability at the time of the first measurement, totryto sort out these issues; most recently, reciprocal-effects modeling has been applied (Marsh, Trautwein, Luüdtke, Köller, & Baumert, 2005). We note the studies that use these more advanced methods. Similarly, when researchers find evidence of correlations between after-school activities (e.g., participation in a computer club) and math performance, it is difficult to know whether participation improves math performance or whether youth with stronger math skills choose to participate in such activities. The latter follows from the expectation that, to some extent, children will create their own environments and seek niches consistent with their interests and abilities (Scarr, 1996; Scarr & McCartney, 1983).

Numerous studies have confirmed the finding that parents’ expectations for their children's academic abilities and success are correlated with the children's self-concept of their own ability and their subsequent performance (e.g., Bleeker & Jacobs, 2004; Parsons, Adler, & Kaczala, 1982). Parents’ level of education correlates with their children's mathematics achievement, even when children's math ability and attitudes are controlled, an effect that holds across cultures (Schiller, Khmelkov, & Wang, 2002). Higher levels of parental involvement with their children's education is correlated with higher levels of children's performance in mathematics (Muller, 1998), although Raymond and Benbow (1986) found that parents were equally supportive of their mathematically talented sons and daughters. Parental involvement also covaries with successful placement of students in higher-ability mathematics groups (Useem, 1992). More specific studies are needed to determine whether parents show sex-differentiated treatment of their children in important matters such as intervening to have them placed in high-math-ability classes.

Lytton and Romney (1991) conducted a meta-analysis of studies of parents’ differential socialization of boys versus girls in western cultures. Although overall they found evidence of similarity in treatment of boys and girls (e.g., warmth d = −.07, discipline d = .07), the studies may not be relevant to the questions addressed in this report. Parents treated males and females similarly in encouraging achievement (d = .02), but this measure did not differentiate areas, such as language arts or mathematics, in which achievement was encouraged. The notable exception to this pattern of similar treatment was encouragement of sex-typed activities and sex-typed perceptions of the child, which was sex-differentiated (d 5 0.34 for mothers, d 5 0.49 for fathers). That is, parents, especially fathers, encouraged sex-typed behavior—particularly, fathers discouraged their sons from playing with dolls. The question, then, is the extent to which these sex-typed experiences may contribute to sex differences in math and science abilities.

Sociologists and psychologists have also studied neighborhood effects—that is, effects outside the home that have an impact on children (e.g., Leventhal & Brooks-Gunn, 2004). One well-sampled study of children in kindergarten and first grade found that boys’ gains in math reasoning were more sensitive to neighborhood resources than were those of girls (Entwistle, Alexander, & Olson, 1994), which is consistent with the earlier suggestion that male development is more sensitive to environmental conditions. The effect was to create more variability among males in their math performance. By middle school, when children were tracked for math classes, males in the high track were outscoring females in the high track, even though sex differences were not significant in the full sample. The researchers traced this greater variability for males to their early sensitivity to neighborhood effects. In the Entwistle et al. study, there were reports that boys in the summer after first grade were more likely than girls to be monitored less closely by their parents, go to recreation centers, and play organized sports, whereas girls were more likely to play in the house and thus had less freedom to move about the neighborhood. Similar patterns continued in middle school. These differential experiences may give boys more spatial experience and, in complex games, more spatial and mathematical experience. Consistent with this idea, Matthews (1986, 1987) found that, by age 11, boys show greater spatial knowledge than girls do—as demonstrated, for example, by making a map of a familiar area—and attributed this difference to girls’ lesser experience of roaming over their environment, which in turn may be related to parents’ greater restrictions placed on girls as well as by child-initiated sex differences in size of the play range, suggesting that girls may opt for activities that include less roaming than those chosen by boys.

Children and adolescents are strongly influenced by peers (Harris, 1995; Rubin, Bukowski, & Parker, 1998). Here we focus on peer influence on academic performance and motivation. Children's math grades are correlated with the average verbal and math skills of the children in their peer group (Kurdek & Sinclair, 2000). Children tend to become part of peer groups who are similar to them in regard to academic motivation or academic performance, making cause-and-effect inferences difficult (Altermatt & Pomerantz, 2003; Kindermann, 1993; Crosnoe, Cavanagh, & Elder, 2003).

Nonetheless, children appear to stereotype mathematics as masculine. In one study, girls rated men as liking mathematics more and being better at mathematics than women, although the girls rated boys and girls as equal on these variables (J. Steele, 2003; see also Heyman & Legare, 2004). In a Finnish study, second-, fourth-, and sixth-grade children were asked to identify the child who was best in their class in language arts and in mathematics (Räty, Kasanen, Kiiskinen, & Nykky, 2004). In language arts, boys and girls were nominated evenly. However, in mathematics, the boys nominated only boys from the second grade on, and the girls began nominating more boys than girls beginning in fourth grade. By middle adolescence, girls generally receive less peer support for science activities than boys do (Stake & Nickens, 2005). Science enrichment programs can be helpful in counteracting these effects, by giving girls a science-supportive peer network (Stake & Nickens, 2005).

Peer influence, of course, is not limited to childhood and adolescence. Holland and Eisenhart (1990) conducted an ethnographic study of females entering college—at either a southern, predominantly White university or a southern, historically Black college—who were planning to major in mathematics or science. The title of their book,Educated in Romance, reflects their finding that these young women lost their way on the science path during college, being swept away by the search for a romantic partner, which reduced their career ambitions. Holland and Eisenhart concluded that faculty and administrators actually had little impact on the women's choices of career and major; the guiding forces came from peer relationships. It remains to be seen whether female students would be swept away at universities such as MIT or CalTech or whether female students who enter these science-intensive environments differ from women who enter other universities. In either case, the peer environment, as well as women's own preferences, during the undergraduate years may result in a loss of women who are prepared to enter graduate training in science and mathematics.

Herzig's (2004) analysis of women choosing or leaving doctoral programs in mathematics also emphasized peer and other contextual influences. To persist in their doctoral program, students must feel integrated into their community of practice, which means that they must not feel isolated, as women may if they are small in number in a graduate program in mathematics, physics, or engineering. Men, in contrast, may not need as much peer support and social integration to persist in these programs.

Schools may exert an influence in multiple ways, including via teachers’ attitudes and behaviors, curricula, ability groupings, and sex composition of classrooms (Roeser, Eccles, & Sameroff, 2000). For example, ability grouping in mathematics tends to benefit high-ability students (Colangelo, Assouline, & Gross, 2004; Mulkey, Catsambis, Steelman, & Crain, 2005). When combined with implicit instruction (e.g., questioning of students’ experimental results) or explicit instruction (e.g,. Klahr & Nigam, 2004; Kuhn & Dean, 2005), hands-on laboratory experiences are especially important for learning in the physical sciences in middle school and high school. An important point for this report is that, although laboratory experiences do not improve the physical-science achievement of boys, they do improve the achievement of girls, thereby helping to close the gender gap in these areas (Burkam, Lee, & Smerdon, 1997; Lee & Burkam, 1996).

A complementary set of studies has investigated whether boys and girls do, in fact, experience different learning environments relevant to mathematics and science, both in school and out of school. In science and mathematics classes, teachers are more likely to encourage boys to ask questions and to explain concepts (American Association of University Women, 1995; Jones & Wheatley, 1990; Kelly, 1988). In one study of high-school geometry classrooms, teachers directed 61% of their praise comments and 55% of their high-level open questions to boys (Becker, 1981). Experiences such as these are thought to give children a deeper conceptual knowledge of, and more interest in, science, although this relation has not been fully established. Moreover, as Kelly (1988) noted, even an apparently small difference between teachers spending 44% of their time with girls and 56% with boys could translate—via extrapolation—to 1,800 more hours with males over a child's school career of 15,000 hours.

Science-education researchers refer to out-of-school learning as informal learning. The quality of students’ informal learning environments correlates with their performance on tests of scientific reasoning ability (Gerber, Carvallo, & Marek, 2001). For example, presence of a computer in the home for educational purposes and use of a home computer predict performance on standardized tests of mathematics (Downey & Yuan, 2005). Compared with high-school girls, high-school boys are more likely to have computers in their homes for educational purposes and are more likely to use them (Downey & Yuan, 2005). When engaged in a science task—playing with magnets—mothers talk about the science process (e.g., they use explanations and generate hypotheses) more with boys than with girls (Tenenbaum, Snow, Roach, & Kurland, 2005). Moreover, the amount of mothers’ science-process talk predicts children's comprehension of readings about science 2 years later. When parents and children use interactive science exhibits at a museum, parents are three times more likely to explain science to boys than to girls (Crowley, Callanan, Tenenbaum, & Allen, 2001). High-school boys are more likely to have participated in a math or science fair and, as with the activities noted above, this activity affects standardized mathematics test performance (Downey & Yuan, 2005). Thus, informal learning environments relevant to mathematics and science appear to differ for boys and girls. However, it is not clear to what extent these relations are due to parental assumptions of the interests and abilities of boys and girls, to differences in the responsiveness of boys and girls to these activities, or to some combination.

Of course, schools do not exert absolute power over students, and students are not passive recipients of their experiences. Students exercise choice in school activities and in informal learning. Crucial to this discussion is students’ choice in high school to take advanced mathematics and science courses. The gender gap in mathematics course enrollment has narrowed over the last several decades, so that by 1998 girls were as likely as boys to have taken advanced mathematics courses, including Advanced Placement calculus (National Science Foundation, 2005). Girls were actually slightly more likely than males to take advanced biology (40.8% of females vs. 33.8% of males), Advanced Placement biology (5.8% vs. 5.0%), and chemistry (59.2% vs. 53.3%). Boys, however, were more likely to take Advanced Placement chemistry (3.3% of males vs. 2.6% of females) and physics (31.0% vs. 26.6%) and were twice as likely to take Advanced Placement physics (2.3% vs. 1.2%; National Science Foundation, 2005). The science pipeline heading toward physics, then, begins to leak early, as fewer girls than boys take the necessary high-school courses to prepare themselves for college-level physics.

Stereotype Threat

Stereotype threat is an influence that has been demonstrated in laboratory settings and may occur in real testing situations. It was initially identified and theorized to explain differences in test performance between talented Black and White college students (C.M. Steele, 1997). C.M. Steele proposed that a negative stereotype about one's group leads to self-doubt and other processes that can then undermine academic performance, perhaps by impairing working memory. This concept was quickly extended from stereotypes about Blacks’ intellectual inferiority to stereotypes about females’ deficiencies in mathematics (R.P. Brown & Josephs, 1999; Quinn & Spencer, 2001; Spencer, Steele, & Quinn, 1999; Walsh, Hickey, & Duffy, 1999). In one experiment, male and female college students with equivalent math backgrounds were tested (Spencer et al., 1999). Half were told that the math test had shown sex differences in the past, and half were told that the test had been shown to be gender fair. Among those who were led to believe that the test was unbiased, there were no sex differences in performance, but among those who believed it showed sex differences, women performed worse than men.

The stereotype-threat effect on males’ and females’ performance on math tests has been replicated numerous times (e.g., Ben-Zeev, Fein, & Inzlicht, 2005; Cadinu, Maass, Rosabianca, & Kiesner, 2005; Ford, Ferguson, Brooks, & Hagadone, 2004; Inzlicht & Ben-Zeev, 2000; Johns, Schmader, & Martens, 2005; Keller & Dauenheimer, 2003, in a naturalistic setting; Marx, Stapel, & Muller, 2005; Quinn & Spencer, 2001; Schmader, Johns, & Barquissau, 2004), although there are occasional failures to replicate, including one in a more typical test-taking setting that used test questions taken from standardized exams (Cullen, Hardison, & Sackett, 2004). Importantly, most of these studies have been conducted with high-math-ability females— precisely those who are most capable of succeeding at careers in mathematics and science. We note here the heated exchange between Sackett, Hardison, and Cullen (2004a, 2004b), who were concerned about the mischaracterization of stereotype threat by the media, and C.M. Steele and Aronson (2004), who responded to their critique. Sackett et al. also raised concerns about the use of covariates and other statistical procedures used to demonstrate stereotype threat. Steele and Aronson responded to the concerns raised by Sackett et al. by referring to the large number of studies that found evidence for stereotype threat and by pointing out that many of these studies do not rely on the use of covariates to demonstrate the effect. This exchange, which was published in one of psychology's leading journals, shows the disagreement over the concept of stereotype threat and its importance in real-life settings. No one has yet conducted a meta-analysis of these stereotype-threat studies, so the size of the effect is unknown, but some studies show large effects (d 5 .67, Quinn & Spencer, 2001; d 5 1.35, Johns et al., 2005). It is also unknown how altering test scores by removing stereotype threat from the testing setting affects the validity of the scores in predicting grades or other indicators of success.

Additional research has elaborated the processes involved in stereotype threat. For example, when solving difficult math problems, females’ ability to formulate problem-solving strategies is reduced under high-stereotype-threat conditions compared with low-stereotype-threat conditions (Quinn & Spencer, 2001). Exposure to sex-stereotyped television commercials reduces females’ math performance (Davies, Spencer, Quinn, & Gerhardstein, 2002), providing evidence of the media as one of the pervasive sociocultural sources of stereotype threat. And females who endorse stereotypes about mathematics asmasculine show larger stereotype-threat effects on their math performance than do females who do not endorse these stereotypes (Schmader et al., 2004). The presenceofamath-competent female role model eliminates the stereotype-threat effect on females’ math performance (Marx & Roman, 2002).

The stereotype-threat research carries two important implications: First, if a simple manipulation of instructions can produce or eliminate sex differences in performance on a mathematics exam, the notion of fixed sex differences in mathematics ability is called into serious question. Stereotype threat remains a somewhat contentious topic, and some would argue that this is a straw argument because no one really believes that mathematical abilityissomefixedorpermanent attributeof anindividual,so the first concern is not valid. Second, stereotype threat is a result of cultural factors—specifically, stereotypes about female inferiority at mathematics—and thus provides evidence of sociocultural influence on sex differences in mathematics performance.

Most of the research on stereotype threat has been conducted in laboratory settings. Does the effect occur in real-world settings with high-stakes tests? To answer this question, Stricker and Ward (2004) collected information about sex and race either before or after high-school students took an Advanced Placement test in calculus. Students who score 3 or above in this exam are often given college credit for calculus, so it is an important test. Stricker and Ward set their criteria for deciding if stereo- type threat was operating in this real-world setting using a standard alpha level of .05 (indicating that the obtained results would occur by chance when the groups really did not differ in fewer than 5 out of 100 replications) and by deciding that they would only consider effect sizes larger than d 5 .20. They concluded that they found no evidence of deleterious effects of stereotype threat on female performance on quantitative tests. In a reanalysis of their data, Danaher and Crandall (in press) refuted the conclusion that stereotype threat was unimportant in real high-stakes testing. They countered that effect sizes need to be considered within a context and that d < .20 is large and meaningful in this context. They calculated that 5.9% additional females and 4.7% fewer males would achieve a passing score of 3 or higher if sex and race were indicated after students take the test instead of before. The result would be 2,789 more females starting college with credit already achieved for calculus. Thus, stereotype threat has been found to have significant consequences, even though the effect size is small.

Training Studies

Environmental input is essential to the development of spatial and mathematical abilities (Baenninger & Newcombe, 1995; Newcombe, 2002). Babies are not born knowing how to work calculus problems. Children acquire these skills through schooling and other experiences (Geary, 1995, 2006). Here we review the evidence from training and schooling studies. A meta-analysis found that spatial ability can indeed be improved with training, with effect sizes ranging between d 5 0.4 and d 5 0.8, depending on the length and specificity of the training (Baenninger & Newcombe, 1989). A more recent meta-analysis of the effects of training and experience on spatial skills confirms the earlier findings (Marulis et al., 2007). The effects of training were similar for males and females; that is, both groups benefited about equally from the training, and there was little evidence that the gap was closed or widened by training. Vasta, Knott, and Gaze (1996), however, showed that the difference could be eliminated by carefully conceptualized training. Unfortunately, most school curricula contain little or no emphasis on spatial learning. Girls, especially, could benefit greatly from such a curriculum.

The most recent development is multimedia software that provides training in three-dimensional spatial-visualization skills (Gerson, Sorby, Wysocki, & Baartmans, 2001). As described earlier, training in such skills has been used successfully with first-year engineering students. Importantly, there were improvements in the retention of female engineering students who took the spatial-visualization course; without the course, the retention rate for females was 47%, whereas with the course it was 77%. These results have held up across multiple years of training with different cohorts.

Studies of the effects of schooling are difficult in the United States because schooling is nearly universal. One design, though, has compared children's growth during the school year with their growth during summers. A study of kindergartners and first graders, for example, found that growth in spatial skills was much more rapid from October to April (when children are in school most of the time) than it was from April to October (when children are in school less of the time; Huttenlocher, Levine, & Vevea, 1998). Importantly, this effect did not occur for all measures; for example, memory performance improved as much over the April-to-October period as it did from October to April, suggesting specificity of the effects of schooling on spatial skills. Similar results for schooling have been found for mathematics (e.g., Downey, von Hippel, & Broh, 2004).

Cross-Cultural Analyses

The International Assessment of Educational Progress tested the math and science performance of 9- and 13-year-olds in 20 nations around the world. The effect sizes for sex differences for selected countries are shown in Table 7 (Beller & Gafni, 1996). Focusing first on the results for mathematics, we see that the sex differences are small in all cases. Most importantly, effect sizes are positive (favoring males) in some countries, negative (favoring females) in other countries, and several are essentially zero. The 2003 TIMSS (National Center for Education Statistics, 2005) found similar results, with some positive and some negative effect sizes, and most less than .10 (see also D.P. Baker & Jones, 1993). In the TIMSS data for eighth graders, the magnitude of the sex differences was 0.09 in Chile (country average score 379), 0.02 in the United States (country average 502), 0.01 in Japan (country average 569), and —0.05 in Singapore (country average 611). That not only the magnitude but also the direction of sex differences in math performance varies from country to country highlights the importance of sociocultural factors in influencing those differences, although it also possible that different genetic pools are underlying some of the differences. Perhaps most importantly, though, the sex difference is very small in most nations.

Table 7. Effect Sizes for Sex Differences in Mathematics and Science Test Performance at Ages 9 and 13 Across Countries.

	Mathematics		Science
Country	9 years	13 years	9 years	13 years
Hungary	‒0.03	‒0.02	0.09	0.25
Ireland	‒0.06	0.19	0.20	0.31
Israel	0.16	0.15	0.23	0.24
Korea	0.28	0.10	0.39	0.31
Scotland	‒0.01	‒0.02	‒0.01	0.20
Spain	0.01	0.18	0.25	0.24
Taiwan	0.03	0.02	0.25	0.08
United States	0.05	0.04	0.09	0.29
All countries	0.04	0.12	0.16	0.26

Note. From Beller & Gafni, 1996, Table 2 and Appendix.

We note here that large differences in the TIMSS math tests were found by the end of secondary school. As described in the summary report: “The results by gender for the secondary students differ from those at the earlier grades. In most of the countries, males had significantly higher average achievement than females in both mathematics literacy and in advanced mathematics” (estimated average d = .38; Mullis, Martin, Fierros, Goldberg, & Stemler, 2000, p. 13).

Focusing next on the results for science performance, as shown in Table 7, we see that the effect sizes more consistently favor males and are somewhat larger, although they are not large for any nation. When the results are subdivided into scientific subdisciplines, sex differences are smallest in life-sciences knowledge (0.11 and 0.20 at ages 9 and 13, respectively, averaged over all countries) and somewhat larger for physical sciences (0.22 and 0.33; Beller & Gafni, 1996). The TIMSS report summarized the findings this way: “The gender differences were more pronounced in science than in mathematics. Still, by the final year of secondary school, males had significantly higher average achievement than females in most countries in both mathematics and science” (Mullis et al., 2000, p. 30).

The data by content area for fourth, eighth, and final secondary-school grades showed that differences in performance by gender vary by content areas and age. For example, in mathematics, males outperformed females in measurement at eighth grade, but females exhibited a slight edge in algebra. In science, males outperformed females in earth science, physics, and chemistry, but not in life science or environmental issues at the same grade level. Large differences favoring males were not found until the final year of secondary school, and these also varied in size as a function of content area.

It is important to note that cross-cultural differences in mathematics performance are very large compared with sex differences in any one country. For example, in one cross-national study of fifth graders, American males (M = 13.1) performed better than fifth-grade American females (M = 12.4) on word problems, but fifth-grade Taiwanese females (M = 16.1) and Japanese females (M = 18.1) performed far better than American males (Lummis & Stevenson, 1990). Environmental factors can be more important than sex in determining the level of mathematics performance.

In perhaps the most sophisticated analysis of cross-national patterns of gender differences in mathematics performance, D.P. Baker and Jones (1993) found that, across nations, the magnitude of the sex difference in mathematics performance for eighth graders correlated significantly with a variety of measures of sex stratification in the countries. For example, the magnitude of the sex difference in math performance correlated −.55, across nations, with the percentage of females in the workforce in those nations: The more that females participate in the labor force (an index of equality), the smaller the sex difference in mathematics achievement. These findings are consistent with Eagly and Wood's (1999) social-structural theory of psychological sex differences.

Sociocultural Influences On Occupational Choice

To understand sex differences in occupational preferences and choices, one must understand the multiple pathways and psychological processes to those choices. A well-tested model of these choices has been proposed by Eccles, using an expectancy-value theory (Eccles, 1983, 1994; Meece, Eccles-Parsons, Kaczala, Goff, & Futterman, 1982).

According to Eccles’ model (Fig. 9), individuals choose a particular occupation and, before that, take the necessary academic courses in high school and college, as a function of two factors: (a) expectations for success (i.e., individuals take on challenges when they expect that they can succeed at them) and (b) perceptions of task value (i.e., individuals take on a challenge when they value the task, perhaps because they intrinsically enjoy the task, perhaps because it has utility value such as a good salary, or for other reasons). Costs are estimated as well (e.g., joining the after-school science club might require giving up cheerleading). Expectations for success are shaped by the individual's task-specific beliefs (self-concept of ability in the relevant domain, perceptions of the difficulty of the task), which in turn are shaped by past events (e.g., grades in school in that subject, standardized test scores), and also by the person's interpretation of those past events (e.g., high grades in mathematics as a result of ability or of effort). Perceptions of task value are shaped by the individual's long-term goals (e.g., becoming a mathematics professor) and short-term goals (e.g., taking the right sequence of undergraduate mathematics courses to qualify for a PhD program in mathematics). These perceptions of task value are shaped in turn by the individual's perceptions of the attitudes and expectations of important socializers (parents, teachers, peers) and the larger cultural milieu (such as the mass media and gender segregation in the occupation). Dozens of studies have provided evidence supporting the model's proposed links, although it has been criticized for not including a measure of ability (e.g., Eccles, Vida, & Barber, 2004; Fredricks & Eccles, 2002; Frome & Eccles, 1998; Jodl, Michael, Malanchuk, Eccles, & Sameroff, 2001; Meece et al., 1982; reviewed by Eccles, 1994).

Fig. 9.

Eccles (1994) model showing how cultural milieu, beliefs, aptitudes, and experiences work together to create beliefs and expectations in developing children and ultimately influence those individuals’ achievement in math and science. Adapted from “UnderstandingWomen’s Educational and Occupational Choices: Applying the Eccles et al. Model of Achievement-Related Choices,” by J.S. Eccles, 1994, Psychology of Women Quarterly, 18, p. 588. Copyright 1994, Blackwell Publishing. Adapted with permission.

How does the model of achievement proposed by Eccles help us understand sex differences in choice of academic courses in high school, major in college, and occupation? At the simplest level, if males and females differ in their expectations for success at math- and science-related tasks, or if they attach different values to success at these tasks, then sex differences in choices will occur. Research has documented sex differences in expected task value and expected success in the areas of science and mathematics, as well as sociocultural forces that influence those expectations. In general, children's math-competence beliefs decline from 1st to 12th grade (Jacobs et al., 2002). Although boys start out with greater math-competence beliefs than girls, by 12th grade there is no sex difference in these beliefs, at least in recent studies (Fredricks & Eccles, 2002; Jacobs et al., 2002; see Wilkins, 2004, for international comparisons; and see Hyde, Fennema, Ryan, Frost, & Hopp, 1990, for a meta-analysis of earlier studies). Reciprocal-effects modeling with longitudinal data indicates that math-competence beliefs predict later standardized-test performance much more strongly than test scores predict competence beliefs (Marsh et al., 2005). Children's valuing of mathematics also declines from 1st to 12th grade, but there are no sex differences in valuing math. What we do not know from these studies is what the sex differences look like in college-age samples, when serious decisions about occupations are made, or how sex differences in interests may interact with these beliefs in determining long-term career choices.

One relevant study examined ninth graders’ intentions to enroll in math courses (Crombie et al., 2005). Although many of the predictors of intentions were the same for boys and girls, the direct path from math competence beliefs to enrollment intentions was significant for girls but not for boys, suggesting that girls may be more influenced by their math self-concept.

Research within this expectancy-value theory has also documented the relation between parents’ sex-stereotyped beliefs and children's sense of competence and achievement in mathematics and science. In one longitudinal study, mothers’ estimates of their sixth-grade children's likelihood of success in mathematics predicted the children's actual math career choices at ages 24 to 25 years (controlling for children's ability); importantly, mothers’ sixth-grade estimates of their children's math-career success were significantly higher for boys than for girls, although there was no control for ability in this study and the authors acknowledge that less subjective measures, such as achievement tests, might have yielded different relations with career choice (Bleeker & Jacobs, 2004). In another study, parents who held stereotypic beliefs about male superiority in mathematics gave significantly higher math-ability estimates to sons than they did to daughters, controlling for the children's actual grades (Jacobs, 1991; see also Jacobs & Eccles, 1992). Parents’ perceptions of their children's math ability may have a stronger influence on children's beliefs in their own ability than their math grades do (Frome & Eccles, 1998). This is a finding that needs to be replicated and studied further.

Similar results have been found for the influence of teachers. For example, teachers’ perceptions of students’math talent early in the school year predict the students’ later math achievement-test scores, even when earlier measures of ability are controlled (Jussim & Eccles, 1992). In short, the Eccles research demonstrates the potential importance of key socializers—especially parents and teachers—in shaping children's self-concepts of their ability, their course choices, and their occupational choices. When the socializers hold stereotypic beliefs about male superiority in mathematics and science, these beliefs can translate to daughters with lower self-concepts of their math and science ability who choose not to pursue careers in science and mathematics.

Correll's (2004) sociological model is similar to that of Eccles, but Correll's model emphasizes a broader principle: that cultural beliefs about sex differences affect the emerging career aspirations of males and females. In a laboratory experiment, participants were told that they were being tested for a (fictitious) ability, “contrast sensitivity,” which was said to be very important for graduate school and employment success. In one condition, participants were told that, on average, males perform better on these tests (male-advantage, MA, condition), and in the other condition, participants were told that there were no gender differences (NGD condition). The task was in fact ambiguous, and all participants were told that they were correct on 13 of 20 items. Afterward, males in the MA condition gave themselves significantly higher contrast-sensitivity ratings than did females in that condition; in the NGD condition, there were no sex differences in ability ratings. Perhaps most importantly, compared with females in the MA condition, males in the MA condition rated themselves as significantly more likely to apply to graduate programs and for jobs requiring high levels of contrast-sensitivity ability; this differences was not found in the NGD condition.

Another line of evidence comes from cross-cultural analyses indicating that sex-stereotypic patterns of course choice and occupational choice vary from one nation to another. For example, female enrollment in 12th-grade math classes ranges from 22% in Japan to 52% in Thailand (Hanson, Schaub, & Baker, 1996; see also Davenport et al., 1998). Female enrollment in physics classes ranges from 13% in Japan to 52% in Thailand, with the United States at 22% (Hanson et al., 1996). For students planning to major in mathematics or science in college, the range is from 13% female in Japan to 38% female in Canada, with the United States at 28%. These variations closely parallel the proportion of women employed as scientists in those countries.

Sex Discrimination And Occupational Success

Psychological scientists have studied sex discrimination in a number of ways. Social psychologists agree that the old-fashioned, overt sexism that existed several decades ago in the United States may have been replaced by unconscious, covert, modern sexism or neosexism in some situations (Jackson, Esses, & Burris, 2001; Masser & Abrams, 1999; Swim & Cohen, 1997). Studies investigating sex bias generally use one of two methodological approaches: (a) experimental studies, in which a work product (e.g., an article) is submitted to raters for evaluation of its quality and half of the raters see it with a stereotypic male name as author and the other half see the same work product but with a stereotypic female name as author; and (b) naturalistic studies examining experiences of sexism or evaluations or hiring of males and females in real work settings. The experimental studies have the advantage of experimental control but may lack external validity; the naturalistic studies supply the latter, and therefore these studies are perceived to be complementary.

A meta-analysis of studies using the experimental paradigm found that, when job applications were evaluated, sex bias occurred (d= −.13 to −.25; Swim, Borgida, Maruyama, & Myers, 1989; the negative value indicates that the female applicant was rated lower than the male). The effect size does not represent a performance difference between males and females but rather a difference in evaluating the work of a male stimulus person compared with that of a female stimulus person. A metaanalysis of experimental research conducted in simulated employment contexts (e.g., when hiring or compensation decisions were measured) found that sex bias in ratings depended on whether the job in question was traditionally sex-typed as male or female (Davison & Burke, 2000). When the job was male sex-typed, males received higher ratings (d = .33) even though identical qualifications had been presented in the experiment. When the job was female sex-typed, females received higher ratings (d= −.26). This pattern suggests that raters’ beliefs about applicants’ future performance may have influenced their ratings. A meta-analysis of field studies of sex bias in ratings of job performance found, overall, little evidence of bias; however, a substantial pro-male bias (d= .32) appeared when only males served as raters (Bowen, Swim, & Jacobs, 2000). The Davison and Burke (2000) meta-analysis, however, did not find male raters to be more biased than female raters (d = .24 and .34, respectively). Therefore, it is an open question as to whether males are more biased in their ratings than females are.

One study investigated fourth-year medical students’ experiences of sex discrimination and sexual harassment (Stratton, McLaughlin, Witte, Fosson, & Nora, 2005). Compared with men, women who had been exposed to discrimination or harassment were significantly more likely to report that the experience influenced their choice of specialty (45% vs. 16%) and residency rankings (25% vs. 11%). General surgery was the area in which women were most likely to experience discrimination or harassment during the residency selection process. This study, based on a large sample (n = 1,314), documents the frequency of talented professional women's exposure to discrimination and the extent to which it affects their career choices. A related study of women in academic medicine found that 40% of the respondents ranked sex discrimination first out of 11 possible factors hindering their careers in that field (P.L. Carr, Szalacha, Barnett, Caswell, & Inui, 2003).

Focusing on earlier stages of the career process, another study surveyed 477 first-year and 324 final-year undergraduates in male-dominated fields (math, science, engineering) and female-dominated fields (arts, education, humanities, social science; J. Steele, James, & Barnett, 2002). Women in the math, science, and engineering fields reported significantly more sex discrimination than men reported in their fields and than women reported in female-dominated fields. Moreover, they also anticipated experiencing more sex discrimination in the future if they went into a career in that field. Women in the math, science, and engineering fields were also the most likely to report thinking about changing their major.

There has been only one study of sexism in the scientific peer-review process that was based on an analysis of peer-review scores (Wenneras & Wold, 1997). In an investigation of the reasons why women in Sweden are less likely to succeed in science and mathematics, two investigators studied the peer-review process that is used to award postdoctoral fellowships. Sweden has been named as the “leading country in the world with respect to equal opportunities for men and women” (p. 343), so it is likely that if sexism were found in their peer-review process, it exists in other countries as well. Scientific peer review is shrouded in secrecy. When the investigators requested the data on peer review from the Swedish Medical Review Council, they were denied access. Similar requests to the National Science Foundation in the United States were met with the response that the data are not available in a format that allows comparisons of women and men (Ceci, Wiliams, & Barnett, 2007). However, the Swedish Freedom of Press Act grants public access to all government documents, except those classified as secret for reasons related to national security. An Administrative Court granted the investigators access to the documents relating to peer review. The investigators found that female applicants for postdoctoral fellowships received lower mean scores in all three of the areas in which they were evaluated: scientific competence, quality of proposed methodology, and relevance of the research proposal. Because final scores are computed by multiplying all three scores, small differences are enlarged with this procedure for computing total scores. Of course, lower mean scores are not evidence of sexism, as it is possible that the women applicants were, in fact, less qualified. To test this possibility, the investigators computed scientific productivity indices six different ways, using variables such as number of publications, number of first-author publications, impact factors as indicators of the quality of each publication, and number of scientific citations. In the authors’ own words: “Did men and women with equal scientific productivity receive the same competence rating by the MRC reviewers? No!” (p. 387). The most productive group of female researchers (total of more than 100 total impact points) were rated as comparable in ability to the least productive male researchers (total impact points less than 20). All other women were rated below all of the men.

Wenneras and Wold (1997) found that being affiliated with a committee member (what they call a “friendship bonus”) and being male were the two most important factors in determining how research applicants were rated. The effect of having a personal relationship with members of the review committee— which included being a student of a member or working on a project with a committee member—was significant even though committee members with relationships with applicants recused themselves from rating these applicants. Still, those relationships were known among the other members of the committee, who apparently were influenced by that knowledge. The authors of this study conclude that the peer-review process in what is arguably the most gender-equal nation in the world is rife with nepotism and sexism. In Sweden, women receive 44% of bio-medical doctoral degrees but hold only 25% of postdoctoral positions and 7% of professional positions. The authors believe that some portion of these discrepancies is caused by sexism. The policy of secrecy has prevented similar investigations into the peer-review process in other countries. Even if nepotism and sexism operate without conscious awareness, they are no less insidious. At a time when the United States and other countries are facing serious shortages of scientists and mathematicians, we can only wonder if biases in the peer-review process are contributing to the loss of talented women in these areas. There are no reasons to believe that scientists in the United States would be any more immune to prejudice and nepotism than those in Sweden; these results provide strong reasons for making the peer-review process more transparent and open for peer review.

Women's Roles

Although there has been a major shift over the last several decades toward equalizing men's and women's roles in the home, employed women still spend significantly more time with their children than men do (Sandberg & Hofferth, 2001). Achieving high levels of success in a math or science career requires substantially more than 40 hours of work per week. In thinking about future careers, women may believe that such a career would interfere with family life, particularly with having children. And, once in a math or science career, women who have children may find themselves choosing between time with children and the extra hours needed to perform brilliantly. Women with engineering degrees, for example, are more likely than their male peers to be working part time, and the most common reason given for the part-time work is family (Morgan, 2000).

Women who choose nontraditional careers, for example in math or science, may be penalized in the marriage market. For instance, women portrayed as being in a traditionally masculine occupation (e.g., orthopedic surgeon, chemical engineer) are rated as less attractive than women in traditionally feminine occupations (Badgett & Folbre, 2003). Women engineers are less likely to be married and more likely to be childless than men engineers are (Jagacinski, 1987). Thus, it appears that women entering careers in science and engineering face more difficult life trade-offs than their male peers do.

One study pitted several of these explanations against each other, using data from the National Longitudinal Survey of Youth, a national probability sample of 12,686 young men and women who ranged in age from 14 to 21 in 1979 and who were followed until 1993 (Okamoto & England, 1999). According to neoclassical economic theory, women choose traditional female jobs such as secretary or teacher because they anticipate interruptions in their employment (e.g., for childbearing and child rearing); therefore, they purportedly choose occupations that can accommodate this pattern. However, in this large data set, teenagers’ anticipation of future employment breaks did not predict whether women were in female or male occupations 14 years later. Being married and having children later in life did. This pattern held only for White women and Latinas. For Black women, having children predicted being in a male occupation. The researchers explored a second hypothesis, driven by gender-socialization theory, holding that children are socialized from an early age and develop sex-typed interests, preferences, and skills as a result. One of these socializing forces is parents and whether they model working in a highly sex-segregated occupation. However, the sex composition of parents’ jobs was unrelated to the composition of the women's jobs. A third hypothesis predicted that women with more liberal sex-role attitudes would be employed in jobs with a lower percentage of females. This hypothesis was confirmed: Women with more liberal sex-role attitudes in 1979 were more likely to be in male jobs in 1993. This study, then, provides some evidence of the influence of women's roles—marriage and children—and women's sex-role attitudes on whether women enter male occupations.

Summary And Conclusions

In this review of the current state of the evidence for cognitive and interest differences between the sexes and their putative biological, evolutionary, and social/environmental origins, we have presented a summary of what is known about sex differences and similarities in mathematical and science abilities based on the best available scientific evidence. The popular media have sensationalized findings of sex differences, often presenting the latest finding without assessing the quality of the research that it was based on or using “person on the street interviews” about beliefs about sex differences as though they were as valid as a carefully executed program of research (e.g., Conlin, 2003). This monograph represents a consensus of expert opinion, from a group of scientists with diverse backgrounds, to the questions about sex and math and science achievement. We addressed questions concerning whether and when (in the life span) there are differences between males and females in the cognitive abilities that are important for success in careers requiring aptitude for and achievement in mathematics and science, and the extent to which sex differences in math and science abilities can be attributed to “innate” explanations, socialization, or the way these two types of influences reciprocally influence each other. In this review, we have focused on a wide range of research in which reasonable data have accumulated that address these issues, which we summarize and draw conclusions from below.

Average Sex Differences In Cognitive Abilities

Psychologists often look for sex differences very early in life as clues to the relative contribution of biological and environmental contributions, reasoning that newborns have had fewer social interactions, so the earlier that sex differences are reliably found, the more likely they are assumed to be biological in origin. This assumption is not fully supported by the biological literature because, for many species, sex differences are not evident in infancy and often do not emerge until the age of reproductive maturation. The simple distinction between cognitive sex differences that emerge early in life and those that emerge later does not rule out environmental effects, because the uterine environment affects the development of a fetus. The role of prenatal environmental factors is an excellent example of the interaction of biological and environmental variables, which often become indistinguishable in their effects. It does not necessarily follow that differences found later in life are caused by social or environmental factors, because there are developmental timelines for biological processes, including the timing of puberty, the development of the forebrain, and the aging processes, all of which are also influenced by the environment. Moreover, the tasks that infants can handle may be qualitatively different from tasks designed for adolescents, even if they are both labeled the same. For example, a verbal or spatial task for an infant is qualitatively different than a verbal or spatial task for an adolescent. With these caveats in mind, the usual finding across tasks is that males and females develop equally well in early cognitive skills that relate to quantitative thinking and knowledge of objects in the environment.

By the end of grade school and beyond, females perform better on assessments of verbal abilities when assessments are heavily weighted with writing and the language-usage items cover topics with which females are familiar; sex differences favoring females are much larger in these conditions than when assessments of verbal abilities do not including writing. In contrast, males excel on certain visuospatial-ability measures. Yet, of all the sex differences in cognitive abilities, differences in quantitative abilities have received the most attention because of the marked differences favoring males at the highest end of the ability distribution and because of their importance in so many occupations. Male performance is more variable than that of females in quantitative and visuospatial abilities, which means that there are also more males at the low-ability end of these distributions. Because males tend to be more variable, the average difference in performance between females and males for most assessments is smaller than it is at the high- and low-ability tails of the distributions, and the size of the average between-sex difference is larger for tests such as the GRE that are administered to selective samples than it is for less selective tests such as the SAT or a high-school admissions test. The fact that females achieve higher grades in school-based math and science tests and lower average scores on standardized exams used for college admissions and graduate school may point to differences in the strategies males and females use to solve novel problems (Gallagher & Cahalan, in press) and to the tendency of females to do better in most school contexts (Willingham & Cole, 1997). Of course, the factors that enter into earning a high grade in a class are also different from those leading to high test scores on a standardized test.

Sex Differences In Math And Science Performance In The Tails Of The Distribution

Substantial evidence suggests that the male advantage in mathematics is largest at the upper end of the ability distribution, a result that could provide important clues to the origin of this sex difference. In addition, a “tilt” favoring visuospatial or mathematical abilities compared to verbal, regardless of level of ability, is more frequently exhibited by males than by females. Females tend to be more balanced in their ability profiles, which may lead them to choose mathematics or science careers less frequently than their male counterparts do. These differences can be seen as early as adolescence, and, therefore, a greater number of males than females may qualify for advanced training in disciplines that place a premium on mathematical reasoning and/or visuospatial abilities. Any differences that exist are increased if interests and activities that are correlated with abilities are considered.

An Evolutionary Account Of Sex Differences In Mathematics And Science

From an evolutionary perspective, sex differences in advanced math and science have not evolved in any direct way but could be indirectly related to differences in interests and to specific brain and cognitive systems that differ for females and males. Evolutionary theories predict sex differences that arise from patterns of intrasexual competitions (for both males and females) and intersexual choice (for both females and males), including pressures that accompany the male-biased activities of hunters and warriors who traveled long distances in novel territory. Although a large body of data was presented that supports this theory, numerous criticisms have been raised as well. Many of its predictions remain to be tested, although several patterns are consistent with observed differences in interest and ability profiles.

Sex Differences in Brain Structure and Function Studies of brain structure and function have suggested some potential biological mechanisms for the observed sex differences in ability. In general, females have a higher percentage of gray-matter brain tissue, whereas males have a higher volume of connecting white-matter tissue—with the exception of the splenium of the corpus callosum, which is more bulbous and, thus, larger in females than in males. Furthermore, male brains show greater volumetric asymmetries than female brains do. The higher white-matter volume seems associated with better spatial performance in males, while the greater bilateral symmetry seems associated with better language processing in females. Although the advent of noninvasive techniques for functional brain imaging has allowed a rapid increase in the number of studies investigating sex differences in the regional functional specialization for cognition, these studies are in their infancy. Future research of this type should involve larger and more carefully selected sample populations to avoid strong and potentially confounding cohort effects, and should employ longitudinal designs. Finally, hormones have been documented to affect cognition through their organizing effects on the brain.

Sociocultural Forces, Sex, And Math And Science Abilities

Sociocultural forces also influence sex differences in math and science abilities, academic-course choices, occupational choices, and occupational success in math and science careers. Compared with girls, boys seem to benefit more from enriched neighborhoods and to be hurt more by deprived neighborhoods. Schools certainly influence students’ learning and performance; research has documented systematic, subtle differences in the ways that teachers treat males compared with the ways they treat females in math and science classrooms. Cross-cultural research demonstrates that the magnitude of sex differences in math performance varies across nations. In no country is the overall sex difference large prior to the end of secondary school, when the size of the sex difference begins to increase, although larger differences sometimes emerge earlier in specific mathematical areas (e.g., geometry). Moreover, the magnitude of the sex difference correlates negatively with measures of gender equality in the country. Many women in math and science areas do report significant sex discrimination, and these experiences likely shape the direction their careers take. Finally, women's roles may be part of the equation, as women still bear more responsibility for child care than do men and they work fewer hours. It also seems that being successful in a nontraditional career, such as engineering, may penalize women in the marriage market.

Conclusion

There cannot be any single or simple answer to the many complex questions about sex differences in math and science. Readers expecting a single conclusion—such as that we can explain sex differences in science and math by knowing about hormones, or by knowing how stereotypes affect performance, or by knowing how our ancestors met the challenges in their lives—are surely disappointed. Just as there are many related questions about sex differences in test scores and career choices, there are many variables that work togethertopresenta level of complexity that is inherent in understanding complicated questions about the way people think and behave. We have presented several conclusions, including a definition of the problem and the systems of variables that makeusboth social and biological animals. There are caveats to these conclusions because of methodological limitations of individual studies. Nonetheless, they are based on sound science, and we relied on meta-analyses of large bodies of research, when those were available. There is no single factor by itself that has been shown to determine sex differences in science and math. Early experience, biological constraints, educational policy, and cultural context each have effects, and these effects add and interact in complex and sometimes unpredictable ways.