Reproduction of Consistent Pulse-Waveform Changes Using a Computational Model of the Cerebral Circulatory System

Abstract

Due to the inaccessibility of the cranial vault, it is difficult to study cerebral blood flow dynamics directly. A mathematical model can be useful to study these dynamics. The model presented here is a novel combination of a one-dimensional fluid flow model representing the major vessels of the circle of Willis (CoW), with six individually parameterized auto-regulatory models of the distal vascular beds. This model has the unique ability to simulate high temporal resolution flow and velocity waveforms, amenable to pulse-waveform analysis, as well as sophisticated phenomena such as auto-regulation.

Previous work with human patients has shown that vasodilation induced by CO₂ inhalation causes 12 consistent pulse-waveform changes as measured by the Morphological Clustering and Analysis of Intracranial Pressure algorithm. To validate this model, we simulated vasodilation and successfully reproduced 9 out of the 12 pulse-waveform changes.

A subsequent sensitivity analysis found that these 12 pulse-waveform changes were most affected by the parameters associated with the shape of the smooth muscle tension response and vessel elasticity, providing insight into the physiological mechanisms responsible for observed changes in the pulse-waveform shape.

1. Introduction

Assessing cerebral blood flow (CBF) dynamics for the care of brain injury patients is critical in order to titrate treatment, monitor brain states, and offer prognostic insights. Due to the inaccessibility of the cranial vault, it is difficult to directly study in humans the physiologic changes in response to different stimuli, in particular, the distal cerebrovascular changes. For example, differentiating between distal cerebral vasodilatation and vasoconstriction can potentially help establish a correct diagnosis of the causes of acute intracranial hypertension¹, acute neurological deterioration due to cerebral vasospasm^{2, 3}, and cerebral metabolic crisis⁴.

Recently, we conducted a series of investigations on how intracranial pressure (ICP) and cerebral blood flow velocity (CBFV) pulse-waveforms change when the cerebrovascular system is exposed to different stimuli. These studies considered changes in metrics derived from the heights and latencies of the sub-peaks of the pulse-waveform. One product of these investigations is an algorithm that can use continuously acquired ICP or CBFV pulses to detect cerebral vascular changes⁵. This algorithm is based on a key finding from our early work that particular intracranial pulse-waveform metrics consistently change, across patients and normal subjects⁶, as the distal vasculature constricts or relaxes in response to carbon dioxide (CO₂) changes. This finding was based on the analysis of experimental data but it remains unexplained why the pulses behave in such a way. While a number of models of cerebral vasculature and autoregulation have been published^7-10, no model to our knowledge has simulated pulse-waveform trends as affected by cerebrovascular phenomena. The objective of this work is to develop a mathematical model and to investigate if it can reproduce the consistent pulse-waveform changes observed experimentally.

A wealth of literature describes models of CBF and ICP in terms of ordinary differential equations^11-16. These models, by Ursino et al, account for the compliance and resistance created by blood vessels, the inward force of the cerebral spinal fluid as well, the ability of the vasculature to auto-regulate blood flow and the changes effected by varying blood CO₂ concentration. While this model is sufficiently sophisticated to describe the phenomena we are interested in, the output cannot be analyzed at a pulse-waveform level.

Another model, described by Alastruey et al. in 2007, does simulate the cerebral blood flow on the pulse-waveform level¹⁷. This model represents the major vessels of the circle of Willis (CoW) as a one-dimensional deformable pipe network with axial blood flow. However, it uses a simplified three-element lumped parameter outflow model as a boundary condition for the terminal (outlet) vessel segment. This boundary condition addresses the viscous resistance of the blood moving through the vasculature and the compliance of the arterial walls, while ignoring the influence of ICP and the autoregulatory response of the distal vasculature to the changes of CBF. A subsequent model by Alastruey et al. did incorporate an autoregulatory boundary condition, but lacked a shared ICP model and the analysis focused on mean flow through the major cerebral vessels, not the specific pulse-waveform patterns.

In this paper, we present a novel combination of the pipe network model from Alastruey where the outlet boundary conditions are substituted with a modified version of the Ursino autoregulatory model and the ICP component of the autoregulatory model shared between all outlet vessels. This combination is advantageous in that it is sophisticated enough to simulate pulse-waveform changes in response to cerebrovascular dynamics, and by benefit of the one dimensional CoW model, reduces the computational requirement without a significant compromise in accuracy¹⁸. To validate this model, we utilized a sensitivity analysis to identify the model parameters with the most control over the transient pulse-waveform changes observed in CO₂ rebreathing experiments, and used these results to reproduce the vasodilation in the model.

2. Methods and Materials

2.1 Overview of the multi-scale model

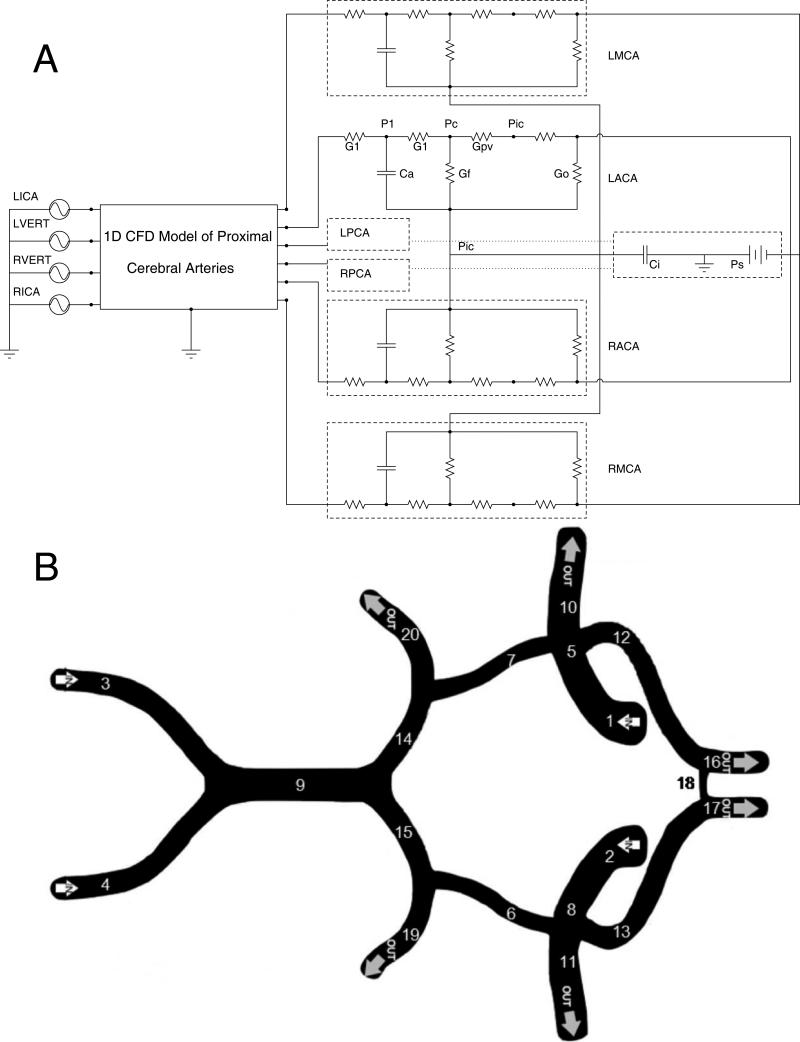
An electrical circuit analog of the model is presented in Figure 1A. The corresponding equations for this model are presented in the supplementary materials. The model is composed of 3 sub-models: The pipe-flow model of the arteries of the neck and CoW, the autoregulatory model of the distal vascular beds, and the ICP model.

Figure 1.

A) A schematic diagram of the model of the cerebral vasculature. The input into the model is the flow through the left and right internal carotid and vertebral arteries (LICA, RICA, LVERT, RVERT). The flow is then computed through a 1 dimensional model of the circle of Willis. The six great vessels, the left and right middle, anterior, and posterior cerebral arteries all employ the Ursino autoregulatory models to represent the downstream vascular beds emanating from these vessels. In this diagram, G1 is the resistance of the capillary beds, C_a is the compliance of the vessel wall, G_f the conductance for the formation of CSF, G_o the outflow conductance of CSF, G_pv is the conductance from the capillary to the location of collapse when the venous bed is modeled as a Starling resistor, P_ic the intracranial pressure, C_i the intracranial compliance, and P_s the pressure of the sagittal sinus. B) The physiological diagram of the circle of Willis with the following segments represented in this model: 1 and 2 are the left and right internal carotid arteries. 3 and 4 are the left and right vertebral arteries. 5 and 8 are the distal segments of the left and right internal carotid arteries. 6 and 7 are the left and right posterior communicating arteries. 9 is the basilar artery. 10 and 11 are the left and right middle cerebral arteries. 12 and 13 are the left and right anterior cerebral arteries. 14 and 15 are the proximal segments of the left and right posterior cerebral arteries. 16 and 17 are the distal A2 segments of the left and right anterior cerebral arteries. 18 is the anterior communicating artery. 19 and 20 are the distal segments of the left and right posterior cerebral arteries. Common and external carotid arteries not shown.

The arteries of the neck and CoW are modeled as a deformable pipe network, consisting of major cerebral vessels, with one dimensional flow in the axial direction of each vessel segment of interest. The temporal evolvements of the velocity and cross sectional area of each pipe (vessel) segment along its axial direction are numerically calculated based on flow dynamics equations. To construct the vascular network for the purpose of flow dynamics simulation, each segment's nominal cross-sectional area, length, and a β term, representing the vessel compliance, are defined; these parameters might be obtained from clinical measurements and with appropriate assumptions. The vessel parameters used for this model were adapted from Alastruey's work and are detailed in Table 1^{17, 19}. The vascular model has three types of boundary conditions: Inlets, junctions between multiple vessel segments, and outlets. The input to this model is the volume flux through the vessel segments that represent the carotid and the vertebral arteries. This flux is calculated by multiplying the velocity measured via TCD by the nominal cross sectional area of the vessel. The measurable data from the model is the velocity of blood through the left and right: anterior cerebral arteries (ACAs), posterior cerebral arteries (PCAs) and middle cerebral arteries (MCAs).

Table 1.

The cross-sectional area, length, elasticity of each vessel in the 1D pipe flow model. As the model is symmetrical, each vessel is only listed once. Physiologic data based on previous modeling results by Alastruey¹⁷.

Vessel	Area (cm2)	Length (cm)	Beta (m pa)
Common Carotid Artery	0.196	17.70	595.24
Internal Carotid Artery (prox)	0.126	17.70	944.83
Internal Carotid Artery (dist)	0.126	0.50	1889.66
External Carotid Artery	0.071	17.70	718.07
Middle Cerebral Artery	0.064	11.90	1360.56
Anterior Cerebral Artery (prox)	0.043	1.20	1096.00
Anterior Cerebral Artery (dist)	0.045	10.30	1133.80
Anterior Communicating Artery	0.017	0.30	718.07
Posterior Communicating Artery	0.017	1.50	680.28
Vertebral Artery	0.058	14.80	642.49
Basilar Artery	0.082	2.90	1511.73
Posterior Cerebral Artery (prox)	0.036	0.50	1020.42
Posterior Cerebral Artery (dist)	0.035	8.60	982.62

The terminal flux from each outlet vessels is extrapolated and used as the input into its respective outlet model of the distal vascular bed. Similarly, the pressure at the entry to the outlet model is the pressure at the exit of the vessel. All of the outlet models are connected by a single ICP model. Parameters in Table 2

Table 2.

The baseline parameters for the six outflow model and the one ICP model

Outlet Model Parameters
r0	0.015 cm
h0	0.003 cm
σ e0	0.143 mmHg
Kσ	10.0
σ coll	62.8 mmHg
T0	2.16 mmHg cm
rm	0.027 cm
rt	0.018 cm
nm	1.83 cm
η	232 mmHg s
Kg	1.43e6 (mmHg s cm)−1
Kv	4.64e3 cm
τ	10 s
G	0.02 mmHg−1
Gpv	1.14 mmHg−1 s−1 ml
Gf	4.2e-4 mmHg−1 s−1 ml
Pan	100 mmHg
qn	12.5 ml s−1
G0	1.9e-3 mmHg−1 s−1 ml
Ps	6.0 mmHg
Intracranial Pressure Model Parameters
Ke	0.11 ml−1
Cm	0.2 mmHg−1 ml
Picn	9.5 mmHg

This model uses 24 vessel segments to describe the connectivity of the CoW (Figure 1B), each with three parameters, and the six outlet models are defined by 20 parameters that interact non-linearly. Lastly the single ICP model has three parameters and serves to couple the outlet models. All parameter values for the outlet and ICP model were based on previous work by Ursino¹². The coupling of these components gives this model 195 degrees of freedom.

2.2 Consistent pulse-waveform changes during CO₂ challenge

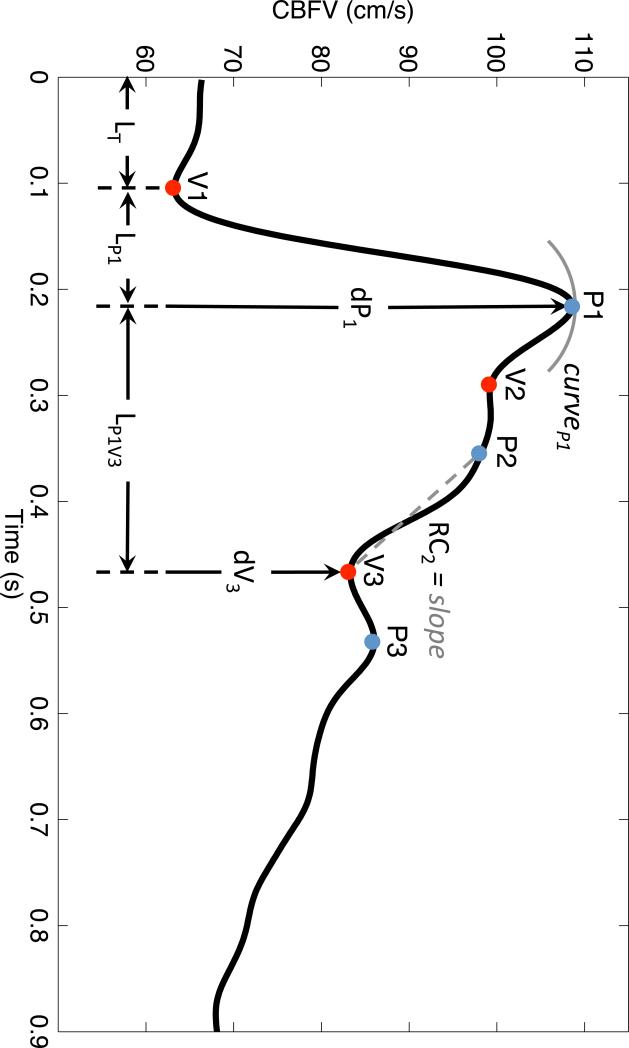
To validate this model we attempted to reproduce the pulse-waveform response of the MCA CBFV associated with hypercapnic vasodilation. To study this process quantitatively, we utilized our recently developed MOCAIP algorithm⁵. MOCAIP is a framework for analyzing pulsatile signals such as CBFV and ICP. The algorithm works by extracting the individual pulses from a continuous signal and identifying the three sub peaks (P1, P2, and P3) and the respective valleys (V1, V2, V3) (Figure 2). From these landmarks 128 pulse-waveform metrics are derived (Table 3).

Figure 2.

A clinical CBFV pulse with the peaks, valleys and selected metrics identified.

Table 3.

The notation used for the 128 MOCAIP metrics. The top portion shows the 28 metrics in the upper portion are basic metrics. Those remaining 100 below are derived metrics calculated as ratios from the basic metrics.

Metric Notation	Description
dV1, dV2, dV3, dP1, dP2, dP3	Amplitude of landmark relative to the minimum point prior to initial rise
LV1P1, LV1P2, LV1P3, LV2P2, LV3P3	Time delay along landmarks
CurveV1, CurveV2, CurvV3, CurvP1, ...	Absolute curvature of each landmark
K1, K2, K3, RC1, RC2, RC3	K1, K2, K3 are the slope of each rising edge and RC1, RC2, RC3 are time-constants of each descending edge
mCBFV, diasV	Mean CBFV and diastolic CBFV
LT	Time delay of V1
mCurv	Mean absolute curvature of the pulse
WaveAmp	Maximum among dP1 and dP3
dP1/dP2, ...	Ratio among landmark amplitudes
LV1P1/LT, ...	Ratio among time delays
CurvV1/CurvV2, ...	Ratio among curvatures
K1/RC1, ...	Ratios among slopes/RCs

A previous study by Asgari et al. examined the CBFV pulse-waveform changes that occurred when patients inhaled a 5% CO₂ mixture²⁰. TCD was recorded during inhalation and after while they returned to normocapnia. For these two phases, a robust least-weighted squares line was fit to the pulse-waveform metrics and, if the trend was significant, determined to be either increasing or decreasing. The magnitude of the slope was not taken into account. The analysis found that 12 pulse-waveform metrics had significant trends that had opposite trends between both phases (Table 4).

Table 4.

The 12 consistent trends identified by Asgari et al.

Metric Trend (Vasodilation)

Positive

dP2

dV2

mCBFV

diasV

K1/RC2

RC3/RC1

LV1P1/LV1P3

LV1P1/LP1P3

LV1P3/LP1P3

Negative

dV1/dV2

dP1/dV2

RC1/RC2

The 12 pulse-waveform metrics for which we attempted to reproduce increases in the model were dP₂ and dV₂ (the heights of P2 and V2, respectively), mCBFV (the mean velocity over a pulse), diasV (the diastolic CBFV), K₁/RC₂ (the slope of the systolic upstroke of the pulse divided by the descending slope of P2), RC₃/RC₁ (the ratio between the descending slopes of P3 and P1), and L_V1P1/L_V1P3, L_V1P1/L_P1P3, L_V1P3/L_P1P3 (each the ratio of latencies between two landmarks in the pulse. e.g. L_V1P1/L_V1P3 is the time between V1 and P1 divided by the time between V1 and P3). The pulse-waveform metrics for which we attempted to reproduce decreases were dV₁/dV₂ (the ratio between V1 and V2), dP₁/dV₂ (the ratio between P1 and V2), and RC₁/RC₂ (the ratio between the descending slopes of P1 and P2).

2.3 Model-based reproduction of consistent pulse-waveform changes

In order to simulate vasodilation in this model we increased the flow into the carotid and vertebral vessels without changing the shape of the waveform.

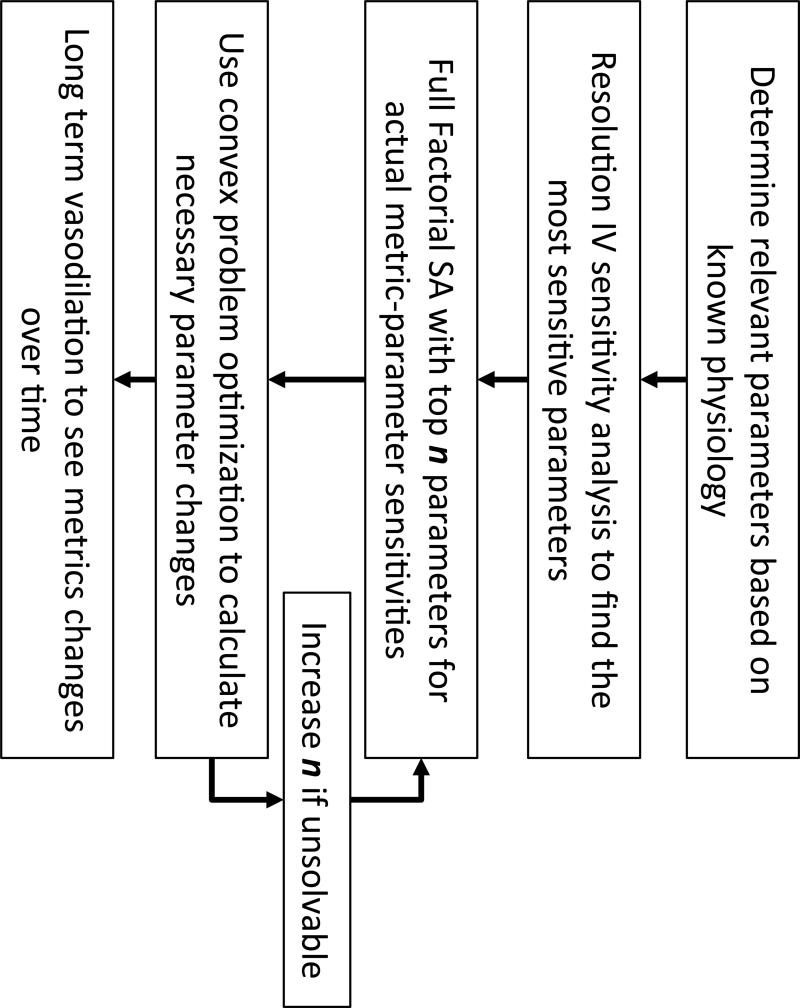
To determine the parameters necessary to simulate our clinical results we first identified the parameters that were physiologically plausible to represent vasodilation associated with CO₂ inhalation. Next, a fractional factorial experiment was used to determine which parameters have a significant effect on the pulse-waveform metrics being investigated. The top n most sensitive parameters were then analyzed using a full factorial experiment that considered all possible two-level combinations of parameter changes. Using the parameter-metric sensitivities obtained from the full factorial analysis, a sensitivity matrix was constructed representing the rate of change for each metric as a linear combination of each parameter's rate of change. This matrix was then used to solve a constrained optimization problem to determine the smallest local magnitude and direction each parameter must shift to replicate the desired changes in the TCD metrics. The workflow is described below and summarized in Figure 3.

Figure 3.

The flow diagram detailing the process of reducing the parameter space and replicating vasodilation

2.3.1 Identifying physiologically relevant parameters and changes

While the total model has 195 different parameters, not all are relevant when studying the effects of CO₂ induced vasodilation. Vasodilation occurs mainly in the distal vascular beds at the level of the resistance arterioles. While there is some evidence of a vasodilation response to CO₂ in the major cerebral arteries, these reports are still controversial²¹. Therefore, for the purpose of this analysis we have excluded the parameters affecting the cross-sectional area of the major vessels of the CoW. All parameter changes were made to each outlet boundary condition equally. Lastly, several of the parameters in the outlet model are biophysical constants, such as the density of blood, so they were omitted from the analysis.

The analysis focused on the parameters associated with the smooth muscle tension of the vessel wall described in Equation 1,

$$T_m=T_0(1+M)\exp \left(-{\mid \frac{r-r_m}{r_t-t_m}\mid }^{n_m}\right)$$ (1)

This equation describes the relationship between the radius (r) of the distal vascular bed and the tension (T_m), where M is an activation factor of cerebral autoregulation that responds to CBF fluctuations. M is controlled by three parameters: G, τ, and q_n, where G and τ denote the gain and the time constant of the autoregulatory function, and q_n is the value of blood flow at which the autoregulatory mechanism exerts its maximum strength. Also considered were the parameters associated with the elastic tension of the vessel wall (Equation 2) (see appendix).

$${\sigma }_e={\sigma }_{e0}\left[\exp \left(K_{\sigma }\frac{r-r_0}{r_0}\right)-1\right]-{\sigma }_{coll}$$ (2)

The parameters controlling the active and elastic tension components combined with the assumption of uniform changes in each of the 6 distal vascular models left 12 parameters to be included in the sensitivity analysis.

2.3.2 Sensitivity analysis experiments

A fractional factorial experiment²² was used to determine the sensitivity of each pulse-waveform metric to changes in the parameter values. To test all possible parameter combinations would require 2¹² simulations and require an infeasible amount of time. The fractional factorial experiment works by increasing several parameters at a time from the ‘off’ value to the ‘on’ value in a single simulation, and averaging the difference between the ‘off’ and ‘on’ simulations for each parameter. The fractional factorial experiment used was of resolution IV (4), meaning that it is possible that two factor interactions were confounded by other two factor interactions. This experimental design allowed us to estimate which subset of parameters had a more substantial effect on the twelve pulse-waveform metrics than the rest. With a reduced set of parameters, a full factorial experiment was performed to compute the sensitivities for each parameter.

The number of parameters used for the full factorial analysis was determined by the minimum set of the most sensitive parameters whose matrix could solve the convex problem (described in section 2.3.3).

Each simulation in the sensitivity analyses lasted for 10 cardiac cycles. The first three cycles allowed the system time to stabilize, and between each subsequent cycle the parameters being tested in the simulation were increased by 5% of their baseline value. This was done to obtain a more robust value for the change of each pulse-waveform metric in response to the parameter changes. Since the vasculature below the neck was not included in this model and the input was through the carotid and vertebral arteries, there could be no substantial increase in CBF caused by the vasodilation. To compensate for this, the input flow was also increased by 6% of its baseline value over the course of the simulation. The average effect of each parameter was calculated and scaled by the change in the parameter to obtain $\frac{\Delta \Phi }{\Delta \mathit{P}}$, where Φ is a pulse-waveform metric and P is a parameter.

2.3.3 Constrained Optimization

To determine the parameter changes necessary to elicit the TCD metric increases and decreases demonstrated clinically a sensitivity matrix was constructed

$$\frac{\partial \Phi }{\partial \mathit{P}}=\left[\begin{array}{ccc}\hfill \frac{\partial {\Phi }_1}{\partial P_1}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\Phi }_1}{\partial P_n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial {\Phi }_m}{\partial P_1}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\Phi }_m}{\partial P_n}\hfill \end{array}\right]$$ (3)

For the metrics that were expected to decrease, the respective sensitivities were negated, such that an increase would be the desired outcome and the objective was to find

$$\begin{array}{c}\hfill \min \Vert \mathit{X}\Vert \hfill \\ \hfill \text{subject to}:\frac{\partial \Phi }{\partial \mathit{P}}\mathbf{X}\succ 0\hfill \end{array}$$ (4)

where ≻ is the component-wise relational operator. This optimization problem was solved using CVX: Matlab Software for Disciplined Convex Programming^{23, 24}.

2.3.4 Time varying simulation of vasodilation

The constrained optimization provided the smallest parameter shifts in the linearized model that could elicit the pulse-waveform changes consistent with clinical results. The next step was to determine whether these parameter changes could replicate these pulse-waveform changes in the full non-linear model. As the changes observed in the CO₂ rebreathing test took place over roughly one minute, the parameter shifts were applied incrementally between each of 60 cardiac cycles of 0.9 seconds each including 4 cycles with no changes to allow the system to reach steady state. The parameter shift between each pulse was 1/60^th X, the value found during the constrained optimization. The input blood flow was increased by 60% of its baseline value to account for the increase in flow through the system. The trends of the relevant MOCAIP metrics were then computed for the simulation. Since the model is fit based on the direction of pulse-waveform metric changes (Eqs. 3-4) and not the magnitude, only the pulse-waveform metric trend direction were compared between the model predictions and clinical data.

2.3.5 Verification of signal quality

Two tests were performed to ensure that the pulse-waveform metric trends produced by the vasodilation simulation met the same criteria as those in found in clinical experiments. To ensure that the pulse-waveform metric trends of the 12 metrics were as significant as the trends found in the CO₂ rebreathing test, the metrics were fit to a line using a weighted least squares algorithm²⁵, and the p-value describing the significance of the trend was compared to the 90^th percentile of trends found in the clinical data.

The additional criteria was that the metric trends are opposite during vasodilation and vasoconstriction. To simulate this, after vasodilation the model was allowed to stabilize while no changes were made to the parameters or flow. This was followed by an incremental decrease in flow and parameter opposite change in parameter shifts. The slopes of the metric trends during this vasoconstriction were compared to those obtained during the vasodilation.

3. Results

3.1 Sensitivity Analysis

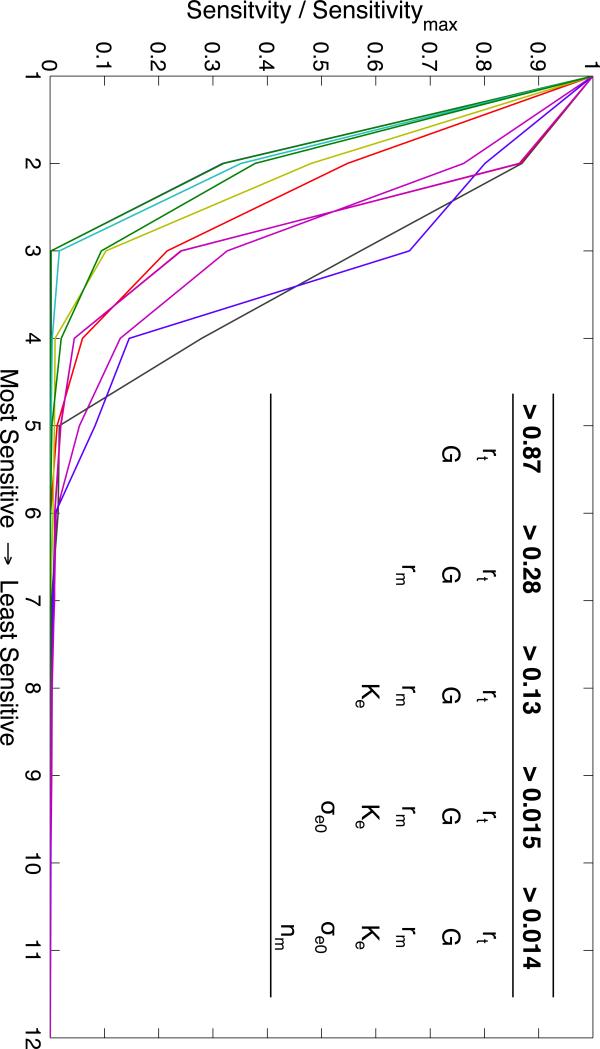
The resolution IV fractional factorial analysis of the 12 parameters provided the sensitivities of each metric to each parameter. The relative sensitivities for each metric are shown in Figure 4. The table inset in Figure 4 shows the sets of parameters greater than a minimum sensitivity threshold. The most sensitive parameters for the 12 pulse-waveform metrics were r_t and G. The three least sensitive parameters were σ_coll, τ, and q_n, which affect the passive elastic tension of the vessel wall, the time delay of autoregulation, and the baseline flow through the distal vasculature, respectively. A full factorial experiment was performed for the 6 most sensitive parameters (σ_e0, r_t, r_m, G, K_e and n ) and the resultant sensitivity matrix $\frac{\partial \mathit{M}}{\partial \mathit{P}}$ was used to solve the convex optimization problem in Eq. 4, solution in Table 5. The solution for the 6 most sensitive parameters showed a decrease in n_m and G (0.3% and 95%), and an increase in σ_e0, r_m, r_t, and K_e (50.7%, 7.5%, 4.2%, 33%). The optimization problem was unsolvable for the 5 most sensitive parameters.

Figure 4.

Each line shows the sorted parameters sensitivities for each metric. The value of each parameter sensitivity is divided by the maximum sensitivity for that metric, giving the most sensitive a value of 1. The inset table shows the thresholds at which the number of parameters that have a greater relative sensitivity increases (e.g. r_t, G, and r_m are the only parameters that have a relative sensitivity greater than 0.28 for any metric).

Table 5.

The solution to the constrained optimization problem. ΔP is the minimum vector such that $\frac{\partial \Phi }{\partial P}\Delta P>0$ for all elements of the product vector.

Parameter	P0	ΔP
σe0 (mmHg)	0.14	0.071
rm (mmHg-cm)	0.03	0.00225
rt (cm)	0.02	0.000849
nm (cm)	1.83	−0.00651
G (mmHg−1)	0.02	−0.0191
Ke (mL−1)	0.11	0.0369

3.2 Simulation of Vasodilation

3.2.1 Flow Characteristics

Over the vasodilation simulation the mean CBFV increased from 0.29m/s to 0.50 m/s (58%). The radius of the distal vasculature increased from 0.016m to 0.0175m. Solving Equation 1 for the initial and final parameter values shows a decrease in active tension of 0.045mmHg for the maximum radius obtained during the simulation

3.2.2 Pulse-Waveform Changes

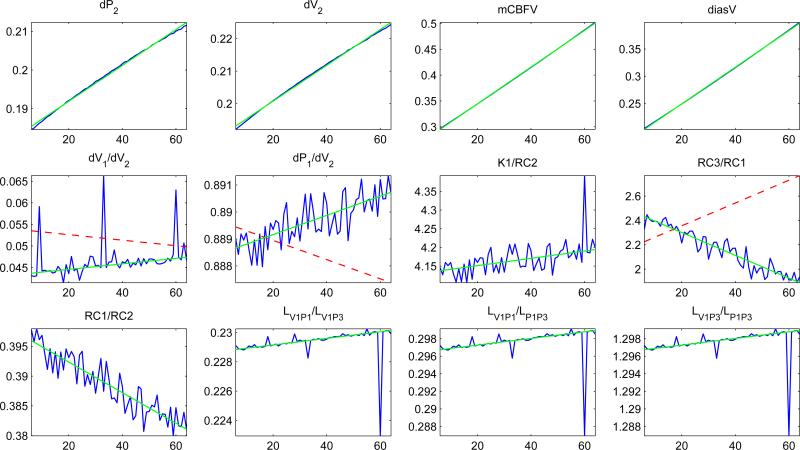
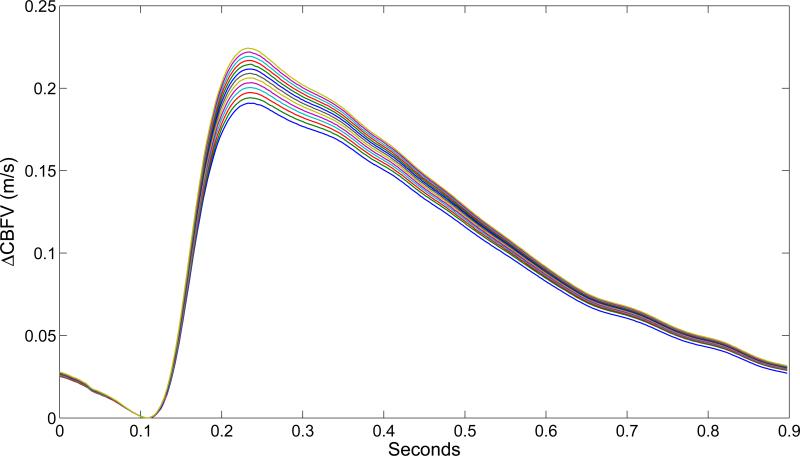
The fit of the 12 pulse-waveform metrics showed that 9 out of the 12 metrics exhibited trends consistent with clinical findings (Figure 5). The three metrics that did not correspond with the clinical indicators of vasodilation were dV₁/dV₂, dP₁/dV₂ and K₁/RC₂. The metrics dP₂, dV₂, mCBFV and diasV all monotonically increased over the simulation. RC₃/RC₁ also increased monotonically. The last three metrics, L_V1P1/L_V1P3, L_V1P1/L_P1P3 and L_V1P3/L_P1P3, show distinct discontinuities around the 60^th cardiac cycle. Figure 6 shows the evolution of the MCA pulse-waveform for every 5^th cardiac cycle aligned at the diastolic point.

Figure 5.

The value of each MOCAIP metric, calculated for each pulse for 55 pulses. The jagged line is the value of the metrics, while the straight solid line is the least squares fit of the actual data. The dashed line (if shown) is the direction the metric was expected to change in according to the clinical data. This line does not necessarily have the slope or intercept of the actual data

Figure 6.

The change in CBFV from diastolic for every 5^th cardiac cycle

3.2.3 Significance of simulated metric trends

The p-values obtained from the weighted least squares fit were lower than those obtained from clinical data for all 12 metrics, indicating that the metric trends obtained from the simulation were more significant than those obtained from clinical data. Furthermore, out of all 128 metrics, 109 had significant trends.

The vasoconstriction simulation showed that all 12 pulse-waveform metrics had opposite trends than in the vasodilation simulation.

4. Discussion

*A list of relevant terms is provided in Table 6

Table 6.

List of terms

Term	Definition
Autoregulation	The process by which the cerebral vasculature adjusts to maintain adequate blood flow
CBFV	Cerebral blood flow velocity
Circle of Willis	Circulatory structure that supplies blood to the brain
Constrained optimization	Solving a convex problem using by minimizing a cost function within given constraints
Craniospinal Compliance	The ability of the craniospinal system to accommodate additional volume
Fractional Factorial Experiment	Uses a carefully chosen subset of the parameter combinations from a full factorial experiment to reduce the necessary number of experimental runs
Full Factorial Experiment	An experimental design in which all combinations of parameters are tested. Requires 2^n experimental runs
Middle Cerebral Artery (MCA)	One of the major cerebral arteries originating from the CoW.
Parameter sensitivity	The degree to which a change in a parameter causes a change in the output
Pulse waveform shape	Shape of a pulsatile signal such as arterial blood pressure or cerebral blood velocity. The MOCAIP algorithm calculates 128 descriptive metric for wach pulse
Vascular active tension	The tension cerebral vasculature casued by the constriction or relaxation of smooth muscle cells in the vascular wall
Vascular elastic tension	The cerebral vasculature's natural resistance to stretching caused by the elastin and collagen fibers in the vascular wall
Vasodilation/Vasoconstriction	The increase/decrease in arteriole radius to maintain adequate cerebral blood flow. Effected by physical, chemical and neural stimuli

In this paper we utilized a model to study the relationship between the physiological state of the cerebral circulatory system and the CBFV pulse-waveform trends. This model was a novel approach, combining a one-dimensional pipe-flow model of the CoW with autoregulatory outlet boundary conditions and an attached model of cerebrospinal fluid circulatory system. To analyze and validate this model, a series of sensitivity analyses were employed to determine the model parameters that most significantly affected the 12 pulse-waveform metrics associated with vasodilation in clinical studies. The sensitivity analysis identified 6 such parameters (Figure 4), which involved the elastic tension caused by collagen and elastin fibers (σ_e0), the shape of the curve describing the tension applied by the arterial smooth muscle for a given arterial radius (r_m, r_t, n_m), as well as the gain of the autoregulatory feedback response to changes in blood flow (G), and the intracranial compliance (K_e). With this information a linearized model was constructed and constrained optimization was used to calculate the minimum shifts for these parameters necessary to replicate the pulse-waveform metric trends reported during vasodilation (Table 5). These parameter shifts were incrementally applied to the full non-linear model during a simulation to simulate vasodilation, resulting in 9 out of the 12 pulse-waveform metrics trending consistently with clinical findings (Figure 5).

4.1 Sensitivity Analysis

The sensitivity analysis focused on determining how sensitive each pulse-waveform metric associated with vasodilation was to each parameter of the model. This analysis showed that the parameters exerting the most control over these pulse-waveform metrics were those related to the active tension (r_m, r_t, n_m), and the intracranial compliance (K_e). This agrees with the physiological changes that occur during the vasodilation process – as the demand for blood increases, the arterial smooth muscles that regulate CBF relax, increasing arterial compliance allowing for a dilation of the vessel radius and increasing blood flow. Furthermore, the increased blood volume will cause an increase in pressure and a decrease in intracranial compliance. The pulse-waveform metrics were also sensitive to the gain of the autoregulatory feedback equation (G), which controls the magnitude of the smooth arterial muscle resistance to increases in CBF. Lastly, the pulse-waveform metrics were also sensitive to changes in the elastic tension parameter (σ_e0).

4.2 Constrained Optimization

The constrained optimization produced the smallest possible parameter vector that could reproduce the desired changes in the linearized model. The minimization allowed us to observe the actual changes in the nonlinear model within the local parameter space. This was successful as the calculated parameter changes were small enough they did not cause the model to reach an unlikely physiological state (negative tension, etc). Furthermore, it is clear that the most significant changes were made to the parameters associated with the tension of the distal vasculature, an expected result as the autoregulatory response is primarily mediated by the arteriole tone²⁶.

4.3 Pulse-waveform metric trends during vasodilation simulation

Of the pulse-waveform metrics whose changes over time matched clinical observations, the four metrics dP₂ (the amplitude of P2), dV₂ (amplitude of the valley between P2-P3), mean CBFV, and diastolic CBFV all increase during the simulation. These metrics are all directly related to an increase in velocity during different phases of the waveform. This can best be explained by a relaxation of the vessel wall. While the change in pressure (0.045mmHg) was small, the purpose of the constrained optimization was to find the minimum parameter shift necessary to cause an increase or decrease in the pulse-waveform metrics.

The pulse-waveform metrics RC₃/RC₁ and RC₁/RC₂ describe the ratios between the P3 and P1 descending slopes, and the P1 and P2 descending slopes, respectively. The RC₃/RC₁ increase and RC₁/RC₂ decrease implies a sharpening of the last two peaks relative to the first peak, best explained by the decrease in intracranial compliance, affected by increase in parameter K_e. During the course of vasodilation, the additional cerebral blood volume may decrease the craniospinal compliance and shift the bandwidth of frequencies of arterial blood pressure pulses that are attenuated. This would shorten the duration between individual peaks and increase the absolute value of the descending slopes, providing the results seen both clinically and in our simulation.

The last three metrics that agree with previous clinical results, L_V1P1/L_V1P3, L_V1P1/L_V1P3, and L_V1P3/L_P1P3 all show spikes during the 60^th cardiac cycle. These metrics describe the relative differences between the latencies of the peaks and valleys of the waveform. The sudden shift in these metrics can be attributed to changes in the point identified as V1.

The noticeable change in the waveform at points V2 and P2 is likely an effect created by the changing dynamics of the system. Throughout the vasodilation simulation, the inputs are always the same other than scaling to account for the flow increase. This change in pulse-waveform shape may be related to the aforementioned change in intracranial compliance. Since the vessels of this model are connected through the communicating arteries, the CBFV waveform for the MCA is actually a weighted sum of the time-delayed flows and reflected waves from the rest of the vasculature. As the craniospinal compliance decreases during vasodilation, the change in capacitance may alter the attenuation range or phase shift of these frequencies. However, there is little literature to our knowledge on the effect of intracranial compliance and the frequency spectrum of the CBFV pulse-waveform.

Of the three pulse-waveform metrics that did not match the clinical results, dV₁/dV₂ and dP₁/dV₂ increased when a decrease was observed in human patients, while K1/RC2 decreased when an increase was observed in human patients. These first two metrics describe an increase in the first peak and valley relative to the second valley in the simulation. Similarly, the third metric shows that the descending slope of the second peak increased in magnitude faster than the ascending slope of the first peak. These changes indicate that the first peak increased relative to the rest of the pulse during the simulation, while the opposite effect was seen during the CO₂ rebreathing test.

To understand why three of the pulse-waveform metric trends did not agree with clinical data, we must consider the effects of a linear analysis of a nonlinear model. While the single level full factorial sensitivity analysis took into account all possible interactions between the seven most sensitive parameters, only the single parameter effects were utilized in the constrained optimization prediction. Furthermore the sensitivity analysis was a single level while these parameters all have non-linear effects on the model. The effects predicted for a 10% change in two parameters does not scale to predict the effects of changing one parameter by 5% and the other by 15%. As a result, the constrained optimization used to predict the parameter changes necessary to replicate clinical data did not cover the entirety of the parameter space.

The discrepancy between the clinically observed and simulated pulse-waveform metric changes can also be explained by the limitations of the model. In this simulation the input was a waveform with constant shape except for a shifting mean. However, this does not take into account the physiological changes that may occur extracranially in response to CO₂ inhalation and affect the pulse-waveform of the flow entering the CoW^{27, 28}. Another factor that may contribute to the changing pulse-waveform observed in response to CO₂ is a changing elasticity of the vessels of the CoW, not identified in previous studies²¹. It is accepted that as arterial elasticity decreases with age^29-32 the reflected wave arrives earlier in the cardiac cycle³³. A change in the elasticity of the major vessels of the CoW could alter the timing of the reflected wave in the cardiac cycle and substantially affect the pulse-waveform of the MCA.

4.4 Comparison of Pulse-waveform Metrics during Vasodilation and Vasoconstriction

Another important result obtained from this model is the identification of 109 pulse-waveform metrics that exhibited opposite trends during the vasodilation and vasoconstriction phases of the simulation. In agreement with our result, it was shown by Asgari et al.^20,25 that for any single patient, approximately 100 metrics produced this pattern. However, as more patients were included in the model, the number of metrics changes that were consistent across all patients decreased, resulting in the set of 12 pulse-waveform metrics considered in this analysis. As this analysis took into account a single set of initial conditions representative of a single patient, there was no inter-subject variability due to anatomical variations in the CoW, state of autoregulation, intracranial compliance etc. Therefore, this modeling result may indicate that an individualized template of pulse-waveform changes during vasodilation or vasoconstriction may offer better sensitivity in detecting those changes in a given patient.

4.5 Clinical Implications

TCD is routinely used in the diagnosis and monitoring of patients with intracranial diseases including vasospasm,^{34, 35} sickle cell,³⁶ and others. However, these established techniques are based on relatively simple morphological features of the TCD pulse-waveform, such as diastolic, systolic, and mean CBFV. Work by Asgari et al. has demonstrated that more sophisticated pulse-waveform metrics can be used to assess other physiological changes, particularly vasodilation and vasoconstriction⁶. The model presented here provides insight into the difficult to measure physiological mechanisms affecting these additional pulse-waveform metrics. Specifically, the sensitivity analysis and validation has suggested several factors that play a role in how the hypercapnic vasodilation response is represented in TCD monitoring. As additional relationships between TCD pulse-waveform metrics and clinical state are identified, this model will be invaluable in understanding the underlying mechanisms.

With the addition of patient-specific vascular geometry and waveforms, it will be possible to fit the model to an individual patient and investigate the state and response to different procedures. Based on the positive results obtained by validating the model based on pulse-waveform trends, we can expand on our previous work using a hidden state estimation approach on a simpler model of the cerebral circulatory system to estimate unobserved variables.³⁷

4.6 Limitations

The sensitivity analysis of this model was limited by the single level fractional factorial analysis. As many of the parameter changes have non-linear effects on the pulse-waveform shape, a sensitivity analysis that uses a multiple level design will further detail the specific relationship between the state of the cerebrovascular system and the CBFV pulse-waveform.

This study was also limited by the use of a generalized model of the cerebral vasculature and input flows. To take advantage of the full potential of this model, data such as angiographically measured vascular geometry and simultaneously measured CBFV can used to produce patient specific simulations.

4.7 Conclusions

Despite the limitations of this initial analysis, it shows that this model of cerebral blood flow is capable of replicating many of the pulse-waveform changes observed during a CO₂ inhalation on human patients. Furthermore, by identifying the parameters that most affect the specific pulse-waveform characteristics and how they relate to the state of the cerebrovascular system as a whole, we gain insight into the specific mechanisms of changes in the brain. These results pave the way for subsequent model analysis and modifications that can further improve our understanding of cerebral circulatory system.