Conformational dynamics of a crystalline protein from microsecond-scale molecular dynamics simulations and diffuse X-ray scattering

Significance

A major challenge of protein crystallography is to accurately describe protein structure variations. Whereas Bragg peaks only yield a picture in which the variations are superimposed, diffuse X-ray scattering (diffraction between the peaks) reports on the way different atoms move together and can be used to increase the accuracy of models. We have performed a molecular-dynamics (MD) simulation of crystalline staphylococcal nuclease, yielding a rich picture of functionally important motions. This simulation is 100-fold longer than previous studies and yields reproducible calculations of diffuse intensity, overcoming a major challenge in the field. Experimental data support the MD models and indicate that diffuse scattering can be used both to validate and to improve MD simulations.

Abstract

X-ray diffraction from protein crystals includes both sharply peaked Bragg reflections and diffuse intensity between the peaks. The information in Bragg scattering is limited to what is available in the mean electron density. The diffuse scattering arises from correlations in the electron density variations and therefore contains information about collective motions in proteins. Previous studies using molecular-dynamics (MD) simulations to model diffuse scattering have been hindered by insufficient sampling of the conformational ensemble. To overcome this issue, we have performed a 1.1-μs MD simulation of crystalline staphylococcal nuclease, providing 100-fold more sampling than previous studies. This simulation enables reproducible calculations of the diffuse intensity and predicts functionally important motions, including transitions among at least eight metastable states with different active-site geometries. The total diffuse intensity calculated using the MD model is highly correlated with the experimental data. In particular, there is excellent agreement for the isotropic component of the diffuse intensity, and substantial but weaker agreement for the anisotropic component. Decomposition of the MD model into protein and solvent components indicates that protein–solvent interactions contribute substantially to the overall diffuse intensity. We conclude that diffuse scattering can be used to validate predictions from MD simulations and can provide information to improve MD models of protein motions.

Proteins explore many conformations while carrying out their functions in biological systems (1–3). X-ray crystallography is the dominant source of information about protein structure; however, crystal structure models usually consist of just a single major conformation and at most a small portion of the model as alternate conformations. Crystal structures therefore are missing many details about the underlying conformational ensemble (4).

Proteins assembled in crystalline arrays, like proteins in solution, exhibit rich conformational diversity (4) and often can perform their native functions (5). Many methods have emerged for using Bragg data to model conformational diversity in protein crystals (6–17). The development of these methods has been important as conformational diversity can lead to inaccuracies in protein structure models (9, 18–20). A key limitation of using the Bragg data, however, is that different models of conformational diversity can yield the same mean electron density.

Whereas the Bragg scattering only contains information about the mean electron density, diffuse scattering (diffraction resulting in intensity between the Bragg peaks) is sensitive to spatial correlations in electron density variations (21–28) and therefore contains information about the way that atomic positions vary together in protein crystals. Because models that yield the same mean electron density can yield different correlations in electron density variations, diffuse scattering provides a means to increase the accuracy of crystallography for determining protein conformational variations (29). Peter Moore (30) and Mark Wilson (31) have argued that diffuse scattering should be used to test models of conformational diversity in X-ray crystallography.

Several pioneering studies used diffuse scattering to reveal insights into correlated motions in proteins (17, 30, 32–49). Some of these studies used diffuse scattering to experimentally validate predictions of correlated motions from molecular-dynamics (MD) simulations (35–37, 40, 42–44). These studies revealed important insights but were limited by inadequate sampling of the conformational ensemble, leading to lack of convergence of the diffuse scattering calculations (35). Microsecond-scale simulations of staphylococcal nuclease were predicted to be adequate for convergence of diffuse scattering calculations (42). Modern simulation algorithms and computer hardware now enable microsecond or longer MD simulations of protein crystals (50).

Here, we present calculations of diffuse X-ray scattering using a 1.1-μs MD simulation of crystalline staphylococcal nuclease. The results demonstrate that we have overcome the past limitation of inadequate sampling. We chose staphylococcal nuclease because the experiments of Wall et al. (49) still represent the only complete, high-quality, 3D diffuse scattering data set from a protein crystal. The calculated diffuse intensity is very similar using two independent halves of the trajectory; the results therefore are reproducible and can be meaningfully compared with the experimental data. The MD simulation provides a rich picture of conformational diversity in the energy landscape of a protein crystal, consisting of at least eight metastable states. Like previous MD studies of crystalline staphylococcal nuclease (42–44), the agreement of the simulation with the total experimental diffuse intensity is excellent, supporting the use of MD simulations to model diffuse scattering data. Unlike previous MD studies, we separately compared the more finely structured, anisotropic component of the diffuse intensity with experimental data. The agreement is substantial but weaker than for the isotropic component, indicating there are inaccuracies in the MD models. Our results therefore point toward using diffuse scattering to improve MD models of protein motions.

Results

Functionally Important Motions of Crystalline Staphylococcal Nuclease.

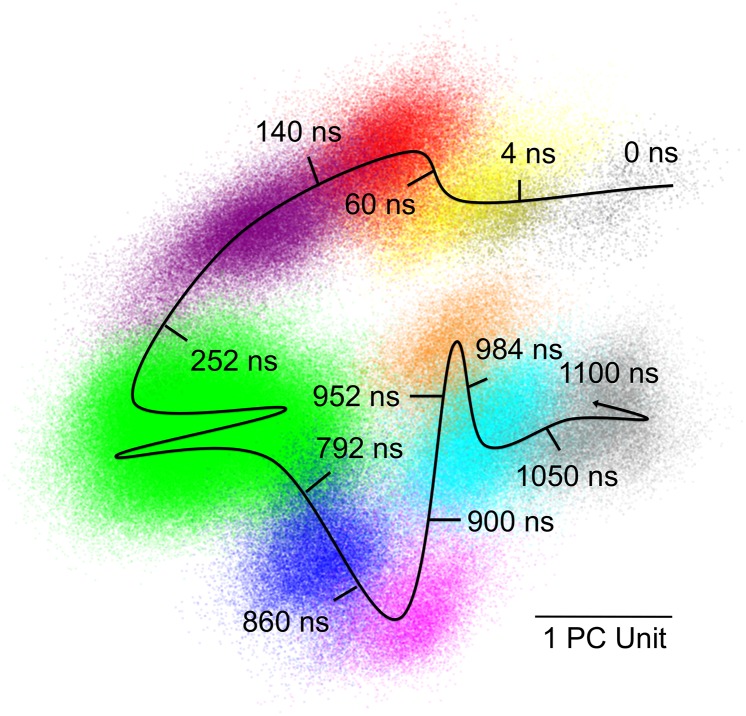
We performed a 1.1-μs MD simulation of a staphylococcal nuclease unit cell (Fig. S1 and Methods), revealing a rich conformational landscape. To analyze the trajectory, we performed principal component analysis (Methods) and gradually added sequential time points to a scatter plot in the space of the two dominant principal components. The points clustered visually into ellipsoidal shaped regions (Fig. 1).

Fig. 1.

Scatter plot of structures extracted from the MD trajectory projected on the first two principal components of the α-carbon position covariance matrix. The first component corresponds to the x axis, and the second corresponds to the y axis. Gray regions correspond to the first 10 ns and last 50 ns of the trajectory; colored regions correspond to metastable states (the yellow region overlaps the first gray region). The curved line indicates the rough trajectory of the system; tick marks indicate approximate times at which state transitions occur.

We identified at least eight metastable states by noting when sharp transitions occurred between the regions (Fig. 1, curved black line with tick marks). The time between the transitions varies considerably from 32 ns (Fig. 1, orange basin) to 540 ns (Fig. 1, green basin); notably, these times are longer than the 10-ns duration of the previous MD simulation of a staphylococcal nuclease unit cell (42) (Fig. 1, gray region). The cyan basin is visited twice: the first time for 52 ns, and the second time for 66 ns. The system spends nearly half the duration of the simulation in the green basin (540 ns); visualization in three dimensions revealed that this basin has a fine structure of substates that, compared with the separations in Fig. 1, lie close together in the space of the dominant principal components.

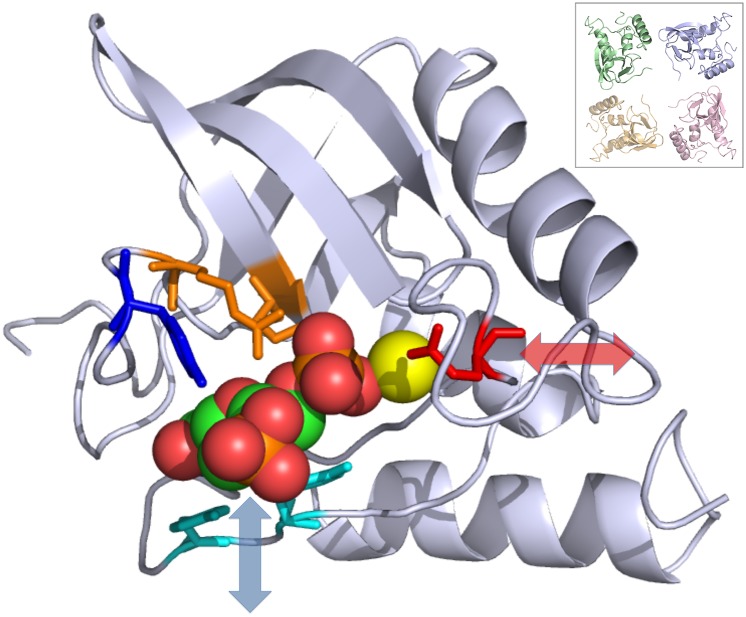
To gain insight into the functional significance of the states in Fig. 1, we created movies to visualize the motions of the two dominant principal components (Movies S1 and S2). Both components are dominated by internal motions rather than overall rotations and translations of the protein. The residues in the active site (51) cluster into localized regions whose motions are highly correlated (Fig. 2): (A) Glu43, at the beginning of the omega loop (Fig. 2, red sticks); (B) Arg35, Tyr85, and Arg87, at the top of the binding pocket (Fig. 2, Arg35 and Arg87 in orange sticks, and Tyr85 in blue sticks); and (C) Tyr113 and Tyr115, at the bottom of the binding pocket (Fig. 2, cyan sticks). Both of the principal components involve substantial motions of regions A and C with little motion in region B. Especially prominent are a clamping motion of region C against region B, which would likely modulate binding interactions (Fig. 2, blue double-headed arrow), and an opening of region A away from region B, modulating the environment of a water molecule putatively involved in the hydrolysis of the 5′-phosphodiester bond (Fig. 2, red double-headed arrow) (52). The motions vary for the four copies of the protein in the unit cell (Fig. 2, Inset): the region C motion is most pronounced for the pink chain; the region A motion is most pronounced for the blue and yellow chains; and the region A and C motions are smallest in the green chain. The states therefore correspond to structures with different active site geometries, resulting in identifiable functional consequences for binding and catalysis.

Fig. 2.

Active-site conformational dynamics in crystalline staphylococcal nuclease. The backbone is rendered using a ribbon, and the P4₁ unit cell packing along the c axis is shown in the Inset (the screw axis translation is into the page, with the green copy closest and the orange copy farthest away). The residues are shown using sticks, proceeding counterclockwise: Glu43 (red), Arg35 (orange on the β-sheet), Arg87 (orange on the loop), Tyr85 (blue), Tyr115 (cyan), and Tyr113 (cyan). The rest of the protein is rendered as a gray cartoon. The inhibitor thymidine 3′,5′-bisphosphate is shown using spheres and the calcium ion using a yellow sphere. Arrows indicate the direction of motion in the two dominant principal components of the microsecond MD simulation. The loop containing Glu43 (red) moves in the approximate direction indicated by the transparent red double-headed arrow. The loop containing Tyr113 and Tyr115 (cyan) moves in the approximate direction indicated by the transparent blue double-headed arrow. The region containing Tyr85 (blue) and Arg35 and Arg87 (orange) moves much less by comparison. The image was created using PyMOL (66).

MD Model of Diffuse Scattering.

Wall et al. (49) obtained 3D experimental diffuse scattering data by averaging measurements of the continuous intensity $D_o\left(\mathbf{s}\right)$ at scattering vectors s in the neighborhood of each Bragg peak. This procedure yielded a single diffuse intensity $D_o\left(hkl\right)$ at integer reciprocal lattice points hkl (SI Text); the diffuse lattice showed the expected P4/m Patterson symmetry, which was used to create an eightfold redundant expanded lattice with symmetry averaged observations (49). We similarly computed the diffuse intensity $D_{md}\left(\mathbf{s}\right)$ at each reciprocal lattice point and expanded the lattice using the P4/m Patterson symmetry (Methods). To assess the reproducibility of diffuse intensity calculations, we compared $D_{md}\left(hkl\right)$ calculated using either the first or second half of the following subsections extracted from the full 1.1-μs trajectory: the first 10 ns; the first 100 ns; and the last 1,000 ns. Correlation coefficients using all of the $D_{md}\left(hkl\right)$ lattice points (∼138,500 in total, of which ∼17,300 are independent, due to symmetry) were calculated between the results obtained using either the first or second half (Methods). Correlations of the total intensity, $r_{12}$, were excellent for each of the three subsections of the trajectory: $r_{12}=$ 0.994 for 10 ns, 0.995 for 100 ns, and 0.998 for 1,000 ns.

We performed a more detailed assessment of the reproducibility by first decomposing the diffuse intensity into components that are distributed either isotropically or anisotropically about the origin (Methods). We then calculated correlations for just the anisotropic component, $D{\prime }_{md}\left(hkl\right)$, which corresponds to the striking 3D features visible in the experimental data (see, e.g., figure 3 of ref. 49). The correlations for the anisotropic intensity, $r{\prime }_{12}$, were lower than for the total intensity: $r{\prime }_{12}=$ 0.646 for 10 ns, 0.654 for 100 ns, and 0.832 for 1,000 ns. The first and second halves of the 1,000-ns trajectory sample a similar range in the dominant principal component (Fig. 1), which is consistent with the high correlation for that trajectory. The difference between the values of $r_{12}$ and $r{\prime }_{12}$ indicates that the total intensity correlation is dominated by the large isotropic component of the signal that varies gradually with resolution. The increase in the anisotropic intensity correlation with simulation time indicates that diffuse scattering calculations become more reproducible for longer simulations, as expected. The fact that $r{\prime }_{12}$ = 0.832 for the 1,000-ns trajectory demonstrates that sampling is not a limitation for our validation of MD models of diffuse X-ray scattering.

Meinhold and Smith (42) analyzed diffuse scattering using an approximation in which the variations in atomic positions are normally distributed. In this case, the diffuse intensity in Eq. 1 can be computed using the covariance matrix of atomic displacements $\langle {\mathbf{u}}_k{\mathbf{u}}_{k^{\prime }}^T\rangle$ between all atom pairs $\left(k,k^{\prime }\right)$ (equation 2 in ref. 42). The reproducibility of diffuse scattering calculations then depends on the reproducibility of these matrix element calculations. Similar to Meinhold and Smith (42), we assessed the reproducibility of the matrix elements by just examining α-carbon coordinates. The covariance matrices were calculated from either the early or late halves of the 1,000-ns trajectory (Methods), and were compared by calculating the Pearson correlation coefficient between all elements. The resulting value of 0.517 is much lower than the values of $r_{12}$ (0.9975) or $r{\prime }_{12}$ (0.832) computed from the diffuse intensity, indicating that calculations of the covariance matrix were not as reproducible as diffuse scattering calculations. A possible explanation is that the diffuse intensity results from the statistically accumulated signal of many atom pairs, whereas the covariance matrix has an element for each individual atom pair.

Experimental Validation of the MD Model.

We compared the MD model to the 64,335 experimental observations collected by Wall et al. (49). The observations were placed on a symmetry expanded diffuse intensity lattice containing 120,845 points (Methods). For each simulation, we multiplied all of the $D_{md}\left(hkl\right)$ by a single scalar weight w and optimized the value of w to minimize the root-mean-squared deviation (RMSD) of the calculated $D_{md}\left(hkl\right)$ with respect to the experimental $D_o\left(hkl\right)$ values. Comparisons were performed by calculating correlation coefficients using the lattice points where both calculations and observations were available (∼118,500, of which ∼14,800 are independent due to symmetry). Correlations were computed for four trajectories, either with or without using hydrogen atoms: 0–10, 0–100, 0–1,100, and 100–1,100 ns (Table S1). The correlation $r_{oc}$ of the total intensity ranged from 0.90 to 0.94 for the all-atom calculations, and from 0.85 to 0.92 for the heavy-atom calculations. The correlations for heavy-atom models were in each case lower than for all-atom models (difference of 0.02–0.05), indicating that adding hydrogens somewhat improves the model of total intensity. The correlations increase as the trajectories increase in duration. Excellent agreement was achieved for the 0- to 1,100-ns and 100- to 1,100-ns all-atom simulations, where $r_{oc}$ = 0.94.

We also calculated Meinhold and Smith’s R-factor–like agreement statistic (equation 3 in ref. 42) between $D_o\left(hkl\right)$ and the total $D_{md}\left(hkl\right)$ computed from the 100- to 1,100-ns simulation. This involved a minimization with respect to an overall weighting factor and baseline shifting of the $D_{md}\left(hkl\right)$. We found a value of 0.029, which is much lower than the minimum value of 0.081 found by Meinhold and Smith (table 2 in ref. 42). The agreement factor therefore is substantially improved for our microsecond simulation compared with their 10-ns simulation.

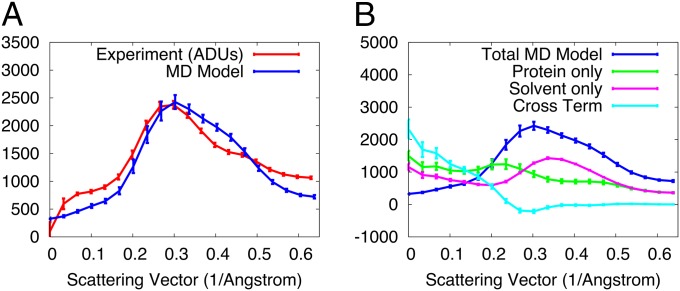
The isotropically averaged diffuse intensity from the MD model and experimental data were very similar (Fig. 3A), which is consistent with the global correlation results. To better understand the origin of the isotropic intensity, we decomposed $D_{md}\left(hkl\right)$ for the 1,000-ns trajectory into protein ($D_{md,p}$), solvent ($D_{md,s}$), and protein–solvent ($D_{md,x}$) terms (Methods). (Note that the contribution of $D_{md,x}$ to the sum is negative.) Each component contributes about equally to the total signal (Fig. 3B).

Fig. 3.

Analysis of isotropic diffuse intensity. (A) Comparison of isotropic diffuse intensity for data (red) to the MD model (blue). (B) Decomposition of the total simulated isotropic intensity (blue) into contributions from protein (green), solvent (magenta), and the protein–solvent cross term (cyan). The total intensity is equal to the protein term plus the solvent term minus the cross term (Methods). In both A and B, the SD of the anisotropic diffuse intensity is indicated using error bars.

The protein and solvent curves are similar to those calculated by Meinhold and Smith (42). The cross term, $D_{md,x}$, starts high at small scattering vectors, dips below zero at about 0.3 Å⁻¹, and settles to zero at ∼0.35 Å⁻¹. To gain further insight into the nature of the correlations implied by this behavior, we fit the cross term to a model of correlations that decay exponentially in real space over a length $\gamma$ (Methods). A reasonable fit was obtained using $\gamma =0.89\pm 0.08$ Å (Fig. S2), suggesting that the cross term is dominated by short-range correlations between the fluctuations of the protein and solvent (Discussion).

As for the model $D{\prime }_{md}$, we calculated the anisotropic component of the experimentally observed diffuse intensity, $D{\prime }_o,$ by subtracting the isotropic component (Methods). For both the experimental data and the MD model, at each resolution the SD of the anisotropic intensity is less than 10% of the isotropic intensity (Fig. 3A, error bars). The anisotropic component therefore is weaker than the isotropic component. The anisotropic intensity due the individual protein, solvent, and protein–solvent cross terms show differences in magnitude (Fig. 3B). At scattering vectors greater than 0.1 Å⁻¹, the protein has the strongest anisotropic intensity (largest green error bars). The protein–solvent cross term is weaker (small cyan error bars), and the solvent is weakest (very small magenta error bars). Below 0.1 Å⁻¹, each component has substantial anisotropic intensity; however, different components nearly cancel, summing to a very small total anisotropic intensity (blue bars).

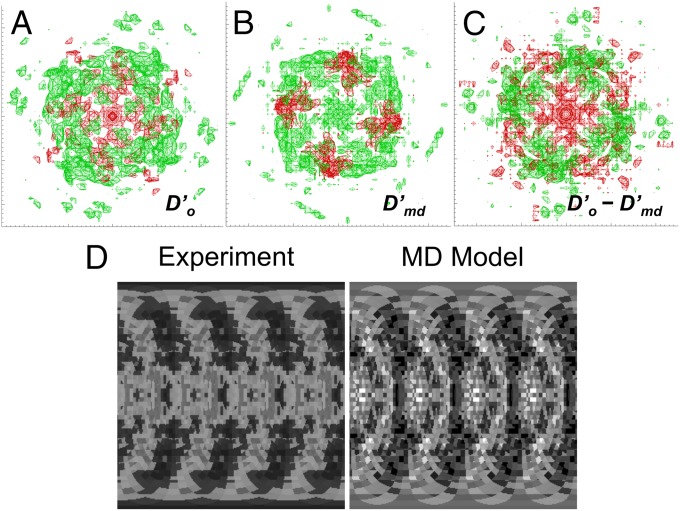
To assess the agreement of the anisotropic component of the MD model ($D{\prime }_{md}$) with experimental data ($D{\prime }_o$), we visualized level surfaces of $D{\prime }_o$ (Fig. 4A), $D{\prime }_{md}$ (Fig. 4B), and $D{\prime }_o-D{\prime }_{md}$ (Fig. 4C). The comparison revealed places where the MD model intensity was either higher (Fig. 4C, green) or lower (Fig. 4C, red) than the experimental intensity. As for the total intensity, to quantify the agreement we calculated the anisotropic correlation coefficient $r{\prime }_{oc}$ (Methods) between $D{\prime }_{md}$ and $D{\prime }_o$ for each of the trajectories, either with or without hydrogens (Table S1). The correlation $r{\prime }_{oc}$ of the anisotropic intensity ranged from 0.35 to 0.43 for the all-atom calculations, and from 0.34 to 0.40 for the heavy-atom calculations. The highest anisotropic correlation ($r{\prime }_{oc}$ = 0.43) is strongly positive, but is lower than the lowest total intensity correlation ($r_{oc}$ = 0.85), indicating that the MD model more accurately describes the isotropic than the anisotropic diffuse intensity. The best all-atom correlation is for the 0- to 10-ns trajectory ($r{\prime }_{oc}$ = 0.43), and the worst is for the 0- to 100-ns trajectory ($r{\prime }_{oc}=$ 0.35). The 0- to 1,000-ns and 0- to 1,100-ns trajectories yield intermediate correlations ($r{\prime }_{oc}$ = 0.40).

Fig. 4.

Comparison of anisotropic diffuse intensity between models and experimental data. (A–C) Isosurfaces in the (A) experimental ($D{\prime }_o$), (B) scaled MD model ($D{\prime }_{md}$), and (C) difference ($D{\prime }_o-D{\prime }_{md}$) intensity maps. Positive intensity is shown in green, and negative intensity in red. All isosurfaces including the difference map are displayed at an intensity level equal to the SD of $D{\prime }_o$ in the solvent ring. The values of $D{\prime }_{md}$ were multiplied by a uniform scale factor to yield the same SD in the solvent ring as $D{\prime }_o$. The x direction in each panel corresponds to the a* axis, varying from −0.5 Å⁻¹ at the left to 0.5 Å⁻¹ at the right; the y direction corresponds to the b* axis, varying from −0.5 Å⁻¹ at the bottom to 0.5 Å⁻¹ at the top. (D) Visualizations of the experimental (Left) and MD model (Right) anisotropic diffuse intensity in the 0.27-Å⁻¹ resolution shell, for which the agreement is best. The images were constructed as in figure 3 of ref. 49, using the shimlt and seesh routines in LUNUS (63, 72). The y direction corresponds to the polar angle in the shell as measured from the c* axis, varying from 0 at the top to π at the bottom of each image. The x direction corresponds to the azimuthal angle as measured from the a* axis in a right-handed sense, varying from −π at the left to π at the right. Pixel values are displayed as the deviation from the mean on a linear gray scale, with −500 corresponding to black, and 500 corresponding to white.

Correlations for heavy-atom models were lower than for all-atom models by 0.01 or less (Table S1), indicating that adding hydrogens did not substantially improve the model of anisotropic intensity. The correlation for the protein component of the MD model ($D_{md,p}$) was $r{\prime }_{oc}$ = 0.38 (not listed in Table S1), which is very similar to that for the entire MD model. This supports the finding that the protein is the dominant contributor to the anisotropic intensity (Fig. 3A, error bars).

We also calculated the anisotropic correlation within resolution shells, and found the highest value was 0.58 in the 0.27 Å⁻¹ resolution shell. Visualization of the experimental and MD model intensity in this shell shows arcs of diffuse intensity extending between the two poles, and rich large-scale features near the equator (Fig. 4D). A liquid-like motions model showed similar patterns (figure 5 in ref. 49), suggesting that they can be explained largely by the protein structure factor (equation 4 in ref. 49).

Discussion

The present 1.1-μs simulation, which is 100-fold longer than the previous 10-ns simulation of a staphylococcal nuclease unit cell (42), revealed eight metastable states with lifetimes that are longer than the duration of the shorter simulation. Analysis of the motions revealed that the basins correspond to structures with different active-site geometries, resulting in identifiable functional consequences for binding and catalysis.

Diffuse scattering can independently validate the predictions of MD simulations. Conversely, interpretation of the diffuse intensity in terms of a multistate conformational ensemble is now possible (Fig. 1). Although there is room for improvement in modeling the isotropic intensity at resolutions exceeding 0.3 Å⁻¹ (Fig. 3A), the agreement of the MD model with the total experimental diffuse intensity is remarkable considering that no free parameters were adjusted. Moreover, this agreement is robust to sampling (Table S1) and to a model perturbation that includes a change of force field (SI Text).

Compared with the total intensity, the MD model had a lower, but still strongly positive, correlation with the anisotropic diffuse intensity. The lower correlation of the anisotropic intensity indicates there are inaccuracies in the MD models. Maximizing the correlation of the anisotropic intensity is therefore a potential strategy for increasing the accuracy of the MD models. For example, both the simulation of a single unit cell with periodic boundary conditions and the assumption of independent unit cells inherent in Eq. 1 might limit the accuracy of the MD model. One way to test this possibility is to simulate larger sections of the crystal with several unit cells (50), as this will enable correlations between unit cells to be included in the model.

Decomposition of the diffuse intensity into protein and solvent components revealed that the protein component $D_{md,p}$ dominates the overall magnitude of the anisotropic intensity (Fig. 3A, error bars). In addition, the MD model of anisotropic intensity using the protein alone ($r{\prime }_{oc}$ = 0.38) was almost as accurate as using the protein and solvent ($r{\prime }_{oc}$ = 0.40). These results support the hypothesis that the anisotropic intensity reports largely on variations in the protein structure (49).

The decomposition also revealed that the protein–solvent interactions contribute a strong negative component to the sum ($D_{md,x}$ is mostly positive in Fig. 3B and enters with a minus sign). Combined with the subatomic correlation length derived from the fit to Eq. 2, these results suggest that the cross term might be mainly due to negative correlations in the density fluctuations that occur in the region between the protein and solvent atoms. One possible explanation for this is that, when atoms move together, the density shifts, resulting in a positive fluctuation ($+\Delta \rho$) for the leading edge density of one atom (e.g., a protein atom) coupled a negative fluctuation ($-\Delta \rho$) for the trailing edge density of a neighboring atom (e.g., a solvent atom) (Fig. S2, Inset).

Increasing the duration of the MD trajectory yielded more reproducible calculations of diffuse intensity and better models of the total intensity. Calculations of the covariance matrix of α-carbon displacements, however, were less reproducible than the calculations of diffuse intensity. In addition, only the cyan basin in Fig. 1 is visited more than once. Thus, even though we have achieved reproducible diffuse scattering calculations using an MD model, the sampling of the conformational ensemble is still incomplete. Millisecond all-atom simulations (53), advanced sampling methods such as parallel tempering (54), and acceleration schemes such as Markov state models (55) and parallel replica MD (56, 57) can be used to pursue increased sampling and improved convergence of the calculations.

Our comparisons point to opportunities for improving models of protein motions using diffuse scattering. For example, if the accuracy of the model of anisotropic diffuse intensity can be improved, it might become possible to use diffuse scattering to improve MD force fields. Indeed, use of NMR data for force field improvement provides an example of the potential impact of diffuse scattering. Early comparisons of MD to NMR data for staphylococcal nuclease revealed differences in the residue-by-residue backbone flexibility (58), and more recent force fields now do a much better job of reproducing the NMR data (59–62). Another possibility is to use diffuse scattering for validating results obtained using schemes for increasing sampling (54–57).

There is also room for improvement in integration of experimental diffuse scattering data from diffraction images. For example, our current methods aim to extract the large-scale features (due to short-range correlations within the unit cell) and to ignore the small-scale, streaked features (due to long-range correlations across unit cells) (63). However, these methods can be improved by accounting for better separation of the large-scale from small-scale features, or a finer sampling of all diffuse features (29). Increased diffuse scattering data collection efforts and advances in X-ray detector technology will further this goal (29).

Methods

MD Simulations.

The 48.5 Å × 48.5 Å × 63.5-Å P1 unit cell model was prepared from the Research Collaboratory for Structural Bioinformatics (RCSB) Protein Data Bank (PDB) (64) (www.rcsb.org) entry 1STN (65) using the UnitCell code in AmberTools (ambermd.org/#AmberTools). The RMSD of the atomic coordinates [calculated using PyMOL (66)] between 1STN and PDB entry 4WOR (49) (the crystal structure refined against the Bragg data) is 0.70 Å, with backbone deviations concentrated in loops near the ligand binding site (Fig. S3). Waters and counterions were added using genbox and genion in GROMACS (67), resulting in a model with 8,904 protein atoms (four proteins arranged in a P4₁ configuration), 6,477 TIP3P water atoms, and 40 Cl⁻ ions (Fig. S1). The OPLS-AA force field (68, 69) was selected. An initial model was prepared using energy minimization followed by 100-ps equilibration in a constant-particle number, -volume, and -temperature (NVT) ensemble at 300 K, using harmonic restraints for the protein atom coordinates. The modified Berendsen thermostat with a 0.1-ps time constant was used for temperature equilibration.

The production 1.1-μs simulation was performed in GROMACS (67) on a 128 core 2.00 GHz Intel Xeon X6550 machine using a 2-fs time step with a constant-particle number, -pressure, and -temperature (NPT) ensemble at 300 K and 1 bar. The Parrinello–Rahman barostat with a 2.0-ps time constant was used for pressure equilibration. At a rate of 44.6-ns system time per day of wall clock time, it took roughly 30 d to complete, including periods of down time. Snapshots were recorded every 2 ps in compressed (.xtc) format, yielding a total of 5.5 × 10⁸ frames in a 31.1-GB file.

Upon the switch from the restrained NVT to the unrestrained NPT simulation, the unit cell dimensions began fluctuating (all scaled simultaneously with the volume fluctuations) and the mean values rapidly shrank by 1.3% of their initial values. The structure also drifted away from the crystal structure: the RMSD between the mean coordinates from the simulation and PDB entry 4WOR was 1.8 Å (1.3 Å) for heavy atoms (α-carbons). These values are similar to those obtained by Meinhold and Smith (42) for their 10-ns simulation: they reported deviations of less than 0.8% in unit cell dimensions, and a RMSD between the mean simulation coordinates and PDB entry 2SNS (52) (an experimentally determined crystal structure available at the time) of 1.7 Å (1.3 Å) for heavy atoms (α-carbons).

MD Model Diffuse Scattering Calculations and Reproducibility.

To calculate the diffuse intensity for a given section of the trajectory, ensembles of atomic coordinates were extracted from the full trajectory in 5-ns chunks. This procedure yielded protein and solvent coordinates of the P1 unit cell in a series of separate files (SI Text).

Each of the files was then processed to calculate the diffuse intensity. The structure factor, $f_n\left(hkl\right)$, for each unit cell structure n was calculated to 1.6-Å resolution at Miller indices hkl using the iotbx package in the computational crystallography toolbox (CCTBX) (70). The average structure factor, ${\langle f_n\left(hkl\right)\rangle }_n$, and the average squared structure factor, ${\langle {\left|f_n\left(hkl\right)\right|}^2\rangle }_n$, were calculated using a modified version of the Phenix (71) Python script get_struct_fact_from_md.py, which we called get_diffuse_from_md.py. Averages for longer sections of the trajectory were accumulated from averages of the 5-ns chunks. The intensity of the diffuse scattering for the first $\left[D_{md1}\left(hkl\right)\right]$ and second $\left[D_{md2}\left(hkl\right)\right]$ parts of the trajectory were calculated using the following equation:

$$D_{md}\left(hkl\right)={\langle {\left|f_n\left(hkl\right)\right|}^2\rangle }_n-{\left|{\langle f_n\left(hkl\right)\rangle }_n\right|}^2.$$ [1]

Eq. 1 appears in the classic text of Guinier (24) and assumes independent unit cell fluctuations. It states that the diffuse intensity is equal to the variance of the unit cell structure factor, and therefore contains information that is distinct from the Bragg peak intensities, which are determined by the square of the mean structure factor (second term of Eq. 1). Eq. 1 is an established method for calculating diffuse scattering from protein MD simulations (35, 42–44).

To decompose the diffuse intensity into isotropic and anisotropic components, reciprocal space was subdivided into concentric spherical shells, each with a thickness equal to the reciprocal unit cell diagonal ($\Delta s$ = 0.0336 Å⁻¹). The isotropic intensity $D_{md}\left(s_n\right)$ was calculated as the mean intensity at scattering vector $s_n$ at the midpoint of each shell n. The anisotropic intensity $D{\prime }_{md}\left(hkl\right)$ was then calculated at each lattice point $hkl$ by subtracting the isotropic intensity $D_{md}\left(s_{hkl}\right)$ from the original signal $D_{md}\left(hkl\right)$. The value of $D_{md}\left(s_{hkl}\right)$ at scattering vector $s_{hkl}$ in the range $(s_n,s_{n+1})$ was obtained by linear interpolation of $D_{md}\left(s_n\right)$. The same method was used to obtain isotropic $\left[D_o\left(s_n\right)\right]$ and anisotropic $\left[D{\prime }_o\left(hkl\right)\right]$ components of the experimentally observed diffuse intensity.

Because the experimental diffuse intensity shows symmetry consistent with the P4₁ symmetry of the unit cell (49), we enforced the P4/m Patterson symmetry (corresponding to the P4₁ unit cell symmetry) by replacing each $D_{md}\left(hkl\right)$ value with the average over all symmetry equivalent hkl positions in the map. The resulting symmetry-expanded map had ∼17,300 independent values on ∼138,500 lattice points with eightfold redundancy. The values were very similar to the original map (Pearson correlation coefficient r_sym = 0.996 for total intensity and $r{\prime }_{sym}=0.789$ for anisotropic intensity).

To assess the reproducibility of diffuse scattering calculations in the MD model, we divided the extracted trajectory into first and second halves of equal duration. We then calculated the simulated diffuse scattering from the first and second parts independently, and compared the results quantitatively. A global comparison of $D_{md}\left(hkl\right)$ and $D{\prime }_{md}\left(hkl\right)$ was made using the Pearson correlation coefficients $r_{12}$ and $r{\prime }_{12}$, respectively.

Covariance Matrices and Principal Components.

To calculate covariance matrices and to perform principal component analysis, the trajectory was adjusted to remove discontinuous jumps of atomic positions to symmetry-related positions during the course of the simulation (trjconv –pbc nojump). Next, the coordinates were adjusted to remove translational drift (trjconv –fit translation) and to preserve the covalent bonding structure of the protein (trjconv –pbc mol). Finally the α-carbon coordinates were selected and used to calculate and diagonalize the covariance matrix (g_covar). Comparisons of covariance matrices and projections of trajectories onto principal components were performed using the tool g_anaeig. Visualization of the energy landscape was performed by displaying the projected coordinates in a 2D scatter plot.

Decomposition into Protein and Solvent Components.

We used Eq. 1 and the equation $D_{md}=D_{md,p}+D_{md,s}-D_{md,x}$ to decompose $D_{md}$ into protein $\left(D_{md,p}=\langle {\left|f_{prot}\right|}^2\rangle -{\left|\langle f_{prot}\rangle \right|}^2\right)$, solvent $\left(D_{md,s}=\langle {\left|f_{solv}\right|}^2\rangle -{\left|\langle f_{solv}\rangle \right|}^2\right)$ and protein–solvent $\left(D_{md,x}=D_{md,p}+D_{md,s}-D_{md}\right)$ terms, where $f_{prot}$ and $f_{solv}$ are the structure factors computed from just the protein or solvent component, respectively. Note that positive values of $D_{md,x}$ contribute negatively to $D_{md}$.

We modeled $D_{md,x}$ using the following function (34, 49):

$$\mathrm{FT}\left[e^{-\gamma r}\right]=\frac{8\pi {\gamma }^3}{{\left[1+{\left(2\pi s\gamma \right)}^2\right]}^2},$$ [2]

where s is the scattering vector, $\gamma$ is the correlation length of atomic displacements, and $\mathrm{FT}\left[e^{-\gamma r}\right]$ indicates the 3D Fourier transform of the real-space function $e^{-\gamma r}$, which decays exponentially with distance r. The fitting of $D_{md,x}$ to Eq. 2 was performed using the nonlinear-least-squares fitting feature of gnuplot (www.gnuplot.info).