Flagellated bacterial motility in polymer solutions

Significance

The way microorganisms swim in concentrated polymer solutions has important biomedical implications, i.e., how pathogens invade the mucosal lining of mammal guts. Physicists are also fascinated by self-propulsion in such complex non-Newtonian fluids. The current standard model of how bacteria propelled by rotary helical flagella swim through concentrated polymer solutions postulates bacteria-sized pores, allowing them relative easy passage. Our experiments using high-throughput methods overturn this standard model. Instead, we show that the peculiarities of flagellated bacteria locomotion in concentrated polymer solutions are due to the fast-rotating flagellum, giving rise to a lower local viscosity in its vicinity. The bacterial flagellum is therefore a nano-rheometer for probing flows at the molecular level.

Abstract

It is widely believed that the swimming speed, v, of many flagellated bacteria is a nonmonotonic function of the concentration, c, of high-molecular-weight linear polymers in aqueous solution, showing peaked $v\left(c\right)$ curves. Pores in the polymer solution were suggested as the explanation. Quantifying this picture led to a theory that predicted peaked $v\left(c\right)$ curves. Using high-throughput methods for characterizing motility, we measured v and the angular frequency of cell body rotation, Ω, of motile Escherichia coli as a function of polymer concentration in polyvinylpyrrolidone (PVP) and Ficoll solutions of different molecular weights. We find that nonmonotonic $v\left(c\right)$ curves are typically due to low-molecular-weight impurities. After purification by dialysis, the measured $v\left(c\right)$ and $\mathrm{\Omega }\left(c\right)$ relations for all but the highest-molecular-weight PVP can be described in detail by Newtonian hydrodynamics. There is clear evidence for non-Newtonian effects in the highest-molecular-weight PVP solution. Calculations suggest that this is due to the fast-rotating flagella seeing a lower viscosity than the cell body, so that flagella can be seen as nano-rheometers for probing the non-Newtonian behavior of high polymer solutions on a molecular scale.

The motility of microorganisms in polymer solutions is a topic of vital biomedical interest. For example, mucus covers the respiratory (1), gastrointestinal (2), and reproductive (3) tracks of all metazoans. Penetration of this solution of biomacromolecules by motile bacterial pathogens is implicated in a range of diseases, e.g., stomach ulcers caused by Helicobacter pylori (4). Oviduct mucus in hens provides a barrier against Salmonella infection of eggs (5). Penetration of the exopolysaccharide matrix of biofilms by swimming bacteria (6) can stabilize or destabilize them in vivo (e.g., the bladder) and in vitro (e.g., catheters). In reproductive medicine (human and veterinary), the motion of sperms in seminal plasma and vaginal mucus, both non-Newtonian polymer solutions, is a strong determinant of fertility (3), and polymeric media are often used to deliver spermicidal and other vaginal drugs (7).

Microorganismic propulsion in non-Newtonian media such as high-polymer solutions is also a hot topic in biophysics, soft matter physics, and fluid dynamics (8). Building on knowledge of propulsion modes at low Reynolds number in Newtonian fluids (8), current work seeks to understand how these are modified to enable efficient non-Newtonian swimming. In particular, there is significant interest in a flapping sheet (9, 10) or an undulating filament (11) (modeling the sperm tail) and in a rotating rigid helix (modeling the flagella of, e.g., Escherichia coli) (12, 13) in non-Newtonian fluids.

An influential set of experiments in this field was performed 40 years ago by Schneider and Doetsch (SD) (14), who measured the average speed, $\overline{v}$, of seven flagellated bacterial species (including E. coli) in solutions of polyvinylpyrrolidone (PVP, molecular weight given as $M=360\hspace{0.5em}\mathrm{kDa}$) and in methyl cellulose (MC, M unspecified) at various concentrations, c. SD claimed that $\overline{v}\left(c\right)$ was always nonmonotonic and peaked.

A qualitative explanation was suggested by Berg and Turner (BT) (15), who argued that entangled linear polymers formed “a loose quasi-rigid network easily penetrated by particles of microscopic size.” BT measured the angular speed, Ω, of the rotating bodies of tethered E. coli cells in MC solutions. They found that adding MC hardly decreased Ω. However, in solutions of Ficoll, a branched polymer, $\mathrm{\Omega }$ is proportional to ${\eta }^{-1}$, where η is the solution’s viscosity, which was taken as evidence for Newtonian behavior. In MC solutions, however, BT suggested that there were E. coli-sized pores, so that cells rotated locally in nearly pure solvent. Magariyama and Kudo (MK) (16) formulated a theory based on this picture and predicted a peak in $v\left(c\right)$ by assuming that a slender body in a linear-polymer solution experienced different viscosities for tangential and normal motions in BT’s “easily penetrated” pores.

This standard model is widely accepted in the biomedical literature on flagellated bacteria in polymeric media. It also motivates much current physics research in non-Newtonian low-Reynolds-number propulsion. Nevertheless, there are several reasons for a fundamental reexamination of the topic.

First, polymer physics (17) casts a priori doubt on the presence of E. coli-sized pores in an entangled solution. Entanglement occurs above the overlap concentration, $c^{\mathrm{\ast }}$, where coils begin to touch. The mesh size at $c^{\mathrm{\ast }}$, comparable to a coil’s radius of gyration, $r_g$, gives the maximum possible pore size in the entangled network. For 360-kDa PVP in water, $r_g\lesssim 60\hspace{0.17em}\mathrm{nm}$ (see below), which is well under the cross section of E. coli (0.8 μm). Thus, the physical picture suggested by BT (15) and used by MK (16) has doubtful validity.

Second, SD’s data were statistically problematic. They took movies, from which cells with “the 10 greatest velocities were used to calculate the average velocity” (14). Thus, their peaks in $v\left(c\right)$ could be no more than fluctuations in measurements that were in any case systematically biased.

Finally, although MK’s theory indeed predicts a peak in $v\left(c\right)$, we find that their formulas also predict a monotonic increase in $\mathrm{\Omega }\left(c\right)$ in the same range of c (Fig. S1), which is inconsistent with the data of BT, who observed a monotonic decrease.

We therefore performed a fresh experimental study of E. coli motility using the same polymer (PVP) as SD, but varying the molecular weight, M, systematically. High-throughput methods for determining v and Ω enabled us to average over $\sim {10}^4$ cells at each data point. Using polymers as purchased, we indeed found peaked $v\left(c\right)$ curves at all M studied. However, purifying the polymers removed the peak in all but a single case. Newtonian hydrodynamics can account in detail for the majority of our results, collapsing data onto master curves. We show that the ratio $v\left(c\right)/\mathrm{\Omega }\left(c\right)$ is a sensitive indicator of non-Newtonian effects, which we uncover for 360-kDa PVP. We argue that these are due to shear-induced changes in the polymer around the flagella.

Below, we first give the necessary theoretical and experimental background before reporting our results.

Theoretical Groundwork: Solving Purcell’s Model

Purcell’s widely used “model E. coli” has a prolate ellipsoidal cell body bearing a single left-handed helical flagellum at one pole (18). Its motion is described by three kinematic parameters: the swimming speed, v, the flagellum angular speed, ω, and the body angular speed, Ω,

$$\mathbf{v}=\left(v,\mathrm{0,0}\right),\hspace{1em}\mathit{\omega }=\left(-\omega ,\mathrm{0,0}\right),\hspace{1em}\mathbf{\Omega }=\left(\mathbf{\Omega },\mathrm{0,0}\right),$$ [1]

with $(v,\omega ,\mathrm{\Omega })>0$. The drag forces and torques $\left(\mathbb{F},\mathrm{\mathbb{N}}\right)$ on the body (subscript b) and flagellum (subscript $f^{\prime }$) are given by

$$\left(\begin{array}{c}{\mathbb{F}}_b\\ {\mathrm{\mathbb{N}}}_b\end{array}\right)=-\left(\begin{array}{cc}{A}_0& 0\\ 0& D_0\end{array}\right)\left(\begin{array}{c}\mathbf{v}\\ \mathbf{\Omega }\end{array}\right),$$ [2]

$$\left(\begin{array}{c}{\mathbb{F}}_f\\ {\mathrm{\mathbb{N}}}_f\end{array}\right)=-\left(\begin{array}{cc}A& B\\ B& D\end{array}\right)\left(\begin{array}{c}\mathbf{v}\\ \mathit{\omega }\end{array}\right),$$ [3]

where $A_0,D_0,A,B,\hspace{0.17em}D\propto {\eta }_s$, the solvent viscosity. Requiring the body and flagellum to be force and torque free, we find

$$\mathrm{\Omega }=\frac{D\left(A_0+A\right)-B^2}{D_0\left(A+A_0\right)}\omega \equiv \beta \omega ,$$ [4]

$$v=\frac{B}{A_0+A}\omega \equiv \gamma \omega ,$$ [5]

where β and γ are viscosity-independent geometric constants. Eqs. 4 and 5 predict that

$$\mathrm{\Omega }=R_{1}v,\hspace{1em}\mathrm{with}\hspace{1em}{R}_1=\beta /\gamma ,$$ [6]

but underdetermine $\left(v,\mathrm{\Omega },\omega \right)$. Closure requires experimental input, in the form of the relationship between the torque developed by the motor, N, and its angular speed, ${\omega }_m$, where

$${\omega }_m=\mathrm{\Omega }+\omega =\left(1+{\beta }^{-1}\right)\mathrm{\Omega }.$$ [7]

Measurements have repeatedly shown (19) that $N\left({\omega }_m\right)$ displays two regimes (Fig. 1), which we model as

$$\omega \le {\omega }_m^c:N=N_0$$ [8a]

$$\omega >{\omega }_m^c:N=\alpha \left({\omega }_m^{\max }-{\omega }_m\right),$$ [8b]

where $\alpha =\left|\mathrm{d}N/\mathrm{d}{\omega }_m\right|=N_0/\left({\omega }_m^{\max }-{\omega }_m^c\right)$ is the absolute slope of $N\left({\omega }_m\right)$ when ${\omega }_m^c<\omega <{\omega }_m^{\max }$. For our purposes later, it is important to realize that Eq. 7 implies an equivalent $N\left(\mathrm{\Omega }\right)$ relation, with associated ${\mathrm{\Omega }}^c$ and ${\mathrm{\Omega }}^{\text{max}}$.

Fig. 1.

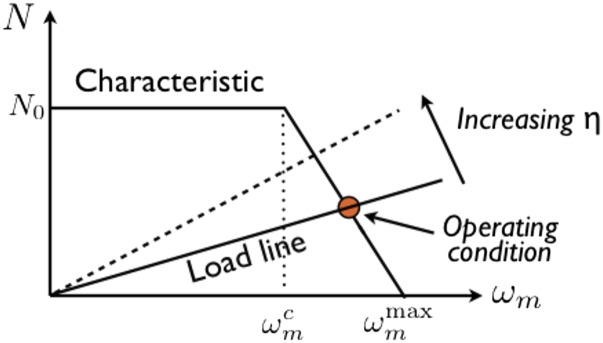
Schematic of the relationship $N\left({\omega }_m\right)$ between the flagellum motor torque, N, and its angular speed, ${\omega }_m$. Intersection with a load-line determines the operating condition. The $N\left(\mathrm{\Omega }\right)$ relation has the same form (cf. Eq. 7).

Eqs. 4, 5, 8a, and 8b completely specify the problem. We can now predict Ω and $v=\mathrm{\Omega }/R_1$, the observables in this work, as functions of solvent viscosity by noting that the motor torque is balanced by the drag torque on the body

$$N=D_0\mathrm{\Omega }=\left(\frac{D_0}{1+{\beta }^{-1}}\right){\omega }_m.$$ [9]

Eq. 9 specifies a load line that intersects with the motor characteristic curve (Fig. 1) to determine the operating condition. For a prolate ellipsoidal cell body with semimajor and semiminor axes a and b, $D_0=16\pi \eta a{b}^2/3$, so that

$$\omega <{\omega }_m^c:\mathrm{\Omega }=\frac{N_0}{D_0}=\left(\frac{3N_0}{16\pi a{b}^2}\right){\eta }^{-1}$$ [10a]

$$\omega >{\omega }_m^c:\mathrm{\Omega }=\frac{{\alpha }^{\mathrm{\ast }}{\mathrm{\Omega }}^{\max }}{{\alpha }^{\mathrm{\ast }}+D_0}=\frac{3{\alpha }^{\mathrm{\ast }}{\mathrm{\Omega }}^{\max }{\eta }^{-1}}{16\pi a{b}^2+3{\alpha }^{\mathrm{\ast }}{\eta }^{-1}},$$ [10b]

where ${\alpha }^{\mathrm{\ast }}=\left|\mathrm{d}N/\mathrm{d\Omega }\right|=N_0/\left({\mathrm{\Omega }}^{\max }-{\mathrm{\Omega }}^c\right)$ is the absolute slope of the $N\left(\mathrm{\Omega }\right)$ relation (cf Fig. 1) in the variable-torque regime.

Recall that BT equated $\mathrm{\Omega }\propto {\eta }^{-1}$ scaling with Newtonian behavior (15). The above results show that this is true in the constant-torque regime $\left(\omega <{\omega }_m^c\right)$ of the motor. Our experiments demonstrate that this is not the only relevant regime.

Experimental Groundwork: Characterizing Polymers

SD used “PVP K-90, molecular weight 360,000” (14), which, according to current standards (20), has a number averaged molecular weight of $M_n=360\hspace{0.5em}\mathrm{kDa}$, and a weight-average molecular weight of $M_w\approx {10}^6\hspace{0.17em}\mathrm{kDa}$. We show in SI Text that SD’s polymer probably has somewhat lower $M_w$ than the current PVP 360 kDa. We used four PVPs (Sigma Aldrich) with stated average molecular weights of $M\sim 10\hspace{0.5em}\mathrm{kDa}$ (no K-number given), 40 kDa (K-30), 160 kDa (K-60), and 360 kDa (K-90). Measured low-shear viscosities, which obeyed a molecular weight scaling consistent with good solvent conditions, yielded (see SI Text for details) the overlap concentrations (17), $c^{\mathrm{\ast }}=0.55\pm 0.01,1.4\pm 0.02,\hspace{0.17em}3.8\pm 0.1$, and $9.5\pm 0.5$ wt.% (in order of decreasing M; Fig. S2 and Table S1). Static light scattering in water gave $M_w\approx 840\hspace{0.5em}\mathrm{kDa}$ for our PVP360k, well within the expected range (20), and $r_g=56\hspace{0.5em}\mathrm{nm}$ (Table S2). We also used Ficoll with $M\sim 70$ kDa and 400 kDa from Sigma Aldrich (Fi70k, Fi400k).

Results

We measured the motility of E. coli in polymer solutions using two new high-throughput methods (Materials and Methods and SI Text). Differential dynamic microscopy (DDM), which involves correlating Fourier-transformed images in time, delivers, inter alia, the mean swimming speed $\overline{v}$ (21, 22). In dark-field flicker microscopy (DFM), we average the power spectrum of the flickering dark-field image of individual swimmers to obtain the mean body angular speed, $\overline{\mathrm{\Omega }}$.

Cells suspended in a phosphate motility buffer were mixed with polymer solution in buffer to reach final desired concentrations and loaded into sealed capillaries for DDM and DFM. The concentrations of cells were low enough to avoid any cell–cell interaction, including polymer-induced depletion aggregation (23)—the absence of the latter being confirmed by microscopy. Separate experiments confirmed that oxygen depletion is negligible over the duration of the measurements.

Native Polymer.

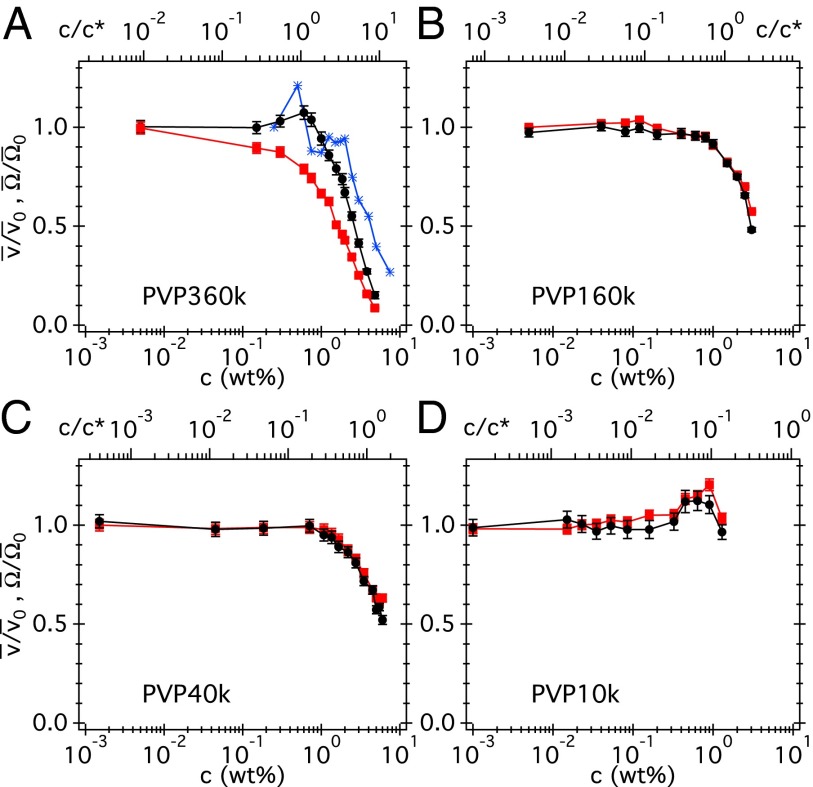
The measured $\overline{v}\left(c\right)$ curves for all four PVP (Fig. S3) and Ficoll (Fig. S4) solutions are all nonmonotonic. The peak we see in PVP360k (Fig. S3) is somewhat reminiscent of SD’s observation (14) for E. coli (Fig. 2A). Interestingly, all $\overline{\mathrm{\Omega }}\left(c\right)$ are also nonmonotonic except for PVP360k (Fig. S3).

Fig. 2.

(A–D) Normalized swimming speed $\overline{v}/{\overline{v}}_0$ (black circles) and body angular speed $\overline{\mathrm{\Omega }}/{\overline{\mathrm{\Omega }}}_0$ (red squares) vs. dialyzed PVP concentration (in weight percent) at four molecular weights, with ${\overline{v}}_0\approx 15\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$ and ${\overline{\mathrm{\Omega }}}_0\approx 20\hspace{0.5em}\mathrm{Hz}$. Top axis: PVP concentration normalized to c*. The blue stars in A are the swimming speeds from SD (14) normalized to the values at their lowest polymer concentration.

Dialyzed Polymers.

The initial rise in $\overline{v}$ and $\overline{\mathrm{\Omega }}$ on addition of native polymers (Figs. S3 and S4) are somewhat reminiscent of the way swimming speed of E. coli rises on adding small-molecule carbon sources (see the example of glycerol in Fig. S5), which cells take up and metabolize to increase the proton motive force. PVP is highly efficient in complexing with various small molecules (20). We therefore cleaned the as-bought, native polymers by repeated dialysis using membranes that should remove low-molecular-weight impurities (Materials and Methods) and then repeated the $\overline{v}\left(c\right)$ and $\overline{\mathrm{\Omega }}\left(c\right)$ measurements (Fig. 2), now reported in normalized form, $\overline{v}/{\overline{v}}_0$ and $\overline{\mathrm{\Omega }}/{\overline{\mathrm{\Omega }}}_0$, with ${\overline{v}}_0$ and ${\overline{\mathrm{\Omega }}}_0$ values at $c=0$ (buffer).

The prominent broad peaks or plateaus seen in the data for native PVP40k and PVP160k have disappeared (the same is true for Fi70k and Fi400k; Fig. S6). A small bump (barely one error bar high) in the data for PVP10k remains. Given the flatness of the data in PVP40k and PVP160k, we believe that the residual peak in PVP10k, whose coils have higher surface to volume ratio, is due to insufficient cleaning. A small peak ($\mathrm{\lesssim }10\text{\%}$ increase) in $\overline{v}\left(c\right)/{\overline{v}}_0$ also remains for PVP360k. For now, what most obviously distinguishes the PVP360k from the other three polymers is that the normalized $\overline{v}\left(c\right)$ and $\overline{\mathrm{\Omega }}\left(c\right)$ for the latter coincide over the whole c range, whereas for PVP360k, they diverge from each other at all but the lowest c.

Newtonian Propulsion.

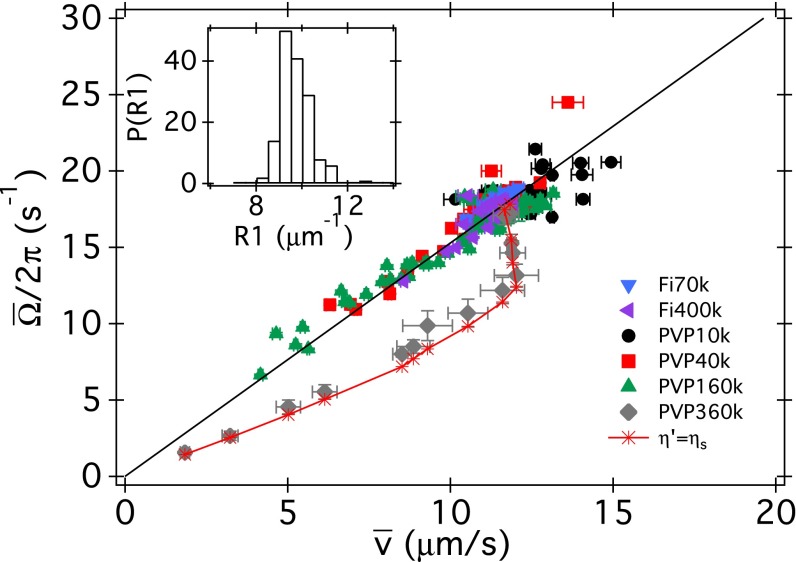
To observe $\overline{v}\left(c\right)/{\overline{v}}_0=\overline{\mathrm{\Omega }}\left(c\right)/{\overline{\mathrm{\Omega }}}_0$ (Fig. 2 B–D) we require $\overline{v}\propto \overline{\mathrm{\Omega }}$, i.e., that Eq. 6 should be valid. This proportionality is directly confirmed by Fig. 3: data for PVP10k, 40k, and 160k collapse onto a single master proportionality at all concentrations. Data for two dialyzed Ficolls also fall on the same master line. The good data collapse shows that there is only very limited sample-to-sample variation in the average body and flagellar geometry, which are the sole determinants of $R_1$ in Eq. 6. The slope of the line fitted to all of the data gives $R_1\approx 9.6\hspace{0.17em}\mu {\mathrm{m}}^{-1}$ (compare $\approx 7\hspace{0.17em}\mu {\mathrm{m}}^{-1}$ in ref. 24). The constancy of the ratio $R_1=\overline{\mathrm{\Omega }}/\overline{v}$ is also be seen from the strongly peaked distribution of this quantity calculated from all individual pairs of $\overline{v}\left(c\right)$ and $\overline{\mathrm{\Omega }}\left(c\right)$ values except those for PVP360k (Fig. 3, Inset). Physically, $R_1$ is an inverse cell body processivity, i.e., on average a bacterium swims forward a distance $R_1^{-1}\approx 0.1\hspace{0.17em}\mu \mathrm{m}$ per body revolution.

Fig. 3.

Mean rotational frequency $\overline{\mathrm{\Omega }}/2\pi$ vs. swimming speed $\overline{v}$ for dialyzed PVP and Ficoll solutions at molecular weights as indicated (there are at least two datasets per each PVP and one dataset for each Ficoll). The line is a linear fit to all data (except PVP360k), giving $R_1=9.6\pm 0.1\hspace{0.17em}\mu {\mathrm{m}}^{-1}$ in Eq. 6. (Inset) Probability distribution of $R_1$ for all datasets except PVP360k. The diamonds are for PVP360k averaged over two datasets with the errors bars being SDs. The stars linked by the full curve are the predicted $\mathrm{\Omega }\left(v\right)$ for PVP360k, according to a model in which the body experiences the full low-shear viscosity of the polymer solution, and the flagella experiences the viscosity of pure buffer, ${\eta }_s$.

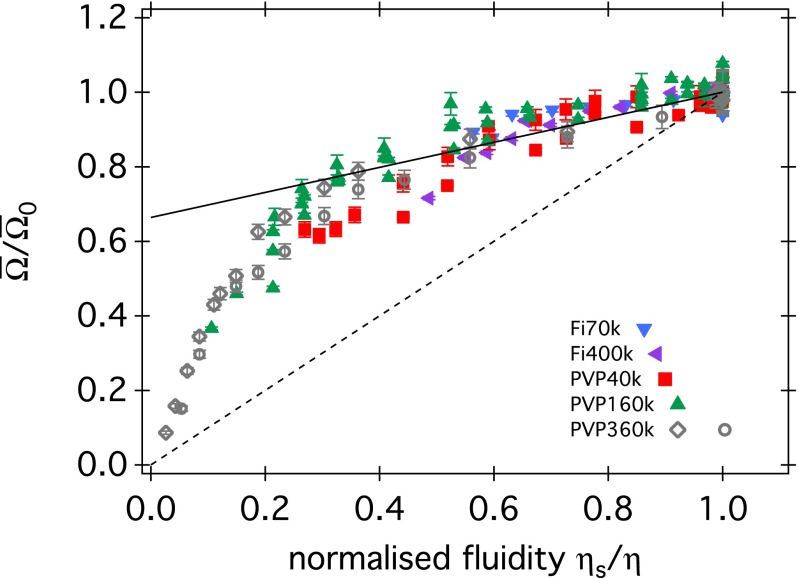
The implication of Fig. 3 is that swimming E. coli sees all our polymer solutions except PVP360k as Newtonian fluids. Interestingly, BT cited the proportionality between Ω and ${\eta }^{-1}$ (rather than Ω and v) as evidence of Newtonian behavior in Ficoll. We show the dependence of body rotation speed normalized by its value at no added polymer, $\overline{\mathrm{\Omega }}/{\overline{\mathrm{\Omega }}}_0$, on the normalized fluidity ${\eta }_s/\eta$ (where ${\eta }_s$ is the viscosity of the solvent, i.e., buffer) for our four PVPs and two Ficolls in Fig. 4, together with the lines used by BT to summarize their MC and Ficoll data. Our data and BT’s MC results (which span $0.2\mathrm{\lesssim }{\eta }_s/\eta <1$) cluster around a single master curve, which, however, is not a simple proportionality. Eqs. 10a and 10b together predict such nonlinear data collapse, provided that the cell body geometry, $\left(a,b\right)$, and the motor characteristics, $\left(N_0,{\mathrm{\Omega }}^c,{\mathrm{\Omega }}^{\max }\right)$, remain constant between datasets. The larger data scatter in Fig. 4 compared with Fig. 3 suggests somewhat larger variations in motor characteristics than in geometry between samples.*

Fig. 4.

Relative rotational body speed $\overline{\mathrm{\Omega }}/\overline{{\mathrm{\Omega }}_0}$ vs. fluidity $\left(1/\eta \right)$, normalized to the fluidity of the motility buffer (c = 0), for all polymer solutions we studied. Full and dashed lines are those used by BT to summarize their MC and Ficoll data, respectively. BT’s MC data spanned a smaller interval $\left(0.2\lesssim {\eta }_s/\eta <1\right)$ than ours.

Of all of the polymers contributing to Fig. 4, PVP360k gave the most extensive coverage over the whole range of fluidity (Fig. 5).^† Eqs. 10a and 10b apply to the low and high fluidity regimes of these data, respectively. Eq. 10a depends on a single motor parameter, $N_0$, and predicts a strict proportionality. Our lowest fluidity data points suggest that at the highest polymer concentrations reached, we are indeed operating in this regime. Using $a=1.2\hspace{0.17em}\mu \mathrm{m}$ and $b=0.43\hspace{0.17em}\mu \mathrm{m}$ (average values from microscopy) to fit Eq. 10a to the lowest fluidity data gives $N_0=1,450\pm 50$ pN⋅nm (Fig. 5, blue), which agrees well with previously measured stall torque (19).

Fig. 5.

Body rotation frequency vs. fluidity averaged over all PVP360k datasets. Blue line, fitting the constant-torque result, Eq. 10a, in the range $0\hspace{0.17em}\mathrm{\lesssim }\hspace{0.17em}\eta \hspace{0.17em}\mathrm{\lesssim }\hspace{0.17em}0.15\hspace{0.5em}\mathrm{c}{\mathrm{P}}^{-1}$. Pink curve, fitting the linear-torque result, Eq. 10b, in the range $\eta \hspace{0.17em}\mathrm{\gtrsim }\hspace{0.17em}0.2\hspace{0.5em}\mathrm{c}{\mathrm{P}}^{-1}$. The thickness of the line/curve indicates uncertainties associated with choosing the boundary between the two kinds of behavior. (Inset) Log-log plot to show that Eq. 10b alone does not fit the data.

The majority of the data away from the lowest fluidities are clearly nonlinear and need to be fitted with Eq. 10b. Doing so with the above value of $N_0$ gives ${\overline{\mathrm{\Omega }}}^c/2\pi =6.6\pm 0.5\hspace{0.5em}{\mathrm{s}}^{\mathrm{-}1}$ and ${\overline{\mathrm{\Omega }}}^{\max }/2\pi =20.5\pm 0.5\hspace{0.5em}{\mathrm{s}}^{\mathrm{-}1}$ (Fig. 5, pink). Given that $\mathrm{\Omega }\propto {\omega }_m$ (Eq. 7), we expect ${\mathrm{\Omega }}^{\max }/{\mathrm{\Omega }}^c={\omega }_m^{\max }/{\omega }_m^c$. Our ratio of ${\overline{\mathrm{\Omega }}}^{\max }/{\overline{\mathrm{\Omega }}}^c\approx 3.1$ compares reasonably with ${\omega }_m^{\max }/{\omega }_m^c\approx 2.3$ for a different strain of E. coli at the same temperature (22 °C) (19).

Thus, Eqs. 10a and 10b give a reasonable account of the data in Fig. 5. We conclude that PVP360k solution is Newtonian as far as body rotation is concerned.

Non-Newtonian Effects and Flagella Nano-Rheology.

Given the above conclusion, the nonlinear $\overline{\mathrm{\Omega }}\left(\overline{v}\right)$ for PVP360k (Fig. 3) suggests a non-Newtonian response at the flagellum. In a minimal model, the flagellum “sees” a different viscosity, ${\eta }^{\prime }\left(c\right)$, than the cell body, which simply experiences the low-shear viscosity of the polymer solution, $\eta \left(c\right)$. Making explicit the viscosity dependence of the resistive coefficients in Eqs. 2 and 3 by writing $A=\widehat{a}\eta$, etc., force and torque balance now read

$$\eta \hspace{0.17em}{\widehat{a}}_0\hspace{0.17em}v={\eta }^{\prime }\left(-\widehat{a}\hspace{0.17em}v+\widehat{b}\hspace{0.17em}\omega \right),$$ [11]

$$\eta \hspace{0.17em}{\widehat{d}}_0\hspace{0.17em}\mathrm{\Omega }={\eta }^{\prime }\left(-\widehat{b}\hspace{0.17em}v+\widehat{d}\hspace{0.17em}\omega \right).$$ [12]

Solving these gives

$$\frac{\mathrm{\Omega }}{v}=\frac{\widehat{d}\left[\left(\frac{\eta }{{\eta }^{\prime }}\right){\widehat{a}}_0+\widehat{a}\right]-{\widehat{b}}^2}{\left(\frac{\eta }{{\eta }^{\prime }}\right){\widehat{d}}_0\widehat{b}}.$$ [13]

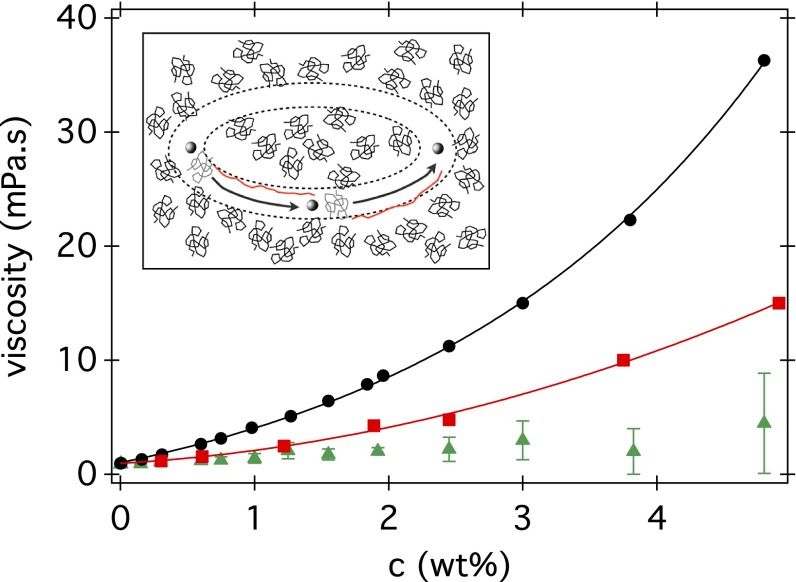
Eq. 11 makes an interesting prediction. If we take ${\eta }^{\prime }\left(c\right)={\eta }_s$ and use previously quoted flagellum dimensions for E. coli (24) to calculate $\left({\widehat{a}}_0,{\widehat{d}}_0;\widehat{a},\widehat{b},\widehat{d}\right)$, it predicts nearly perfectly the observed nonlinear $\overline{\mathrm{\Omega }}\left(\overline{v}\right)$ relationship for PVP360k (Fig. 3). Details are given in SI Text, where we also predict the observed peak in $\overline{v}\left(c\right)$ (Fig. 2 and Fig. S7). To check consistency, we proceed in reverse and treat the flagellum as a nano-rheometer. Given the measured $\overline{v}\left(c\right)$ in PVP360k, we deduce the viscosity seen by the flagellum, ${\eta }^{\prime }\left(c\right)$, at shear rate $\dot{\gamma }\approx {10}^4\hspace{0.17em}{\mathrm{s}}^{-1}$ (SI Text and Fig. 6). In Fig. 6 we also show the low-shear viscosity of PVP360k solutions measured using conventional rheometry. Indeed, over most of the concentration range, we find ${\eta }^{\prime }\approx {\eta }_s$. (Note that the highest c data points are subject to large uncertainties associated with measuring very low swimming speeds.) Thus, our data are consistent with the flagellum seeing essentially just the viscosity of the pure solvent (buffer). Macroscopically, this corresponds to extreme shear thinning. Is this a reasonable interpretation?

Fig. 6.

Viscosities of PVP360k solutions: low-shear values from rheometry (filled circle); microrheology data obtained using 980-nm beads at 10⁴ Hz (red square); and ${\eta }^{\prime }$ deduced from swimming data (green triangle). Lines are best fits (SI Text). (Inset) Schematic showing three snapshots of a section of a flagellum (sphere, $\approx 40\hspace{0.5em}\mathrm{nm}$) cutting through a solution of polymer coils ($\approx 120\hspace{0.17em}\mathrm{nm}$) (with a circular path). Coils, which are initially in the path of the flagellum section (gray), become stretched out (red), leaving a coil-sized channel of solvent.

For a helical flagellum of thickness d and diameter D rotating at angular frequency ω, the local shear rate is ${\dot{\gamma }}_f\sim \omega D/d$ (we neglect translation because $v\ll \omega D$). For an E. coli flagellar bundle, $d\approx 40\hspace{0.5em}\mathrm{nm}$, $D\approx 550\hspace{0.5em}\mathrm{nm}$, and $\omega \approx 2\pi \times 115\hspace{0.5em}\mathrm{rad}/\mathrm{s}$ (24), giving ${\dot{\gamma }}_f\mathrm{\lesssim }{10}^4\hspace{0.17em}{\mathrm{s}}^{\mathrm{-}1}$ in the vicinity of the flagellum. The Zimm relaxation time of a polymer coil is ${\tau }_Z\sim 4\pi {\eta }_s{r}_g^3/k_{B}T$, where $k_{B}T$ is the thermal energy. Using ${\eta }_s={10}^{-3}\hspace{0.5em}\mathrm{Pa\cdot s}$ and $r_g\sim 60\hspace{0.5em}\mathrm{nm}$, we find ${\tau }_Z\sim 1\hspace{0.5em}\mathrm{ms}$ for our PVP360k at room temperature. Because ${\mathrm{\Omega }}^{-1}\gg {\tau }_Z$, the cell body does not perturb significantly the polymer conformation. However, ${\dot{\gamma }}_f^{-1}\sim 0.1{\tau }_Z$, so that the polymer may be expected to shear thin in both dilute $\left(c<c^{\mathrm{\ast }}\right)$ (25) and semidilute $\left(c\hspace{0.17em}\mathrm{\gtrsim }\hspace{0.17em}{c}^{\mathrm{\ast }}\right)$ (26) solutions. Low-shear rate data collected using rheometry and high-frequency microrheological data collected using 1-μm beads and interpreted using the Cox–Merz rule (27) (see SI Text for details) show that there is indeed significant shear thinning of our PVP360k polymer (Fig. 6 and Fig. S8), although not as extreme as thinning down to ${\eta }_s$.

Anisotropic elastic stresses (9–11, 13) and shear thinning (28, 29) have been proposed before as a possible cause of non-Newtonian effects in biological swimmers. However, in the usual sense, these are continuum concepts arising from experiments on the millimeter (rheometry) or micrometer (microrheology) scale. Neither is obviously applicable to an ∼40-nm segment of flagellum moving through somewhat larger polymer coils $\left(r_g\sim 60\hspace{0.5em}\mathrm{nm}\right)$. One of the very few explorations of the …probe ∼ polymer size regime to date found a highly nonlinear time dependent response with a shear-thinning steady state that matched bulk rheometry data, albeit with quite stiff polymers (λ-phage DNA) (30). The relevant physics may be similar to, but perhaps more complex than, the active microrheology of colloidal suspensions using probes that are approximately the same size as the colloids (31). A qualitative picture (Fig. 6, Inset) may be as follows. A section of the flagellum traveling at $\omega D/2\sim 200\hspace{0.17em}\mu \text{m}/\text{s}$ takes $\sim 0.3{\tau }_Z$ to traverse $\sim r_g$. Thus, polymer coils in its vicinity are strongly stretched as quasi-stationary objects and the flagellum effectively carves out an $\sim 2r_g$-wide channel practically void of polymers. Each flagellum section revisits approximately the same spatial location with a period $2\pi /\omega \sim 10\hspace{0.5em}\mathrm{ms}$ (because the translation per turn is low). Although this time is larger than the single chain relaxation time ${\tau }_Z$, the time required for collective relaxation and diffusion of a large number of strongly stretched polymer chains is significantly larger than that. Effectively, then, the flagellum moves inside a channel with viscosity $\to {\eta }_s$. Moreover, under strong local elongation of the kind we suggested, it is also possible that polymers may break (32). This separate, but related, mechanism could change the mechanical properties of the solution around the flagellum.

We note that previous experiments of E. coli swimming in MC (15, 33) used polymers and worked in concentration regimes where shear thinning effects are insignificant. There is already indirect evidence of this in Fig. 4, where data from BT (15) collapse onto a Newtonian master curve for $\overline{\mathrm{\Omega }}\left({\eta }^{-1}\right)$. More directly, these previous studies used methyl celluloses with viscosity grade around 4,000 cP in the range of 0–0.3 wt.% (15) and at 0.18 wt.% (33). The shear thinning of such polymers has been measured (polymer AM4 in ref. 34) and fitted to a power law: $\eta \sim {\dot{\gamma }}^{n-1}$; at c = 0.25 wt.% and 0.5 wt.%: $n=1.00$ and 0.961, respectively. Thus, at the concentrations used before (15, 33), shear thinning is very weak or absent, and the solutions behave as Newtonian.

Summary and Conclusions

We measured the average swimming speed and cell body rotation rate in populations of E. coli bacteria swimming in different concentrations of solutions of the linear polymer PVP (nominal molecular weights of 10, 40, 160, and 360 kDa, these probably were number-averaged values) and the branched polymer Ficoll (70 and 400 kDa). We dialyzed each polymer to remove small-molecular impurities that can be metabolized by the cells to increase their swimming speed. The collapse of data for all polymers except PVP360k onto a single proportionality relationship between swimming speed and body rotation rate, $\overline{\mathrm{\Omega }}\left(\overline{v}\right)$ (Fig. 3), demonstrates that these solutions behave as Newtonian fluids as far as E. coli propulsion is concerned.

Significant nonlinearities in $\overline{\mathrm{\Omega }}\left(\overline{v}\right)$ were found for E. coli swimming in PVP360k solutions. Further analysis showed that the motion of the cell body remained Newtonian: the measured $\overline{\mathrm{\Omega }}\left({\eta }^{-1}\right)$ can be fitted to results derived from Newtonian hydrodynamics (Eqs. 10a and 10b; Fig. 5). Thus, there must be non-Newtonian effects at the flagellum. The observed deviations from Newtonian behavior can be quantitatively accounted for by a simple model in which the flagellum sees the viscosity of pure buffer. This result is consistent with significant shear thinning observed at the micrometer level in PVP360k solutions using microrheology, although we suggest that molecular effects must be taken into account because the polymer and flagellum filament have similar, nanometric dimensions. The effects we are considering, which arise from high shear rates, are absent from experiments using macroscopic helices as models for viscoelastic flagella propulsion (13).

Shear thinning is not the only possible effect in the vicinity of a flagellum creating local deformation rates of $\sim {10}^4\hspace{0.5em}{\text{s}}^{-1}$. Higher-molecular-weight polymers that are more viscoelastic than PVP 360 kDa will show significant elastic effects. Interestingly, it is known that double-stranded DNA could be cut at a significant rate at $\dot{\gamma }\sim {10}^4\hspace{0.5em}{\mathrm{s}}^{\mathrm{-}1}$ (35). An E. coli swimming through a high-molecular-weight DNA solution should therefore leave behind a trail of smaller DNA and therefore of lower-viscosity solution, making it easier for another bacterium to swim in the wake. The latter may have important biomedical implications: the mucosal lining of normal mammalian gastrointestinal tracks and of diseased lungs can contain significant amounts of extracellular DNA. Exploration of these issues will be the next step in seeking a complete understanding of flagellated bacterial motility in polymeric solution.

Materials and Methods

Cells.

We cultured K12-derived WT E. coli strain AB1157 as previously detailed (21, 22). Briefly, overnight cultures were grown in Luria-Bertani (LB) broth using a shaking incubator at 30 °C and shaking speed of 200 rpm. A fresh culture was inoculated as 1:100 dilution of overnight grown cells in 35 mL tryptone broth (TB) and grown for 4 h (to late exponential phase). Cells were washed three times with motility buffer (MB, pH = 7.0, 6.2 mM K₂HPO₄, 3.8 mM KH₂PO₄, 67 mM NaCl, and 0.1 mM EDTA) by careful filtration (0.45-μm HATF filter; Millipore) to minimize flagellar damage and were resuspended in MB to variable cell concentrations.

Polymers.

Native.

PVP and Ficoll from Sigma-Aldrich were used at four (10, 40, 160, and 360 kDa) and two (70 and 400 kDa) nominal molecular weights, respectively. Polymer stock solutions were prepared and diluted with MB.

Dialysis.

The polymer stock solutions were dialyzed in tubes with 14-mm-diameter and 12-kDa cutoff (Medicell International) against double-distilled water. The dialysis was performed over 10 d with daily exchange of the water. The final polymer concentration was determined by measuring the weight loss of a sample during drying in an oven at 55 °C and subsequent vacuum treatment for 6 h. Polymer solutions at several concentration were prepared by dilution using MB.

Motility Measurement.

Bacterial suspensions were gently mixed with the polymer solutions to a final cell density of $\approx 5\times {10}^8\hspace{0.17em}\mathrm{cells}/\mathrm{mL}$. An $\approx 400‐\mu \mathrm{m}$-deep flat glass sample cell was filled with $\approx 150\hspace{0.5em}\mu \text{L}$ of suspension and sealed with petroleum jelly to prevent drift. Immediately after, two movies, one in phase-contrast illumination (∼40 s long, Nikon Plan Fluor 10×Ph1 objective, NA = 0.3, Ph1 phase-contrast illumination plate at 100 frames/s and 500² pixels) and one in dark-field illumination (∼10 s long, Nikon Plan Fluor 10×Ph1 objective, NA = 0.3, Ph3 phase-contrast illumination plate, either 500 or 1,000 frames/s, 500² pixels) were consecutively recorded on an inverted microscope (Nikon TE300 Eclipse) with a Mikrotron high-speed camera (MC 1362) and frame grabber (Inspecta 5, 1-Gb memory) at room temperature $\left(22\pm 1{\hspace{0.17em}}^{°}\mathrm{C}\right)$. We image at 100 μm away from the bottom of the capillary to avoid any interaction with the glass wall.

We measured the swimming speed from the phase contrast movies using the method of DDM as detailed previously (21, 22). The dark field movies were analyzed to measure the body rotation speed using the method of DFM, in which we Fourier transform the power spectrum of the flickering image of individual cells, and identify the lowest frequency peak in the average power spectrum (Fig. S9) as the body rotation frequency as in previous work (24, 36); the difference here is that DFM is a high-throughput method (SI Text).

Rheology.

We measured the low-shear viscosity η of polymer solutions using a TA Instruments AR2000 rheometer in cone-plate geometry (60 cm, 0.5°). Passive microrheology was performed using diffusing wave spectroscopy in transmission geometry with 5-mm-thick glass cuvettes. The setup (LS Instruments) uses an analysis of the measured mean square displacement (MSD) of tracer particles as detailed previously (37). Tracer particles (980-nm-diameter polystyrene) were added to the samples at 1 wt% concentration. The transport mean free paths $l^{\mathrm{\ast }}$ of the samples were determined by comparing the static transmission to a reference sample (polystyrene with 980 nm diameter at 1 wt% in water). The shear rate-dependent viscosity η was obtained from the frequency dependent storage and loss moduli using the Cox–Merz rule (27).