The origin of risk aversion

Significance

Risk aversion is one of the most widely observed behaviors in the animal kingdom; hence, it must confer certain evolutionary advantages. We confirm this intuition analytically in a binary-choice model of decision-making—risk aversion emerges from mindless decision-making as the evolutionarily dominant behavior in stochastic environments with correlated reproductive risk across the population. The simplicity of our framework suggests that our results are likely to apply across species. From a policy perspective, our results underscore the importance of addressing systematic risk through insurance markets, capital markets, and government policy. However, our results also highlight the potential dangers of sustained government intervention, which can become a source of systematic risk in its own right.

Abstract

Risk aversion is one of the most basic assumptions of economic behavior, but few studies have addressed the question of where risk preferences come from and why they differ from one individual to the next. Here, we propose an evolutionary explanation for the origin of risk aversion. In the context of a simple binary-choice model, we show that risk aversion emerges by natural selection if reproductive risk is systematic (i.e., correlated across individuals in a given generation). In contrast, risk neutrality emerges if reproductive risk is idiosyncratic (i.e., uncorrelated across each given generation). More generally, our framework implies that the degree of risk aversion is determined by the stochastic nature of reproductive rates, and we show that different statistical properties lead to different utility functions. The simplicity and generality of our model suggest that these implications are primitive and cut across species, physiology, and genetic origins.

Risk aversion is one of the most fundamental properties of human behavior. Ever since pioneering work by Bernoulli (1) on gambling and the St. Petersburg Paradox in the 17th century, considerable research has been devoted to understanding human decision-making under uncertainty. Two of the most well-known theories are expected utility theory (2) (an axiomatic formulation of rational behavior under uncertainty) and prospect theory (3) (a behavioral theory of decision-making under uncertainty). Several measures of risk aversion have been developed, including curvature measures of utility functions (4, 5), human subject experiments and surveys (6, 7), portfolio choice for financial investors (8), labor–supply behavior (9), deductible choices in insurance contracts (10, 11), contestant behavior on game shows (12), option prices (13), and auction behavior (14).

Despite its importance and myriad applications in the past several decades, few economists have addressed the question: where does risk aversion come from? Biologists and ecologists have documented risk aversion in nonhuman animal species—often called risk-sensitive foraging behavior—ranging from bacteria to primates (15–19). Recently, the neural basis of risk aversion has also received much attention, because researchers discovered that the activity of a specific brain region correlates with risk-taking and risk-averse behavior (20–22).

Evolutionary principles have been applied by economists to a variety of economic behaviors and concepts, including altruism (23, 24), the rate of time preference (25), and utility functions (26–29)^†. In particular, Robson (26) proposes an evolutionary model of risk preferences, in which he assumes an increasing concave relation between an individual’s number of offspring and the amount of resources available to that individual, and given this concave “biological production function,” Robson (26) shows that expected utility arises from idiosyncratic environmental risk and that nonexpected utility arises from systematic risk. In the context of financial markets, evolutionary models have also been proposed to capture market selection (30) and the geometric mean principle or Kelly criterion (31). Additionally, as an alternative to the traditional view that markets are always and everywhere efficient and that “prices fully reflect all possible information” (32, 33), the Adaptive Markets Hypothesis (34) provides an evolutionary perspective of financial markets.

More recently, Brennan and Lo (35) have proposed a binary-choice model that provides an evolutionary framework for generating a variety of behaviors that are considered anomalous from the perspective of traditional economic models (i.e., loss aversion, probability matching, and bounded rationality). In this framework, natural selection yields standard risk-neutral optimizing economic behavior when reproductive risk is idiosyncratic (i.e., uncorrelated across individuals within a given generation). However, when reproductive risk is systematic (i.e., correlated among individuals within a given generation), some seemingly irrational behaviors, such as probability matching and loss aversion, become evolutionarily dominant.

In this paper, we extend the binary-choice model (35) and focus on the origin of utility and risk aversion. We show that risk aversion emerges as a consequence of systematic risk and that risk neutrality emerges as a consequence of idiosyncratic risk, regardless of the species and without the need for any biological production function—concave or otherwise. This result suggests that the degree and type of risk aversion are determined by the stochastic nature of reproductive risk, and we show how different environments lead to different stable utility functions over time. This approach provides an alternate and more fundamental explanation of risk aversion, and the fact that our results do not depend on any exogenously specified production function suggests that risk aversion is a much more primitive feature of all organisms. Moreover, the simplicity of our framework and the direct relation between reproductive success and risk aversion provide an equally simple explanation for the large amount of heterogeneity in risk aversion observed in empirical studies (7–11): variation in the amount of systematic risk in reproductive success.

When applied to economic contexts, our results imply a link between the expected returns of risky assets, such as equities, and systematic reproductive risk, which in turn, is correlated with aggregate financial risk. This relation is consistent with the well-known equilibrium risk/reward tradeoff first proposed by Sharpe (36). However, our theoretical derivation of this relation does not depend on preferences or general equilibrium and is solely a consequence of natural selection under systematic reproductive risk.

Our model consists of an initial population of individuals, each assigned a purely arbitrary behavior with respect to a binary-choice problem, and it is assumed that offspring behave in an identical manner to their parents. Therefore, those behaviors leading to greater reproductive success will lead to higher growth rates and become more representative in the general population. Environments with different types of reproductive risks will lead to different optimal behaviors, and in the limit, only certain types of behaviors—corresponding to specific types of preferences or utility functions—will survive in such environments.

By studying the impact of selection on behavior rather than genes, we are able to derive evolutionary implications that cut across species, physiology, and genetic origins. In the same way that different magnifications of a microscope reveal different details of a specimen, applying evolutionary principles to behavioral variations leads to different insights that may be more relevant for economics, psychology, and behavioral ecology. Our focus on behavior as the object of selection is a different lens through which the effects of evolution may be studied.

The Binary-Choice Model

Consider individuals that live for one period, produce a random number of offspring asexually, and then die. During its life (we use the pronoun it, because the individual need not be human), individual i makes only one decision: choose one of two possible actions, a and b, which results in one of two corresponding random numbers of offspring, $x_{a,i}$ and $x_{b,i}$. These two random variables summarize the impact of the environment on the reproductive success of the individual, and they are assumed to be the weighted sum of two components:

$$\{\begin{array}{l}{x}_{a,i}=\lambda z_a+\left(1-\lambda \right)y_{a,i}\\ x_{b,i}=\lambda z_b+\left(1-\lambda \right)y_{b,i}.\end{array}$$ [1]

The first component of the weighted sum, $\left(z_a,z_b\right)$, is assumed to be independently and identically distributed over time and identical for all individuals in a given generation; hence, we refer to it as systematic risk, because one individual experiences the same reproductive outcome as others that choose the same action. The second component, $\left(y_{a,i},y_{b,i}\right)$, is assumed to be independently and identically distributed both over time and across individual i in a given generation; hence, we refer to it as idiosyncratic. Both components are described by some well-behaved probability distributions (SI Appendix), and λ is a real number between zero and one.

Each individual chooses a with some probability $f\in \left[\mathrm{0,1}\right]$ and b with probability $1-f$. We shall henceforth refer to f as the individual’s behavior, because it completely determines how the individual chooses between a and b. Note that f can be zero or one; hence, we are not requiring individuals to randomize, although randomization will be derived as a consequence of natural selection under certain conditions. Denoted by $x_i^f$ is the random number of offspring produced by individual i of type f; then, $x_i^f=I_i^f{x}_{a,i}+\left(1-I_i^f\right)x_{b,i}$, where $I_i^f$ is the Bernoulli random variable that equals 1 with probability f and 0 otherwise.

Furthermore, offspring behave in a manner identical to their parents (i.e., they choose between a and b according to the same f); hence, the population may be viewed as being segmented into groups of distinct type f. This assumption is tantamount to assuming perfect genetic transmission of traits from one generation to the next, which provides a clearer analysis of the interaction between natural selection and the stochastic properties of reproduction implicit in the environment. However, mutation can easily be incorporated into this framework at the expense of analytical simplicity (37). We also assume that the initial population contains an equal number of all types, and we normalize this common initial population to be one for each type without loss of generality.

We wish to emphasize the difference between reproductive success with systematic $\left(z_a,z_b\right)$ and idiosyncratic $\left(y_{a,i},y_{b,i}\right)$ risk, which points to the central role that systematic risk plays in shaping the evolution of behavior and preferences. In the case of systematic risk, the number of offspring is given by the same two random variables, $\left(z_a,z_b\right)$, for all individuals. If two individuals choose the same action a, both will generate the same number of random offspring $z_a$ (i.e., their reproductive success is perfectly correlated). In this sense, fecundity is systematic. However, for $\left(y_{a,i},y_{b,i}\right)$, the randomness in the number of offspring is strictly idiosyncratic in the sense that the correlation between the number of offspring for two individuals i and j is zero, even if both individuals choose the same course of action. Idiosyncratic fecundity implies that, even if all individuals in a given population choose the same action, there will still be considerable cross-sectional variability in the number of offspring produced in any generation.

Using Eq. 1, we can rewrite $x_i^f$ as a combination of systematic and idiosyncratic risks:

$$x_i^f=\lambda z_i^f+\left(1-\lambda \right)y_i^f,$$

where

$$\{\begin{array}{l}{z}_i^f=I_i^f{z}_a+\left(1-I_i^f\right)z_b\\ y_i^f=I_i^f{y}_{a,i}+\left(1-I_i^f\right)y_{b,i}.\end{array}$$

The coefficient $\lambda \in \left[\mathrm{0,1}\right]$ indicates the proportion of systematic risk in the environment. When $\lambda =1$, all reproductive risk is systematic; when $\lambda =0$, all reproductive risk is idiosyncratic, and when $0<\lambda <1$, both types of risk are present. In a particular environment described by λ, the total number of offspring of type f in generation T is denoted by $n_T^f$. It is easy to show that the average of the log population $T^{-1}\log n_T^f$ converges in probability to the log geometric average growth rate:

$${\alpha }_{\lambda }\left(f\right)={\mathbb{E}}_z\left[\log \left(\lambda z^f+\left(1-\lambda \right){\mathbb{E}}_y\left[y^f\right]\right)\right],$$ [2]

where ${\mathbb{E}}_z$ denotes the expectation taken with respect to $z^f$, and ${\mathbb{E}}_y$ denotes the expectation taken with respect to $y^f$. Eq. 2 can also be written as

$${\alpha }_{\lambda }\left(f\right)={\mathbb{E}}_z\left[\text{log}\left(f{\omega }_a^{\lambda }+\left(1-f\right){\omega }_b^{\lambda }\right)\right],$$ [3]

where

$$\{\begin{array}{l}{\omega }_a^{\lambda }=\lambda z_a+\left(1-\lambda \right){\mathbb{E}}_y\left[y_a\right],\\ {\omega }_b^{\lambda }=\lambda z_b+\left(1-\lambda \right){\mathbb{E}}_y\left[y_b\right].\end{array}$$

Maximizing Eq. 3 yields the evolutionarily dominant or growth-optimal behavior in environment-λ (35):

$$f_{\lambda }^{\mathrm{\ast }}=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_a^{\lambda }/{\omega }_b^{\lambda }\right]>1\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_b^{\lambda }/{\omega }_a^{\lambda }\right]<1\hfill \\ \text{solution}\hspace{0.17em}\text{to}\hspace{0.17em}\left(5\right)\hfill & \text{if}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_a^{\lambda }/{\omega }_b^{\lambda }\right]\ge 1\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_b^{\lambda }/{\omega }_a^{\lambda }\right]\ge 1\hfill \\ 0\hfill & \text{if}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_a^{\lambda }/{\omega }_b^{\lambda }\right]<1\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbb{E}}_z\left[{\omega }_b^{\lambda }/{\omega }_a^{\lambda }\right]>1,\hfill \end{array}$$ [4]

where $f_{\lambda }^{\mathrm{\ast }}$ is defined implicitly in the second case of Eq. 4 by

$$0={\mathbb{E}}_z\left[\frac{{\omega }_a^{\lambda }-{\omega }_b^{\lambda }}{f{\omega }_a^{\lambda }+\left(1-f\right){\omega }_b^{\lambda }}\right].$$ [5]

The three possible behaviors described in Eq. 4 reflect the relative reproductive success of the two choices. Choosing a deterministically will be optimal if choice a exhibits unambiguously higher expected relative fecundity; choosing b deterministically will be optimal if the opposite is true. Randomizing between a and b will be optimal if neither choice has a clear-cut reproductive advantage. This last outcome is perhaps the most counterintuitive, because it is suboptimal from an individual’s perspective (35).

When $\lambda =0$ (pure idiosyncratic risk), the optimal behavior $f^{\mathrm{\ast }}$ can only be 0 or 1, corresponding to purely deterministic choice. In this case, the individually optimal choice—to select the action that yields the highest expected number of offspring—coincides with the evolutionarily dominant strategy (SI Appendix has additional discussion and examples). However, when $\lambda >0$ (a portion of reproductive risk is systematic), the evolutionarily dominant behavior $f^{\mathrm{\ast }}$ can be between 0 and 1, in which case individuals exhibit randomizing behavior. Although mixed strategies are well-known in the evolutionary game theory literature (38), those strategies emerge from sophisticated strategic interactions between rational optimizing players—in our framework, randomization is mindless behavior produced solely through natural selection. SI Appendix provides several examples for common distributions of relative fecundity ${\omega }_a^{\lambda }/{\omega }_b^{\lambda }$, and Fig. S1 illustrates how $f^{\mathrm{\ast }}$ depends on the parameters selected for the examples.

Now imagine a large population with individuals who are exposed to different reproductive risks—some individuals are only exposed to idiosyncratic risk ($\lambda =0$), some individuals are only exposed to systematic risk ($\lambda =1$), and some individuals are exposed to a mix of both risks. The same parameters apply to their offspring. These different groups of individuals have different behaviors in terms of Eq. 4 as well as different growth rates.

Individual Preferences

We assume that there exists an objective function $V_{\lambda }\left(z,y\right)$ that describes an individual’s preference, where z represents systematic risk and y represents idiosyncratic risk, in the sense that $\left(z_1,y_1\right)$ is favored over $\left(z_2,y_2\right)$ if and only if $V_{\lambda }\left(z_1,y_1\right)>V_{\lambda }\left(z_2,y_2\right)$. In other words, the individual maximizes $V_{\lambda }\left(z,y\right)$ to determine its choice over random outcomes.

The objective function $V_{\lambda }\left(z,y\right)$ can take any form. For example, $V_{\lambda }\left(z,y\right)={\max }_{z+y}\mathbb{E}\left[U\left(z+y\right)\right]$ corresponds to expected utility that does not distinguish between systematic and idiosyncratic risks. However, some functions will give individuals an evolutionary advantage over others in the population; we derive the evolutionarily dominant function in environments with varying proportions of systematic risk.

When $\lambda =1$, the individual faces only systematic risk. The evolutionarily dominant behavior $f^{\mathrm{\ast }}$ is given by $f^{\mathrm{\ast }}=\arg {\max }_f{\mathbb{E}}_z\left[\text{log}\left(z^f\right)\right]$; hence, the evolutionarily implied individual maximization criterion is

$$V_{\lambda =1}\left(z,y\right)={\mathbb{E}}_z\left[\text{log}\left(z\right)\right].$$

This function is simply the expected log utility of the total number of offspring, which Bernoulli (1) proposed in 1738 to resolve the St. Petersburg Paradox.

When $\lambda =0$, the individual faces only idiosyncratic risk. The dominant behavior $f^{\mathrm{\ast }}$ in this case is given by $f^{\mathrm{\ast }}=\arg {\max }_f\text{log}\left({\mathbb{E}}_y\left[y^f\right]\right)$. Therefore, the evolutionarily implied individual maximization criterion is

$$V_{\lambda =0}\left(z,y\right)={\mathbb{E}}_y\left[y\right].$$

This function is expected linear utility of the total number of offspring. In other words, the optimal criterion for an individual is simply the expected value—individuals are risk neutral in this environment.

In the general case in which $0<\lambda <1$, reproductive risk contains both systematic and idiosyncratic components. The implied individual maximization criterion from the evolutionary perspective is, therefore,

$$V_{\lambda }\left(z,y\right)={\mathbb{E}}_z\left[\text{log}\left(\lambda z+\left(1-\lambda \right){\mathbb{E}}_y\left[y\right]\right)\right].$$ [6]

This objective function does not conform to the traditional expected utility framework, in which the individual’s behavior can be represented as the outcome of a constrained optimization of the expected value of a concave function of the total number of offspring: $\lambda z+\left(1-\lambda \right)y$. The idiosyncratic component gives rise to a linear expectation in y, and the systematic component gives rise to a logarithmic function of z and the expectation in y. Risk aversion emerges as a consequence of systematic risk, and risk neutrality emerges as a consequence of idiosyncratic risk, regardless of the species. This characteristic is a novel implication of natural selection that has not appeared, to our knowledge, in prior studies of human or animal risk preferences. We explore this implication further in the next section.

Risk Aversion and Systematic Risk

From Eq. 6, it is clear that the level of risk aversion is determined by natural selection as a function of the level of systematic risk in the environment. Suppose an individual is faced with a random number of offspring $\lambda z+\left(1-\lambda \right)y$, and $\left(1-\lambda \right)\mu ={\mathbb{E}}_y\left[\left(1-\lambda \right)y\right]$ is the expectation of the idiosyncratic component. As a function of z, Eq. 6 can be written as the expected utility function $V_{\lambda }\left(z,y\right)={\mathbb{E}}_z\left[U_{\lambda ,\mu }\left(z\right)\right]$, where

$$U_{\lambda ,\mu }\left(z\right)=\text{log}\left(\lambda z+\left(1-\lambda \right)\mu \right).$$ [7]

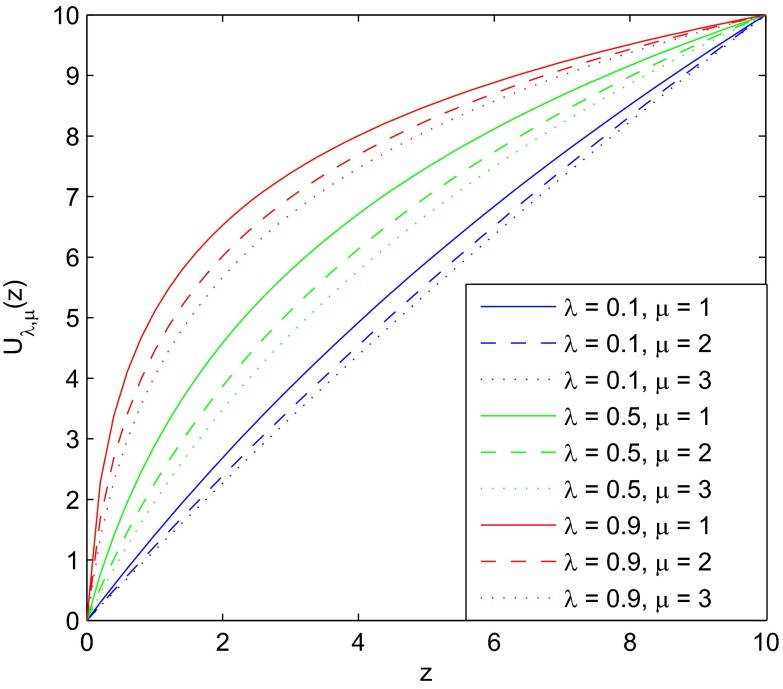
This expression defines a class of utility functions with utility measured as a function of the number of offspring arising from the systematic component. Different amounts of systematic risk in the environment correspond to different evolutionarily dominant utility functions. Fig. 1 shows nine example utility functions with $\lambda =0.1,\hspace{0.17em}0.5,\hspace{0.17em}\text{and}\hspace{0.17em}0.9$ and $\mu =1,\hspace{0.17em}2,\hspace{0.17em}\text{and}\hspace{0.17em}3$. All nine utility functions are normalized by an affine transformation that sets $U_{\lambda ,\mu }\left(0\right)=0$ and $U_{\lambda ,\mu }\left(10\right)=10$.

Fig. 1.

Utility functions implied by environments with different portions of systematic risk and different levels of idiosyncratic risk: $\lambda =0.1$ represents a low level of systematic risk, $\lambda =0.9$ represents a high level of systematic risk, $\mu =1$ represents a low level of idiosyncratic risk, and $\mu =3$ represents a high level of idiosyncratic risk. All nine utility functions are normalized by setting $U_{\lambda ,\mu }\left(0\right)=0$ and $U_{\lambda ,\mu }\left(10\right)=10$.

We can see from Fig. 1 that variation in the proportion (λ) of systematic risk drives the concavity of utility functions, whereas variation in the level of idiosyncratic risk (μ) also plays a role in determining the level of risk aversion. More specifically, we consider the Arrow–Pratt measure of absolute risk aversion of $U_{\lambda ,\mu }(\cdot )$:

$$A_{\lambda ,\mu }\left(z\right)=-\frac{U_{\lambda ,\mu }″\left(z\right)}{U_{\lambda ,\mu }\prime \left(z\right)}=\frac{1}{z+\left(\frac{1}{\lambda }-1\right)\mu },$$ [8]

and the Arrow–Pratt–De Finetti measure of relative risk aversion of $U_{\lambda ,\mu }(\cdot )$:

$$R_{\lambda ,\mu }\left(z\right)=z{A}_{\lambda ,\mu }\left(z\right)=\frac{1}{1+\left(\frac{1}{\lambda }-1\right)\frac{\mu }{z}}\hspace{0.17em}.$$ [9]

As the number of offspring gets larger, absolute risk aversion gets smaller, whereas relative risk aversion gets larger:

$$\{\begin{array}{cc}{A}_{\lambda ,\mu }\left(z_1\right)\ge A_{\lambda ,\mu }\left(z_2\right)& \text{if}\hspace{1em}{z}_1\le z_2,\\ R_{\lambda ,\mu }\left(z_1\right)\le R_{\lambda ,\mu }\left(z_2\right)& \text{if}\hspace{1em}{z}_1\le z_2.\end{array}$$

Moreover, both measures of risk aversion are increasing functions of the proportion-λ of systematic risk:

$$\{\begin{array}{cc}{A}_{{\lambda }_1,\mu }\left(z\right)\le A_{{\lambda }_2,\mu }\left(z\right)& \text{if}\hspace{1em}{\lambda }_1\le {\lambda }_2,\\ R_{{\lambda }_1,\mu }\left(z\right)\le R_{{\lambda }_2,\mu }\left(z\right)& \text{if}\hspace{1em}{\lambda }_1\le {\lambda }_2,\end{array}$$

and decreasing functions of the level of idiosyncratic risk-μ:

$$\{\begin{array}{cc}{A}_{\lambda ,{\mu }_1}\left(z\right)\ge A_{\lambda ,{\mu }_2}\left(z\right)& \text{if}\hspace{1em}{\mu }_1\le {\mu }_2,\\ R_{\lambda ,{\mu }_1}\left(z\right)\ge R_{\lambda ,{\mu }_2}\left(z\right)& \text{if}\hspace{1em}{\mu }_1\le {\mu }_2.\end{array}$$

In other words, risk aversion arises from natural selection in environments with systematic risk. More generally, the degree of risk aversion is determined by the stochastic nature of the environment: the more systematic risk that is in the environment, the more risk averse are the evolutionarily dominant utility functions.

Testable Implications

Although our theory of the evolutionary origin of risk aversion is a highly simplified mathematical caricature of reality, its implications should be empirically verifiable if the theory has captured the most relevant features of decision-making under uncertainty, which we claim. Although formal tests of these implications are beyond the scope of this study, in this section, we describe several methods for conducting such tests to illustrate the potential practical relevance of the theory.

Biology and Behavioral Ecology.

Because the individuals in our theory are not assumed to be intelligent beings—they need not even possess CNSs—the theory’s implications should apply to the full cross-section of the animal kingdom for which risk-sensitive foraging behavior has been observed (15–19). Therefore, one direct test of our theory is to perform controlled experiments on nonhuman animal species, in which the amount of systematic and idiosyncratic reproductive risk is varied and the impact of these variations on behavior is documented and compared with the theory’s predictions (4).

A particularly promising species with which to conduct such experiments is bacteria, which engage in remarkably varied and sophisticated behaviors (19, 39–46). Although an individual bacterium is clearly mindless, colonies of bacteria, such as Paenibacillus vortex, have been observed to engage in seemingly intelligent behavior, such as competition, collaborative foraging, and cell-to-cell chemotactic and physical communication (19). Moreover, this setting most closely matches two key assumptions of our theory: asexual reproduction (bacteria reproduce by binary fission and other forms of cellular division) and no environmental resource constraints (unless purposely imposed by the experimenter).

A direct test of our theory may be constructed by focusing on a simple behavior, such as chemotaxis—cell movement in response to gradients in the concentration of a specific chemical agent, which is usually a food source—and manipulating the environment to generate systematic or idiosyncratic risk. Given the speed with which bacteria reproduce, the growth-optimal chemotactic behavior should be observable within a short timespan. Although such behavior can ultimately be traced to genetic structures (45), our complementary approach of linking behavior directly to reproductive outcomes may yield additional insights into the common evolutionary origins of risk preferences.

Financial Economics.

A less direct test of our theory may be performed by applying statistical inference to retrospective data on human behavior. Although the outcome is likely to be considerably noisier and more difficult to interpret because of the complexity of human cognitive abilities, the simplicity of our evolutionary framework suggests that risk aversion is an extremely primitive adaptation possessed by most animal species. Nevertheless, human evolutionary biology is at odds with several of our theory’s assumptions, including asexual semelparous reproduction and no resource constraints. Moreover, current human lifespans make controlled experiments with human subjects impractical. However, our theory’s growth-optimal behavior may be a reasonable approximation to human decision-making over long timespans, in which case a statistical hypothesis test of the theory can be conducted using historical data involving financial risk and reward. The challenge is to identify scenarios in which human decision-making is driven primarily by this adaptation and no other cognitive mechanisms, such as strategic, cooperative, altruistic, or ethical behaviors, and distinguish between systematic and idiosyncratic reproductive risk in these scenarios.

One possible context is the stock markets of developed economies, which reflect the decisions of many investors facing both systematic and idiosyncratic risks [although we are using these terms in a different sense than Sharpe (36), who focused on systematic and idiosyncratic financial risks, it is not hard to see how this type of risk might be related to reproductive risk over long timespans]. The impact of economy-wide shocks, such as natural disasters, technological hazards, and financial crises, can proxy for systematic risk (47), and low-frequency, high-impact events have been used in the financial economics literature to explain a variety of asset-pricing anomalies, including high equity risk premia, low risk-free rates, and excess volatility in stock returns (48, 49), all of which yield a high level of implied risk aversion in expected utility rational expectations equilibrium models. However, an example of idiosyncratic reproductive risk is infant mortality caused by accidental suffocation (50), preterm birth (51, 52), and congenital malformations (53). Although each of these risks may contain a systematic component (e.g., birth defects caused by environmental pollutants in a given geographical region), this component should become less influential in country-level data.

An indirect hypothesis test of our theory can then be performed by comparing the estimated risk aversion of populations with varying exposures to systematic risk—those populations with greater systematic risk should be more risk averse. Measures of risk aversion can be obtained from several sources, including human subject experiments and surveys (6, 7), portfolio choices for financial investors (8), labor–supply behavior (9), deductible choices in insurance contracts (10, 11), contestant behavior on game shows (12), option prices (13), and auction behavior (14).

By comparing aggregate risk aversion across countries with high and low amounts of systematic reproductive risk, an indirect econometric test of the evolutionary origin of risk aversion may be constructed.

Discussion

Risk aversion is one of the most widely observed behaviors in the animal kingdom; hence, it stands to reason that it must confer certain evolutionary advantages. This intuition is confirmed in our simple but general binary-choice model of behavior, in which risk aversion emerges from mindless behavior as the evolutionarily dominant behavior in stochastic environments with correlated reproductive risk across the population. Our evolutionary framework shows how the stochastic properties of the environment shape preferences, yielding specific utility functions that depend on the nature of reproductive risk. Logarithmic utility and linear utility arise as special cases for the two extremes of pure systematic and idiosyncratic risk, respectively. However, for environments containing a mixture of both types of risk, there is a continuum of evolutionarily dominant behaviors that do not conform to expected utility theory. The simplicity of our framework suggests that our results are likely to apply across species and that the degree of risk aversion in animal behavior is significantly influenced by the stochastic properties of the environment as it affects fecundity.

These results are closely related to but distinct from those in the extant literature on evolution and economic behavior (25, 26, 28–29)^‡. In particular, the seminal paper by Robson (26) on the evolutionary origins of utility functions specifies an increasing concave relation between the number of offspring and the amount of resources available to a given individual, from which the relation between expected/nonexpected utility and systematic/idiosyncratic risk follows naturally. In particular, Robson (26) shows that “properties of risk aversion or risk preference for gambles over commodities derive from a biological production function relating expected offspring to commodities” (ref. 26, p. 405), where this “biological production function” is exogenously specified to be increasing and concave (the concavity hypothesis).

Our model highlights a different and simpler origin of risk aversion—the stochastic nature of the environment—without reference to any biological production function. By developing a formal theory of the evolution of preferences in stochastic environments in the context of the simplest possible nontrivial choice problem (a binary choice), we show that the origin of risk aversion is considerably more primitive than previously thought. Moreover, we derive a class of utility functions that emerges from natural selection as the proportion of systematic risk-λ in the environment that is varied (Eqs. 7, 8, and 9), which may explain the large amount of heterogeneity in risk preferences observed in empirical studies (7–11).

Other studies have also made use of the concavity hypothesis to generate risk aversion (27, 28), and this specification can also be incorporated into our binary-choice framework to yield similar results (35). There is no doubt that the concavity hypothesis provides one explanation for risk aversion, simply because decreasing marginal returns is a common pattern found in nature. However, the economics literature is also replete with examples of nondecreasing marginal returns in both consumption and production. For example, early research on nonconvex preferences (which implies nonconcave utility functions) (54–57) has motivated a large and diverse literature on general equilibrium with nonconvexities [e.g., the Shapley Folkman Lemma (58) that guarantees existence of approximate general equilibria with many consumers]. From the producer perspective, nondecreasing marginal returns have been considered since 1926 (59), giving rise to an extensive literature on monopolies, oligopolies, externalities, and regulatory policy designed to correct such market failures. In fact, the concavity hypothesis is necessarily restrictive in hardwiring, a particular degree of risk aversion (i.e., curvature), after a particular concave function is specified. No single function can explain the large degree of heterogeneity observed in human risk preferences or the state-dependent nature of risk aversion, unless these features are also exogenously specified in multiple time-varying state-dependent biological production functions.

We have purposely avoided the use of any such function, because we wish to highlight the more fundamental role that stochastic environments play in generating risk aversion. Our simple binary-choice framework shows that a concave biological production function is unnecessary for generating risk aversion, which in our setting, is simply a consequence of natural selection operating in stochastic environments with systematic risk, irrespective of any additional functional transformations. Moreover, a byproduct of our simpler framework is a natural explanation for the large heterogeneity in risk preferences observed in empirical studies: natural variation in the proportion of systematic risk across a geographically diverse population. Because our binary-choice model is so simple and because its results follow from a minimal set of assumptions, its implications are likely to apply much more generally across species, time, and contexts.

The evolutionary origins of strategic behavior have also been considered (27, 28), and natural selection can also produce overconfidence (60) and altruism (23), both of which emerge as a result of more complex environmental conditions. In contrast, our framework does not require any strategic interactions, and individual decision-making is deliberately mindless, allowing us to determine the most fundamental links between stochastic environments and adaptive behavior.

Extensions of the binary-choice framework include regime-switching environmental conditions (37), mutation through sexual reproduction (37), resource-constrained environments (which generate strategic interactions), and emergence of intelligent behavior and bounded rationality (61). A recent study^‡ considers an evolutionary framework in continuous time and distinguishes between systematic variations that are instantaneous drops in population size and future shifts in death and birth rates. The former corresponds to the systematic environmental risk in our model, whereas the latter is closely related to extensions to regime-switching environments (37).

Our results have several broader implications for financial economics and public policy. The role of systematic risk in shaping individual and aggregate behavior provides a more fundamental channel through which the relation between systematic financial risk and expected asset returns defined by Sharpe (36) can arise [as long as systematic reproductive risk is positively correlated with systematic financial risk, which is implied by the concave reproduction function described by Robson (26)]. However, unlike the fixed preferences assumed in the Capital Asset Pricing Model by Sharpe (36), our framework implies that preferences vary over time and across environmental conditions; hence, large systematic financial shocks can lead to more risk aversion over time and vice versa.

From a policy perspective, our results underscore the importance of addressing systematic risk through insurance markets, capital markets, and government policy to allow individuals to transfer or mitigate such risks. If not properly managed, systematic risk can lead to increases in risk aversion, implying higher risk premia and borrowing costs and lower economic growth. However, our results also highlight the potential dangers of sustained government intervention, which can become a source of systematic risk in its own right (62, 63).