Abstract
Consider a linear model Y = X β + z, where X = Xn,p and z ~ N(0, In). The vector β is unknown and it is of interest to separate its nonzero coordinates from the zero ones (i.e., variable selection). Motivated by examples in long-memory time series (Fan and Yao, 2003) and the change-point problem (Bhattacharya, 1994), we are primarily interested in the case where the Gram matrix G = X′X is non-sparse but sparsifiable by a finite order linear filter. We focus on the regime where signals are both rare and weak so that successful variable selection is very challenging but is still possible.
We approach this problem by a new procedure called the Covariance Assisted Screening and Estimation (CASE). CASE first uses a linear filtering to reduce the original setting to a new regression model where the corresponding Gram (covariance) matrix is sparse. The new covariance matrix induces a sparse graph, which guides us to conduct multivariate screening without visiting all the submodels. By interacting with the signal sparsity, the graph enables us to decompose the original problem into many separated small-size subproblems (if only we know where they are!). Linear filtering also induces a so-called problem of information leakage, which can be overcome by the newly introduced patching technique. Together, these give rise to CASE, which is a two-stage Screen and Clean (Fan and Song, 2010; Wasserman and Roeder, 2009) procedure, where we first identify candidates of these submodels by patching and screening, and then re-examine each candidate to remove false positives.
For any procedure β̂ for variable selection, we measure the performance by the minimax Hamming distance between the sign vectors of β̂ and β. We show that in a broad class of situations where the Gram matrix is non-sparse but sparsifiable, CASE achieves the optimal rate of convergence. The results are successfully applied to long-memory time series and the change-point model.
Keywords and phrases: Asymptotic minimaxity, Graph of Least Favorables (GOLF), Graph of Strong Dependence (GOSD), Hamming distance, multivariate screening, phase diagram, Rare and Weak signal model, sparsity, variable selection
1 1. Introduction
Consider a linear regression model
| (1.1) |
The vector β is unknown but is sparse, in the sense that only a small fraction of its coordinates is nonzero. The goal is to separate the nonzero coordinates of β from the zero ones (i.e., variable selection). We assume σ, the standard deviation of the noise is known, and set σ = 1 without loss of generality.
In this paper, we assume the Gram matrix
| (1.2) |
is normalized so that all of the diagonals are 1, instead of n as often used in the literature. The difference between two normalizations is non-essential, but the signal vector β are different by a factor of .
We are primarily interested in the cases where
The signals (nonzero coordinates of β) are rare (or sparse) and weak.
The Gram matrix G is non-sparse or even ill-posed (but it may be sparsifiable by some simple operations; see details below).
In such cases, the problem of variable selection is new and challenging.
While signal rarity is a well-accepted concept, signal weakness is an important but a largely neglected notion, and many contemporary researches on variable section have been focused on the regime where the signals are rare but strong. However, in many scientific experiments, due to the limitation in technology and constraints in resources, the signals are unavoidably weak. As a result, the signals are hard to find, and it is easy to be fooled. Partially, this explains why many published works (at least in some scientific areas) are not reproducible; see for example Ioannidis (2005).
We call G sparse if each of its rows has relatively few ‘large’ elements, and we call G sparsifiable if G can be reduced to a sparse matrix by some simple operations (e.g. linear filtering or low-rank matrix removal). The Gram matrix plays a critical role in sparse inference, as the sufficient statistics X′Y ~ N(G β, G). Examples where G is non-sparse but sparsifiable can be found in the following application areas.
- Change-point problem. Recently, driven by researches on DNA copy number variation, this problem has received a resurgence of interest (Niu and Zhang, 2012; Olshen et al., 2004; Tibshirani and Wang, 2008). While existing literature focuses on detecting change-points, locating change-points is also of major interest in many applications (Andreou and Ghysels, 2002; Siegmund, 2011; Zhang et al., 2010). Consider a change-point model
where θ = (θ1, …, θp)′ is a piece-wise constant vector with jumps at relatively few locations. Let X = Xp,p be the matrix such that X(i, j) = 1{j ≥ i}, 1 ≤ i, j ≤ p. We re-parametrize the parameters by(1.3)
so that βk is nonzero if and only if θ has a jump at location k. The Gram matrix G has elements G(i, j) = min{i, j}, which is evidently non-sparse. However, adjacent rows of G display a high level of similarity, and the matrix can be sparsified by a second order adjacent differencing between the rows. Long-memory time series. We consider using time-dependent data to build a prediction model for variables of interest: Yt = ∑j βj Xt−j + εt, where {Xt} is an observed stationary time series and {εt} are white noise. In many applications, {Xt} is a long-memory process. Examples include volatility process (Fan and Yao, 2003; Ray and Tsay, 2000), exchange rates, electricity demands, and river’s outflow (e.g. the Niles). Note that the problem can be reformulated as (1.1), where the Gram matrix G = X′X is asymptotically close to the auto-covariance matrix of {Xt} (say, Ω). It is well-known that Ω is Toeplitz, the off-diagonal decay of which is very slow, and the matrix L1-norm of which diverges as p → ∞. However, the Gram matrix can be sparsified by a first order adjacent differencing between the rows.
Further examples include jump detections in (logarithm) asset prices and time series following a FARIMA model (Fan and Yao, 2003). Still other examples include the factor models, where G can be decomposed as the sum of a sparse matrix and a low rank (positive semi-definite) matrix. In these examples, G is non-sparse, but it can be sparsified either by adjacent row differencing or low-rank matrix removal.
1.1. Non-optimality of L0-penalization method for rare and weak signals
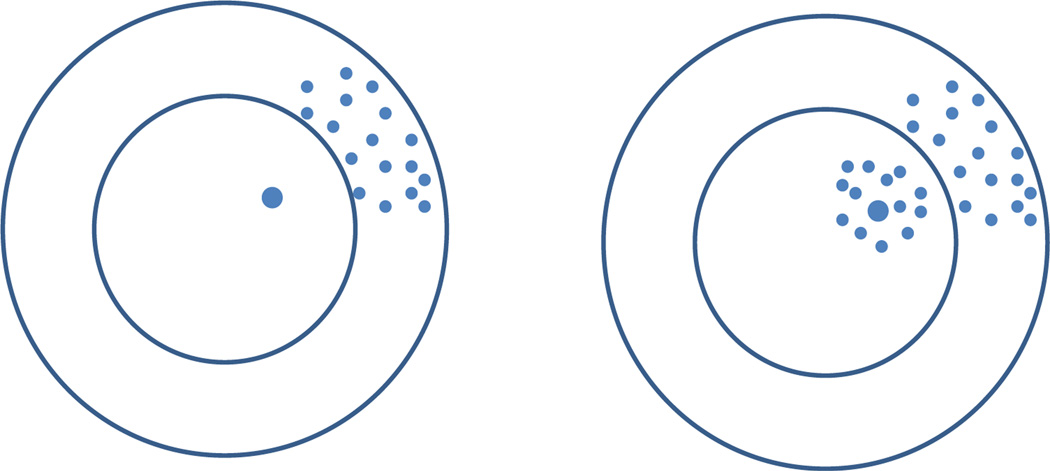
When the signals are rare and strong, the problem of variable selection is more or less well-understood. In particular, Donoho and Stark (1989) (see also Donoho and Huo (2001)) have investigated the noiseless case where they reveal a fundamental phenomenon. In detail, when there is no noise, Model (1.1) reduces to Y = X β. Now, suppose (Y, X) are given and consider the equation Y = X β. In the general case where p > n, it was shown in Donoho and Stark (1989) that under mild conditions on X, while the equation Y = X β has infinitely many solutions, there is a unique solution that is very sparse. In fact, if X is full rank and this sparsest solution has k nonzero elements, then all other solutions have at least (n − k + 1) nonzero elements; see Figure 1 (left).
Fig 1.
Illustration for solutions of Y = X β + z in the noiseless case (left; where z = 0) and the strong noise case (right). Each dot represents a solution (the large dot is the ground truth), where the distance to the center is the L0-norm of the solution. In the noiseless case, we only have one very sparse solution, with all other being much denser. In the strong noise case, signals are rare and weak, and we have many very sparse solutions that have comparable sparsity to that of the ground truth.
In the spirit of Occam’s razor, we have reasons to believe that this unique sparse solution is the ground truth we are looking for. This motivates the well-known method of L0-penalization, which looks for the sparsest solution where the sparsity is measured by the L0-norm. In other words, in the noiseless case, the L0-penalization method is a “fundamentally correct” (but computationally intractable) method.
In the past two decades, the above observation has motivated a long list of computable global penalization methods, including but are not limited to the lasso, SCAD, MC+, each of which hopes to produce solutions that approximate that of the L0-penalization method.
These methods usually use a theoretic framework that contains four intertwined components: “signals are rare but strong”, “the true β is the sparsest solution of Y = X β”, “probability of exact recovery is an appropriate loss function”, and “L0-penalization method is a fundamentally correct method”.
Unfortunately, the above framework is no longer appropriate when the signals are rare and weak. First, the fundamental phenomenon found in Donoho and Stark (1989) is no longer true. Consider the equation Y = X β + z and let β0 be the ground truth. We can produce many vectors β by perturbing β0 such that two models Y = X β + z and Y = X β0 + z are indistinguishable (i.e., all tests—computable or not—are asymptotically powerless). In other words, the equation Y = X β + z may have many very sparse solutions, where the ground truth is not necessarily the sparsest one; see Figure 1 (right).
In other words, when signals are rare and weak:
The situation is much more complicated than that considered by Donoho and Stark (1989), and the principle Occam’s razor may not be relevant.
“Exact Recovery” is usually impossible, and the Hamming distance between the sign vectors of β̂ and β is a more appropriate loss function.
The L0-penalization method is no longer “fundamentally correct”, if the signals are rare/weak and Hamming distance is the loss function.
In fact, it was shown in Ji and Jin (2012) and Jin, Zhang and Zhang (2012) that in the rare/weak regime, even when X is very simple and when the tuning parameter is ideally set, the L0-penalization method is not rate optimal in terms of the Hamming distance. See Ji and Jin (2012) and Jin, Zhang and Zhang (2012) for more discussions. In Section 3, we further present a simple example showing that a slightly revised method has a better numeric performance than the L0-penalization method.
1.2. Limitation of UPS
That the L0-penalization method is rate non-optimal implies that many other penalization methods (such as the lasso, SCAD, MC+) are also rate non-optimal in the Rare/Weak regime.
A natural question is what could be a rate optimal variable selection procedure when the signals are Rare/Weak. To address this problem, Ji and Jin (2012) proposed a method called Univariate Penalization Screening (UPS), and showed that UPS achieves the optimal rate of convergence in Hamming distance under certain conditions.
UPS is a two-stage Screen and Clean (Wasserman and Roeder, 2009) method, at the heart of which is marginal screening. The main challenge that marginal screening faces is the so-called phenomenon of “signal cancellation”, a termed coined by Wasserman and Roeder (2009). The success of UPS hinges on relatively strong conditions, under which signal cancellation has negligible effects.
1.3. Variable selection when G is non-sparse but sparsifiable
Motivated by the application examples aforementioned, we are primarily interested in the Rare/Weak cases where G is non-sparse but can be sparsified by a finite-order linear filtering. That is, if we denote the linear filtering by a p × p matrix D, then the matrix DG is sparse in the sense that each row has relatively few large entries, and all other entries are relatively small. In such a challenging case, we should not expect either the L0-penalization method or the UPS to be rate optimal; this motivates us to develop a new approach.
Our strategy is to exploit the sparsity of DG. Multiplying both sides of (1.1) by X′ and then by D gives
| (1.4) |
On one hand, sparsifying is helpful for both matrices DG and DGD′ are sparse, which can be largely exploited to develop better methods for variable selection. On the other hand, “there is no free lunch”, and sparsifying also causes serious issues:
The post-filtering model (1.4) is not a regular linear regression model.
If we apply a local method (e.g., UPS, Forward/Backward regression) to Model (1.4), we face so-called challenge of information leakage.
In Section 2.4, we carefully explain the issue of information leakage, and discuss how to deal with it.
While sparsifying may help in various ways, it does not mean that it is a trivial task to derive optimal procedures from Model (1.4). For example, if we apply the L0-penalization method naively to Model (1.4), we then ignore the correlations among the noise, which can not be optimal. If we apply the L0-penalization with the correlation structures incorporated, we are essentially applying the L0-penalization method to the original regression model (1.1), leading to a non-optimal procedure again.
1.4. Covariance Assisted Screening and Estimation (CASE)
To exploit the sparsity in DG and DGD′, and to deal with the issues (a)–(b) we just mentioned, we propose a new variable selection method which we call Co-variance Assisted Screening and Estimation (CASE). The main methodological innovation of CASE is to use linear filtering to create graph sparsity and then to exploit the rich information hidden in the ‘local’ graphical structures among the design variables, which the lasso and many other procedures do not utilize.
In the core of CASE is covariance assisted multivariate screening. Screening is a well-known method of dimension reduction in Big Data. However, most literature to date has been focused on univariate screening or marginal screening (Fan and Song, 2010; Genovese et al., 2012). Extending marginal screening to (brute-force) m-variate screening, m > 1, means that we examine all size-m sub-models, and has two major concerns:
Computational infeasibility. A brute-force m-variate screening has a computation complexity of O(pm), which is usually not affordable.
Screening inefficiency. Among the different size-m sub-models, for most of them, the m-nodes are not connected in a sparse graph, called Graph of Strong Dependence (GOSD), which is constructed from the Gram matrix G—without using the response vector Y. As a result, many of such sub-models can be excluded from screening by merely using G, not Y. Therefore, a much more efficient screening procedure than the brute-forth m-variate is to remove all size-m sub-models where the nodes do not form a connected subgraph of the aforementioned sparse graph, and only screen the remaining ones.
In a broad context, GOSD only has Lpp connected size-m sub-graphs, where Lp is a multi-log(p) term to be introduced later. As a result, CASE is a computationally efficient and “fundamentally correct” method when the signals are rare/weak and the Gram matrix is non-sparse and sparsifiable.
1.5. Objective of the paper
The objective of the paper is three-fold:
To develop a theoretic framework that is appropriate for the regime where signals are rare/weak, and G is non-sparse but is sparsifiable.
To appreciate the ‘pros’ and ‘cons’ in variable selection when we attempt to sparsify the Gram matrix G, and to investigate how to fix the ‘cons’.
To show that CASE is asymptotic minimax and yields an optimal partition of the so-called phase diagram.
The phase diagram is a relatively new criterion for assessing the optimality of procedures. Call the two-dimensional space calibrated by the signal rarity and signal strength the phase space. The phase diagram is the partition of the phase space into different regions where in each of them inference is distinctly different. The notion of phase diagram is especially appropriate when signals are rare and weak.
The proposed study is challenging for many reasons:
We focus on a very challenging regime, where signals are rare and weak, and the design matrix is non-sparse or even ill-posed. Such a regime is important from a practical perspective, but has not been carefully explored in the literature.
The goal of the paper is to develop procedures in the rare/weak regime that are asymptotic minimax in terms of Hamming distance, to achieve which we need to find a lower bound and an upper bound that are both tight. Compared to most works on variable selection where the goal is to find procedures that yield exact recovery for sufficiently strong signals, our goal is comparably more ambitious, and the study it entails is more delicate.
To find the precise demarcation for the partition of the phase diagram usually needs very delicate analysis. The study associated with the change-point model is especially challenging and long.
1.6. Content and notations
The paper is organized as follows. Section 2 depict the main results of this paper: we formally introduce CASE and establish its asymptotic optimality. Section 3 presents simulation studies, and Section 4 contains conclusions and discussions.
Throughout this paper, D = Dh,η, d = D(X′Y), B = DG, H = DGD′, and 𝒢* denotes the GOSD (In contrast, dp denotes the degree of GOLF and Hp denotes the Hamming distance). Also, ℝ and ℂ denote the sets of real numbers and complex numbers respectively, and ℝp denotes the p-dimensional real Euclidean space. Given 0 ≤ q ≤ ∞, for any vector x, ‖x‖q denotes the Lq-norm of x; for any matrix M, ‖M‖q denotes the matrix Lq-norm of M. When q = 2, ‖M‖q coincides with the matrix spectral norm; we shall omit the subscript q in this case. When M is symmetric, λmax(M) and λmin(M) denote the maximum and minimum eigenvalues of M respectively. For two matrices M1 and M2, M1 ≽ M2 means that M1 − M2 is positive semi-definite.
2. Main results
This section is arranged as follows. Sections 2.1–2.6 focus on the model, ideas, and the method. In Section 2.1, we introduce the Rare and Weak signal model. In Section 2.2, we formally introduce the notion of sparsifiability. The starting point of CASE is the use of a linear filter. In Section 2.3, we explain how linear filtering helps in variable selection by simultaneously maintaining signal sparsity and yielding the covariance matrix nearly block diagonal. In Section 2.4, we explain that linear filtering also causes a so-called problem of information leakage, and how to overcome such a problem by the technique of patching. After all these ideas are discussed, we formally introduce the CASE in Section 2.5. In Section 2.6, we discuss the computational complexity and show that CASE is computational feasible in a broad context.
Sections 2.7–2.9 focus on the asymptotic optimality of CASE. In Section 2.7, we introduce the asymptotic minimax framework where we use Hamming distance as the loss function. In Section 2.9, we study the lower bound for the minimax Hamming risk, and in Section 2.9, we show that CASE achieves the minimax Hamming risk in a broad context.
In Section 2.10–2.11, we applied our results to the long-range memory time series and the change-point model. For each of them, we derive explicit formulas for the rate of convergence and use it to derive the phase diagram.
2.1. Rare and Weak signal model
Our primary interest is in the situations where the signals are rare and weak, and where we have no information on the underlying structure of the signals. In such situations, it makes sense to use the following Rare and Weak signal model; see Candès and Plan (2009); Donoho and Jin (2008); Jin, Zhang and Zhang (2012). Fix ε ∈ (0, 1) and τ > 0. Let b = (b1, …, bp)′ be the p × 1 vector that is realizations from
| (2.5) |
and let Θp(τ) be the set of vectors
| (2.6) |
We model β by
| (2.7) |
where μ ∈ Θp(τ) and ◦ is the Hadamard product (also called the coordinate-wise product). In Section 2.7, we further restrict μ to a subset of Θp(τ).
In this model, βi is either 0 or a signal with a strength ≥ τ. Since we have no information on where the signals are, we assume that they appear at locations that are randomly generated. We are primarily interested in the challenging case where ε is small and τ is relatively small, so the signals are both rare and weak.
Definition 2.1. We call Model (2.5)–(2.7) the Rare and Weak signal model RW(ε, τ, μ).
We remark that the theory developed in this paper is not tied to the Rare and Weak signal model, and applies to more general cases. For example, the main results can be extended to the case where we have some additional information about the underlying structure of the signals such as the Ising model (Ising, 1925).
2.2. Sparsifiability, linear filtering, and GOSD
As mentioned before, we are primarily interested in the case where the Gram matrix G can be sparsified by a finite-order linear filtering.
Fix an integer h ≥ 1 and an (h + 1)-dimensional vector η = (1, η1, …, ηh)′. Let D = Dh,η be the p × p matrix satisfying
| (2.8) |
The matrix Dh,η can be viewed as a linear operator that maps any p × 1 vector y to Dh,ηy. For this reason, Dh,η is also called an order h linear filter Fan and Yao (2003).
For α > 0 and A0 > 0, we introduce the following class of matrices:
| (2.9) |
Matrices in ℳp(α, A0) are not necessarily symmetric.
Definition 2.2. Fix an order h linear filter D = Dh,η. We say that G is sparsifiable by Dh,η if for sufficiently large p, DG ∈ ℳp(α, A0) for some constants α > 1 and A0 > 0.
In the long memory time series model, G can be sparsified by an order 1 linear filter. In the change-point model, G can be sparsified by an order 2 linear filter.
The main benefit of linear filtering is that it induces sparsity in the Graph of Strong Dependence (GOSD) to be introduced below. Recall that the sufficient statistics Ỹ = X′Y ~ N(G β, G). Applying a linear filter D = Dh,η to Ỹ gives
| (2.10) |
where d = D(X′Y), B = DG, and H = DGD′. Note that no information is lost when we reduce from the model Ỹ ~ N(G β, G) to Model (2.10), as D is non-singular.
At the same time, if G is sparsifiable by D = Dh,η, then both the matrices B and H are sparse, in the sense that each row of either matrix has relatively few large coordinates. In other words, for a properly small threshold δ > 0 to be determined, let B* and H* be the regularized matrices of B and H, respectively:
It is seen that
| (2.11) |
where each row of B* or H* has relatively few nonzeros. Compared to (2.10), (2.11) is much easier to track analytically, but it contains almost all the information about β.
The above observation naturally motivates the following graph, which we call the Graph of Strong Dependence (GOSD).
Definition 2.3. For a given parameter δ, the GOSD is the graph 𝒢* = (V, E) with nodes V = {1, 2, …, p} and there is an edge between i and j when any of the three numbers H*(i, j), B*(i, j), and B*(j, i) is nonzero.
Definition 2.4. A graph 𝒢 = (V, E) is called K-sparse if the degree of each node ≤ K.
The definition of GOSD depends on a tuning parameter δ, the choice of which is not critical, and it is generally sufficient if we choose δ = δp = 1/ log(p); see Section B.1 in the supplemental materials for details. With such a choice of δ, it can be shown that in a general context, GOSD is K-sparse, where K = Kδ does not exceed a multi-log(p) term as p → ∞ (see Lemma B.1).
2.3. Interplay between the graph sparsity and signal sparsity
With these being said, it remains unclear how the sparsity of 𝒢* helps in variable selection. In fact, even when 𝒢* is 2-sparse, it is possible that a node k is connected—through possible long paths—to many other nodes; it is unclear how to remove the effect of these nodes when we try to estimate βk.
Somewhat surprisingly, the answer lies in an interesting interplay between the signal sparsity and graph sparsity. To see this point, let S = S(β) be the support of β, and let be the subgraph of 𝒢* formed by the nodes in S only. Given the sparsity of 𝒢*, if the signal vector β is also sparse, then it is likely that the sizes of all components of (a component of a graph is a maximal connected subgraph) are uniformly small. This is justified in the following lemma which is proved in Jin, Zhang and Zhang (2012).
Lemma 2.1. Suppose 𝒢* is K-sparse and the support S = S(β) is a realization from , where ν0 is the point mass at 0 and π is any distribution with support ⊆ ℝ\{0}. With a probability (from randomness of S) at least 1 − p(eεK)m+1, decomposes into many components with size no larger than m.
In this paper, we are primarily interested in cases where for large p, ε ≤ p−ϑ for some parameter ϑ ∈ (0, 1) and K is bounded by a multi-log(p) term. In such cases, the decomposability of holds for a finite m, with overwhelming probability.
Lemma 2.1 delineates an interesting picture: The set of signals decomposes into many small-size isolated signal islands (if only we know where), each of them is a component of , and different ones are disconnected in the GOSD. As a result, the original p-dimensional problem can be viewed as the aggregation of many separated small-size subproblems that can be solved parallelly. This is a key insight of this paper.
Note that the decomposability of attributes to the interplay between the signal sparsity and the graph sparsity, where the latter attributes to the use of linear filtering. The decomposability is not tied to the specific model of β in Lemma 2.1, and holds for much broader situations (e.g. when b is generated by a sparse Ising model (Ising, 1925)).
2.4. Information leakage and patching
While it largely facilitates the decomposability of the model, we must note that the linear filtering also induces a so-called problem of information leakage. In this section, we discuss how linear filtering causes such a problem and how to overcome it by the so-called technique of patching.
The following notation is frequently used in this paper.
Definition 2.5. For ℐ ⊂ {1, 2, …, p}, 𝒥 ⊂ {1, ⋯, N}, and a p × N matrix X, Xℐ denotes the |ℐ} × N sub-matrix formed by restricting the rows of X to ℐ, and X𝒥, ℐ denotes the |𝒥| × |ℐ| sub-matrix formed by restricting the columns of X to ℐ and rows to 𝒥.
Note that when N = 1, X is a p × 1 vector, and Xℐ is an |ℐ| × 1 vector.
To appreciate information leakage, we first consider an idealized case where each row of G has ≤ K nonzeros. In this case, there is no need for linear filtering, so B = H = G and d = Ỹ. Recall that consists of many signal islands and let ℐ be one of them. It is seen that
| (2.12) |
and how well we can estimate βℐ is captured by the Fisher Information Matrix Gℐ,ℐ (Lehmann and Casella, 1998).
Come back to the case where G is non-sparse. Interestingly, despite the strong correlations, Gℐ,ℐ continues to be the Fisher information for estimating βℐ. However, when G is non-sparse, we must use a linear filtering D = Dh,η as suggested, and we have
| (2.13) |
Moreover, letting 𝒥 = {1 ≤ j ≤ p : D(i, j) ≠ 0 for some i ∈ ℐ}, it follows that
By the definition of D, |𝒥| > |ℐ|, and the dimension of the following null space ≥ 1:
| (2.14) |
Compare (2.13) with (2.12), and imagine the oracle situation where we are told the mean vector of dℐ in both. The difference is that, we can fully recover βℐ using (2.12), but are not able to do so with only (2.13). In other words, the information containing βℐ is partially lost in (2.13): if we estimate βℐ with (2.13) alone, we will never achieve the desired accuracy.
The argument is validated in Lemma 2.2 below, where the Fisher information associated with (2.13) is strictly “smaller” than Gℐ,ℐ; the difference between two matrices can be derived by taking ℐ+ = ℐ and 𝒥+ = 𝒥 in (2.15). We call this phenomenon “information leakage”.
To mitigate this, we expand the information content by including data in the neighborhood of ℐ. This process is called “patching”. Let ℐ+ be an extension of ℐ by adding a few neighboring nodes, and define similarly 𝒥+ = {1 ≤ j ≤ p : D(i, j) ≠ 0 for some i ∈ ℐ+} and Null(ℐ+, 𝒥+). Assuming that there is no edge between any node in ℐ+ and any node in ,
| (2.15) |
The Fisher Information Matrix for βℐ under Model (2.15) is larger than that of (2.13), which is captured in the following lemma.
Lemma 2.2. The Fisher Information Matrix associated with Model (2.15) is
| (2.16) |
where U is any |𝒥+| × (|𝒥+| − |ℐ+|) matrix whose columns form an orthonormal basis of Null(ℐ+, 𝒥+).
When the size of ℐ+ becomes appropriately large, the second matrix in (2.16) is small element-wise (and so is negligible) under mild conditions (see details in Lemma A.3). This matrix is usually non-negligible if we set ℐ+ = ℐ and 𝒥+ = 𝒥 (i.e., without patching).
Example 1. We illustrate the above phenomenon with an example where p = 5000, G is the matrix satisfying G(i, j) = [1 + 5|i − j|]−0.95 for all 1 ≤ i, j ≤ p, and D = Dh,η with h = 1 and η = (1, −1)′. If ℐ = {2000}, then Gℐ,ℐ = 1, but the Fisher information associated with Model (2.13) is 0.5. The gap can be substantially narrowed if we patch with ℐ+ = {1990, 1991, …, 2010}, in which case the Fisher information in (2.16) is 0.904.
Although one of the major effects of information leakage is a reduction in the signal-to-noise ratio, this phenomenon is very different from the well-known “signal cancelation” or “partial faithfulness” in variable selection. “Signal cancellation” is caused by correlations between signal covariates, and CASE overcomes this problem by using multivariate screening. However, “information leakage” is caused by the use of a linear filtering. From Lemma 2.2, we can see that the information leakage appears no matter for what signal vector β. CASE overcomes this problem by the patching technique.
2.5. Covariance Assisted Screening and Estimation (CASE)
In summary, we start from the post-filtering regression model
We have observed the following.
Signal Decomposability. Linear filtering induces sparsity in GOSD, a graph constructed from the Gram matrix G. In this graph, the set of all true signal decomposes into many small-size signal islands, each signal island is a component of GOSD.
Information Patching. Linear filtering also causes information leakage, which can be overcome by delicate patching technique.
Naturally, these motivate a two-stage Screen and Selection approach which we call Covariance Assisted Screening and Estimation (CASE). CASE contains a Patching and Screening (PS) step, and a Patching and Estimation (PE) step.
PS-step. We use sequential χ2-tests to identify candidates for each signal island. Each χ2-test is guided by 𝒢*, and aided by a carefully designed patching step. This achieves multivariate screening without visiting all submodels.
PE-step. We re-investigate each candidate with penalized MLE and certain patching technique, in hope of removing false positives.
For the purpose of patching, the PS-step and the PE-step use tuning integers ℓps and ℓpe, respectively. The following notations are frequently used in this paper.
Definition 2.6. For any index 1 ≤ i ≤ p, {i}ps = {1 ≤ j ≤ p : |j − i| ≤ ℓps}. For any subset ℐ of {1, 2, …, p}, ℐps = ∪i∈ℐ{i}ps. Similar notation applies to {i}pe and ℐpe.
We now discuss two steps in detail. Consider the PS-step first. Fix m > 1. Suppose that 𝒢* has a total of T connected subgraphs with size ≤ m, which we denote by , arranged in the ascending order of the sizes, with ties breaking lexicographically.
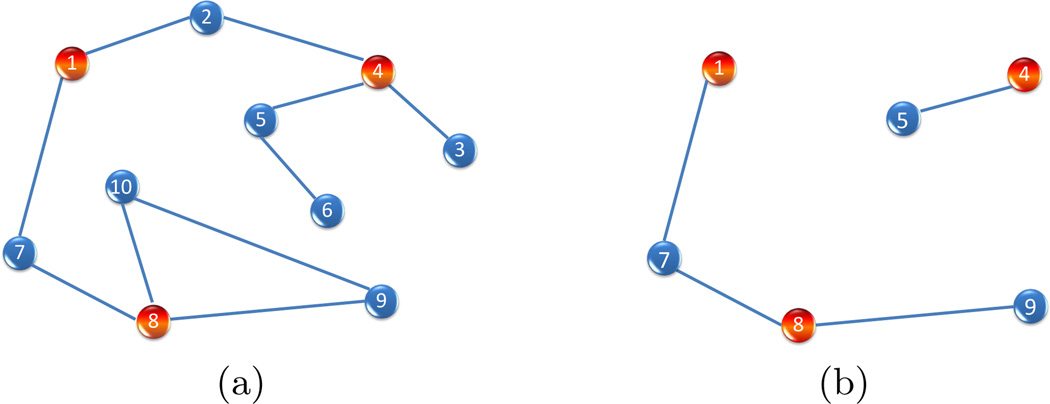
Example 2(a). We illustrate this with a toy example, where p = 10 and the GOSD is displayed in Figure 2(a). For m = 3, GOSD has T = 30 connected subgraphs, which we arrange as follows. Note that are singletons, are connected pairs, and are connected triplets:
{1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {10}
{1, 2}, {1, 7}, {2, 4}, {3, 4}, {4, 5}, {5, 6}, {7, 8}, {8, 9}, {8, 10}, {9, 10}
{1, 2, 4}, {1, 2, 7}, {1, 7, 8}, {2, 3, 4}, {2, 4, 5}, {3, 4, 5}, {4, 5, 6}, {7, 8, 9}, {7, 8, 10}, {8, 9, 10}.
Fig 2.
Illustration of Graph of Strong Dependence (GOSD). Red: signal nodes. Blue: noise nodes. (a) GOSD with 10 nodes. (b) Nodes of GOSD that survived the PS-step.
In this example, the multivariate screening exams sequentially only the 30 submodels above to decide whether any variables have additional utilities given the variables recruited before, via χ2-tests. The first 10 screening problems are just the univariate screening. After that, starting from bivariate screening, we examine the variables given those selected so far. Suppose that we are examining the variables {1, 2}. The testing problem depends on how variables {1, 2} are selected in the previous steps. For example, if variables {1, 2, 4, 6} have already been selected in the univariate screening, there is no new recruitment and we move on to examine the submodel {1, 7}. If the variables {1, 4, 6} have been recruited so far, we need to test if variable {2} has additional contributions given variable {1}. If the variables {4, 6} have been recruited in the previous steps, we will examine whether variables {1, 2} together have any significant contributions. Therefore, we have never run regression for more than two variables. Similarly, for trivariate screening, we will never run regression for more than 3 variables. Clearly, multivariate screening improves the marginal screening in that it gives significant variables chances to be recruited if it is wrongly excluded by the marginal method.
We now formally describe the procedure. The PS-step contains T sub-stages, where we screen 𝒢t sequentially, t = 1, 2, …, T. Let 𝒰(t) be the set of retained indices at the end of stage t, with 𝒰(0) = ∅ as the convention. For 1 ≤ t ≤ T, the t-th sub-stage contains two sub-steps.
(Initial step). Let N̂ = 𝒰(t−1) ∩𝒢t represent the set of nodes in 𝒢t that have already been accepted by the end of the (t − 1)-th sub-stage, and let F̂ = 𝒢t \ N̂ be the set of other nodes in 𝒢t.
- (Updating step). Write for short ℐ = 𝒢t. Fixing a tuning parameter ℓps for patching, introduce
where W is a random vector and Q can be thought of as the covariance matrix of W. Define WN̂, a subvector of W, and QN̂, N̂, a submatrix of Q, as follows:(2.17)
Introduce the test statistic(2.18)
For a threshold t = t(F̂, N̂) to be determined, we update the set of retained nodes by 𝒰(t) = 𝒰(t−1) ∪ F̂ if T(d, F̂, N̂) > t, and let 𝒰(t) = 𝒰(t−1) otherwise. In other words, we accept nodes in F̂ only when they have additional utilities.(2.19)
The PS-step terminates when t = T, at which point, we write , and so
In the PS-step, as we screen, we accept nodes sequentially. Once a node is accepted in the PS-step, it stays there till the end of the PS-step; of course, this node could be killed in the PE-step. In spirit, this is similar to the well-known forward regression method, but the implementation of two methods are significantly different.
The PS-step uses a collection of tuning thresholds
A convenient choice for these thresholds is to let t(F̂, N̂) = 2q̃ log(p)|F̂| for a properly small fixed constant q̃ > 0. See Section 2.9 (and also Sections 2.10–2.11) for more discussion on the choices of t(F̂, N̂).
In the PS-step, we use χ2-test for screening. This is the best choice when the coordinates of z are Gaussian and have the same variance. When the Gaussian assumption on z is questionable, we must note that the χ2-test depends on the Gaussianity of a′z for all p-different a, not on that of z. Therefore, by similar arguments as above, the performance of χ2-test is relatively robust to nonGaussianity. If circumstances arise that the χ2-test is not appropriate (e.g., misspecification of the model, low quantity of the data), we may need an alternative, say, some non-parametric tests. In this case, if the efficiency of the test is nearly optimal, then the screening in the PS-step would continue to be successful.
How does the PS-step help in variable selection? In Section A, we show that in a broad context, provided that the tuning parameters t(F̂, N̂) are properly set, the PS-step has two noteworthy properties: the Sure Screening (SS) property and the Separable After Screening (SAS) property. The SS property says that contains all but a negligible fraction of the true signals. The SAS property says that if we view as a subgraph of 𝒢* (more precisely, as a subgraph of 𝒢+, an expanded graph of 𝒢* to be introduce below), then this subgraph decomposes into many disconnected components, each having a moderate size.
Together, the SS property and the SAS property enable us to reduce the original large-scale problem to many parallel small-size regression problems, and pave the way for the PE-step. See Section A for details.
Example 2(b). We illustrate the above points with the toy example in Example 2(a). Suppose after the PS-step, the set of retained indices is {1, 4, 5, 7, 8, 9}; see Figure 2(b). In this example, we have a total of three signal nodes, {1}, {4}, and {8}, which are all retained in and so the PS-step yields Sure Screening. On the other hand, contains a few nodes of false positives, which will be further cleaned in the PE-step. At the same time, viewing it as a subgraph of 𝒢*, decomposes into two disconnected components, {1, 7, 8, 9} and {4, 5}; compare Figure 2(a). The SS property and the SAS property enable us to reduce the original problem of 10 nodes to two parallel regression problems, one with 4 nodes, and the other with 2 nodes.
We now discuss the PE-step. Recall that ℓpe is the tuning parameter for the patching of the PE-step, and let {i}pe be as in Definition 1.6. The following graph can be viewed as an expanded graph of 𝒢*.
Definition 2.7. Let 𝒢+ = (V, E) be the graph where V = {1, 2, …, p} and there is an edge between nodes i and j when there exist nodes k ∈ {i}pe and k′ ∈ {j}pe such that there is an edge between k and k′ in 𝒢*.
Recall that is the set of retained indices at the end of the PS-step.
Definition 2.8. Fix a graph 𝒢 and its subgraph ℐ. We say ℐ ⊴ 𝒢 if ℐ is a connected subgraph of 𝒢, and ℐ ⊲ 𝒢 if ℐ is a component (maximal connected subgraph) of 𝒢.
Fix 1 ≤ j ≤ p. When , CASE estimates βj as 0. When , viewing as a subgraph of 𝒢+, there is a unique subgraph ℐ such that . Fix two tuning parameters upe and υpe. We estimate βℐ by minimizing
| (2.20) |
where θ is an |ℐ| × 1 vector where each nonzero coordinate ≥ υpe, and ‖θ‖0 denotes the L0-norm of θ. Putting these together gives the final estimator of CASE, which we denote by β̂case = β̂case(Y; δ, m, 𝒬, ℓps, ℓpe, upe, υpe, Dh,η, X, p).
CASE uses tuning parameters (δ, m, 𝒬, ℓps, ℓpe, upe, υpe). Earlier in this paper, we have briefly discussed how to choose (δ, 𝒬). As for m, usually, a choice of m = 3 is sufficient unless the signals are relatively ‘dense’. The choices of (ℓps, ℓpe, upe, υpe) are addressed in Section 2.9 (see also Sections 2.10–2.11).
2.6. Computational complexity of CASE, comparison with multivariate screening
The PS-step is closely related to the well-known method of marginal screening, and has a moderate computational complexity.
Marginal screening selects variables by thresholding the vector d coordinate-wise. The method is computationally fast, but it neglects ‘local’ graphical structures, and is thus ineffective. For this reason, in many challenging problems, it is desirable to use multivariate screening methods which adapt to ‘local’ graphical structures.
Fix m > 1. An m-variate χ2-screening procedure is one of such desired methods. The method screens all k-tuples of coordinates of d using a χ2-test, for all k ≤ m, in an exhaustive (brute-force) fashion. Seemingly, the method adapts to ‘local’ graphical structures and could be much more effective than marginal screening. However, such a procedure has a computational cost of O(pm) (excluding the computation cost for obtaining X′Y from (X, Y); same below) which is usually not affordable when p is large.
The main computational innovation of the PS-step is to use a graph-assisted m-variate χ2-screening, which is both effective in variable selection and efficient in computation. In fact, the PS-step only screens k-tuples of coordinates of d that form a connected subgraph of 𝒢*, for all k ≤ m. Therefore, if 𝒢* is K-sparse, then there are ≤ Cp(eK)m+1 connected subgraphs of 𝒢* with size ≤ m; so if K = Kp is no greater than a multi-log(p) term (see Definition 2.10), then the computational complexity of the PS-step is only O(p), up to a multi-log(p) term.
Example 2(c). We illustrate the difference between the above three methods with the toy example in Example 2(a), where p = 10 and the GOSD is displayed in Figure 2(a). Suppose we choose m = 3. Marginal screening screens all 10 single nodes of the GOSD. The brute-force m-variate screening screens all k-tuples of indices, 1 ≤ k ≤ m, with a total of such k-tuples. The m-variate screening in the PS-step only screens k-tuples that are connected subgraphs of 𝒢*, for 1 ≤ k ≤ m, and in this example, we only have 30 such connected subgraphs.
The computational complexity of the PE-step consists two parts. The first part is the complexity of obtaining all components of , which is O(pK) and where K is the maximum degree of 𝒢+; note that for settings considered in this paper, does not exceed a multi-log(p) term (see Lemma B.2). The second part of the complexity comes from solving (2.20), which hinges on the maximal size of ℐ. In Lemma A.2, we show that in a broad context, the maximal size of ℐ does not exceed a constant l0, provided the thresholds 𝒬 are properly set. Numerical studies in Section 3 also support this point. Therefore, the complexity in this part does not exceed p · 3l0. As a result, the computational complexity of the PE-step is moderate. Here, the bound O(pK + p · 3l0) is conservative; the actual computational complexity is much smaller than this.
How does CASE perform? In Sections 2.7–2.9, we set up an asymptotic framework and show that CASE is asymptotically minimax in terms of the Hamming distance over a wide class of situations. In Sections 2.10–2.11, we apply CASE to the long-memory time series and the change-point model, and elaborate the optimality of CASE in such models with the so-called phase diagram.
2.7. Asymptotic Rare and Weak model
In this section, we add an asymptotic framework to the Rare and Weak signal model RW(ε, τ, μ) introduced in Section 2.1. We use p as the driving asymptotic parameter and tie (ε, τ) to p through some fixed parameters.
In particular, we fix ϑ ∈ (0, 1) and model the sparse parameter ε by
| (2.21) |
Note that as p grows, the signal becomes increasingly sparse. At this sparsity level, it turns out that the most interesting range of signal strength is . For much smaller τ, successful recovery is impossible. For much larger τ, the problem is relatively easy. In light of this, we fix r > 0 and let
| (2.22) |
At the same time, recalling that in RW(ε, τ, μ), we require μ ∈ Θp(τ) so that |μi| ≥ τ for all 1 ≤ i ≤ p. Fixing a > 1, we now further restrict μ to the following subset of Θp(τ):
| (2.23) |
Definition 2.9. We call (2.21)–(2.23) the Asymptotic Rare and Weak model ARW(ϑ, r, a, μ).
Requiring the strength of each signal ≤ aτp is mainly for technical reasons, and hopefully, such a constraint can be removed in the near future. From a practical point of view, since usually we do not have sufficient information on μ, we prefer to have a larger a: we hope that when a is properly large, is broad enough, so that neither the optimal procedure nor the minimax risk needs to adapt to a.
Towards this end, we impose some mild regularity conditions on a and the Gram matrix G. Let g be the smallest integer such that
| (2.24) |
For any p × p Gram matrix G and 1 ≤ k ≤ p, let be the minimum of the smallest eigenvalues of all k × k principle sub-matrices of G. Introduce
| (2.25) |
For any two subsets V0 and V1 of {1, 2, …, p}, consider the optimization problem
up to the constraints that if i ∈ Vk and otherwise, where k = 0, 1, and that in the special case of V0 = V1, the sign vectors of θ(0) and θ(1) are unequal. Introduce
The following lemma is elementary, so we omit the proof.
Lemma 2.3. For any G ∈ ℳ̃p(c0, g), there is a constant C = C(c0, g) > 0 such that .
In this paper, except for Section 2.11 where we discuss the change-point model, we assume
| (2.26) |
Under such conditions, is broad enough and the minimax risk (to be introduced below) does not depend on a. See Section 2.8 for more discussion.
For any variable selection procedure β̂, we measure the performance by the Hamming distance
where the expectation is taken with respect to β̂. Here, for any p × 1 vector ξ, sgn(ξ) denotes the sign vector (for any number x, sgn(x) = 1, 0, −1 when x < 0, x = 0, and x > 0 correspondingly).
Under ARW(ϑ, r, a, μ), β = b ◦ μ, so the overall Hamming distance is
where Eεp is the expectation with respect to the law of b. Finally, the minimax Hamming distance under ARW(ϑ, r, a, μ) is
In next section, we will see that the minimax Hamming distance does not depend on a as long as (2.26) holds.
In many recent works, the probability of exact support recovery or oracle property is used to assess optimality, e.g. Fan and Li (2001); Zhao and Yu (2006). However, when signals are rare and weak, exact support recovery is usually impossible, and the Hamming distance is a more appropriate criterion for assessing optimality. In comparison, study on the minimax Hamming distance is not only mathematically more demanding but also scientifically more relevant than that on the oracle property.
2.8. Lower bound for the minimax Hamming distance
We view the (global) Hamming distance as the aggregation of ‘local’ Hamming distances. To construct a lower bound for the (global) minimax Hamming distance, the key is to construct lower bounds for ‘local’ Hamming errors. Fix 1 ≤ j ≤ p. The ‘local’ Hamming error at index j is the risk we make among the neighboring indices of j in GOSD, say, {k : d(j, k) ≤ g}, where g is as in (2.24) and d(j, k) is the geodesic distance between j and k in the GOSD. The lower bound for such a ‘local’ Hamming error is characterized by an exponent , which we now introduce.
For any subset V ⊂ {1, 2, …, p}, let IV be the p × 1 vector such that the j-th coordinate is 1 if j ∈ V and 0 otherwise. Fixing two subsets V0 and V1 of {1, 2, …, p}, introduce
| (2.27) |
with and
| (2.28) |
The exponent is defined by
| (2.29) |
The following notation Lp is frequently used in this paper.
Definition 2.10. Lp, as a positive sequence indexed by p, is called a multi-log(p) term if for any fixed δ > 0, limp→∞ Lppδ = ∞ and limp→∞ Lpp−δ = 0.
It can be shown that provides a lower bound for the ‘local’ minimax Hamming distance at index j, and that when (2.26) holds, does not depend on a; see Lemma 16 in Jin, Zhang and Zhang (2012) for details. In the remaining part of the paper, we will write it as for short.
At the same time, in order for the aggregation of all lower bounds for ‘local’ Hamming errors to give a lower bound for the ‘global’ Hamming distance, we need to introduce Graph of Least Favorables (GOLF). Towards this end, recalling g and ρ(V0, V1) as in (2.24) and (2.28), respectively, let
and when there is a tie, pick the one that appears first lexicographically. We can think as the ‘least favorable’ configuration at index j.
Definition 2.11. GOLF is the graph 𝒢◇ = (V, E) where V = {1, 2, …, p} and there is an edge between j and k if and only if .
The following theorem is similar to Theorem 14 in Jin, Zhang and Zhang (2012), so we omit the proof.
Theorem 2.1. Suppose (2.26) holds so that does not depend on the parameter a for sufficiently large p. As p → ∞, , where dp(𝒢◇) is the maximum degree of all nodes in 𝒢◇.
In many examples, including those of primary interest of this paper,
| (2.30) |
In such cases, we have the following lower bound:
| (2.31) |
2.9. Upper bound and optimality of CASE
In this section, we show that in a broad context, provided that the tuning parameters are properly set, CASE achieves the lower bound prescribed in Theorem 2.1, up to some Lp terms. Therefore, the lower bound in Theorem 2.1 is tight, and CASE achieves the optimal rate of convergence.
For a given γ > 0, we focus on linear models with the Gram matrix from
where we recall that the two terms on the right hand side are defined in (2.9) and (2.25), respectively. The following lemma is proved in Section B.
Lemma 2.4. For , the maximum degree of nodes in GOLF satisfies dp(𝒢◇) ≤ Lp.
Combining Lemma 2.4 with Theorem 2.1, the lower bound (2.31) holds for our settings.
For any linear filter D = Dh,η, let
be the so-called characterization polynomial. We assume the following regularity conditions.
Regularization Condition A (RCA). For any root z0 of φη(z), |z0| ≥ 1.
Regularization Condition B (RCB). There are constants κ > 0 and c1 > 0 such that (see Section 1.7 for the definition of ).
For many well-known linear filters such as adjacent differences, seasonal differences, etc., RCA is satisfied. Also, RCB is only a mild condition since κ can be any positive number. For example, RCB holds in the change-point model and long-memory time series model with certain D matrices. In general, κ is not 0 because when DG is sparse, DGD′ is very likely to be approximately singular and the associated value of can be small when k is large. This is true even for very simple G (e.g. G = Ip, D = D1,η and η = (1, −1)′).
At the same time, these conditions can be further relaxed. For example, for the change-point problem, the Gram matrix has barely any off-diagonal decay, and does not belong to . Nevertheless, with slight modification in the procedure, the main results continue to hold.
CASE uses tuning parameters (δ, m, 𝒬, ℓps, ℓpe, upe, υpe). The choice of δ is flexible, and we usually set δ = 1/ log(p). For the main theorem below, we treat m as given. In practice, taking m to be a small integer (say, ≤ 3) is usually sufficient, unless the signals are relatively dense (say, ϑ < 1/4). The choice of ℓps and ℓpe are also relatively flexible, and letting ℓps be a sufficiently large constant and ℓpe be (log(p))ν for some constant ν < (1 − 1/α)/(κ+1/2) is sufficient, where α is as in Definition 2.2, and κ is as in RCB.
At the same time, in principle, the optimal choices of (upe, υpe) are
| (2.32) |
which depend on the underlying parameters (ϑ, r) that are unknown to us. Despite this, our numeric studies in Section 3 suggest that the choices of (upe, υpe) are relatively flexible; see Sections 3–4 for more discussions.
Last, we discuss how to choose 𝒬 = {t(F̂, N̂) : (F̂, N̂) are defined as in the PS-step}. Let t(F̂, N̂) = 2q log(p), where q > 0 is a constant. It turns out that the main result (Theorem 2.2 below) holds as long as
| (2.33) |
where q0 > 0 is an appropriately small constant, and for any subsets (F, N),
| (2.34) |
here,
| (2.35) |
with
| (2.36) |
and
| (2.37) |
where QF,N = (Bℐps,F)′(Hℐps,ℐps)−1(Bℐps, N) with ℐ = F ∪ N, and QN,F, QF,F and QN,N are defined similarly. Compared to (2.17), we see that QF,N, QF,N, QN,F and QN,N are all submatrices of Q. Hence, ω̃(F, N) can be viewed as a counterpart of ω(F, N) by replacing the submatrices of Gℐ,ℐ by the corresponding ones of Q.
From a practical point of view, there is a trade-off in choosing q: a larger q would increase the number of Type II errors in the PS-step, but would also reduce the computation cost in the PE-step. The following is a convenient choice which we recommend in this paper:
| (2.38) |
where 0 < q̃ < c0r/4 is a constant and c0 is as in .
We are now ready for the main result of this paper.
Theorem 2.2. Suppose that for sufficiently large p, , Dh,ηG ∈ ℳp(α, A0) with α > 1, and that RCA-RCB hold. Consider β̂case = β̂case(Y; δ, m, 𝒬, ℓps, ℓpe, upe, υpe, Dh,η, X, p) with the tuning parameters specified above. Then as p → ∞,
| (2.39) |
Combine Lemma 2.4 and Theorem 2.2. Given the parameter m is appropriately large, both the upper bound and the lower bound are tight and CASE achieves the optimal rate of convergence prescribed by
| (2.40) |
Theorem 2.2 is proved in Section A, where we explain the key idea behind the procedure, as well as the selection of the tuning parameters.
2.10. Application to the long-memory time series model
The long-memory time series model in Section 1 can be written as a regression model:
where the Gram matrix G is asymptotically Toeplitz and has slow off-diagonal decays. Without loss of generality, we consider the idealized case where G is an exact Toeplitz matrix generated by a spectral density f:
| (2.41) |
In the literature (Chen, Hurvich and Lu, 2006; Moulines and Soulier, 1999), the spectral density for a long-memory process is usually characterized as
| (2.42) |
where ϕ ∈ (0, 1/2) is the long-memory parameter, f*(ω) is a positive symmetric function that is continuous on [−π, π] and is twice differentiable except at ω = 0.
In this model, the Gram matrix is non-sparse but it is sparsifiable. To see the point, let η = (1, −1)′ and let D = D1,η be the first-order adjacent row-differencing. On one hand, since the spectral density f is singular at the origin, it follows from the Fourier analysis that
and hence G is non-sparse. On the other hand, it is seen that
where we recall that B = DG and note that ĝ denotes the Fourier transform of g. Compared to f(ω), ωf(ω) is non-singular at the origin. Additionally, it is seen that B ∈ ℳp(2 − 2ϕ, A), where 2 − 2ϕ > 1, so B is sparse (similar claim applies to H = DGD′). This shows that G is sparsifiable by adjacent row-differencing.
In this example, there is a function that only depends on (ϑ, r, f) such that
where the subscript ‘lts’ stands for long-memory time series. The following theorem can be derived from Theorem 2.2, and is proved in Section B.
Theorem 2.3. For a long-memory time series model where |(f*)″(ω)| ≤ C|ω|−2, the minimax Hamming distance satisfies . If we apply CASE where , η = (1, −1)′, and the tuning parameters are as in Section 2.9, then
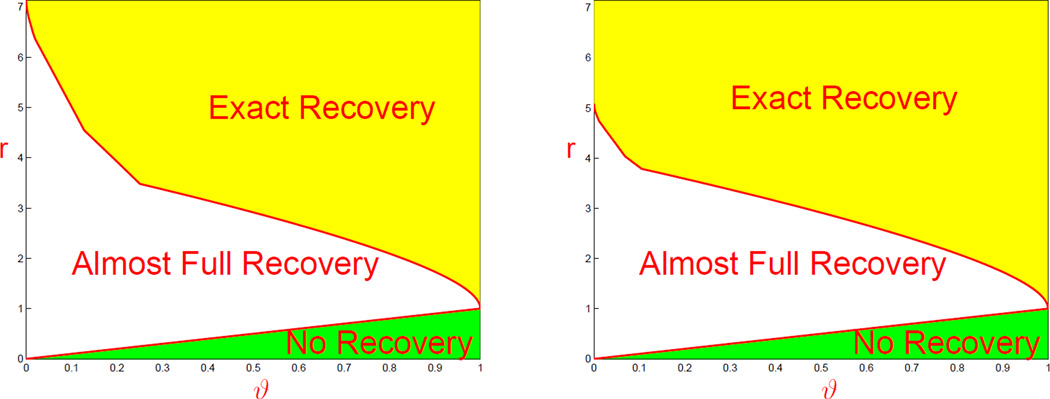
Theorem 2.3 can be interpreted by the so-called phase diagram. Phase diagram is a way to visualize the class of settings where the signals are so rare and weak that successful variable selection is simply impossible (Ji and Jin, 2012). In detail, for a spectral density f and ϑ ∈ (0, 1), let be the unique solution of . Note that characterizes the minimal signal strength required for exact support recovery with high probability. We have the following proposition, which is proved in Section B.
Lemma 2.5. Under the conditions of Theorem 2.3, if (f*)″(0) exists, then is a decreasing function in ϑ, with limits 1 and as ϑ → 1 and ϑ → 0, respectively.
Call the two-dimensional space {(ϑ, r): 0 < ϑ < 1, r > 0} the phase space. Interestingly, there is a partition of the phase space as follows.
Region of No Recovery {(ϑ, r): 0 < r < ϑ, 0 < ϑ < 1}. In this region, the minimax Hamming distance ≳ pεp, where pεp is approximately the number of signals. In this region, the signals are too rare and weak and successful variable selection is impossible.
Region of Almost Full Recovery . In this region, the minimax Hamming distance is much larger than 1 but much smaller than pεp. Therefore, the optimal procedure can recover most of the signals but not all of them.
Region of Exact Recovery . In this region, the minimax Hamming distance is o(1). Therefore, the optimal procedure recovers all signals with probability ≈ 1.
Because of the partition of the phase space, we call this the phase diagram.
From time to time, we wish to have a more explicit formula for the rate and the critical value . In general, this is a hard problem, but both quantities can be computed numerically when f is given. In Figure 3, we display the phase diagrams for the autoregressive fractionally integrated moving average process (FARIMA) with parameters (0, ϕ, 0) (Fan and Yao, 2003), where
| (2.43) |
Take ϕ = 0.35, 0.25 for example, , 5.08 for small ϑ.
Fig 3.
Phase diagrams corresponding to the FARIMA(0, ϕ, 0) process. Left: ϕ = 0.35. Right: ϕ = 0.25.
2.11. Application to the change-point model
The change-point model in the introduction can be viewed as a special case of Model (1.1), where β is as in (2.7), and the Gram matrix satisfies
| (2.44) |
For technical reasons, it is more convenient not to normalize the diagonals of G to 1.
The change-point model can be viewed as an ‘extreme’ case of what is studied in this paper. On one hand, the Gram matrix G is ‘ill-posed’ and each row of G does not satisfy the condition of off-diagonal decay in Theorem 2.2. On the other hand, G has a very special structure which can be largely exploited. In fact, if we sparsify G with the linear filter D = D2,η, where η = (1, −2, 1)′, it is seen that B = DG = Ip, and H = DGD′ is a tri-diagonal matrix with H(i, j) = 2 · 1{i = j} − 1{|i − j| = 1} − 1{i = j = p}, which are very simple matrices. For these reasons, we modify the CASE as follows.
Due to the simple structure of B, we don’t need patching in the PS-step (i.e., ℓps = 0).
For the same reason, the choices of thresholds t(F̂, N̂) are more flexible than before, and taking t(F̂, N̂) = 2q log(p) for a proper constant q > 0 works.
Since H is ‘extreme’ (the smallest eigenvalue tends to 0 as p → ∞), we have to modify the PE-step carefully.
In detail, the PE-step for the change-point model is as follows. Given ℓpe, let 𝒢+ be as in Definition 1.7. Recall that denotes the set of all retained indices at the end of the PS-step. Viewing as a subgraph of 𝒢+, and let be one of its components. The goal is to split ℐ into N different subsets
and for each subset ℐ(k), 1 ≤ k ≤ N, we construct a patched set ℐ(k),pe. We then estimate βℐ(k) separately using (2.20). Putting βℐ(k) together gives our estimate of βℐ.
The subsets are recursively constructed as follows. Denote l = |ℐ|, M = (ℓpe/2)1/(l+1), and write
First, letting k1 be the largest index such that jk1 − jk1 − 1 > ℓpe/M, define
Next, letting k2 < k1 be the largest index such that jk2 − jk2−1 > ℓpe/M2, define
Continue this process until for some N, 1 ≤ N ≤ l, kN = 1. In this construction, for each 1 ≤ k ≤ N, if we arrange all the nodes of ℐ(k),pe in the ascending order, then the number of nodes in front of ℐ(k) is significantly smaller than the number of nodes behind ℐ(k).
In practice, we introduce a suboptimal but much simpler patching approach as follows. Fix a component ℐ = {j1, ⋯, jl} of 𝒢+. In this approach, instead of splitting it into smaller sets and patching them separately as in the previous approach, we patch the whole set ℐ by
| (2.45) |
and estimate βℐ using (2.20). Our numeric studies show that two approaches have comparable performances.
Define
| (2.46) |
where ‘cp’ stands for change-point. Choose the tuning parameters of CASE such that
| (2.47) |
that , and that (recall that we take t(F̂, N̂) = 2q log(p) for all (F̂, N̂) in the change-point setting). Note that the choice of ℓpe is different from that in Section 2.5. The main result in this section is the following theorem which is proved in Section B.
Theorem 2.4. For the change-point model, the minimax Hamming distance satisfies . Furthermore, the CASE β̂case with the tuning parameters specified above satisfies
It is noteworthy that the exponent has a phase change depending on the ratios of r/ϑ. The insight is, when , the minimax Hamming distance is dominated by the Hamming errors we make in distinguishing between an isolated change point and a pair of adjacent change points, and when , the minimax Hamming distance is dominated by the Hamming errors of distinguishing the case of consecutive change point triplets (say, change points at {j − 1, j, j − 1}) from the case where we don’t have a change point in the middle of the triplets (that is, the change points are only at {j − 1, j + 1}).
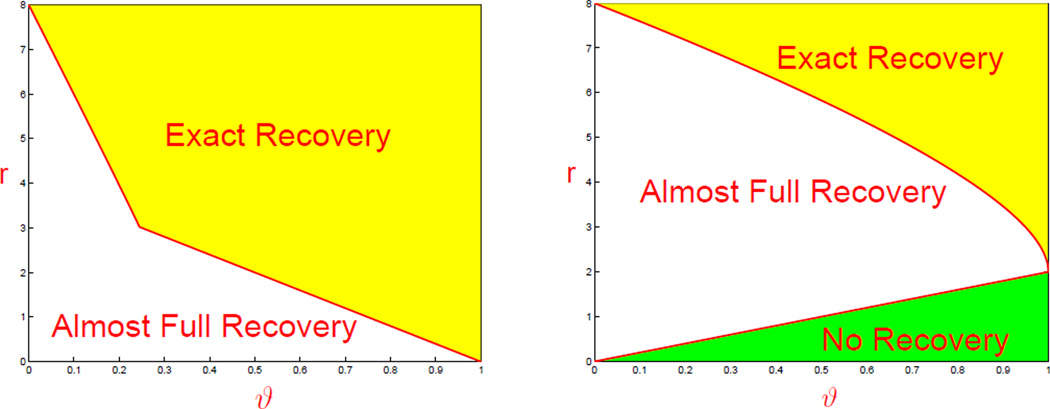
Similarly, the main results on the change-point problem can be visualized with the phase diagram, displayed in Figure 4. An interesting point is that, it is possible to have almost full recovery even when the signal strength parameter τp is as small as . See the proof of Theorem 2.4 for details.
Fig 4.
Phase diagrams corresponding to the change-point model. Left: CASE; the boundary is decided by (left part) and 4(1 − ϑ) (right part). Right: hard thresholding; the upper boundary is decided by and the lower boundary is decided by 2ϑ.
Alternatively, one may use the following approach to the change-point problem. Treat the liner change-point model as a regression model Y = X β+ z as in Section 1 (Page 2), and let W = (X′X)−1X′Y be the least-squares estimate. It is seen that W ~ N(β, Σ), where we note that Σ = (X′X)−1 is tridiagonal and coincides with H. In this simple setting, a natural approach is to apply a coordinate-wise thresholding to locate the signals. But this neglects the covariance of W in detecting the locations of the signals and is not optimal even with the ideal choice of thresholding parameter t0, since the corresponding risk satisfies
The proof of this is elementary and omitted. The phase diagram of this method is displayed in Figure 4, right panel, which suggests the method is non-optimal.
Other popular methods in locating multiple change-points include the global methods (Harchaoui and Lévy-Leduc, 2010; Olshen et al., 2004; Tibshirani, 1996; Yao and Au, 1989) and local methods (Niu and Zhang, 2012). The global methods are usually computationally expensive and can hardly be optimal due to the strong correlation nature of this problem. Our procedure is related to the local methods but is different in important ways. Our method exploits the graphical structures and uses the GOSD to guide both the screening and cleaning, but SaRa does not utilize the graphical structures and can be shown to be non-optimal.
To conclude the section, we remark that the change-point model constitutes a special case of the settings we discuss in the paper, where setting some of the tuning parameters is more convenient than in the general case. First, for the change point model, we can simply set δ = 0 and ℓps = 0. Second, there is an easy-to-compute preliminary estimator available. On the other hand, the performance of CASE is substantially better than the other methods in many situations. We believe that CASE is potentially a very useful method in practice for the change-point problem.
3. Simulations
We conducted a small-scale numeric study where we compare CASE and several popular variable selection approaches, with representative settings. The study contains two parts, Section 3.1 and Section 3.2, where we investigate the change-point model and the long-memory time series model, respectively.
We set m = 2 so that in the screening stage of CASE, bivariate screening is the highest order screening we use. At least for examples considered here, using a higher-order screening does not have a significant improvement. For long-memory time series, we need a regularization parameter δ (but we don’t need it for the change-point model). The guideline for choosing δ is to make sure the maximum degree of GOSD is 15 (say) or smaller. In this section, we choose δ = 2.5/ log(p). The maximum degree of GOSD is much higher if we choose a much smaller δ; in this case, CASE has similar performance, but is computationally much slower.
In this section, sp = pεp for convenience. The core tuning parameters for CASE are (𝒬, upe, υpe, ℓps, ℓpe). We streamline these tuning parameters in a way so they only depends on two tuning parameters (sp, τp) (calibrating the sparsity and the minimum signal strength, respectively). Therefore, essentially, CASE only uses two tuning parameters. Our experiment shows that the performance of CASE is relatively insensitive to these two tuning parameters. Furthermore, these two tuning parameters can be set in a data driven fashion, especially in the change-point model. See details below.
3.1. Change-point model
In this section, we use Model (1.3) to investigate the performance of CASE in identifying multiple change-points. For a given set of parameters (p, ϑ, r, a), we set εp = p−ϑ and . First, we generate a (p − 1) × 1 vector β by , where U(s, t) is the uniform distribution over [s, t] (when s = t, U(s, t) represents the point mass at s). Next, we construct the mean vector θ in Model (1.3) by θj = θj−1 + βj−1, 2 ≤ j ≤ p. Last, we generate the data vector Y by Y ~ N(θ, Ip).
CASE, when applied to the change-point model, requires tuning parameters (m, 𝒬, ℓpe, upe, υpe). Denote by sp ≡ pεp = p1−ϑ the average number of signals. Given (sp, τp), we determine the tuning parameters as follows: Take m = 2, ℓps = 0, ℓpe = 10 log(p/sp), and υpe = τp. 𝒬 contains thresholds t(F, N) for each pair of sets (F, N); we take t(F, N) = 2q(F, N) log(p) with
| (3.48) |
where ϑ = log(p/sp), and ω̃ = ω̃(F, N) is given in (2.37). With these choices, CASE only depends on two parameters (sp, τp).
Experiment 1a. In this experiment, we compare CASE with the lasso (Tibshirani, 1996), SCAD (Fan and Li, 2001) (penalty shape parameter a = 3.7), MC+ (Zhang, 2010) (penalty shape parameter γ = 1.1), and SaRa. For tuning parameters λ > 0 and h > 0 (integer), SaRa takes the following form:
The tuning parameters for the lasso, SCAD, MC+, and SaRa are ideally set (pretending we know β). For CASE, all tuning parameters depend on (sp, τp), so we implement the procedure using the true values of (sp, τp); this yields slightly inferior results than that of setting (sp, τp) ideally (pretending we know β, as we do in the lasso, SCAD, MC+, SaRa), so our comparison in this setting is fair. Note that even when (sp, τp) are given, it is unclear how to set the tuning parameters of the lasso, SCAD, MC+, and SaRa.
Fix p = 5000 and a = 1. We let ϑ range in {0.3, 0.45, 0.6, 0.75} and τp range in {3, 3.5, ⋯, 6.5}. The parameters fall into the regime where exact-recovery is impossible. Table 1 reports the average Hamming errors of 100 independent repetitions. We see that CASE consistently outperforms other methods, especially when ϑ is small, i.e., signals are less sparse.
Table 1.
Hamming errors in Experiment 1a. It is a change-point model with p = 5000. The tuning parameters for CASE are set from the true (sp, τp), and the tuning parameters of other methods are set to minimize the Hamming error.
| ϑ | sp | τp | ||||||
|---|---|---|---|---|---|---|---|---|
| 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | |||
| 0.3 | 338.4 | CASE | 105.8 | 63.9 | 37.6 | 18.5 | 8.9 | 4.8 |
| lasso | 371.7 | 370.0 | 371.5 | 370.1 | 371.5 | 369.8 | ||
| SCAD | 370.6 | 368.3 | 370.5 | 368.2 | 369.3 | 369.2 | ||
| MCP | 374.0 | 372.1 | 374.3 | 372.5 | 373.6 | 373.1 | ||
| SaRa | 175.6 | 144.0 | 107.8 | 73.7 | 49.0 | 32.3 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.45 | 108.3 | CASE | 50.1 | 35.5 | 26.3 | 20.0 | 12.8 | 6.2 |
| lasso | 103.2 | 104.1 | 103.8 | 103.8 | 104.9 | 104.3 | ||
| SCAD | 101.8 | 102.7 | 102.1 | 102.0 | 102.9 | 102.5 | ||
| MCP | 103.7 | 104.7 | 104.4 | 104.3 | 105.4 | 104.8 | ||
| SaRa | 78.9 | 72.0 | 66.2 | 63.4 | 61.9 | 60.4 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.6 | 30.2 | CASE | 14.4 | 11.1 | 8.9 | 6.7 | 5.0 | 3.9 |
| lasso | 29.3 | 29.2 | 29.3 | 29.7 | 27.7 | 29.3 | ||
| SCAD | 27.7 | 27.7 | 27.9 | 27.4 | 26.1 | 27.1 | ||
| MCP | 29.8 | 29.8 | 29.8 | 30.2 | 28.4 | 29.8 | ||
| SaRa | 20.4 | 17.0 | 13.6 | 10.9 | 8.6 | 6.8 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.75 | 8.4 | CASE | 3.5 | 2.9 | 2.4 | 1.8 | 1.6 | 1.3 |
| lasso | 8.2 | 8.3 | 8.5 | 8.8 | 8.0 | 8.5 | ||
| SCAD | 6.8 | 7.0 | 7.0 | 6.9 | 6.6 | 6.6 | ||
| MCP | 8.7 | 8.8 | 9.1 | 9.2 | 8.7 | 9.1 | ||
| SaRa | 5.2 | 4.5 | 3.8 | 3.0 | 2.4 | 2.0 | ||
We also observe that the three global penalization methods, lasso, SCAD and MCP, perform unsatisfactorily, with Hamming errors comparable to the expected number of signals sp. It suggests that the global penalization methods are not appropriate for the change-point model when the signals are rare and weak. Similar conclusion can be drawn in most experiments in this section. To save space, we only report results of the lasso, SCAD and MCP in this experiment.
Experiment 1b. In this experiment, we investigate the performance of CASE with estimated (sp, τp) is estimated by SaRa, which we call the adaptive CASE. In detail, we estimate (εp, τp) by and , where the tuning parameters (λ, h) of SaRa is determined by minimizing which is a slight modification of Bayesian Information Criteria (BIC).
For experiment, we use the same setting as in Experiment 1a. Table 2 reports the average Hamming errors of CASE, SaRa and the adaptive CASE based on 100 independent repetitions. First, the adaptive CASE, which is CASE with estimated (sp, τp), has a very similar performance to CASE. Second, although the adaptive CASE uses SaRa as the preliminary estimator, its performance is substantially better than that of SaRa (and other methods in the same setting; see Experiment 2a).
Table 2.
Hamming errors in Experiment 1b. It has the same setting as Experiment 1a. “adCASE” refers to the adaptive CASE, where (sp, τp) are estimated from SaRa. The tuning parameters in SaRa are selected using a modified BIC.
| ϑ | sp | τp | ||||||
|---|---|---|---|---|---|---|---|---|
| 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | |||
| 0.3 | 338.4 | CASE | 105.8 | 63.9 | 37.6 | 18.5 | 8.9 | 4.8 |
| adCASE | 100.3 | 63.6 | 37.8 | 18.6 | 8.9 | 4.8 | ||
| SaRa | 190.7 | 162.0 | 131.3 | 98.0 | 68.2 | 47.1 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.45 | 108.3 | CASE | 50.1 | 35.5 | 26.3 | 20.0 | 12.8 | 6.2 |
| adCASE | 48.6 | 33.9 | 26.0 | 20.8 | 16.6 | 9.7 | ||
| SaRa | 86.1 | 76.7 | 71.4 | 66.7 | 65.0 | 62.8 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.6 | 30.2 | CASE | 14.4 | 11.1 | 8.9 | 6.7 | 5.0 | 3.9 |
| adCASE | 14.0 | 11.0 | 8.8 | 6.5 | 4.8 | 3.4 | ||
| SaRa | 35.7 | 28.5 | 24.1 | 19.9 | 15.8 | 11.9 | ||
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |||
| 0.75 | 8.4 | CASE | 3.5 | 2.9 | 2.4 | 1.8 | 1.6 | 1.3 |
| adCASE | 3.7 | 3.0 | 2.2 | 1.8 | 1.5 | 1.3 | ||
| SaRa | 13.3 | 11.5 | 8.0 | 5.2 | 4.0 | 2.9 | ||
Experiment 2. In this experiment, we consider the post-filtering model, Model (1.4), associated with the change-point model, and illustrate that the seeming simplicity of this model (where D is the second-order differencing, G = Ip, and DGD′ is tri-diagonal) does not mean it is a trivial setting for variable selection. In particular, if we naively apply the L0/L1-penalization to the post-filtering model, we end up with naive soft/hard thresholding; we illustrate our point by showing that CASE significantly outperforms naive thresholding (since we use Hamming distance as the loss function, there is no difference between soft and hard thresholding). For both CASE and naive thresholding, we set tuning parameters assuming (εp, τp) as known. The threshold of naive thresholding is set as (r + 2ϑ)2/(2r) · log(p), where ϑ = log(p/sp) and ; this threshold choice is know as theoretically optimal.
Fix p = 106 and a = 1 (so that the signals have equal strengths). Let ϑ range in {0.35, 0.5, 0.75}, and τp range in {5, ⋯, 13}. Table 3 reports the average Hamming errors of 50 independent repetitions, which show that CASE outperforms the naive hard thresholding in most cases, especially when ϑ is small or τp is small. It suggests that the post-filtering model remains largely non-trivial, and to deal with it we need sophisticated methods.
Table 3.
Hamming errors of Experiment 2. It is a change-point model with p = 106. “nHT” refers to the naive hard thresholding. Any global penalization methods directly applied to the post-filtering model are equivalent to the naive hard thresholding.
| ϑ | sp | τp | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||
| 0.35 | 7943 | CASE | 956.7 | 332.6 | 117.5 | 49.1 | 24.1 | 13.9 | 10.6 | 7.7 | 7.3 |
| nHT | 4430.5 | 2381.3 | 1085.8 | 418.1 | 139.7 | 41.9 | 11.0 | 2.5 | 0.5 | ||
| 0.50 | 1000 | CASE | 195.3 | 68.8 | 20.8 | 5.0 | 1.3 | 0.7 | 0.4 | 0.1 | 0.2 |
| nHT | 767.9 | 489.0 | 250.8 | 105.3 | 38.4 | 12.4 | 3.5 | 0.7 | 0.2 | ||
| 0.75 | 32 | CASE | 9.3 | 3.1 | 2.3 | 0.4 | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 |
| nHT | 31.1 | 25.6 | 15.7 | 8.3 | 3.2 | 1.8 | 0.5 | 0.0 | 0.0 | ||
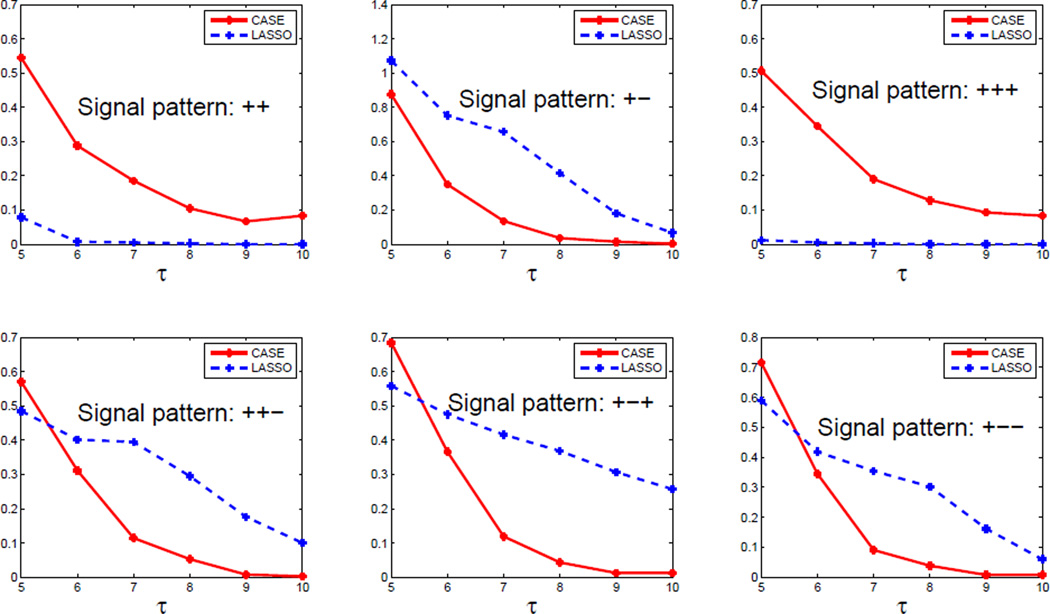
Experiment 3. In this experiment, we let a > 1 so the signals may have different strengths. Fix (p, ϑ, τp) = (5000, 0.50, 4.5), and let a range from 1 to 3 with increment 0.5. We investigate a case where the signals have the “half-positive-half-negative” sign pattern, i.e., , and a case where the the signals have the “all-positive” sign pattern, i.e., . We compare CASE with SaRa for different values of a and sign-patterns (we do not include the lasso, SCAD, MC+ in this particular experiment, for at least for the experiments reported above, they are inferior to SaRa). The tuning parameters for both CASE and SaRa are set ideally as in Experiment 1a. The results of 50 independent repetitions are reported in Table 4, which suggest that CASE uniformly outperforms SaRa for various values of a and the two sign patterns.
Table 4.
Hamming errors in Experiment 3. It is a change-point model, p = 5000, ϑ = 0.5, sp = 70.7 and τp = 4.5. “Half-half” and “all-positive” refer to two different sign patterns. The value a is the ratio between the maximum and minimum signal strength.
| a | ||||||
|---|---|---|---|---|---|---|
| 1 | 1.5 | 2 | 2.5 | 3 | ||
| half-half | CASE | 14.26 | 6.32 | 5.50 | 4.78 | 4.56 |
| SaRa | 24.98 | 18.96 | 16.56 | 14.00 | 12.50 | |
| all-positive | CASE | 13.44 | 6.18 | 4.90 | 5.38 | 4.14 |
| SaRa | 24.26 | 18.58 | 16.80 | 13.66 | 12.12 | |
3.2. Long-memory time series model
In this section, we consider the long-memory time series model with a focus on the FARIMA(0, ϕ, 0) process Fan and Yao (2003). Fix (p, ϕ, ϑ, τp, a), where ϕ is the long-memory parameter. We first let X = G1/2 where G is constructed according to (2.41)–(2.43). We then generate the vector β by . Finally, we generate Y ~ N(X β, Ip).
CASE uses tuning parameters (m, δ, ℓps, 𝒬, ℓpe, upe, υpe), which are set in the same way as in the change-point model, except for two differences. First, we need a regularization parameter δ which is set as 2.5/ log(p) (recall that we don’t need such a tuning parameter in the change-point model). Second, we take ℓps = ℓpe/2.
Experiment 4a. In this experiment, we compare CASE with the lasso, SCAD (shape parameter a = 3.7) and MC+ (shape parameter γ = 2). Similarly, the tuning parameters of CASE are set as above assuming that (sp, τp) are known, and the tuning parameters are set ideally to minimize the Hamming error (assuming β is known). By similar argument as in Experiment 1a, the comparison is fair.
We fix p = 5000, ϕ = 0.35 and a = 1. Let ϑ range in {0.35, 0.45, 0.55}, and τp range in {4, ⋯, 9}. Table 5 reports the average Hamming errors of 100 independent repetitions. The results suggest that CASE outperforms lasso and SCAD, and has a comparable performance to that of MC+.
Table 5.
Hamming errors in Experiment 4a. The Gram matrix is the population covariance matrix of the FARIMA(0, φ, 0) process with φ = 0.35, and p = 5000. The tuning parameters for CASE are set with true (sp, τp), and the tuning parameters of other methods are set to minimize the Hamming error.
| ϑ | sp | τp | |||||
|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | 7 | 8 | |||
| 0.35 | 253.7 | CASE | 118.0 | 60.7 | 26.3 | 9.5 | 4.3 |
| lasso | 145.2 | 91.6 | 60.2 | 37.4 | 26.0 | ||
| SCAD | 140.6 | 87.0 | 42.8 | 19.5 | 8.0 | ||
| MCP | 108.6 | 50.2 | 20.4 | 7.4 | 2.6 | ||
| 0.45 | 108.3 | CASE | 60.3 | 27.7 | 11.8 | 4.0 | 1.9 |
| lasso | 65.6 | 40.0 | 23.2 | 13.5 | 7.7 | ||
| SCAD | 64.0 | 37.7 | 19.6 | 9.2 | 3.9 | ||
| MCP | 52.0 | 23.6 | 8.6 | 3.0 | 1.0 | ||
| 0.55 | 46.2 | CASE | 27.9 | 13.4 | 4.3 | 1.4 | 0.5 |
| lasso | 27.8 | 16.0 | 8.0 | 3.9 | 2.1 | ||
| SCAD | 27.0 | 15.2 | 7.0 | 3.1 | 1.2 | ||
| MCP | 23.4 | 10.6 | 3.1 | 0.7 | 0.2 | ||
Experiment 4b. We use the same setting as in Experiment 4a, except that we force the signals to appear in adjacent pairs with opposite signs. In detail, β is generated such that , where ν(a,b) is a point mass at (a, b) ∈ ℝ2. This concerns a setting where “signal cancellation” has more important effect than that in Experiment 4b. Table 6 reports the average Hamming errors of 100 independent repetitions. We see that CASE significantly outperforms all the other methods.
Table 6.
Hamming errors in Experiment 4b. It has the same setting as Experiment 4a, except that the signals always appear in adjacent pairs with opposite signs.
| ϑ | sp | τp | |||||
|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | 7 | 8 | |||
| 0.35 | 253.7 | CASE | 138.6 | 60.8 | 23.3 | 7.2 | 1.8 |
| lasso | 223.0 | 158.9 | 97.9 | 54.8 | 27.1 | ||
| SCAD | 257.5 | 156.8 | 95.1 | 52.1 | 25.1 | ||
| MCP | 206.7 | 129.2 | 68.6 | 33.4 | 13.6 | ||
| 0.45 | 108.3 | CASE | 75.7 | 36.4 | 13.3 | 3.7 | 0.9 |
| lasso | 100.0 | 84.7 | 58.4 | 32.2 | 15.9 | ||
| SCAD | 99.2 | 83.2 | 56.6 | 30.6 | 14.9 | ||
| MCP | 98.1 | 76.0 | 44.8 | 21.5 | 8.9 | ||
| 0.55 | 46.2 | CASE | 38.6 | 20.0 | 8.9 | 3.6 | 1.0 |
| lasso | 45.4 | 40.1 | 31.0 | 20.6 | 10.9 | ||
| SCAD | 45.0 | 39.4 | 30.1 | 19.6 | 9.9 | ||
| MCP | 44.9 | 38.4 | 26.3 | 14.8 | 6.8 | ||
It is noteworthy that MC+ behaves much more satisfactory in Experiment 4a than here, and the main reason is MC+ does not adequately address “signal cancellation”. At the same time, since one of the major advantage of CASE is that it addresses adequately the “signal cancellation”, it has satisfactory performance in both Experiment 4a and 4b.
Experiment 5. In some of the experiments above, we set the tuning parameters of CASE assuming (sp, τp) as known. It is therefore interesting to investigate how the misspecification of (sp, τp) affects the performance of CASE. Fix p = 5000 and ϕ = 0.35. We consider two combinations of (ϑ, τp): (ϑ, τp) = (0.35, 6), (0.55, 5). The vector β is generated in the same way as in Experiment 4b, with the signals appearing in adjacent pairs. We fix one parameter of (sp, τp) and mis-specify the other (since sp is not on the same scale as τp, the results are reported based on the misspecification of (ϑ, τp), instead of (sp, τp); recall here sp = p1−ϑ). We then apply CASE with tuning parameters set base on the misspecified (sp, τp). Table 7 reports the average Hamming errors of 50 independent repetitions. It is seen that the errors remain quite at within a wide range of misspecified (ϑ, τp). This suggests that CASE is relatively insensitive to the misspecification of (sp, τp).
Table 7.
Hamming errors in Experiment 5. The Gram matrix is the population covariance matrix of the FARIMA(0, φ, 0) process with φ = 0.35, and p = 5000. The signals appear in adjacent pairs with opposite signs. CASE is applied with misspecified values ϑ̃ and τ̃p. The Hamming errors of the lasso are 97.9 and 40.1 for the two settings, respectively.
| ϑ = 0.35, τp = 6 sp = 253.7 |
ϑ̃ | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
| 27.8 | 24.8 | 23.2 | 23.2 | 24.5 | 26.3 | 48.9 | ||
| τ̃p | 4 | 5 | 5.5 | 6 | 6.5 | 7 | 8 | |
| 47.3 | 30.2 | 25.3 | 23.2 | 23.9 | 26.9 | 42.7 | ||
| ϑ = 0.55, τp = 5 sp = 46.2 |
ϑ̃ | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 |
| 21.8 | 19.0 | 19.3 | 19.8 | 21.7 | 25.5 | 25.4 | ||
| τ̃p | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | |
| 23.8 | 22.2 | 20.8 | 19.8 | 21.0 | 23.9 | 29.0 | ||
Experiment 6. We investigate the performance of CASE under various structures in the signal vector β. Fix p = 5000, ϕ = 0.35, ϑ = 0.75 and let τp range in {5, ⋯, 10}. We force the signals to appear in adjacent pairs or triplets. Denote by ‘+−’ the signal pattern ‘pairs of opposite signs’, by ‘++’ the pattern ‘pairs of the same sign’, and similarly for other signal patterns. For each pattern, say ‘+−’, β is generated by first generating a (p/2) × 1 vector θ by , and then letting β2j−1 = θj and β2j = θj. Figure 5 displays the results of 50 independent repetitions. We see that in the four patterns ‘+−’, ‘+ + −’, ‘+ − +’ and ‘+ − −’, CASE uniformly outperforms the lasso when τp ≥ 6.
Fig 5.
Hamming errors in Experiment 6. The Gram matrix is the population covariance matrix of the FARIMA(0, ϕ, 0) process with ϕ = 0.35, and p = 5000. We fix ϑ = 0.75 so that sp = 32. The signals are generated with six different patterns, where under each pattern, the signals appear in adjacent pairs or triplets.
4. Discussion
Variable selection when the Gram matrix G is non-sparse is a challenging problem. We approach this problem by first sparsifying G with a finite order linear filter, and then constructing a sparse graph GOSD. The key insight is that, in the post-filtering data, the true signals live in many small-size components that are disconnected in GOSD, but we do not know where. We propose CASE as a new approach to variable selection. This is a two-stage Screen and Selection method, where we first use a covariance-assisted multivariate screening to identify candidates for such small-size components, and then re-examine each candidate with penalized least squares. In both stages, to overcome the problem of information leakage, we employ a delicate patching technique.
We develop an asymptotic framework focusing on the regime where the signals are rare and weak so that successful variable selection is challenging but is still possible. We show that CASE achieves the optimal rate of convergence in Hamming distance across a wide class of situations where G is non-sparse but sparsifiable. Such optimality cannot be achieved by many popular methods, including but not limited to the lasso, SCAD, and Dantzig selector. When G is non-sparse, these methods are not expected to behave well even when the signals are strong. We have successfully applied CASE to two different applications: the change-point problem and the long-memory times series.
Compared to the well-known method of marginal screening (Fan and Song, 2010; Wasserman and Roeder, 2009), CASE employs a covariance-assisted multivariate screening procedure, so that it is theoretically more effective than marginal screening, with only a moderate increase in the computational complexity. CASE is closely related to the graphical lasso (Friedman, Hastie and Tibshirani, 2008; Meinshausen and Bühlmann, 2006), which also attempts to exploit the graph structure. However, the setting considered here is very different from that in Friedman, Hastie and Tibshirani (2008); Meinshausen and Bühlmann (2006) and our emphasis on optimality is also very different.
The paper is closely related to the recent work Jin, Zhang and Zhang (2012) (see also Ji and Jin (2012)), but is different in important ways. The work in Jin, Zhang and Zhang (2012) is motivated by recent literature of Compressive Sensing and Genetic Regulatory Network, and is largely focused on the case where the Gram matrix G is sparse in an unstructured fashion. The current work is motivated by the recent interest on DNA-copy number variation and long-memory time series, and is focused on the case where there are strong dependence between different design variables so G is usually non-sparse and some times ill-posed. To deal with the strong dependence, we have to use a finite-order linear filter and delicate patching techniques. Additionally, the current paper also studies applications to the long-memory time series and change-point problem which have not been considered in Jin, Zhang and Zhang (2012). Especially, the studies on the change-point problem encompasses very different and very delicate analysis on both the derivation of the lower bound and upper bound which we have not seen before in the literature. For these reasons, the two papers have very different scopes and techniques, and the results in one paper cannot be deduced from those in the other.
In this paper, we are primarily interested in the linear model, Model (1.1), but CASE is applicable in much broader settings. For example, in Model (1.1), we assume that the coordinates of z have the same variance σ2, and σ is known (and so without loss of generality, we assume σ = 1). When σ is unknown, the main results in this paper continue to hold, provided that we can estimate σ consistently (say, except for a probability of o(p−2), there is an estimate σ̂ such that |σ̂ / σ − 1| = o(1). Such an estimator can be obtained by adapting the scaled-lasso approach by Sun and Zhang (2012) or the refitted cross validation by Fan, Guo and Hao (2012) to to the post-filtering model (1.4). Correspondingly, we need to modify the tuning parameters of CASE slightly. For example, in the PS-step, 𝒬 is replaced by σ̂2𝒬 ≡ {σ̂2t(F, N)}, and in the PE-step, upe is replaced by σ̂upe, and υpe is replaced by σ̂υpe, respectively.
Also, in Model (1.1), we have assumed that the coordinates of z are Gaussian distributed. Such an assumptions can also be relaxed. In fact, in the core of CASE is the analysis of low-dimensional sub-vectors of Ỹ = X′Y, where we note that each coordinate of Ỹ has the form of b0 + a′z for some constant b0 and n × 1 non-stochastic vector a. Note that a only depend on the design matrix and the index of the coordinate of Ỹ (so there are p different vectors a at most). Essentially, the Gaussian assumption is only required for a′z for all p different choices of a. Note that even when z is non-Gaussian, a′z could be approximately Gaussian for all p different choices of a by Central Limit Theorem; this holds, for example, for the long-memory time series considered in the paper. As a result, the Gaussian assumption on z can be largely relaxed.
The main results in this paper can be extended in many other directions. For example, we have used a Rare and Weak signal model where the signals are randomly generated from a two-component mixture. The main results continue to hold if we choose to use a much more relaxed model, as long as the signals live in small-size isolated islands in the post-filtering data.
Also, we have focused on the change-point model and the long-memory time series model, where the post-filtering matrices have polynomial off-diagonal decay and are sparse in a structured fashion. CASE can be extended to more general settings, where the sparsity of the post-filtering matrices are unstructured, provided that we modify the patching technique accordingly: the patching set can be constructed by including nodes which are connected to the original set through a short-length path in the GOSD 𝒢*.
Still another extension is that the Gram matrix can be sparsified by an operator D, but D is not necessary linear filtering. To apply CASE to this setting, we need to design specific patching technique. For example, when D−1 is sparse, for a given ℐ, we can construct ℐpe = {j : |D−1(i, j)| > δ1, for some i ∈ ℐ}, where δ1 is a chosen threshold.
The paper is closely related to recent literature on DNA copy number variation and financial data analysis, but is different in focus and scope. It is of interest to further investigate such connections. To save space, we leave explorations along this line to the future.
Supplementary Material
Acknowledgements
The authors would like to thank Ning Hao, Philippe Rambour and David Siegmund for helpful pointers and comments.
Footnotes
Supported in part by National Science Foundation DMS-0704337 and DMS-1206464, the National Institute of General Medical Sciences of the National Institutes of Health through Grant Numbers R01GM100474 and R01-GM072611.
Supported in part by NSF CAREER award DMS-0908613.
SUPPLEMENTARY MATERIAL
Supplementary Material for “Covariance Assisted Screening and Estimation” (http://www.e-publications.org/ims/support/dowload/imsart-ims.zip). Owing to space constraints, the technical proofs are relegated a supplementary document.
References
- Andreou E, Ghysels E. Detecting multiple breaks in financial market volatility dynamics. Journal of Applied Econometrics. 2002;17:579–600. [Google Scholar]
- Bhattacharya P. Some aspects of change-point analysis. Lecture Notes-Monograph Series. 1994:28–56. [Google Scholar]
- Candès EJ, Plan Y. Near-ideal model selection by 1 minimization. The Annals of Statistics. 2009;37:2145–2177. [Google Scholar]
- Chen WW, Hurvich CM, Lu Y. On the correlation matrix of the discrete Fourier transform and the fast solution of large Toeplitz systems for long-memory time series. Journal of the American Statistical Association. 2006;101 [Google Scholar]
- Donoho DL, Huo X. Uncertainty principles and ideal atomic decomposition. Information Theory, IEEE Transactions on. 2001;47:2845–2862. [Google Scholar]
- Donoho D, Jin J. Higher criticism thresholding: optimal feature selection when useful features are rare and weak. Proceedings of the National Academy of Sciences. 2008;105:14790–14795. doi: 10.1073/pnas.0807471105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoho DL, Stark PB. Uncertainty principles and signal recovery. SIAM Journal on Applied Mathematics. 1989;49:906–931. [Google Scholar]
- Fan J, Guo S, Hao N. Variance estimation using refitted cross-validation in ultrahigh dimensional regression. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2012;74:37–65. doi: 10.1111/j.1467-9868.2011.01005.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- Fan J, Song R. Sure independence screening in generalized linear models with NP-dimensionality. The Annals of Statistics. 2010;38:3567–3604. [Google Scholar]
- Fan J, Xue L, Zou H. Strong oracle optimality of folded concave penalized estimation. arXiv preprint arXiv:1210.5992. 2012 doi: 10.1214/13-aos1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Yao Q. Nonlinear time series: nonparametric and parametric methods. Springer; 2003. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9:432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genovese CR, Jin J, Wasserman L, Yao Z. A comparison of the lasso and marginal regression. The Journal of Machine Learning Research. 2012;98888:2107–2143. [Google Scholar]
- Harchaoui Z, Lévy-Leduc C. Multiple change-point estimation with a total variation penalty. Journal of the American Statistical Association. 2010;105 [Google Scholar]
- Ioannidis JP. Why most published research findings are false. PLoS medicine. 2005;2:e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ising E. A contribution to the theory of ferromagnetism. Z. Phys. 1925;31:253–258. [Google Scholar]
- Ji P, Jin J. UPS delivers optimal phase diagram in high-dimensional variable selection. The Annals of Statistics. 2012;40:73–103. [Google Scholar]
- Jin J, Zhang C-H, Zhang Q. Optimality of Graphlet Screening in high dimensional variable selection. arXiv preprint arXiv:1204.6452. 2012 [Google Scholar]
- Lehmann EL, Casella G. Vol. 31. Springer; 1998. Theory of point estimation. [Google Scholar]
- Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso. The Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- Moulines E, Soulier P. Broadband log-periodogram regression of time series with long-range dependence. The Annals of Statistics. 1999;27:1415–1439. [Google Scholar]
- Niu YS, Zhang H. The screening and ranking algorithm to detect DNA copy number variations. The Annals of Applied Statistics. 2012;6:1306–1326. doi: 10.1214/12-AOAS539SUPP. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Venkatraman E, Lucito R, Wigler M. Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics. 2004;5:557–572. doi: 10.1093/biostatistics/kxh008. [DOI] [PubMed] [Google Scholar]
- Ray BK, Tsay RS. Long-range dependence in daily stock volatilities. Journal of Business & Economic Statistics. 2000;18:254–262. [Google Scholar]
- Siegmund DO. Personal communication. 2011 [Google Scholar]
- Sun T, Zhang C-H. Scaled sparse linear regression. Biometrika. 2012;99:879–898. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996:267–288. [Google Scholar]
- Tibshirani R, Wang P. Spatial smoothing and hot spot detection for CGH data using the fused lasso. Biostatistics. 2008;9:18–29. doi: 10.1093/biostatistics/kxm013. [DOI] [PubMed] [Google Scholar]
- Wasserman L, Roeder K. High dimensional variable selection. Annals of statistics. 2009;37:2178–2201. doi: 10.1214/08-aos646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Y-C, Au S. Least-squares estimation of a step function. Sankhyā: The Indian Journal of Statistics, Series A. 1989:370–381. [Google Scholar]
- Zhang C-H. Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics. 2010;38:894–942. [Google Scholar]
- Zhang NR, Siegmund DO, Ji H, Li JZ. Detecting simultaneous changepoints in multiple sequences. Biometrika. 2010;97:631–645. doi: 10.1093/biomet/asq025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao P, Yu B. On model selection consistency of Lasso. The Journal of Machine Learning Research. 2006;7:2541–2563. [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. Journal of the American statistical association. 2006;101:1418–1429. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.